Ultrafast visualization of phase transitions in nonequilibrium warm dense matter

Abstract

Intense ultrafast laser excitation brings materials into highly nonequilibrium states with complex solid–liquid phase transitions. These ultrafast processes yield warm dense matter (WDM) conditions characterized by comparable thermal and Fermi energies, and strong ion–ion coupling. Here, we review recent studies employing mega-electron-volt ultrafast electron diffraction to resolve the structural dynamics of nonequilibrium WDM created by femtosecond laser heating of solids. For the study of warm dense gold, the results showed homogeneous melting that occurs within tens of picoseconds at absorbed energy densities of 0.4–1.4 MJ/kg. These results constrained the electron–ion coupling rate and revealed the melting sensitivity to nucleation seeds. For the study of radiation-damaged tungsten, the results showed a melting transition below the melting temperature. Molecular dynamics simulations suggested that this melting behavior is driven by vacancy defect clusters from radiation damage. These studies provided atomic-level insights into the melting behavior of materials under extreme conditions.

Graphic abstract

Introduction

The advent of ultrafast lasers^1,2,3 has enabled time-resolved measurements of physical processes and chemical reactions at temporal resolutions better than a trillionth of a second (10⁻¹² s, or 1 ps). This time scale is particularly important for studying the structural dynamics of materials.^4,5 For example, the frequencies of phonon oscillations and molecular vibrations are on the order of 10¹² Hz to 10¹⁴ Hz.⁶ Reinforced by the chirped pulse amplification (CPA), a technique that was recognized by the Nobel Prize in Physics in 2018, ultrafast lasers have become sufficiently powerful to alter physical properties of materials over a broad range of parameter space, and to drive irreversible phase transitions. In condensed matter physics studies, in the experiments employing ultrafast laser pulses, the intense optical field can break atomic bonds and cause phase transitions. In nuclear physics research, intense ultrafast lasers can be used to produce relativistic electrons to ignite hot plasmas that can fuse lighter elements into heavier atoms and potentially unleash unlimited clean energy. Nonetheless, capturing the atomic and molecular motions during ultrafast laser-induced phase transitions represent the frontiers of many disciplines and have become possible using the techniques of ultrafast x-ray or electron diffractions.^7,8,9

Compared with x-rays, electrons have 10⁴–10⁶ times larger scattering cross sections, making them a better probe to study nanometer-thick samples. The elastic mean-free paths of electrons are comparable with typical optical penetration depth in conductive materials, further enhancing their detection efficiency as a probe for pump-probed experiments. Furthermore, electrons have much smaller scattering angles, making it easier to register a large momentum transfer range of the scattering signal. This is especially important for the construction of pair correlation function later described in the text. Last, high energy electrons form a nearly flat Ewald sphere in the reciprocal space, facilitating its interception with reciprocal lattice and therefore providing simultaneous access to many orders of diffraction peaks. This feature benefits the diffraction measurements with single-crystalline samples.

Ultrafast-electron diffraction (UED) with picosecond resolution was first demonstrated by Williamson et al. in 1984,⁸ at the dawn of the invention of the CPA technology. In that experiment, they utilized 25 keV electron pulses of 20 ps long, emitted from a streak camera, to probe the melting of aluminum. Since then, there have been tremendous efforts to improve the performance of UED with the common goal of packing more electrons in an ever shorter pulse. In particular, the utilization of mega-electron-volt (MeV) electrons, produced by radio frequency acceleration-based photoemission guns, has significantly boosted the performance of UED.^10,11,12,13 Due to the reduced space charge effect, this device provides high peak currents (∼100 mA), enabling measurements with extremely high signal-to-noise ratios. Furthermore, multiple elastic scattering effects are less probable in nanometer thin films at these energies due to their relatively large elastic mean-free path compared to keV electrons. Here, we are focusing on the application of MeV-UED to study the structural dynamics of the so-called warm dense matter (WDM).

As an intermediate phase between condensed matter and plasma, WDM refers to material states where the thermal energy of the electrons is comparable with their Fermi energy, and the potential energy between the ions is larger than their kinetic energy.^14,15 Generally, this corresponds to near solid density matter at temperatures on the order of 1–100 eV (1 eV ≈ 1.16 × 10⁴ K).¹⁶ Under these conditions, the energy density of the material system is typically in the range of 10¹⁰ –10¹² J/m³ (or 0.1–10 Mbar, 1 Mbar = 10¹¹ J/m³ = 10¹¹ Pa). WDM is attracting increasing attention due to its wide occurrence. For instance, these extreme states of matter widely exist in the interiors of giant planets such as Jupiter and Saturn,¹⁷ and they are also found as the important transient states in solid-to-plasma transitions induced by ultrafast laser ablation of materials.¹⁸ However, the knowledge of WDM is still a missing puzzle between condensed matter physics and plasma physics. The extreme temperatures impose tremendous challenges to condensed matter theory, and the partially degenerate electrons and strongly coupled ions deviate immensely from ideal plasma conditions. Although much progress has been made, there remain many outstanding questions about the fundamental properties of WDM. Notable examples include the electron–ion energy relaxation rate, lattice dynamics and dielectric properties under nonequilibrium conditions that are also known to be important for other areas of materials research.

Advanced levels of theory have been developed and applied to solve problems of WDM physics. For instance, density functional theory (DFT) combined with molecular dynamics (MD) simulations has been widely used to understand the complex interplay between the electronic and ionic systems in WDM.^19,20,21 However, high-precision experimental data are required to test and improve these models. For the scheme of using ultrafast lasers to create WDM, the laser excitation deposits energy to the sample much faster than the onset of thermal expansion, leading to a uniformly heated state with well-defined temperature and density. Ultrafast spectroscopy using electromagnetic waves from terahertz, and optical to x-ray frequencies have been implemented to investigate the materials under these extreme conditions.^{22,23,24,25,26,27} These diagnostics, however, provide information on the electronic properties, and the ionic structure would have to be inferred indirectly. On the other hand, time-resolved electron diffraction experiments^9,28,29,30 enable one to visualize the evolution of the atomic structure, providing direct insight into the changes of ionic properties during the formation of WDM.

In this article, we will discuss the recent advances made using the technique of MeV-UED in understanding the solid-to-liquid phase transitions under highly nonequilibrium WDM conditions. We will highlight two examples that have emerged from our earlier investigation on the ultrafast melting of gold and tungsten with radiation-induced defects.

Formation of WDM by isochoric laser heating

Experimental studies of WDM are challenging. This is in part due to its high energy density that can lead to significant hydrodynamic expansion. Data obtained from such an expanding system are generally integrated over mixed conditions of both temperature and density, making it difficult to interpret the data. To mitigate the gradient effects, a key experimental platform by isochoric laser heating of solids has been developed for WDM studies.^14,31,32 In this scheme, the solid target is excited by an intense femtosecond (fs) laser pulse and its thickness is chosen to be comparable with the optical penetration depth. This allows the sample to be uniformly heated along the longitudinal direction.

Consider an example of a 30-nm-thick gold (Au) foil irradiated by a focused 400-nm, fs-laser pulse (Figure 1). The laser pulse energy is first absorbed by the electrons via 5d—6sp interband transitions. These absorption processes take place near the front surface that matches with the optical penetration depth (∼15 nm). Immediately after the excitation, the electrons are in a highly nonequilibrium state and carry kinetic energies that are slightly above the Fermi energies (∼5.5 eV for Au). These electrons then penetrate ballistically into a deeper part of the sample at velocities of approximately 10⁸ cm/s. The ballistic range of these electrons is ∼110 nm in Au,³³ much longer than the sample thickness. Due to the energy barrier naturally set up by the work function of the material (4.8 eV for Au), most of the ballistic electrons are reflected at the metal-vacuum interface, while the few escaped electrons will be dragged back by the space charge field near the interface and continue to transport in the film till the ballistic range is reached. The ballistic transport and refluxing of the excited electrons result in a uniform energy deposition in the nanofoil even before the thermalization (∼600 fs after excitation³⁴) of the excited electrons is yet achieved.

Figure 1

Formation of warm dense matter (WDM) by isochoric laser heating of solids. (a) Electron density of states (eDOS) for face-centered-cubic Au calculated at T_e = 0 K and Fermi–Dirac distributions (centered about the chemical potential, µ) at T_e = 300 K, 10,000 K and 20,000 K. The horizontal arrow indicates a 5d → 6sp interband transition via photoexcitation at a photon energy ħω = 3.1 eV (400 nm). The vertical arrow indicates the work function (+ 4.8 eV) of gold. The eDOS data are taken from Reference 36. (b) A schematic diagram showing the formation of WDM by isochoric laser heating of a freestanding Au nanofoil.¹⁴

On the other hand, the temperature of the lattice remains nearly the same before the electron thermalization and is increased subsequently through electron–ion coupling processes. Thermal energy exchange between the electron and lattice systems can be approximated with the two-temperature model (TTM)³⁵ that solves the evolution of electron temperature T_e and ion temperature T_i using the following two equations:

$$ C_{e} \left( {T_{\text{e}} } \right)\frac{{\partial T_{\text{e}} }}{\partial t} = - g_{{{\text{ei}}}} \left( {T_{{\text{e}}} - T_{{\text{i}}} } \right) + S\left( t \right), $$

(1)

$$ C_{{\text{i}}} \left( {T_{{\text{i}}} } \right)\frac{{\partial T_{{\text{i}}} }}{\partial t} = g_{{{\text{ei}}}} \left( {T_{{\text{e}}} - T_{{\text{i}}} } \right), $$

(2)

where $C_{{\text{e}}} \left( {T_{{\text{e}}} } \right)$ and $C_{{\text{i}}} \left( {T_{{\text{i}}} } \right)$ are the electron and ion heat capacities, $g_{{{\text{ei}}}}$ is the electron–ion coupling strength and $S\left( t \right)$ is the source term that describes the energy deposition rate of the laser pulse. Here, $S\left( t \right)$ is obtained from the experiments. Among the other three parameters, $g_{{{\text{ei}}}}$ remains elusive under WDM conditions and is the least known parameter in the TTM model. $C_{{\text{e}}} \left( {T_{{\text{e}}} } \right)$ can be obtained from DFT calculations for most of the metals (see Reference 36), and $C_{{\text{i}}} \left( {T_{{\text{i}}} } \right)$ can be either derived from the Debye model for constant volume approximation,⁶ or obtained from existing experimental or theoretical data. Examples of TTM simulations for warm dense Au at an absorbed energy density ε = 1.17 MJ/kg are shown in Figure 3c; the results obtained using the $g_{{{\text{ei}}}}$ derived from UED experiments imply an electron–ion thermal equilibrium time of ∼100 ps. In reality, this equilibration time could be shorter because TTM does not account for the energy consumed during hydrodynamic expansion and phase transition. For excitation conditions with final temperatures at thermal equilibrium well below the melting point of the material, $g_{{{\text{ei}}}}$ can be measured rather directly using ultrafast electron diffuse scattering, a recently developed extension of UED described by Durr et al. in this issue of MRS Bulletin.³⁷ However, the application of this approach to WDM conditions will pose a significant challenge to the sample delivery aspect of the pump-probed experiment since diffuse scattering intensity is many orders of magnitude lower than that of the diffraction peaks and its precise measurement requires an accumulation of hundreds of thousands of shots.^38,39

Electron diffraction theory

The general theory for electron diffraction is well established.⁴⁰ Here, we summarize the basic equations employed for the analysis of the diffraction data and for modeling the attenuation of the diffraction peaks due to Debye–Waller effect.

In electron diffraction experiments, the diffraction intensity is commonly obtained by radially averaging the diffraction signal, and is expressed as a function of the momentum transfer $Q = 4\uppi \sin \uptheta /\uplambda$, where $\theta$ is the scattering angle, and $\lambda$ is the de Broglie wavelength of the electrons. The scattering intensity $I\left( Q \right)$ is given by:⁴⁰

$$ I\left( Q \right) = \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{i = 1}^{N} f_{i} f_{j} \frac{{\sin \left( {Qr_{ij} } \right)}}{{Qr_{ij} }}, $$

(3)

where r_ij is the distance between atom i and atom j, f_i (f_j) is the electron atomic form factor for the ith (jth) atom. The structure factor $S\left( Q \right)$ can be obtained by dividing the above equation by $\mathop \sum \limits_{i = 1}^{N} f_{i}^{2}$. For a monatomic system, the expression of $S\left( Q \right)$ is given by:

$$ S\left( Q \right) = 1 + \frac{1}{N}\mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{i \ne j}^{N} \frac{{\sin \left( {Qr_{ij} } \right)}}{{Qr_{ij} }}. $$

(4)

The sine Fourier transform of $S\left( Q \right)$ yields the pair correlation function, H(r), which is given by:

$$ H\left( r \right) = 4\pi r^{2} \left[ {\rho \left( r \right) - \rho_{0} } \right] = \frac{2r}{\pi }\mathop \int \limits_{0}^{\infty } Q\left[ {S\left( Q \right) - 1} \right]\sin \left( {Q r} \right)dQ. $$

(5)

According to Equation 5, H(r) describes the deviation of atomic density $\rho \left( r \right)$ from the average atomic density $\rho_{0}$ as a function of radial distance r from an average atomic origin.

The intensity drop of diffraction peaks in laser-excited solids can be caused by both the increasing thermal vibrations of atoms and structural changes. The former contribution is related to the smearing effect of lattice planes and can be described by Debye–Waller factor (DWF), denoted by D:

$$ D\left( {T_{\text{i}} ,Q,{\Theta }_{D} } \right) = \exp \left( { - \frac{1}{3}\langle{u^{2}}\rangle Q^{2} } \right), $$

(6)

where Θ_D is the Debye temperature and $\langle{u^{2}}\rangle$ is the atomic mean square displacement (MSD) about its equilibrium position. An expression for $\langle{u^{2}}\rangle$, developed by Debye⁴¹ and applicable to cubic crystals with a single atomic species, is given by:

$$ \langle{u^{2}}\rangle = \frac{{9h^{2} }}{{4\pi^{2} M\kappa_{B} {\Theta }_{D} }}\left[ {\frac{1}{4} + \left( {\frac{{T_{\text{i}} }}{{{\Theta }_{D} }}} \right)^{2} \mathop \int \limits_{0}^{{{\Theta }_{D} /{T_{\text{i}} }}} \frac{x}{\exp \left( x \right) - 1}dx} \right], $$

(7)

where h is the Planck constant, $\kappa_{\text{B}}$ is the Boltzmann constant and M is the atomic mass. Note that Θ_D is a physical quantity that is related to the interatomic potential energy (IPE) of the material. Theoretical studies on the effect of intense electronic excitations on IPE predicted a phonon hardening effect with an increase of Θ_D in warm dense Au.²⁰ Since $\langle{u^{2}}\rangle$ is a function of both T_i and Θ_D, the validation of this affect will require an accurate knowledge of T_i when using the DWF method.

Based on Equation 6, one can derive an expression for the normalized intensity of diffraction peaks as typically measured in UED experiments, $I\left( t \right)/I_{0}$, where I(t) is the scattering intensity at time t and I₀ is the reference obtained from the unpumped sample or from the negative time delays; $I\left( t \right)/I_{0}$ is given by the following equation:

$$ I\left( t \right)/I_{0} = \exp \left\{ { - \frac{1}{3}\left[ \langle{u^{2}\rangle \left( t \right) - \langle{u_{0}^{2} }}\rangle \right] \cdot Q^{2} } \right\}, $$

(8)

where $\langle{u_{0}^{2}}\rangle$ is the MSD at the ambient condition. Equations 7 and 8 together with the temperature results from TTM Equations 1 and 2 will allow to simulate the temporal evolution of DWF in laser-excited solids.

Ultrafast melting of gold

The melting of Au induced by intense ultrafast laser excitation is of particular interest. Early ultrafast interferometry measurements performed by Ao et al.⁴² inferred that under nonequilibrium temperature conditions, the melting transitions of Au occur in strongly superheated conditions, requiring 50% more energy density for lattice structure disassembly than in equilibrium conditions. In the meantime, DFT-MD calculations were performed to understand the effect of intense laser irradiation on semiconductors and metals.²⁰ The simulation results suggested a phonon hardening effect in warm dense Au; strong electronic excitation reduces the screening of the attractive interatomic potential, leading to a significant increase of the phonon frequency; this results in hardening of the lattice with an increasing Θ_D and a higher melting temperature.

Subsequently, Ernstorfer et al.²⁹ claimed an experimental evidence of electronic bond hardening in ultrafast laser heated Au. In that experiment, 55 keV ultrafast electrons were employed to resolve the evolution of the diffraction signal for polycrystalline (PC) Au as it underwent a solid–liquid phase transition. The measured decay of (220) diffraction peak intensities were compared with TTM simulations combined with DWF defined by Equations 6, 7, and 8. The T_e-dependent $g_{\text{ei}}$ from DFT calculations by Lin et al.³⁶ was used in TTM. The simulation results were found to agree better with the experiments when using a T_e-dependent Θ_D other than a constant Θ_D. However, the T_e-dependent $g_{\text{ei}}$ was later found to be significantly overestimated by a pump-probed experiment measuring the ac conductivity of warm dense Au.⁴³ This meant that the rise of T_i would be overestimated in the TTM calculations done in Reference 29, as such the agreement with the experiments using a T_e-dependent Θ_D would be questionable.

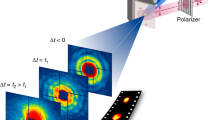
More recently, Mo et al.⁴⁴ performed a similar experiment on the ultrafast melting of Au using 3.2 MeV electrons as the electron probe. Both PC and single-crystal (SC) Au were studied in this experiment. The schematic of the setup is shown in Figure 2a, with single-shot diffraction patterns of SC Au taken at different time delays. The evolution of the scattering signal measured at absorbed energy density ε = 1.17 MJ/kg (∼5 times the complete melting threshold) is shown in Figure 2b. These results show three distinctive characteristics: (1) the decay of Laue diffraction peaks due to DWF and phase changes; (2) an overall increase of thermal diffuse background; and (3) the rise of liquid scattering signal.

Figure 2

Mega electron volt-ultrafast electron diffraction (MeV-UED) studies of the ultrafast solid–liquid phase transition in gold. (a) Schematic of the experimental setup; the diffraction patterns are single-shot diffraction patterns of single-crystal (SC) Au captured at the selective time delays for ε = 1.17 MJ/kg. (b) Temporal evolution of the scattering signal for SC Au at ε = 1.17 MJ/kg. (c) Melting time for both SC and polycrystalline (PC) Au measured by MeV-UED; for comparison, the reported lattice disassembly times of PC Au nanofoils (30-nm-thick) measured using the frequency domain interferometry (FDI) technique are also shown. The MeV-UED data are taken from Reference 44 and the FDI data are taken from References 42 and 45.

Figure 2c shows the melting time directly determined from the diffraction data for both SC and PC Au with ε ≥ 0.4 MJ/kg.⁴⁴ In this regime homogeneous nucleation is the dominant melting mechanism, resulting in a melting time of a few tens of ps. Below 0.4 MJ/kg, heterogeneous nucleation from surfaces or grain boundaries was found to be the dominant melting mechanism, resulting in a melting time from hundreds of ps to nanoseconds.⁴⁴ Figure 2c also shows the results for PC Au measured with the technique of frequency domain interferometry (FDI).^42,45 Excellent agreement was found between UED and FDI on the melting time of PC Au. Comparing PC Au with SC Au, the results show that at energy densities below 1 MJ/kg, PC Au melts substantially faster due to the additional nucleation seeds from the grain boundaries and crystal defects.⁴⁶ However, this difference diminishes at higher energy densities as homogeneous nucleation becomes faster at stronger superheating conditions,⁴⁷ surpassing the speed of grain boundary assisted melting.

Figure 3a shows the decay of (220) peak for Au measured at ε $\approx$ 1.2 MJ/kg. Both MeV-UED data (SC Au)⁴⁴ and keV-UED data (PC Au)²⁹ are shown. An overall agreement is found between the two data sets except at time delays above 10 ps. In the MeV-UED measurement, T_i after the melting time was determined by comparing the measured liquid structure factor with results from DFT-MD calculations; cf. Figure 3b. The initial temperature of the solid and the ion temperature of the liquid characterized during the melting process constrain the effective $g_{{{\text{ei}}}}$ using TTM. The evolution of T_e and T_i computed from TTM simulations using $g_{{{\text{ei}}}}$ determined from the aforementioned method and DFT calculations by Lin et al.³⁶ are shown in Figure 3c. The rise of T_i is greatly overestimated using the theoretical $g_{{{\text{ei}}}}.$ On the other hand, when the experimentally determined $g_{{{\text{ei}}}}$ is applied to calculate T_i, the T_e-dependent Θ_D from phonon hardening theory can no longer correctly predict the decay of (220), as indicated in Figure 3a. As a matter of fact, the inferred Θ_D from the UED data showed a rapid decay with the temperature.⁴⁴

Figure 3

Lattice heating and disordering in warm dense gold measured by ultrafast electron diffraction (UED) experiments. (a) Measured decay of Laue diffraction peak (220) from MeV-UED (red squares)⁴⁴ and keV-UED (green circles)²⁹ experiments at a similar ε (~ 1.2 MJ/kg). Solid lines are two-temperature model (TTM) simulations of Debye–Waller factor: Θ_D(T_i) derived from (220) decay with constant $g_{{{\text{ei}}}}$ (blue solid and dashed lines), Θ_D(T_e)²⁰ with constant $g_{{{\text{ei}}}}$ (magenta line) and with $g_{{{\text{ei}}}}$ from density functional theory (DFT) calculations³⁶ (gray line). (b) Liquid scattering data from MeV-UED measurement of single-crystal (SC) gold (top) and polycrystalline (PC) gold (bottom), in comparison with their best fit data from DFT-molecular dynamics (MD) simulations.⁴⁴ (c) Temporal evolution of T_e and T_i from TTM simulations with different $g_{{{\text{ei}}}}$ at ε = 1.17 MJ/kg. The constant $g_{{{\text{ei}}}}=4.9$ × 10¹⁶ W/m³/K is derived by solving for the ion temperature at complete melt (17 ps), taking into account the energy consumed by latent heat, as indicated by the red star.⁴⁴ (d) Summary of the electron–ion coupling strength in gold reported thus far from both experiments and theoretical calculations. The solid blue and red squares represent the MeV-UED measurements on SC and PC gold, respectively.⁴⁴ The hollow discrete data points are determined from experiments below melting threshold: White,⁴⁸, Nicoul,⁴⁹ Ligges,⁵⁰ Wright,⁵¹ Hohlfeld,³³ Elsayed-Ali,⁵² Hostetler,⁵³ and Groeneveld.⁵⁴ Solid and dashed curves represent theoretical results from Medvedev,⁵⁵ Smirnov,⁵⁶ Lin,³⁶ Holst,²¹ Brown,⁵⁷ and Petrov.⁵⁸

Figure 3d shows the T_e-dependent $g_{{{\text{ei}}}}$ results determined from the MeV-UED experiment,⁴⁴ comparing with results reported thus far including both experimental measurements^{33,48,49,50,51,52,53,54} and theoretical calculations.^{21,36,55,56,57,58} UED measurements indicate approximately a factor of 2 increase in $g_{{{\text{ei}}}}$ when T_e increases from room temperature to 18,000 K. This trend agrees well with theoretical calculations from Medvedev et al.,⁵⁵ but is slower than other theoretical results including the one from Lin et al.³⁶ Again, the deviations in theoretical calculations using various models signify the challenge in studying WDM physics, and high-precision experimental data are essential for their validation. This calls for more experimental measurements on different materials to understand the electron–ion coupling strength at high electronic temperatures.

Ultrafast melting of radiation-damaged tungsten

Ultrafast laser heating can suppress surface melting and lead to a fast homogeneous nucleation in a superheated solid, as discussed in the previous section. In the classical picture of homogeneous melting, the formation of an initial liquid nucleus is aided by thermal fluctuations without preferential nucleation sites.⁵⁹ This picture, however, fails to account for the potentially important roles of point defects, dislocations and multiple barriers along melting paths.^60,61 Recent theoretical studies⁶² found that the melting of a solid occurs via multiple, competing pathways involving the formation of point defects and dislocations; at temperatures approaching superheating, the melting mechanism is, however, driven by Lindemann’s vibrational instability.⁶³

Direct experimental observations of nucleation processes and the potential formation of defects are challenging due to their small time and length scales. For equilibrium melting studies, in the seminal work conducted by Wang et al.,⁶⁴ micrometer-size colloidal crystals were used as the model systems and their slow motion nucleation processes were directly imaged and measured with video microscopy techniques. These results showed that melting of superheated colloidal crystals is driven by large displacement amplitudes rather than any defects, in agreement with the theoretical predictions by Samanta et al.⁶² For ultrafast laser-induced melting, the application of time-resolved electron diffraction techniques^8,9,29,44 has provided atomic-level information on the kinetics of phase transformations. However, there are few experiments exploring the possible formation of defects during ultrafast melting processes nor the impact of crystal defects and impurities on the melting kinetics. In the experiments on the melting of SC and PC Au films,⁴⁴ the shorter melting time for PC Au is attributed to its increasing nucleation seeds from grain boundaries of nanocrystalline structures and the additional crystal defects. However, detailed understanding on the melting kinetics of solids with defects is still lacking.

Within this context, Mo et al. reported a time-resolved electron diffraction experiment studying laser-induced melting in solids embedded with external point defects.⁶⁵ These defects were produced by 200-keV Cu⁺ ion bombardment to 30-nm-thick tungsten (W) films at room temperature. The pump-probed experiment of the radiation-damaged W was then performed using the same setup as described in “Ultrafast melting of gold” section: the melting was induced by fs-laser heating and the ensuing phase transition was probed in transmission electron diffraction mode using 3.2 MeV electrons. Here, the maximum T_i of the heated samples was slightly above the nominal melting temperature T_m in which condition heterogeneous melting is expected and the melting sensitivity to defects is the highest, as shown by the melt time results of Au in Figure 2c.

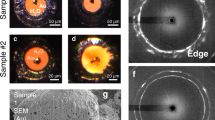
Figure 4a–b shows the temporal evolution of the diffraction signals for the pristine and radiation-damaged W at the same absorbed pump fluence of 46 mJ/cm². The results clearly showed that the structure of the pristine W was mostly crystalline by the end of 20 ps, indicated by the residual signal strength of the solid diffraction peaks. This incomplete melting behavior is expected as the pump fluence is below the complete melting threshold. In contrast, radiation-damaged W underwent a full solid–liquid phase transition, indicated by the disappearance of the solid diffraction peaks and the emergence of two broad peaks of the liquid structure factor. Quantitative information on the structural changes of the two samples can be gained by the atomic pair correlation function, H(r). Before the laser excitation (Figure 4c), H(r) results exhibited long-range correlations as expected in a crystalline material. Noticeable height reduction was observed for the radiation-damaged sample, implying the loss of the coordination number resulted from the displacement damage. This coordination number loss was calculated to be 0.6 ± 0.3 from the first measured atomic peak, amounting to approximately 5% of vacancy population. At the delay time of 20 ps, the atomic peaks for pristine W remain well defined in spite of the intensity reduction, confirming the presence of long-range crystalline order. In contrast, radiation-damaged W showed a much lower peak height, and noticeable broadening and merging of peaks. These changes implied a substantial loss of the long-range order in radiation-damaged W.

Figure 4

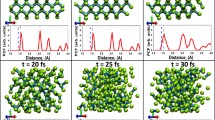
MeV-ultrafast electron diffraction (UED) measurement of the ultrafast solid–liquid phase transition in radiation-damaged tungsten. (a) Temporal evolution of the electron scattering signal for pristine W at an absorbed fluence of 46 mJ/cm². (b) The same as (a) but for W subjected to 10 displacement per atom (dpa) of radiation damage. (c, d) The experimental pair correlation functions, H(r), for both pristine and 10-dpa W captured before (denoted as reference) and after (20 ps) the laser excitation. (e, f) Molecular dynamics (MD) simulated H(r) at the same time delays for pristine and irradiated W with 5% vacancy defects. The interatomic spacings of the first four atomic peaks for bcc W are labeled by P1–P4.⁶⁵

The determination of the vacancy population allowed to set up the initial condition for MD simulations of radiation-damaged W. With this and using the extended Finnis–Sinclair potential⁶⁶ for W and a constant $g_{{{\text{ei}}}}$ of 2 × 10¹⁷ W/m³/K derived from the UED experiment, MD simulations were able to reproduce the two different melting behaviors between pristine and radiation-damaged W, with representative H(r) results shown in Figure 4e–f. By examining the atomic trajectories from simulations, it was found that local nanovoids in radiation-damaged W played a crucial role in promoting the overall melting. They were observed to amorphize immediately after the lattice heating (Figure 5a), which then acted as nucleation centers for the melting transition.

Figure 5

Early-stage behavior for the melting dynamics of radiation-damaged W. (a) Molecular dynamics (MD) snapshots of the atomic trajectory (close-up) captured before 5 ps for the irradiated W that illustrate the local amorphization around one big nanovoid. Connectivity of the atoms are coded in different colors: red spheres have a connectivity of 13 to 14 and represent crystalline atoms, green spheres have connectivity of 11 to 12 and represent strongly undercoordinated atoms, and blue spheres have a connectivity of less than 11 and represent atoms in an amorphous/disordered state. (b) MD simulation results of the temporal evolution for the lattice temperature of the pristine and irradiated W following the laser excitation. (c) Schematic illustrating the Gibbs free energy, ∆G(r), of homogeneous melting viewed from the perspective of classical nucleation theory.⁶⁵

Considerable amorphization of crystals around nanovoids had occurred within 5 ps, at which time T_i was still below T_m of W (Figure 5b). This undercooled nucleation process can be understood with the classical nucleation theory that considers the Gibbs free energy change, ∆G(r), upon the formation of a spherical solid nucleus of radius r in an undercooled liquid:^46,59

$$ \Delta G\left( r \right)\; = \; - \frac{4}{3}\pi r^{3} \Delta G_{V} \; + \;4\pi r^{2} \gamma_{{{\text{sl}}}}, $$

(9)

where $\Delta G_{{{V}}}$ is the difference in volumetric free energy density between the solid and liquid, and $\gamma_{{{\text{sl}}}}$ is the interfacial tension at the liquid–solid interface. A schematic of ∆G(r) is shown in Figure 5c. For small undercooling ∆T = T_m − T, an expression for the critical nucleus size $r^{*}$ that corresponds to the location of barrier height ∆G^∗ is given by $r^{*} \; = \;2\gamma_{{{\text{sl}}}} T_{{\text{m}}} /\left( {\Delta H_{{\text{m}}} \Delta T} \right)$ with ∆H_m the latent heat. For $r > r^{*}$, the solid cluster is thermodynamically unstable as its dissolution leads to the decrease of ∆G, and otherwise for $r > r^{*}$ the growth of the cluster is favored. The expression of $r^{*}$ can be formulated to yield the critical undercooling temperature, $T^{*}$:⁴⁶

$$ T^{*} = T_{m} \left[ {1 - \frac{{2\gamma_{sl} }}{{\Delta H_{m} }}\frac{1}{r}} \right], $$

(10)

which corresponds to the equilibrium between the solid cluster and the surrounding liquid. When $T > T^{*}$, the dissolution of the solid cluster tends to reduce ∆G(r) and hence it is kinetically favored. Equation 10 implies that $T^{*}$ will drop with decreasing the size of the solid cluster. For instance, using the following parameters for W, ∆H_m = 5.4 × 10⁹ J/m^{3 67} and $\gamma_{{{\text{sl}}}}$ = 0.59 J/m^{2 68}, $T^{*}$ = 2888 K for a solid cluster with r = 1 nm, which is only 78% of the melting temperature for W. This explains the MD simulation results of the radiation-damaged samples. The initial amorphization processes of nanovoids in the early heating stage separates the big crystal into many small nanocrystallites. This in turn suppresses the melting temperature and leads to the observed homogeneous melting.

Conclusion and outlook

In this article, we review a new class of experiments that investigated the structural dynamics of nonequilibrium WDM produced by femtosecond laser heating of solids, using the technique of MeV-UED. In the experiment of warm dense Au, the results showed that at absorbed laser energy density above 0.4 MJ/kg, the melting mechanism is dominated by homogeneous liquid nucleation. The melt time is shorter in polycrystalline samples than in single-crystal samples. Such difference is more prominent at lower energy densities, which indicates that grain boundary and defect assisted liquid nucleations are important near the onset of homogeneous melting. Comparing the structure factor with density functional theory calculations, the ion temperature after the complete melting was determined and indicated a superheated state. The liquid ion temperatures were applied to constrain the T_e dependence of $g_{{{\text{ei}}}}$ in warm dense Au, which were found to be consistent with the recent theoretical calculations from Medvedev et al.,⁵⁵ but lower than other existing theoretical results including the widely used one from Lin et al.³⁶

In the experiment of radiation-damaged W, the results showed that W highly populated with point defects underwent a melting transition below the melting temperature, in contrast with the incomplete melting behavior found in the pristine case. Molecular dynamics simulations showed good agreement with the experiments and provided atomic-level information on the nucleation process. Simulations showed that the initiation of amorphization at randomly distributed nanovoids in the early heating stage separated the big crystal into many small nanocrystallites, which steered the melting process along the path where melting continues below the equilibrium melting temperature and resulted in a rapid collapse of the crystal structure.

The results from these two experiments provided critical information to test and improve the kinetic theories of melting under nonequilibrium WDM conditions with strong implications for ultrafast laser–matter interactions. Furthermore, the visualization of different melting mechanisms in Au has showcased that MeV-UED can be implemented to understand material responses to extreme heat flux conditions, and the successful application to study radiation-damaged W suggested that MeV-UED is a potential tool for in situ study of radiation damage to materials in harsh environments.

The two experiments discussed here demonstrated that MeV electrons provide not only femtosecond temporal resolution, but also sufficient signal-to-noise ratios for single-shot measurements of transient atomic structure in nanoscale materials. In addition to high-Z materials such as Au and W that have large scattering cross sections, recent single-shot experiments have demonstrated that MeV electron diffraction can also measure lower-Z elements such as copper, iron, aluminum and even amorphous materials like amorphous germanium and amorphous silicon dioxide; similar data quality are achievable by increasing the accumulation of data shots. Therefore, we expect that this technique will be suitable to study the structural dynamics for a wide range of materials in WDM states. Apart from solids, the recent demonstration of liquid phase MeV-UED using a continuous flow liquid sheet jet^69,70 made it a promising alternative to study the chemical bond dynamics for liquids under extreme conditions.⁷¹

In addition to WDM science, MeV-UED could be also a strong candidate for studying dynamic compression physics. First, electron diffraction can measure the lattice strain by tracking the diffraction peak shifts due to external loading. Second, MeV electrons permit to access a large Q range and multiple orders of diffraction peaks. This will allow for a potential three-dimensional view of the lattice deformation, and accurate determination of the structure factor and possible phase transitions at high pressures. Therefore, combining MeV-UED with dynamic compression techniques such as using high-power lasers, would make it a candidate platform for investigating a broad range of high-pressure and high strain-rate phenomena, ranging from melting line,⁷² plastic deformation⁷³ to phase transitions.⁷⁴