Local microstructure and micromechanical stress evolution during deformation twinning in hexagonal polycrystals

Abstract

Deformation twinning is a prevalent plastic deformation mode in hexagonal close-packed (HCP) materials, such as magnesium, titanium, and zirconium, and their alloys. Experimental observations indicate that these twins occur heterogeneously across the polycrystalline microstructure during deformation. Morphological and crystallographic distribution of twins in a deformed microstructure, or the so-called twinning microstructure, significantly controls material deformation behavior, ductility, formability, and failure response. Understanding the development of the twinning microstructure at the grain scale can benefit design efforts to optimize microstructures of HCP materials for specific high-performance structural applications. This article reviews recent research efforts that aim to relate the polycrystalline microstructure with the development of its twinning microstructure through knowledge of local stress fields, specifically local stresses produced by twins and at twin/grain–boundary intersections on the formation and thickening of twins, twin transmission across grain boundaries, twin–twin junction formation, and secondary twinning.

Introduction

The class of structural hexagonal close-packed (HCP) metals, such as Mg, Zr, and Ti and their alloys, has the exciting potential to provide an unprecedented combination of desirable properties to a broad range of structural applications in need of more advanced materials than those currently in use [1, 2, 3, 4, 5, 6]. Successful incorporation of HCP metals into engineering designs is, however, hindered by their more highly anisotropic plastic deformation behavior and stronger sensitivity to changes in temperature and strain rates compared to those of simpler cubic crystal structures, such as face-centered cubic (FCC) or body-centered cubic (BCC) metals [7, 8, 9, 10, 11, 12]. This complexity is due in part to the fact that HCP metals deform not only by slip but also by deformation twinning [13, 14, 15, 16].

Deformation twinning continues to receive a lot of attention in the materials research community, since it is not understood as well as plastic slip and its effects on material performance can be more significant than those of slip. Slip can occur homogeneously across each crystal and generate a gradual lattice rotation with each increment in strain [13, 15, 17, 18, 19]. Twins, on the other hand, generate heterogeneous lamellar shaped domains within the crystal where the lattice rotation and shear can occur abruptly with each strain increment [13, 20]. Furthermore, since the twin domain is reoriented from that of the parent grain, twins introduce intragranular boundaries, which strongly resist the motion of dislocations gliding within the grain and within the twin [21, 22, 23, 24, 25]. This is one of the many reasons why the effects of deformation twinning on deformation behavior, ductility, formability, and failure of HCP metals can be dominant.

To date, the tools that have been used to understand and study twinning vary over many length and time scales, from first-principles density functional theory [26, 27], molecular dynamics [26, 28, 29, 30, 31, 32, 33, 34], continuum dislocation and defect theory [35, 36, 37], phase field modeling [38, 39], single crystal plasticity, and polycrystalline plasticity [40, 41, 42, 43, 44, 45, 46]. While these modeling methods have collectively advanced our understanding of twinning, they do not cover the mesoscopic range representing the actual discrete twin domains inside a crystal or among a set of crystals. This subgrain regime is a critically important length-scale regime. Twins generate highly localized stress–strain fields inside their parent grain and neighboring grains that can only be resolved in this regime [47, 48, 49]. These heterogeneous fields can potentially influence the formation of additional twins, twin thickening, recrystallization kinetics, and fracture [43, 50, 51, 52, 53, 54, 55].

In recent years, major advances in both three-dimensional mechanics modeling [41, 43, 44, 47, 56, 57] and experimental characterization [22, 23, 24, 48, 49, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71] of polycrystal microstructures have been made in this mesoscopic regime. Together, they have helped to initiate the development of novel models for deformation twin formation and growth. It is now possible to calculate the spatially resolved mechanical fields within deformed microstructures where the structure and topology of grains and grain boundaries can be represented. Within such microstructural frameworks, modeling the formation, propagation, and thickening of discrete twin lamellae within grains and from grain boundaries is feasible. At the same time, with the development of 3D electron backscattered diffraction [72] and in situ nondestructive high-energy X-ray diffraction microscopy [48, 59, 63], it is possible to map twins within the local grain structure. Such information can directly inform and help to advance the development of spatial–temporal models for twinning.

Many insightful and valuable findings are being reported from microstructural modeling studies of discrete twin lamellae during deformation. The aim of this article is to review these endeavors and the role that experimental characterization has played in motivating and guiding model development. We highlight the insight gained by these studies, such as the local stresses produced by twins and at twin/grain–boundary intersections, the stress measures responsible for twin formation and thickening, and driving stresses responsible for twin–twin interactions, twin transmission across grain boundaries, and secondary twinning. This article is structured as follows. It begins with a very brief background on deformation twinning. Next, we introduce the local stresses associated with twinning using experimental and computational modeling efforts. Then, we discuss the connection between local stresses and twinning microstructure development. The chapter ends with some possible future directions.

Deformation twinning in HCP metals

In HCP crystals, the loading condition with respect to c-axis orientation results in the activation of different types of twinning modes. For example, tensile twins $\left\{ {10\bar 12} \right\}$ and $\left\{ {11\bar 21} \right\}$ form when the loading condition extends the crystal along the c-axis, and compression twins $\left\{ {11\bar 22} \right\}$ and $\left\{ {10\bar 11} \right\}$ form when the loading condition results in contraction of the c-axis [13, 15, 16]. Due to the symmetry of the HCP structure, each twin type has six variants, which are crystallographically equivalent but independently oriented. Each twin type has a characteristic shear s, which restores a crystal lattice in a twin orientation [13, 15, 16]. The value of s depends on the c/a ratio and type of twin [16]. For Mg (c/a = 1.624), Zr (c/a = 1.593), and Ti (c/a = 1.588), the twinning shear for the $\left\{ {10\bar 12} \right\}$ tensile twin is ∼12.9%, ∼16.8, and ∼17.4%, respectively.

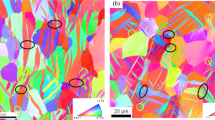
While most of these twin types have been observed in HCP metals under various deformation conditions [15, 16, 22, 23, 24, 73], the $\left\{ {10\bar 12} \right\}$ tensile twin type is the most frequently occurring one among the structural HCP metals. Figure 1 presents Electron Back Scatter Diffraction (EBSD) images of $\left\{ {10\bar 12} \right\}$ twins in pure Mg [74], Zr [23] and commercially pure Ti [9] compressed to 3%, 10%, and 5% strains, respectively.

Figure 1

Experimental evidence showing $\left\{ {10\bar 12} \right\}$ deformation twinning in different HCP metal systems: (a) polycrystal magnesium compressed to 3% (standard stereographic triangle showing the compression direction). Reprinted with permission from Ref. 74; (b) polycrystal zirconium compressed to 10% (standard stereographic triangle showing plane normal direction and compression direction, which is horizontal in the figure). Reprinted with permission from Ref. 23; (c) polycrystal titanium compressed to 5% (standard stereographic triangle showing plane normal direction and the compression direction, lying in the vertical direction in the figure). Reprinted with permission from Ref. 9.

The twinning process can be viewed broadly as a sequence of three steps. In lieu of actual experimental images, which can be challenging to obtain, Fig. 2 illustrates these three stages. Stage I corresponds to the creation of an embryo (nucleation), which begins at the atomic scale. This step, twin nucleation, has been extensively studied over the last few decades using atomistic calculations, dislocation dissociation reactions, and probability modeling [26, 27, 28, 42, 45, 74, 75, 76]. Stage II is associated with the growth of a twin embryo into a twin lamella. This stage starts with the embryo, initially nanoscale in size, changing its aspect ratio as it propagates under stress within the crystal, and ends with the twin lamella usually terminating at the grain boundaries of the parent grain [23, 24, 42, 77]. While some twin lamellae have been seen to terminate inside the grain [78] they are observed, more often, to span the entire grain [22, 23, 24]. Mostly, just propagated twins, i.e., stage II twins, are of plate-like shapes with almost uniform thickness. Stage III involves thickening or expansion of the twin or twins after propagation to the boundaries of its or their parent grain. The twins commonly seen at the resolution typical of EBSD, as in Fig. 1, are either in stage II or stage III.

Figure 2

Schematic representation of sequential processes associated with twinning: (a) Nucleation: formation of twin nuclei at a given grain boundary and also inside a grain; (b) propagation: propagation of a twin nucleus into the parent crystal; (c) growth: migration of the twin boundary and thickening of the lamella; (d) transmission: propagation of twin across the grain boundary. Multiple twin formation: (e) and (f) nucleation of another twin with the same or a different variant, which leads to parallel twins or twin–twin junction scenarios, respectively; (g) formation of a different type of twin inside a primary twin, which leads to double twinning or secondary twinning.

Twins accommodate strain by moving their boundaries; and stage III is when the twins reach a volume wherein they can accommodate a nonnegligible amount of strain for the deforming parent grain. The twin microstructure, including the number of twins, their thickness, and their crystallography (variants), is largely determined by the manner in which twins in stage III grow within the microstructure. The studies reviewed in this article seek to understand how microstructure properties govern the formation of stage III twins from stage II twins, which are of almost uniform thickness.

Figure 2 illustrates the possible ways by which twins have been observed to grow: twin thickening, twin transmission, or multiple twin formation. Twin thickening increases the volume of the twin domain. Specifically, the boundaries of stage II twins with almost uniform thickness migrate inhomogeneously based on the micromechanical fields, and as a result, most commonly twins grow to lenticular shapes [44]. If the domain is unsuitably oriented for easy glide, the domain is then plastically “hard.” Consequently, the twin thickening process could increase material flow stress and hardening rate [46, 79]. Twin transmission, on the other hand, propagates the twins across grain boundary and forms adjoining twin pairs (ATPs) [22, 51, 68, 80]. This process can continue across several grains and, thus, will develop twin chains [21, 78]. In addition, at times, two twins could nucleate simultaneously from the common grain boundary and lead to the adjoining twin-pair configuration [68]. Both the ATPs and twin chains can result in local strain concentrations and, thus, increase the likelihood for instabilities such as void nucleation, cracking, and premature failure [55, 82, 83]. Activation of multiple twins within the same parent grain can develop three different twinning microstructures. First, a parallel twin microstructure [see Fig. 2(e)] develops when twins of the same type and same variant are activated at different locations. Parallel twins increase the Hall–Petch-type barrier for dislocation motion, by reducing the mean free path for glide to that of the spacing between adjacent twins, and consequently the strain hardening behavior [74, 84]. Second, activation of different twin variants within a grain creates twin–twin junctions [see Fig. 2(f)], which significantly increases the strain-hardening rate and also acts as a preferential site for damage nucleation [71, 85, 86, 87]. Third, the formation of a twin inside another twin is also observed as a likely mode of twin propagation, and it is referred as double twinning [see Fig. 2(g)]. The twin shear is enhanced within the same twin domain, and its occurrence affects the mechanical and failure response in different ways than those of the other propagation modes [54, 88, 89, 90].

Local stresses associated with twinning

The deformation twin domain is associated with a homogeneous, characteristic shear and lattice reorientation. At the grain-scale level, the crystal immediately surrounding the twin domain reacts mechanically to the twinning shear and lattice reorientation prevailing inside the twin domain. Local stresses within and in the vicinity of the twin domain are internal stresses that have a net zero stress over the volume of the material. Considering the case of an unconstrained twin, which can be realized when a twin resides within a single crystal and spans from one free surface to the other, the shape change imposed by the twin is manifested on the free surfaces, as shown in Fig. 3(a). The shearing action imposed by the twin is unconstrained, and the reaction stresses that develop in the single crystal away from the free surfaces are minimal. This scenario is often realized in micro-pillar experiments, for instance [91, 92]. If, on the other hand, the twin resides within a grain belonging to a polycrystalline aggregate, the surrounding material, comprising the parent grain and possibly neighboring grains, constrains the twin shear and shape change imposed by the twin. An example that occurs often is shown in Fig. 3(b), wherein the neighboring grains restrict the shear associated with the twin domain, and as a result, the reaction from the surrounding crystal introduces a backstress in the twin domain and a forward stress in the neighboring grain. The intensity and extent of these internal stresses depend on the elastic and plastic properties of the parent and surrounding neighboring grains. These internal localized stress fields can affect how the twin microstructure develops under straining. Knowledge of these locally induced twin stresses is essential for understanding how twins may propagate.

Figure 3

Schematic representation of deformation twin with different surroundings (a) free surface (constraint free) and (b) neighboring grains.

Experimental characterization of local micro-mechanical fields

Several recent experimental efforts using X-ray synchrotron and/or high-resolution EBSD (HR-EBSD) techniques have focused on characterizing the local stresses associated with twinning. Aydiner et al. [93] measured the evolution of average stresses in the twin and in the parent grain in HCP AZ31 Mg alloy using synchrotron X-ray diffraction. As shown in Fig. 4(a), two different variants of $\left\{ {10\bar 12} \right\}$ tensile twins are activated at an applied stress of ∼40 MPa. The twin-plane resolved shear stress in the twin is significantly lower than that in the parent grain, which clearly provides evidence for the twinning shear transformation-induced stress reversal in the twin domain. Under further loading, the field of the resolved shear stress on the plane and direction for the twin, referred to as the twin resolved shear stress (TRSS), intensifies in both the twin and the parent grain. These measurements provided the average stress response in the twin and parent grain.

Figure 4

Experimentally measured stresses associated with twinning. (a) Average stress in the $\left\{ {10\bar 12} \right\}$ tensile twin and in the parent grain of AZ31 Mg alloy. Stresses were measured using synchrotron X-rays, and the stresses in the twin lamellae are significantly different from the parent grain. Reprinted with permission from Ref. 93. (b) and (c) HR-EBSD–based strain mapping of $\left\{ {11\bar 22} \right\}$ and $\left\{ {10\bar 12} \right\}$ twins in Ti, respectively. These stresses were obtained from the surface and so they do not represent a twin that resides inside a bulk polycrystal. (b) and (c) Reprinted with permission from Refs. 94 and 49, respectively (open access articles). (d) Cauchy stress variation across a $\left\{ {10\bar 12} \right\}$ twin in a bulk AZ31 Mg polycrystal using differential aperture X-ray microscopy (DAXM) synchrotron experiment. Reprinted from Ref. 63, which is an open access article distributed under the terms of the Creative Commons CC BY license, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Later, Guo et al. [94] and Basu et al. [49] employed the HR-EBSD technique to measure the spatially resolved stress and strain within and in the vicinity of $\left\{ {11\bar 22} \right\}$ compression twins [see Fig. 4(b)] and $\left\{ {10\bar 12} \right\}$ tensile twins [see Fig. 4(c)] in HCP Ti. The TRSS distribution at the twin tip is highly positive compared to that at the lateral side of the $\left\{ {11\bar 22} \right\}$ compression twin, which is negative, acting against twinning. This twin-induced stress field suggests that twin propagation is more favorable than lateral thickening. Similarly, the TRSS distribution across the $\left\{ {10\bar 12} \right\}$ tensile twin interface shows significant heterogeneity. These stress profiles, however, are obtained from a surface measurement, which questions whether surface stresses can be representative of those in bulk. Balogh et al. [48] used X-ray synchrotron with the differential aperture X-ray microscopy (DAXM) technique to map the spatially resolved elastic strain within and in the vicinity of the $\left\{ {10\bar 12} \right\}$ tensile twin within a bulk AZ31 Mg alloy. Their findings show that the elastic strain varies significantly within the twin and that it differs from the parent grain. But in this work, the elastic strain was measured along an arbitrary direction, which did not permit calculation of the full strain tensor. More recently, Arul Kumar et al. [63] performed a similar X-ray synchrotron experiment with the DAXM technique to measure complete elastic strain and stress tensors in the vicinity of a tensile twin in AZ31 Mg alloy, which is shown in Fig. 4(d). While these experimental techniques were able to provide stress distributions, they were for a particular twin within a particular microstructure configuration. To aid in developing a comprehensive understanding, crystallography-based micromechanical modeling can provide further insight into the microstructural factors that influence the stresses and strains associated with twinning.

Computational methods for micro-mechanical fields around twins

Modeling calculations at complementary scales to the foregoing measurements have been carried out in recent years to quantify the local stresses and strains associated with twinning. Two types of full-field, spatially resolved polycrystal models, such as crystal plasticity Fast Fourier Transform (CPFFT) and crystal plasticity finite element method (CPFEM), have been advanced to simulate discrete twin domains within individual grains [40, 41, 43, 44, 51, 58, 95, 96, 97]. To model the twin domain, the boundary of the domain, the twinning orientation, and the characteristic twin shear need to be imposed homogeneously throughout the domain. Studies focused on local stress states around twin lamellae in HCP crystals have for the most part been conducted using CPFFT, and therefore, results from this technique will be featured here. We will also include a CPFEM study on double twinning in an Mg alloy [98].

Brief background on the CPFFT twinning model

The CPFFT modeling approach used in most of the calculations discussed here is built upon the infinitesimal elasto-visco-plasticity technique [99, 100]. A detailed presentation of the general CPFFT formulation can be found in Lebensohn et al. [100]. CPFFT was originally developed to calculate and relate the effective and local responses associated inter and intragranular stress states resulting from the heterogeneity in elastic and plastic properties between grains in polycrystalline materials. The CPFFT formulation was more recently extended to incorporate deformation twins [44]. For the sake of self-consistency and background, the formulation pertaining to modeling explicit twin lamellae is briefly reviewed here.

The constitutive behavior of an elasto-visco-plastic material under an infinitesimal strain approximation with shear transformation can be written as follows:

$${{\sigma }}\left( x \right) = C\left( x \right):\>{{{\varepsilon }}^{{\rm{el}}}}\left( x \right) = C\left( x \right)\left( {{{\varepsilon }}\left( x \right) - {{{\varepsilon }}^{{\rm{pl}}}}\left( x \right) - {{{\varepsilon }}^{{\rm{tr}}}}\left( x \right)} \right)\quad ,$$

(1)

where σ(x) is the Cauchy stress, C(x) is the elastic stiffness tensor, and ε^el(x) is the elastic strain at a material point x. In this work, we consider deformation twinning as a shear transformation process. The elastic strain can be written as the difference between the total strain ε(x) and the plastic strain ε^pl(x) due to dislocation slip and the transformation strain ε^tr(x) associated with twinning. We solve the problem for the local stress field at material point x by using an implicit time discretization of the following form:

$$\eqalign{ & {{{\sigma }}^{t + {{\Delta }}t}}\left( x \right) = C\left( x \right):\left( {{\varepsilon ^{t + {{\Delta }}t}}\left( x \right) - {{{\varepsilon }}^{{\rm{pl}},t}}\left( x \right) - {{{{\dot \varepsilon }}}^{{\rm{pl}},t + {{\Delta }}t}}\left( x \right),{{{\sigma }}^{t + {{\Delta }}t}}} \right) \cr & \;\;\;{{\Delta }}t - {{{\varepsilon }}^{{\rm{tr}},t}}\left( x \right) - {{\Delta }}{{{\varepsilon }}^{{\rm{tr}},t + {{\Delta }}t}}\left( x \right)\quad , \cr} $$

(2)

where

$${{{\dot \varepsilon }}^{{\rm{pl}}}}\left( x \right) = \sum\limits_{s = 1}^N {{m^{\rm{s}}}\left( x \right){{{{\dot \gamma }}}^{\rm{s}}}\left( x \right)} \quad ,$$

(3)

and

$${{{\dot \gamma }}^s}\left( x \right) = {{{\dot \gamma }}_0}{\left( {{{\left| {{{\boldsymbol{m}}^s}\left( x \right):\>{{\sigma }}\left( x \right)} \right|} \over {{{\tau }}_{\rm{c}}^s}}} \right)^n} \times {\rm{sgn}}\left( {{{\boldsymbol{m}}^{\rm{s}}}\left( x \right):\>{{\sigma }}\left( x \right)} \right)\quad .$$

(4)

In Eqs. (3) and (4), ${{\boldsymbol{m}}^s} = {1 \over 2}\left( {{{\boldsymbol{b}}^s} \otimes {{\boldsymbol{n}}^s} + {{\boldsymbol{n}}^s} \otimes {{\boldsymbol{b}}^s}} \right)$ is the symmetric part of the Schmid tensor and b^s and n^s are the unit vectors along the slip direction and normal to the glide plane. The tensor quantities ${{{\dot \gamma }}^{\rm{s}}}$ and ${{\tau }}_{\rm{c}}^{\rm{s}}$ are, respectively, the shear rate and critical resolved shear stress (CRSS) associated with slip system s, and n is the stress exponent. Numerically, the twin shear transformation is imposed in successive shear increments

$${{\Delta }}{{{\varepsilon }}^{{\rm{tr}}}}\left( x \right) = {{\bf{m}}^{{\rm{tw}}}}\left( x \right){{\Delta }}{{{\gamma }}^{{\rm{tw}}}}\left( x \right)\quad ,$$

(5)

at all points within the twin domain. Otherwise, outside of the twin domain, ${{\Delta }}{{{\varepsilon }}^{{\rm{tr}}}}\left( x \right)$ is zero. The tensor ${{\boldsymbol{m}}^{{\rm{tw}}}} = {1 \over 2}\left( {{{\boldsymbol{b}}^{{\rm{tw}}}} \otimes {{\boldsymbol{n}}^{{\rm{tw}}}} + {{\boldsymbol{n}}^{{\rm{tw}}}} \otimes {{\boldsymbol{b}}^{{\rm{tw}}}}} \right)$ is the symmetric part of the Schmid tensor associated with the twinning system, where b^tw and n^tw are unit vectors along the twinning direction and the twin plane normal, respectively. The number of increments required to reach the characteristic twinning shear s^tw is

$${{\Delta }}{{{\gamma }}^{{\rm{tw}}}}\left( x \right) = {{{s^{{\rm{tw}}}}} \over {{N^{{\rm{twincr}}}}}}\quad .$$

(6)

The time increment Δt(=10⁻⁴ s) and the number of increments to achieve the twinning transformation N^twincr are set sufficiently low and high, respectively, to ensure convergence.

Simulation details: A model tri-crystal microstructure consisting of a $\left\{ {10\bar 12} \right\}$ tensile twin in a parent grain and two neighboring grains is shown in Fig. 5(a). The model is a periodic unit cell and is discretized into 510 × 510 × 3 voxels with an outer (buffer) layer that is 10 voxels thick, representing the surrounding polycrystalline material. These dimensions provide a spatially resolved stress distribution that is unaffected by the boundary conditions, corners of the unit cell, and junctions formed by the parent grain, neighboring grains, and the buffer layer. For most cases, the crystal orientation of the parent grain is assumed to be (0°, 0°, 0°) (in the Bunge convention), i.e., the c-axis is aligned with the z-direction, and the texture of the homogeneous buffer layer is random. Before twinning, the simulation cell is subjected to compression along the y-direction, which is perpendicular to the c-axis of the parent grain. This loading condition produces a Schmid factor close to 0.5 for the $\left( {01\bar 12} \right)\left[ {0\bar 111} \right]$ tensile twin variant. In these simulations, a set of voxels in the parent grain is preselected for the twin domain following the theoretical crystallography for the twin. The twin domain is defined by two parallel interfaces, corresponding to the crystallographic twinning plane with a separation distance that yields a twin volume fraction of ∼1.0% for the parent grain. The inclination of the twinning plane with respect to the compression axis for the $\left( {01\bar 12} \right)\left[ {0\bar 111} \right]$ variant depends on the c/a ratio of the HCP material being modeled. For instance, for Mg, Ti, and Zr, the plane angle is 43.1°, 42.5°, and 42.6°, respectively.

Figure 5

CPFFT calculated twin stress distributions generated by a twin lamella in Ti. (a) Tri-crystal setup consisting of a central grain “grain-1” containing a twin and two neighboring grains, with the same orientation on each side. Reprinted with permission from Ref. 51. (b) The twin-plane resolved shear stress (TRSS) distribution after twinning, and (c) the TRSS profile along twin boundary before and after twinning for the orientations of grain-1 and grain-2 is (0°, 0°, 0°) and (0°, 30°, 0°), respectively, in Bunge convention.

At all stages in the simulation, the deformation is accommodated by a combination of elasticity and plasticity. The material properties used in the constitutive law are the elastic stiffness tensor, the preferred slip modes, and the CRSS values for activating them. The single crystal elastic constants [101], in GPa, for Mg at 298 K: C₁₁ = 58.58, C₁₂ = 25.02, C₁₃ = 20.79, C₃₃ = 61.11, and C₄₄ = 16.58; for Zr at 77 K: C₁₁ = 154.2, C₁₂ = 67.8, C₁₃ = 64.8, C₃₃ = 171.6, and C₄₄ = 35.8; and for Ti at 298 K: C₁₁ = 162.4, C₁₂ = 92.0, C₁₃ = 69.0, C₃₃ = 180.7, and C₄₄ = 46.7. The elastic anisotropic indicesa¹ for Mg are 1.09, 1.01, and 1.23; for Zr are 0.78, 1.21, and 1.42; and for Ti are 1.06, 0.75, and 1.21, where 1.0 represents an elastically isotropic material [102]. These indices indicate that Ti is elastically more anisotropic than Mg and less so than Zr. Plasticity is accommodated by basal 〈a〉, prismatic 〈a〉, and pyramidal 〈c + a〉 slip systems for all three metals, and the corresponding CRSS values, in MPa, for Mg [74] are 3.3, 35.2, and 86.2; for Zr [103] are 700.0, 20.0, and 160.0; and for Ti [104, 105] are 120.0, 60.0, and 180.0. The CRSS value, in MPa, of the tensile twin for its activation in Mg [74], Zr [103] and Ti [104] is 20.0, 102.0, and 125.0, respectively.

In most cases, the simulation of twinning shear transformation is performed sequentially. First, the unit cell is subjected to an initial compression along the y-direction. Along the other two directions 1 and 3, zero average stress is enforced. The choice of compressive strain ensures that the resolved shear stress in the twin plane along the twin direction (TRSS) is slightly greater than the CRSS for twinning. Second, while the load is applied, the twinning process involving twin reorientation followed by the shear transformation is then performed. The preselected voxels belonging to the twin domain are reoriented and, then, the local twinning shear is enforced.

Assessment of twinning microstructures

Statistical characterization of twins

In postmortem evaluations of deformed materials, deformation twins are seen to form heterogeneously across a grain microstructure. Extracting relationships between the microstructure and twin development from such studies cannot be properly assessed by analyzing just one or even a few grains in the microstructure. To establish correlations between the microstructure and twins, a statistical analysis needs to be performed.

As an example, recent statistical results of the $\left\{ {10\bar 12} \right\}$ tensile twin in Mg, Zr, and Ti are briefly reviewed. These three data sets are by far not the only statistical data analyses that have been carried out [22, 23, 24], and they have many aspects in common. They all deform by predominantly one type of twin. They are all pure polycrystalline metals: high-purity polycrystalline Mg, high-purity polycrystalline Zr, and commercially pure Ti. And they have similar initial textures, a rolling basal texture, and, hence, similar grain misorientation distributions [22, 23, 24]. All three materials were compressed at 10⁻³/s in an in-plane direction to activate $\left\{ {10\bar 12} \right\}$ twinning. To develop a sufficient number of incipient twins in many grains, Zr was deformed at 77 K, and Mg and Ti were deformed at room temperature. The amount of plastic strain at which they were examined postmortem was relatively small: 3–5% for Mg and 5–10% for Zr and Ti, which is significantly lower than the corresponding failure strain. At higher levels of strain, the twins would tend to dominate the microstructure, making it difficult to identify the role of microstructure in their initial development.

Under their respective temperatures, strain rate conditions, and strain levels, the materials twinned significantly such that many grains contained fine twins that were visible in EBSD (see Fig. 1). Using automated EBSD software, large data sets were generated by analyzing several distinct EBSD scans [22, 23]. The number of grains and twins investigated totaled 2339 and 8550 for Mg, 639 and 1065 for Zr, and 4678 and 2331 for Ti. Using this statistical analysis, several correlations are made between the parent grain size or orientation and the properties of child twins, such as their individual thickness, spacing between parallel twins, and variant types. Other interesting data extended outside of the parent and included the nearest neighbor, such as parent/neighbor misorientation and connectivity of twins across boundaries. Still others were related to the frequency of subgranular twin structures, such as twin–twin intersections and double twinning. Since these studies, as well as other statistical analyses of twinning, focused separately on different materials, material effects were not investigated. In this review, we focus on microstructural features that affected mechanisms of twin propagation and take the opportunity to examine the effect of material on twinning microstructure development.

Model setup for local stress states

To understand the twin propagation process and its connections with the microstructure, we first present the stress field produced by a single $\left\{ {10\bar 12} \right\}$ tensile twin lamella modeled explicitly using CPFFT [43, 44]. Figure 5 shows the calculated local stresses for a tensile twin in HCP Ti, as an example. Figure 5(a) shows the tri-crystal model setup, and Fig. 5(b) presents the calculated TRSS distribution after twinning and Fig. 5(c), the distribution specifically along the twin boundary. The distribution is not uniform, nor is it symmetric, which is a result of the twin shear imposed homogeneously within the twin domain. In particular, the TRSS along the twin boundary is negative, signifying an antitwinning stress.

Figure 5(c) also compares the TRSS distribution in the positions corresponding to the twin boundary before and after twinning. The two vertical dashed lines represent the grain boundaries. It shows that the TRSS has changed from a positive and uniform stress before twinning to the negative one seen in Fig. 5(b), where the larger change occurs at the twin tips compared to the central portion of the twin. The difference is referred to as a “twin backstress.” The amount of stress reversal that leads to a nonzero backstress decreases with twin volume fraction [44]. However, it is not possible to obtain nonzero backstresses even for a twin embryo that is even smaller relative to the grain size than a twin lamella.

The TRSS profile along the twin interface in Fig. 5(c) indicates that the twin “backstress” is high at the twin tip compared to part of the twin in the interior of the parent. Therefore, under further straining, this central portion of the twin, as opposed to the twin tip, becomes the preferable site for twin thickening. In the neighboring grains, a stress concentration develops in the vicinity of the twin tip. For the sake of further discussion, we refer to this stress field as “forward stress,” to suggest that it can drive forward plasticity or twinning. Similar distribution characteristics are obtained for Mg and Zr, and for different neighboring grain orientations.

Twin growth process

Many experimental and modeling literature studies have shown a strong connection between twinning and twin growth with the crystallographic orientation of the parent with respect to the applied loading direction, which is commonly represented in terms of twin Schmid factor [23, 24, 77, 94, 106, 107, 108, 109, 110]. The common understanding is that twins in the grains that are favorably oriented for twinning (high Schmid factor ones) can grow more easily than in grains not favorably oriented for twinning (low Schmid factor ones). Apart from this dominant grain orientation aspect, other microstructural features can play an important role in the twin growth process, which is presented in the following sections.

Experimental observation on twin thickness

Over the years, a commonly reported finding in many metals, not only those of HCP crystal structure, is that polycrystals with smaller average grain sizes develop lower twin volume fractions [21, 22, 23, 24, 109, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121]. This frequent observation has motived the application of the Hall–Petch scaling law, originally used for slip, to twinning. This law was first used to explain the higher yield stresses or fracture strains with decreasing grain size. For twinning, it has been applied in a similar way, such as a twinning stress that increases according to ${1 \over {\sqrt D }}$, where D is the grain size. In the 2D orientation map, which many of the experimental studies have used, the grain size D refers to the diameter of the grain that has been cut by the section.

Figure 6 compiles the distributions from three studies for the individual twin thickness as a function of D of its parent. The twin thickness is calculated by fitting an ellipse to the individual twins, and the true twin thickness is estimated using the minor axis of the fitted ellipse and the relative inclination between twinning plane normal and the sample surface normal. All studies reported a grain size effect on twin thickness, with larger grains containing thicker twins, a result that is consistent with prior reports that higher twin volume fractions are seen for materials with larger average grain sizes. When all three datasets are plotted on the same scale, the grain size effect differs in the three materials. The grain size dependency on twin thickness is strong in Ti and less so in Mg, and not apparent in Zr. On an absolute scale, the twin thicknesses tend to be larger for Mg and Ti than Zr.

Figure 6

Effect grain size on twin thickness distribution for $\left\{ {10\bar 12} \right\}$ tensile twin in HCP Mg, Zr, and Ti. Twins are thick in Mg and Ti compared to Zr. And the grain size sensitivity on twin thickness is high in Ti compared to Mg and Zr. Reprinted with permission from Ref. 24.

Microstructural effects on twin boundary stresses and twin growth

To explain material effects on twin thickness, the local stress fields around twins in Mg, Ti, and Zr using CPFFT are compared. For the twin to thicken, the twin boundary would want to expand by migration, where the TRSS is positive and exceeds a critical threshold, say a preassigned CRSS. Figure 5 shows the TRSS stress component along the twin boundary after the parent grain has been deformed sufficiently to form a twin. The TRSS here is negative, indicating that it is an antitwin state and more applied stress is needed to raise the TRSS along the boundary to meet the threshold CRSS for further growth. The intensity of the antitwinning backstress is affected by the response of the surrounding material. In the case of twin lamellae that span the entire grain, the response of the neighboring grains, where the twin tips meet the grain boundaries, would influence the magnitude of the antitwinning backstress.

To examine neighbor effects on twin growth, we consider the effect of neighbor orientation on the stress S_TB, which is defined as the TRSS at the site in the central part of the twin, where the value of the backstress is the lowest, and thus, twin expansion is likely to first initiate. The S_TB was determined by taking the average of the TRSS in the central part of the twin boundary, shown as region Σ in Fig. 5(c). Figures 7(a)–7(c) show the evolution of S_TB for a single twin of the same size and type and parent orientation for three materials (Mg, Zr, and Ti). The neighbor orientations are selected to cover a broad range of plastic responses. Several curves are shown for each material, corresponding to these different neighboring orientations. To demonstrate, a total of six different neighbors are selected. The neighboring grain orientations and the corresponding relative position of slip modes with a twin are listed in Table I.

Figure 7

CRSS normalized evolution of S_TB in (a) Mg, (b) Zr, and (c) Ti for different neighboring grain cases given in Table I. Reprinted with permission from Ref. 43. Neighbor orientation map of the twin backstress for (d) Mg, (e) Zr, and (f) Ti. A total of 221 different neighboring grain orientations are considered for the same parent grain orientation. With respect to the parent grain orientation, the neighboring grain orientation is denoted by two angles: c-axis misorientation and a-axis misorientation. Reprinted with permission from Ref. 50.

TABLE I Neighbor grain crystallographic orientations along the crystal frame and the corresponding relative position along twin direction of the best oriented slip systems for each mode. The relative position is defined as follows: m′ = (bt·bs)(nt·ns), where bt and nt are the twin direction and twin plane normal, respectively. bs and ns are the slip direction and slip plane normal, respectively [17]. The crystal wireframe of the neighbor orientations looking along the z-axis.

In Figs. 7(a)–7(c), before additional strain is applied, S_TB is close to zero for all cases and for all three metals. As additional strain is imposed, S_TB evolves nonlinearly as a result of the development of plasticity in the localized region around the twin-tip–grain boundary junction. In all materials, the strain evolution of S_TB exhibits a dependence on the neighboring grain orientation.

In the case of Mg, it is possible in all grain neighborhoods to increase the applied stress such that eventually the S_TB exceeds the CRSS for twinning. This is not the case for Ti and Zr. This conclusion is consistent with the experimental results shown in Fig. 6; that is, relatively thick twins are seen in Mg, expanding in some cases to overtake the grain, as the stress is increased, but not often in Ti or Zr [22].

Specifically, in Mg, the neighboring grain oriented for the easiest basal slip (0°, 30°, and 0°) provides the lowest S_TB, and less additional stress needs to be applied in order for S_TB > CRSS. In contrast, the neighbor oriented for the harder pyramidal slip (30°, 0°, and 0°) generates the highest S_TB, and hence more stress is required to overcome it and grow the twin for Mg. These differences are only due to a change in the neighboring orientation since in all scenarios, the parent grain and twin orientation remained fixed. Thus, an important implication from these calculations is that criteria based on parent grain properties alone, such as orientation, twin variant, and average grain stress, may not be sufficient to determine whether freshly formed twins would grow under the applied stress.

The results for Mg can be compared with the same calculations of S_TB (normalized by CRSS) for the same six grain neighbors for Zr and Ti in Table I. For Zr, in Fig. 7(b), a notable distinction is that S_TB does not evolve in the same manner as in Mg. First, unlike Mg, the initial values of the backstresses for some neighboring orientations (C2, C3, C4, and C6) are relatively high, with the ratio S_TB/CRSS being well below zero. In some cases, the S_TB only increases slightly as additional strain is applied, without reaching the CRSS (C3 and C6). In other cases, the S_TB does not evolve or worsens (C2 and C4). Only for neighboring grain orientations (C1 and C5), where the S_TB/CRSS is initially positive, can an additional applied stress overcome the backstress and make S_TB increase above the CRSS. These outcomes can be connected with the type of slip activated in the neighboring grain at the twin/GB junction. For those neighbors (C1 and C5 in Table I) that support further twin growth with an increase in stress (S_TB/CRSS > 1), the preferred slip mode is prismatic 〈a〉 slip, which is the easiest slip mode in Zr, and the backstresses are relatively small in value. In contrast, those neighbors oriented for the harder pyramidal 〈c + a〉 slip mode (C0, C2, and C4 in Table I) can make it difficult for subsequent twin expansion, since the backstresses generated are large.

Similar to Mg and Zr, we calculate S_TB at the TB in the case of an isolated twin with different neighboring grain orientations for Ti. Figure 7(c) shows the strain evolution of the ratio between S_TB and CRSS. The S_TB ratio is negative, and with increasing strain, it increases for all cases of grain neighbor orientation. In most cases, except two of them, the S_TB is able to exceed the CRSS, suggesting that further expansion is possible. The ability for the applied strain to grow the twin in Ti exhibits some sensitivity to neighboring grain orientation, more so than Mg, but less so than Zr. As mentioned, Ti is plastically softer and less anisotropic than Zr. Therefore, compared to Zr, the values of the backstresses in Ti would be smaller and less sensitive to the neighboring grain orientation. From these studies, we find that with all else being the same, the backstresses that develop in the twin in Zr are more sensitive to the neighboring grain orientation, compared to Mg and Ti. The values of the backstress in Zr are much larger than its CRSS for twinning than those in Mg and Ti.

In the prior paragraphs, stresses for twin growth are studied considering the effect of a small number of neighboring grain orientations. To compare the range of backstresses possible for each material, twinning simulations are performed for neighboring grain orientations that span the entire orientation space of neighboring grains. Figures 7(d)–7(f) display calculated backstress maps for the entire space of neighboring orientations for Mg, Zr, and Ti [50]. The orientation is a relative one, defined as the orientation of the neighbor with respect to the parent grain and is denoted by two angles: one corresponding to an in-plane rotation and another to the c-axis misorientation. These maps show that the magnitudes and anisotropy in the backstress are much higher for Zr and Ti than Mg. In the case of Mg, the backstress is particularly low (∼22 MPa) for the neighboring grain when the c-axis misorientation ranges from 0° to ∼25° and from ∼65° to 90°, but slightly higher (∼25 MPa) for the c-axis misorientation range from ∼25° to ∼65°. In the case of Zr, the backstress is lower (∼75 MPa) for the c-axis misorientation range from 0° to ∼45° and substantially higher (∼105 MPa) for the c-axis misorientation range from ∼45° to 90°. The backstress distribution for Ti is similar to that of Zr.

Grain size effect: In addition to material and neighboring grain orientation, experimental studies indicate that grain size affects twin thickness. To determine whether grain size would affect the twin-induced backstress, calculations for the same parent/twin were repeated for a broad range of grain sizes. Figures 8(a) and 8(b) show the calculated TRSS profile along the twin–grain matrix boundary for two normalized grain sizes, where the grain size is normalized by the twin thickness, D* (=D/t) = 15 and 46 for Mg [116], and D* = 12 and 46 for Ti [122]. For both materials, the backstress away from the twin ends, particularly the S_TB at the center of the grain, is larger in the case of the smaller grain.

Figure 8

Calculations aiming to elucidate the effect of grain size on twin expansion in Mg. (a) The TRSS profile along the twin boundary for a parent grain size of D* (=D/t), 15 and 46, where t is the twin thickness and D is the parent grain size. Reprinted with permission from Ref. 116. (b) Similar TRSS profile for Ti for a parent grain size of D* (=D/t), 12 and 46. Variation in twin backstress as a function of grain size for (c) Mg and (d) Ti. (b)–(d) Reprinted with permission from Ref. 122.

The calculations were carried out for D* ranging from 9.0 to 46.0. Figures 8(c) and 8(d) show the average backstress in the twin domain S_B as a function of D* for both Mg and Ti, respectively. These plots use the Hall–Petch axes as a way to elucidate the varying sensitivities to grain size among the two materials. As seen, the average twin backstress, S_B, increases as D* decreases for both Mg and Ti. On these axes, we observe that the calculated backstresses S_B follow a linear relationship, signifying that S_B is proportional to (D/t)^−1/2. The values of S_B for Ti, however, are on average 2–3 times larger, and consequently, the Hall–Petch scaling coefficients are almost 2–3 times smaller in Mg than that in Ti, being 114.45 and 247.18 for Mg and Ti, respectively. The larger Hall–Petch coefficient for Ti indicates that the reduction in grain size increases the backstress and decreases the twin thickening propensity more significantly in Ti. This finding provides some rationale for the much stronger grain size effect on twin thickness for Ti than Mg (see Fig. 6).

The grain size effect applies to twin lamellae that span the grain and can be explained by the intense backstresses generated where the twin intersects the grain boundary. The backstress concentrates at the twin tips, and this intensity can extend back onto the twin several times that of the twin thickness. When the reaction stress fields from the two ends are sufficiently close to interact, the result is an increase in the backstress. As D and the distance between these two “twin-tip” fields increase, the backstress reduces. In the limit that the twin becomes extremely long, the fields are sufficiently far apart that the tip fields no longer interact and the S_TB saturates.

So far, grain size effects on local stress fields and potential for growth are studied for a neighboring grain orientation with a slight misorientation of ∼5° from the orientation of the central parent grain, a case that would represent a typical grain within a strongly textured material. We find that this neighboring crystal orientation is, in fact, not plastically soft or accommodating, leading to a relatively high backstress along the lateral area of the twin. However, a neighboring grain well oriented to accommodate the shearing action of the twin, mostly with its easy basal slip system, would be considered a “plastically soft” neighbor. Less backstress would result in less applied load needed to increase the local stress in the twin boundary to a level where the twin can grow again. In contrast, a neighboring grain that is oriented poorly for basal slip must activate relatively large amounts of the harder pyramidal slip in order to accommodate the shearing of the twin. It would constitute a “plastically hard” neighbor. A higher backstress in the twin would result, and consequently, more applied load would be required to grow the twin.

For Mg and Ti, calculations were performed for two distinct neighboring grain orientations, one plastically hard neighbor (pyramidal slip for both Mg and Ti) and another plastically soft neighbor (basal for Mg and prismatic for Ti), which are presented in Figs. 8(c) and 8(d), respectively. As expected for both Mg and Ti, the plastically harder the neighboring grain, the more severe the grain size constraint is, and thus the higher twin backstress for the same twin in the same parent. The strong influence of grain neighbor orientation effect could explain why not all grains of similar size and orientation [22, 23, 24] form twins. It provides insight for designing microstructures that hamper twinning for the sake of increasing formability. Furthermore, grain neighbors that are plastically hard provide an even higher grain size constraint that could make grain refinement even more effective on suppressing twinning.

Twin transmission process

Experimental observation on twin transmission

Twins can expand by extending into their neighboring grain, a phenomenon often referred to as twin transmission. Partial evidence of twin transmission in postmortem microscopy analyses are observations of ATPs, which are two twins belonging to different grains that meet at the same point in the grain boundary [22, 51, 66, 68, 80, 81, 123]. ATPs could have formed in one of two ways: (i) as two twins that formed simultaneously from a common grain boundary or (ii) in a sequence, starting with one twin transmitting into the other grain across the grain boundary. Distinguishing scenarios (i) and (ii) is not possible from postmortem analyses, but, nonetheless, it identifies a boundary location from which a paired twin formation event took place.

Figures 9(a) and 9(b) show the variation in the fraction of grain boundaries with ATPs with grain boundary misorientation angle for both Mg and Zr. In both cases, a sizable fraction of $\left\{ {10\bar 12} \right\}$ twins were identified as twins belonging to ATPs, and these ATPs were found over a wide range of misorientation angles. For both materials, the propensity for ATPs decreases with increasing grain boundary misorientation angle. The relationship is nonlinear, where the likelihood for twin transmission is high at low misorientation angles and decreases rapidly with increasing misorientation angle. A cut-off misorientation angle appears, above which twin transmissions are rarely observed, and is approximately 50° for Mg and slightly greater than 60° for Zr.

Figure 9

Statistical distribution of twin transmission frequency as a function of grain boundary misorientation angle in (a) Mg and (b) Zr. Reprinted from Ref. 51, which is an open access article distributed under the terms of the Creative Commons CC BY license, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Similar results have been reported in other HCP metal systems, such as AZ31 Mg alloy, Ti, and Re. In all cases, the propensity for ATPs was found to decrease with increasing misorientation angle [22, 51, 68, 81, 123]. The cut-off misorientation angle for ATPs of the $\left\{ {10\bar 12} \right\}$ twin type in Ti is 50°, which is closer to that of Mg and lower than that of Zr [68]. Similarly, Kacher and Minor [81] report twin transmission of $\left\{ {11\bar 21} \right\}$ tensile twins in HCP Re, and the cut-off misorientation angle for ATPs is much lower at 25°. The influence of the nearest grain neighborhood can add to the substantial spatial variations observed in typical twinned microstructures, where, in the most exceptional cases, some areas that happen to connect a string of favorably misoriented grains will produce twin chains.

Twin-tip stresses and twin transmission

In prior work, the stresses generated at the tip of the twin were analyzed to determine whether they were sufficient to extend the twin either in its own parent crystal or as a new twin in the neighboring grain [scenario (2) in ATP formation]. Figure 5 provides an example of the localized intense forward stress field that can be created around the twin tip, having terminated at the grain boundary, in the adjacent grain. Plotted there is the TRSS corresponding to the primary twin. As a measure of the stress needs to extend the twin or form a new one, the average TRSS, called TRSS_tip, in the stress concentrated volume Ω ahead of the twin tip is calculated. When the twin tip lies in the perfect parent grain (containing no other defects), TRSS_tip = TRSS_SX, corresponding to the particular situation in which twin propagation can be expected, without the need for an increase in the applied driving force. When the twin-tip stressed region lies in the neighboring grain, TRSS_tip will depend on the orientation of that grain with respect to the load and the twin system.

Toward using the forward stress as a way of identifying twin transmission propensity, the maximum TRSS_tip among all six twin variants of the neighboring grain is first determined. Then, in order to compare transmissibility across different neighbor orientations and materials, the TRSS ratio = max [TRSS_tip]/TRSS_SX is used. Figure 10 shows the changes in the TRSS ratio for different grain neighbor misorientation angles for three metals: Mg, Zr, and Ti [51]. We observe from the calculations that for all HCP metals, the TRSS ratio decreases with the misorientation angle, signifying a reduction in the propensity for twin transmission. The sensitivity of the TRSS ratio follows remarkably well the experimentally measured dependencies of twin transmission on misorientation angle (see Fig. 9). The material influences are also predicted, wherein the reduction in the TRSS ratio with misorientation is more pronounced in Mg than in Zr and Ti. The calculation even forecasts, consistent with experimental observations, that the cut-off misorientation angle is approximately 50° for Mg, 66° for Zr, and 60° for Ti.

Figure 10

Variation of the TRSS ratio (5TRSS_tip/TRSS_SX) in twin-tip region X versus the grain boundary misorientation angle for HCP (a) Mg, (b) Zr, and (c) Ti. Reprinted from Ref. 51, which is an open access article distributed under the terms of the Creative Commons CC BY license, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

The key difference that distinguishes Mg from Zr and Ti is its plastic anisotropy. Zr and Ti are plastically more anisotropic than Mg, leading to greater sensitivity in the orientation of the neighbor on its deformation response. Zr deforms mainly by two modes, prismatic slip and pyramidal slip, whereas Mg and Ti deform by three modes. The use of two rather than three slip modes makes Zr more anisotropic than Mg and Ti. Furthermore, the differences among the slip strengths in Ti are greater than those in Mg. In a recent study [97], the effect of plastic anisotropy on twin transmissibility across grain boundaries was probed for a range of Mg alloys using the TRSS ratio as an indicator. In the calculation, alloying had the effect of changing the differences among the slip strengths of the three predominant modes of slip. There, it was found that the more anisotropic the Mg alloy, the more likely twin transmission is promoted [97].

A noteworthy outcome emerges from the calculations for Zr and Ti. For some grain neighbors with low misorientation angle, the propensity for propagating the twin tip is even higher than for a single crystal with no misorientation angle (TRSS ratio >1). This finding implies that for these special grain neighbors in Zr and Ti, the driving force for propagating the twin across the GB is even higher than that for propagating the same twin within its parent grain. This twin-transmission “boost” is not predicted for Mg, and this difference provides another indication that plastic deformation properties matter. Its existence in Zr and Ti but not Mg is consistent with the experimentally observed trend that, particularly at low misorientation angles, Zr is more likely to transmit than Mg. Yet, since not all low-misorientation angle GBs are associated with a boost in Zr and Ti, obtaining experimental validation would require knowing the full grain boundary character and not just the misorientation angle.

Multiple twin formation

Experimental observation on parallel twins

To accommodate the imposed deformation, instead of thickening already existing twins, grains sometime activate new twins. If the newly activated twin type and its variant are the same as that of the existing twin, then it will develop a parallel twinning microstructure. Arrays of parallel twins are often observed in the EBSD images of HCP Mg, Zr, and Ti (see Fig. 1). Figure 11(a) shows the effect of grain size on the formation of multiple parallel twins in Mg, Zr, and Ti. In all cases, the number of twins per grain increases with increasing grain size, but the rate of increase is particularly striking in Zr. A grain of a given size in Zr accommodates more twins than grains of the same size in Mg and Ti. Also, in Mg and Ti, the number of twins per twinned grain varies from 1 to 2 as the grain area increases from 50 to 600 µm², whereas in Zr, the number of twins per twinned grain increases from 2 to 15 for the same range of grain area from 50 to 600 µm². The grain size effect on the parallel twin formation is much stronger in Zr than Mg and Ti.

Figure 11

Experimental characterization and FFT-based local stress calculation for parallel twin formation. (a) Experimentally observed the correlation between grain size and number of twins per grain. Reprinted with permission from Ref. 24. The number of twins per grain increases with grain size, and the dependency is significant in Zr compared to Mg and Ti. (b) FFT tri-crystal setup with parallel twins in the central grain (grain-1). The spacing between parallel twins is s. (c)–(f) TRSS distribution with twin spacing, s = 0, 2t, 8t, and 20t, respectively. Here, t is the twin thickness. (g)–(i) The difference between average twin stress of parallel twins with different spacing and single isolated twin for Mg, Zr, and Ti, respectively. (b)–(i) Reprinted with permission from Ref. 43.

Local twin stresses and parallel twin spacing

To gain some insight on twin spacing, the CPFFT model is applied to study the stress fields that develop when two adjacent, parallel and identical twins exist in the same parent grain. Figure 11(b) displays a schematic of the two-twin model, where the twin thickness is t and their spacing s is the minimum distance between their (inner) boundaries, s = nt, where n is an integer. In simulation, the two twins are inserted simultaneously under load. Figures 11(c)–11(f) show the TRSS field produced by an isolated twin and a pair of twins with spacing 2t, 8t, and 20t in a Zr tri-crystal model setup. At a spacing of 2t, when the two twins are closely spaced, their stress fields overlap. When they are spaced 8t apart, these fields appear to be on the cusp of interacting. By 20t, their fields are well separated. The interaction between the two twins has not changed the fact that the backstress is the largest at the twin-tip/GB junction and decays in value toward the center of the grain. However, the backstress depends on spacing s and, more importantly, their values are higher, on average, than that of an isolated twin. The interaction increases the backstress, especially when the two twins are closely spaced. This increase in backstress can hamper their growth to a greater degree than if these twins were isolated.

To further examine the variation in their backstress with twin spacing s, the average twin TRSS in one of the twin domains, S_ave, for different spacings is plotted. Using the isolated twin case as the reference, Figs. 11(g)–11(i) show the difference between the S_ave and S_ave,0 of an isolated case as a function of spacing s. It suggests that the critical spacing is around 8t and 15t for Zr and Ti, respectively, in which the difference becomes nearly zero. Above this spacing, there are no additional hampering effects on the TRSS from neighboring twins. For Mg, on the other hand, the twin–twin interaction effect will hamper propagation even at large separations.

One contribution to the backstress field acting on the twin comes from the constraint that the neighboring grain provides on the localized shear imposed by the twin lamella. Another contribution comes from the reaction in the parent grain to the shear transformation. As seen in earlier calculations for an isolated twin, for the same parent and twin and material, the extent of the backstress field depends on the orientation of the grain neighbors. Thus, the neighboring grain properties should affect the interaction between two twins in the parent and, hence, the critical twin spacing beyond which their mutual interaction becomes negligible.

To examine neighbor effects, the simulations are repeated for neighbor orientations corresponding to cases 1 and 4 (see Table I). These results are included in Fig. 11, and they reveal that while the grain neighbor affects the magnitude of the backstress field, S_ave evolves with s in a similar manner as with the other neighboring orientations. For Zr, S_ave reduces to that of the single isolated twin S_ave,0 by s ∼ 9t for cases 1 and 4. Thus, changing the neighbor orientation in these cases does not significantly alter the critical spacing for Zr. Similarly, changing the neighbor orientation does not alter the conclusion that the critical spacing for Mg exceeds 20t, which could physically extend beyond the grain size. In Mg, the presence of another twin, even when it is distant (over 20 times in thickness), hampers twin growth more so than if it were isolated.

The analysis in Fig. 11 implies that compared to Mg, tensile twins in Ti and Zr will tend not to grow as thick and the number of twins per grain will be larger. This tendency agrees with the notion discussed earlier. Since Ti and Zr are elastically and plastically more anisotropic than Mg, the difference in the elastic and plastic properties of the matrix domain in between the two twins is greater. For the parent orientation simulated, the matrix is stiffer than the twin for accommodating shear parallel to the twin plane, and the plastic strain fields induced by twins are less extended in Ti and Zr than in Mg. Consequently, the interaction between two twins would be weaker and the critical spacing would be smaller.

Experimentally observed twin–twin junctions

Instead of activating the same type and same variant twin, sometimes a grain may activate different variants, leading to the formation of twin–twin junctions. Twin–twin junctions are observed to vary statistically within deformed microstructures. Within a Zr polycrystal of 1200 grains, there were 1975 twins, 831 of which were part of a twin–twin junction. Twin–twin junctions have been shown to play distinctive roles, compared to isolated twins, in their interactions with gliding dislocations, twin thickening, strain hardening, and void formation and fracture [62, 71, 85, 109, 124, 125, 126]. Yu et al. [71] studied the effect of twin–twin junctions on the strain hardening rate and yield stress in a HCP Mg single crystal. Figure 12(a) displays an EBSD image of tensile twin junctions in single crystal Mg formed during cyclic loading along the $\left[ {10\bar 10} \right]$ direction. Figure 12(b) shows that with increasing number of cycles, the number of twin–twin junction increases, causing an increase in both yield and the strain hardening rate. A similar finding was reported by Jiang et al. [125] in the AZ31 Mg alloy. Twin–twin junctions affect the development of the twinning microstructure; once formed, they are less likely to thicken, promoting proliferation of twinning by forming new twins rather than thickening the newly joined ones in an Mg alloy [62] and Zr [109]. El Kadriri et al. [62] demonstrated this effect by closely examining two grains with roughly the same Schmid factor: one showed a single twin variant and the other had two intersecting twin variants [see Figs. 12(b1) and 12(b2)]. Upon further loading, the preexisting twins grew in the former grain, but not in the latter. At the same time, in the twin intersecting grain, new twins formed [see Figs. 12(b3), 12(b4), and 12(b2)]. While the twins grew steadily thicker with strain for both grains, the twin thickness is higher for the grain with single variant twin than the grain with two different variants.

Figure 12

(a) Effect of twin–twin junctions on mechanical response: (a1) EBSD image shows the twin–twin junction microstructure in single crystal Mg and (a2) effect of twin junctions on yield stress and strain hardening response in single crystal Mg under cyclic loading. Reprinted with permission from Ref. 71. (b) Effect of twin–twin junctions on further twinning microstructure development: (b1) and (b2) EBSD image showing a grain with parallel twins of the same variant (grain-1) and a grain with twin–twin junction (grain-2). (b3), (b4), and (b5) Evolution of twin volume fraction, average twin thickness, and number of twins with strain for grain-1 and grain-2, respectively. For the same twin volume fraction, grain-1 accommodates with a smaller number of thick twins and grain-2 accommodates with a greater number of thin twins. Reprinted with permission from Ref. 62.

Local stresses and twin junction formation

The local stresses involved in twin–twin junction formation, in the stage before contact to after contact, were studied in a recent work using CPFFT [127]. Figure 13(a) shows a schematic representation of the simulation setup. This setup consists of one orientation (grain) finely discretized, which contains two co-zone twin variants T1 $\left( {\left( {10\bar 12} \right)\left[ {\bar 1011} \right]} \right)$ and T4 $\left( {\left( {\bar 1012} \right)\left[ {10\bar 11} \right]} \right)$. For this combination of grain orientations and loading conditions, the twin plane normal and twin shear directions of both twin variants lie in the Y–Z plane. In this setup, T1 is presumed to be the preexisting twin, and a newly formed twin, T4, approaches T1 under an applied load.

Figure 13

(a) Model setup for twin–twin interaction simulation. (b) Twin-plane resolved shear stress (T1-TRSS) profile along the top interface of T1 for different spacing, s/t = 2.0, 1.5, 1.0, and 0.5. The TRSS profile confirms that the formation of the twin–twin junction is attractive. Twin-plane resolved shear stress (T4-TRSS) profile along (c) the top and (d) bottom interface of T1 with impinging T4. TRSS profile along the top interface prevents the penetration of T4 into T1, and the same TRSS profile along the bottom interface suggests that the nucleation of T4 on the opposite side of T1 is possible and may lead to the formation of a “twin-crossing” configuration. Two vertical dashed lines correspond to the points in the twin boundary where T4 would impinge on T1, i.e., twin–twin junction points. Reprinted with permission from Ref. 127.

To examine the different stages in junction formation, a series of simulations were performed with different spacings s between T1 and T4, wherein T1 is the recipient twin and T4 is the impinging twin. Figure 13(b) shows the T1-TRSS profiles along the twin boundary from A to B for different spacings s between the tip of twin T4 and the boundary of T1. Along most of the recipient T1 boundary, the TRSS is negative, an antitwinning stress, meaning the T1 boundary would not migrate. An exception exists in the region where the T4 tip is close to the T1 boundary, where the T1-TRSS is locally enhanced, becoming in fact more localized and intense as s/t decreases. Localization of intense stress is a consequence of the shape of the stress profile ahead of the T4 twin tip. Generally, the TRSS field is intense and narrow near the twin tip and reduces in intensity as one move away from the twin tip. As T4 approaches T1, the highest stress region produced at the T4 tip draws closer to the T1 boundary. Concomitantly, we see the T1 boundary stress produced by T4 growing more intense and concentrated. This result indicates that the T1 boundary would migrate toward T4, as T4 approaches T1. Therefore, junction formation can be accomplished by boundary migration of the recipient twin T1.

Once T1 and T4 have made contact, an important question that has been asked is how the two twins “cross,” wherein the same twin variant of one twin lies on both sides of another twin. A few microscopy studies of deformed single crystals and polycrystals have suggested that the two twins interpenetrate [71, 126, 128, 129, 130]. Sun et al. [128] speculated, from postmortem analysis, that one twin partially penetrates the other. A recent study by Yu et al. [71] studied the stress state and crystallography of the overlapped domain in a twin–twin junction and concluded that it is not consistent with a reoriented domain and twin formation is unfavorable in this region. Instead, they argue that a new twin of the same variant impinges from the opposite side, grows by thickening, and appears as if it had been transmitted through the recipient twin.

To understand the process, CPFFT calculations were carried out to analyze the stress fields associated with a newly formed twin–twin junction. The fields of the T4-TRSS component in particular can help determine whether the impinging twin would continue to propagate after making contact and, if so, how. Figure 13(c) shows the T4-TRSS profile along the top interface of T1 (see inset), where T1 and T4 contact each other. Within the region below the T4 tip, inside the T1 boundary, an antitwinning stress for T4 develops, marked by the generation of a large, negative T4-TRSS stress. This would suggest that interpenetration of T4 into T1 in the overlapped twin domain would not be supported. Figure 13(d) shows the calculated T4-TRSS along the T1 boundary opposite the contact point (see inset) to determine whether T4 would reform on the other side of the T1 twin. The T4-TRSS is notably higher along the parts of the boundary where the T4 twin tip meets T1 (between the dashed lines). In this region, a new twin is likely to form, of the same type and variant as T4. Taken together, the local stress calculations indicate that the T4 twin variant, upon making contact with T1, would not likely transmit through the existing twin. It would form and eventually propagate from the T1 boundary on the opposite side of the junction, creating the appearance of a crossed-twin structure.

Double twinning in HCP metals

For a given orientation and loading condition, only a few combinations of twin modes are possible. For example, if a grain is favorably oriented for tensile twinning, it usually will not simultaneously activate compression twins under the same loading state. However, the large reorientation due to tensile twinning may reorient the twin domain to favor compression twinning. Activation of a twin inside another twin is referred to as double twinning [131]. Several combinations of double twinning are possible as reported in the literature, including $\left\{ {10\bar 11} \right\} - \left\{ {10\bar 12} \right\}$ [53, 88, 106, 132, 133] and $\left\{ {10\bar 12} \right\} - \left\{ {10\bar 12} \right\}$ [90, 134] in magnesium and its alloys and $\left\{ {11\bar 22} \right\} - \left\{ {10\bar 12} \right\}$ [135, 136, 137, 138] and $\left\{ {10\bar 12} \right\} - \left\{ {10\bar 12} \right\}$ [139] in titanium and its alloys. Figure 14 displays an example of $\left\{ {11\bar 22} \right\} - \left\{ {10\bar 12} \right\}$ double twinning in titanium [135].

Figure 14

(a)–(c) $\left\{ {11\bar 22} \right\} - \left\{ {10\bar 12} \right\}$ double twinning microstructure in titanium. Here, 1, 2, and 3 refer to the parent grain, $\left\{ {11\bar 22} \right\}$ primary compression twin, and $\left\{ {10\bar 12} \right\}$ secondary tensile twin, respectively. Reprinted with permission from Ref. 135. (d)–(f) Crack formation at $\left\{ {10\bar 11} \right\} - \left\{ {10\bar 12} \right\}$ double twinning interfaces (white arrows) in a magnesium alloy. Reprinted from Ref. 88. CPFEM modeling of double twinning in an AZ31 Mg alloy. Distribution of von-Mises stress (g) before and (h) after the formation of $\left\{ {10\bar 11} \right\}$ compression twin, and (i) after the formation of $\left\{ {10\bar 12} \right\}$ tensile twin inside the compression twin. Reprinted with permission from Ref. 98. Reference 88 is an open access article distributed under the terms of the Creative Commons CC BY license, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

The presence of double twinning affects material strength, ductility, and failure response. For instance, Lentz et al. [88] showed that nonparallel networks of $\left\{ {10\bar 11} \right\} - \left\{ {10\bar 12} \right\}$ double twinning interfaces [shown in Figs. 14(d)–14(f)] can act as strong barriers to slip in an Mg–Li alloy, leading to both simultaneous strengthening and high strains to failure. Other observations reported cracks or voids at $\left\{ {10\bar 11} \right\} - \left\{ {10\bar 12} \right\}$ double twins in Mg alloys [53]. Statistical characterization of double twins has focused on variant selection [90, 105, 108, 132, 135, 136, 138, 139, 140, 141], and less so on characteristics of twinning microstructures comprising double twins.

Modeling of double twinning

Recently, Ardeljan and Knezevic [98] studied the formation of $\left\{ {10\bar 11} \right\} - \left\{ {10\bar 12} \right\}$ double twinning in AZ31 Mg alloy using the CPFEM framework. Here, a synthetically generated 3D polycrystalline granular microstructure was modeled using a standard finite element (FE) homogenization method, while each grain of the polycrystal is discretized into a set of FE integration points. Material constitutive response is simulated at the FE integration point level using crystal plasticity theory. The constitutive model allowed the plastic strain to be accommodated by crystallographic slip and deformation twinning, wherein twinning is represented as a pseudo-slip mechanism. Once the predefined critical value of twinning activity is reached, the particular material point is deemed a twin element. At this stage, the twinning shear and reorientation are explicitly established. A similar approach is employed for the formation of a twin inside another twin, i.e., double twinning. Details of the plastic deformation mechanism and the associated hardening equations are incorporated into a UMAT subroutine within the Abaqus FE solver.

To study $\left\{ {10\bar 11} \right\} - \left\{ {10\bar 12} \right\}$ double twinning in detail, the largest grain (located centrally) with a favorable orientation for twinning, which is located centrally in the polycrystal, was selected. First, the polycrystal was subjected to preferred prestraining to activate a compression twin in the selected grain. As shown in Fig. 14(g), the macroscopically imposed strain developed a heterogeneous stress field within the grains and at the grain boundaries, which identifies the location and the variant of the $\left\{ {10\bar 11} \right\}$ compression twin. Within the explicitly modeled compression twin domain, significantly large local stress concentrations develop, favoring the activation of an internal $\left\{ {10\bar 12} \right\}$ tensile twin [see Fig. 14(h)]. In addition, the selection of the tensile twin variant is also decided by the $\left\{ {10\bar 11} \right\}$ twin-induced local stresses, which is different from that which would be identified by the Schmid factor. The model then permits a $\left\{ {10\bar 12} \right\}$ tensile twin to form inside the compression twin, producing an explicit double twin. The local stresses generated from the double twin suggest that the double-twin boundary is susceptible to void nucleation and may lead to premature failure.

Conclusions and future research

The class of HCP metals, such as Mg, Zr, and Ti, and their alloys have outstanding intrinsic properties that make them attractive for structural applications. Yet in many cases, incorporation of HCP metals into engineering designs is hindered by their complex deformation and damage behavior compared to other structural metals, such as Al and Ni alloys, in use in many of today’s load-bearing structures. This complexity in the deformation response of HCP metals results from its deformation mechanisms, which include not only multiple slip processes, but also the seemingly random formation, growth, and proliferation of deformation twins throughout the microstructure.

Twins generate highly localized stress–strain fields inside their parent grain and neighboring grains. The important characteristics of these fields prevail over the mesoscale regime, above the atomic scale but below the micron scale of the size of an individual grain. These heterogeneous fields can potentially influence the formation of additional twins, twin thickening, recrystallization kinetics, and fracture. In this article, we review recent results from micromechanical models that are able to calculate the spatially resolved mechanical fields due to twins within deformed microstructures, where the structure and topology of grains, twins, and grain boundaries are explicitly represented. Also included is the valuable role that experimental characterization has played in motivating and guiding model development. We highlight the insight gained by these studies, such as the local stresses produced by twins and at twin/grain–boundary intersections, the stress measures responsible for twin formation and thickening, and driving stresses responsible for twin–twin interactions, twin transmission across grain boundaries, and secondary twinning.

Although not discussed here, these same tools offer a platform for studying twinning-induced damage and failure. While some efforts have begun in this area, it will be critical for eventual certification of HCP microstructures to involve these tools to examine the role of twinning in void and crack formation [82, 83, 142, 143, 144]. It is also recognized that most of the model analyses reviewed here are 2D, since this is representative of most studies carried out to date. Recent characterization and modeling studies have suggested that the interaction and growth processes of twins in the third dimension are unlike those seen in 2D analyses [72, 145, 146]. Extension of experimental characterization twinning studies and calculation of localized stress states in 3D ought to reveal new insight that would complete our understanding of the development of a twinning microstructure in the bulk material [146, 147]. We have focused our examples on pure metals, but most material candidates are alloys or two-phase HCP-based metals. The mesoscale models here can be straightforwardly modified for alloys [11, 97, 98, 148]. Important questions that remain are the differing effects of solutes with migrating twin boundaries, with the grain boundaries where twins intersect or form, and the plastic properties of the grains. Last, as we have alluded to here, many breakthroughs in understanding twin growth processes have been driven by observations from in situ deformation studies [61, 63, 64, 65, 91, 149]. Continuing efforts toward capturing fast-acting twins in situ hold, in our view, the most promise in advancing understanding on the effects of microstructure and material properties on twin formation, propagation, and growth.