Introduction

Pharmacokinetic (PK) modeling relies heavily on mass and species balances. Such balances are described by ordinary differential equations (ODEs) or partial differential equations (PDEs), depending on the level of detail that is of interest. For example, compartmental models consist of sets of ODEs describing the rates of accumulation of drug in individual compartments due to exchange flows between compartments, or due to elimination of drug. Under steady state conditions, where the rates of the accumulation do not change with time, the ODEs become algebraic equations.

Accumulation, flow, and irreversible elimination are not peculiar to pharmacokinetics. In fact, numerous physical processes involving storage, transfer, and loss, such as the conduction of electricity in circuits, fluid flow through porous media, sound waves, conductive heat transfer, and chemical flow and conversion in reactors, are modeled using differential equations. These differential equations are built from relationships between forces and flows, and conservation principles. The question may be asked: to what extent can we apply what is learned from one class of processes to another, in particular pharmacokinetics?

Before the widespread use of digital computers to solve the differential equations of pharmacokinetics, analog electrical circuits and oscilloscopes were used to visualize pharmacokinetics. In such circuits, charge represents amount of drug, voltage represents concentration, current represents drug flow or elimination (excretion or metabolism), and capacitance and conductance represent apparent volume and clearance, respectively. The ratio of conductance to capacitance is a rate constant. (These analogies were recognized as early as 1964 by Riggs (1). The third traditional electrical circuit element, the inductor, has no analog in pharmacokinetics.) When hepatic clearance concepts were introduced, some researchers borrowed from chemical reactor models of varying complexity (2), including models that required a partial differential equation description in time and space. At steady state, the PDEs reduce to spatial ODEs.

Recently, Benet and coworkers published two papers contending that many concepts and results of pharmacokinetics can be clarified using Kirchhoff’s laws, derived initially for electrical systems (3,4). In a paper published between the Benet contributions, Korzekwa and Nagar argued that Kirchhoff’s laws cannot account for certain processes (5). Further criticisms of the use of Kirchhoff’s laws in PK modeling, specifically of hepatic processes, are presented in a recent paper by Rowland et al. (6). The present commentary is a contribution to the discussion.

Kirchhoff’s Laws and Pharmacokinetics

Kirchhoff’s voltage law (KVL) states that the sum of voltage drops around a loop in an electrical circuit is zero (7,8,9). A corollary is that the voltage difference between two points, or “nodes” of a circuit is independent of the “path” between the two nodes. A second corollary is that voltage is well defined at any node. Since concentration in pharmacokinetic systems is analogous to voltage, the KVL analog in pharmacokinetics is that concentration is well defined at any “node,” e.g., point or compartment with known apparent volume.

Kirchhoff’s current law (KCL) states that the sum of all currents flowing into a node is zero. Depending on the sense of current direction, it can equivalently be stated that the sum of all currents flowing into the node must equal the sum of currents flowing out of that node (7,8,9). The notion of a current flowing through a wire or a resistor is well understood, but what is the “current” flowing through a capacitor? It is the rate of accumulation of charge across the capacitor plates, which equals the “displacement current” that “flows” through the medium separating the plates (7).

By analogy, the mass balance equation for the one compartment body model,

$${V}_{d}\frac{dC}{dt}=-C{L}_{E}C+{R}_{in}(t)$$
(1)

where C is plasma concentration, t is time, Vd is apparent volume of distribution, CLE is elimination clearance, and Rin(t) is the rate of drug administration into plasma, is simply “KCL” applied to the drug “currents” Rin(t), CLEC, and \({V}_{d}dC/dt\). Figure 1a depicts the one compartment model.

Fig. 1
figure 1

a Schematic of one compartment body model. b A compartment (or node) with two parallel elimination clearances, CL1 and CL2. These two clearances can be added to produce \(C{L}_{\mathrm{tot}}=C{L}_{1}+C{L}_{2}\)

Full size image

If Rin(t) is constant, then eventually \(dC/dt\) vanishes, and at steady state, we have \({C}_{ss}={R}_{in}/C{L}_{E}\), or rearranging, \(C{L}_{E}={R}_{in}/{C}_{ss}\). If on the other hand we start with C(0) = 0, administer a finite dose, assume that elimination clearance is constant, and let \({\int }_{0}^{\infty }{R}_{in}(t)dt=F\cdot \mathrm{Dose}\), where F is fraction absorbed, then integration of Eq. 1 yields \(C{L}_{E}=F\cdot \mathrm{Dose}/{\int }_{0}^{\infty }C(t)dt=F\cdot \mathrm{Dose}/\mathrm{AUC}\). This well-known relation is independent of dosing pattern. In particular, it does not depend on any “clearance” processes associated with absorption into the systemic circulation, as suggested by Benet and Sodhi (4).

A final observation with regard to KCL (mass balance) is that it need not apply only to nodes but it may also apply to regions (8,9). For a pharmacokinetic example, the rate of change of amount of drug in an organ is equal to the rate of arterial flow of drug into the organ minus the rate of venous flow of drug out, minus the rate of elimination of drug from the organ, even though concentrations may vary geographically within the organ. (Lymph flow is assumed negligible.) We will return to this point later.

The Parallel Rule

Consider a single node, or compartment in a pharmacokinetic system as illustrated in Fig. 1b. Let the volume of that node be denoted by V, and assume two independent parallel clearance processes, CL1 and CL2 emanating from the node. Then, according to KCL, the total clearance for drug leaving the node is

$$C{L}_{\mathrm{tot}}=C{L}_{1}+C{L}_{2}$$
(2)

Now define the rate constants for the individual processes, \({k}_{1}=C{L}_{1}/V\) and \({k}_{2}=C{L}_{2}/V\). Then the rate constant for the combined processes in parallel is

$${k}_{\mathrm{tot}}=C{L}_{\mathrm{tot}}/V=(C{L}_{1}+C{L}_{2})/V={k}_{1}+{k}_{2}$$
(3)

Equations 2 and 3 are equivalent to Eqs. 6 and 8 of Benet and Sodhi (4). A familiar example is when total body elimination is due to renal (R) and hepatic (H) processes operating in parallel from the common plasma compartment. Then, \(C{L}_{E}=C{L}_{R}+C{L}_{H}\) and \({k}_{E}={k}_{R}+{k}_{H}\).

Rules for Processes in Sequence

In circuit theory, parallel processes are complemented by in series processes, so it is tempting to assume that such complementarity also exists in pharmacokinetics, and Benet and Sodhi have argued as such. However, Korzekwa and Nagar have demonstrated that such translation is not always possible (5). Here, we further pursue the latter authors’ argument.

We begin by paraphrasing Eqs. 7 and 9 of Benet and Sodhi for two “in series” processes: \(1/C{L}_{\mathrm{tot}}=1/C{L}_{1}+1/C{L}_{2}\) and \(1/{k}_{\mathrm{tot}}=1/{k}_{1}+1/{k}_{2}\) (4). These two equations will generally not hold at the same time, unless the volume terms associated with the two processes are identical. It seems however that there should be models for which either one is true. Figure 2a and b illustrate such models. Both models have two compartments in sequence, with the first compartment (“1”) having input rate Rin(t), and the second compartment (“2”) having elimination clearance CLE. The two compartments have respective volumes V1 and V2. The model in Fig. 2a, which shall be called the “series model,” includes a completely reversible bidirectional “exchange” clearance term, \(C{L}_{1\leftrightarrow 2}\). The model in Fig. 2b will be called the “relay” model; in this model, transfer from 1 to 2 is unidirectional and its associated clearance is denoted by \(C{L}_{1\to 2}\).

Fig. 2
figure 2

Models of in sequence pharmacokinetics processes, with differing clearance properties between compartments 1 and 2. a “Series” model with completely reversible clearance between 1 and 2. b “Relay” model with unidirectional clearance from 1 to 2. c General model with non-negative but not necessarily equal clearances between 1 and 2 (5)

Full size image

The mass balance equations for the concentrations in 1 and 2 for the series model of Fig. 2a are

$${V}_{1}\frac{d{C}_{1}}{dt}={R}_{in}(t)-C{L}_{1\leftrightarrow 2}{C}_{1}+C{L}_{1\leftrightarrow 2}{C}_{2}$$
(4a)
$${V}_{2}\frac{d{C}_{2}}{dt}=C{L}_{1\leftrightarrow 2}{C}_{1}-C{L}_{1\leftrightarrow 2}{C}_{2}-C{L}_{E}{C}_{2}$$
(4b)

When Rin is constant, the system settles to a stationary state with time derivatives vanishing, leading to the steady state solutions

$${C}_{1,ss}=\left(\frac{1}{C{L}_{1\leftrightarrow 2}}+\frac{1}{C{L}_{E}}\right){R}_{in}$$
(5a)
$${C}_{2,ss}={R}_{in}/C{L}_{E}$$
(5b)

The rate of input into 1 is Rin; the net rate of transfer between 1 and 2 is

$$C{L}_{1\leftrightarrow 2}({C}_{1,ss}-{C}_{2,ss})=C{L}_{1\leftrightarrow 2}\left(\frac{1}{C{L}_{1\leftrightarrow 2}}+\frac{1}{C{L}_{E}}-\frac{1}{C{L}_{E}}\right){R}_{in}={R}_{in}$$
(6a)

and the rate of elimination from 2 is

$$C{L}_{E}{C}_{2,ss}=C{L}_{E}({R}_{in}/C{L}_{E})={R}_{in}$$
(6b)

i.e., flows of drug in, through, and out the system are equal at steady state, as they must be since there are no parallel elimination pathways in this model. Taking compartment 1 as the reference, the “total” clearance from 1 is

$$CL_{\mathrm{tot},\mathrm{series}}=\frac{R_{in}}{C_{1,ss}}=\left(\frac1{CL_{1\leftrightarrow2}}+\frac1{CL_E}\right)^{-1}=\frac{CL_{1\leftrightarrow2}CL_E}{CL_{1\leftrightarrow2}+CL_E}$$
(7a)

or equivalently,

$$\frac1{CL_{\mathrm{tot},\mathrm{series}}}=\frac1{CL_{1\leftrightarrow2}}+\frac1{CL_E}$$
(7b)

which is compatible with Benet and Sodhi’s Eq. 7, and with it the series rule derived from Kirchhoff’s laws (3).

For a nonsteady input, it is straightforward to show by integrating Eqs. 4a and 4b over all time and assuming zero initial drug in the two compartments, that

$$\frac{\int_0^\infty R_{in}(t)dt}{\int_0^\infty C_1(t)dt}=\left(\frac1{CL_{1\leftrightarrow2}}+\frac1{CL_E}\right)^{-1}=CL_{\mathrm{tot},\mathrm{series}}$$
(8a)

and

$$\frac{{\int }_{0}^{\infty }{R}_{in}(t)dt}{{\int }_{0}^{\infty }{C}_{2}(t)dt}=C{L}_{E}$$
(8b)

Now CLE is a “direct” clearance since it represents direct elimination from 2, whereas \(C{L}_{\mathrm{tot},\mathrm{series}}\) represents transport of drug from 1 to the elimination site through an intermediate compartment, i.e., 2. The term \(C{L}_{\mathrm{tot},\mathrm{series}}\) is what this author has previously called a “generalized clearance” (10). This distinction will be reintroduced in the later discussion of oral absorption.

We now calculate the mean residence times in 1, 2, and the whole system, tot. There are several ways to do this (11); here, we divide amounts by flows at steady state. Thus

$$MR{T}_{1}={V}_{1}{C}_{1,ss}/{R}_{in}={V}_{1}\left(\frac{1}{C{L}_{1\leftrightarrow 2}}+\frac{1}{C{L}_{E}}\right)$$
(9a)
$$MR{T}_{2}={V}_{2}{C}_{2,ss}/{R}_{in}=\frac{{V}_{2}}{C{L}_{E}}$$
(9b)

and

$$MRT_{\mathrm{tot},\mathrm{series}}=MRT_1+MRT_2=V_1\left(\frac1{CL_{1\leftrightarrow2}}+\frac1{CL_E}\right)+\frac{V_2}{CL_E}=\frac{V_1}{CL_{1\leftrightarrow2}}+\frac{V_1+V_2}{CL_E}$$
(9c)

Notice that MRT2 as presented here is the mean time a drug molecule spends in 2, whereas \(MR{T}_{\mathrm{tot}}\) is the mean time that a molecule will spend in the whole system before it is eliminated from 2. Defining the rate constants \({k}_{1}=C{L}_{1\leftrightarrow 2}/{V}_{1}\), \({k}_{2}=C{L}_{E}/({V}_{1}+{V}_{2})\) and \({k}_{\mathrm{tot}}=1/MR{T}_{\mathrm{tot}}\) yields\(1/{k}_{\mathrm{tot}}=1/{k}_{1}+1/{k}_{2}\), which superficially resembles Benet and Sodhi’s Eq. 9. Unfortunately, k2 is not a “proper” rate constant, which would be derived as the clearance emanating from a single compartment divided by the volume of that compartment.

Analogous calculations for the relay model of Fig. 2b can be carried out. Here, the mass balance equations are

$${V}_{1}\frac{d{C}_{1}}{dt}={R}_{in}(t)-C{L}_{1\to 2}{C}_{1}$$
(10a)
$${V}_{2}\frac{d{C}_{2}}{dt}=C{L}_{1\to 2}{C}_{1}-C{L}_{E}{C}_{2}$$
(10b)

At steady state, with constant Rin,

$${C}_{1,ss}={R}_{in}/C{L}_{1\to 2}$$
(11a)
$${C}_{2,ss}={R}_{in}/C{L}_{E}$$
(11b)

and decidedly, \({R}_{in}\ne {(1/C{L}_{1\to 2}+1/C{L}_{E})}^{-1}{C}_{1,ss}\), as would be predicted by the series rule. In fact, clearance with respect to 1 is

$$C{L}_{\mathrm{tot},\mathrm{relay}}={R}_{in}/{C}_{1,ss}=C{L}_{1\to 2}$$
(12)

On the other hand,

$$MR{T}_{1}=\frac{{V}_{1}}{C{L}_{1\to 2}}$$
(13a)
$$MR{T}_{2}=\frac{{V}_{2}}{C{L}_{E}}$$
(13b)
$$MR{T}_{\mathrm{tot},\mathrm{relay}}=\frac{{V}_{1}}{C{L}_{1\to 2}}+\frac{{V}_{2}}{C{L}_{E}}$$
(13c)

the last of which is congruent to \(1/{k}_{\mathrm{tot}}=1/{k}_{1}+1/{k}_{2}\), with proper rate constants \({k}_{1}=C{L}_{1\to 2}/{V}_{1}\) and \({k}_{2}=C{L}_{E}/{V}_{2}\).

The series and relay models are special cases of the more general model of Korzekwa and Nagar (5), in which nonnegative but possibly different clearance terms, \(C{L}_{1\to 2}\) and \(C{L}_{2\to 1}\) (see Fig. 2c), are associated with mass transfer between compartments 1 and 2. The two clearances might differ, for example, when active transporters are involved in drug influx and/or efflux. Analyzing as above, the following results are obtained:

$${C}_{1,ss}={R}_{in}\left(\frac{C{L}_{2\to 1}+C{L}_{E}}{C{L}_{1\to 2}C{L}_{E}}\right)$$
(14a)
$${C}_{2,ss}={R}_{in}/C{L}_{E}$$
(14b)
$$CL_{\mathrm{tot}}=R_{in}/C_{1,ss}=\frac{CL_{1\rightarrow2}CL_E}{CL_{2\rightarrow1}+CL_E}$$
(14c)
$$MRT_{\mathrm{tot}}=V_1\left(\frac{CL_{2\rightarrow1}+CL_E}{CL_{1\rightarrow2}CL_E}\right)+\frac{V_2}{CL_E}$$
(14d)

Equation 14c can also be obtained by adapting Cleland’s partitioning analysis (5,12). These expressions reduce to the series results when \(C{L}_{1\to 2}=C{L}_{2\to 1}=C{L}_{1\leftrightarrow 2}\), and the relay results when \(C{L}_{2\to 1}=0\).

The in sequence models described above are cast in terms of “whole” concentrations, and corresponding “whole” clearance and volume terms. With some effort, the models can be recast in terms of unbound concentrations, clearances, and volumes. Doing so is conceptually most important for the series model, since reversibility of transport should refer to unbound drug. (We thank a reviewer for pointing this out.)

Applications

Models of Elimination from the Liver

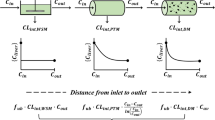
Because it is an important organ of elimination by metabolism and biliary excretion, clearance from the liver has been the subject of extensive experimental and theoretical investigations over the past several decades. Theoretical approaches have been based primarily on chemical reactor models, including the well stirred model (WSM), the parallel tube model (PTM), and the dispersion model (DM), where WSM and PTM are limiting cases of DM (13,14,15,16,17,18,19).

Experiments have been conducted with isolated perfused rat livers (18,19,20). In one set of experiments, a bolus of an inert tracer is introduced into the arterial stream, and tracer concentration is monitored as a function of time in the venous output. Analyses of the experimental residence time distributions of the inert tracers in the liver, which depend on hepatic blood flow, QH, conclude that DM best describes the data (19). In a second set of experiments, a constant concentration of drug, \({C}_{\mathrm{in}}\), is delivered into the arterial stream, and the steady state venous concentration of drug, \({C}_{\mathrm{out}}\), is measured (18,20). The extraction ratio, \(ER=({C}_{\mathrm{in}}-{C}_{\mathrm{out}})/{C}_{\mathrm{in}}\) is then determined, followed by the hepatic clearance, \(C{L}_{H}=ER\cdot {Q}_{H}\). As reviewed by Sodhi et al. (20), virtually all evidence gathered for the second set of experiments favors WSM. Thus, the two types of experiments present conflicting conclusions.

Quantitatively, WSM predicts, for drugs not suffering permeability limitations, that

$$CL_H=\frac{fuCL_{\mathrm{int}}\;Q_H}{fuCL_{\mathrm{int}}+Q_H}$$
(15)

where fu is fraction unbound of the drug (21). In their recent papers (3,4), Benet et al. observed that this relation can be inverted to the form

$$\frac{1}{C{L}_{H}}=\frac{1}{{Q}_{H}}+\frac{1}{fuC{L}_{\mathrm{int}}}$$
(16)

which bears a striking resemblance to the series formula (Eq. 7a). The interpretation was that there are two processes in series that determine drug elimination, namely, hepatic blood flow and intrinsic clearance (metabolism and biliary excretion) acting on unbound drug. It was postulated, to paraphrase, that if one accepts the series analogy, then there is no need or possibility to discriminate among WSM, PTM, and DM using clearance data.

Unfortunately, this reasoning ignores the fact that not all drug is extracted as it passes through the liver. Instead, drug molecules partition between two parallel pathways, namely, the intrinsic clearance pathway and venous exit from the liver. The correct use of the Kirchhoff analogy is as follows. Drug enters the liver as an arterial “current,” \({i}_{\mathrm{in}}={Q}_{H}{C}_{\mathrm{in}}\). It then divides, at steady state, into an elimination current, \({i}_{\mathrm{elim}}=fuC{L}_{\mathrm{int}}{C}_{\mathrm{ave}}\), where \({C}_{\mathrm{ave}}\) is the volume averaged drug concentration in the liver micro-vessels, and a venous exit current \({i}_{\mathrm{out}}={Q}_{H}{C}_{\mathrm{out}}\). By KCL, \({i}_{\mathrm{in}}={i}_{\mathrm{elim}}+{i}_{\mathrm{out}}\), or

$$Q_HC_{\mathrm{in}}=fuCL_{\mathrm{int}}\;C_{\mathrm{ave}}+Q_HC_{\mathrm{out}}$$
(17)

The extraction ratio is

$$ER=\frac{i_{\mathrm{elim}}}{i_{\mathrm{in}}}=\frac{fuCL_{\mathrm{int}}\;C_{\mathrm{ave}}}{Q_HC_{\mathrm{in}}}=\frac{fuCL_{\mathrm{int}}\;C_{\mathrm{ave}}}{fuCL_{\mathrm{int}}C_{\mathrm{ave}}+Q_HC_{\mathrm{out}}}$$
(18)

and

$$CL_H=ER\cdot Q_H=\frac{fuCL_{\mathrm{int}}\;C_{\mathrm{ave}}\;Q_H}{fuCL_{\mathrm{int}}\;C_{\mathrm{ave}}+Q_H\;C_{\mathrm{out}}}$$
(19)

Inverting,

$$\frac{1}{C{L}_{H}}=\frac{1}{{Q}_{H}}+\frac{1}{fuC{L}_{int}}\left(\frac{{C}_{out}}{{C}_{ave}}\right)$$
(20)

Equations 19 and 20 revert to Eqs. 15 and 16 only when \({C}_{\mathrm{ave}}={C}_{\mathrm{out}}\), i.e., under WSM. It is therefore not possible to use arguments based on Kirchhoff’s laws to resolve the contradiction between the interpretation of the tracer experiments in terms of DM and the apparent success of WSM over other models in accounting for hepatic clearance of drugs. Related arguments are presented by Rowland et al. (6).

For PTM, \({C}_{\mathrm{ave}}=({C}_{\mathrm{in}}-{C}_{\mathrm{out}})/\mathrm{ln}({C}_{\mathrm{in}}/{C}_{\mathrm{out}})\), and using \(ER=({C}_{\mathrm{in}}-{C}_{\mathrm{out}})/{C}_{\mathrm{in}}\), it is found that

$$\frac1{CL_H}=\frac1{Q_H}+\frac1{fuCL_{\mathrm{int}}}\left[\frac{-(1-ER)\ln(1-ER)}{ER}\right]$$
(21)

Using Eqs. 16 and 20, and \(C{L}_{H}=ER\cdot {Q}_{H}\), the following formulas are derived for estimating intrinsic clearance given WSM and PTM:

$$\mathrm{WSM}:CL_{\mathrm{int}}=\frac{Q_H}{fu}\left[\frac{ER}{1-ER}\right]$$
(22)
$$\mathrm{PTM}:CL_{\mathrm{int}}=\frac{Q_H}{fu}\left[-\ln(1-ER)\right]$$
(23)

Constancy of estimated \(C{L}_{\mathrm{int}}\) following experimental variations of QH and/or fu and consequent changes in ER would provide evidence for the correctness of either model. Plots of the bracketed dimensionless functions of ER are presented in Fig. 3. For DM, a class of functions lying between those plotted is expected. It is recognized that Eq. 22 is equivalent to Eqs. 15 and 16, while Eq. 23 is a rearrangement of \(ER=1-\mathrm{exp}(fuC{L}_{\mathrm{int}}/{Q}_{H})\) from the literature (16,17).

Fig. 3
figure 3

Bracketed dimensionless functions of ER in Eqs. 22 and 23

Full size image

The above analyses can be extended to include the effects of slow drug permeation through hepatocyte membranes, and the contributions of luminal influx and efflux transporters. Here, these effects are summarized by net influx and efflux clearances, \(C{L}_{\mathrm{influx}}\) and \(C{L}_{\mathrm{efflux}}\), recognizing that in the absence of transporters, these two clearances will be equal. To account for these contributions, we replace \(C{L}_{int}\) in the preceding equations with

$$C{L}_{\mathrm{net}}=\frac{C{L}_{\mathrm{influx}}C{L}_{\mathrm{int}}}{C{L}_{\mathrm{efflux}}+C{L}_{\mathrm{int}}}$$
(24)

(NB this clearance acts on the unbound drug, as does \(C{L}_{\mathrm{int}}\) in the usual context.) Eq. 24 is congruent with Eq. 14c and with most of the literature, with the exception of the papers by Benet et al. (3,4), which postulate (in our notation), that

$$C{L}_{\mathrm{net}}=\frac{(C{L}_{\mathrm{influx}}-CL{^{\prime}}_{\mathrm{efflux}})C{L}_{\mathrm{int}}}{(C{L}_{\mathrm{influx}}-CL{^{\prime}}_{\mathrm{efflux}})+C{L}_{\mathrm{int}}}$$
(25)

i.e. the difference \(C{L}_{\mathrm{influx}}-CL{^{\prime}}_{\mathrm{efflux}}\) is lumped into a single net clearance coefficient acting on unbound drug. (A prime is placed on efflux clearance here to emphasize that it differs from \(C{L}_{\mathrm{efflux}}\) as modeled in Eq. 24.) Comparing Eqs. 24 and 25, we find that

$$CL{^{\prime}}_{\mathrm{efflux}}=C{L}_{\mathrm{influx}}\left[\frac{(C{L}_{\mathrm{efflux}}-C{L}_{\mathrm{influx}})/C{L}_{\mathrm{int}}}{1+(C{L}_{\mathrm{efflux}}-C{L}_{\mathrm{influx}})/C{L}_{\mathrm{int}}}\right]$$
(26)

The bracketed term can be positive, negative, or infinite, depending on the values of \(C{L}_{\mathrm{influx}}\), \(C{L}_{\mathrm{efflux}}\), and CLint, all of which are positive. It is therefore evident that Eq. 25 as a generalized expression is problematic.

We close this discussion by reiterating that the present use of KCL is nothing other than a rephrasing of the Fick principle (1), i.e., molar balance of drug considering all of its possible fates after entering the liver. We also recognize that there is strong evidence against uniformity of enzymatic processes and biliary excretion throughout the liver (16), so one may expect the presented models to be valid only in an average sense. Finally, other complications such as saturable, Michaelis–Menten enzyme, and transporter kinetics have not been addressed here. However, none of these caveats detract from the basic identification of KCL as a statement of molar balance.

Oral Absorption

We first consider the simplest model of oral absorption, with first order drug absorption into the systemic circulation, where drug obeys first-order disposition, with no loss due to first pass absorption (F = 1). In this model, it is assumed that transport from the gut to the systemic circulation is unidirectional. The model therefore corresponds to the relay model scheme in Fig. 2b, with 1 being the gut and 2 the system circulation, with corresponding volumes of distribution \({V}_{1}={V}_{\mathrm{gut}}\) and \({V}_{2}={V}_{\mathrm{sys}}\). The absorption (a) and elimination (e) clearances are \(C{L}_{1\to 2}=C{L}_{a}\) and \(C{L}_{E}=C{L}_{e}\), and the corresponding rate constants are \({k}_{a}=C{L}_{a}/{V}_{\mathrm{gut}}\) and \({k}_{e}=C{L}_{e}/{V}_{\mathrm{sys}}\). The well known time course for systemic drug concentration, \({C}_{sys}(t)\) following a “bolus” dose to the gut, \({R}_{in}(t)={\mathrm{Dose}}_{\mathrm{oral}}\cdot \delta (t)\), where \(\delta (t)\) is the Dirac delta function, is (22)

$$C_{\mathrm{sys},\mathrm{relay}}(t)=\frac{{\mathrm{Dose}}_{\mathrm{oral}}\cdot k_a}{V_{\mathrm{sys}}}\left(\frac{e^{-k_et}-e^{-k_at}}{k_a-k_e}\right),t>0$$
(27)

This expression (the Bateman function) follows from integrating Eqs. 10. By the usual \({\mathrm{Dose}}_{\mathrm{oral}}/AU{C}_{\mathrm{sys}}\) calculation, we arrive at \({CL}_{e}={k}_{e}{V}_{\mathrm{sys}}\), as expected.

For later purposes, we also calculate \({\mathrm{Dose}}_{\mathrm{oral}}/AU{C}_{\mathrm{gut},\mathrm{relay}}\). Integrating Eq. 10a alone, we have \({C}_{\mathrm{gut},\mathrm{relay}}(t)=({\mathrm{Dose}}_{\mathrm{oral}}/{V}_{\mathrm{gut}}){e}^{-{k}_{a}t}\) and \({\mathrm{Dose}}_{\mathrm{oral}}/AU{C}_{\mathrm{gut},\mathrm{relay}}=C{L}_{a}\). This quantity, besides being the clearance of drug from the gut into to systemic circulation, is the generalized clearance from gut to final elimination from the circulation (10). (In this respect, \(C{L}_{a}=C{L}_{1\to 2}\) is also the generalized clearance from gut to circulation in the presently discussed model, where absorption is unidirectional).

For completeness, recall the result for mean residence time in the whole body (23)

$$MRT_{\mathrm{tot},\mathrm{relay}}=\frac{\int_0^\infty tC_{\mathrm{sys},\mathrm{relay}}(t)dt}{\int_0^\infty C_{\mathrm{sys},\mathrm{relay}}(t)dt}=\frac1{k_a}+\frac1{k_e}$$
(28)

The inverse rate constants are the mean times spent by drug in the gut and in the systemic circulation. Equation 28 is a direct analog of Eq. 13c, in which was \(MR{T}_{\mathrm{tot}}\) calculated by the steady state method.

Now consider the series model (Fig. 2a), with reversible drug transport between gut lumen and systemic circulation. We can use the same recent definitions, except to note that \(C{L}_{a}=C{L}_{1\leftrightarrow 2}\) and that we need to define a new “efflux” rate constant, \({k}_{\mathrm{eff}}=C{L}_{a}/{V}_{\mathrm{sys}}\). The equations for systemic and gut lumen concentrations feature nontrivial exponential decay eigenvalues and coefficients, so we shall not report them here. Of more interest are clearances and mean residence times, which are calculated using analogs of Eqs. 7–9:

$$CL_{\mathrm{sys},\mathrm{series}}={\mathrm{Dose}}_{\mathrm{oral}}/AUC_{\mathrm{sys},\mathrm{series}}$$
(29a)
$$CL_{\mathrm{gut},\mathrm{series}}={\mathrm{Dose}}_{\mathrm{oral}}/AUC_{\mathrm{gut},\mathrm{series}}={(1/CL_a+1/CL_e)}^{-1}$$
(29b)
$$MRT_{\mathrm{sys},\mathrm{series}}=V_{\mathrm{sys}}/CL_e=1/k_e$$
(29c)
$$MRT_{\mathrm{gut}.\mathrm{series}}=V_{\mathrm{gut}}(1/CL_a+1/CL_e)=1/k_a+V_{\mathrm{gut}}/CL_e$$
(29d)
$$MRT_{\mathrm{tot}.\mathrm{series}}=\frac{V_{\mathrm{gut}}}{CL_a}+\frac{V_{\mathrm{gut}}+V_{\mathrm{sys}}}{CL_e}=\frac1{k_a}+\frac1{k_e}+\frac{V_{\mathrm{gut}}}{CL_e}$$
(29e)

Typical estimates for \({V}_{\mathrm{gut}}\) are of order 100–250 mL (24), whereas \({V}_{\mathrm{sys}}\) is at least 2 L and can be orders of magnitude larger (25). The last term in Eq. 29e is therefore considerably smaller than the second term and can be practically ignored.

The present analysis shows that the expression \({(1/C{L}_{a}+1/C{L}_{e})}^{-1}\), which Benet and Sodhi claim to be the valid value of clearance in oral (or otherwise extravascular) delivery, is actually the generalized clearance from gut lumen to elimination, given the series model. In contrast to the relay model, there is no generalized clearance from gut to systemic circulation, since in the series model, there is also reverse transport from circulation to gut lumen. Finally, note that the present analysis would apply to other extravascular routes.

Extravascular Absorption and Bioavailability

Benet and Sodhi (4) note that there are examples of drugs whose dose corrected extravascular bioavailabilities exceed 100%. In particular, they cite a study by Grahnén et al. (26), in which the mean apparent oral bioavailability of cimetidine in human subjects, as determined by dose corrected AUC ratios, was 110.6%, whereas taking ratios of fractions recovered unchanged in the urine yielded a mean apparent bioavailability of 59.5%. While confidence intervals of these estimates were not reported, assume for now that they are narrow. Then, the pharmacokinetic system cannot be linear. If it was, then for any concentration-time relationship of drug in plasma, C(t), following a dose, Dose, the fraction excreted unchanged in the urine would be

$$fe=\frac1{\mathrm{Dose}}\int_0^\infty CL_RC(t)dt=\frac{CL_RAUC}{\mathrm{Dose}}$$
(30)

where CLR is pulled out of the integral because the system is linear. Denoting “extravascular” and “intravascular” by “ev” and “iv,”

$$\frac{fe_{ev}}{fe_{iv}}=\frac{{(AUC/\mathrm{Dose})}_{ev}}{{(AUC/\mathrm{Dose})}_{iv}}$$
(31)

since the CLR terms in the numerator and denominator cancel. Thus, assuming perfect measurement, the two techniques for assessing bioavailability should yield the same result; since they do not, the system is nonlinear. The left and right ratios in Eq. 31, multiplied by 100%, are denoted by Grahnén et al. as Ffe and FAUC (26).

Suppose now that renal elimination of unchanged drug contains a saturable secretory component, see for example Weiner and Roth (27). Then, CLR will be concentration dependent, in a decreasing manner, and it is not possible to pull it outside the integral in Eqs. 30, and 31 will not hold. When drug is at high concentrations, the fraction that is eliminated in the urine will decrease, and the contribution to the drug’s AUC will increase, so one should expect \({F}_{AUC}>{F}_{fe}\). Further, if FAUC measured at low doses is reasonably close to 100%, then it would not be surprising for FAUC to exceed 100% at higher doses where renal elimination is partially saturable.

In the Grahnén study, the i.v. bolus dose of cimetidine was 100 mg, while the oral doses were 100, 400, and 800 mg. The i.v. disposition showed a rapid distribution and a slower elimination phase, with no apparent saturability of elimination. During the elimination phase, plasma concentration was below 1 μg/ml. For oral dosing at 100 mg, the values of Ffe and FAUC were below 100 and approximately equal, suggesting linear pharmacokinetics. For the higher oral doses, however, FAUC was larger than Ffe in all but one case. Also, plots of plasma concentration in response to a 400-mg oral dose showed long exposures to drug near 2 μg/ml. Even higher and longer exposures would be expected given an 800 mg oral dose. Thus, saturable renal elimination is a potential explanation for the difference between Ffe and FAUC, and for FAUC exceeding 100%, even though Grahnén et al. claim dose independent pharmacokinetics. As a final note, a weak but visible negative correlation was observed between Ffe and FAUC for the higher oral doses (Fig. 3 of Grahnén et al.). This would be consistent with our explanation.

Discussion and Conclusion

This commentary has attempted to resolve certain disputes regarding the use of Kirchhoff’s laws in pharmacokinetics. Actually, Kirchhoff’s laws are not the real issue, since their physiological meanings are that concentrations are well defined (KVL) and that mass or molar balances hold (KCL). There is no dichotomy between Kirchhoff’s laws and differential equations, once it is realized that time derivatives of amounts can be considered “currents.” In the electrical circuit and more general engineering literatures, Kirchhoff’s laws are used to set up differential equations describing system behavior (8,9,28), and the same can hold true for pharmacokinetics. We note in passing that Kirchhoff’s laws apply also to nonlinear systems and even to systems whose properties change with time.

The real issue is how to treat in sequence processes. While Benet and coworkers treat them as series processes, Korzekwa and Nagar provide examples where the series rule does not hold, and we augment their case by presenting the limiting case of relay processes. All of these processes fit within the framework of Kirchhoff’s laws.

We conclude this commentary by providing non-pharmacokinetic analogies, which highlight the difference between series and relay processes. When two resistors are placed in series, the current flow is reduced compared to what it would be if either of the two resistors was exposed to the same voltage. The presence of the second resistor thus impinges on the current flow through the first resistor, and vice versa. Quantitatively, the resistances add. On the other hand, swimmers in a relay race will complete their legs with times that are not dependent on those of their teammates. Their times will add, however.