Background

Wavefront sensing, i.e., the detection of relative phase shifts in propagating waves provides essential information in imaging applications where the scattering process affects the phase of the probing wave. Examples which highlight the importance of being able to detect phase shifts of waves passing through transparent objects include imaging of unstained cells under the optical microscope and imaging of soft matter (e.g., DNA, viruses, proteins and other macromolecules, polymers, etc.) in the transmission electron microscope (TEM). In 1953, Frits Zernike received the Nobel Prize in Physics for the development of phase contrast microscopy, a technique which allows part of the phase information carried by a wave to be converted into an amplitude signal, making it detectable as part of the intensity variations in the image. In 1971, Dennis Gabor received the Nobel Prize in Physics for developing the holographic principle [1], a technique by which the phase of a wave could be extracted by post-processing images. Later, iterative [2, 3] and deterministic [4–7] mathematical formulations and associated computer algorithms were developed by which both phase and amplitude of a wave could be recovered from intensity measurements at different planes along the optic axis, a so-called focal series.

One very popular approach toward wavefront reconstruction from intensity measurements at different planes of focus is the transport of intensity equation (TIE) [5, 8] which, due to its simple mathematical formulation and straightforward computational implementation, has attracted much attention in research communities as diverse as cold atom clouds [9], digital optical holography [10], and medical X-ray imaging [11].

Many algorithms such as the fast Fourier transform [6], the finite element method [12, 13], multigrid methods [14], a special symmetrization approach [15], each requiring Neumann, Dirichlet, or periodic boundary conditions have been proposed and applied for solving the TIE.

For wavefront reconstruction from focal series of images, the high spatial frequency components of the phase are well-defined by the data, but the low spatial frequency components are largely determined by the boundary conditions, which are usually unknown. Gureyev et al. [16, 17] and later Zuo et al. [18] introduced hard-edge apertures or, more generally non-uniform illumination during the experiment and thus physically enforced Neumann boundary conditions, allowing orthogonal series expansion-based approaches to be used to solve the TIE. Such an approach to make the boundary conditions physically accessible may be feasible in some setups, but not generally. In the TEM, for example, the field of view is often so small that no aperture with perfectly abrupt edges exists, in particular not at atomic resolution.

There have been attempts to improve the recovery of low spatial frequency information in the context of the TIE by reformulating it as a total-variation optimization problem, [19, 20]; however, these approaches require a piecewise constant phase. Other approaches include the application of structured illumination [21]; the experimentally much more complicated interferometric setup [22]; or prior knowledge of the measurement variation [23]. Therefore the problem of faithfully recovering low spatial frequency components of arbitrarily shaped phases remains, at least for a very large range of applications of wave front sensing.

In this work, we propose a simple iterative algorithm, gradient flipping (GF), with an emphasis on objects that are non-periodic and non-piecewise linear. GF imposes sparsity on the gradient of the phase by either driving a certain percentage of the phase gradient to zero, or forcing all phase gradients below a certain positive threshold to zero. By combining the conventional Fourier method to solve the TIE with principles adapted from the charge-flipping algorithm in crystallography, GF determines boundary conditions on the phase, while preserving consistency with the higher frequencies of the experimental data.

In this research work, first the TIE and its conventional Fourier solution are introduced; then, the gradient-flipping algorithm is presented and it is demonstrated with simulations that the GF algorithm retrieves the boundaries and low spatial frequencies of two test objects. Furthermore, experimental results on a fly wing are presented in the experiment section; and, finally, conclusions are drawn.

The transport of intensity equation

The TIE is a second-order elliptical, non-separable, and inhomogeneous partial differential equation which relates the irradiance as well as the variation of the irradiance along the direction of propagation to a Laplacian-like function of the phase:

$$\vec{\nabla }_{ \bot } \cdot \left[ {I(\vec{r})\vec{\nabla }_{ \bot } \varphi (\vec{r}_{ \bot } )} \right] = -k\frac{{\partial I(\vec{r})}}{{\partial z}}$$
(1)

where k denotes the wave number of the incident radiation, and \(\vec {r}_\bot\) is a vector in the plane normal to the optic axis. \(\frac{\partial I\left( \vec {r}\right) }{\partial z}\) denotes the variation of intensity along the optical axis z. This quantity is most often approximated by the simple first-order finite difference approximation

$$\begin{aligned} \frac{\partial I\left( \vec {r} \right) }{\partial z} \approx \frac{ I\left( \vec {r}, +\Delta z \right) - I\left( \vec {r}, -\Delta z \right) }{2 \Delta z} \end{aligned}$$
(2)

Here \(\Delta z\) is a small distance along the optic axis. If the image \(I(\vec {r})\) is recorded in the exact focus of the imaging system, then \(I\left( \vec {r}, +\Delta z \right)\) and \(I\left( \vec {r}, -\Delta z \right)\) are images recorded under over-focus and under-focus condition, respectively. Note that \(I\left( \vec {r} \right)\) has to be non-zero, for this equation to have a well-defined solution.

Expression (1) can be rewritten in the following form

$$\begin{aligned} \varphi \left( \vec {r}_\bot \right) = -k \nabla ^{-2} \vec {\nabla }_\bot \cdot \frac{\vec {\nabla }_\bot \nabla ^{-2} \frac{\partial I\left( \vec {r}\right) }{\partial z}}{I\left( \vec {r} \right) }, \end{aligned}$$
(3)

where \(\nabla ^{-2} = (\vec {\nabla }_\bot \cdot \vec {\nabla }_\bot )^{-1}\). A detailed discussion on the validity and range of applicability of Eq. (3) can be found in [24].

The nature of this equation implies that boundary conditions must be applied to solve it. Assuming different boundary conditions will yield different solutions for the phase \(\varphi \left( \vec {r}_\bot \right)\). A number of different algorithms have been developed to solve the TIE (e.g., [6, 15, 16, 25–29]), many of which are based on the very popular approach by Paganin and Nugent [6] which makes use of the fact that

$$\begin{aligned} \nabla ^{-2} f\left( \vec {r}_\bot \right) = \mathcal {F}^{-1} \left\{ \left| \vec {q}_\bot \right| ^{-2} \mathcal {F} \left[ f\left( \vec {r}_\bot \right) \right] \right\}, \end{aligned}$$
(4)

where \(\mathcal {F}\) and \(\mathcal {F}^{-1}\) are the two-dimensional forward and inverse Fourier transform, respectively, and \(\vec {q}_\bot\) is the two-dimensional reciprocal space coordinate in the plane of \(f\left( \vec {r}_\bot \right)\). At \(|q_\bot | = 0\) this expression diverges, so at that reciprocal space point one can simply multiply by zero instead. This is a physically legitimate procedure, since this defines the mean value of the phase—a physically undefined quantity—as zero.

This expression is straightforward to implement computationally, since it makes the expression (3) fully deterministic. However, using discrete Fourier transforms periodic boundary conditions are implicitly imposed. Also for iterative approaches, such as finite element [12, 13] or multigrid [27] methods the boundary conditions must be specified and are often chosen to either be periodic, or of the Neumann type, or even both [27].

In the context of wavefront sensing, the investigated objects often have sparse phase gradients

$$\begin{aligned} \vec {G}\left( \vec {r}\right) = \vec {\nabla _\bot }\varphi \left( \vec {r} \right) =-k \frac{\vec {\nabla _\bot } \nabla ^{-2} \frac{\partial I\left( \vec {r}\right) }{\partial z}}{I\left( \vec {r} \right) }. \end{aligned}$$
(5)

This means that they contain areas where the phase is rather flat. Examples of such sparse objects include live cells in biological, biochemical, or biophysical applications, a large fraction of objects (e.g., nanoparticles) observed in the TEM, but also objects that extend well beyond the detected field of view, but have regions of constant optical thickness (e.g., the experimental example shown below).

Gradient flipping

Gradient flipping (GF), is based on the charge-flipping (CF) algorithm which was originally developed for X-ray crystallography [30] where it is very effective in finding sparse solutions of the charge density consistent with experimental diffraction data.

GF pads the input data \(I(\vec {r})\) with its mean value so that the padded image is twice as large along each of its two dimensions as the original image [31]. Also \(\partial I\left( \vec {r}\right) / \partial z\) is padded to the same size, with zeros around its perimeter. The data in the padded area are then iteratively updated such that the phase gradient within the area corresponding to the measurement either has a certain percentage driven to zero, or has the gradient in all pixels the absolute value of which is below a certain positive threshold minimized.

The GF algorithm iterates between \(\vec {G}(\vec {r})\) in Eq. 5 and the following expression for \(\partial I\left( \vec {r}\right) / \partial z\):

$$\begin{aligned} D\left( \vec {G}'\right) = \frac{-\vec {\nabla }\cdot I(\vec {r})\vec {G}'(\vec {r})}{k}, \end{aligned}$$
(6)

where gradient flipping is applied as

$$\begin{aligned} \vec {G}'\left( \vec {r_\bot }\right) = {\left\{ \begin{array}{ll} \vec {G}\left( \vec {r_\bot }\right) &{} \text{ if } \left\| \vec {G}\left( \vec {r_\bot }\right) \right\| _1 > \delta \\ -\beta \vec {G}\left( \vec {r_\bot }\right) &{} \text{ if } \left\| \vec {G}\left( \vec {r_\bot }\right) \right\| _1 \le \delta . \end{array}\right. } \end{aligned}$$
(7)

The parameter \(\beta\) is chosen slightly below 1, i.e., \(\beta = 0.97\) in order to improve convergence. Furthermore, \(\delta\) defines a threshold between 5 and 20 % of the maximum value of \(\Vert \vec {G}\left( \vec {r_\bot }\right) \Vert _1\), this proved to keep the balance between perturbation and algorithmic stability as suggested in [30].

At each iteration the left-hand side of (6) is updated with the experimental data \(dI^\mathrm{{exp.}}_z \left( \vec {r_\bot }\right)\) by

$$\begin{aligned} dI_z \left( \vec {r_\bot }\right) = {\left\{ \begin{array}{ll} D\left( \vec {G}'\right) &{} \text{ if } \vec {r_\bot } \in \text {padded area} \\ \mathcal {F}^{-1}\left[ h \mathcal {F}\left( D\left( \vec {G}'\right) \right) + \left( 1-h\right) \mathcal {F}\left( dI^\mathrm{{exp.}}_z \left( \vec {r_\bot }\right) \right) \right] &{} \text{ if } \vec {r_\bot } \in \text {experimental area}, \end{array}\right. } \end{aligned}$$
(8)

where h is defined in reciprocal space as

$$\begin{aligned} h \left( \vec {q}_\bot \right) = \exp \left( -R_{LP}^2 \left| \vec {q}_\bot \right| ^{-2} \right) . \end{aligned}$$
(9)

The mask h acts as a Gaussian low-pass filter for the flipped gradient \(\vec {G}'(\vec {r})\) with a characteristic length of \(2 \pi R_{LP}\). This updating rule thus preserves the high spatial frequencies from the measurements, which are generally well-defined by the experiments, and lets the low-frequency information, which is only weakly present in the measurements, be dictated by the gradient flipping.

\(dI_z \left( \vec {r}\right)\) is initialized with the experimental values \(dI^\mathrm{{exp.}}_z \left( \vec {r}\right)\) and zero-padded. Then it is fed into an iterative procedure which loops over the operations defined in expressions (3), (5), (7), and (8), feeding the updated \(dI_z \left( \vec {r_\bot }\right)\) again into expression (3). Convergence is reached when successive estimates of the phase are sufficiently similar. Figure 1 shows a flowchart of the proposed algorithm.

Fig. 1
figure 1

The flowchart of the proposed TIE-based algorithm

Full size image

Free parameters δ and R LP

A careful selection of the threshold parameter \(\delta\) is a matter of great importance owing to its role as a trade-off between stabilization and perturbation of the algorithm. The threshold is defined as \(\delta = \zeta \sigma,\) where \(\sigma\) is the standard deviation of the phase gradient and \(\zeta\) is a constant. As shown in Fig. 2, despite the variation of \(\sigma\) during the initial iterations, it remains almost constant throughout the rest of the proposed iterative algorithm. This confirms the eligibility of \(\sigma\) to be a reasonable basis for the optimum choice of \(\delta\). Following the suggestion of Oszlányi et al. [30], we chose the value of \(\zeta\) between 1.0 and 1.2.

Fig. 2
figure 2

Plot of \(\sigma\) as a function of iterations, an almost constant value of \(\sigma\) furnishes a basis for selecting optimum \(\delta\)

Full size image

The characteristic length scale of the mask h in (8), \(R_{LP}\), is the second free parameter in the proposed algorithm and is determined entirely from the experimental data by setting it to the value that minimizes \(\chi ^2\) in (10). The \(\chi ^2\) figure-of-merit is defined as,

$$\begin{aligned} \chi ^2 =\frac{\sum _{x,y,z} \left[ I^\mathrm{{sim.}}\left( \vec {r},z,R_{LP}\right) -I^\mathrm{{exp.}}\left( \vec {r},z,\right) \right] ^2}{\sum _{x,y,z} I^\mathrm{{exp.}}\left( \vec {r},z,\right) }, \end{aligned}$$
(10)

where the values of z being summed over all the under- and over-focus at which the experimental images have been recorded, and x and y span the area of those images. Furthermore, \(I^\mathrm{{sim.}}(\vec {r}_\bot ,R_{LP})\) are the images simulated from the phase \(\varphi (\vec {r},R_{LP})\) that has been reconstructed with \(R_{LP}\) and the amplitude \(A(\vec {r}) = \sqrt{I(\vec {r},z=0)}\). \(I^\mathrm{{exp.}}\left( \vec {r},z\right)\) denotes the experimental data.

Simulations

In this section the performance of GF is demonstrated on simulations of two specimens: the projection of a cube and a L-shaped membrane.

Projected cube

Images of a test object are simulated for a wavelength of \(\lambda = 500\) nm, a defocus step of \(\Delta f = 1\) mm, a numerical aperture of 0.3, and a pixel size of 1 μm. Figure 3 shows an under-focused, and an over-focused image, as well as the finite difference estimate of the intensity variation along the optical axis determined from those. The images were padded by a factor close to 2, i.e., from \(624 \times 624\) to \(1200 \times 1200\) pixels.

Fig. 3
figure 3

a Under-focused b Over-focused c Finite difference estimate of the intensity variation according (2)

Full size image

The threshold \(\delta\) was set to \(6.64\,e^{-4}\), corresponding to a \(\zeta\) of 1.2. From the graph in Fig. 4 it is apparent that \(\chi ^2\) is minimal for values of \(R_{LP}\) greater than 17.77 μm and \(R_{LP}\) is thus set to this value.

Fig. 4
figure 4

\(\chi ^2\) as a function of \(R_{LP}\)

Full size image

Figure 5b shows the retrieved phase by means of the proposed approach and Fig. 5a displays the original phase of the wave used to simulate the input data shown in Fig. 3. In Fig. 5c the boundaries of the original phase and its reconstruction are compared.

Fig. 5
figure 5

a Original phase. b Reconstructed phase by proposed method. c Line profile extracted along the red line in each of the phase maps

Full size image

L-shaped membrane

To further investigate the performance of the proposed algorithm for properly recovering also slowly varying phases, we constructed a phase object with the phase given by a continuous function that is not piecewise constant (Fig. 6a), namely the L-shaped membrane; this function can be obtained by the MATLAB expression ’membrane()’. Figure 6c shows the phase map retrieved by means of the FFT approach, which assumes periodic boundary conditions, while Fig. 6b shows the reconstruction obtained by the symmetrization method [15]. As clearly shown in Fig. 6d, the proposed algorithm yields a more accurate reconstruction than the aforementioned approaches. Furthermore, from Fig. 6d it is clear that GF retrieves the boundaries much better.

Fig. 6
figure 6

a Original phase obtained by the Matlab expression ’membrane()’, phase reconstructed by means of (b) the symmetrization method (Neumann boundary conditions), c the FFT approach (periodic boundary conditions), d and the approach proposed here. e Line profile extracted along the red line shown at the top of (a) in each of the phase maps

Full size image

For this reconstruction the parameter \(\delta\) has been set such that the number of pixels being flipped corresponded to one quarter of the total number of the pixels in the field of view. And \(R_{LP}\) has chosen to be 34.52 μm by minimizing \(\chi ^2\).

Experiment

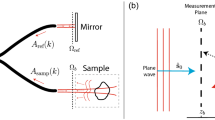
The GF algorithm is tested further using experimental data acquired from the simple optical setup shown in Fig. 7. The system comprised a laser with integrated collimator emitting green light at a wavelength of \(\lambda = 520\) nm, two lenses with a focal length of \(f = 150\) mm, an iris diaphragm, and a for constructing the new \(2048 \times 2048\) pixel CCD detector. The wing of a fly was used as a test object positioned at a distance r in front of the first lens, with \(f<r<2f\). The diaphragm was placed at the back focal plane of the first lens in order to limit the numerical aperture of the system to about 0.1. Images at the three focal planes \(z=-\Delta z\), \(z=0\), and \(z=+\Delta z\) were acquired by translating the camera along the optic axis with a defocus step of \(\Delta z = 1\) mm.

Fig. 7
figure 7

Experimental setup: the wing of a fly is imaged by a NA-limiting 4f system at a magnification of \(M \approx 1\). The focal series in Fig. 8 was acquired by shifting the detector by \(\pm 1\) mm

Full size image

All three images were dark-current corrected, and a gain reference image with no object in place was used for normalization. Since a difference in defocus leads to a difference in contrast between these three images and motivated by the fact that \(I(\vec {r},+\Delta z) + I(\vec {r},-\Delta z) \approx 2 I(\vec {r})\) the two defocused images \(I(\vec {r},\pm \Delta z)\) were registered to the focused image \(I(\vec {r})\) by iterating the following two steps until convergence:

  1. Step 1:

    Shift \(I(\vec {r},+\Delta z)\) to the position of the maximum of the cross correlation of that image with \(2 I(\vec {r})-I(\vec {r},-\Delta z)\), and

  2. Step 2:

    Shift \(I(\vec {r},-\Delta z)\) to the position of the maximum of the cross correlation of that image with \(2 I(\vec {r})-I(\vec {r},+\Delta z)\),

each time using the shifted defocused image from the previous iteration for constructing the new reference.

The under-focused and over-focused image, as well as \(dI^\mathrm{{exp.}}_z \left( \vec {r_\bot }\right)\) computed according to (8) are shown in Fig. 8. Setting \(\zeta = 1.2\) converged to a \(\delta\) value of \(5.22\times 10^{-5}\). Furthermore, the minimum of \(\chi ^2\) occurs at \(R_{LP} = 91.2\) μm (see Fig. 9). The algorithm was iterated for 20 epochs with the above-mentioned parameters.

Fig. 8
figure 8

a Under-focused image b Over-focused image c Finite difference estimate of the intensity derivative along the optical axis

Full size image
Fig. 9
figure 9

Plot of \(\chi ^2\) as function of \(R_{LP}\) (in \(\mu\)m)

Full size image

Figure 10 shows phase maps \(\varphi \left( \vec {r_\bot }\right)\) reconstructed by three different techniques: (a) the conventional FFT method applying (3) and (4), (b) the symmetrization mirror padding approach proposed by Volkov et al. [15], and (c) the GF scheme proposed here. For both the conventional FFT method (a), as well as the proposed GF algorithm (c) the experimental data were padded as described above to result in data of twice the original image dimensions.

Fig. 10
figure 10

Phase maps reconstructed by three different approaches: a the conventional FFT method (incl. padding), b the mirror padding scheme by Volkov et al. [15], and c our GF algorithm [same padding as for (a)]. d Diagonal line profiles extracted from each of the three reconstructions

Full size image

All three phase maps shown in Fig. 10 are consistent with the experimental data, but the applied boundary conditions differ. The reconstructed phase maps shown in Fig. 10a, b are unphysical, because in both cases the phase shift inside the wing drops below the phase shift in the empty area. The FFT reconstruction shown in Fig. 10a also features a severe overall phase slope in the empty area which cannot be deemed physical.

The line profiles across the reconstructed phase maps show good agreement between the three different reconstruction results for fine details, but they also highlight the large differences at low spatial frequencies.

Conclusion

In this work, we proposed a simple iterative algorithm, gradient flipping (GF), which imposes sparsity on the phase gradient by either driving a certain percentage of values to zero, or forcing all values below a certain positive threshold to zero. By combining the conventional Fourier method with these principles adapted from the charge-flipping algorithm in crystallography, GF determines boundary conditions on the phase, while preserving consistency with the higher frequencies of the experimental data.

It was shown with simulations and experiments of non-periodic and non-piecewise linear objects that these boundary conditions contribute to GF’S much improved lower spatial frequencies compared to that of the more conventional FFT method and symmetrization method.