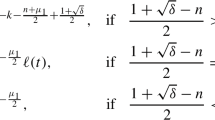Abstract
This paper is concerned with the Cauchy problem for semilinear wave equation with space-dependent scattering damping and combined nonlinearities. The blowup results of solution are established by introducing proper test functions. Moreover, upper bound lifespan estimates of a solution to the Cauchy problem with small initial values are derived. To the best of our knowledge, the results in Theorems 1.1–1.2 are new.
Similar content being viewed by others
1 Introduction and main results
In this work, we consider the following Cauchy problem of wave equation with space-dependent damping and combined nonlinearities:
where \(\mu >0\), \(\beta >1\), \(p>1\), \(q>1\), \(n\geq 2\). The compactly supported nonnegative initial values satisfy \((f,g)\in H^{1}(\mathbb{R}^{n})\times L^{2}(\mathbb{R}^{n})\) (\(n\geq 2\)) and
In addition, \(f(x)\), \(g(x)\not \equiv 0\).
The study of formation of singularity for semilinear wave equation has a long history (see detailed illustrations in [3, 5, 9, 11, 22–25, 27–30, 33, 34, 39–42] and the references therein). In fact, problem (1.1) originates from the following three problems:
and
Problem (1.3) is known as the Strauss conjecture (see [35]), which shows that the solution blows up in finite time when \(1< p\leq p_{S}(n)\) (\(n\geq 2\)) and \(p_{S}(1)=+\infty \) for \(n=1\), whereas the solution exists globally in time when \(p>p_{S}(n)\). Here \(p_{S}(n)\) is the Strauss critical exponent, which is the positive root of the quadratic equation
Problem (1.4) is known as the Glassey conjecture (see [6]), where the Glassey critical exponent is \(p_{G}(n)=\frac{n+1}{n-1}\). It is shown in [4] that the Cauchy problem of heat equation (1.5) possesses the Fujita critical exponent \(p_{F}(n) =1+\frac{2}{n}\).
Scholars investigated the blowup dynamics of a semilinear wave equation with damping term
where \(h(u_{t})=\frac{\mu}{(1+t)^{\beta}}u_{t}\), \(\frac{\mu}{(1+|x|)^{\beta}}u_{t}\) (\(\mu >0\), \(\beta \in \mathbb{R}\)) and \(f(u,u_{t})=|u|^{p},|u_{t}|^{p}\), \(|u_{t}|^{p}+|u|^{q}\) (\(p>1\), \(q>1\)). When the critical exponent of the damped wave equation (1.6) is related to the Srauss exponent \(p_{S}(n)\) or the Glassey exponent \(p_{G}(n)\), we say that the equation behaves like that of the wave equation. This means that the damping term in the equation makes no effect. When the critical exponent is related to the Fujita exponent \(p_{F}(n)\), we say that the damping term makes an effect. According to the range of β, we use the following table to show the effect of damping terms (we can see it in [18, 21]).
Blowup and global existence results in connection with the semilinear wave equation with time-dependent damping \(\frac{\mu}{(1+t)^{\beta}}u_{t} \) are established in [1, 13, 16, 20, 31, 37, 38]. Energy estimates of solution to semilinear wave equation with space-dependent damping are derived in [14, 15, 36]. Nishihara et al. [32] investigated the blowup and global existence for a semilinear wave equation with space- and time-dependent damping. In the present paper, we mainly concentrate on the problem with space-dependent scattering damping case \(\frac{\mu}{(1+|x|)^{\beta}}u_{t}\) (\(\beta >1\)). Namely, the behavior of a solution is similar to that of the wave equation in this case. Lai and Tu [17] considered upper bound lifespan estimates of a solution to the wave equation with space-dependent damping \(\frac{\mu}{(1+|x|)^{\beta}}u_{t}\) (\(\beta >2\), \(n\geq 2\)) and \(f(u,u_{t})=|u|^{p}\), \(|u_{t}|^{p}\) for both subcritical and critical exponents. Especially, for the power nonlinearity \(|u|^{p}\) (\(\frac{n}{n-1}< p\leq p_{S}(n)\)) and derivative-type nonlinearity \(|u_{t}|^{p}\) (\(1< p\leq p_{G}(n)\)), they obtained the same critical exponents and upper bound lifespan estimates of solutions as in the situation without damping by using the test function method. Lai et al. [17] obtained upper bound lifespan estimate of solution when \(f(u,u_{t})=|u|^{p}\) and \(\beta >1\). Meanwhile, the lifespan estimate for the case \(1< p<\frac{n}{n-1}\) was also improved.
We are in the position to present some known results related to the semilinear wave equation (1.6) with combined nonlinearities \(f(u,u_{t})=|u_{t}|^{p}+|u|^{q}\). Han and Zhou [10] obtained an upper bound lifespan estimate of solution to the Cauchy problem without damping term by constructing a proper test function and solving ordinary differential inequalities. Hidano et al. [12] established the sharp lower bound lifespan estimate of a solution to the problem. Dai et al. [2] derived the sharp lifespan estimate of a solution to the nonlinear wave equation when \(p\geq q_{S}(n)\) and \(q=q_{S}(n)\) (\(n=2, 3\)), where \(q_{S}(n)\) is the Strauss critical exponent of the semilinear wave equation with power nonlinearity \(|u|^{q}\). Lai and Takamura [19] illustrated blowup results and upper bound lifespan estimates of a solution to the problem with time-dependent damping term \(\frac{\mu}{(1+t)^{\beta}}u_{t}\) (\(\beta >1\)) by using a multiplier and iteration argument. Blowup of a solution to the problem with scale-invariant damping \(\frac{\mu}{ 1+t }u_{t} \) was investigated by applying test function approach (see [7, 8]). Liu and Wang [26] consider problem (1.1) for the more general nonlinearity \(f(u,u_{t})=c_{1}|u_{t}|^{p}+c_{2}|u|^{q}\) on asymptotically Euclidean manifolds. Upper bound lifespan estimates of solution with different values of \(c_{1}\) and \(c_{2}\) are obtained. In addition, the existence of a solution is established.
Inspired by the works [10, 17, 19, 21], we consider blowup and upper bound lifespan estimates of a solution to problem (1.1). To our best knowledge, the blowup for the space-dependent damped wave equation with combined nonlinearities has not been discussed yet. The purpose of this paper is to fill this gap. We establish upper bound lifespan estimates of a solution. It is worth mentioning that in this paper, we employ the test function method different from the technique in [10, 19]. We bear in mind that lifespan estimates of solutions to the problems with space-dependent damping \(\frac{\mu}{(1+|x|)^{\beta}}u_{t}\) (\(\beta >2\)) and \(f(u,u_{t})=|u|^{p}, |u_{t}|^{p}\) are investigated in [21]. Thanks to the work [17], we obtain upper bound lifespan estimates of a solution to problem (1.1) with \(\frac{\mu}{(1+|x|)^{\beta}}u_{t}\) (\(\beta >1\)) and combined nonlinearities \(|u_{t}|^{p}+|u |^{q}\) (see the new results in Theorems 1.1–1.2 in this paper).
The main results in this paper are described as follows.
Theorem 1.1
Let \(n\geq 2\), \(\mu >0\), and \(\beta >1\), and let f and g satisfy (1.2). Suppose that problem (1.1) has an energy solution u such that
Then we have the following lifespan estimates of solution:
where C is a positive constant.
Theorem 1.2
Let \(n\geq 2\), \(\mu >0\), and \(\beta >1\), and let f and g satisfy (1.2). Suppose that problem (1.1) has an energy solution u such that
Then the lifespan estimates of solution satisfy
Remark 1.1
In Theorem 1.1, for \(\max \{1+\frac{1}{2(n-1)},\frac{2}{n-1}\}< p<\frac{n+1}{n-1}\) and \(\frac{n}{n-1}< q<2p-1\), we have
where we have used the fact \(2p-1<1+\frac{4}{(n-1)p-2}\) for \(p<\frac{n+1}{n-1}\). When \(\max \{1,\frac{2}{n-1}\}< p<\frac{n+1}{n-1}\) and \(\max \{2p-1,\frac{n}{n-1}\}< q<1+\frac{4}{(n-1)p-2}\), we obtain
We use Fig. 1 to make a simple description for \(n=2\).
The case \(n=2\) in Theorem 1.1
For \(p,q\in B\cup C \cup E\), we have the first lifespan estimate in (1.7). For \(p,q\in A\cup B\cup C\cup D\), we obtain the second lifespan estimate in (1.7), whereas for \(p,q\in B\), the second lifespan estimate in (1.7) is better than the first one. For \(p,q\in C\), the first lifespan estimate in (1.7) is better than the second one.
Remark 1.2
In Theorem 1.2, for \(1< q< p<\frac{n+1}{n-1}\) or \(\frac{n+1}{n-1}< p\) (\(n=2,3\)), \(\frac{n+1}{n-1}< p<\frac{n-1}{n-3}\) (\(n>3\)), \(1< q<\frac{2p}{(n-1)(p-1)}\), we have
When \(1< p< q<\frac{n+1}{n-1}\), we have
Similarly, we use Fig. 2 to illustrate the specific comparison for \(n=2\).
The case \(n=2\) in Theorem 1.2
For \(p,q\in F\cup G\cup H\), we obtain the first lifespan estimate in (1.8). For \(p,q\in G\cup H\cup I\), we have the second lifespan estimate in (1.8). For \(p,q\in G\), the first lifespan estimate in (1.8) is better than the second one, and for \(p,q\in H\), the second lifespan estimate in (1.8) is better than the first one.
Remark 1.3
Let \(n\geq 2\), \(\mu >0\), and \(\beta >1\). The assumptions in Theorems 1.1 and 1.2 hold. Combining the results in [17, 21] with (1.7) and (1.8), we derive
where
\(p_{S}(n)\) denotes the Strauss critical exponent, and \(p_{G}(n)\) represents the Glassey critical exponent.
Throughout this paper, C denotes a positive constant independent of ε, which may vary from line to line.
2 Preliminaries
In this section, we present several basic definitions and lemmas.
Definition 2.1
A function u is called an energy solution of problem (1.1) on \([0,T)\) if
satisfies \(u(0,x)=\varepsilon f(x)\) and \(u_{t}(0,x)=\varepsilon g(x)\). Moreover, we have
where \(\varphi (t,x)\in C_{0}^{\infty}([0,T)\times \mathbb{R}^{n})\) and \(T\in (1,T(\varepsilon ))\). Here \(T(\varepsilon )\) represents the upper bound lifespan estimate of a solution to problem (1.1), which satisfies
Definition 2.2
The cutoff function \(\eta (t)\in C^{\infty}([0,\infty ))\) is defined by
which satisfies \(|\eta '(t)|,|\eta ''(t)|< C\). Let \(\eta _{T}(t)=\eta (t/T)\) and \(\gamma >1\). We have that
Lemma 2.3
(Lemma 3.1 in [21])
If \(\beta >0\), then for all \(\alpha \in \mathbb{R}\) and a fixed constant R, there exists a positive constant C such that
Lemma 2.4
(Lemma 2.5 in [17])
Let \(n\geq 2\), \(\beta >1\), and \(\mu \geq 0\). Then the equation
admits a solution \(\phi (x)\). Moreover, there exists a constant \(C_{1}\in (0,1)\) such that
Let \(\psi (t,x)=e^{-t}\phi (x)\). Then we have
3 Proof of Theorem 1.1
In this section, we illustrate the proof of Theorem 1.1.
3.1 Case \(p\geq q\)
First, we choose \(\varphi (t,x)=\eta _{T}^{2q'}\) as the test function, where \(q'\) satisfies \(\frac{1}{q}+\frac{1}{q'}=1\). From (2.1) we obtain
where we have used the fact that \(\partial _{t}\eta _{T}(0)=0\) and \(\eta _{T}(T)=0\).
Using the Hölder and Young inequalities, we have that for \(q>\frac{n}{n-1}\),
Combining (3.1)–(3.3), we deduce
where \(C_{1}(f,g)=C(\int _{\mathbb{R}^{n}}g(x)\,dx+\int _{\mathbb{R}^{n}} \frac{\mu}{(1+|x|)^{\beta}}f(x)\,dx)\).
Let \(\varphi (t,x)=\partial _{t}\Phi _{1}(t,x)\), where \(\Phi _{1}(t,x)=-\eta _{T}^{2q'}\psi (t,x)=-\eta _{T}^{2q'}e^{-t} \phi (x)\), and \(\psi (t,x)\) is defined in Lemma 2.4. Applying (2.1), we have
where we have employed the fact \(\partial _{t}\Phi _{1}(0,x)=\phi (x)\). Since
and
we have
It follows that
where we have applied Lemma 2.4.
We are in the position to derive the estimates for \(I_{3}\), \(I_{4}\), and \(I_{5}\).
Employing Lemma 2.3 leads to
A direct calculation gives rise to
which implies
where \(C_{2}(f,g)=C(\int _{\mathbb{R}^{n}}g(x)\phi (x)\,dx+\int _{\mathbb{R}^{n}}(1+ \frac{\mu}{(1+|x|)^{\beta}}) f(x)\phi (x)\,dx)\).
Combining (3.4) and (3.9) and using the assumptions \(\max \{1, \frac{2}{n-1}\}< p<\frac{4n-2}{n-1}\), \(\frac{n}{n-1}< q<1+\frac{4}{(n-1)p-2}\), and \(q\leq p\), we obtain
On the other hand, according to (3.5), we derive
Taking into account (3.5) and (3.10)–(3.12) and using the Young inequality, we have
Therefore, for \(1< p<\frac{n+1}{n-1}\) and \(1< q\leq p\), we have that
3.2 Case \(p< q\)
Taking \(\varphi (t,x)=\eta _{T}^{2p'}\) in (2.1) yields
Applying the fact that \(p< q\) and \(q>\frac{n}{n-1}\), we deduce
Combining (3.14)–(3.16), we get
We set \(\varphi (t,x)=\partial _{t}\Phi _{2}(x,t)\) in (2.1), where \(\Phi _{2}(x,t)=-\eta _{T}^{2p'}\psi (x,t)=-\eta _{T}^{2p'}e^{-t} \phi (x)\). Therefore we have
Similarly to the deduction in (3.9), we obtain
From (3.17) and (3.19) the conditions \(\max \{1, \frac{2}{n-1}\}< p<\frac{4n-2}{n-1}\) and \(\max \{p,\frac{n}{n-1}\}< q<1+\frac{4}{(n-1)p+2}\) lead to
By (3.18) we have
Combining (3.18) and (3.20)–(3.22), for \(1< p<\min \{q,\frac{n+1}{n-1}\}\) and \(q>1\), we have
This completes the proof of Theorem 1.1.
4 Proof of Theorem 1.2
Taking \(\varphi (t,x)=\eta _{T}^{2k}\psi (t,x)\) in (2.1), where \(k=\max \{p',q'\}\) and \(\psi (t,x)=e^{-t}\phi (x)\), we obtain
A direct calculation shows that
and
It follows that
Employing (2.2), we have
Combining (4.1)–(4.4), we deduce
On the other hand, we take \(\varphi (t,x)=\partial _{t}\Phi (t,x)\) in (2.1), where \(\Phi (t,x)=-\eta _{T}^{2k}\psi (t,x)=-\eta _{T}^{2k}e^{-t}\phi (x)\). Similarly to the derivation in (3.5) and (3.18), we acquire
It follows that
Similarly, we conclude that
Employing the fact \(\partial _{t}\Phi =\eta _{T}^{2k}\psi -2k\eta _{T}^{2k-1}\partial _{t} \eta _{T}\psi \geq \eta _{T}^{2k}\psi >0\) and (4.5)–(4.9), we have
which implies
for \(p>1\) (\(n=2,3\)), \(1< p<\frac{n-1}{n-3}\) (\(n>3\)), and \(1< q<\frac{2p}{(n-1)(p-1)}\).
On the other hand, (4.2)–(4.4) yield
From (4.1) and (4.11)–(4.13) we obtain
which implies
for \(p>1\) and \(1< q<\frac{n+1}{n-1}\). The proof of Theorem 1.2 is finished.
Availability of data and materials
Data sharing not applicable to this paper as no data sets were generated or analyzed during the current study.
References
D’Abbicco, M., Lucente, S., Reissig, M.: A shift in the Strauss exponent for semilinear wave equations with a not effective damping. J. Differ. Equ. 259, 5040–5073 (2015)
Dai, W., Fang, D.Y., Wang, C.B.: Global existence and lifespan for semilinear wave equations with mixed nonlinear terms. J. Differ. Equ. 267, 3328–3354 (2019)
Du, Y., Metcalfe, J., Sogge, C.D., Zhou, Y.: Concerning the Strauss conjecture and almost global existence for nonlinear Dirichlet-wave equations in 4-dimensions. Commun. Partial Differ. Equ. 33(7–9), 1487–1506 (2008)
Fujita, H.: On the blowing up of solutions of the Cauchy problem for \(u_{t}=\Delta u+u^{1+\alpha}\). J. Fac. Sci., Univ. Tokyo, Sect. I 13, 109–124 (1966)
Georgiev, V., Lindblad, H., Sogge, C.D.: Weighted Strichartz estimates and global existence for semilinear wave equations. Am. J. Math. 119, 1291–1319 (1997)
Glassey, R.T.: Mathematical reviews to “Global behavior of solutions to nonlinear wave equations in three space dimensions”. Sideris, Comm. Part. Diff. Equa., (1983)
Hamouda, M., Hamza, M.A.: Blow-up for wave equation with the scale-invariant damping and combined nonlinearities. Math. Methods Appl. Sci. 44, 1127–1136 (2021)
Hamouda, M., Hamza, M.A.: Improvement on the blow-up of the wave equation with the scale invariant damping and combined nonlinearities. Nonlinear Anal., Real World Appl. 59, 103275 (2021)
Han, W.: Concerning the Strauss conjecture for the sub-critical and critical cases on the exterior domain in two space dimensions. Nonlinear Anal. 84, 136–145 (2013)
Han, W., Zhou, Y.: Blow-up for some semilinear wave equations in multi-space dimensions. Commun. Partial Differ. Equ. 39, 651–665 (2014)
Hidano, K., Metcalfe, J., Smith, H.F., Sogge, C.D., Zhou, Y.: On abstract Strichartz estimates and the Strauss conjecture for non-trapping obstacles. Trans. Am. Math. Soc. 362(5), 2789–2809 (2010)
Hidano, K., Wang, C.B., Yokoyama, K.: Combined effects of two nonlinearities in lifespan of small solutions to semilinear wave equations. Math. Ann. 366, 667–694 (2016)
Ikeda, M., Sobajima, M.: Lifespan of solutions to semilinear wave equation with time dependent critical damping for specially localized initial data. Math. Ann. 372(3–4), 1017–1040 (2018)
Ikehata, R.: Some remarks on the wave equation with potential type damping coefficients. Int. J. Pure Appl. Math. 21, 19–24 (2005)
Ikehata, R., Takeda, H.: Uniform energy decay for wave equations with unbounded damping coefficients. Funkc. Ekvacioj 63, 133–152 (2020)
Imai, T., Kato, M., Takamura, H., Wakasa, K.: The lifespan of solutions of semilinear wave equations with the scale-invariant damping in two space dimensions. J. Differ. Equ. 269, 8387–8424 (2020)
Lai, N.A., Liu, M.Y., Tu, Z.H., Wang, C.B.: Lifespan estimates for semilinear wave equations with space dependent damping and potential (2021). arXiv:2102.10257v1
Lai, N.A., Takamura, H.: Blow-up for semilinear damped wave equations with sub-Strauss exponent in the scattering case. Nonlinear Anal. 168, 222–237 (2018)
Lai, N.A., Takamura, H.: Non-existence of global solutions of wave equations with weak time dependent damping and combined nonlinearity. Nonlinear Anal., Real World Appl. 45, 83–96 (2019)
Lai, N.A., Takamura, H., Wakasa, K.: Blow-up for semilinear wave equations with the scale invariant damping and super-Fujita exponent. J. Differ. Equ. 263(9), 5377–5394 (2017)
Lai, N.A., Tu, Z.H.: Strauss exponent for semilinear wave equations with scattering space dependent damping. J. Math. Anal. Appl. 489, 124189 (2020)
Lai, N.A., Zhou, Y.: An elementary proof of Strauss conjecture. J. Funct. Anal. 267(5), 1364–1381 (2014)
Lai, N.A., Zhou, Y.: Finite time blow-up to critical semilinear wave equation outside the ball in 3-D. Nonlinear Anal. 125, 550–560 (2015)
Lai, N.A., Zhou, Y.: Non-existence of global solutions to critical semilinear wave equations in exterior domain in high dimensions. Nonlinear Anal., Real World Appl. 143, 89–104 (2016)
Lai, N.A., Zhou, Y.: Blow-up for initial boundary value problem of critical semilinear wave equation in 2-D. Commun. Pure Appl. Anal. 17(4), 1499–1510 (2018)
Liu, M.Y., Wang, C.B.: Blow-up for small-amplitude semilinear wave equations with mixed nonlinearities on asymptotically Euclidean manifolds. J. Differ. Equ. 269(10), 8573–8596 (2020)
Metcalfe, J., Sogge, C.D.: Global existence for high dimensional quasilinear wave equations exterior to star shaped obstacles. Discrete Contin. Dyn. Syst. 28(4), 1589–1601 (2012)
Ming, S., Lai, S.Y., Fan, X.M.: Lifespan estimates of solutions to quasilinear wave equations with scattering damping. J. Math. Anal. Appl. 492, 124441 (2020)
Ming, S., Lai, S.Y., Fan, X.M.: Blow-up for a coupled system of semilinear wave equations with scattering dampings and combined nonlinearities. Appl. Anal. 101(8), 2996–3016 (2022)
Ming, S., Yang, H., Fan, X.M.: Formation of singularities of solutions to the Cauchy problem for semilinear Moore–Gibson–Thompson equations. Commun. Pure Appl. Anal. 21(5), 1773–1792 (2022)
Nishihara, K.: Asymptotic behavior of solutions to the semilinear wave equation with time-dependent damping. Tokyo J. Math. 34, 327–343 (2011)
Nishihara, K., Sobajima, M., Wakasugi, Y.: Critical exponent for the semilinear wave equations with a damping increasing in the far field. Nonlinear Differ. Equ. Appl. 25(6), 55 (2018)
Schaeffer, J.: The equation \(\Box u =|u|^{p}\) for the critical value of p. Proc. R. Soc. Edinb. 101, 31–44 (1985)
Smith, H.F., Soggee, S.D., Wang, C.B.: Strichartz estimates for Dirichlet wave equations in two dimensions with applications. Trans. Am. Math. Soc. 364, 3329–3347 (2012)
Strauss, W.A.: Nonlinear scattering theory at low energy. J. Funct. Anal. 41(1), 110–133 (1981)
Todorova, G., Yordanov, B.: Weighted \(L^{2}\)-estimates for dissipative wave equations with variable coefficients. J. Differ. Equ. 246, 4497–4518 (2009)
Wakasa, K.: The lifespan of solutions to semilinear damped wave equations in one space dimension. Commun. Pure Appl. Anal. 15, 1265–1283 (2016)
Wakasugi, Y.: Critical exponent for the semilinear wave equation with scale invariant damping. Four. Anal. Tren. Math., 375–390 (2014)
Wang, C.B.: Long time existence for semilinear wave equations on asymptotically flat space times. Commun. Partial Differ. Equ. 42(7), 1150–1174 (2017)
Yordanov, B., Zhang, Q.S.: Finite time blow-up for critical wave equations in high dimensions. J. Funct. Anal. 231, 361–374 (2006)
Zhou, Y.: Blow-up of solutions to semilinear wave equations with critical exponent in high dimensions. Chin. Ann. Math. 28, 205–212 (2007)
Zhou, Y., Han, W.: Lifespan of solutions to critical semilinear wave equations. Commun. Partial Differ. Equ. 39, 439–451 (2014)
Acknowledgements
The authors would like to express their sincere gratitude to the anonymous referees for a number of valuable comments and suggestions. The author Sen Ming would like to express his sincere thank to Professor Yi Zhou for his guidance and encouragements during the postdoctoral study in Fudan University. The authors would like to express their gratitude to Professor Ning-An Lai for his useful suggestions.
Funding
The project is supported by Natural Science Foundation of Shanxi Province of China (No. 201901D211276), Fundamental Research Program of Shanxi Province (Nos. 20210302123021 and 20210302123045), Innovative Research Team of North University of China (No. TD201901), Science and Technology Innovation Project of Higher Education Institutions in Shanxi (No. 2020L0277), and Science Foundation of North University of China (No. XJJ201922).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yao, J., Ming, S. & Fan, X. Blowup for semilinear wave equation with space-dependent damping and combined nonlinearities. Adv Cont Discr Mod 2022, 47 (2022). https://doi.org/10.1186/s13662-022-03719-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-022-03719-3