1 Introduction

The primary theme of the paper is the Euler equations of isentropic gas dynamics in Eulerian coordinates,

$$ \textstyle\begin{cases} {\gamma }_{\tau }+(\gamma v)_{\eta }=0, \\ (\gamma v)_{\tau }+ (\gamma v^{2}+P )_{\eta }=0, \end{cases} $$
(1)

with Riemann initial values

$$ (\gamma ,v)|_{\tau =0}= \textstyle\begin{cases} ({\gamma }_{-}, v_{-}), & \eta < 0, \\ ({\gamma }_{+}, v_{+}), & \eta >0, \end{cases} $$
(2)

where v, \(p(\gamma )\), and γ are the velocity, pressure, and density, respectively, We assume that \(v_{-}>v_{+}\) and the pressure function is

$$ P=\varepsilon p(\gamma ) $$
(3)

with p satisfying

$$ \textstyle\begin{cases} {p}'(\gamma )>0, \\ {p}'(\gamma )+\gamma {p}''(\gamma )\geq 0. \end{cases} $$
(4)

Equations (1) can be expressed by the hyperbolic system for conservation laws:

$$ U_{\tau }+ F(U)_{\eta }=0 $$
(5)

with

$$ U= \begin{pmatrix} \gamma \\ \gamma v \end{pmatrix} ,\qquad F(U)= \begin{pmatrix} \gamma v \\ \gamma v^{2}+\epsilon p(\gamma ) \end{pmatrix} . $$

As \(\epsilon \rightarrow 0\), (1) becomes the zero-pressure limiting scheme

$$ \textstyle\begin{cases} {\gamma }_{\tau }+(\gamma v)_{\eta }=0, \\ (\gamma v)_{\tau }+ (\gamma v^{2} )_{\eta }=0. \end{cases} $$
(6)

Many scientists have researched the alternatives to the zero-pressure gas dynamics [1–8]. Brenier and Grenier [9] provided uncountable viscous particles possessing momentum and mass preserved under collision to enhance the dynamics of one-dimensional pressureless gas (4). Bouchut [1] proved the presence of the system entropy solution (6) for the Riemann case, and the associated numerical findings affirmed that the alternatives have the concentration of the density, that is, the delta wave. Grenier and Brenier [9] and Rykov and Sinai [2] initially obtained work delta wave entropy alternatives for the Cauchy problem irrespective of the pressureless gas; see Huang, Ding, and Wang [7] with distinct original information classes. Wang and Ding [8] first demonstrated the uniqueness when the original information were features. With a distinct technique, Bouchut [10] had the same outcome. Finally, Wang and Huang [5, 11, 12] demonstrated the uniqueness when measuring radon in the original information under circumstances of energy and Oleinik entropy. See Huang [13–15] for overall pressure-free system. Regarding the two-dimensional Riemann case of pressureless gas dynamics, see [6, 16–18], and the references therein.

Let us now turn to the Euler scheme isentropic (1). The Euler system officially refers as a dynamics of zero gas pressure (6) in a situation whereby pressure gets close to zero or nonzero. Chen and Lin [19] initially demonstrated the development of vacuum states and δ-shocks of the Riemann solutions to the Euler equations (1) as the stress comes to zero, which describes the concentration and cavitation phenomenon exactly in mathematics. We demonstrated the same concentration phenomenon in [20–22] as the stress tends to a nonzero constant. All operations of [19] are carried out only for the gas dynamics of γ-law. In current research, we demonstrate the same concentration phenomenon in a general pressure mode for \(P=\epsilon p(\gamma )\) as \(\epsilon \rightarrow 0\), where the pressure p satisfies (4). To the best of our knowledge, the scheme Riemann problem (1) was not previously considered in the literature as \(\epsilon \rightarrow 0\).

The rest of the work is structured as follows. In Sect. 2, we report some preliminaries on the delta wave solution for the pressure-free gas dynamical system (6). In Sect. 3, we establish the classical Riemann solutions to the Euler equations. In Sect. 4, we depict the limiting behavior of the Riemann solution to the Euler equations (1) in the forming of delta wave. Section 5 reports the Lax–Friedrichs numerical scheme [23, 24] of first order.

2 Preliminaries

Alternatives to the pressure-free method have been explored in (6) involving delta wave, backed on a sleek curve, [6], the solution is a delta function.

Suppose that \(S=\{(\eta (s),\tau (s)):c< s< d\}\) is a smooth curve, we define

$$ \bigl\langle {w(\tau )\delta _{S},\phi (\eta ,\tau )} \bigr\rangle = \int _{c}^{d}{w \bigl( \tau (s) \bigr)\phi \bigl( \eta (s),\tau (s) \bigr)\sqrt{\eta '(s)^{2}+\tau '(s)^{2}}}\,ds $$
(7)

for \(\phi \in C^{\infty }_{0}(\mathbb{R}^{2}_{+})\). The delta function weight is denoted by \(w(\cdot )\). For the Riemann case with \(v_{-}>v_{+}\), the Dirac-measured solution with parameter σ can be expressed by

$$ \gamma (\eta ,\tau )=\gamma _{0}(\eta ,\tau )+w( \tau )\delta _{S},\qquad v(\eta ,\tau )=v_{0}(\eta ,\tau ), $$
(8)

with \(S=\{(\sigma {\tau },\tau ): 0<\tau <\infty \}\),

$$\begin{aligned}& \gamma _{0}(\eta ,\tau )= \textstyle\begin{cases} \gamma _{-},& \eta < \sigma {\tau }, \\ \gamma _{+},& \eta >\sigma {\tau }, \end{cases}\displaystyle \\ & v_{0}(\eta ,\tau )= \textstyle\begin{cases} v_{-},& \eta < \sigma {\tau }, \\ \sigma ,& \eta =\sigma {\tau }, \\ v_{+},&\eta >\sigma {\tau }, \end{cases}\displaystyle \end{aligned}$$

and

$$ w(\tau )=\frac{\tau }{\sqrt{1+\sigma ^{2}}} \bigl(\sigma [\gamma ]-[\gamma {v}] \bigr). $$
(9)

For across, the discontinuity \([h ]:=h_{+}-h_{-}\) represents the function jump. The Dirac-measured alternative \((\gamma ,\gamma {v})\) established above is said to be a “delta wave” to the pressureless gas dynamics (6) if

$$\begin{aligned}& \langle {\gamma ,\psi _{\tau }}\rangle +\langle { \gamma {v},{\psi }_{\eta }} \rangle =0, \end{aligned}$$
(10)
$$\begin{aligned}& \langle {\gamma {v},\psi _{\tau }}\rangle + \bigl\langle {\gamma {v^{2}},{\psi }_{\eta }} \bigr\rangle =0 \end{aligned}$$
(11)

for all \(\psi \in C_{0}^{\infty }(\mathbb{R}_{+}^{2})\). The insight into the distribution is taken as

$$ \begin{aligned} &\langle {\gamma ,\phi }\rangle = \int _{0}^{\infty } \int _{-\infty }^{ \infty }\gamma _{0}(\eta ,\tau )\phi (\eta ,\tau )\,d\eta \,dt+ \bigl\langle {w( \tau )\delta _{S},\phi (\eta ,\tau )} \bigr\rangle , \\ &\langle {\gamma {v},\phi }\rangle = \int _{0}^{\infty } \int _{-\infty }^{ \infty }\gamma _{0}(\eta ,\tau )v_{0}(\eta ,\tau )\phi (\eta ,\tau )\,d\eta \,d\tau + \bigl\langle { \sigma w(\tau )\delta _{S},\phi (\eta ,\tau )} \bigr\rangle \end{aligned} $$

for all \(\phi \in C_{0}^{\infty }(\mathbb{R}_{+}^{2})\), from which we have

$$ [\gamma ]{\sigma }^{2}-2 [\gamma {v} ]{\sigma }+ \bigl[\gamma {v^{2}} \bigr]=0. $$

Thus σ is determined in a unique way as

$$ \sigma = \frac{\sqrt{\gamma _{+}}{v_{+}}+\sqrt{\gamma _{-}}{v_{-}}}{\sqrt{\gamma _{+}}+\sqrt{\gamma _{-}}} $$
(12)

under the entropy axiom \(v_{-}>\sigma >v_{+}\) [6].

Remark 2.1

In a geometrical sense the entropy axiom \(v_{-}>\sigma >v_{+}\) implies that any characteristic lines generated in the x-axis enter into the Delta wave \(\eta =\sigma \tau \); see Fig. 1. The results give us the plethora of particles concentrated on \(\eta =\sigma \tau \) with the increase in time τ. Thus by (10) we get

$$ \sqrt{1+\sigma ^{2}} {w(\tau )}= \int _{\eta -v_{-}{\tau }}^{\eta -v_{+}{ \tau }}\gamma (y,0)\,dy, $$

[6, 13].

Figure 1
figure 1

The concentration of mass

Full size image

3 Riemann solutions

Next, we can take the Riemann case (1) and (2) in the scenario \(v_{-}>v_{+}\). The eigenvalues of system (1) are

$$ \lambda _{1}(\gamma ,v)=v-\sqrt{\varepsilon p^{\prime }( \gamma )},\qquad \lambda _{2}(\gamma ,v)=v+\sqrt{\varepsilon p^{\prime }( \gamma )}. $$
(13)

There should be a general pressure under assumption (4). We can take a particular smooth solution along the line \(S=\{(\sigma {\tau },\tau ): 0<\tau <\infty \}\) with bounded jump. Then for the discontinuity of system (1), by the Rankine–Hugoniot relation we have

$$ \begin{aligned} &\sigma [\gamma ]=[\gamma {v}], \\ &\sigma [\gamma {v}]= \bigl[\gamma {v^{2}}+\varepsilon p(\gamma ) \bigr], \end{aligned} $$
(14)

so that we obtain

$$\begin{aligned}& \sigma =\frac{[\gamma {v}]}{[\gamma ]}, \\& v=v_{-}\pm \sqrt{ \biggl(\frac{1}{\gamma _{-}}- \frac{1}{\gamma } \biggr) \bigl(\varepsilon p(\gamma )-\varepsilon p(\gamma _{-}) \bigr)} \end{aligned}$$

with σ, \((\gamma _{-},v_{-})\), and \((\gamma _{+},v_{+})\) showing the shock speed and the left and right states, respectively.

1-shock curve \(S_{1}(\gamma _{-},v_{-})\):

The Lax entropy inequality [25] yields

$$ \lambda _{1}(\gamma ,v)< \sigma < \lambda _{1}(\gamma _{-},v_{-}) $$

and

$$ \sigma -v_{-}< -\sqrt{\epsilon p^{\prime }( \gamma _{-})}< 0. $$
(15)

So by applying the Rankine–Hugoniot condition, we arrive at

$$ (\sigma - v_{-}) (\gamma - {\gamma }_{-})=\gamma (v - {v_{-}}),$$

which shows that \(\gamma -\gamma _{-}\) and \(v-v_{-}\) possess distinct signs. If \(v>v_{-}\), then \(\gamma <\gamma _{-}\), and

$$ \sigma -v_{-}=\frac{\gamma }{\gamma -\gamma _{-}}(v-v_{-})=-\sqrt{ \frac{\epsilon \gamma }{\gamma _{-}}}\sqrt{ \frac{p(\gamma _{-})-p(\gamma )}{\gamma _{-}-\gamma }}=-\sqrt{ \frac{\epsilon \gamma }{\gamma _{-}}} \sqrt{p'(\bar{\gamma })} $$

for some \(\bar{\gamma }\in (\gamma ,\gamma _{-})\). From (4) we get

$$ \sqrt{\epsilon {p}'(\gamma _{-})}-\sqrt{ \frac{\epsilon \gamma }{\gamma _{-}}}\sqrt{ {p}'(\bar{\gamma })}\geq \sqrt{ \frac{\epsilon }{\gamma _{-}}} \bigl(\sqrt{{\gamma _{-}} {p}'( \gamma _{-})}- \sqrt{\bar{\gamma } {p}'(\bar{\gamma }) \bigr)}\geqslant 0, $$

which yields

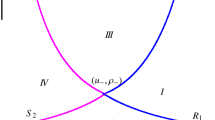
$$ \sigma -v_{-}\geqslant -\sqrt{\epsilon p'(\gamma _{-})}, $$
(16)

a contradiction to (15). Therefore we obtain the shock curve \(S_{1}(\gamma _{-},v_{-})\) in the phase plane for the first family (see Fig. 2):

$$ v=v_{-} -\sqrt{ \biggl(\frac{1}{\gamma _{-}}- \frac{1}{\gamma } \biggr) \bigl(\epsilon p( \gamma )-\epsilon p(\gamma _{-}) \bigr)},\quad \gamma >\gamma _{-}, v< v_{-}. $$
(17)

In this way, we can obtain the shock curve \(S_{2}(\gamma _{-},v_{-})\) for the second family:

$$ v=v_{-} -\sqrt{ \biggl(\frac{1}{\gamma _{-}}- \frac{1}{\gamma } \biggr) \bigl(\epsilon p( \gamma )-\epsilon p(\gamma _{-}) \bigr)}, \quad \gamma < \gamma _{-}, v< v_{-}. $$
(18)

We are especially interested in the case \(S_{1}+S_{2}\), where there is a unique state of intermediate \((\gamma _{*},v_{*})\), which gives \((\gamma _{*},v_{*}) \in {S_{1}(\gamma _{-},v_{-})}\) and \((\gamma _{+},v_{+})\in {S_{2}(\gamma _{*},v_{*})}\), that is,

$$\begin{aligned}& v_{*}=v_{-}-\sqrt{ \biggl( \frac{1}{\gamma _{-}}-\frac{1}{\gamma _{*}} \biggr) \bigl(\epsilon p(\gamma _{*})-\epsilon p(\gamma _{-}) \bigr)}, \quad \gamma _{*}>\gamma _{-}, v_{*}< v_{-}, \end{aligned}$$
(19)
$$\begin{aligned}& v_{+}=v_{*}-\sqrt{ \biggl( \frac{1}{\gamma _{*}}-\frac{1}{\gamma _{+}} \biggr) \bigl(\epsilon p(\gamma _{+})-\epsilon p(\gamma _{*}) \bigr)}, \quad \gamma _{+}< \gamma _{*}, v_{+}< v_{*}, \end{aligned}$$
(20)

with the shock speeda

$$ \sigma _{1}= \frac{\gamma _{*}v_{*}-\gamma _{-}v_{-}}{\gamma _{*}-\gamma _{-}}, \qquad \sigma_{2}= \frac{\gamma _{+}v_{+}-\gamma _{*}v_{*}}{\gamma _{+}-\gamma _{*}}, $$
(21)

respectively. The RIE solution in this regard is

$$ (\gamma ,v) (\eta ,\tau )= \textstyle\begin{cases} (\gamma _{-},v_{-}), &\eta < \sigma _{1}\tau , \\ (\gamma _{*},v_{*}), &\sigma _{1}\tau < \eta < \sigma _{2}\tau , \\ (\gamma _{+},v_{+}), &x>\sigma _{2}\tau . \end{cases} $$
(22)

4 Formation of delta wave

Assume that \(v_{-}>v_{+}\) for the limiting manner of Riemann solutions for the Euler system of the isentropic fluids with initial data as ϵ tends to 0. So we have to show that the limit is the delta wave solution to the pressureless gas dynamics (6).

4.1 The limiting behavior of Riemann solution

The coupled shock curves (17) and (18) come closer to the line \(v=v_{-}\) as ϵ approaches 0, so for all RIE data with \(v_{-}>v_{+}\), the Riemann solution possesses two shocks only if \(\epsilon >0\) is small, as shown in Fig. 2. Thus it suffices to consider \(S_{1}+S_{2}\) as ϵ approaches 0. From (19) and (20) an identity of \(\gamma _{*}\) is attained:

$$ \begin{aligned} v_{-} -v_{+} &= \sqrt{ \biggl(\frac{1}{{\gamma }_{-}}- \frac{1}{{\gamma }_{*}} \biggr) \bigl(\epsilon p({\gamma }_{*})- \epsilon p({\gamma }_{-}) \bigr)} + \sqrt{ \biggl( \frac{1}{{\gamma }_{*}}- \frac{1}{{\gamma }_{+}} \biggr) \bigl(\epsilon p({ \gamma }_{+})- \epsilon p({\gamma }_{*}) \bigr)} \\ &=\sqrt{\frac{\epsilon p(\gamma _{*})}{\gamma _{-}}- \frac{\epsilon p(\gamma _{-})}{\gamma _{-}} - \frac{\epsilon p(\gamma _{*})}{\gamma _{*}}+ \frac{\epsilon p(\gamma _{-})}{\gamma _{*}}} \\ &\quad {}+\sqrt{ \frac{\epsilon p(\gamma _{+})}{\gamma _{*}} - \frac{\epsilon p(\gamma _{*})}{\gamma _{*}}- \frac{\epsilon p(\gamma _{+})}{\gamma _{+}}+ \frac{\epsilon p(\gamma _{*})}{\gamma _{+}}}. \end{aligned} $$
(23)

Thus we obtain the following:

Figure 2
figure 2

The shock curves in the phase plane

Full size image

Lemma 4.1

\(\lim_{\epsilon \rightarrow 0} \gamma _{*} = +\infty \).

Proof

Let \(\liminf_{\epsilon \rightarrow 0} \gamma _{*}=\Lambda \) and \(\limsup_{\epsilon \rightarrow 0} \gamma _{*}=\Theta \). For \(\Lambda <\Theta \), by the continuity of \(\varepsilon p(\gamma _{*})\) there is a sequence \(\{\epsilon _{n}: n\geq 1\}\subseteq (0,1)\) such that

$$ \lim_{n\to \infty }\epsilon _{n}=0, \quad \text{and}\quad \lim_{n\to \infty } \gamma _{*}(\epsilon _{n})=c $$

for some \(c\in (\Lambda ,\Theta )\).

Considering the right side of (23) and replacing the sequence thereafter imposing the limit give

$$ \lim_{n\to \infty } \biggl( { \frac{\epsilon p({\gamma _{*}}(\epsilon _{n}))}{\gamma _{\pm }}- \frac{\epsilon p(\gamma _{\pm }(\epsilon _{n}))}{\gamma _{\pm }}- \frac{\epsilon p(\gamma _{*}(\epsilon _{n}))}{\gamma _{*}}+ \frac{\epsilon p(\gamma _{\pm })(\epsilon _{n}))}{\gamma _{*}}} \biggr)=0, $$

which contradicts (23) with the surmising \(v_{-}>v_{+}\). Thus \(\Lambda =\Theta \).

For \(\Lambda =\Theta \in (0,\infty )\), \(\lim_{\epsilon \to 0} \gamma _{*}(\epsilon )=\Lambda \). A contradiction can be reached if we take the limit in (23). So \(\Lambda =\Theta =0\) or \(\Lambda =\Theta =\infty \). Nevertheless, the entropy case implies \(\gamma _{*}>\max \{\gamma _{-},\gamma _{+}\}\), and we get \(\lim_{\epsilon \rightarrow 0}\gamma _{*}(\epsilon )= \Lambda =\Theta =\infty \). □

Lemma 4.2

\(\lim_{\epsilon \rightarrow 0}{\epsilon p({{\gamma }_{*}}( \epsilon ))} = a = ( \frac{\sqrt{\gamma _{+}\gamma _{-}}(v_{-}-v_{+})}{\sqrt{\gamma _{+}}+\sqrt{\gamma _{-}}} )^{2}\).

In the right-hand side of (23), taking the limit, we obtain

$$ \lim_{\epsilon \to 0} \biggl( { \frac{\epsilon p(\gamma _{*})}{\gamma _{\pm }}- \frac{\epsilon p(\gamma _{\pm })}{\gamma _{\pm }}- \frac{\epsilon p(\gamma _{*})}{\gamma _{*}}+ \frac{\epsilon p(\gamma _{\pm })}{\gamma _{*}}} \biggr)=\lim _{ \epsilon \rightarrow 0} \frac{\gamma _{*} -\gamma _{\pm }}{\gamma _{*} \gamma _{\pm }} \bigl(\epsilon p( \gamma _{*})-\epsilon p(\gamma _{\pm }) \bigr)= \frac{a}{{\gamma }_{\pm }} $$

and

$$ v_{-} -v_{+} = \sqrt{\frac{a}{\gamma _{-}}}+ \sqrt{ \frac{a}{\gamma _{+}}}, $$

which leads to \(a= ( \frac{\sqrt{\gamma _{+}\gamma _{-}}(v_{-}-v_{+})}{\sqrt{\gamma _{+}}+\sqrt{\gamma _{-}}} )^{2}\).

Moreover, we have

$$ \lim_{\epsilon \rightarrow 0}{\epsilon p \bigl({{\gamma }_{*}}( \epsilon ) \bigr)} = a = \biggl( \frac{\sqrt{\gamma _{+} \gamma _{-}}(v_{-}-v_{+})}{\sqrt{\gamma _{+}}+\sqrt{\gamma _{-}}} \biggr)^{2}. $$
(24)

Proposition 4.1

We have

$$ \lim_{\epsilon \rightarrow 0}{v_{*}} = \lim _{ \epsilon \rightarrow 0}{\sigma _{1}} = \lim_{\epsilon \rightarrow 0}{ \sigma _{2}} = \sigma $$
(25)

and

$$ \lim_{\epsilon \rightarrow 0}{\gamma _{*}(\sigma _{2}- \sigma _{1})}= \sigma [\gamma ]-[\gamma {v}], $$
(26)

where \(\sigma = \frac{\sqrt{\gamma _{-}}v_{-}+\sqrt{\gamma _{+}}v_{+}}{\sqrt{\gamma _{-}}+\sqrt{\gamma _{+}}}\).

Proof

By simple calculation we get

$$\begin{aligned}& \lim_{\epsilon \rightarrow 0} v_{*}= v_{-} -\lim _{ \epsilon \rightarrow 0}{\sqrt{ \frac{\epsilon p(\gamma _{*})}{\gamma _{-}}- \frac{\epsilon p(\gamma _{+})}{\gamma _{-}}- \frac{\epsilon p(\gamma _{*})}{\gamma _{*}}+ \frac{\epsilon p(\gamma _{-})}{\gamma _{*}}}} = v_{-} -\sqrt{ \frac{a}{\gamma _{-}}} = \sigma , \\& \lim_{\epsilon \rightarrow 0}{ \sigma _{1} } = \lim _{ \epsilon \rightarrow 0} \frac{\gamma _{*}v_{*}-\gamma _{-}v_{-}}{\gamma _{*}-\gamma _{-}} = v_{-} + \lim _{\epsilon \rightarrow 0}{ \frac{\gamma _{*}}{\gamma _{-} -\gamma _{*}}(v_{-} - v_{*})} = \sigma , \\& \lim_{\epsilon \rightarrow 0}{ \sigma _{2} } = \lim _{ \epsilon \rightarrow 0} \frac{\gamma _{+}v_{+}-\gamma _{*}v_{*}}{\gamma _{+}-\gamma _{*}} = v_{+} + \lim _{\epsilon \rightarrow 0}{ \frac{\gamma _{*}}{\gamma _{+} -\gamma _{*}}(v_{+} - v_{*})} = \sigma , \end{aligned}$$

and

$$ \begin{aligned} \lim_{\epsilon \rightarrow 0}{ \gamma _{*}(\sigma _{2}- \sigma _{1})} &=\lim _{\epsilon \rightarrow 0}{\gamma _{*} \biggl( \frac{\gamma _{+}v_{+}-\gamma _{*}v_{*}}{\gamma _{+}-\gamma _{*}}- \frac{\gamma _{*}v_{*}-\gamma _{-}v_{-}}{\gamma _{*}-\gamma _{-}} \biggr)} \\ &=\lim_{\epsilon \rightarrow 0}{\gamma _{*} \biggl( \frac{[\gamma {v}]}{\gamma _{+}-\gamma _{*}}+ \frac{-\gamma _{-}v_{-}[\gamma ]+\gamma _{*}v_{*}[\gamma ]}{(\gamma _{*}-\gamma _{-})(\gamma _{*}-\gamma _{+})} \biggr)} \\ &=\sigma [\gamma ]-[\gamma v]. \end{aligned} $$

 □

Remark 4.1

The results show that the delta wave velocity σ is the limiting value of the speed particle \(v_{*}\) and coupled shocks velocity \(\sigma _{1}\), \(\sigma _{2}\). We can illustrate it as the catching up of 1-shock with the coupled shock, whereas overlap of the coupled shocks forms a delta wave. In addition, multiplying (26) with τ, we may readily notice a mass concentration situation; see also Remark 2.1.

4.2 The formation of delta wave

Here we demonstrate that the Riemann solution in the sense of distributions is the delta wave of the zero-pressure gas dynamics (6).

Theorem 4.1

Let \((\gamma _{\epsilon }(\eta ,\tau ),m_{\epsilon }(\eta ,\tau ))= (\gamma _{\epsilon }(\eta ,\tau ),\gamma _{\epsilon }(\eta ,\tau ){u_{\epsilon }( \eta ,\tau )})\) be the solutions having two shocks for the Riemann case (1) and (2) with surmising \(v_{-}>v_{+}\). If \(\epsilon \rightarrow 0\), then \((\gamma _{\epsilon }(\eta ,\tau ),m_{\epsilon }(\eta ,\tau ))\) converges to

$$ \bigl(\gamma (\eta ,\tau ),m(\eta ,\tau ) \bigr)= \bigl(\gamma _{0}( \eta ,\tau )+w_{1}( \tau )\delta _{S},\gamma _{0}(\eta ,\tau )v_{0}(\eta , \tau )+w_{2}( \tau )\delta _{S} \bigr) $$

in the distribution sense. The singular part \(\gamma (\eta ,\tau )\) and \(m(\eta ,\tau )\) of the limit function is a weighted Dirac measurement with the associated weight given as

$$ w_{1}(\tau )= \frac{\tau }{\sqrt{1+\sigma ^{2}}} \bigl(\sigma [ \gamma ]-[ \gamma {v}] \bigr)\quad \textit{and}\quad w_{2}(\tau )= \frac{\tau }{\sqrt{1+\sigma ^{2}}} \bigl(\sigma [\gamma {v}]- \bigl[\gamma {v^{2}} \bigr] \bigr), $$
(27)

respectively.

Proof

1. From (22) we know that if we take \(\zeta =\frac{\eta }{\tau }\), \(\gamma _{\epsilon }(\zeta )= \gamma _{\epsilon }(\zeta {\tau },\tau )\), and \(v_{\epsilon }(\zeta )= v_{\epsilon }(\zeta {\tau },\tau )\), then the Riemann solutions become

$$ \bigl(\gamma _{\epsilon }(\xi ),v_{\epsilon }(\xi ) \bigr)= \textstyle\begin{cases} (\gamma _{-},v_{-}),& \zeta < \sigma _{1}, \\ (\gamma _{*},v_{*}), & \sigma _{1}< \zeta < \sigma _{2}, \\ (\gamma _{+},v_{+}), & \zeta >\sigma _{2}, \end{cases} $$

and \((\gamma _{\epsilon }(\zeta ),v_{\epsilon }(\zeta ))\) solve the equations

$$ \textstyle\begin{cases} -\zeta ({\gamma )_{\zeta }}+(\gamma {v})_{\zeta }=0, \\ -\zeta {(\gamma {v})}_{\zeta }+(\gamma {v^{2}}+\epsilon p(\gamma ))_{ \zeta }=0. \end{cases} $$
(28)

So for all \(\psi (\cdot ) \in C^{\infty }_{0}(\mathbb{R})\), \((\gamma _{\epsilon }(\zeta ),v_{\epsilon }(\zeta ))\) will satisfy

$$\begin{aligned}& \int _{-\infty }^{\infty }\gamma _{\epsilon }(\zeta ) \psi (\zeta )\,d\zeta = \int _{-\infty }^{\infty }\gamma _{\epsilon }(\zeta ) \bigl(v_{\epsilon }(\zeta )- \zeta \bigr){{\psi }'(\zeta )}\,d\zeta , \end{aligned}$$
(29)
$$\begin{aligned}& \begin{aligned} &\int _{-\infty }^{\infty }\gamma _{\epsilon }(\zeta )v_{\epsilon }(\zeta ){ \psi (\zeta )}\,d\zeta \\ &\quad = \int _{-\infty }^{\infty }\gamma _{\epsilon }( \zeta )v_{\epsilon }(\zeta ) \bigl({v_{\epsilon }(\zeta )-\zeta } \bigr){\psi }'(\zeta )\,d\zeta + \int _{-\infty }^{\infty }\epsilon p \bigl(\gamma _{\epsilon }(\zeta ) \bigr){ \psi }'(\zeta )\,d\zeta . \end{aligned} \end{aligned}$$
(30)

2. For (29), we have

$$ \begin{aligned} & \int ^{\infty }_{-\infty }\gamma _{\epsilon }(\zeta ) \bigl(v_{\epsilon }(\zeta )- \zeta \bigr){\psi }'(\zeta )\,d\zeta \\ &\quad = \int _{-\infty }^{\sigma _{1}}\gamma _{-}(v_{-}- \zeta ){\psi }'( \zeta )\,d\zeta + \int _{\sigma _{2}}^{\infty }\gamma _{+}(v_{+}- \zeta ){ \psi }'(\zeta )\,d\zeta + \int _{\sigma _{1}}^{\sigma _{2}}\gamma _{*}(v_{*}- \zeta ){\psi }'(\zeta )\,d\zeta \\ &\quad = { \biggl(}\gamma _{-}v_{-}\psi (\sigma _{1})+\gamma _{-} \int _{- \infty }^{\sigma _{1}}\psi (\zeta )\,d\zeta -\gamma _{-}\sigma _{1}\psi ( \sigma _{1}) { \biggr)} \\ &\qquad {}+ \biggl(-\gamma _{+}v_{+}\psi (\sigma _{2}) + \gamma _{+} \int _{\sigma _{2}}^{\infty }\psi (\zeta )\,d\zeta +\gamma _{+}\sigma _{2}\psi (\sigma _{2}) \biggr)+ \int _{\sigma _{1}}^{ \sigma _{2}}\gamma _{*}(v_{*}- \zeta ){\psi }'(\zeta )\,d\zeta . \end{aligned} $$

In addition, we have

$$ \begin{aligned} & \int _{\sigma _{1}}^{\sigma _{2}}\gamma _{*}(v_{*}- \zeta ){\psi }'( \zeta )\,d\zeta \\ &\quad =\gamma _{*}v_{*} \bigl(\psi (\sigma _{2})-\psi (\sigma _{1}) \bigr)+\gamma _{*} \int _{\sigma _{1}}^{\sigma _{2}}\psi (\zeta )\,d\zeta -\gamma _{*} \bigl( \sigma _{2}\psi (\sigma _{2})- \sigma _{1}\psi (\sigma _{1}) \bigr) \\ &\quad =\gamma _{*}(\sigma _{2}-\sigma _{1}) \biggl(v_{*} \frac{\psi (\sigma _{2})-\psi (\sigma _{1})}{\sigma _{2}-\sigma _{1}}+ \frac{\int _{\sigma _{1}}^{\sigma _{2}}\psi (\zeta )\,d\zeta }{\sigma _{2}-\sigma _{1}}- \frac{\sigma _{2}\psi (\sigma _{2})-\sigma _{1}\psi (\sigma _{1})}{\sigma _{2}-\sigma _{1}} \biggr), \end{aligned} $$

which converges to

$$ \bigl(\sigma [\gamma ]-[\gamma {v}] \bigr) \bigl(\sigma \psi '( \sigma )+\psi (\sigma )- \bigl( \sigma \psi (\sigma ) \bigr)' \bigr)=0 $$

by Proposition 4.1. Then sending ϵ to 0 in (29) gives

$$ \lim_{\epsilon \rightarrow 0} \int _{-\infty }^{\infty } \bigl( \gamma _{\epsilon }( \zeta )-\gamma _{0}(\zeta ) \bigr)\psi (\zeta )\,d\xi = \bigl( \sigma [ \gamma ]-[\gamma {v}] \bigr)\psi (\sigma ), $$
(31)

where \((\gamma _{0}(\zeta ),v_{0}(\zeta ))=(\gamma _{\pm },v_{\pm })\), \(\pm (\zeta -\sigma )>0\).

3. Following the same way, for (30), we can obtain

$$\begin{aligned} &\lim_{\epsilon \rightarrow 0} \int _{-\infty }^{\infty } \gamma _{\epsilon }(\zeta )u_{\epsilon }(\zeta ) \bigl(v_{\epsilon }(\zeta )- \zeta \bigr){\psi }'(\zeta )\,d\zeta \\ &\quad = \bigl(\sigma [\gamma {v}]- \bigl[\gamma {v^{2}} \bigr] \bigr)\psi ( \sigma )+ \int _{-\infty }^{ \infty }\gamma _{0}(\zeta )v_{0}(\zeta )\psi (\zeta )\,d\zeta \end{aligned}$$

and

$$ \begin{aligned} &\int _{-\infty }^{\infty }\epsilon p \bigl(\gamma _{\epsilon }(\zeta ) \bigr){\psi }'( \zeta )\,d\zeta \\ &\quad = \int _{-\infty }^{\sigma _{1}}\epsilon p(\gamma _{-}){ \psi }'(\zeta )\,d\zeta + \int _{\sigma _{2}}^{\infty }\epsilon p(\gamma _{+}){ \psi }'(\zeta )\,d\zeta + \int _{\sigma _{1}}^{\sigma _{2}}\epsilon p( \gamma _{*}){\psi }'(\zeta )\,d\zeta \\ &\quad =\epsilon p(\gamma _{-})\psi (\sigma _{1})-\epsilon p(\gamma _{+}) \psi (\sigma _{2})+\epsilon p(\gamma _{*}) (\sigma _{2}-\sigma _{1}) \frac{\psi (\sigma _{2})-\psi (\sigma _{1})}{\sigma _{2}-\sigma _{1}} \\ &\quad \rightarrow 0 \quad \text{as } \epsilon \to 0. \end{aligned} $$

Thus we obtain the limit of (30):

$$ \lim_{\epsilon \rightarrow 0} \int _{-\infty }^{\infty } \bigl( \gamma _{\epsilon }( \zeta )v_{\epsilon }(\zeta )-\gamma _{0}(\zeta )v_{0}( \zeta ) \bigr)\psi (\zeta )\,d\zeta = \bigl(\sigma [\gamma {v}]- \bigl[\gamma {v^{2}} \bigr] \bigr) \psi (\sigma ). $$
(32)

4. For all \(\psi (\eta ,\tau ) \in C^{\infty }_{0}(\mathbb{R}^{2}_{+})\), based on the transformation of the coordinates \((\eta ,\tau )= (\zeta {\tau },\tau )\), send \(\psi (\zeta )=\psi (\zeta {\tau },\tau )=\psi (\eta ,\tau )\) and \((\gamma _{0}(\zeta ),v_{0}(\zeta ))=(\gamma _{0}(\zeta {\tau },\tau ),v_{0}( \zeta {\tau },\tau ))=(\gamma _{0}(\eta ,\tau ), v_{0}(\eta ,\tau ))\). Then multiplying (31) and (32) by τ and integrating, we get

$$ \begin{aligned} &\lim_{\epsilon \rightarrow 0} \int _{0}^{\infty }\tau \int _{- \infty }^{\infty } \bigl(\gamma _{\epsilon }( \zeta {\tau },\tau )-\gamma _{0}( \zeta {\tau },\tau ) \bigr)\psi ( \zeta {\tau },\tau )\,d{\zeta }\,d\tau \\ &\quad =\lim_{\epsilon \rightarrow 0} \int _{0}^{\infty } \int _{- \infty }^{\infty }(\gamma _{\epsilon }(\eta , \tau )-\gamma _{0}(\eta , \tau )\psi (\eta ,\tau )\,d\eta \,d\tau \\ &\quad = \int _{0}^{\infty }\tau \bigl(\sigma [\gamma ]-[\gamma {v}] \bigr)\psi ({\sigma } \tau ,\tau )\,d\tau \end{aligned} $$

and

$$ \begin{aligned} \lim_{\epsilon \rightarrow 0} \bigl\langle \gamma _{\epsilon }(\eta , \tau ),\psi (\eta ,\tau ) \bigr\rangle &= \bigl\langle \gamma _{0}(\eta ,\tau ), \psi (\eta ,\tau ) \bigr\rangle + \biggl\langle \frac{\tau (\sigma [\gamma ]-[\gamma {v}])}{\sqrt{1+\sigma ^{2}}}{ \delta }_{S},\psi (\eta ,\tau ) \biggr\rangle \\ &= \bigl\langle \gamma _{0}(\eta ,\tau )+w_{1}(\tau ){ \delta }_{S},\psi ( \eta ,\tau ) \bigr\rangle . \end{aligned} $$

Similarly, from (32) we have

$$ \lim_{\epsilon \rightarrow 0} \bigl\langle \gamma _{\epsilon }(\eta , \tau )v_{\epsilon }(\eta ,\tau ),\psi (\eta ,\tau ) \bigr\rangle = \bigl\langle \gamma _{0}(\eta ,\tau )v_{0}(\eta ,\tau )+w_{2}(\tau ){\delta }_{S}, \psi (\eta ,\tau ) \bigr\rangle . $$

Hence the Riemann solution for (1)–(2) surely converges to the delta wave

$$ \bigl(\gamma (\eta ,\tau ),\gamma (\eta ,\tau )v(\eta ,\tau ) \bigr)= \bigl( \gamma _{0}( \eta ,\tau )+w_{1}(\tau )\delta _{S},\gamma _{0}(\eta ,\tau )v_{0}( \eta , \tau )+w_{2}(\tau )\delta _{S} \bigr) $$

in the distribution sense. □

5 Numerical results

Here we show a set of representative numerical outcomes for the Euler scheme (1) with original Riemann information (2). A number of iterative numerical tests have been conducted to verify that the proof does not coincide with numerical objects. The initial values in (1)–(2) are solved by \(p(\gamma ) = \gamma ^{2} +\gamma ^{3}\). This model of pressure satisfies general assumption (4). We take the following initial data:

$$ (\gamma ,v) (\eta ,0)= \textstyle\begin{cases} (1.0,1.5)& \text{for }\eta < 0, \\ (0.2,0.0)& \text{for }\eta >0. \end{cases} $$

For (5) to be discretized, we apply the following explicit conservative approach:

$$\begin{aligned} U^{n+1}_{j}=U^{n}_{j}- \frac{\triangle \tau }{\triangle \eta } \bigl(f^{n}_{j+ \frac{1}{2}} -f^{n}_{j-\frac{1}{2}} \bigr), \end{aligned}$$

where △η is the spatial size, △τ is time step, and \(f^{n}_{j+\frac{1}{2}}\) is the numerical flux. For the simplicity, we use the local first-order Lax–Friedrichs scheme [23]:

$$ f^{n}_{j+\frac{1}{2}}=\frac{1}{2} \bigl(f \bigl(U^{n}_{j} \bigr)+f \bigl(U^{n}_{j+1} \bigr)-\alpha \bigl(U^{n}_{j+1}-U^{n}_{j} \bigr) \bigr), $$

and

$$ \lambda _{\max } \bigl(U^{n}_{j+1} \bigr)\}, \lambda _{\max }(V)=\max \{v-c,v+c \}, \alpha =\max \{\lambda _{\max } \bigl(U^{n}_{j} \bigr), $$

with \(c=\sqrt{p'(\gamma )}\) denoting the velocity sound. Using the stability axiom, we got the time step \(\triangle \tau =\mathrm{CFL}\cdot \frac{\triangle x}{\max_{i}|\lambda _{\max }(V_{i})|}\), where CFL is the short form of the Courant–Friedrichs–Lewyor number [21]. As demonstrated in Figs. 3–4, the intermediate state of the density approaches infinity, and the velocity becomes constant as ϵ is close to zero. As the limit is applied, the overlap of the coupled shocks generates the delta wave, which solves the zero-pressure gas dynamics (6), (2). Thus we conclude that the infinite amplitude is retained by the solutions if the strict hyperbolicity degenerates. In this situation the system of equations (1) is a model. For the numerous selection of ϵ (i.e., \(\epsilon = 0.1, 0.007, 0.0015, 0.00009\), and the time \(\tau = 0.2\)), the numerical simulation is done by taking \(\mathrm{CFL} =1\) with 200 points and is shown in Figs. 4–5. The density producing a Dirac measure is depicted on the left sides of Figs. 4–5. Similarly, the right sides of Figs. 5–6 present the changes in velocity as decreasing using the space variable η as horizontal and velocity v as vertical, which guarantee a step function in the following.

Figure 3
figure 3

Velocity (right) and density (left) for \(\epsilon =0.1\)

Full size image
Figure 4
figure 4

Velocity (right) and density (left) for \(\epsilon =0.007\)

Full size image
Figure 5
figure 5

Velocity (right) and density (left) for \(\epsilon =0.0015\)

Full size image
Figure 6
figure 6

Velocity (right) and density (left) for \(\epsilon =0.00009\)

Full size image

It is illustrated that the delta wave for the zero gas dynamics (6) appears in a way of an efficient numerical approach for the Euler system by considering the limit of pressureless in the solutions. In addition to this technique, we can explore a lot of attractive physical phenomena by employing the proposed approach to evaluate solutions for different types of problems.

6 Conclusion

Finally, we conclude that the limiting values of Riemann solutions to the Euler equations are derived in isentropic gas dynamics fulfilling the general pressure law. We have also provided the zero-pressure gas dynamics of delta wave in distributional form made by the limiting values of the required solution. We have given some numerical approximations for the phenomena of concentration representation. As a future suggestion, the stability of the vacuum state and the case of nonisentropic Euler equations can be analyzed and investigated.