1 Introduction

In audio signal processing, adaptive filters are frequently used to model systems with thousands of taps. To reduce the computational burden, frequency-domain adaptive filters (FDAFs), particularly partitioned-block FDAFs (PBFDAFs), are commonly employed [1,2,3,4,5,6,7]. By utilizing the fast Fourier transform (FFT) for the calculation of the block convolution and correlation, the FDAFs offer significant computational advantages over time-domain and sub-band adaptive filters [8,9,10,11]. However, the FDAF algorithm might not be suitable for certain real-time applications that demand a very low input–output latency. The PBFDAF algorithm can alleviate this limitation by dividing the whole impulse response into shorter and equal-length sub-blocks. The block convolution can be accomplished through a series of shorter block convolutions [12,13,14]. The PBFDAF algorithm reduces the algorithm latency, but at the expense of lower convergence speed [15]. In recent years, deep neural networks (DNNs) have been integrated with the FDAF algorithms to enhance their convergence performance [16,17,18].

The constrained and unconstrained PBFDAFs are two prevalent versions of PBFDAFs [19,20,21]. The unconstrained PBFDAFs omit the gradient constraint on the time-domain weight vector, and hence, FFT computations are reduced in the weight update of each partition [19, 22]. When a specific adaptive filtering algorithm is developed, it is of importance to study the statistical convergence behaviors [1, 23,24,25,26,27,28,29]. Considerable effort has been dedicated to investigate the convergence properties of PBFDAFs [24,25,26,27,28,29]. More recently, a thorough analysis of the PBFDAF algorithm is conducted and some interesting properties are discovered in [27,28,29]. Specifically, the transient and steady-state convergence behaviors of the PBFDAFs with 50% overlap in exact-modeling scenarios are described by the theoretical models in [27] and [29]. Subsequently, following a similar approach as in [27], the statistical performance of the PBFDAFs in under-modeling cases is comprehensively investigated in [28]. However, the analysis of the unconstrained PBFDAFs presented in [28] is somewhat difficult to follow due to the singularity of the autocorrelation matrix governing the mean convergence mode. Additionally, the steady-state filter weight vector depends on its initialization, and the mean square deviation (MSD) is influenced by the initial conditions. Consequently, the MSD cannot accurately reflect the true system modeling capability of the unconstrained PBFDAFs

To resolve the aforementioned problems, this paper provides a new theoretical framework for the deficient-length unconstrained PBFDAFs in a system identification scenario. Motivated by methods in [28] and [29], the presented analysis is based on a modified filter weight vector. We firstly perform the mean analysis of the unconstrained PBFDAFs algorithm. Our findings reveal that the steady-state modified weight vector is independent of the initial values and converges to the unique Wiener solution. We also show that the unconstrained PBFDAFs can recover more coefficients of the unknown plant than the constrained version in certain cases, which is not revealed before and is a very nice property for system identification purpose. We then derive closed-form expressions for the steady-state values of MSD and extra mean square error (EMSE). The MSD calculated using the modified filter weight vector is lower than that obtained from the original one, which indicates that the unconstrained PBFDAFs exhibit a stronger system modeling capability than previously assumed. Moreover, the presented statistical analysis of the unconstrained PBFDAFs is much easier to follow compared to our previous work [28]. Finally, simulations support the theoretical results based on the proposed theoretical model.

2 Unconstrained PBFDAFs

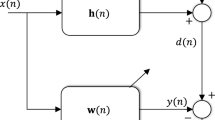
In this paper, the system identification is considered as the adaptive filtering task. The input–output relation of the linear time-invariant system is described by

$$\begin{aligned} d(n)={{\textbf{x}}(n)^T}{{\textbf{w}}_{\textrm{o}}}+v(n), \end{aligned}$$
(1)

where \(\textbf{x}(n) = [x(n),\ldots ,x(n-M+1)]^T\) is the input signal vector of length M, \(\textbf{w}_{\textrm{o}} = [w_0,\ldots ,w_{M-1}]^{T}\) is the parameter vector of the system, d(n) is the desired response, v(n) is the zero-mean additive noise and \((\cdot )^T\) denotes transpose operation. To obtain the parameter vector \(\textbf{w}_{\textrm{o}}\), one can solve the well-known Wiener–Hopf equations. However, this non-iterative solution requires substantial data and computational resources to compute unknown statistical matrices, such as the autocorrelation matrix of the reference signal. In scenarios such as acoustic echo control and acoustic feedback cancelation, it is preferable to estimate the impulse response iteratively using adaptive filtering algorithms due to their computational efficiency and effective tracking capability [1].

We now introduce the unconstrained PBFDAF algorithm, which processes data in blocks rather than individual samples. Once a block of data is collected, the PBFDAF algorithm performs the block convolution and weight updates. The adaptive filter of length \(M_{1}=PL\) is partitioned into P subfilters, each with a length of L. This paper focuses on the under-modeling scenario, i.e., the length of the parameter vector is longer than that of adaptive filter \((M_1 < M)\). The time-domain input signal vector, desired signal vector, output vector and error signal vector for the kth block are defined as follows

$$\begin{aligned} {\textbf{x}}_p(k)= & {} \left[ x((k-p-1)L),\ldots ,x((k-p+1)L-1)\right] ^T, \end{aligned}$$
(2)
$$\begin{aligned} {\textbf{d}}(k)= & {} \left[ d(kL),\ldots ,d((k+1)L-1)\right] ^T, \end{aligned}$$
(3)
$$\begin{aligned} {\textbf{y}}(k)= & {} \left[ y(kL),\ldots ,y((k+1)L-1)\right] ^T, \end{aligned}$$
(4)
$$\begin{aligned} {\textbf{e}}(k)= & {} \left[ e(kL),\ldots ,e((k+1)L-1)\right] ^T. \end{aligned}$$
(5)

The output of the PBFDAFs follows

$$\begin{aligned} {\textbf{y}}(k) = {\textbf{G}}_{01}{\textbf{F}}^{-1}\sum \limits _{p = 0}^{P-1}\varvec{\mathcal {X}}_p(k)\hat{\textbf{W}}_p(k), \end{aligned}$$
(6)

where \(\varvec{\mathcal {X}}_p(k) = \textrm{diag}\{{\textbf{F}}{\textbf{x}}_p(k)\}\) is the input matrix in the frequency domain of dimension \(N=2L\), \(\textrm{diag}(\cdot )\) generates a diagonal matrix, \({\textbf{F}}\) is the \(N \times N\) FFT matrix and \(\hat{\textbf{W}}_p(k)\) is the frequency-domain weight vector. The window matrix \({\textbf{G}}_{01}= [{\textbf{0}}_{L}, {\textbf{I}}_{L}]\) is used to discard the filter output corresponding to circular convolution, where \({\textbf{0}}_{L}\) is a zero matrix of dimension L and \({\textbf{I}}_{L}\) denotes the \(L \times L\) identity matrix.

The time-domain error signal is

$$\begin{aligned} {\textbf{e}}(k) = {\textbf{d}}(k)- {\textbf{y}}(k). \end{aligned}$$
(7)

Using FFT, the vector \({\textbf{e}}(k)\) can be transformed to frequency domain, denoted as \({\textbf{E}}(k)={\textbf{F}}[{{\textbf{0}}_{L{\times }1},{\textbf{e}}^T(k)}]^T\). Then, the unconstrained PBFDAF algorithm update is given by [1, 12]

$$\begin{aligned} \hat{\textbf{W}}_p(k+1) = \hat{\textbf{W}}_p(k) + \mu {\mathbf {\Lambda }}^{-1}{\varvec{\mathcal {X}}}_{p}^{H}(k){\textbf{E}}(k), \end{aligned}$$
(8)

where \(\mu\) is the step size and \((\cdot )^H\) denotes Hermitian operations. The matrix \({\mathbf {\Lambda }}=E\left[ {\varvec{\mathcal {X}}}_{p}^{H}(k){\varvec{\mathcal {X}}}_{p}(k)\right]\) and \({\mathbf {\Lambda }}= {\textbf{I}}_{N}\) represent the normalized and unnormalized PBFDAFs, respectively.

3 Statistical analysis

This section starts with a summary of the analysis results for the deficient-length unconstrained PBFDAFs algorithm developed in [28]. Following this, we construct a modified filter weight vector for an alternative performance analysis. We then proceed to analyze the convergence behaviors of the unconstrained PBFDAFs. It should be mentioned that the presented analysis is based on the results in [28], but it provides a more comprehensive understanding of the performance characteristics of the underlying algorithm.

3.1 Analysis of deficient-length unconstrained PBFDAF in [28]

By transforming the frequency-domain weight vector \(\hat{\textbf{W}}_p(k)\) back to time domain, we have

$$\begin{aligned} \hat{\textbf{w}}_p(k) = {\textbf{F}}^{-1}\hat{\textbf{W}}_p(k)= [{\hat{w}}_{p,0}(k),\ldots ,{\hat{w}}_{p,N-1}(k)]^T. \end{aligned}$$
(9)

In [29], it is demonstrated that the output vector \({\textbf{y}}(k)\) can be expressed in terms of the vectors \(\hat{\textbf{w}}_p(k)\) as

$$\begin{aligned} \hat{\textbf{y}}(k) = \sum \limits _{p=0}^{P-1}{\textbf{X}}_p(k)\hat{\textbf{w}}_p(k)={\textbf{X}}_a(k)\hat{\textbf{w}}(k), \end{aligned}$$
(10)

where \(\hat{\textbf{w}}(k)=[\hat{\textbf{w}}_0^T(k),\ldots , \hat{\textbf{w}}_{P-1}^T(k)]^T\) represents the augmented filter weight vector of length NP, \({\textbf{X}}_p(k)= {\textbf{G}}_{01}{\textbf{F}}^{-1} \varvec{\mathcal {X}}_p(k){\textbf{F}} = [{\textbf{x}}_{p,0}(k),\ldots , {\textbf{x}}_{p,N-1}(k)]\) is the time-domain input matrix of size \(L \times N\) and \({\textbf{X}}_a(k)=\left[ {\textbf{X}}_0(k), \ldots ,{\textbf{X}}_{P-1}(k)\right]\) is the augmented input matrix of size \(L \times NP\)

The parameter vector of the unknown plant can be divided into two parts \({{\textbf{w}}_{\textrm{o}}}= [{\textbf{w}_{*}^T},{\textbf{w}_{r}^T}]^T\). The modeling part of the system \({\textbf{w}_{*}}= [{\textbf{w}_{0}^T},\ldots ,{\textbf{w}_{P-1}^T}]^T\) corresponds to the first \(M_1\) coefficients of the parameter vector \(\textbf{w}_{\textrm{o}}\), where \({\textbf{w}_{p}}= [{{w}_{pL},\ldots ,{w}_{(p+1)L-1}}]^T\) is a vector of length L. The under-modeling part \({\textbf{w}_{r}}=\left[ {w}_{PL},\ldots ,{w}_{M-1}\right] ^T\) is of length \(M_2=M-M_1\). We define the weight-error vector as

$$\begin{aligned} \tilde{\textbf{w}}(k) = \overline{\textbf{w}}-\hat{\textbf{w}}(k), \end{aligned}$$
(11)

where \(\overline{\textbf{w}}=[{\overline{\textbf{w}}}_0^T,\ldots ,{\overline{\textbf{w}}}_{P-1}^T]^T\) is the zero-padded parameter vector of length NP and \({\overline{\textbf{w}}}_p=[{\textbf{w}}_p^T,{\textbf{0}}_{1\times L}]^T\). As shown in [28], the update equation of the weight-error vector is given by

$$\begin{aligned} \begin{aligned} \tilde{\textbf{w}}(k+1) =&\tilde{\textbf{w}}(k)-\mu {\varvec{\theta }}{\textbf{X}}_{a}^T(k) {\textbf{X}}_{a}(k)\tilde{\textbf{w}}(k) \\&-\mu {\varvec{\theta }}{\textbf{X}}_{a}^T(k){\textbf{X}}_{r}(k){\textbf{w}}_r(k) \\&-\mu {\varvec{\theta }}{\textbf{X}}_{a}^T(k){\textbf{v}}(k), \end{aligned} \end{aligned}$$
(12)

where \({\varvec{\theta }}=\textrm{blkdiag}({\varvec{\sigma }},\ldots ,{\varvec{\sigma }})\) is the \(NP{\times }NP\) block diagonal matrix, \({\varvec{\sigma }} = ({{\textbf{F}}^{-1} {\mathbf {\Lambda }}{\textbf{F}} })^{-1}\) and \({\textbf{X}}_{r}(k)=\left[ {\textbf{x}}_{r}(kL),\ldots , {\textbf{x}}_{r}(kL+L-1)\right] ^T\) is the \(L \times M_2\) input matrix with \({\textbf{x}}_{r}(n)=\left[ x(n-PL),\ldots ,x(n-M+1)\right] ^T\). Using (12), the expectation of the weight-error vector \(\tilde{\textbf{w}}(k)\) is given by

$$\begin{aligned} \begin{aligned} E[\tilde{\textbf{w}}(k+1)] =&(\textbf{I}-\mu {E[{\textbf{A}}_{0}(k)]})E[\tilde{\textbf{w}}(k)] \\&-E[{\textbf{B}}_{0}(k)]{\textbf{w}}_{r}(k), \end{aligned} \end{aligned}$$
(13)

where \({\textbf{A}}_{0}(k)={\varvec{\theta }}{\textbf{X}}_{a}^T(k) {\textbf{X}}_{a}(k)\), \({\textbf{B}}_{0}(k)={\varvec{\theta }}{\textbf{X}}_{a}^T(k){\textbf{X}}_{r}(k)\) and \(E(\cdot )\) is the statistical expectation operator.

The convergence characteristics of the deficient-length unconstrained PBFDAFs are accurately described by the theoretical model proposed in [28]. However, this model has two limitations. First, the analysis of the mean and mean square performance is mathematically complicated. This is because of the correlation matrix \({E[{\textbf{A}}_{0}(k)]}\) is singular and has zero eigenvalues. Second, because the correlation matrix \({E[{\textbf{A}}_{0}(k)]}\) is rank-deficient, the filter coefficients are dependent on their initial values in the steady state. In [30], the behaviors of several popular adaptive filtering algorithms are investigated when the covariance matrix of the input signal is singular. A similar convergence behavior of the LMS algorithm is revealed in [30], e.g., the steady-state weights are biased and depend on the weight initialization. However, it should be mentioned that the deficient rank of the input covariance matrix is due to the underlying signal characteristic in [30], while it is caused by the overlap between successive partitions in the PBFDAF algorithm. In [29], we have demonstrated that the bias in the steady-state weights of the unconstrained PBFDAF can be eliminated, allowing PBFDAF to recover the true impulse response in exact-modeling scenarios. Hence, the MSD calculated using the weight-error vector cannot accurately reflect the system modeling capability of the unconstrained PBFDAFs.

3.2 Proposed model

To overcome the above difficulties, we now present an alternative theoretical model, which was originally applied to analyze the performance of the unconstrained PBFDAF in exact-modeling scenarios [29]. In [28], the main difficulty in performance analysis lies in the singularity of correlation matrix \({E[{\textbf{A}}_{0}(k)]}\) since there are identical columns in the augmented input matrix \({\textbf{X}}_a(k)\). Specifically, we have \({\textbf{x}_{p,0}(k)}={\textbf{x}_{p+1,L}(k)}\) for \({0\le p \le P-2}\). This motivates us to remove the identical columns in the matrix \({\textbf{X}}_a(k)\). Subsequently, we construct a new weight vector \({\hat{\textbf{h}}(k)}\) to remain the time-domain output vector \({\textbf{y}}(k)\) unchanged.

To illustrate our main idea, we partition the adaptive filter of length \(M_1 = 2\) into \(P = 2\) blocks, i.e., \(L = 1\). The output of the filter is calculated by

$$\begin{aligned} \textbf{y}(k)=\left[ \begin{array}{llll} x(k)&x(k-1)&x(k-1)&x(k-2) \end{array}\right] \left[ \begin{array}{c} \hat{w}_{0,0}(k) \\ \hat{w}_{0,1}(k) \\ \hat{w}_{1,0}(k) \\ \hat{w}_{1,1}(k) \end{array}\right] . \end{aligned}$$
(14)

By removing the same columns of the data matrix and reconstructing the weight vector in (14), the output vector \({\textbf{y}}(k)\) can also be expressed by

$$\begin{aligned} \textbf{y}(k)=\left[ \begin{array}{lll} x(k)&x(k-1)&x(k-2) \end{array}\right] \left[ \begin{array}{c} \hat{w}_{0,0}(k) \\ \hat{w}_{0,1}(k) + \hat{w}_{1,0}(k) \\ \hat{w}_{1,1}(k) \end{array}\right] . \end{aligned}$$
(15)

Since the data matrix in (14) contains the identical columns, its correlation matrix is singular. As suggested in [28], the steady-state values of \(\hat{w}_{0,1}(k)\) and \(\hat{w}_{1,0}(k)\) depend on their initial values. In contrast, the data matrix in (15) does not contain any identical columns and its correlation matrix is invertible. Hence, the steady-state coefficients \(\hat{w}_{0,1}(k) + \hat{w}_{1,0}(k)\) do not depend on its initial values. Our subsequent study shows that this property not only simplifies the convergence behavior analysis but also allows us to focus on the influence of the under-modeling part on the steady-state performance of the algorithm. Finally, based on the proposed model, we demonstrate that the modeling part of the system can be recovered in certain cases

In general, by deleting the columns of \({\textbf{x}_{p,L}(k)}\) \({0\le p \le P-2}\) in the augmented input matrix \({\textbf{X}}_a(k)\), we obtain the modified input matrix \({\textbf{X}}_b(k)\) with dimensions \(L \times (NP-P+1)\). The modified input matrix \({\textbf{X}}_b(k)\) and input matrix \({\textbf{X}}_a(k)\) are related through the following equations

$$\begin{aligned}{} & {} {{\textbf{X}}_{b}(k)}= {{\textbf{X}}_{a}(k)} {\varvec{\beta }}. \end{aligned}$$
(16)
$$\begin{aligned}{} & {} {{\textbf{X}}_{a}(k)}= {{\textbf{X}}_{b}(k)} {\varvec{\alpha }}, \end{aligned}$$
(17)

where the matrices \({\varvec{\beta }}\) and \({\varvec{\alpha }}\) are of size \((NP-P+1) \times NP\) and \(NP \times (NP-P+1)\), respectively. We generate the matrix \({\varvec{\beta }}\) by removing the \((2p-1)L\)th \((p = 1,\ldots , P-1)\) columns of the identity matrix \({\textbf{I}_{NP}}\). We generate the matrix \({\varvec{\alpha }}\) by first constructing a matrix \({\varvec{\alpha }}_{0}\), where the \(2p-1)L\)th \((p = 1,\ldots , P-1)\) rows of the identity matrix \({\textbf{I}_{NP}}\) are added to the 2pLth row. Then, by removing \((2p-1)L\)th \((p = 1,\ldots , P-1)\) rows of the matrix \({\varvec{\alpha }}_{0}\), we obtain the matrix \({\varvec{\alpha }}_{0}\).

Substituting (17) into (10), we may express the output vector \({\textbf{y}}(k)\) as [29]

$$\begin{aligned} {\textbf{y}}(k)= {{\textbf{X}}_{b}(k)} {\hat{\textbf{h}}(k)}, \end{aligned}$$
(18)

where \({\hat{\textbf{h}}(k)} ={\varvec{\alpha }} {\hat{\textbf{w}}(k)} = [{\hat{\textbf{h}}_{0}^{T}(k)},\ldots , {\hat{\textbf{h}}_{P-1}^{T}(k)}]^{T}\) is the modified weight vector of length \(NP-P+1\),

$$\begin{aligned}{} & {} \begin{aligned} \hat{\textbf{h}}_0(k) =&{[\underbrace{\hat{w}_{0,0}(k), \ldots , \hat{w}_{0, L-1}(k)}_L,} \\ {}&\underbrace{\hat{w}_{0, L+1}(k), \ldots , \hat{w}_{0,N-1}(k)}_{L-1}]^T, \end{aligned}\\{} & {} \begin{aligned} \hat{\textbf{h}}_p(k) =&{[\underbrace{\hat{w}_{p,0}(k) +\hat{w}_{p-1,L}(k), \ldots , \hat{w}_{p, L-1}(k)}_L,} \\ {}&\underbrace{\hat{w}_{p, L+1}(k), \ldots , \hat{w}_{p,N-1}(k)}_{L-1}]^T, {1 \le p \le P-2 } \end{aligned}\\{} & {} \begin{aligned} \hat{\textbf{h}}_{P-1}(k)=&{[\underbrace{\hat{w}_{P-1,0}(k) +\hat{w}_{P-2,L}(k), \ldots , \hat{w}_{P-1, L-1}(k)}_L,} \\ {}&\underbrace{\hat{w}_{P-1, L}(k), \ldots , \hat{w}_{P-1,N-1}(k)}_{L}]^T. \end{aligned} \end{aligned}$$

Using the modified matrix \({{\textbf{X}}_{b}(k)}\), the desired signal vector \({\textbf{d}}(k)\) can be expressed as

$$\begin{aligned} {\textbf{d}}(k)= {{\textbf{X}}_{b}(k)} {{\textbf{h}}_{\textrm{o}}}+ {\textbf{X}}_{r}(k){\textbf{w}}_{r}(k)+{\textbf{v}}(k), \end{aligned}$$
(19)

where \({{\textbf{h}}_{\textrm{o}}} = {\varvec{\alpha }}{\overline{\textbf{w}}} =[{{\textbf{h}}_{0}^{T}},\ldots , {{\textbf{h}}_{P-1}^{T}}]^{T}\) is the modified augmented weight vector with \({{\textbf{h}}_{p}} = [{\textbf{w}}_p^T,{\textbf{0}_{1 \times (L-1)}}]^{T}\) for \(0 \le p \le P-2\) and \({{\textbf{h}}_{P-1}} = [{\textbf{w}}_{P-1}^T,{\textbf{0}_{1 \times L}}]^{T}\). The modified weight-error vector is given by

$$\begin{aligned} {\tilde{\textbf{h}}(k)} = {{\textbf{h}}_{\textrm{o}}}-{\hat{\textbf{h}}(k)}. \end{aligned}$$
(20)

Substituting (18) and (19) into (7), we may rewrite the error vector as

$$\begin{aligned} {\textbf{e}}(k)= {{\textbf{X}}_{b}(k)} {\tilde{\textbf{h}}(k)}+ {\textbf{X}}_{r}(k){\textbf{w}}_{r}(k)+{\textbf{v}}(k). \end{aligned}$$
(21)
Fig. 1
figure 1

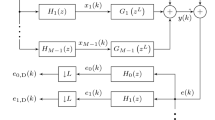
Connection between the theoretical model in [28] and the proposed model

Full size image

The connection between the theoretical model in [28] and the proposed model is depicted in Fig. 1. The elements \([\bar{\textbf{w}}, \textbf{X}_{a}(k),\hat{\textbf{w}}(k)]\) and \([{\textbf{h}_{\textrm{o}}}, \textbf{X}_{b}(k),\hat{\textbf{h}}(k)]\) are the primary components of the model in [28] and that of the proposed model, respectively. The primary components of the two models can be related by the matrices \(\varvec{\alpha }\) and \(\varvec{\beta }\). As shown in (18) and (19), the two model are equivalent in calculating the output \({\textbf{y}}(k)\) and the desired signal vector \({\textbf{d}}(k)\). Hence, the mean square convergence behavior of the algorithm can be described by the proposed model.

3.3 Mean convergence behavior

Two assumptions are used for the following derivation. [A1] The noise signal v(n) and the input signal x(n) are independent and both have zero mean. [A2] Independence assumption: The input matrix \({{\textbf{X}}_{b}(k)}\) and the weight vector \({\hat{\textbf{h}}(k)}\) and are mutually independent [1].

Premultiplying the matrix \({\varvec{\alpha }}\) on both sides of (12) and using (17), we obtain

$$\begin{aligned} \begin{aligned} {\tilde{\textbf{h}}(k+1)}=&{\tilde{\textbf{h}}(k)}-{\mu } {{\textbf{A}}(k)} {\tilde{\textbf{h}}(k)} - {\mu } {{\textbf{B}}(k)} {{\textbf{w}}_{r}} \\&- {\mu } {\varvec{\alpha }} {\varvec{\theta }} {{\textbf{X}}_{a}^T(k)} {\textbf{v}}(k), \end{aligned} \end{aligned}$$
(22)

where \({{\textbf{A}}(k)}= {\varvec{\alpha }} {\varvec{\theta }}{\textbf{X}}_{a}^T(k) {\textbf{X}}_{a}(k){\varvec{\beta }}\) and \({{\textbf{B}}(k)}= {\varvec{\alpha }} {\varvec{\theta }}{\textbf{X}}_{a}^T(k) {\textbf{X}}_{r}(k)\). Using the independence assumption [A2], we have

$$\begin{aligned} \begin{aligned} E[{\tilde{\textbf{h}}(k+1)}]=&[{\textbf{I}}-{\mu }E({{\textbf{A}}(k)})] E[{\tilde{\textbf{h}}(k)}] \\&- {\mu } {E[{{\textbf{B}}(k)}] } {\textbf{w}}_r. \end{aligned} \end{aligned}$$
(23)

Since the matrix \(E[{{\textbf{A}}(k)}]\) does not contain any identical columns, it does not have zero eigenvalues and is invertible. Hence, the steady-state value of the weight-error vector is

$$\begin{aligned} E[{\tilde{\textbf{h}}(\infty )}]= -{(E[{{\textbf{A}}(k)}])^{-1}} {{E[{{\textbf{B}}(k)}]}} {\textbf{w}}_r. \end{aligned}$$
(24)

It is apparent that the steady-state weight-error vector \({\tilde{\textbf{h}}(\infty )}\) is independent of the initial weight-error vector \({\tilde{\textbf{h}}(0)}\), which is quite different from the original weight-error vector \({\tilde{\textbf{w}}(k)}\).

We now investigate the Wiener solution of the modified weight-error vector \({\tilde{\textbf{h}}(k)}\) and examine whether it converges to the Wiener solution. By replacing the modified weight-error vector \({\tilde{\textbf{h}}(k)}\) with a fixed vector \({\tilde{\textbf{h}}}\) in (21), we may write the MSE as

$$\begin{aligned} \begin{aligned} J&= \frac{1}{L}{E{\Vert {\textbf{e}}(k) \Vert }^2} \\&= \frac{1}{L}({\tilde{\textbf{h}}}^T {\textbf{R}}_b {\tilde{\textbf{h}}} +{\tilde{\textbf{h}}}^T{\textbf{R}}_{br} {\textbf{w}}_r + {\textbf{w}}_r^T {\textbf{R}}_{br}^T {\tilde{\textbf{h}}}) + {\sigma }_v^2, \end{aligned} \end{aligned}$$
(25)

where \({\textbf{R}}_b = E[{{\textbf{X}}_{b}^T(k)} {{\textbf{X}}_{b}(k)}]\) and \({\textbf{R}}_{br}=E[{{\textbf{X}}_{b}^T(k)} {{\textbf{X}}_{r}(k)}]\). The Wiener solution of (24) satisfies

$$\begin{aligned} \frac{\partial J}{\partial {\tilde{\textbf{h}}}} = 2{\textbf{R}}_b{\tilde{\textbf{h}}}+2{\textbf{R}}_{br}{\textbf{w}}_r = {\textbf{0}}. \end{aligned}$$
(26)

Since the matrix \(\textbf{R}_b\) is full rank, we can obtain the Wiener solution using (26)

$$\begin{aligned} {\tilde{\textbf{h}}}_{\textrm{opt}} = - {\textbf{R}}_b^{-1}{\textbf{R}}_{br}{\textbf{w}}_r. \end{aligned}$$
(27)

Equation (27) indicates that, within our theoretical framework, the Wiener solution is uniquely determined by the under-modeling part and the statistical characteristics of the input signal. In contrast, the theoretical model proposed in [28] results in infinitely many Wiener solutions. In Appendix A, we demonstrated that \(E[{\tilde{\textbf{h}}(\infty )}]={\tilde{\textbf{h}}}_{\textrm{opt}}\), which indicates that the modified weight-error vector \({\tilde{\textbf{h}}}(k)\) converges to the Wiener solution. Moreover, the correlation matrix \({\textbf{R}}_{br}\) is nonzero regardless of the input signal. Consequently, the vector \(E[{\tilde{\textbf{h}}(\infty )}]\) is not a zero vector and \({\hat{\textbf{h}}}(k)\) cannot converge to \({{\textbf{h}}}_{\textrm{o}}\) in the mean sense.

As aforementioned, the vector \(E[{\hat{\textbf{h}}(\infty )}]\) does not match \({{\textbf{h}}}_{\textrm{o}}\) that consists of the first PL elements of the unknown plant. Does it mean that we cannot obtain any useful information about the unknown plant from \({\hat{\textbf{h}}}(k)\)? The answer is no as we will immediately show.

3.3.1 White noise input

We will demonstrate that we can recover (calculate) the first \(PL+L\) coefficients of the parameter vector \(\textbf{w}_{\textrm{o}}\) for white noise input. For \(M_2 \ge L\), the under-modeling vector can be divided into two parts \({{\textbf{w}}_r} = [{{\textbf{w}}_{r1}^T},{{\textbf{w}}_{r2}^T}]^T\), where \({{\textbf{w}}_{r1}} = [w_{PL},\ldots ,w_{PL+L-1}]\) and \({{\textbf{w}}_{r2}} = [w_{PL+L},\ldots ,w_{PL+M_2-1}]\). For \(M_2 < L\), we may zero-pad the vector \({{\textbf{w}}_r}\) to obtain \({{\textbf{w}}_{r0}} = [{{\textbf{w}}_r^T},{\textbf{0}}_{1 \times (L-M_2)}]^T\).

For white noise input signal, the matrix \({\textbf{R}}_{br}\) can be represented as

$$\begin{aligned} {\textbf{R}}_{br} = \begin{bmatrix} {\textbf{0}}_{(NP-P-L+1) \times L} &{} {\textbf{0}}_{(NP-P-L+1) \times (M_2-L)} \\ {\textbf{K}} &{} {\textbf{0}}_{L \times (M_2-L)} \\ \end{bmatrix}, \end{aligned}$$
(28)

where \({\textbf{K}} = {\textrm{diag}} \{{\sigma }_x^2[L,L-1,\ldots ,1]^T\}\) is a \(L \times L\) diagonal matrix and \({\sigma }_x^2 = E[x^2(n)]\) is the variance of the input signal. We partition the matrix \({\textbf{R}}_{b}^{-1}\) into four submatrices

$$\begin{aligned} {\textbf{R}}_{b}^{-1} = \begin{bmatrix} {\textbf{R}_1} &{} {\textbf{R}_2} \\ {\textbf{R}_3} &{} {\textbf{R}_4} \\ \end{bmatrix}, \end{aligned}$$
(29)

where \({\textbf{R}_1}\), \({\textbf{R}_2}\), \({\textbf{R}_3}\) and \({\textbf{R}_4}\) are the submatrix of dimensions \((NP-P-L+1) \times (NP-P-L+1)\), \((NP-P-L+1) \times L\), \(L \times (NP-P-L+1)\) and \(L \times L\), respectively. Substituting (28) and (29) into (27), we obtain

$$\begin{aligned} E[{\tilde{\textbf{h}}(\infty )}] = -\begin{bmatrix} {\textbf{R}_2} {\textbf{K}} {\textbf{w}_{r1}} \\ {\textbf{R}_4} {\textbf{K}} {\textbf{w}_{r1}} \\ \end{bmatrix}. \end{aligned}$$
(30)

Note that for white noise input, only the first L entries of vector \({\textbf{w}_{r}}\) contribute to the bias of the steady-state filter weight vector \(E[{\tilde{\textbf{h}}(\infty )}]\). We split \(E[{\hat{\textbf{h}}(\infty )}]\) into

$$\begin{aligned} E[{\hat{\textbf{h}}(\infty )}] = \begin{bmatrix} {\hat{\textbf{h}}_1(\infty )} \\ {\hat{\textbf{h}}_2(\infty )} \\ \end{bmatrix}, \end{aligned}$$
(31)

where the vectors \({\hat{\textbf{h}}_1(\infty )}\) and \({\hat{\textbf{h}}_2(\infty )}\) are of length \(NP-P-L+1\) and L, respectively. Using (30) and (31), we have

$$\begin{aligned} {\hat{\textbf{h}}_2(\infty )} = {\textbf{R}_4} {\textbf{K}} {\textbf{w}_{r1}}. \end{aligned}$$
(32)

Using (32), We can then obtain

$$\begin{aligned} {\textbf{w}_{r1}} = {\textbf{K}^{-1}} {\textbf{R}_4^{-1}} {\hat{\textbf{h}}_2(\infty )}. \end{aligned}$$
(33)

Substituting (33) into (30), we obtain the vector \({\tilde{\textbf{h}}(\infty )}\) and \({\textbf{h}_{\textrm{o}}}\) can be computed by

$$\begin{aligned} {\textbf{h}}_{\textrm{o}} =E[{\hat{\textbf{h}}(\infty )}] + E[{\tilde{\textbf{h}}(\infty )}]. \end{aligned}$$
(34)

Since the modeling part \(\textbf{w}_{*}\) of length PL can be recovered by (34) and the first L coefficient of the under-modeling part \({\textbf{w}_{r}}\) can be recovered by (33), we obtain the first \(PL+L\) coefficients of the weight vector \({\textbf{w}_{o}}\) from the weight vector \(E[{\hat{\textbf{h}}(\infty )}]\), which is referred to as \({\breve{\textbf{h}}} = [{\textbf{w}}_{*}^T, {\textbf{w}_{r1}^{T}}]^{T}\).

3.3.2 Correlated input

At this point, we investigate the recovery of the true weight vector \(\textbf{w}_{\textrm{o}}\) for correlated input. By permuting the entries of the vector \(E[{\hat{\textbf{h}}(\infty )}]\), we obtain the vector \({\hat{\textbf{b}}} = [{\hat{\textbf{b}}}_1^T,{\hat{\textbf{b}}}_2^T]\), where

$$\begin{aligned}{} & {} \begin{aligned} \hat{\textbf{b}}_1 =&E[\underbrace{{\hat{w}_{0,0}(\infty )}, \ldots , {\hat{w}_{0,L-1}(\infty )}}_L, \\ {}&\underbrace{{\hat{w}_{1,0}(\infty )} + {\hat{w}_{0,L}(\infty )}, \ldots , {\hat{w}_{1,L-1}(\infty )}}_L, \ldots \\ {}&\underbrace{ {\hat{w}_{P-1, 0}(\infty )} + \hat{w}_{P-2, L+1}(\infty ), \ldots , \hat{w}_{P-1,L-1}(\infty )}_{L}]^T, \end{aligned}\\{} & {} \begin{aligned} \hat{\textbf{b}}_2 =&E[\underbrace{{\hat{w}_{0,L+1}(\infty )}, \ldots , {\hat{w}_{0,N-1}(\infty )}}_{L-1}, \\ {}&\underbrace{{\hat{w}_{1,L+1}(\infty )}, \ldots , {\hat{w}_{1,N-1}(\infty )}}_{L-1}, \ldots \\ {}&\underbrace{ {\hat{w}_{P-1, L}(\infty )}, \ldots , \hat{w}_{P-1,N-1}(\infty )}_{L}]^T, \end{aligned} \end{aligned}$$

are of lengths PL and \(PL-P+1\), respectively. The vector \({\hat{\textbf{b}}}\) and \(E[{\hat{\textbf{h}}(\infty )}]\) can be related as

$$\begin{aligned} {\hat{\textbf{b}}} = {\textbf{P}} {E[{\hat{\textbf{h}}(\infty )}]}, \end{aligned}$$
(35)

where \({\textbf{P}}\) is a \((NP-P+1) \times (NP-P+1)\) permutation matrix. Premultiplying both sides of (34) by the permutation matrix \({\textbf{P}}\), we have

$$\begin{aligned} {{\textbf{b}}_{\textrm{o}}} = {\hat{\textbf{b}}} + {\tilde{\textbf{b}}}, \end{aligned}$$
(36)

where \({{\textbf{b}}_{\textrm{o}}} = {\textbf{P}}{{\textbf{h}}_{\textrm{o}}} = [ {\textbf{w}_{*}^{T}, {\textbf{0}}_{1 \times (PL-P+1)}} ]^{T}\) and \({\tilde{\textbf{b}}} = {\textbf{P}} E[{\tilde{\textbf{h}}(\infty )}]\). Using (27), the vector \({\tilde{\textbf{b}}}\) can be represented as \({\tilde{\textbf{b}}} = {\textbf{Q}} {\textbf{w}_{r}}\), where \({\textbf{Q}} = - {\textbf{P}} {\textbf{R}}_b^{-1} {\textbf{R}}_{br}\) is of dimension \((NP-P+1) \times M_2\). We split \({\textbf{Q}}\) as \({\textbf{Q}} = [{\textbf{Q}}_{1}^{T},{\textbf{Q}}_{2}^{T}]^{T}\), where the submatrices \({\textbf{Q}}_{1}\) and \({\textbf{Q}}_{2}\) are of dimensions \(PL \times M_2\) and \((PL-P+1) \times M_2\), respectively. We then rewrite (36) as

$$\begin{aligned} \begin{bmatrix} {\textbf{w}_{*}} \\ {\textbf{0}}_{(PL-P+1) \times 1} \\ \end{bmatrix} = \begin{bmatrix} {\hat{\textbf{b}}_1} \\ {\hat{\textbf{b}}_2} \\ \end{bmatrix} + \begin{bmatrix} {{\textbf{Q}}_{1} {\textbf{w}_{r}} } \\ {{\textbf{Q}}_{2} {\textbf{w}_{r}} } \\ \end{bmatrix}. \end{aligned}$$
(37)

Provided that the matrix \({ {\textbf{Q}}_{2} }\) is of full column rank, \({\textbf{w}_{r}}\) can be obtained by

$$\begin{aligned} {\textbf{w}_{r}} = - ( {\textbf{Q}}_{2}^{T} {\textbf{Q}}_{2} )^{-1} {\textbf{Q}}_{2}^{T} {\hat{\textbf{b}}_2}. \end{aligned}$$
(38)

Substituting (38) into (37), the modeling part \({\textbf{w}_{*}}\) can be expressed as

$$\begin{aligned} {\textbf{w}_{*}} = {\hat{\textbf{b}}_1} + {\textbf{Q}}_{1}{\textbf{w}_{r}}. \end{aligned}$$
(39)

Using (38) and (39), the true impulse response \({{\textbf{w}}}_{\textrm{o}}\) can be recovered.

To guarantee that \({ {\textbf{Q}}_{2} }\) is of full column rank, it should have \(M_2 \le PL-P+1\). However, this is not a sufficient condition. For instance, for a first-order autoregressive (AR) process as input, the matrix \({ {\textbf{Q}}_{2} }\) has rank at most L, and hence, the true impulse response cannot be recovered in this case.

The results in Sects. 3.3.1 and 3.3.2 are of particularly interest and show we can indeed obtain useful information about the true system impulse response using the unconstrained PBFDAFs. Specifically, the unconstrained PBFDAFs can recover more coefficients of the unknown plant than the constrained version in certain cases. Also, we can use (32) to determine whether the unconstrained PBFDAF is sufficient length or deficient length. In other words, if \({\hat{\textbf{h}}_2(\infty )}\) is a zero vector (or very close to a zero vector), it indicates that \({\textbf{w}_{r}}\) is a zero vector and we are using a sufficient-length adaptive algorithm.

3.4 Mean square convergence behavior

Using (21) and invoking the independence assumption, the EMSE produced by the algorithm is

$$\begin{aligned} \begin{aligned} {\xi }_{ex}(k) =&\frac{1}{L} {\textrm{tr}} (E[{\tilde{\textbf{h}}(k)}{\tilde{\textbf{h}}^T(k)}] {{\textbf{R}}_b } \\&+ E[{\tilde{\textbf{h}}(k)}{\textbf{w}_{r}^T}]{{\textbf{R}}_{br}^T } \\ {}&+ E[{\textbf{w}_{r}}{\tilde{\textbf{h}}^T(k)}]{{\textbf{R}}_{br} } \\&+ E[{\textbf{w}_{r}}{\textbf{w}_{r}^T}]{{\textbf{R}}_{rr} } ), \end{aligned} \end{aligned}$$
(40)

where \({{\textbf{R}}_{rr}} = E[{\textbf{X}_{r}^{T}(k)}{\textbf{X}_{r}(k)}]\). The last three terms of (40) are introduced by the under-modeling part \({\textbf{w}_{r}}\). To continue with our analysis, it is required to calculate the covariance matrix \(E[{\tilde{\textbf{h}}(k)}{\tilde{\textbf{h}}^T(k)}]\). Using (22), we have

$$\begin{aligned} \begin{aligned} E[{\tilde{\textbf{h}}(k+1)}{\tilde{\textbf{h}}^T(k+1)}] =&E[{\tilde{\textbf{h}}(k)}{\tilde{\textbf{h}}^T(k)}] \\&-\mu E[{\textbf{A}(k)} {\tilde{\textbf{h}}(k)}{\tilde{\textbf{h}}^T(k)}] \\&-\mu E[{\textbf{B}(k)} {\textbf{w}_{r}} {\tilde{\textbf{h}}^T(k)}] \\&-\mu E[{\tilde{\textbf{h}}(k)} {\tilde{\textbf{h}}^T(k)}{\textbf{A}^{T}(k)} ] \\&-\mu E[{\tilde{\textbf{h}}(k)} {\textbf{w}_{r}^T} {\textbf{B}^{T}(k)} ] \\&+ {\mu }^2 E[{\textbf{A}(k)} {\tilde{\textbf{h}}(k)} {\tilde{\textbf{h}}^T(k)} {\textbf{A}^{T}(k)} ] \\&+ {\mu }^2 E[{\textbf{B}(k)} {\textbf{w}_{r}} {\tilde{\textbf{h}}^T(k)} {\textbf{A}^{T}(k)}] \\&+ {\mu }^2 E[{\textbf{A}(k)} {\tilde{\textbf{h}}(k)} {\textbf{w}_{r}^T} {\textbf{B}^{T}(k)} ] \\&+ {\mu }^2 E[{\textbf{B}(k)} {\textbf{w}_{r}} {\textbf{w}_{r}^T} {\textbf{B}^{T}(k)}] \\&+ {\mu }^2 {{\sigma }_{v}^2} E[{\varvec{\alpha }} {\varvec{\theta }}{\textbf{X}_{a}^{T}(k)}{\textbf{X}_{a}(k)}{\varvec{\theta }^T}{\varvec{\alpha }^{T}}]. \end{aligned} \end{aligned}$$
(41)

To facilitate the derivation of the recursion of the covariance matrix, we introduce the vectorization operator \({\textrm{vec}}({\cdot })\), which stacks the input matrix into one column. Applying the operator \({\textrm{vec}}({\cdot })\) to the matrix product \({\textbf{M}} {\textbf{Q}} {\textbf{N}}\), we have [31]

$$\begin{aligned} {\textrm{vec}}({\textbf{M}} {\textbf{Q}} {\textbf{N}}) = ({\textbf{N}}^{T} {\otimes } {\textbf{M}}) {\textrm{vec}} ({\textbf{Q}}), \end{aligned}$$
(42)

where \({\otimes }\) denotes the Kronecker product.

We define the vectorization of the covariance matrix as \({{\textbf{z}}(k)}= {\textrm{vec}}({\tilde{\textbf{h}}(k)}{\tilde{\textbf{h}}^T(k)})\). Using (41) and (42), \({{\textbf{z}}(k)}\) satisfies the difference equation

$$\begin{aligned} {{\textbf{z}}(k+1)} ={\textbf{H}}{{\textbf{z}}(k)} + {\varvec{\theta }}(k), \end{aligned}$$
(43)

where the matrices \({\textbf{H}}\) and \({\varvec{\theta }}(k)\) are

$$\begin{aligned}{} & {} {\textbf{H}} ={\textbf{I}}- {\mu }{\textbf{D}} + {\mu }^2{\textbf{J}}, \end{aligned}$$
(44)
$$\begin{aligned}{} & {} {\varvec{\theta }}(k) = \sum \limits _{i=1}^{4} {{\varvec{\theta }}_{i}(k)}. \end{aligned}$$
(45)

The matrices \({\textbf{D}}\) and \({\textbf{J}}\) in (44) are given by \({\textbf{D}} = E[{\textbf{A}(k)}] {\otimes } {\textbf{I}} + {\textbf{I}} {\otimes } E[{\textbf{A}(k)}]\) and \({\textbf{J}} = E[{\textbf{A}(k)} {\otimes } {\textbf{A}(k)}]\). The vectors \({{\varvec{\theta }}_{i}(k)}\) in (45) are given by

$$\begin{aligned}{} & {} \begin{aligned} {{\varvec{\theta }}_{1}(k)} =&(-{\mu } E[{\textbf{B}(k)}] {\otimes } {\textbf{I}} + {\mu }^2 E[{\textbf{B}(k)} {\otimes } {\textbf{A}(k)}]) \\&{\times } {\textrm{vec}} ({\tilde{\textbf{h}}(k)} {\textbf{w}_{r}^T} ), \end{aligned}\end{aligned}$$
(46)
$$\begin{aligned}{} & {} \begin{aligned} {{\varvec{\theta }}_{2}(k)} =&(-{\mu } {\textbf{I}} {\otimes } E[{\textbf{B}(k)}] + {\mu }^2 E[{\textbf{A}(k)} {\otimes } {\textbf{B}(k)} ]) \\&{\times } {\textrm{vec}} ( {\textbf{w}_{r}} {\tilde{\textbf{h}}^T(k)}), \end{aligned}\end{aligned}$$
(47)
$$\begin{aligned}{} & {} \begin{aligned} {{\varvec{\theta }}_{3}(k)} =&{\mu }^2 E[{\textbf{B}(k)} {\otimes } {\textbf{B}(k)} ] {\times } {\textrm{vec}} ( {\textbf{w}_{r}} {\textbf{w}_{r}^T}), \end{aligned}\end{aligned}$$
(48)
$$\begin{aligned}{} & {} \begin{aligned} {{\varvec{\theta }}_{4}(k)} =&{\mu }^2 {{\sigma }_{v}^2} {\textrm{vec}} [E({\varvec{\alpha }} {\varvec{\theta }}{\bar{\textbf{X}}_{a}^{T}(k)}{\bar{\textbf{X}}_{a}(k)}{\varvec{\theta }^T}{\varvec{\alpha }^{T}})], \end{aligned} \end{aligned}$$
(49)

where \({{\sigma }_{v}^2}\) is the additive noise variance. We then obtain the MSD learning curve

$$\begin{aligned} {\delta }_{m}(k) = {\textrm{tr}} (E[{\tilde{\textbf{h}}(k)}{\tilde{\textbf{h}}^T(k)}]) ={\textrm{tr}}( {\textrm{vec}}^{-1} [ {\textbf{z}}(k)]). \end{aligned}$$
(50)

Since the control matrix \({\textbf{H}}\) is invertible, the steady-state value of the vector \({{\textbf{z}}(k)}\) is

$$\begin{aligned} {\textbf{z}}(\infty ) = ({\textbf{I}} - {\textbf{H}})^{-1} {\varvec{\theta }}(\infty ). \end{aligned}$$
(51)

Using (51), the steady-state value of the EMSE is given by

$$\begin{aligned} \begin{aligned} {\xi }_{ex}(\infty ) =&\frac{1}{L} {\textrm{tr}} ( {\textrm{vec}}^{-1} [ {\textbf{z}}(\infty )]{{\textbf{R}}_b } \\&+ E[{\tilde{\textbf{h}}(\infty )}{\textbf{w}_{r}^T}]{{\textbf{R}}_{br}^T } \\ {}&+ E[{\textbf{w}_{r}}{\tilde{\textbf{h}}^T(\infty )}]{{\textbf{R}}_{br} } \\ {}&+ E[{\textbf{w}_{r}}{\textbf{w}_{r}^T}]{{\textbf{R}}_{rr} } ). \end{aligned} \end{aligned}$$
(52)

In [28], the MSD is evaluated using the original weight vector \({\hat{\textbf{w}}(k)}\) which depends on the initialization \({\hat{\textbf{w}}(0)}\). Here, we evaluate the MSD using the modified weight vector \({\hat{\textbf{h}}(k)}\) that is independent of the initialization \({\hat{\textbf{h}}(0)}\). Also, we observe from (51) and (52) that the steady-state MSD and EMSE are influenced by the degree of under-modeling and the system noise level.

We now show that as the step size \(\mu\) converges to zero, the steady-state modified MSD does not decrease to zero. Substituting (44) and (45) into (51), we get

$$\begin{aligned} \begin{aligned} {\textbf{z}}(\infty )&= (- {\mu }{\textbf{D}} + {\mu }^2{\textbf{J}})^{-1 }\sum \limits _{i=1}^{4} {{\varvec{\theta }}_{i}(k)} \\&= {\mu }^{-1}(- {\textbf{D}} + {\mu }{\textbf{J}})^{-1} \sum \limits _{i=1}^{4}{ {{\varvec{\theta }}_{i}(k)}}. \end{aligned} \end{aligned}$$
(53)

In Appendix B, we prove that as the step size \(\mu\) converges to zero, the vector \({\textbf{z}}(\infty )\) converges to

$$\begin{aligned} \begin{aligned} {\textbf{z}}(\infty )_{ \mu \rightarrow 0} =&-{\textbf{D}}^{-1} (E[{\textbf{B}(k)} {\otimes } {\textbf{I}} ]) \times {\textrm{vec}} ({\tilde{\textbf{h}}(k)} {\textbf{w}_{r}^T} ) \\&+ ({\textbf{I}} {\otimes } E[{\textbf{B}(k)}]) \times {\textrm{vec}} ( {\textbf{w}_{r}} {\tilde{\textbf{h}}^T(k)}). \end{aligned} \end{aligned}$$
(54)

As shown in (54), the MSD will not decrease to zero due to the influence of under-modeling part \({\textbf{w}_{r}}\). Substituting (52) into (49) and (53), we have the minimum value \({\delta }_{m,min}(\infty )\) and \({\xi }_{ex,min}(\infty )\) for the MSD and EMSE, respectively.

The aim of this paper is not to replace the model in [28] with the presented one, but the presented model can be used as useful supplement to the model in [28], as will be explained. The mean weight behavior \(E[\hat{\textbf{w}}(k)]\) of the deficient-length unconstrained PBFDAF has been described in [28], while the presented model describes mean the weight behavior \(E[\hat{\textbf{h}}(k)]\) instead. The model in [28] and the presented model are indeed equivalent in describing the MSE performance of the deficient-length unconstrained PBFDAF. However, the steady-state MSD calculated using the vector \(\hat{\textbf{h}}(k)\) is smaller than that obtained using the vector \(\hat{\textbf{w}}(k)\). This is because the MSD calculated with \(\hat{\textbf{h}}(k)\) is independent of its initial condition \(\hat{\textbf{h}}(0)\). Consequently, the unconstrained PBFDAFs exhibit better modeling capability than previously assumed. Also, in the under-modeling scenarios, the steady-state MSD and EMSE have nonzero lower bounds regardless of the step size. In contrast, for the unconstrained PBFDAFs with sufficient length, both MSD and EMSE tend to zero as the step size is decreased [27]. A comparison of the theoretical model in [28] and the proposed theoretical is summarized in Table 1.

Table 1 Comparison of the theoretical model in [28] and the proposed theoretical model
Full size table

4 Simulation results

The proposed theoretical model is verified via Monte Carlo simulations (over 1000 independent runs). We consider a system identification scenario where the system to be modeled has an impulse response of length \(M = 15\). The adaptive filter, with a total length of \(M_1 = 8\), is partitioned into two subfilters \(P=2\), each of length \(L=4\). The reference signal x(n) is either white uniform noise or an AR(15) process generated by applying the filter \(H(z)={1}/{(1+0.3z^{-1} + 0.3z^{-7} - 0.4z^{-15})}\) to white Gaussian noise. The white noise v(n) is scaled to achieve a signal-to-noise ratio (SNR) of 10 dB.

Fig. 2
figure 2

Transient behavior of the modified weight-error vector \({\tilde{\textbf{h}}}(k)\)

Full size image
Fig. 3
figure 3

Steady-state behavior of the modified weight-error vector \({\tilde{\textbf{h}}}(k)\)

Full size image

We study the mean convergence behavior for correlated inputs. Figure 2 shows the transient behavior of the mean modified weight-error vector \(E[{\tilde{\textbf{h}}(k)}]\) with a step size of 0.03. For clarity, the learning curves of the first six entries of the weight-error vector \(E[{\tilde{\textbf{h}}(\infty )}]\) are presented. As shown in Fig. 1, the experimental results closely match the predicted learning curves calculated by (23). Figure 3 presents the steady-state modified weight-error vector \(E[{\tilde{\textbf{h}}(\infty )}]\). The theoretical predictions, calculated via (24), correspond well with the experimental results, and the mean weight-error vector \(E[{\tilde{\textbf{h}}(\infty )}]\) is nonzero. This implies the modified weight vector \({\tilde{\textbf{h}}(k)}\) converges to a biased solution, i.e., the deficient-length unconstrained PBFDAFs cannot converge to \(\textbf{h}_{\textrm{o}}\) that consists of the first PL coefficients of unknown plant.

Fig. 4
figure 4

Recovery of the weight vector \({\breve{\textbf{h}}}\) for white inputs. a Steady-state weight vector \({\hat{\textbf{b}}_1}\). b Recovered weight vector \({\breve{\textbf{h}}}\)

Full size image
Fig. 5
figure 5

Recovery of the weight vector \({\breve{\textbf{h}}}\) for correlated inputs. a Steady-state weight vector \({\hat{\textbf{b}}_1}\). b Recovered weight vector \({{\textbf{w}}}_{\textrm{o}}\)

Full size image
Fig. 6
figure 6

Learning curves of the deficient-length unconstrained PBFDAFs. a MSD. b EMSE

Full size image
Fig. 7
figure 7

Steady-state MSD and EMSE as a function of step size. a MSD. b EMSE

Full size image

Figure 4 shows the recovery of the weight vector \({\breve{\textbf{h}}}\) for white input. Figure 4a illustrates the steady-state weight vector \({\hat{\textbf{b}}_1}\) corresponding to the samples that lack a recovery weight vector. The vector \({\hat{\textbf{b}}_1}\) is obtained from (37). Due to the influence of under-modeling part, the steady-state weight vector \({\hat{\textbf{b}}_1}\) does not match the modeling part \({\textbf{w}_{*}}\) for white noise input. Figure 4b presents the vector \({\breve{\textbf{h}}}\) obtained from (33) and (34). It is apparent that the first \(PL+L\) coefficients of the true weight vector \({{\textbf{w}}_{\textrm{o}}}\) can be recovered for white noise input.

We demonstrate that the unknown parameter vector can be recovered when using the AR(15) process as input. Figure 5a suggests that the weight vector \({\hat{\textbf{b}}_1}\) and the steady-state weight vector \(E[{\hat{\textbf{w}}_{\textrm{cn}}(\infty )}]\) of the constrained PBFDAFs do not match the modeling part \({{\textbf{w}}_{\mathrm {*}}}\). The results of the constrained PBFDAFs are obtained from [28]. Figure 5b shows that the vector \({{\textbf{w}}_{\textrm{o}}}\) calculated by (38) and (39) is consistent with the impulse response. Figures 4 and 5 confirm that more coefficients of the unknown plant can be recovered using the unconstrained PBFDAFs compared to the constrained PBFDAFs, which is not revealed in the previous works. This is because the steady-state weight vector \(E[{\hat{\textbf{h}}(\infty )}]\) is independent on the initialization of the filter coefficient and we can extract part of steady-state weight error from the vector \(E[{\hat{\textbf{h}}(\infty )}]\).

We examine the mean square convergence behavior for correlated inputs. Figure 6 the learning curves of the MSD and EMSE. The theoretical learning curves of the MSD and EMSE are obtained from (50) and (51), respectively. The used step sizes are 0.03 and 0.1. As shown in Fig. 6, there is a good agreement between theoretically derived learning curve and the experimental learning curve. We also repeat this experiment using SNR = 30 dB and obtain the very similar learning curves as that in Fig. 6, which is because the MSD and EMSE are dominated by the under-model part and the system noise does not affect the steady-state MSD and EMSE significantly in this case.

Figure 7 depicts the variation of the MSD and EMSE across a range of step sizes from 0.003 to 0.62. The stability bound of the step size is obtained by the method introduced in [27]. The MSD and EMSE of the constrained version are calculated via (77) and (78) in [28], respectively. Specifically, the unconstrained PBFDAF shows a higher MSD but a lower EMSE than the constrained PBFDAF, which is consistent with the results in [28]. Figure 7a illustrates that the steady-state MSD derived from the modified weight vector \({\tilde{\textbf{h}}(k)}\) is lower than that obtained from \({\tilde{\textbf{w}}(k)}\). This reduction in MSD is attributed to the steady-state MSD, and \({\delta }_{m}(\infty )\) does not depend on the initial conditions of the adaptive coefficients. In exact-modeling scenarios, the steady-state MSD and EMSE of the unconstrained PBFDAFs decrease as the step size is reduced [29]. However, in under-modeling scenarios, the steady-state MSD and EMSE remain almost unchanged when the step size is very small due to the under-modeling part \({\textbf{w}_{r}}\). Additionally, the values \({\delta }_{m,min}(\infty )\) and \({\xi }_{ex,min}(\infty )\) accurately represent the lower bounds for the steady-state MSD and EMSE, respectively.

5 Conclusion

This paper provided a new statistical performance analysis of the deficient-length unconstrained PBFDAFs. Our findings indicate that the theoretical analysis is significantly simplified and more comprehensible compared to our previous work in [28] due to the utilization of the new weight vector \({\hat{\textbf{h}}(k)}\). The developed theoretical model reveals new properties of unconstrained PBFDAFs in under-modeling scenarios and provides insights into the convergence behavior of the unconstrained PBFDAFs. For instance, the first \(PL+L\) coefficients of the unknown plant can be recovered using the unconstrained PBFDAF for white noise input, whereas the constrained PBFDAF of the same order can only identify the first PL entries. In certain cases, the true impulse response can be recovered using the unconstrained PBFDAF for correlated input. A comparison of steady-state MSD shows that the modified weight vector yields a lower MSD than the original one, which indicates that the unconstrained PBFDAFs exhibit a stronger system modeling capability than previously assumed. The theoretical model matches the simulation results well.