1 Introduction

The autonomic control of circulation, attributed to the sympathetic and parasympathetic branches of the autonomic nervous systems, is important for maintaining homeostasis. Dysfunction of the autonomic control could lead to the development of various cardiovascular and other diseases, including myocardial infarction and arterial hypertension; therefore, diagnostics of the autonomic control is important for prevention and therapy of cardiovascular diseases [1,2,3,4,5]. Development of pathologies, transition between different stages of sleep and active experiments, such as passive orthostasis, or completion of cognitive tasks, are also reflected in the dynamics of the autonomic control of circulation, making it important for fundamental understanding of several important biological objects, including central nervous system, respiratory system, and cardiovascular system [6,7,8]. Among other things, the autonomic control maintains proper heart rate and mean arterial pressure in the aorta by modulating the heart rate [9] and arterial pressure [10, 11].

The dynamics of the autonomic control of the mean arterial pressure could be modeled using a time-delayed controller, and such systems often exhibit self oscillations [12]. More recent and complex models also take into account the autonomic control of both heart rate and arterial pressure [13,14,15,16]. Self oscillations, related to the autonomic control of heart rate, can be observed in the heart rate variability representing the sequence of time intervals between the heart contractions, typically estimated from the electrocardiogram (ECG) as a distance between the R peaks (RR intervals or RRI) [17]. The frequency of the oscillations is 0.04–0.15 Hz, in the literature they are referred to as the low-frequency (LF) oscillations [17]. The LF oscillations are also present in the photoplethysmogram (PPG) signals, but they are related to the autonomic control of the mean arterial pressure [10].

The LF oscillations in the RRI and PPG are coupled and exhibit intervals of phase synchronization, which can last up to hundreds of seconds and alternate with the intervals of asynchronous behavior [6, 18, 19]. Relative duration of the synchronous intervals is smaller in people with impaired autonomic control and is perspective for medical diagnostics and therapy of myocardial infarction and arterial hypertension [20,21,22,23]. Other characteristics of coupling, based on the phase dynamics modeling, are perspective for stress detection [24, 25], somnology [26], and investigation of aging [27].

However, experimental ECG and PPG signals are nonstationary and noisy and have complex, broadband spectral distributions. Duration of the experimental signals is also often limited. Analysis of biological signals demands careful selection of the data analysis techniques and their parameters. Unfortunately, when analyzing the experimental data, there are no references, and the accuracy of the various data analysis techniques cannot be reliably measured or compared, and therefore, the methods are often tested on the model signals.

In case of phase synchronization detection, a model with a priori known phases of the LF oscillations, and a priory known pattern of synchronization could be used as a test object. In our opinion, the model should fit the following criteria: model time-series, phases, power spectra of the RRI, ECG, and PPG signals, and the pattern of phase synchronization between the LF oscillations must be quantitatively similar to the experimental data; the phases of the LF oscillations in RRI and PPG must be known a priori; the borders of the intervals of phase synchronization between the LF oscillations must be known a priori. There are few mathematical models, which fit some of those criteria. In our study, we aimed to develop a model that fits them all. The proposed models of the ECG and PPG signals were used to test and tune the method for detection of phase synchronization proposed in [18].

2 Materials and methods

2.1 Modeling the phase difference

The proposed model starts with the simulation of the difference between the phases of the LF oscillations in the PPG and RRI signals. Kralemann with the coauthors [28] define the phase φ(t) of an oscillation as “the uniformly growing variable, which measures the fraction of the time within one undisturbed cycle”. A phase of an undisturbed system can be modeled using the following phase oscillator:

$$\dot{\varphi }\left( t \right) = 2\pi f.$$
(1)

In this simple case, the resulting phase is a function that increases at a constant rate of f radians per second. To simulate the phases of more complex oscillations (i.e., of biological origin), more complex equations are required. The resulting phase will still be a uniformly growing variable, but the growth rate can vary in time. We use this definition of phase when modeling the phases of LF oscillations in the RRI and PPG signals (see Sect. 2.2) using noisy phase oscillators.

Another case is the phase estimated from the time-series. Common approach is to reconstruct a two-dimensional embedding of the limit cycle or a strange attractor, using, for example, Hilbert transform. Then, the phase is introduced as an angle variable on the limit cycle/strange attractor. Due to technical reasons, for complex oscillation, this empirical phase is observant-dependent and may not be a “uniformly grooving variable”, and does not fit the classical definition. Therefore, it sometimes referred as a “protophase”, and Kralemann et al. [28] explore the techniques to bridge the gap between the protophase and correct observant-independent phase. We use protophase to introduce the model heart rate (see Sect. 2.3), and because we are only interested in the duration of the limit cycle and dealing with relatively simple oscillations, we do not apply any algorithms to correct the protophase.

In the case of phase synchronization of two coupled oscillators, their phases increase at the same rate. In that case, the phase difference is a horizontal line, or close to a horizontal line when noises are present. The difference between the asynchronous phases is a sloped line, with the angle of the slope depending on the difference between the frequencies of the oscillations.

The LF oscillations in the PPG and RRI signals exhibit alternating irregular intervals of phase synchronization and asynchronous behavior, so we modeled the phase difference of the LF oscillations as a sequence of alternating horizontal and sloped sections (Fig. 1) with added colored noise, which generation is explained in the next subsection. The duration of the horizontal and sloped sections, and the angles of the slopes were taken directly from the experimental data, as described further.

Fig. 1
figure 1

Experimental (bold black line) and simulated (red line) differences between the LF oscillations in the RRI and PPG signals. Semi-transparent bars mark intervals of phase synchronization. Thin black line drawn over the red line represents the simulated phase difference without added noise

Full size image

We analyzed 2-h ECG and PPG recordings from ten healthy subjects, 20–34 years of age. Data were recorded in a quiet, temperature-controlled room. All signals were sampled at 250 Hz and digitized at 14 bits. The records of respiration were used to control evenness of the breathing. All experimental signals were recorded using a standard electroencephalograph analyzer EEGA-21/26 ‘Encephalan-131-03’ [Medicom MTD Ltd, Taganrog, Russia (www.medicom-mtd.com/en/products/eega.html)]. To extract the phases, estimate the phase difference, and detect horizontal, synchronization related, sections of the phase difference, we used the methods proposed in [18]. The aforementioned characteristics of the phase difference were stored in a database, and the values were selected at random to generate the simulated phase difference.

2.2 Modeling the phases

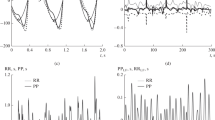
We simulated the phases of the LF oscillations in the RRI and PPG signals, \(\varphi_{{{\text{LF}}}}^{{{\text{RR}}}} (t)\) and \(\varphi_{{{\text{LF}}}}^{{{\text{PPG}}}} (t)\), using a set of phase oscillators. The phases were modeled in such a way that their difference was equal to the phase difference simulated during the previous step. For the horizontal sections, we used the following equations: \(\dot{\varphi }_{{{\text{LF}}}}^{{{\text{RR}}}} (t) = 2\pi f_{{{\text{LF}}}} + \xi_{{{\text{LF}}}}^{{{\text{RR}}}} (t)\), \(\dot{\varphi }_{{{\text{LF}}}}^{{{\text{PPG}}}} (t) = 2\pi f_{{{\text{LF}}}} + \xi_{{{\text{LF}}}}^{{{\text{PPG}}}} (t)\), where \(f_{{{\text{LF}}}}\) = 0.1 Hz, and \(\xi_{{{\text{LF}}}}^{{{\text{RRI}}}} \left( t \right)\) and \(\xi_{{{\text{LF}}}}^{{{\text{PPG}}}} \left( t \right)\) are colored noises. For the sloped sections, we used the following equations: \(\dot{\varphi }_{{{\text{LF}}}}^{{{\text{RR}}}} (t)\) = 2π \(f_{{{\text{LF}}}}\) + \(\xi_{{{\text{LF}}}}^{{{\text{RRI}}}} \left( t \right)\) + 0.5θ and \(\dot{\varphi }_{{{\text{LF}}}}^{{{\text{PPG}}}} (t)\) = 2π \(f_{{{\text{LF}}}}\) + \(\xi_{{{\text{LF}}}}^{{{\text{PPG}}}} \left( t \right)\) – 0.5θ, where θ is the increment rate of the phase difference. The resulting phases are shown in Fig. 2a, b.

Fig. 2
figure 2

The unwrapped phases of the LF oscillations in the RRI signal (a) and PPG signal (b), simulated phases are shown in red, and the black line corresponds to the averaged experimental phase, with the gray surrounding area showing the standard deviation. Panel (c) shows the averaged power spectra of the noise in the detrended experimental unwrapped phases of the LF oscillations in the RRI (red) and PPG (black) time-series

Full size image

To generate the colored noise in the individual phases (\(\xi_{{{\text{LF}}}}^{{{\text{RRI}}}} \left( t \right)\) and \(\xi_{{{\text{LF}}}}^{{{\text{PPG}}}} \left( t \right)\)), we estimated the spectral characteristics of the noise present in the experimental signals. The experimental PPG and RRI signals were filtered using 0.04–0.15 Hz band-pass filter, and then detrended using a moving-average algorithm with a window of 20 s. The power spectra \(\overline{S}_{{{\text{LF}}}}^{{{\text{PPG}}}} \left( f \right)\) and \(\overline{S}_{{{\text{LF}}}}^{{{\text{RRI}}}} \left( f \right)\) of the detrended phases of the LF oscillations in the PPG and RRI signals were averaged across all ten recordings (Fig. 2c). The resulting spectra were approximated using an exponential function. The noises were generated as AAFT surrogates, based on the approximated spectra, since the AAFT surrogates preserved the spectral properties of the original signals. The final phase difference ΔφLF was calculated as a difference between the noisy \(\varphi_{{{\text{LF}}}}^{{{\text{RR}}}} (t)\) and \(\varphi_{{{\text{LF}}}}^{{{\text{PPG}}}} (t)\) signals, and therefore, noise present in ΔφLF is a combination of the \(\xi_{{{\text{LF}}}}^{{{\text{RRI}}}} \left( t \right)\) and \(\xi_{{{\text{LF}}}}^{{{\text{PPG}}}} \left( t \right)\).

As shown in Fig. 2, the power spectra of the raw RRI and PPG signals also contain VLF (0.015–0.04 Hz) and HF (0.15–0.4 Hz) spectral components [17]. The phases of these spectral components \(\phi_{{{\text{VLF}}}}^{{{\text{RR}}}} \left( t \right)\), \(\varphi_{{{\text{HF}}}}^{{{\text{RR}}}} (t)\), \(\phi_{{{\text{VLF}}}}^{{{\text{PPG}}}} \left( t \right)\) and \(\phi_{{{\text{HF}}}}^{{{\text{PPG}}}} \left( t \right)\) were generated similarly to \(\varphi_{{{\text{LF}}}}^{{{\text{RR}}}} (t)\) and \(\varphi_{{{\text{LF}}}}^{{{\text{PPG}}}} (t)\).

2.3 Modeling PPG and ECG signals

To model the PPG and ECG signals, we adopted the approach from [29, 30]. The heart rate was defined as a radian frequency of the following dynamical system:

$$\dot{x}\left( t \right) = \alpha \left( t \right)x\left( t \right) - \omega \left( t \right)y\left( t \right),$$
(2)
$$\dot{y}\left( t \right) = \alpha \left( t \right)y\left( t \right) + \omega \left( t \right)x\left( t \right).$$
(3)

In (2) and (3), \(\alpha = 1 - \sqrt {x^{2} \left( t \right) + y^{2} \left( t \right)}\), ω(t) is the heart rate

$$\omega \left( t \right) = 2\pi /\left( {\frac{1}{{\omega_{0} }} + \sum\limits_{{i = {\text{VLF,LF,HF}}}} {k_{i}^{{{\text{HRV}}}} \cos \left( {\varphi_{i}^{{{\text{HRV}}}} \left( t \right)} \right)} } \right),$$
(4)

where \(\phi_{i}^{{{\text{HRV}}}} (t)\), i = VLF, LF, HF, are the phases of the oscillations in the VLF, LF, and HF bands, generated during the previous stage, \(\omega_{0}\) is an intrinsic heart rate, and \(k_{i}^{{{\text{HRV}}}}\) are dimensional coefficients, which independently regulate the depths of the frequency modulation of the heart rate in the VLF, LF, and HF bands.

Equations (2) and (3) were solved numerically using the fourth-order Runge–Kutta approach, with integration step of 0.004 s. The variables x(t) and y(t) are not directly present in any other part of the model, and they are used to calculate the protophase of the heart: \(\varphi_{{{\text{HR}}}} \left( t \right) = {\text{arctg}}\left( {y\left( t \right)/x\left( t \right)} \right)\). The protophase \(\varphi_{{{\text{HR}}}} \left( t \right)\) is also not directly present in the following expressions; instead, we use it to calculate the beginning of the next cardiac cycle, which begins when \(\varphi_{{{\text{HR}}}} \left( t \right)\) reaches a value divisible by 2π rad. Then, we calculated Tn(t), which was the amount of time passed since the beginning of the current cardiac cycle, where n is a sequential number of the current cardiac cycle. This variable was used when modeling the shapes of the ECG and PPG signals.

To model the shape of the single ECG cycle, we used the following expression:

$${\text{ECG}}\left( t \right) = \sum\limits_{i = P,Q,R,S,T} {\frac{{s_{i}^{{{\text{RR}}}} }}{{\left( {b_{i}^{{{\text{RR}}}} } \right)^{2} }}e^{{ - \left( {T_{n} (t) - T_{i}^\text{RR} } \right)^{2} }} } .$$
(5)

The model is a combination of five bell curves, each simulated a specific peak on the ECG signal (P, Q, R, S or T), with specific width and amplitude, set by the dimensionless coefficients \(s_{i}^\text{RR}\) and \(b_{i}^\text{RR}\), respectively. The center of each curve corresponds to a moment in time, when \(Tn\left( t \right) - T_{i}^\text{RR} = 0\) (see Table 1).

Table 1 Parameters of the mathematical model
Full size table

We modeled the shape of a single PPG cycle using a very similar approach

$${\text{PPG}}\left( t \right) = \sum\limits_{{i = {\text{VLF,LF,HF}}}} {k_{i}^{{{\text{PPG}}}} \cos \left( {\phi_{i}^{PPG} \left( t \right)} \right)} + 2\sum\limits_{i = An,Cat} {a_{i} \gamma_{i} \left( t \right)\Gamma_{i} \left( t \right)}$$
(6)

The model is a combination of two skewed bell curves, representing the anacrotic (An) and catacrotic (Cat) waves of a real PPG, and three modulating signals in the VLF, LF, and HF bands. The phases \(\phi_{i}^{{{\text{PPG}}}} \left( t \right)\) are the phases of the corresponding modulating signals, generated during the previous stage, \(k_{i}^\text{PPG}\) are dimensionless coefficients, that independently regulate the depths of modulation in different bands, and since the amplitude of the PPG(t) signal has no physiological meaning, the coefficients are dimensionless. Parameters ai regulate the amplitudes of the anacrotic and catacrotic PPG rises. Symbols \(\gamma_{i} \left( t \right)\) and \(\Gamma_{i} \left( t \right)\) denote the skewed bell curves

$$\gamma_{i} \left( t \right) = \frac{1}{{b_{i} \sqrt {2\pi } }}e^{{\left( { - s_{i} \left( {\frac{{T_{n}^{\gamma } \left( t \right) - T_{i} }}{{b_{i} }}} \right)^{2} } \right)}} ,$$
(7)
$$\Gamma_{i} \left( \tau \right) = \int\limits_{0}^{1} {\gamma_{i} \left( \tau \right){\text{d}}\tau } ,$$
(8)

where si, bi, and Ti are parameters regulating the asymmetry, height, and location of the anacrotic and catacrotic PPG rises, \(T_{n}^{\gamma } \left( t \right)\) is a nonlinear function of time since the beginning of current cardiac cycle Tn(t). The first 0.5 s from the beginning of the cardiac cycle contain both the anacrotic and catacrotic PPG rises, and during that section, \(T_{n}^{\gamma } \left( t \right)\) = Tn(t). After 0.5 s, \(T_{n}^{\gamma } \left( t \right)\) increases at a different rate, set by expression (9), and always reaches 1 by the end of a cardiac cycle

$$\dot{T}_{n}^{\gamma } \left( t \right) = \frac{0.5}{{(T_{n}^{c} - 0.5)}},$$
(9)

where \(T_{n}^{c}\) is a duration, in seconds, of the current cardiac cycle. Then, \(T_{n}^{\gamma } \left( t \right)\) was smoothed using a moving-average filter with a time-window of 31 discrete steps. Introduction of the \(T_{n}^{\gamma } \left( t \right)\) was necessary to reach two conflicting goals:

  • The pulse wave should still elongate during the long cardiac cycles, and shorten during short cardiac cycles.

  • Despite the overall lengths of the PPG wave changing from cycle to cycle, it was necessary to keep the time intervals between the beginnings of the cardiac cycles and the anacrotic rises constant, as seen in healthy subjects [31].

Parameters of the model are listed in Table 1, they were fitted to quantitatively simulate the average spectral and statistical characteristics of the real PPG, ECG, and RRI signals.

2.4 Method for detection of synchronization

We used the approach, proposed in [18], to detect the intervals of phase synchronization between the LF oscillations, related to the autonomic control of circulation. The first stage of the algorithm was to calculate the RRI time-series. Complying with the recommendations [17], we interpolated the non-equidistant RRI time-series using β-splines, and later, we resampled the interpolated data at a sample rate of 5 Hz. The RRI and PPG time-series were filtered using a rectangular band-pass filter with the bandpass of 0.04–0.15 Hz [17]. The Hilbert–Huang transform was applied to the filtered signals to obtain the instantaneous phases. To detect the intervals of synchronization, we calculated the slope of the phase difference. If the slope was less than a threshold value \(|\alpha|\), the interval was considered to be an interval of synchronization. We excluded the intervals of synchronization shorter than l seconds to combat stochastic fluctuations.

To increase the sensitivity and specificity, the algorithm [18] was modified to also track the duration of the intervals of asynchronous behavior. If the interval was shorter than n seconds, it was merged with neighboring synchronous intervals.

2.5 Mean phase coherence

To compare the reference model phases \(\varphi_\text{LF}^\text{HRV} \left( t \right)\) and \(\varphi_\text{LF}^\text{PPG} \left( t \right)\) to the phases of the LF oscillations extracted from the model RRI and PPG signals, we used the mean phase coherence index [32]. It was calculated as follows:

$$\rho = \left| {\frac{1}{N}\sum\nolimits_{n = 1}^{N} {e^{{j(\varphi_{1} (t_{n} ) - \varphi_{2} (t_{n} ))}} } } \right|,$$
(10)

where j is the imaginary unit, N is the number of points in the time-series, and \(\varphi_{1} (t_{n} )\) and \(\varphi_{2} (t_{n} )\) are the phases. The index ρ = 1 means total synchronization; ρ = 0 corresponds to the uniform distribution of the phase differences, i.e., incoherent phases.

3 Results

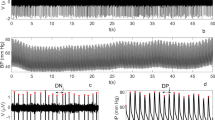
The time-series and power spectra of the model signals are shown in Fig. 3.

Fig. 3
figure 3

Model and experimental time-series and power spectra: a experimental ECG (black) and PPG (red), b model ECG (black) and PPG (red), c experimental RRI, d model RRI, e experimental RRI power spectra (black) and PPG power spectra (red), and f model RRI power spectra (black) and PPG power spectra (red)

Full size image

Figure 3a–d illustrates that the model reproduce the shapes of the experimental ECG, PPG, and RRI signals. The model, however, does not take into account the measurement noises or changes in the shape of PQRST complex or PPG waves (see Discussion). The power spectra of the experimental and model time-series are shown in Fig. 3e and f, respectively. The model reproduces the oscillations in VLF, LF, and HF bands. The parameters of the model also allow for independent tuning of spectral power density in VLF, LF, and HF frequency bands. An automated algorithm was used to fit the spectral power density in the model RR signal to the average experimental data with an error of less than 1%. The power was set to 334 ms2, 308 ms2, and 309 ms2 in the VLF, LF, and HF bands, respectively.

Likewise, the spectral power density in the VLF, LF, and HF bands of the PPG signal was also tuned to fit the experimental values of the ratio between the spectral power density in the respective frequency band and the area around the heart rate (ω0 – 0.1; ω0 + 0.1 Hz). The average model and experimental values for those ratios were 1.34, 3.53, and 3.05 for the VLF, LF, and HF bands, respectively.

To test the method proposed in [18], we generated 100 sets of model ECG and PPG signals, each 20 min long (120 periods). Figure 4 shows examples of the differences between the LF oscillations in real RRI and PPG signals, reference model phase differences, and phase differences empirically estimated from model data. The mean phase coherence between the reference model phases and phases extracted from the model time-series was 0.95 ± 0.01 (mean value ± standard error) for PPG and 0.95 ± 0.01 for RRI.

Fig. 4
figure 4

Time-series of the differences between the LF oscillations in RRI and PPG: a experimental phase difference, b model phase differences, where the reference phase difference is shown in black, and the difference between the LF oscillations extracted from model RRI and PPG is shown in blue, with red segments corresponding to detected intervals of phase synchronization. Gray bars mark the true intervals of synchronization

Full size image

We tested different sets of parameters (b, \(|\alpha|\), l, n), when applying the method to the model ECG and PPG. For the b parameter, which represents the width of the smoothing window, we tested values from 5 s (halved period of the LF oscillations) upward to 90 s with the step of 5 s; for the \(|\alpha|\) parameter, which represent the threshold value for the slope of approximating line, we tested the values from 0.001 to 0.3 with the step of 0.001; for the l parameter, which represents the minimal length of a synchronous interval, the range was set from 6 to 20 s with the step of 1 s; for the n parameter, which represents the minimal length of an asynchronous interval, the range was set from 0 to 7 s with the step of 1 s. The resulting receiver-operating characteristic (ROC curve) is shown in Fig. 5. The area under the curve (AUC) was 0.75. The parameters, corresponding to the point of the ROC curve closest to the perfect classifier [FPR = 0, TPR = 1] were: b = 20 s, \(\left| \alpha \right| = 0.023\), l = 10 s, and n = 3 s. With this set of parameters, the sensitivity was 0.69, and specificity was 0.60.

Fig. 5
figure 5

The ROC curves for unmodified method (black) and modified and refined method (red)

Full size image

We also tested the unmodified method from [18]. The resulting ROC curve is also shown in Fig. 5, and the AUC was 0.71. When using optimal parameters, the sensitivity reached 0.64, and specificity reached 0.63.

When sensitivity was set to 0.70, the unmodified method had specificity of 0.54, and modified method had specificity of 0.59. When sensitivity was set to 0.90, the unmodified method had specificity of 0.34, and modified method had specificity of 0.37. When using the meta-parameters proposed in [18] (b = 13 s, \(\left| \alpha \right| = 0.01\), l = 16 s), the unmodified method demonstrated sensitivity of 0.28 and specificity of 0.84, the modified method demonstrated sensitivity of 0.29 and specificity of 0.84.

4 Discussion

The proposed mathematical models were used to generate synthetic ECG and PPG signals with preset phases of the LF oscillations, related to modulation of heart rate and arterial pressure. This functionality is not presented in previously available models. The shape, spectral, and statistical properties of the model signals qualitatively and to a degree quantitatively reproduce the real data.

The models of ECG and PPG signals were combined with the proposed algorithm for generation of synthetic phase difference that preserve the statistical characteristics of the difference between the LF oscillations in the loops of autonomic control of circulation. The resulted combination provides tools for objective testing and refinement of the methods aimed to process the nonstationary and noisy signals, reflecting the dynamics of the loops of the autonomic control, and detect intervals of synchronization.

The testing demonstrated that when extracting the phases of the LF oscillations from RRI and PPG signals, the resulting phase difference is smoothed, and some information about the HF oscillations is lost. The loss of information is probably related to the nature of a non-equidistant RRI, since the RRI is sampled at an irregular sample rate of only about 1 Hz (heart rate). As a result, some information about the position of synchronous intervals is also lost. This decreases the accuracy of the method, and only 70% of synchronous intervals are detected when using optimal parameters. Those results also provide estimation of the accuracy, that is expected when analyzing the real biological signals.

In our opinion, this application of mathematical modeling is useful for testing and refining of the methods, designed to detect coupling and synchronization between the experimental signals [32,33,34,35]. An advantage of the proposed model over previously available models [30] is functionality to preset the pattern of synchronization between the LF oscillations, then that the individual phases of the LF oscillations are fitted to the phase difference. This provides reference values, which can be used to test and compare different approaches to detection of the phase synchronizations. Easy access to the individual phases also provides reference values when testing the algorithms for introduction of the phases.

As mentioned earlier, in the present study, the phases were generated to fit the phase difference; however, it is also possible to use the phases extracted from experimental time-series or generated by coupled oscillators. This functionality could be used to test the methods for detection of directional coupling.

In addition, the phases of the VLF, LF, and HF oscillations in both RRI and PPG signals are introduced to the models in similar manner. The present study was limited to the investigation of the synchronization between the LF oscillations, but the models could be used to test the methods for detection of coupling between the VLF or HF oscillations, which is an interesting topic for further studies.

The models also have several limitations. We only introduced the frequency modulation of the ECG signal; however, in real signals, both the amplitude of the P, Q, R, S, and T peaks and the mean value of the signals are non-constant, which may have prominent effect on the accuracy of phase synchronization detection. Likewise, the shape of the real individual PPG waveforms changes over time, and in the model, the shape is constant.

We also did not study the effects of measurement noises, which can potentially distort the PPG power spectra or introduce errors when detecting the R peaks in the ECG time-series, but this investigation is planned for the future.

5 Conclusion

We have developed mathematical models of the ECG and PPG signals, with preset and, therefore, a priori known phases of the low-frequency oscillations, related to the autonomic control of heart rate and arterial pressure. We have also proposed a method for generation of the difference between the phases of the low-frequency oscillations.

The developed models were used to generate a testing dataset, consisting of signals that reproduce the statistical and spectral characteristics of the real ECG, PPG, and RRI signals, including the irregular alternations between the intervals of synchronization and desynchronization between the LF oscillations in PPG and RRI.

The previously proposed method for detection of phase synchronization between the above-mentioned LF oscillations was modified and tested against the model dataset. The parameters of the method were refined to achieve better accuracy. The refined method reached the sensitivity of 0.69, specificity of 0.60, and AUC of 0.75, when using the following meta-parameters \(\left| \alpha \right| = 0.023\), b = 20 s, l = 10 s, and n = 3 s. The performance improved, since the unmodified approach reached the sensitivity of 0.64, specificity of 0.63, and AUC of 0.71.

The results suggest that accuracy of the method is lower, than previously assumed, but we consider this estimation to be more credible, due to a more accurate simulation of the real data processing routine, including filtration of the broadband experimental signals and introduction of the phases using the Hilbert Transform.