1 Introduction

Ferrofluids are colloidal suspensions of single-domain ferromagnetic particles in a carrier liquid.

The typical size of the particles in modern ferrofluids is about 10–20 nm. One of the most interesting, from the point of view of the basic research, and important from the viewpoint of applications peculiarities of the fluids, is the ability to control transport (hydrodynamic, diffusion, thermal) phenomena in them with the help of an applied magnetic field, easily achievable in the laboratory and industrial conditions (see, for example, Ref. [1]).

Diffusion phenomena in ferrofluids determine many important properties of these systems, and their behavior in various technological and bio-medical applications. In very dilute systems, where any interactions between particles are negligible, the coefficient of the ferroparticle diffusion can be determined by the classical Einstein formula for the diffusion coefficient of a Brownian particle. When the interparticle interactions are significant, this coefficient depends on the particle concentration and applied magnetic field, as well. Theoretical investigations of the diffusion and magnetophoretic transport in magnetic fluids with an account of magnetic, hydrodynamic, and steric interactions between the particles are presented in [2,3,4,5]. It is shown that in a magnetic field, the diffusion coefficient is anisotropic—its magnitude along the field differs from that in the perpendicular direction.

The models [2,3,4,5] deal with weakly and moderately interacting particles, not able to form any heterogeneous structures. However, observations demonstrate that linear chains, bulk dense drops, and other structures take place in many modern ferrofluids. The applied magnetic field stimulates the appearance of these structural transformations (see, for example, [6,7,8,9,10]). Since the wavelength of the visual light is much more than the size of the particles in ferrofluids, the linear chains cannot be detected optically, but they have been observed by using electronic microscopes in [6, 7]. Note that usually, the chains appear when the concentration of the particles, able to the bulk condensation, is below some threshold one. Above that, the bulk “drops” are expected. Estimate of this threshold concentration presents a very difficult theoretical and experimental problem.

The typical size of the bulk drops in ferrofluids is about several microns. Usually, they are well seen in optical microscopes [8,9,10].

The appearance of the internal heterogeneous structures affects significantly magnetic, rheological, transport, and other properties of ferrofluids [11,12,13]. The effect of chains on the diffusion and magnetophoretic transport in ferrofluids have been studied theoretically in [13]. Any interactions between the chains have been ignored in this consideration. The goal of this work is the analysis of the interchain interaction on the diffusion and magnetophoretic transport in ferrofluids.

2 Physical model and the main approximations

We will use a simple model of the chain-like aggregates, developed in Ref. [14]. In spite of simplifications, this model has allowed us to describe the rheological properties of various magnetic fluids with the single-domain and cluster particles, as well [15,16,17,18].

In the framework of the model [14], the ferrofluid particles are considered to be identical ferromagnetic spheres with diameter d and magnetic moment m, fixed in the particle body. It is supposed that the particles can form only the linear chain-like structures. Following references [14,15,16,17,18], we will suppose that the energy of the dipole–dipole interaction between the nearest particles in the chain is significantly more than the thermal energy kT. This condition is necessary for the appearance of any heterogeneous aggregates in a ferrofluid. We neglect the thermal fluctuations of the chain shape and orientations of the particle moments in the chain. In the other words, the chains are modeled by straight rigid rod-like aggregates; the particle magnetic moments are aligned along the chain axis. The criterion of this approximation applicability is discussed in Ref. [14]. For maximal simplification of calculations, we consider the limiting case of very strong applied magnetic field \(\mathbf{H} _{0}\), when the Zeeman energy of the particle interaction with the field is much more than kT. Therefore, magnetic moments of the particles are aligned along with the field \(\mathbf{H} _{0}\). In the frame of this approach, we can consider the chains as aligned in the field direction. The interchain interaction will be considered in the well-known pair approximation. This means that interaction only between two chains will be taken into account; effect of any other third chain will be neglected.

The approximation of the rigid rod-like chains, of course, is a very strong simplification. A model of the flexible chains in an arbitrary magnetic field has been proposed in [19]. However, this model leads to bulky calculations. At the same time, results of [15, 16] show that the model of the rod-like chains allows getting quite reasonable estimates for ferrofluid rheological properties. It gives us the background to consider this model as a robust foundation for the description of the transport phenomena in ferrofluids.

3 Macroscopical flux of the particles

According to the general Einstein–Batchelor formula [19], the flux density \(\mathbf{j} _{n}\) of the particles united in the n-particle chains can be presented as \({\mathbf {j}}_{n}=-n g_{n}\varvec{\beta }_{n}:\nabla \mu \). Here, \(g_{n}\) is a number of the n-particle chains in a unit volume of the system; \(\mu \) is the chemical potential of the particles; \(\varvec{\beta }_{n}\) is tensor of the hydrodynamical mobility of the chain. The explicit form of components of \(\varvec{\beta }_{n}\) will be discussed below. The tensor character of the mobility is explained by the anisotropic shape and orientation of the chains.

The total flux density is

$$\begin{aligned} {\mathbf {j}}=-\left( \sum ^{\infty }_n {n g_n \varvec{\beta }_n}\right) :\nabla \mu . \end{aligned}$$
(1)

The chemical potential \(\mu \) of the particles depends on their volume concentration \(\varphi \) and the absolute value H of the local magnetic field. Thus, one can present

$$\begin{aligned} \nabla \mu =\frac{\partial \mu }{\partial \varphi } \nabla \varphi +\frac{\partial \mu }{\partial H} \nabla H. \end{aligned}$$
(2)

The relation (2) must be added by the Maxwell equations for the magnetic field \({\mathbf {H}}\). These equations can be written down as

$$\begin{aligned} \mathrm{div}({\mathbf {H}}+{\mathbf {M}})=0, \quad \mathrm{rot}\, {\mathbf {H}}=0. \end{aligned}$$
(3)

Here, M is the fluid magnetization. In the limiting case of the strong magnetic field

$$\begin{aligned} {\mathbf {M}}=\varphi M_p\frac{{{\mathbf {H}}}}{H}. \end{aligned}$$
(4)

Here, \(M_p\) is the magnetization of the particle material.

Let us present

$$\begin{aligned} \varphi =\varphi _0+\varphi ',{{\mathbf {H}}}={{\mathbf{H}}}_0+{{\mathbf {h}}}, \end{aligned}$$
(5)

where \(\varphi _0\) and \({{{\mathbf {H}}}}_0\) are the uniform mean particles volume concentration and magnetic field in the suspension. We will suppose that the strong, inequalities \(\varphi _0>>\varphi '\) and \(H_0>>h\) are held.

In the linear approximation with respect to \(\varphi '\) and h, Eqs. (2), (3) can be rewritten as

$$\begin{aligned}&\nabla \mu =\frac{\partial \mu }{\partial \varphi _0}\nabla \varphi '+\frac{\partial \mu }{\partial H_0}\nabla h, \end{aligned}$$
(6)
$$\begin{aligned}&\left( 1+\frac{M_p \varphi _0}{H_0}\right) \mathrm{div}{\mathbf{h}}+\frac{M_p}{H_0}({{{\mathbf {H}}}}_0\cdot \nabla )\varphi ' \nonumber \\&\quad -\frac{M_p \varphi _0}{{H_0}^2}({{{\mathbf {H}}}}_0\cdot \nabla )({{\mathbf {h}}}{\cdot {{\mathbf {H}}}}_0)=0, \end{aligned}$$
(7)
$$\begin{aligned}&\mathrm{rot}\,{{\varvec{h}}}=0. \end{aligned}$$
(8)

Equation (7) allows us to find a relation between \({\mathbf{h}}\) and \(\varphi '\) and to rewrite \(\nabla \mu \) in the form linear with respect to \(\nabla \varphi '\), i.e., in the standard form for the diffusion flux.

4 Distribution function \(\varvec{g_{n}}\) and thermodynamic functions of the system

Let us consider a unit representative volume of the ferrofluid. We will suppose that this volume contains a tremendous number of particles; the particle size is much less than the characteristic distance of change of the particle concentration.

We will denote the number of n-particle chains in this volume as \(g_{n}\). Let us suppose that the usual approximation of the local thermodynamic equilibrium is held. In other words, in each moment of time, the thermodynamical state of every elementary volume of the fluid can be considered as equilibrium. In the framework of the chosen approximations, the free energy F of the unit volume of the fluid can be presented as [14]

$$\begin{aligned} F= & {} kT\sum ^{\infty }_{n=1}{\mathrm{g}}_n\left[ \ln \frac{{\mathrm{g}}_{\mathrm{n}}v}{e}-\varepsilon (n-1)+\frac{1}{2}\sum ^{\infty }_k{B_{nk}v{\mathrm{g}}_{\mathrm{k}}}\right] \nonumber \\&-\mu _0\frac{\varphi }{v}\mathrm{\ }mH, \nonumber \\ \varepsilon= & {} \frac{\mu _0}{2\pi }\frac{m^2}{d^3kT}\, \ \ v=\frac{\pi }{6}d^3. \end{aligned}$$
(9)

The first term in the square brackets (9) corresponds to the entropy of an ideal gas of the chains. The second term presents the internal energy of the chain, which is estimated as the energy of interaction between the neighbor particles in the chains; the third one presents the energy of the chain interaction estimated in the pair approximation; \(B_{nk}\) is the dimensionless, related to kT, second virial coefficient of the interchain interaction, v is the particle volume, and H is the local magnetic field.

The equilibrium state of the elementary unit volume corresponds to the distribution function \(g_{n}\) providing the minimum of the free energy F under the normalization condition

$$\begin{aligned} \sum _{n=1}^{\infty }ng_{n} =\frac{\varphi }{ v}. \end{aligned}$$
(10)

Here, \(\varphi \) is the volume concentration of the particles in the unit volume.

Standard minimization of F (see details in 14) leads to the following equation for the function \(g_{n}\):

$$\begin{aligned} \ln \frac{{\mathrm{g}}_\mathrm{nv}}{e}-\varepsilon (n-1)+\sum ^{\infty }_k{B_{nk}v{\mathrm{g}}_{\mathrm{k}}-\Lambda n=0}. \end{aligned}$$
(11)

Here, \(\Lambda \) is the Lagrange multiplier to be determined substituting solution of (11) into the normalization condition (10). This leads to a system of non-linear equations of the integral type with respect to \(g_n\) and \(\Lambda \). Equations of this type do not have an exact analytical solution. However, their solution can be found using the method of iterations.

To this end, we present Eq. (11) in the form

$$\begin{aligned} g_n= & {} \frac{1}{v}x^n \exp \left( -\varepsilon -v\sum ^{\infty }_k{B_{nk}{\mathrm{g}}_{\mathrm{k}}}\right) ,\nonumber \\ x= & {} \exp (\Lambda \mathrm{+}\varepsilon ). \end{aligned}$$
(12)

In zero iteration, we will neglect any interactions between the chains and put \(B_{nk}\)=0 in Eqs. (9), (11), (12). Substituting (12) into (10), neglecting the terms \(B_{nk}\), after calculations, we get

$$\begin{aligned} g_{0n}= & {} \frac{1}{v}x^n_0\exp (-\varepsilon ), \nonumber \\ x_0= & {} \exp ({\Lambda }_0)=\frac{1+y-\sqrt{1+2y}}{y},\ \ y=2\varphi \exp (\varepsilon ).\nonumber \\ \end{aligned}$$
(13)

Here and below, the subscript 0 means “zero iteration”. To get the first approximation, in the right part of (12), we use \(g_{0k}\) instead of \(g_k\)

$$\begin{aligned} g_{1n}=\frac{1}{v}x^n_1\exp \left( -\varepsilon -v\sum ^{\infty }_k{B_{nk}{\mathrm{g}}_{\mathrm{0k}}}\right) . \end{aligned}$$
(14)

The subscript 1 means “the first iteration”. One can determine \(x_{1}\) using the iteration (14) in the normalization condition (10). This procedure can be continued. Analysis [14] shows that when the concentration \(\varphi \) is in the range of several percent and \(\varepsilon \) is not large, the iteration scheme converges quite fast. We will restrict ourselves by the first iteration.

By definition, the chemical potential of the particles in the elementary unit volume is

$$\begin{aligned} \mu= & {} v\frac{\partial F}{\partial \varphi }=v\sum ^{\infty }_{n=1}{\frac{\partial F}{\partial g_n}\frac{\partial g_n}{\partial \varphi }=v\Lambda \sum ^{\infty }_{n=1}{n\frac{\partial g_n}{\partial \varphi }}}-\mu _0mH.\nonumber \\ \end{aligned}$$
(15)

Differencing both parts of Eq. (10) over \(\varphi \), one gets

$$\begin{aligned} v\sum ^{\infty }_{n=1}{n\frac{\partial g_n}{\partial \varphi }=1}. \end{aligned}$$
(16)

Thus, the chemical potential can be calculated as

$$\begin{aligned} \mu =\Lambda \mathrm{-}{\mu }_0mH. \end{aligned}$$
(17)

5 Second virial coefficient \(\varvec{B_{nk}}\)

The dimensionless second virial coefficient can be presented as

$$\begin{aligned} B_{nk}={B_{nk}}^{st}+{B_{nk}}^m. \end{aligned}$$
(18)

Here, the term \({B_{nk}}^{st}\) corresponds to the sterical interaction of the chains; \({B_{nk}}^m\)—to the magnetic interaction.

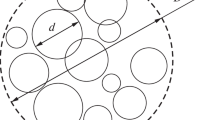
To estimate \({B_{nk}}^{st}\), let us remind that the second virial approximation is applicable when the volume concentration \(\varphi \) of the particles is low or moderate. In this case, the mean distance between the chains must be significantly more than the particle diameter d. Therefore, one can neglect the details of the “necklace” shape of the chains and model them as straight spherocylinders. Using the results of the classical Onsager theory, [20] taking into account that the chains are parallel, we get

$$\begin{aligned} {B_{nk}}^{st}=8+6(n+k-2). \end{aligned}$$
(19)

Let us estimate now the magnetic part \({B_{nk}}^m\) of the dimensional virial coefficient. By definition, it can be presented as

$$\begin{aligned} {B_{nk}}^m=\frac{1}{v}\int {\left[ 1-\exp (-u_{nk}({\mathbf{R}}))\right] d{{\mathbf {R}}}}. \end{aligned}$$
(20)

Here, u is dimensionless, related to kT, energy of magnetic interaction between the n- and k-particles chains; R is the radius-vector, linking centers of some chosen particles in the chains. We will choose the “lowest” particles, illustrated in Fig. 1.

Fig. 1
figure 1

A sketch of the interaction of n- and k-particle chains as well as the cylindrical coordinate system, used for calculation of the integrals in Eqs. (20), (22). Explanations are given in the text

Full size image

The energy \(u_{nk}\) of the dipole–dipole interaction of particles, united in the chains is (see Fig. 1)

$$\begin{aligned} u_{nk}= & {} -\frac{\varepsilon }{2}\sum ^n_{i=1}{\sum ^k_{j=1}{\frac{3{\left( j+z-i\right) }^2-(z^2+\rho ^2)}{{(z^2+\rho ^2)}^{5/2}}}},\nonumber \\ z= & {} \frac{R_z}{d},\quad \rho =\frac{R_\rho }{d}. \end{aligned}$$
(21)

For maximal simplification of calculations, we restrict ourselves by the situation when the mean value of the dimensionless energy \(u_{nk}\) of the dipole–dipole interaction between the chains is about one or less. In this case, we can expand the exponent in (20) into the power series; in the first approximation, one gets

$$\begin{aligned} {B}_{nk}^{m}=\frac{1}{v}\int {u_{nk}({\mathbf {R}})d{\mathbf {R}}}. \end{aligned}$$
(22)

Note that in the opposite case, when this mean dimensionless energy is significantly more than one, the chains condensation into the dense bulk phases must take place. This phase transition is beyond our consideration here.

De Gennes and Pincus have shown in [21] that, because the potential of the dipole–dipole interaction slowly decays with the interparticle distance, the integrals in (20), (22) converge conditionally; the results of the integration are determined by the shape of the volume of integration over the radius-vector R. The correct shape in the form of an infinitely long cylinder with the axis aligned along the applied field (along the axis Oz here) has been justified in [22]. Using the approach [22], we can present the integral in (20), (22) as

$$\begin{aligned} \frac{1}{v}\int {u_{nk}({{\mathbf {R}}})d{{\mathbf {R}}}}= & {} \frac{2\pi }{v}\int ^{\infty }_1{\int ^{\infty }_{-\infty }{u_{nk}(z,{\mathbf \rho })\mathrm{d}z\rho \mathrm{d}\rho }}\nonumber \\&+\varepsilon d^3\sum ^n_{i=1}\sum ^k_{j=1}(Q(n-1+j-i)\nonumber \\&+Q(k-1+i-j)),\nonumber \\ Q(x)= & {} \int ^1_0{\int ^{\infty }_{x+\sqrt{1-\rho ^2}}{u_{nk}(z,\rho )\mathrm{d}z \rho \mathrm{d}\rho }}.\nonumber \\ \end{aligned}$$
(23)

Note that the integral over z is internal; it is to be calculated first. The integral over \(\rho \) is to be calculated second. This order of integration is principally important to get the correct results.

Calculations show that the first integral in the brackets of (22) equals zero. After integrations, the function Q can be presented as

$$\begin{aligned} Q(x)=\frac{1}{2}\int ^1_0{\frac{\sqrt{1-y\ }+x}{{\left( 1+x^2+2x\sqrt{1-y\ }\right) }^{3/2\ }}\mathrm{d}y}. \end{aligned}$$
(24)

Combining Eqs. (22)–(24), we determine the magnetic part \({B_{nk}}^m\) of the second virial coefficient. The total coefficient \(B_{nk}\) can be found using relations (18), (19), (22)–(24).

6 Transport coefficients

Let us return to Eq. (1) for the particle flux density \({{\varvec{j}}}\). The problem of calculation of the components \(\beta _{n\parallel }\) and \(\beta _{n\bot }\) of the hydrodynamic mobility tensor \(\varvec{\beta }_{{\mathbf {n}}}\) of the neck-shaped chain is still unsolved. To get transparent estimates, we will model the n-particles chain by the ellipsoid of revolution with the aspect ratio (ratio of the major to the minor axis) equal to n and diameter equal to the particle diameter d. Note that the volume of this ellipsoid is the same as the total volume of the n particles in the chain. Therefore, the volume concentration \(\varphi \) of the ellipsoids coincides with the concentration of the particles in the fluid.

In the pair approximation between the particles, one can present

$$\begin{aligned} \beta _{n\parallel }={\beta _{n\parallel }}^0\left( 1-\ {\varphi K}_{n\parallel }\right) ,\ \ \beta _{n\bot }={\beta _{n\bot }}^0\left( 1-\ {\varphi K}_{n\bot }\right) .\nonumber \\ \end{aligned}$$
(25)

Here, \({\beta _{n\parallel }}^0\) and \({\beta _{n\bot }}^0\) are the mobilities of the single ellipsoids in an infinitive volume of the liquid; parameters \(K_{n\parallel }\), \(K_{n\bot }\) reflect the effects of the hydrodynamic interaction between the ellipsoids. For the hard spherical particles (n=1), they were determined by Batchelor [23] \(K_{1\parallel }=K_{1\bot }=6.55.\) At the same time, the dimensionless steric second virial coefficient for the identical spheres is \(B^{st}_{11}=8\).

To the best of our knowledge for non-spherical particles, the parameters \(K_{n\parallel }\), \(K_{n\bot }\) have not been determined. Here, we will ignore them; this means that we will concentrate on the effects of the steric and magnetic interaction between the chains.

Below, we consider two simple, however, quite typical situations when the vectors \(\nabla \varphi '\) and \({{{\mathbf {H}}}}_0\) are parallel and perpendicular.

Gradient of the particles concentration \(\nabla \varphi '\) is parallel to the field \({{{\mathbf {H}}}}_0\).

Let us introduce the Cartesian coordinate system, with the axis Oz directed along the field \({{{\mathbf {H}}}}_0\) and \(\nabla \varphi \mathrm{'}\). This means, in part, that \(\varphi \mathrm{'}\) depends only on the coordinate z. The symmetry consideration dictates that the vector \({{\mathbf {h}}}\) also must be directed along Oz and depend only on the coordinate z. Taking it into account, one gets from Eq. (7)

$$\begin{aligned} \frac{\partial h}{\partial z}=-M_p\frac{\partial \varphi '}{\partial z}. \end{aligned}$$
(26)

Substituting (26) into (6), taking into account Eq. (17), we come to the following relation:

$$\begin{aligned} \frac{\partial \mu }{\partial z}=\left[ \frac{\partial \Lambda }{\partial \varphi _0}+\mu _0mM_p\right] \frac{\partial \varphi '}{\partial z}=\left[ \frac{\partial \Lambda }{\partial \varphi _0}+\mu _0{M_p}^2v\right] \frac{\partial \varphi '}{\partial z}.\nonumber \\ \end{aligned}$$
(27)

Combining (1) and (27), one gets

$$\begin{aligned} j_{\parallel }=-D_{\parallel }\frac{\partial \varphi '}{\partial z}, \quad D_{\parallel }=\left[ \frac{\partial \Lambda }{\partial \varphi _0}+\mu _0{M_p}^2v\right] \sum ^{\infty }_{n=1}{ng_n\beta _{n\parallel }}.\nonumber \\ \end{aligned}$$
(28)

The subscript \(\parallel \) here marks components of vectors and tensors in the direction of the field \({{{\mathbf {H}}}}_0\).

Gradient of concentration is perpendicular to \({{\mathbf{H}}}_0\).

In this case, from relation (7), we get h=0; therefore, Eq. (1) can be rewritten as

$$\begin{aligned} j_{\bot }=-D_{\bot }\frac{\partial \varphi '}{\partial x},\quad D_{\bot }=\frac{\partial \Lambda }{\partial \varphi _0}\sum ^{\infty }_{n=1}{ng_n\beta _{n\bot }}. \end{aligned}$$
(29)

The subscript \(\bot \) marks the components in the direction perpendicular to \({{{\mathbf {H}}}}_0\).

7 Results

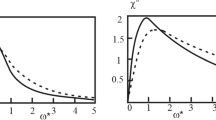
Figure 2 demonstrates the results of calculations of the mean number of particles in the chain

$$\begin{aligned} {<}n{>}=\frac{\sum ^{\infty }_{n=1}{ng_n}}{\sum ^{\infty }_{n=1}{g_n}}=\frac{\varphi }{v\sum ^{\infty }_{n=1}{g_n}} \end{aligned}$$
(30)

obtained in the zero (\(g_n=g_{0n}\)) and first (\(g_n=g_{1n}\)) iterations. Our analysis shows that the sterical interaction between chains increases the mean number \(<{n>}\), whereas the magnetic interaction decreases their mean size. The physical nature of that is in the fact that the absolute value of the mean negative energy of the chain–chain magnetic interaction decreases when the length of the chain increases. In contrast, the energy of the steric interaction between the chains is less than the one between the separate particles with the same volume concentration. These energetical factors provoke a reduction of the chain length because of magnetic interaction between them and an increase of the length because of the steric one. The reduction of <n> demonstrates that the effect of the magnetic interaction dominates over the steric ones.

Fig. 2
figure 2

The mean number of particles in the chains \(<{n}>\) versus their total volume concentration \(\varphi \) in the ferrofluid for two parameters e of the interparticle dipole–dipole interaction. Curves 0 and 1—the numbers of the iteration of the distribution function \(g_{n}\) calculation

Full size image

Note that for the system parameters, used in the calculations, illustrated in Fig. 2, the difference between the second (not shown here for brevity) and the first iterations of the mean number \(<n>\) calculations is not significant—about several percent.

Some results of calculations of the dimensionless components \(D_{\parallel }/D^0\) and \(D_{\bot }/D^0\) of the diffusion tensor are shown in Figs. 3 and 4. Here, \({\ D}^0=kT/3\pi \eta d\) is the classical Einstein coefficient of the single particle diffusion.

Fig. 3
figure 3

The ratio of the diffusion tensor components \(D_{\parallel }\) (a) and \(D_{\bot }\) (b) to the Einstein diffusion coefficient \({D}{}^{0}\) of the single particle. Parameter of the dipole–dipole interaction e=4. Figures 0 and 1 near the curves mean the zero and first iterations of the function g\({}_{n}\)

Full size image
Fig. 4
figure 4

The same as in Fig. 3 for e = 6

Full size image

The results demonstrate that the appearance of the chains significantly reduces both components of the diffusion tensor. Note that at vanishing concentrations \(\varphi \ \), our calculations give \(D_{\parallel },D_{\bot }\approx D^0\) as it should be.

The interchain interaction decreases the diffusion coefficients. This reduction takes place, because this interaction decreases the derivate \(\partial \mu /\partial \varphi \). The diffusion coefficient \(D_{\parallel }\) in the field direction nonmonotonic, with a minimum, depends on the particle concentration, whereas the coefficient in the perpendicular direction monotonically decreases with the total concentration [24].

8 Conclusion

The obtained results show that appearance of the chains in ferrofluids significantly reduces the diffusion coefficients both in the directions along and perpendicular to the applied magnetic field.

The physical reason of that is the reduction of hydrodynamic mobility for the main part of the particles united in the chains. The interchain interaction additionally decreases the diffusion coefficients. This reduction takes place, because this interaction decreases the derivate \(\partial \mu /\partial \varphi \). The diffusion coefficient \(D_{\parallel }\) in the field direction nonmonotonic, with a minimum, depends on the particle concentration, whereas the coefficient \(D_{\bot }\) in the perpendicular direction monotonically decreases with the total concentration.

Note that the real ferrofluids are polydisperse. However, an account of the polydispersity leads to very cumbersome mathematics. That is why, here, we restricted ourselves by the simplest model of the monodisperse ferrofluid, considering it as a “first step” towards the transport phenomena in the real systems.