Propagation of the autofocusing Lommel–Gaussian vortex beam with I-Bessel beam in turbulent atmosphere

Abstract

By the Fourier transformation upon an autofocusing Lommel–Gaussian vortex beam (LGVB) with J-Bessel beam, a novel autofocusing LGVB with I-Bessel beam is generated, and then the generated beam propagation in turbulence-free channel and turbulent atmosphere is investigated. Results demonstrate that under similar beam intensity profile parameters, a LGVB with J-Bessel beam has stronger anti-diffraction effect than a LGVB with I-Bessel beam in short-distance transmission, while a LGVB with I-Bessel beam has better autofocusing properties in long-distance transmission. Also, with the increase in topological charge, the intensity profile of the LGVB with I-Bessel beam remains almost unchanged within a certain distance, while it enlarges and the maximum intensity reduces beyond the certain distance. Additionally, when the ring radius approaches to a Gaussian beam waist, a LGVB with I-Bessel beam would degenerate into a LGVB with J-Bessel beam. Besides, impact of refractive index structure parameter and wavelength on the received probability of the LGVB with I-Bessel beam are also studied, and it is showed that the received probability decreases with the increase in the refractive index structure parameter or wavelength. This work could extend potential applications of LGVB with I-Bessel beam in free-space optical communication.

1 Introduction

The vortex beam is a special type of beam carrying orbital angular momentum (OAM) [1, 2], such as hollow Gaussian vortex beams [3, 4], high-order Bessel beams [5,6,7], Airy vortex beams [8, 9], perfect vortex beams [10,11,12], etc., which have become a research hotspot in recent years. Different OAM modes of the vortex beam are orthogonal to each other, which could be utilized to expand the channel capacity of the optical communication system. The OAM modes of the vortex beam are applied to signal encoding [13], because the number of OAM mode is not limited, in theory, a code element could carry an infinite amount of information. However, when the vortex beam is transmitted in turbulence atmosphere, the vortex structure is significantly distorted, and the beam intensity distribution is also uneven. The distortion and expansion of the spiral phase and spectrum could lead to crosstalk between different modes of vortex beams, which reducing the signal-to-noise ratio of the communication system and causing a decline in communication quality in practical applications [14,15,16].

At present, non-diffraction vortex beams are used as the beam source of free optical communication to mitigate turbulence effects [17, 18]. Lommel–Gaussian vortex beam (LGVB) is a typical non-diffraction vortex beam, whose essence is an infinite linear superposition of Bessel modes with the identical axial projections of wave vector [19]. It has a very narrow beam radius, and the central spot radius does not change with propagation distance. The self-healing properties of the LGVB improves the phase distortion and drift effect caused by the turbulent atmosphere, which is of great significance to explore its propagation in turbulent atmosphere [20, 21]. In 2016, the Fourier transformation of the Bessel beam was proposed to generate a perfect vortex beam (PVB). This novel beam has the properties that the radius remains unchanged with the increase in the OAM mode, that is, the PVB radius of different orders is the same, which has important application value in the fields of particle manipulation, quantum information coding and free-space optical communication [22,23,24,25]. In 2020, the beam-keeping characteristics of PVB propagating in turbulence atmosphere were investigated, it is found that the beam-keeping characteristics of PVB propagating in different atmospheric turbulence were greatly improved by adjusting the beam radius and ring width of PVB [26]. In addition, the self-focusing effect of a perfect optical vortex beam on the atmosphere power spectrum was studied, the beam could achieve long-distance transmission in turbulent atmosphere on account of its unique self-focusing effect, while its initial profile is not affected by changes in topological charge. However, to our knowledge, the Fourier transformation of the LGVB and the influences of the obtained beam propagating in turbulence-free and turbulence atmosphere have not yet been researched.

In this work, the anti-diffraction effect of the LGVB with the first kind Bessel function (J-Bessel beam) and the autofocusing properties of the LGVB with the modified Bessel function of first kind (I-Bessel beam) in the turbulence-free channel are investigated, and the influences of the LGVB with I-Bessel beam propagation in turbulence atmosphere are studied. Firstly, analytical expression of the LGVB with I-Bessel beam is obtained by using the Fourier transformation formula. Then, the correlation function of the LGVB with I-Bessel beam in turbulence atmosphere is established by Rytov approximation, and the signal OAM modal probability density of the beam is derived. Further, we study the effects of propagation distance, topological charge and ring radius on the autofocusing properties by the intensity and phase distribution of the LGVB with I-Bessel beam, and influence of wavelength and refractive index structure constant on the received probability of the LGVB with I-Bessel beam are also analyzed and discussed. Finally, the obtained results are summarized.

2 Theoretical formulation

At the original plane, the Lommel mode is essentially a linear combination of Bessel modes, and the complex amplitude of the non-diffraction LGVB with J-Bessel beam at propagation distance z = 0 is expressed [27]

$$E_{J} \left( {r,\varphi } \right) = \sum\limits_{q = 0}^{\infty } {\left( {ic} \right)^{2q} J_{{m_{0} + 2q}} \left( {\frac{\eta r}{w}} \right)} \exp \left[ {i\left( {m_{0} + 2q} \right)\varphi } \right]\exp \left( { - \frac{{r^{2} }}{{w^{2} }}} \right),$$

(1)

where $\eta = k\sin \left( \theta \right)w$ represents the profile of the LGVB, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }$ denotes the wave number with wavelength λ, w is the Gaussian beam waist, θ is defined as Bessel cone angle, (r,φ) determine radial and angle coordinate, m₀ means the topological charge and c indicates dimensionless asymmetric parameter. A simple lens could act as an optical Fourier transformer, which can be written mathematically as [28]

$$E_{I} \left( {\tilde{r}_{p} ,\tilde{\varphi }_{p} } \right) = \frac{k}{i2\pi f}\int_{0}^{\infty } {\int_{0}^{2\pi } {E_{J} \left( {r,\varphi } \right)} } r{\text{d}}r{\text{d}}\varphi \exp \left[ { - \frac{ik}{f}r\tilde{r}_{p} \cos \left( {\tilde{\varphi }_{p} - \varphi } \right)} \right],$$

(2)

where $(\tilde{r}_{p} ,\tilde{\phi }_{p} )$ represents radial and angle coordinate after Fourier transformation, and f is the focal length of the lens.

Substituting Eq. (1) into Eq. (2), LGVB with J-Bessel beam could be transformed into the LGVB with I-Bessel beam, based on the Bessel function identity [29] and standard integral

$$E_{I} \left( {\tilde{r}_{p} ,\tilde{\varphi }_{p} } \right) = A_{0} \sum\limits_{q = 0}^{\infty } {\left( {ic} \right)}^{2q} \exp \left( { - \frac{{\tilde{r}_{p}^{2} }}{{w_{1}^{2} }}} \right)I_{{m_{0} + 2q}} \left( {\frac{{2\tilde{r}_{p} r_{0} }}{{w_{1}^{2} }}} \right)\exp \left[ {i\left( {m_{0} + 2q} \right)\tilde{\varphi }_{p} } \right],$$

(3)

where A₀ is constant amplitude, $w_{1} = 2f/kw$ indicates the Gaussian beam waist at the focus, $I_{{m_{0} + 2q}} \left( \cdot \right)$ represents the (m + 2q)th order of the first kind of modified Bessel function. When the LGVB with I-Bessel beam propagates through turbulence-free channel at propagation distance z from the source plane, the complex amplitude of the beam in the receiver plane could be determined by using the extended Huygens–Fresnel principle [30]

$$E_{I} \left( {\rho ,\theta ,z} \right) = \frac{k}{i2\pi z}\exp \left( {ikz} \right)\int_{0}^{\infty } {\int_{0}^{2\pi } {E_{I} \left( {\tilde{r}_{p} ,\tilde{\varphi }_{p} } \right)} } \exp \left\{ {\frac{ik}{{2z}}\left[ {\rho^{2} + \tilde{r}_{p}^{2} - 2\rho \tilde{r}_{p} \cos \left( {\theta - \tilde{\varphi }_{p} } \right)} \right]} \right\}\tilde{r}_{p} {\text{d}}\tilde{r}_{p} {\text{d}}\tilde{\varphi }_{p} .$$

(4)

Similarly, the complex amplitude of the LGVB with J-Bessel beam in turbulence-free channel is obtained

$$E_{J} \left( {\rho ,\theta ,z} \right) = \frac{k}{i2\pi z}\exp \left( {ikz} \right)\int_{0}^{\infty } {\int_{0}^{2\pi } {E_{J} \left( {r,\varphi } \right)} } \exp \left\{ {\frac{ik}{{2z}}\left[ {\rho^{2} + r^{2} - 2\rho r\cos \left( {\theta - \varphi } \right)} \right]} \right\}r{\text{d}}r{\text{d}}\varphi .$$

(5)

Substituting Eqs. (1) and (3) into Eqs. (5) and (4) for numerical integration, separately, the complex amplitude of the LGVB with J- and I-Bessel beams in the turbulence-free channel can be calculated

$$E_{J} \left( {\rho ,\theta ,z} \right) = \sum\limits_{q = 0}^{\infty } {\left( {ic} \right)}^{2q} \frac{{kA_{0} }}{{2n_{0} z}}\exp \left( {il\theta } \right)\exp \left( {\frac{{ikr^{2} }}{2z}} \right)\exp \left( { - \frac{{\alpha_{0}^{2} + \beta_{0}^{2} }}{{4n_{0} }}} \right)I_{l} \left( {\frac{{\alpha_{0} \beta_{0} }}{{2n_{0} }}} \right)\exp \left( {ikz} \right),$$

(6.1)

$$E_{I} \left( {\rho ,\theta ,z} \right) = \sum\limits_{q = 0}^{\infty } {\left( {ic} \right)^{2q} \frac{k}{{2n_{1} z}}\exp \left( {il\theta } \right)\exp \left( {\frac{{ikr^{2} }}{2z}} \right)\exp \left( {\frac{{\alpha_{1}^{2} - \beta_{1}^{2} }}{{4n_{1} }}} \right)J_{l} \left( {\frac{{\alpha_{1} \beta_{1} }}{{2n_{1} }}} \right)\exp \left( {ikz} \right)} ,$$

(6.2)

with

$$l = m_{0} + 2q,n_{0} = \frac{1}{{w^{2} }} - \frac{ik}{{2z}},\alpha_{0} = \frac{\eta }{w},\beta_{0} = - \frac{kr}{z},n_{1} = \frac{1}{{w_{{^{1} }}^{2} }} - \frac{ik}{{2z}},\alpha_{1} = \frac{{2r_{0} }}{{w_{{^{1} }}^{2} }},\beta_{1} = - \frac{kr}{z}.$$

(7)

Equation (6.1) is the linear superposition of the first kind Bessel function and the exponential term, while the Eq. (6.2) is the linear superposition of the modified Bessel function of first kind and the exponential term. From different exponential terms and Bessel functions, the theoretical value of the Eq. (6.1) decreases rapidly after exceeding a Rayleigh distance z, whereas the theoretical value of the Eq. (6.2) has a maximum value at z = z₀, which means that the LGVB with I-Bessel beam has a autofocusing properties at the Rayleigh distance. This prediction would be verified in the numerical results. In the following part, the normalized probability density distribution at the receiving plane would be discussed. To describe the OAM mode of LGVB with I-Bessel beam more intuitively, the function $E_{I} \left( {\rho ,\theta ,z} \right)$ can be written in the form of spiral harmonic function exp(imθ) as follow [31]

$$E_{I} \left( {\rho ,\theta ,z} \right) = \frac{1}{{\sqrt {2\pi } }}\sum\limits_{m} {R_{l,m} \left( {\rho ,z} \right)\exp \left( {im\theta } \right)} ,$$

(8)

where $R_{l,m} \left( {\rho ,z} \right)$ is given by the integral

$$R_{l,m} \left( {\rho ,z} \right) = \frac{1}{{\sqrt {2\pi } }}\int_{0}^{2\pi } {E_{I} \left( {\rho ,\theta ,z} \right)\exp \left( { - im\theta } \right){\text{d}}\theta } ,$$

(9)

By combining Eqs. (6–2)-(9), the mode probability density of the LGVB with I-Bessel beam in turbulence atmosphere channel is determined [32]

$$\left\langle {\left| {R_{l,m} \left( {\rho ,z} \right)} \right|^{2} } \right\rangle = \frac{1}{2\pi }\int_{0}^{2\pi } {\int_{0}^{2\pi } { \, E_{I} \left( {\rho ,\theta ,z} \right)E_{I}^{ * } \left( {\rho ^{\prime},\theta ^{\prime},z} \right) \times \left\langle {\exp \left[ {\psi \left( {\rho ,\theta ,z} \right) + \psi^{ * } \left( {\rho ^{\prime},\theta ^{\prime},z} \right)} \right]} \right\rangle {\text{d}}\theta {\text{d}}\theta ^{\prime}} } ,$$

(10)

where $\left\langle \cdot \right\rangle$ is expressed as the ensemble average over turbulence atmosphere medium, and * indicates the complex conjugate. The non-Kolmogorov probability spectrum is used to describe the effect of turbulence atmosphere on the OAM of the LGVB with I-Bessel beam. According to the quadratic approximation of the wave structure function [33], the relationship is given

$$\left\langle {{\text{exp}}\left[ {\psi \left( {\rho ,\theta ,z} \right) + \psi^{ * } \left( {\rho ^{\prime},\theta ^{\prime},z} \right)} \right]} \right\rangle \approx \exp \left( { - \frac{{2\rho^{2} - 2\rho^{2} \cos \left( {\theta - \theta ^{\prime}} \right)}}{{\sigma_{0}^{2} }}} \right),$$

(11)

here, $\sigma_{0}$ is the spatial coherence radius of the spherical wave in the anisotropic non-Kolmogorov turbulence, and takes the form [34]:

$$\sigma_{0} = \left\{ {\frac{{\zeta_{x}^{2} + \zeta_{y}^{2} }}{{2\zeta_{x}^{2} \zeta_{y}^{2} }}\frac{{\pi^{2} k^{2} zA\left( \alpha \right)C_{n}^{2} }}{{6\left( {\alpha - 2} \right)}} \times \left[ {\kappa^{2 - \alpha } \gamma \exp \left( {\frac{{\kappa_{0}^{2} }}{{\kappa_{{^{l} }}^{2} }}} \right)\Gamma \left( {2 - \frac{\alpha }{2},\frac{{\kappa_{0}^{2} }}{{\kappa_{{^{l} }}^{2} }}} \right) - 2\kappa_{0}^{4 - \alpha } } \right]} \right\}^{{ - \frac{1}{2}}} ,$$

(12.1)

with

$$A\left( \alpha \right) = \Gamma \left( {\alpha - 1} \right)\frac{{\cos \left( {\pi \alpha /2} \right)}}{{4\pi^{2} }},\gamma = 2\kappa_{0}^{2} - 2\kappa_{l}^{2} + \alpha \kappa_{l}^{2} ,$$

(12.2)

where ζ_x and ζ_y are, respectively, anisotropic factors of turbulence atmosphere in the x and y direction, $\kappa_{l} = {{C\left( \alpha \right)} \mathord{\left/ {\vphantom {{C\left( \alpha \right)} l}} \right. \kern-0pt} l}$, $\kappa_{0} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } L}} \right. \kern-0pt} L}$, $C\left( \alpha \right) = \left[ {A\left( \alpha \right)\Gamma \left( {\frac{5 - \alpha }{2}} \right)\frac{2\pi }{3}} \right]^{{\frac{1}{\alpha - 5}}}$, l is the inner scale and L is the outer scale, $C_{n}^{2}$ denotes the generalized refractive index structure parameter, α is defined as the power spectrum index. By solving the Eq. (10), the more general integral formula for the average probability distribution at the receiver plane could be obtained

$$\left\langle {\left| {R_{l,m} \left( {\rho ,z} \right)} \right|^{2} } \right\rangle = \sum\limits_{q = 0}^{\infty } {c^{4q} \frac{{k^{2} \pi }}{{2n_{1} n_{1}^{ * } z^{2} }}} \exp \left( {\frac{{\alpha_{1}^{2} - \beta_{1}^{2} }}{{4n_{1} }} + \frac{{\alpha_{1}^{2} - \beta_{1}^{2} }}{{4n_{1}^{ * } }} - \frac{{2\rho^{2} }}{{\sigma_{0}^{2} }}} \right)J_{l} \left( {\frac{{\alpha_{1} \beta_{1} }}{{2n_{1} }}} \right)J_{l} \left( {\frac{{\alpha_{1} \beta_{1} }}{{2n_{1}^{ * } }}} \right)I_{m - l} \left( {\frac{{2r^{2} }}{{\sigma_{0}^{2} }}} \right).$$

(13)

For designated OAM mode m = m₀, the normalized received probability of the LGVB with I-Bessel beam with OAM mode m propagating in anisotropic turbulence atmosphere is

$$P_{{m,m_{0} }} \left( {D,z} \right) = \frac{{\int_{0}^{D/2} {\left\langle {\left| {R_{l,m} \left( {\rho ,z} \right)} \right|^{2} } \right\rangle \rho d\rho } }}{{\sum\limits_{m = - \infty }^{\infty } {\int_{0}^{D/2} {\left\langle {\left| {R_{l,m} \left( {\rho ,z} \right)} \right|^{2} } \right\rangle \rho d\rho } } }},$$

(14)

where D is the diameter of the detector aperture. $P_{{m,m_{0} }} \left( \cdot \right)$ is the received probability of the orbital angular momentum, that is, the OAM mode m detected at the receiving plane is equal to the OAM mode m₀ carried by the LGVB with I-Bessel beam at the transmitting plane.

Equations 6, 7, 13 and 14 are the final analytical expressions in this paper, with which one could analyze the propagation of the LGVB with J- and I-Bessel beams in turbulent-free channel and discuss the received probability distribution of the LGVB with I-Bessel beam in turbulent atmosphere.

3 Numerical results

In this section, the numerical simulations of the LGVB with J- and I-Bessel beam in the turbulence-free channel and turbulent atmosphere were discussed, and the parameter values in the following numerical simulation are α = 3.3, $C_{n}^{2}$ = 10^–14 m^−2/3, μ_x = 2, μ_y = 2, η = 8, λ = 1.55 μm, r₀ = 0.04 m, w = 0.008 m, w₁ = 0.04 m, L₀ = 50 m, l₀ = 0.001 m, m = 2, m₀ = 2.

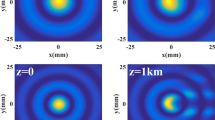
Figures 1 and 2 show the normalized intensity and phase distribution of the LGVB with J- and I-Bessel beams in the x–y plane with propagation distance z, respectively. It could be seen from Fig. 1 that the intensity of the LGVB with J-Bessel beam decreases with the increase in propagation distance z, and the intensity profile begins to expand at about 400 m. For the LGVB with I-Bessel beam in Fig. 2, when it is transmitted to about 400 m, the intensity profile obviously focuses, and the beam intensity does not decrease but increases, reaching the peak value at about 800 m. The comparison shows that LGVB with J-Bessel beam has better anti-diffraction effect than the LGVB with I-Bessel beam in short-distance transmission, while the LGVB with I-Bessel beam has better autofocusing properties in long-distance transmission. Compared with the phase structure in Figs. 1 and 2, it seems that the dark core size of the LGVB with J-Bessel beam enlarges slowly, while the dark core size of the LGVB with I-Bessel beam first reduces and then enlarges, and with the increase in propagation distance z, the phase structure of the LGVB with I-Bessel beam is more obviously disturbed.

Fig. 1

a Evolution of the normalized intensity distribution of LGVB with J-Bessel beam in the turbulence-free channel versus the propagation distance z, and normalized intensity and phase distribution of LGVB with J-Bessel beam in the x–y plane for b1–b2 z = 0 m, c1–c2 z = 400 m, d1–d2 z = 800 m, e1–e2 z = 1200 m, f1–f2 z = 1600 m and g1–g2 z = 2000 m

Fig. 2

a Evolution of the normalized intensity distribution of LGVB with I-Bessel beam in the turbulence-free channel versus the propagation distance z, and normalized intensity and phase distribution of LGVB with I-Bessel beam in the x–y plane for b1–b2 z = 0 m, c1–c2 z = 400 m, d1–d2 z = 800 m, e1–e2 z = 1200 m, f1–f2 z = 1600 m and g1–g2 z = 2000 m

Since the LGVB with I-Bessel beam is obtained by the Fourier transformation of the LGVB with J-Bessel beam, the anti-diffraction effect of the LGVB with I-Bessel beam is still retained, and the contour size can be preserved within 400 m, this distance range is regarded as anti-diffraction range. After beam propagation exceeds 400 m, the intensity profile shrinks and focuses, changing from single-ring intensity mode to multi-ring intensity mode, and the intensity of the LGVB with I-Bessel beam would decrease first and then increase with the increase in propagation distance z, and decrease again after reaching a certain peak intensity, this distance range could be considered as the autofocusing range. The effect of topological charge m₀ on beam propagation in turbulent-free channel is shown in Fig. 3. It is found that intensity profile of the LGVB with I-Bessel beam remains almost unchanged with the change of m₀ within 400 m, and in the autofocusing range, the intensity profile enlarges with the increase of m₀, while the maximum intensity of the beam reduces with the increase of m₀.

Fig. 3

Evolution of the normalized intensity distribution of LGVB with I-Bessel beam in turbulence-free channel versus different topological charges a m₀ = 2, b m₀ = 5 and c m₀ = 8

Figure 4 shows the evolution of intensity distribution of the LGVB with I-Bessel beam in the r-z plane versus ring radius r₀. With the decrease in r₀, the distance range required for the autofocusing properties of the LGVB with I-Bessel beam decreases. When r₀ equals to 0.024, the autofocusing properties of the LGVB with I-Bessel beam are no longer obvious, and when r₀ equals to w, the autofocusing properties disappear, the LGVB with I-Bessel beam degrades to the LGVB with J-Bessel beam propagation mode. Besides, with the increase in r₀, the radius size of the LGVB with I-Bessel beam enlarges, and the number of side lobes in the autofocusing range also increases.

Fig. 4

Evolution of the normalized intensity distribution of LGVB with I-Bessel beam in turbulence-free channel versus different ring radius a r₀ = 0.08, b r₀ = 0.04 and c r₀ = 0.008

The effect of turbulence atmosphere on LGVB with I-Bessel beam transmission along the axial direction is depicted in Fig. 5. Different observation cross sections are taken to study the variation of signal OAM modal probability density of the LGVB with I-Bessel beam along the propagation distance z, and it is found that the signal OAM mode probability density decreases rapidly due to turbulent disturbance of the spiral phase of the beam. However, due to the autofocusing properties, the probability density of the signal OAM mode of the beam is recovered to a certain extent in the autofocusing range. For the different distances of the LGVB with I-Bessel beam, the probability density of the signal OAM mode decreases first and then increases, and the probability density at about z = 400 m to z = 800 m are greater than the probability density at about distance z = 800 m to z = 1200 m. Choosing the appropriate propagation distance z is conducive to the transmission quality of the beam in turbulence atmosphere.

Fig. 5

Signal OAM mode probability density of LGVB with I-Bessel beam propagation in the turbulence atmosphere under different distance z

The received probability P_m,m0 of LGVB with I-Bessel beam is affected by the refractive index structure parameter $C_{n}^{2}$ as shown in Fig. 6. It is clear to seen that the received probability curve decreases rapidly with the increase in propagation distance z, when the propagation distance reaches the far field, the downward trend of the received probability curve slows down. With the increase in $C_{n}^{2}$, the received probability P_m,m0 is closer to 0.05.

Fig. 6

Received probability of OAM signal modes carried by LGVB with I-Bessel beam versus propagation distance z in turbulence atmosphere with different generalized refractive index structure parameter $C_{n}^{2}$

The selection of the wavelength of the light source in free-space optical communication is the key to improving communication efficiency, so that the effect of wavelength λ on the LGVB with I-Bessel beam in turbulence atmosphere is investigated. As shown in Fig. 7, it could be seen that as the propagation distance z increases, the received probability curve tends to decrease, at a certain propagation distance, the received probability gradually decreases as the wavelength λ increases.

Fig. 7

Received probability of OAM signal modes carried by LGVB with I-Bessel beam versus propagation distance z in turbulence atmosphere with different wavelength λ

4 Conclusions

By the Fourier transformation on an autofocusing Lommel–Gaussian vortex beam (LGVB) with J-Bessel beam, a novel autofocusing LGVB with I-Bessel beam is generated. The generated beam propagation in turbulence-free channel is investigated, and the normalized received probability of the LGVB with I-Bessel beam propagation in turbulence atmosphere is also considered. Results indicate that the anti-diffraction effect of the LGVB with J- and I-Bessel beams could be maintained within a distance of about 400 m, and beyond this distance the intensity profile of the LGVB with J-Bessel beam expands, while the intensity profile of the LGVB with I-Bessel beam focuses and then expands. It is worth mentioning that the influence of topological charge m₀ on the beam intensity is very limited in the anti-diffraction range, while the beam intensity reduces significantly with the increase in topological charge m₀ in the autofocusing range. Besides, it is found that the autofocusing properties of the LGVB with I-Bessel beam are related to the ring radius r₀: when r₀ tends to 0.008, the beam’s autofocusing properties disappear, and a LGVB with I-Bessel beam degenerates into a LGVB with I-Bessel beam. Furthermore, for the LGVB with I-Bessel beam, the smaller the generalized refractive index structure parameter $C_{n}^{2}$, the greater the received probability P_m,m0 of the beam in turbulent atmosphere, and as the wavelength λ increases, the curve of received probability P_m,m0 decays faster. This work could extend potential applications of LGVB with I-Bessel beam in free space optical communication.

Appendix

On Substitution from Eqs. (6.2), (11) into Eq. (10) and utilizing Eq. (12), the integral formula for the average probability distribution at the receiving plane becomes:

$$\begin{aligned} \left\langle {\left| {R_{l,m} \left( {\rho ,z} \right)} \right|^{2} } \right\rangle & = \frac{1}{2\pi }\int_{0}^{2\pi } {\int_{0}^{2\pi } {E_{I} \left( {\rho ,\theta ,z} \right)} E_{I}^{ * } \left( {\rho ^{\prime},\theta ^{\prime},z} \right) \times \left\langle {\exp \left[ {\psi \left( {\rho ,\theta ,z} \right) + \psi^{ * } \left( {\rho ^{\prime},\theta ^{\prime},z} \right)} \right]} \right\rangle {\text{d}}\theta {\text{d}}\theta ^{\prime}} \\ & =\frac{1}{2\pi }\sum\limits_{q = 0}^{\infty } {\left( {ic} \right)^{2q} } \sum\limits_{q^{\prime} = 0}^{\infty } {\left( {ic} \right)^{2q^{\prime}} } \int_{0}^{2\pi } {\int_{0}^{2\pi } {\frac{{k^{2} }}{{4n_{1} n_{1}^{*} z^{2} }}\exp \left( {\frac{{\alpha_{1}^{2} - \beta_{1}^{2} }}{{4n_{1} }}} \right)J_{l} \left( {\frac{{\alpha_{1} \beta_{1} }}{{2n_{1} }}} \right)} } \\ & \quad \times \frac{k}{{2n_{1} z}}\exp \left[ {i2\left( {q - q^{\prime}} \right)\theta } \right]\exp \left( {\frac{{\alpha_{1}^{2} - \beta_{1}^{2} }}{{4n_{1}^{*} }}} \right)J_{l} \left( {\frac{{\alpha_{1} \beta_{1} }}{{2n_{1}^{*} }}} \right) \\ & \quad \times \exp \left[ { - i\left( {m - m_{0} - 2q^{\prime}} \right)\left( {\theta - \theta ^{\prime}} \right)} \right]\exp \left( { - \frac{{2\rho^{2} - 2\rho^{2} \cos \left( {\theta - \theta ^{\prime}} \right)}}{{\sigma_{0}^{2} }}} \right){\text{d}}\theta {\text{d}}\theta ^{\prime}, \\ \end{aligned}$$

(15)

where l = m₀ + 2q is topological charge. Utilizing the following formula:

$$\begin{aligned} & \int_{0}^{2\pi } {\exp \left[ { - ix\theta + y\cos \left( {\theta - \theta ^{\prime}} \right)} \right]{\text{d}}\theta = 2\pi \exp \left( { - ix\theta ^{\prime}} \right)I_{x} \left( y \right)} , \\ & \int_{0}^{2\pi } {\exp \left( {is\phi } \right){\text{d}}\phi = \left\{ {\begin{array}{*{20}c} {2\pi } & {{\text{if}}\;m = 0,} \\ { 0} & {{\text{if}}\;m \ne 0,} \\ \end{array} } \right.} \\ \end{aligned}$$

(16)

a more convenient analytical expression can be obtained

$$\left\langle {\left| {R_{l,m} \left( {\rho ,z} \right)} \right|^{2} } \right\rangle = \sum\limits_{q = 0}^{\infty } {c^{4q} \frac{{k^{2} \pi }}{{2n_{1} n_{1}^{ * } z^{2} }}} \exp \left( {\frac{{\alpha_{1}^{2} - \beta_{1}^{2} }}{{4n_{1} }} + \frac{{\alpha_{1}^{2} - \beta_{1}^{2} }}{{4n_{1}^{ * } }} - \frac{{2\rho^{2} }}{{\sigma_{0}^{2} }}} \right)J_{l} \left( {\frac{{\alpha_{1} \beta_{1} }}{{2n_{1} }}} \right)J_{l} \left( {\frac{{\alpha_{1} \beta_{1} }}{{2n_{1}^{ * } }}} \right)I_{m - l} \left( {\frac{{2r^{2} }}{{\sigma_{0}^{2} }}} \right).$$

(17)