1 Introduction

During the last few decades, the observational inputs by High Red Shift type Ia Super-nova (SN Ia) changed the scenario view of the universe. The notable discovery is that due to negative pressure and positive energy density, the expansion of the universe is expanding with acceleration [1,2,3,4,5,6,7,8]. This discovery is further confirmed by the results of Cosmic Microwave Background Radiation (CMBR) [9, 10] and the Large Scale Structure (LSS) [11] data. The analysis of nine years of cosmological results by Wilkinson Microwave Anisotropy Probe (WMAP) [12, 13] and PLANK (XVI) [14] confirmed that dark energy and dark matter are basic constituents of the current universe. Dark energy constitutes 69% of total energy in the present observable universe, 5% for baryonic matter, and 26% for the non-baryonic dark matter if the Lambda-(Cold Dark Matter) CDM model of the universe is correct. For our universe, the easiest candidate for dark energy is the cosmological constant, which fills the space homogeneously with constant energy density. Dark energy models can be well-known by the equation of state (EoS) parameter, given by, ωd = pd/ρd, where pd and ρd are the pressure energy density of dark energy, respectively. The value of ωd is close to − 1 due to negative pressure energy density, or it may change with time t. For ωd = − 1, it represents the standard Lambda-CDM cosmological model. For slightly ωd < − 1 or ωd > − 1, it portrays the phantom or quintessence dark energy cosmological models of the universe.

The existence of dark energy and dark matter are the two notable discoveries in this decade that changed the entire modern cosmology. The observational data from 33 relaxed galaxy clusters A586 by Abell [15], and Baryon Oscillation Spectroscopic Survey (BOSS), mainly for the clustering properties of dark matter in contrast with the homogeneity of dark energy [16], display the interaction between dark energy and dark matter. Hence, one could propose cosmological models in which dark energy and dark matter interact with each other [17]. The interaction between dark matter and dark energy is possible because dark matter fluid is also poorly constrained in nature and for general relativity it requires that total momentum to be conserved, but not partial ones. The interacting dark energy and dark matter models are known to solve the coincidence problem [18,19,20,21,22,23].

In recent years, many radically different cosmological models have been proposed, a dynamical dark energy (quintessence field) [24], the nonlinear f(R) models or modified gravity [25] and inhomogeneous cosmologies [26]. Also, interacting dark energy cosmological models are investigated where dark energy and dark matter do not evolve separately but interact with each other in a non-gravitational way [27 and references therein]. Recently, Ray and Baruah [28] presented two-fluid cosmological models in five-dimensional Kaluza–Klein space-newtime taking a deceleration parameter (\(q\)) as a linear function of Hubble parameter(\(H)\) as \(q=-1+\beta H\).

The nature and physical properties of dark matter are not known at present. Dark matter is the most preferred candidate, represented by a Weakly Interacting Massive Particles (WIMPs) in hypothetically point of view. Khail and Harko [29 and references there] show that dark matter may be a direct consequence of the presence of an extra force and extra force is due to the presence of extra dimensions. The search for dark matter in a direct or indirect way is currently under way. Dark energy is best described in two forms: one is the cosmological constant, and other is scalar or quintessence field. Taking dark energy as the cosmological constant form is impossible due to the too large value of the cosmological constant obtained from quantum field theory. If dark energy is varying in nature, it may be perhaps due to a quintessence field or modified gravitational theories, viz. higher curvature terms or effects of higher dimensions.

The present article deals with new exact solutions of interacting and non-interacting two-fluid cosmological models filled with barotropic matter (due to dark matter nature and physical properties unknown) and dark energy in five-dimensional Kaluza [30]–Kelin [31] spacetime. The article is organised in the following sections. In Section 2, we formulate the Einstein’s field equation for five-dimensional Kaluza–Klein spacetime for two-fluid source. The cosmological models are obtained for non-interacting two-fluid source in Sect. 3, and in Sect. 4, the proposed cosmological models are obtained for interacting two-fluid source. The physical properties associated with different fluid and cosmological parameters are discussed with current observation values for both interacting and non- interacting two-fluid source. Finally, in Sect. 5, we conclude the works with major findings in research article.

2 Five-dimensional space–time and field equations

The line element of five-dimensional Kaluza–Klein space–time is given by [32],

$${\text{d}}{s}^{2}=-{\text{d}}{t}^{2}+{b}^{2}\left({\text{d}}{x}^{2}+{\text{d}}{y}^{2}+{\text{d}}{z}^{2}\right)+{a}^{2}{{\text{d}}\sigma }^{2}$$
(1)

where \(a\) and \(b\) are functions of time \((t)\) only.

Taking 8πG = 1 and c = 1, Einstein’s field equations are given by,

$$R_{{{\text{ij}}}} - \frac{1}{2}g_{{{\text{ij}}}} { }R = - T_{{{\text{ij}}}} .$$
(2)

Here, \({T}_{{\text{ij}}}={T}_{{\text{ij}}}^{({\text{m}})}+{T}_{{\text{ij}}}^{({\text{d}})}\) is the energy–momentum tensor for two-fluid source, where one fluid corresponds to model the barotropic fluid (\({T}_{{\text{ij}}}^{({\text{m}})}\)) and another fluid portrays the dark energy of the universe (\({T}_{{\text{ij}}}^{({\text{d}})}\)), given as in [33].

$${T}_{{\text{ij}}}^{({\text{m}})}={(p}_{{\text{m}}}+{\rho }_{{\text{m}}}) {u}_{i}^{{\text{m}}}{u}_{j}^{{\text{m}}}-{p}_{{\text{m}} }{g}_{{\text{ij}}}$$
(3)
$${T}_{{\text{ij}}}^{({\text{d}})}={(p}_{{\text{d}}}+{\rho }_{{\text{d}}}) {u}_{i}^{{\text{d}}}{u}_{j}^{{\text{d}}}-{p}_{{\text{d}} }{g}_{{\text{ij}}}$$
(4)

\(p_{{\text{m}}} \,{\text{and}}\;\rho_{{\text{m}}} \,\) are pressure and energy density of barotropic fluid, whereas the \(p_{{\text{d}}} \,{\text{and}}\;\rho_{{\text{d}}} \,\) are pressure and energy density of dark fluid respectively.

Taking the five-velocity given as in [34]

$$u_{i}^{{\text{m}}} = \left( {1,0,0,0,0} \right)\;\,\& \;\, u_{i}^{{\text{d}}} = \left( {1,0,0,0,0} \right),$$
(5)

which satisfies the conditions,

$${g}^{{\text{ij}}}{u}_{i}^{{\text{m}}}{u}_{j}^{{\text{m}}}=1\,\, \&\,\, {g}^{{\text{ij}}}{u}_{i}^{{\text{d}}}{u}_{j}^{{\text{d}}}=1.$$
(6)

Using Eqs. (3) to (6), the surviving field Eq. (2) in co-moving coordinate system for the metric (1) is given by:

$$3\frac{{\dot{a}\dot{b}}}{ab} + 3\frac{{\dot{b}^{2} }}{{b^{2} }} = \rho_{{\text{m}}} + \rho_{{\text{d}}}$$
(7)
$$3\frac{{\ddot{b}}}{b} + 3\frac{{\dot{b}^{2} }}{{b^{2} }} = - (p_{{\text{m}}} + p_{{\text{d}}} )$$
(8)
$$2\frac{{\ddot{b}}}{b} + \frac{{\ddot{a}}}{a} + \frac{{\dot{b}^{2} }}{{b^{2} }} + 2\frac{{\dot{a}\dot{b}}}{ab} = - (p_{{\text{m}}} + p_{{\text{d}}} )$$
(9)

The EoS parameter of the barotropic fluid and dark fluid is connected by relation:

$${p}_{{\text{m}}}={\omega }_{{\text{m}}}\ {\rho }_{{\text{m}}}$$
(10)
$${p}_{{\text{d}}}={\omega }_{{\text{d}}}\ {\rho }_{{\text{d}}}$$
(11)

where \({\omega }_{{\text{m}}}\) and \({\omega }_{{\text{d}}}\) are the EoS parameter of the barotropic fluid and dark fluid, respectively.

These are five Eqs. (7–11) with six unknowns, viz.\({p}_{{\text{m}}},{p}_{{\text{d}}},{\rho }_{{\text{m}}}, {\rho }_{d}, a\ {\text{and}}\ b\), respectively. Thus, to get a solution, we require one additional relation. This relationship may be taken to involve field variable.

3 Models with non-interacting two fluids

From Eqs. (8) and (9), an equation connecting a and b is obtained:

$$\frac{{\ddot{b}}}{b} - \frac{{\ddot{a}}}{a} + 2\frac{{\dot{b}^{2} }}{{b^{2} }} - 2\frac{{\dot{a}\dot{b}}}{ab} = 0$$
(12)

The usual conservation law for Einstein’s field equations is \(\nabla^{{\text{j}}} \left( {T_{{{\text{ij}}}} } \right) = 0\). It leads us to conservation equations, \({\nabla }^{{\text{j}}}\left({T}_{{\text{ij}}}^{\left({\text{m}}\right)}\right)=0\ \&\ {\nabla }^{j}\left({T}_{{\text{ij}}}^{\left({\text{d}}\right)}\right)=0\), when two fluids are non-interacting each other as follows,

$$\dot{\rho }_{{\text{m}}} + \left( {3\frac{{\dot{b}}}{b} + \frac{{\dot{a}}}{a}} \right)\left( {\rho_{{\text{m}}} + p_{{\text{m}}} } \right) = 0$$
(13)
$$\dot{\rho }_{{\text{d}}} + \left( {3\frac{{\dot{b}}}{b} + \frac{{\dot{a}}}{a}} \right)\left( {\rho_{{\text{d}}} + p_{{\text{d}}} } \right) = 0$$
(14)

Using Eqs. (10) in (13) and the integration of Eq. (13) leads to

$$\rho_{{\text{m}}} = \rho_{0} \left( {{\text{ab}}^{3} } \right)^{{ - (1 + \omega_{{\text{m}}} )}}$$
(15)

where \(\;\rho_{0} \,\) is an integrating constant. Consequently, we obtain \(p_{{\text{d}}} \,{\text{and}}\;\rho_{{\text{d}}} \,\) in terms of field parameter \(a\left(t\right) {\text{and}}\ b(t)\) as:

$$\rho_{{\text{d}}} = 3\frac{{\dot{a}\dot{b}}}{ab} + 3\frac{{\dot{b}^{2} }}{{b^{2} }} - \rho_{0} \left( {{\text{ab}}^{3} } \right)^{{ - (1 + \omega_{{\text{m}}} )}}$$
(16)
$$p_{{\text{d}}} = - \left[ {3\frac{{\ddot{b}}}{b} + \frac{{\dot{b}^{2} }}{{b^{2} }} + \omega_{{\text{m}}} \rho_{0} \left( {{\text{ab}}^{3} } \right)^{{ - (1 + \omega_{{\text{m}}} )}} } \right]$$
(17)

Integration of Eq. (12) leads to,

$$\left( {\frac{{\dot{b}}}{b} - \frac{{\dot{a}}}{a}} \right)\left( {{\text{ab}}^{{3}} } \right) = \alpha$$
(18)

where \(\;\alpha \,\) is a constant. From Eq. (18) we observe the following three cases for parameter \(\alpha\)

  1. (i)

    For \(\alpha <0\) implying that \(a\left(t\right)>b(t)\), it portrays the early phase of radiation dominant universe where the fifth dimension \(a\left(t\right)\) is more significant compared to scale factor \(b\left(t\right)\).

  2. (ii)

    For \(\alpha =0\) implying that \(a\left(t\right)=b(t)\), it portrays the phase of universe where the fifth dimension \(a\left(t\right)\) is equals to scale factor \(b\left(t\right)\).

  3. (iii)

    For \(\alpha >0\) implying that \(b\left(t\right)>a(t)\), it represent the present phase of matter dominant universe where the scale factor \(b\left(t\right)\) is more significant compared to scale factor \(a\left(t\right)\).

By using the transformation

$${\text{ab}}^{3} = U(t)$$
(19)

We obtain the field parameter \(a\left(t\right)\, {\text{and}}\ b(t)\),

$$a(t) = U^{\frac{1}{4}} e^{{ - \,\frac{3\alpha }{4}\int {\frac{{{\text{d}}t}}{U}} }} ,\;b(t) = U^{\frac{1}{4}} e^{{\,\frac{\alpha }{4}\int {\frac{{{\text{d}}t}}{U}} }} .$$
(20)

Taking the different forms of \(U(t)\), we obtain the field parameter \(a\left(t\right) \,{\text{and}}\ b(t)\) from Eq. (20). Consequently, we find the expressions for \(\rho_{{\text{m}}} ,\rho_{{\text{d}}} \,\,{\text{and}}\;p_{{\text{d}}} \,\) from Eqs. (15), (16) and (17).

The expressions for the scale factor (\(l\)), matter energy density (\({\Omega }_{{\text{m}}}\)), dark energy density (\({\Omega }_{{\text{d}}}\)), Hubble parameter (H), shear scalar (\({\sigma }^{2}\)) and deceleration parameter (\(q\)) are given by in terms of parameter (\(U\)):

$$l= {U}^{\frac{1}{4}}, H=\frac{\dot{l}}{l}=\frac{\dot{U}}{4U},\theta =4H=\frac{\dot{U}}{U},{ \sigma }^{2}= \frac{1}{2}\left[\sum_{i=1}^{i=4}{\left(\frac{{\dot{l}}_{i}}{{l}_{i}}\right)}^{2}-4{\left(\frac{\dot{l}}{l} \right)}^{2}\right]=\frac{3 {\alpha }^{2}}{8 {U}^{2}\vphantom{_{1_{1_{1_{1_{1_{1_{1}}}}}}}}},$$
$$q=\frac{d}{dt}\left(\frac{1}{H}\right)-1=\frac{3 {\dot{U}}^{2}-4U\ddot{U}} {{\dot{U}}^{2}},{\Omega }_{{\text{m}}}=\frac{{\rho }_{{\text{m}}}}{6{H}^{2}}=\frac{8 {\rho }_{0} {U}^{(1-{\omega }_{{\text{m}}})}}{3 {\dot{U}}^{2}}$$
$${\Omega }_{{\text{d}}}=\frac{{\rho }_{d}}{6{H}^{2}}=\frac{3\left({\dot{U}}^{2}-{\alpha }^{2}\right)-8 {\rho }_{0} {U}^{\left(1-{\omega }_{{\text{m}}}\right)} }{3 {\dot{U}}^{2}}$$
(21)

In cosmology, the jerk parameter is defined as the third derivative of the field parameters with respect to cosmic time with no unit. It is given by

$$j\left(t\right)=q+2{q}^{2}-\frac{\dot{q}}{H}$$
(22)

Taking the power law form for \(U(t)\),

$$U\left(t\right)={t}^{{\text{n}}},n\ne 1$$
(23)

The resulting solutions are given by as follows

$$a(t) = t^{\frac{n}{4}} e^{{ - \,\frac{3\alpha }{{4(1 - n)}}t^{(1 - n)} }} ,\;b(t) = t^{\frac{n}{4}} e^{{\,\frac{\alpha }{4(1 - n)}t^{(1 - n)} }} ,\;\rho_{{\text{m}}} = \rho_{0} t^{{ - n(1 + \omega_{{\text{m}}} )}}$$
$$\rho_{{\text{d}}} = 3\frac{{(nt^{(n - 1)} - \alpha )(nt^{(n - 1)} + \alpha )}}{{8t^{2n} }} - \rho_{0} t^{{ - n(1 + \omega_{{\text{m}}} )}} ,$$
$$p_{d} = \frac{{n(3 - n)t^{(2n - 2)} + n\alpha \;t^{(n - 1)} - \alpha^{2} }}{{4t^{2n} }} - \omega_{m} \rho_{0} t^{{ - n(1 + \omega_{m} )}} ,$$
(24)

where \({\rho }_{0}\) is the positive constant of integration.

Using Eqs. (11) and (24), we find the equation of state of dark field in terms of time as:

$$\omega_{{\text{d}}} = 2\left[ {\frac{{n(3 - n)t^{(2n - 2)} + n\alpha \;t^{(n - 1)} - \alpha^{2} - 4\omega_{{\text{m}}} \rho_{0} t^{{n(1 - \omega_{{\text{m}}} )}} }}{{3(nt^{(n - 1)} - \alpha )\;(nt^{(n - 1)} + \alpha ) - \alpha^{2} - 8\rho_{0} t^{{n(1 - \omega_{{\text{m}}} )}} }}} \right]$$
(25)

For the special case \(U\left(t\right)=t\), the field and cosmological parameters are given by

$$a\left(t\right)={t}^{\left(\frac{1-3\alpha }{4}\right)}, b\left(t\right)={t}^{\left(\frac{1+\alpha }{4}\right)}, \frac{b\left(t\right)}{a(t)}={t}^{\alpha }$$
$${\rho }_{{\text{m}}}= \frac{{\rho }_{0}}{{t}^{(1+{\omega }_{{\text{m}}})}}, {\rho }_{{\text{d}}}=\frac{3}{8}\left[\frac{(1-{\alpha }^{2})}{{t}^{2}}\right]-\frac{{\rho }_{0}}{{t}^{\left(1+{\omega }_{{\text{m}}}\right)}},{p}_{{\text{d}}}=\left[\frac{(2+\alpha -{\alpha }^{2})}{4{t}^{2}}\right]-\frac{{\omega }_{{\text{m}}} {\rho }_{0}}{{t}^{(1+{\omega }_{{\text{m}}})}}$$
$$\theta =4H=\frac{1}{t},{\sigma }^{2}=\frac{3}{8}\frac{{\alpha }^{2}}{{t}^{2}},q=3 , {\Omega }_{{\text{m}}}+{\Omega }_{d}=1-{\alpha }^{2}, j\left(t\right)=21$$
(26)

For \(\alpha =0\), \(a\left(t\right)=b\left(t\right)={t}^{1/4}\). For the interval \(-1\le \alpha \le 0\), the scale factor \(a\left(t\right)\) is more significant than the physical scale factor \(b\left(t\right)\), whereas for the interval \(\alpha >0,\) the physical scale factor \(b\left(t\right)\) is more significant compared to scale factor \(a\left(t\right)\). For \(\alpha >0,\) the scale factor \(b\left(t\right)\) is more significant compared to scale factor\(a\left(t\right)\). For \(\alpha =5/3,\) \(a\left(t\right)=\frac{1}{t}\) and \(b\left(t\right)={t}^{2/3}\), which implies that the model isotropies as \(t\to \infty\) and asymptotically approaches to Einstein–de Sitter universe or matter dominated universe. For \(\alpha =1,\) \(a\left(t\right)=\frac{1}{\sqrt{t}}\) and \(b\left(t\right)={t}^{1/2}\), it implies that the model represents early phase of radiation dominated universe.

Taking the EoS parameter of \({\omega }_{{\text{m}}}\) as constant between 0 and 1 and \({\omega }_{{\text{d}}}\) as a function of time because the recent cosmological data from SNIa, CMB and LSS [9,10,11] favours dynamically evolving dark energy. We further investigate the field parameters for the value of \(n>3\) and \(\alpha\) can take any positive or negative value.

For \(n>3\), \({\rho }_{{\text{m}}}\) decreases monotonically as t increases. \({\rho }_{{\text{d}}}\) is negative for \(0<t<{t}_{{\text{d}}}\) and vanishes at \(t={t}_{{\text{d}}}\). For \(t>{t}_{{\text{d}}}\), \({\rho }_{{\text{d}}}\) initially increases till it attains its maximum value and decreases monotonically afterwards, as shown in Fig. 1. For \(t>{t}_{{\text{d}}}\), \({\rho }_{{\text{d}}}/{\rho }_{{\text{m}}}\) increase monotonically as t increases, as shown in Fig. 2.

Fig. 1
figure 1

Plot of \({\rho }_{{\text{m}}}\) and \({\rho }_{{\text{d}}}\) versus time t for \({\rho }_{0}=10,n=9,\alpha =3\) and \({\omega }_{{\text{m}}}=0\)

Full size image
Fig. 2
figure 2

Plot of \({\rho }_{{\text{d}}}/{\rho }_{{\text{m}}}\) versus time t for \({\rho }_{0}=10,n=9,\alpha =3\) and \({\omega }_{{\text{m}}}=0\)

Full size image

Also, it is observed that \({\omega }_{d}\) becomes insignificant at \(t={t}_{{\text{c}}}\), where \({t}_{{\text{c}}}\) is the time obtained by solving the equation for the particular value of \(n,\alpha ,{\omega }_{{\text{m}}}\ {\text{and}}\ {\rho }_{0}\) [35, 36],

$$3n^{2} t_{c}^{{\left( {2n - 2} \right)}} - 4\alpha^{2} - 8\rho_{0} t_{c}^{{n\left( {1 - \omega_{{\text{m}}} } \right)}} = 0.$$
(27)

For \(t\le {t}_{c}\), \({\omega }_{d}\) is positive, whereas it is negative for \(t>{t}_{{\text{c}}}.\) It indicates that our model is a dusty universe at the initial time and converted to dark energy dominated phase after \(t={t}_{{\text{c}}}\), as shown in Fig. 3.

Fig. 3
figure 3

Plot of EoS parameter \({\omega }_{{\text{d}}}\) versus time t for \({\rho }_{0}=10,n=9,\alpha =3\) and \({\omega }_{{\text{m}}}=0\)

Full size image

From Eq. (21), we obtain the cosmological parameters:

$${l}_{1}={l}_{2}={l}_{3}={t}^{\frac{n}{4}}{e}^{\frac{\alpha }{4(1-n)}{t}^{(1-n)}}, {l}_{4}={t}^{\frac{n}{4}}{e}^{- \frac{3\alpha }{4(1-n)}{t}^{(1-n)}}, l={t}^{\frac{n}{4}}$$
$$H=\frac{n}{4 t},\theta =\frac{n}{t},{ \sigma }^{2}=\frac{3 {\alpha }^{2}}{8 {t}^{2n}}, q=\frac{4}{n}-1,j\left(t\right)=\frac{\left(n-4\right)\left(n-8\right)}{{n}^{2}}, {\Omega }_{{\text{m}}}=\frac{8 {\rho }_{0} {t}^{n(1-{\omega }_{{\text{m}}})}}{3 {n}^{2}{t}^{(2n-2)}}$$
$${\Omega }_{{\text{d}}}=\frac{3\left({n}^{2}{t}^{(2n-2)}-{\alpha }^{2}\right)-8 {\rho }_{0} {t}^{n(1-{\omega }_{{\text{m}}})} }{3 {n}^{2}{t}^{(2n-2)}}, {\Omega }_{{\text{m}}}+{\Omega }_{{\text{d}}}=1-{\left(\frac{\alpha }{{n t}^{(n-1)}}\right)}^{2}$$
(28)

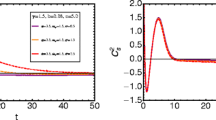
For \(n>1\), \({l}_{1},{l}_{2}{,l}_{3}\to 0\mathrm{\ and }\ {l}_{4}\to finite\ quantity\) as \(l\to 0\); thus, the singularity at \(t=0\) is barrel type. It implies that the universe starts with a one-dimensional universe and the fifth dimension \(a\left(t\right)\) is more significant in early times. For \(n=4\), deceleration parameter \(q\) becomes insignificant. For \(n>4\), \(q\) is negative and approaches to \(-1\) for \(n\to \infty\), whereas for \(n<4\), \(q\) is positive. The jerk parameter is positive for \(n<4\ \&\ n>8\), whereas for \(4<n<8\), \(j(t)\) is negative and approaches to \(1\) for \(n\to \infty\), as shown in Fig. 4.

Fig. 4
figure 4

Plot of j(t) and q for different values of n

Full size image

Recent observations suggest that dark energy dominates the present universe and has effects on our cosmic acceleration. This acceleration can be realized with negative pressure and positive energy density and not satisfied the strong energy conditions. This violation of energy conditions results in the opposite gravitational effect, and the universe gets a jerk from the earlier deceleration phase to the current acceleration phase [11].

Our model satisfies these conditions for \(n>8\) where \(q\) is negative and \(j(t)\) is positive. We investigate our model further for the value \(n=9\), and the field and cosmological parameters are given by taking \({\rho }_{0}=10,\alpha =3\) and \({\omega }_{{\text{m}}}=0\).

$${\rho }_{{\text{m}}}= \frac{10}{{t}^{9}} ,{\rho }_{{\text{d}}}=\frac{243 {t}^{16}-80{t}^{9}-27}{8{t}^{18}}, {p}_{{\text{d}}}=\frac{-54 {t}^{16}+27 {t}^{8}-9}{4{t}^{18}}$$
$$\theta =4H=\frac{9}{t},{\sigma }^{2}=\frac{27}{{8t}^{18}},q=-\frac{5}{9} ,j\left(t\right)=\frac{5}{81}, {\Omega }_{{\text{m}}}+{\Omega }_{{\text{d}}}=1-\frac{1}{9 {t}^{16}}$$

\({\rho }_{{\text{m}}}>0\) for all \(t\) and decreases monotonically as t increases. For \(t=0.921\), \({\rho }_{{\text{d}}}\) becomes insignificant and initially increases till it attains maximum value and decreases monotonically afterwards. For \(t=0.970\), \({\rho }_{d}\) becomes equals to \({\rho }_{{\text{m}}}\) and \({{ \rho }_{{\text{d}}}/\rho }_{{\text{m}}}\) increases monotonically afterwards. \({p}_{{\text{d}}}<0\) for all \(t\), and \({\omega }_{{\text{d}}}\) becomes insignificant for \(t=0.932\) and negative for \(t>0.932\). For \(t\to \infty\), \({\omega }_{{\text{d}}}\) approaches to value\(-0.44\). For \(t\to \infty\), \({\Omega }_{{\text{m}}}+{\Omega }_{{\text{d}}}\) approaches to value \(1\).

For large \(n\), the jerk parameter approaches to value one which is consistent with the current lambda-CDM model of the universe. For \(n=2.2\), the jerk parameter reduces to value \(j \approx 2.16\) and \(q=0.818\). The values of jerk parameter j = 2.16+0.81−0.75 and deceleration parameter \(q=-0.81\pm 0.14\) are obtained from the combination of three kinematical data sets, viz. the gold sample of type Ia supernovac [2], SNIa data from the SNLS project [37] and the X-ray galaxy cluster distance measurement [38].

From Eq. (28), we observe that \({\Omega }_{{\text{m}}}\) decrease as t increases. For \(t>{t}_{{\text{d}}}\), \({\Omega }_{{\text{d}}}\) initially increases till it attains maximum value and becomes constant as t increases, as shown in Fig. 5.

Fig. 5
figure 5

Plot of \({\Omega }_{{\text{m}}} and {\Omega }_{{\text{d}}}\) versus time t for \({\rho }_{0}=10,n=9,\alpha =3\) and \({\omega }_{{\text{m}}}=0\)

Full size image

From Eq. (28), the total density parameter (\(\Omega\)) is given by

$$\Omega ={\Omega }_{{\text{m}}}+{\Omega }_{{\text{d}}}=1-{\left(\frac{\alpha }{{n t}^{\left(n-1\right)}}\right)}^{2}.$$
(29)

The total density parameter (\(\Omega\)) depends upon the value of \(\alpha\ {\text{and}}\ n\) as shown in Fig. 6. This implies that initially ordinary matter density dominates the universe, but the late phase of the universe dark energy dominates the universe which is responsible for accelerated expansion of the current universe. For \(t\to \infty\) and \(n>1\), \(\Omega\) approaches to value \(1\).

Fig. 6
figure 6

Plot of \(\Omega\) versus time t for \(n=9\) and \(\alpha =3\)

Full size image

4 Models with interacting two fluids

For the interaction between dark fluid and barotropic fluid, the continuity equations for dark fluid and barotropic fluids are given as:

$$\dot{\rho }_{{\text{m}}} + \left( {3\frac{{\dot{b}}}{b} + \frac{{\dot{a}}}{a}} \right)\left( {\rho_{{\text{m}}} + p_{{\text{m}}} } \right) = Q$$
(30)
$$\dot{\rho }_{{\text{d}}} + \left( {3\frac{{\dot{b}}}{b} + \frac{{\dot{a}}}{a}} \right)\left( {\rho_{{\text{d}}} + p_{{\text{d}}} } \right) = - Q$$
(31)

For \(Q > 0\) or \(Q < 0\) expresses energy transfer from dark energy to dark fluid or dark fluid to dark energy. The forms of \(Q\) considered in literature are completely arbitrarily, with the obvious requirement to depend only on time due to homogeneity and isotropy. The usual choices of \(Q\) are (i) \(Q = \alpha \kappa \rho_{{{\text{dm}}}} \dot{\phi }\)(in string theory or scalar-tensor theory or Brans–Dicke theory) [39, 40], (ii) \(Q = 3b^{2} H\rho_{{{\text{MCG}}}}\) (in Modified Chaplygin Gas) [41], (iii) \(Q = 3\beta H(\rho_{{{\text{dm}}}} + \rho_{{{\text{de}}}} )\;or\;Q = 3\eta H\rho_{{{\text{dm}}}}\) [42, 43].

We can take here \(Q\) as expressed by Amondola et al. [37], Gou et al. [42],

$$Q = 3H\sigma \rho_{{\text{m}}}$$
(32)

where \(\sigma\) is the positive coupling constant.

From Eqs. (30) and (32), the fluid parameter \({\rho }_{{\text{m}}}\) is given by

$$\rho_{{\text{m}}} = \rho_{0} \left( {{\text{ab}}^{3} } \right)^{{ - (1 + \omega_{{\text{m}}} - \sigma )}} .$$
(33)

Consequently, we obtain \(p_{{\text{d}}} \,{\text{and}}\;\rho_{{\text{d}}} \,\) in terms of field parameter \(a(t)\,\,{\text{and}}\;b(t)\,\) as

$$\rho_{{\text{d}}} = 3\frac{{\dot{a}\dot{b}}}{ab} + 3\frac{{\dot{b}^{2} }}{{b^{2} }} - \rho_{0} \left( {{\text{ab}}^{3} } \right)^{{ - (1 + \omega_{{\text{m}}} - \sigma )}}$$
(34)
$$p_{{\text{d}}} = - \left[ {3\frac{{\ddot{b}}}{b} + \frac{{\dot{b}^{2} }}{{b^{2} }} + \omega_{{\text{m}}} \rho_{0} \left( {{\text{ab}}^{3} } \right)^{{ - (1 + \omega_{{\text{m}}} - \sigma )}} } \right]$$
(35)

From Eq. (20), the fluid parameters for interacting case are given by

$$\begin{aligned}&\rho_{{\text{m}}} = \rho_{0} t^{{ - n(1 + \omega_{{\text{m}}} - \sigma )}} ,\;\;\rho_{{\text{d}}} = 3\frac{{(nt^{(n - 1)} - \alpha )(nt^{(n - 1)} + \alpha )}}{{8t^{2n} }} - \rho_{0} t^{{ - n(1 + \omega_{{\text{m}}} - \sigma )}} ,\\ &\;\;p_{{\text{d}}} = \frac{{n(3 - n)t^{(2n - 2)} + n\alpha \;t^{(n - 1)} - \alpha^{2} }}{{4t^{2n} }} - \omega_{{\text{m}}} \rho_{0} t^{{ - n(1 + \omega_{{\text{m}}} - \sigma )}}\end{aligned}$$
(36)

Using Eqs. (34) and (35) in Eq. (11), we obtain the equation of state of dark field in terms of time as

$${\omega }_{{\text{d}}}=2\left[\frac{n\left(3-n\right){t}^{(2n-2)}+n\alpha {t}^{(n-1)}-{\alpha }^{2}-4{\omega }_{{\text{m}}}{\rho }_{0}{t}^{n(1-{\omega }_{{\text{m}}}+\sigma )}}{3\left(n{t}^{(n-1)}-\alpha \right)\left(n{t}^{(n-1)}+\alpha \right)-{\alpha }^{2}-8{\rho }_{0}{t}^{n(1-{\omega }_{{\text{m}}}+\sigma )}}\right]$$
(37)

Assuming the value of coupling constant (\(\sigma\)) in between \(0<\sigma <1\) [44], we have noted that for \(\sigma\) nearer to zero, the behaviour of physical parameters is the same as in a non-interacting case. For \(\sigma\) nearer to one, \({\rho }_{{\text{m}}}\) decreases slowly and \({\rho }_{{\text{d}}}\) has no effect and \({\rho }_{{\text{d}}}/{\rho }_{{\text{m}}}\) increases as t increases slowly compared to when two fluids are non-interacting, as shown in Fig. 7.

Fig. 7
figure 7

Plot of \({\rho }_{{\text{d}}}/{\rho }_{{\text{m}}}\) versus time t for\({\rho }_{0}=10,n=9,\alpha =3\), \({\omega }_{{\text{m}}}=0\) and \(\sigma =0.6\)

Full size image

Also, it is observed that \({\omega }_{d}\) becomes insignificant at \(t={t}_{{\text{c}}}^{*}\), where \({t}_{{\text{c}}}^{*}\) is the time obtained by solving the equation for the particular value of \(n,\alpha ,{\omega }_{{\text{m}}},\sigma\ {\text{and}}\ {\rho }_{0}\) [35, 36],

$$3n^{2} t_{{\text{c}}}^{*(2n - 2)} - 4\alpha^{2} - 8\rho_{0} t_{{\text{c}}}^{{*n(1 - \omega_{{\text{m}}} + \sigma )}} = 0.$$

For \(t<{t}_{{\text{c}}}^{*}\), \({\omega }_{d}\) is positive, whereas it is negative for \(t>{t}_{{\text{c}}}^{*}.\) Here we have noted that the behaviour of \({\omega }_{{\text{d}}}\) is similar to non-interacting case but here \({t}_{{\text{c}}}^{*}<{t}_{{\text{c}}}\) due to including the coupling constant (\(\sigma\)) term, as shown in Fig. 8.

Fig. 8
figure 8

Plot of EoS parameter \({\omega }_{{\text{d}}}\) versus time t for \({\rho }_{0}=10,n=9,\alpha =3\), \({\omega }_{{\text{m}}}=0\) and \(\sigma =0.6\)

Full size image

The cosmological parameters are same as given by Eq. (26) except the matter energy density (\({\Omega }_{{\text{m}}}\)) and dark energy density (\({\Omega }_{{\text{d}}}\)). \({\Omega }_{{\text{m}}}\) and \({\Omega }_{{\text{d}}}\) are given by

$${\Omega }_{{\text{m}}}=\frac{{\rho }_{{\text{m}}}}{6{H}^{2}}=\frac{8 {\rho }_{0} {t}^{n(1-{\omega }_{{\text{m}}}+\sigma )}}{3 {n}^{2}{t}^{(2n-2)}}, {\Omega }_{{\text{d}}}=\frac{3\left({n}^{2}{t}^{(2n-2)}-{\alpha }^{2}\right)-8 {\rho }_{0} {t}^{n(1-{\omega }_{{\text{m}}}+\sigma )} }{3 {n}^{2}{t}^{(2n-2)}}$$
(38)

From Eqs. (29) and (38), we observe that total energy density \((\Omega )\) is independent of the coupling constant (\(\sigma\)) term and remains the same for both interacting and non-interacting cases. It implies that the value of \(Q\) is very small and approaches zero, and favours the interaction between dark energy and dark fluid as the nature of the dark fluid is also poorly constrained.

5 Conclusions

In this paper, we have investigated interacting and non-interacting two-fluid cosmological models filled with dark energy and barotropic fluid in Kaluza-Klein space-times. We have obtained two-fluid cosmological models taking the EoS parameter \({\omega }_{{\text{d}}}\) as a function of time because recent observational data favours dynamically evolving dark energy [9,10,11]. The EoS parameter \({\omega }_{{\text{d}}}\) tends to \(-2/3\) for large \(n\), and it portrays the quintessence dark energy cosmological models of universe. Our presented two-fluid model is a dusty universe at an initial time and converted to dark energy dominated phase after \(t>{t}_{{\text{c}}}\ or\ t>{t}_{{\text{c}}}^{*}\) for interacting or non-interacting case. We have observed that for taking the coupling constant (\(\sigma\)) nearer to one, \({\rho }_{{\text{m}}}\) decreases slowly and \({\rho }_{{\text{d}}}\) has no effect and \({\rho }_{{\text{d}}}/{\rho }_{{\text{m}}}\) increases as t increases slowly in comparison to when the two fluids are non-interacting to each other.

All the expressions for cosmological parameters are same for interacting and non-interacting case, except the matter and dark energy density expression. Also, total energy density \((\Omega )\) is independent of the coupling constant (\(\sigma\)) term and remains the same for both interacting and non-interacting cases. \(\Omega\) approaches to value \(1\) as \(t\to \infty\). It implies that in the early phase of the universe ordinary matter density dominates but in the late phase of universe dark energy dominates in the universe that is responsible for accelerated expansion of the current universe.

For large \(n\), \(q\to -1\ {\text{and}}\ j(t)\to 1\); thus, our model is consistent with the current lambda-CDM model of universe, which is the best cosmological model to describe the current accelerated expansion and structure formation of the universe. Recently, Panigrahi, Paul and Chatterjee [45] presented a higher-dimensional cosmological model to explain the accelerating of the universe with a Chaplygin type of gas. In his finding, they analytically and graphically showed the analysis of flip time that early flip occurs for higher dimensions and rate of dimensional reduction is faster for higher dimensions.

The precise nature and more constraint on cosmological parameters can be obtained by the analysis of cosmological data of Baryon Acoustic Oscillations (BAO) [46, 47], Weak Lancing (WL) [48,49,50] and Galaxy Clusters and Redshift-Space Distortion (RSD) [51, 52] at low redshift.