1 Introduction

At the end of the last century, the works that reveal relations between non-commutative (NC) geometry and quantum theories of gravity gathered a great deal of attention [1,2,3,4,5]. Essentially, the fuzziness of spacetime was first proposed by Snyder and Yang in the middle of the last century to regularize the ultraviolet divergences of quantum field theories [6, 7]. NC quantum mechanics (NCQM) is sometimes addressed as an approximation of the noncommutative field theories which handle the problems of a finite number of low-energy limited particles that are bounded in the same NC space [8, 9].

In fact, non-relativistic NCQM formalism is first formulated by Chaturvedi et al. in 1993, [10]. There, they kept the time commutative, to preserve the unitarity of the theory, and deformed the usual Heisenberg algebra to assure the spatial non-commutativity. Later, other authors used the Moyal product [11], which leads an appropriate realization of NC operators, to introduce NC parameter to the NCQM formalism [12,13,14]. In the last three decades very important problems of physics, for example quantum hall effect [15,16,17], Landau problem [18,19,20], quantum harmonic oscillator problem in two and three dimensions [20,21,22], central potentials [23], Aharonov-Bohm effect [24, 25], spectra of Rydberg atoms [26], Bose-Einstein statistics [27] are extensively investigated.

In literature, we observe a great number of works that prefer to employ the phase-space (PS) extension of the configuration-space NCQM [28, 29, 31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. It is shown that the extended algebra of the PSNCQM, namely Heisenberg-Weyl algebra, can be mapped onto the standard algebra through Seiberg-Witten transformation [39]. Here, the interesting feature is that the physical predictions, i.e. the probabilities, expectation values, and eigenvalues of operators, are independent of the particular choice of the map [37]. Several other important aspects of the PSNCQM are revealed in detail in [44]. These features encouraged scientists to examine important physical problems via PSNCQM such as the Berry phase [35], quantum gravitational well [29, 30], quantum cosmology [38, 39], and entanglement [43]. Besides, oscillator dynamics for the Dirac [40], Klein-Gordon [36], harmonic [22], Duffin-Kemmer-Petiau [46] and Pauli [47] cases are investigated in PSNCQM formalism.

On the other hand, we notice an increasing interest in studies dealing with the Dunkl derivative. This is not surprising, since the Dunkl derivative operator has a rich structure. In fact the origin of Dunkl-derivative dates back to the middle of the last century, like NC space-time. In 1950, instead of deriving the equations of motion from the commutation relation, Wigner tried to derive the opposite, namely the commutation relations from the equation of motion [48]. He found that it is not always possible to obtain a unique relation, at least in the harmonic oscillator problem. In 1951, Yang employed a reflection operator and solved one-dimensional quantum harmonic oscillator with strict definitions of Hilbert space and expansion theory [49]. His findings cleared Wigner’s doubts. Using the Yang operator, Watanabe defined the Yang Hamiltonian and showed that this Hamiltonian is self-adjoint [50]. However, when the Yang operator acts on a constant number, it gives a non-zero value instead of zero. To remove this inconsistency, Dunkl defined the new derivative operator, which will be named after him, by of a combination of differential and discrete parts with the reflection operator term [51, 52]. Since then, the Dunkl operator has been used in many studies in physics, because its reflection operator causes solutions to have different structures according to parity [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69]. In particular, in 2013, in a series of two papers, Genest et al. considered an isotropic Dunkl-harmonic oscillator in the plane by displacing the Dunkl derivative with the partial derivative and discussed the superintegrability of the model [53, 54]. Then, they revisited the problem in three spatial dimensions [55]. Two years later, they examined the non-relativistic Dunkl-Coulomb problem in the same context [56]. In 2019, Mota et al. used this approach in the relativistic regime and obtained an exact solution of the Dunkl-Dirac oscillator which is under the influence of an external magnetic field [63]. Last year, they solved the Dunkl-Klein-Gordon equation in two dimensions with the Coulomb potential [66]. Very recently, the Dunkl-Klein-Gordon oscillator solutions are found in two and three dimensions, respectively in [67,68,69].

We believe that the Dunkl derivative formalism in a fuzzy PS could provide very interesting results. With this motivation, we consider a two-dimensional Dunkl harmonic oscillator in noncommutative space and intend to derive the energy eigenvalues and their corresponding eigenfunctions within perturbation methods. We organize the manuscript as follows: In Sect. 2, we construct the two dimensional Dunkl-Hamiltonian operator of the harmonic oscillator in the NCPS. After converting the Cartesian-based Dunkl-operator to polar coordinates-based Dunkl operator, in Sect. 3, we obtain the eigenenergies and their corresponding eigenstates of the model analytically. In the final section, we conclude the manuscript.

2 Two dimensional non-commutative Dunkl harmonic oscillator

The time-independent perturbation theory is based on the assumption in which the Hamiltonian of the system can be divided into two parts, such that an exact solution of one of them can be obtained and the other part can be approximated with the help of these solutions. Therefore, we have to derive the Hamiltonian of the system we are considering. To this end, at first we need to express the non-commutative Hamiltonian, and then, extend it by replacing the partial derivatives with the Dunkl ones. Accordingly, we start by writing the non-commutative harmonic oscillator Hamiltonian in two dimensions

$$\begin{aligned} H^{NC}=\frac{1}{2m}\bigg [(P_{x}^{NC})^{2}+(P_{y}^{NC})^{2}\bigg ] +\frac{1}{2}m\omega ^{2}\bigg [(x^{NC})^{2}+(y^{NC})^{2}\bigg ], \end{aligned}$$
(1)

where the non-commutative momentum and position operators are defined as [22]

$$\begin{aligned} P_{x}^{NC}=\, & {} P_{x}+\frac{\eta }{2}y, \end{aligned}$$
(2a)
$$\begin{aligned} P_{y}^{NC}=\, & {} P_{y}-\frac{\eta }{2}x, \end{aligned}$$
(2b)
$$\begin{aligned} x^{NC}=\, & {} x-\frac{\theta }{2}P_{y}, \end{aligned}$$
(2c)
$$\begin{aligned} y^{NC}=\, & {} y+\frac{\theta }{2}P_{x}. \end{aligned}$$
(2d)

Here, \(\eta\) and \(\theta\) are the NCPS parameters. Then, we substitute these operators in Eq. (1), and express the non-commutative Hamilton operator in the form of

$$\begin{aligned} H^{NC}=\bigg [\frac{(1+m^{2} \omega ^{2}\frac{\theta ^{2}}{4})}{2m}\bigg ](p_{x}^{2}+p_{y}^{2})+\bigg [\frac{(\frac{\eta ^{2}}{4}+m^{2} \omega ^{2})}{2m}\bigg ]({x}^{2}+{y}^{2})+\bigg [\frac{(\eta +m^{2} \omega ^{2}\theta )}{2m}\bigg ](yp_{x}-xp_{y}). \end{aligned}$$
(3)

Next, we change the partial derivatives with the Dunkl ones [53]. It is worth noting that partial derivatives only appear in the momentum operators, \(p_{x}\) and \(p_{y}\). Therefore, we consider

$$\begin{aligned} p_{x}\longrightarrow p_{x}^{\mu _{1}}=\frac{\hbar }{i} D_{x}^{\mu _{1}}= & {} \frac{\hbar }{i}\bigg [\frac{\partial }{\partial x}+\frac{\mu _{1}}{x}(1-R_{1})\bigg ], \end{aligned}$$
(4)
$$\begin{aligned} p_{y}\longrightarrow p_{y}^{\mu _{2}}=\frac{\hbar }{i} D_{y}^{\mu _{2}}= & {} \frac{\hbar }{i}\bigg [\frac{\partial }{\partial y}+\frac{\mu _{2}}{y}(1-R_{2})\bigg ], \end{aligned}$$
(5)

where the Wigner parameters, \(\mu _1\) and \(\mu _2\), are two positive constants [56]. Besides, the reflection operators, \(R_{1}\) and \(R_{2}\), satisfy

$$\begin{aligned} R_{1}f(x,y)=f(-x,y)\quad ,\quad R_{2}f(x,y)=f(x,-y)\quad ,\quad R_{1}^{2}=1\quad ,\quad R_{1} x=-xR_{1}\quad ,\quad R_{2} y=-yR_{2}. \end{aligned}$$
(6)

By using the Dunkl-momentum operators defined in Eqs. (4) and (5), we construct all necessary operators of the Hamiltonian in polar coordinates, such as

$$\begin{aligned} p_{x}^{2}+p_{y}^{2}\longrightarrow -\hbar ^{2}\left[ \frac{\partial ^{2}}{\partial \rho ^{2}}+\left( 1+2\mu _{1}+2\mu _{2}\right) \frac{1}{\rho }\frac{\partial }{\partial \rho }-\frac{B_{\phi }}{\rho ^{2}} \right] \end{aligned}$$
(7)

and

$$\begin{aligned} {{\mathcal {L}}_{z}}=yp_{x}-xp_{y}\longrightarrow {\frac{\hbar }{i}}\left[ -\frac{\partial }{\partial \phi }+\mu _{1} \tan \phi (1-R_{1})-\mu _{2}\cot \phi (1-R_{2}) \right] \end{aligned}$$
(8)

where \(B_{\phi }\) is given by

$$\begin{aligned} B_{\phi }=-\frac{\partial ^{2}}{\partial \phi ^{2}}+\frac{\mu _{1}(1-R_{1})}{\cos ^{2}\phi }+\frac{\mu _{2}(1-R_{2})}{\sin ^{2}\phi } -2(\mu _{2}\cot \phi -\mu _{1}\tan \phi )\frac{\partial }{\partial \phi }, \end{aligned}$$
(9)

and the Dunkl orbital angular momentum operator is directly related to this operator. As a result, we consider

$$\begin{aligned} {{\mathcal {L}}_{z}^{2}}={\hbar ^{2}}\left( B_{\phi }+2\mu _{1}\mu _{2}(1-R_{1}R_{2})\right) . \end{aligned}$$
(10)

After performing some simple algebra, we express the non-commutative Dunkl-harmonic oscillator Hamiltonian as

$$\begin{aligned} H_{Dunkl}=-\frac{\hbar ^{2}}{2m}\left( 1+m^{2} \omega ^{2}\frac{\theta ^{2}}{4}\right) \left( \frac{\partial ^{2}}{\partial \rho ^{2}}+\frac{\left( 1+2\mu _{1}+2\mu _{2}\right) }{\rho }\frac{\partial }{\partial \rho }-\frac{B_{\phi }}{\rho ^{2}} \right) +\frac{\frac{\eta ^{2}}{4}+m^{2} \omega ^{2}}{2m}\rho ^{2}+\frac{\left( \eta +m^{2} \omega ^{2}\theta \right) }{2m}{{\mathcal {L}}_{z}} \end{aligned}$$
(11)

Obviously, for \(\mu _{1}=\mu _{2}=\theta =\eta = 0\), we return to the ordinary Hamiltonian of the harmonic oscillator in the non-commutative phase-space for polar coordinates.

3 Separated solutions

In this section, we intend to derive the binding energy of the two-dimensional Dunkl-harmonic oscillator via polar coordinates. In order to state the impact of non-commutativity, first we revisit the well-known commutative case, where the Dunkl-Hamiltonian satisfies

$$\begin{aligned} H_{Dunkl}(\rho ,\phi )\psi _{n_{\rho },n_{\phi }}^{R_{1},R_{2}}(\rho ,\phi )=E_{n_{\rho }, n_{\phi }}\psi _{n_{\rho },n_{\phi }}^{R_{1},R_{2}}(\rho ,\phi ). \end{aligned}$$
(12)

We assume that the wavefunction can be separable to

$$\begin{aligned} \psi _{n_{\rho },n_{\phi }}^{R_{1},R_{2}}(\rho ,\phi )=\Psi _{n_{\rho }}^ {R_{1},R_{2}}(\rho )\Phi _{n_{\phi }}^{R_{1},R_{2}}(\phi ). \end{aligned}$$
(13)

Therefore, by applying Eq. (13) on Eqs. (9) and (10), we can reach the following concepts

$$\begin{aligned}{} & {} R_{i}\psi (\rho ,\phi )=s_{i}\psi (\rho ,\phi )\,\,\text {with}\,(s_{i}=\pm 1\,\,\text {and}\,i=1,2),\end{aligned}$$
(14)
$$\begin{aligned}{} & {} B_{\phi }\Phi _{n_{\phi }}(\phi )=q^{2}\Phi _{n_{\phi }}(\phi ),\end{aligned}$$
(15)
$$\begin{aligned}{} & {} {{\mathcal {L}}_{z}^{2}}\Phi _{n_{\phi }}(\phi )={\hbar ^{2}}\left( q^{2}{+}2\mu _{1}\mu _{2} (1-s_{1}s_{2})\right) \Phi _{n_{\phi }}(\phi ),\end{aligned}$$
(16)
$$\begin{aligned}{} & {} {{\mathcal {L}}_{z}}\Phi _{n_{\phi }}(\phi )={\hbar }\sqrt{q^{2}{+}2\mu _{1} \mu _{2}(1-s_{1}s_{2})}\Phi _{n_{\phi }}(\phi ) \end{aligned}$$
(17)

Consequently, by substituting Eq. (13) into Eq. (11), we have as follows

$$\begin{aligned}{} & {} \left[ -\frac{\hbar ^{2}}{2m}\left( 1+m^{2} \omega ^{2}\frac{\theta ^{2}}{4}\right) \left( \frac{\partial ^{2}}{\partial \rho ^{2}}+\frac{\left( 1+2\mu _{1}+2\mu _{2}\right) }{\rho }\frac{\partial }{\partial \rho }-\frac{q^{2}}{\rho ^{2}} \right) +\frac{\frac{\eta ^{2}}{4}+m^{2} \omega ^{2}}{2m}\rho ^{2}\right. \nonumber \\{} & {} \left. +\frac{{\hbar }\left( \eta +m^{2} \omega ^{2}\theta \right) }{2m}\sqrt{q^{2}{+}2\mu _{1}\mu _{2}(1-s_{1}s_{2})}\right] \Psi (\rho )=E\Psi (\rho ) \end{aligned}$$
(18)

and angular part

$$\begin{aligned} \left[ -\frac{\partial ^{2}}{\partial \phi ^{2}}+\frac{\mu _{1}(1-R_{1})}{\cos ^{2}\phi }+\frac{\mu _{2}(1-R_{2})}{\sin ^{2}\phi }-2(\mu _{2} \cot \phi -\mu _{1}\tan \phi )\frac{\partial }{\partial \phi } \right] \Phi (\phi )=q^{2}\Phi (\phi ) \end{aligned}$$
(19)

If we consider \(\cos ^{2}\phi =u\), then we obtain the eigenfunctions \(\Phi (\phi )\) of Eq. (19) as follows

$$\begin{aligned} & \quad \Phi _{{n_{\phi } }}^{{s_{1} ,s_{2} }} (\phi ) = \cos \phi ^{{\frac{1}{2}\left( { - 2\mu _{1} + 1 + |2\mu _{1} - s_{1} |} \right)}} \left( {1 - \cos ^{2} \phi } \right)^{{\frac{1}{4}\left( { - 2\mu _{2} + 1 + |2\mu _{2} - s_{2} |} \right)}} \\ & \quad \times P_{{n_{\phi } }}^{{\left( {\frac{1}{2}|2\mu _{1} - s_{1} |,\frac{1}{2}|2\mu _{2} - s_{2} |} \right)}} \left( {1 - 2\cos ^{2} \phi } \right), \\ \end{aligned}$$
(20)

where \(P_{m}^{(\alpha ,\beta )}(x)\) is a Jacobi polynomial. Based on these results, we can derive the eigenvalues of Eq. (19) are as follows

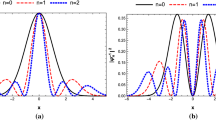
$$\begin{aligned} q^{2}= & {} -2 \mu _{1} \mu _{2}-\mu _{1}-\mu _{2}+4 n_{\phi }^{2}+2 n_{\phi } \bigg ({|2\mu _{1}-s_{1}|+|2\mu _{2}-s_{2}|}+2\bigg )+{|2\mu _{1}-s_{1}|}\nonumber \\{} & {} \quad +{|2\mu _{2}-s_{2}|\left( 1+\frac{1}{2}|2\mu _{1}-s_{1}| \right) } +\frac{3}{2} \end{aligned}$$
(21)

Therefore Eq. (18) can be transformed into the following polar equation using the results of eqs. (14 - 17). In Fig. 1, we have plotted Angular part eigenfunction versus \(\phi\) (\(0<\phi <2\pi\)), for different even and odd parities with \(\mu _{1}=\mu _{2}=0.5\) in \(n=0,1,2\). Then we obtain the energy spectrum of the Dunkl equation as follows:

$$\begin{aligned} E_{n_{\rho },q}={\mathcal {G}}_{3}\sqrt{q^{2}+2(1-s_{1}s_{2})\mu _{1}\mu _{2}}+2 \hbar \sqrt{{\mathcal {G}}_{1}{\mathcal {G}}_{2}}\left( 1+2 n_{\rho }+\sqrt{q^{2}+(\mu _{1}+\mu _{2})^{2}}\right) \end{aligned}$$
(22)

therefore, the wave function of Eq. (18) is

$$\begin{aligned} \Psi _{n_{\rho },q}(\rho )=e^{-\frac{1}{2} x^2 \sqrt{\frac{{\mathcal {G}}_{2}}{{\mathcal {G}}_{1} \hbar ^2}}} x^{-\mu _{1}-\mu _{2}+\sqrt{q^2+(\mu _{1}+\mu _{2})^2 }} L_{n_{\rho }}^{\sqrt{q^2+(\mu _{1}+\mu _{2})^2 }}\left( \sqrt{\frac{{\mathcal {G}}_{2}}{{\mathcal {G}}_{1}} \hbar ^2} x^{2}\right) \end{aligned}$$
(23)

with

$$\begin{aligned} {\mathcal {G}}_{1}=\frac{(1+m^{2} \omega ^{2}\frac{\theta ^{2}}{4})}{2m}\quad ,\quad {\mathcal {G}}_{2}=\frac{(\frac{\eta ^{2}}{4}+m^{2} \omega ^{2})}{2m}\quad ,\quad {\mathcal {G}}_{3}=\frac{{\hbar }(\eta +m^{2} \omega ^{2}\theta )}{2m} \end{aligned}$$
(24)

On the other hand, by considering \(\theta =\eta =0\) in Eq. (18), the corresponding eigenvalue obtain as

$$\begin{aligned} E_{n_{\rho },q}=\hbar \omega \left( 1+2 n_{\rho }+\sqrt{q^{2}+(\mu _{1}+\mu _{2})^{2}}\right) \end{aligned}$$
(25)

also for limit state of Dunkl parameters with \(\mu _{1}=\mu _{2}=0\), we have

$$\begin{aligned} E_{n_{\rho },q}=\hbar \omega \left( 1+2 n_{\rho }+|q|\right) \end{aligned}$$
(26)

Therefore, we return to the ordinary eigenvalue of the harmonic oscillator in the polar coordinates. In Figs. 2 and 3 we have plotted energy versus \(\omega\) and \(\eta\). we observe that when \(\omega\) and \(\eta\) increases the energy eigenvalue increases. Figures 2 and 3 also presents the energy spectrum for positive and negative parities. We also demonstrate some of the wave eigenfunctions for different values of quantum number n, in Fig. 4.

Fig. 1
figure 1

Angular part eigenfunction versus \(\phi\) (\(0<\phi <2\pi\)), for different n with \(\mu _{1}=\mu _{2}=0.5\)

Full size image
Fig. 2
figure 2

Energy spectrum differs for positive and negative parities versus \(\omega\) with \(n_{\phi }=2,\,m=1,\,\eta =\theta =0.2,\, \mu _{1}=\mu _{2}=0.5,\, s_{1}=s_{2}=+1\)

Full size image
Fig. 3
figure 3

Energy spectrum differs for positive and negative parities versus \(\eta\) with \(n_{\phi }=2,\,m=1,\,\omega =\theta =0.2,\, \mu _{1}=\mu _{2}=0.5,\, s_{1}=s_{2}=+1\)

Full size image
Fig. 4
figure 4

The ground and first two excited positive parity eigenfunctions versus \(\rho\) with \(n_{\phi }=2,\,m=1,\,\eta =\theta =0.2,\, \mu _{1}=\mu _{2}=0.5,\, s_{1}=s_{2}=+1\) and \(\omega =0.5\)

Full size image

4 Conclusion

In this manuscript, we examine two dimensional Dunkl-harmonic oscillator problem in a non-commutative phase space. In the context of time-independent polar coordinates, we derive eigenvalues and the corresponding eigenstates in terms of associated Laguerre polynomials. We show that considering Dunkl operator leads to different results than its ordinary state according to the even and odd parities.