1 Introduction

In recent years, the effects of the generalized uncertainty principle (GUP) and the extended uncertainty principle (EUP) have attracted great interest of researchers to study them on various quantum mechanical systems (see, e.g., Refs. [1, 2]). Indeed, it is well known that the application of GUP has come to mimic the effect of quantum gravity, whereas the EUP reflects the concept of space-time curvature. These algebraic deformations are characterized by modification of the canonical commutation relations of the position and momentum operators and imply the appearance of a nonzero minimal length (or momentum) in their uncertainty relations, which must be modified to include additional constraints in the framework of the gravitational field, as well as the term proportional to the cosmological constant. For this reason, the GUP is effective in the field of Planck-scale, whereas the EUP is important to understand quantum effects over macroscopic distances [3]. As a result, the EUP can be used to describe the effect of the cosmological horizon on single-particle quantum mechanics [4].

Since the final development of the deformation of quantum mechanical theory, several authors solved many problems with different methods [5,6,7,8,9,10,11,12,13]. In particular, there is a great interest to study the effects of the EUP and GUP algebra on the Dirac oscillator (DO) system. The latter is an important subject because it has become applied in various fields of physics, and appears in mathematical physics [14,15,16], nuclear physics [17, 18] and non-commutative geometry [19, 20]. It should be noted that the Dirac oscillator potential can be used for studying the electronic properties of charge carriers in graphene [21]. It is also extremely important in quantum chromodynamics (QCD), where it can be used to estimate quark masses [22]. Historically, Ito et al were the first to propose the idea of the DO [23], and it was subsequently developed by Moshinsky and Szczepaniak [24]. Moshinsky named this system a “Dirac oscillator” because in the non-relativistic limit, the Dirac Hamiltonian for this system contains the ordinary harmonic oscillator plus spin-orbit coupling. Also, the first experiment of DO was implemented in Ref. [25]. In addition, a number of papers have addressed DO analysis with deformed algebra, among them, the one-dimensional DO in the presence of the new GUP from the concept of doubly special relativity [26], the GUP Dirac oscillator in the configuration space representation [27], a two-dimensional DO under the influence of GUP [28], the effect of minimal length in one and three dimensions [29, 30], the EUP Dirac oscillator in one dimension [8, 31] and in three dimensions [32]. All these papers have used the wave equation method and they have some common results such that the effect of modified algebra on the DO causes the appearance of the phenomenon of hard confinement. Furthermore in Ref. [31], the authors have shown that the EUP context makes the energy levels of the one-dimensional DO have an upper bound.

On the other hand, the Feynman path integral formulation also found its luck in this type of problem, there are some authors who have taken care of this method in the quantum theory area. For example, Benzair et al. have presented the DO propagator in one dimension and two dimensions with deformed commutation relation of the Heisenberg uncertainty principle (HUP), respectively [33, 34]. Moreover in Ref. [35], the authors have formulated the propagator of the DO in one dimension and in the context of EUP. Complementary to these research, in particular Ref. [33], our work will aim to study the two-dimensional DO in the position space representation using the path integration technique in the context of EUP based on the following generalization of momentum and position operators

$$\begin{aligned} \hat{P}_{i}=\imath \hbar (1+\alpha \textbf{X}^{2})\frac{\partial }{\partial x^{i} },\hat{X}_{i}=\hat{x}_{i},i=1,2, \end{aligned}$$
(1)

with \(\alpha\) is a small and positive parameter. The number-case ( \(i=1,2\)) of (\(\hat{X}_{i}=\hat{x}_{i}\equiv (\hat{x},\hat{y})\), \(\hat{P}_{i}\equiv (\hat{P}_{x},\hat{P}_{y})\)) denotes the coordinates and the momenta components operators. While \(\textbf{X}^{2}\) being the vector module.

The deformed momentum operator in (1) makes the algebra of quantum mechanics different from the usual canonical commutation relations, where the non-commutative between position and momentum operators becomes as

$$\begin{aligned} \left[ \hat{X}_{i},\hat{P}_{j}\right] =\imath \hbar \delta _{ij}\left( 1+\alpha \textbf{X}^{2}\right) , \end{aligned}$$
(2)

where \(\delta _{ij}\) is the Kronecker symbol, which gives 1 if the variables are equal, and 0 otherwise. In the cosmological context, the numerical value of \(\alpha\) in the natural units is \(\alpha \sim 10^{-77}\)Mev\(^{2}\) [4]. In this EUP example, the modified commutation relation in Eq. (2) is exactly the formalism of quantum mechanics on (anti)-de Sitter space (Ads), and the HUP should be modified \(\Delta x_{i}\Delta p_{j}\ge \frac{\delta _{ij} }{2}(1-\frac{\Gamma }{3}\left( \Delta x_{i}\right) ^{2})\) by introducing a term proportional with the cosmological constant (\(\Gamma =-3\alpha\)) [11, 36]. Also, this deformation leads to the following non-commutative momentum operators

$$\begin{aligned}{}[\hat{P}_{i},\hat{P}_{j}]=2\imath \hbar \alpha \left( \hat{X}_{j}\hat{P}_{i}-\hat{X}_{i}\hat{P}_{j}\right) . \end{aligned}$$
(3)

The components of the position operators are assumed to commute with each other

$$\begin{aligned}{}[\hat{X}_{i},\hat{X}_{j}]=0. \end{aligned}$$
(4)

We can easily remark that the momentum operator in Eq. (2) is not Hermitian anymore on Hilbert space \(L\left( \mathbb {R}^{2},d^{2}x\right) .\) So we must work on the subspace instead of all Hilbert space \(L\left( \mathbb {R}^{2},d^{2}x/\left( 1+\alpha \textbf{x}^{2}\right) \right)\), where the scalar product between two functions becomes

$$\begin{aligned} \left\langle f\mid g\right\rangle _{\alpha }=\int \frac{d^{2}x}{1+\alpha \textbf{x}^{2}}f^{\star }(\textbf{x})g(\textbf{x}), \end{aligned}$$
(5)

and the closure relation corresponding to the state \(|x\rangle\) is

$$\begin{aligned} \int d_{\alpha }^{2}x|\textbf{x}\rangle \langle \textbf{x}|=\mathbb {I}, \end{aligned}$$
(6)

Here, \(d_{\alpha }^{2}x\) is the deformed measure defined by \(d_{\alpha } ^{2}x=d^{2}x/\left( 1+\alpha \textbf{x}^{2}\right) .\) As a consequence, their projection relation is easily given by

$$\begin{aligned} \langle \textbf{x}|\textbf{x}^{\prime }\rangle _{\alpha }=(1+\alpha \textbf{x}^{2})\delta ^{2}(\textbf{x}-\textbf{x}^{\prime }). \end{aligned}$$
(7)

In the case \(\alpha =0\), we recover the usual projection relation \(\langle \textbf{x}|\textbf{x}^{\prime }\rangle _{\alpha \rightarrow 0} =\delta ^{2}(\textbf{x}-\textbf{x}^{\prime }).\)

For the time component, we assume that no deformation on the time-coordinate

$$\begin{aligned} \langle x_{0}|x_{0}^{\prime }\rangle =\delta (x_{0}-x_{0}^{\prime }),\text { and }\int dx_{0}|x_{0}\rangle \langle x_{0}|=1. \end{aligned}$$
(8)

The modification of the non-commutative between position and momentum operators in Eq. (2) leads to the following constraint of the minimal uncertainty in momentum measurements \((\Delta P_{i})_{\text {min}}=\hbar \sqrt{\alpha }/2\) and the maximal uncertainty in position measurements \(\left( \Delta X_{i}\right) _{\text {max}}=1/\sqrt{\alpha }\).

The rest of this paper is organized as follows, in Sec. II, we formulate the Green function for the relativistic Dirac oscillator with the modified commutation relation defined in Eq. (2), and it is expressed in Cartesian space-time coordinates. But without using Grassmann variables proved in [37], it is based on making the path integration over the elements of the Green function matrix. This approach has already been used in Refs. [33, 38]. Thanks to the spherical coordinate transformation we have succeeded in separating the angular part from the radial part in section III, which gives the Poschl–Teller radial-propagator [34, 39]. In section IV, the exact energy eigenvalues and their corresponding normalized wave functions are deduced. In Sec. V, we get the thermodynamic functions for the Dirac oscillator with EUP in the high-temperature regime and plot them. Finally, we draw our conclusion in section VI.

2 Green function in Cartesian coordinates

In this section, we construct the relativistic Green function for \((2+1)-\)dimensional Dirac oscillator propagator in a position space representation and in the EUP framework. The propagator of DO is defined as the causal Green function:

$$\begin{aligned} \left( {\gamma }^{\mu }\hat{\Pi }_{\mu } {-m}\right) {S} ^{\left( \alpha \right) c}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a} ,x_{0a}\right) =-\left( 1+\alpha \textbf{x}_{b}^{2}\right) \delta ^{3}\left( x_{b}-x_{a}\right) . \end{aligned}$$
(9)

Here, \({\gamma }-\)matrices satisfy the usual commutation relation \(\left\{ {\gamma }^{\mu },{\gamma }^{\nu }\right\} =2\eta ^{\mu \nu }\) with \(\eta ^{\mu \nu }=\)diag\((1,-1,-1)\) and \(\mu =0,1,2.\)

From [24], we can write \(\hat{\Pi }_{\mu }\) as

$$\begin{aligned} \hat{\Pi }_{0}=\imath \frac{\partial }{\partial t}, \varvec{\hat{\Pi } }=\varvec{\hat{P}}-im\omega {\gamma }^{0}\varvec{\hat{X}}, \end{aligned}$$
(10)

where \(\varvec{\hat{P}}\equiv (\hat{P}_{x},\) \(\hat{P}_{y})\) and \(\varvec{\hat{X}}=(\hat{X},\) \(\hat{Y})\) are operators that achieve the non-commutative relations are shown in Eqs. (2), (3) and (4). The \(2\times 2\) Dirac matrices can be chosen as the Pauli matrices, and they obey the following relations

$$\begin{aligned} {\gamma }^{0}=\sigma ^{3},{\gamma }^{1}={\gamma }^{0}\sigma ^{1},{\gamma }^{2}={\gamma }^{0}\sigma ^{2}. \end{aligned}$$
(11)

Throughout the paper, we set that \(\hbar =c=1.\) The \(\omega\) represents the oscillator frequency and m is the rest mass of a particle. Let us point out that Eq. (10) is obtained from the propagator of the Dirac equation in two dimensions by the minimal coupling substitution \(\hat{P}_{i} \rightarrow \hat{P}_{i}-im\omega {\gamma }^{0}\hat{X}_{i}\) [24].

As we know, the Schwinger proper-time method gives the relation between the global Green function and the Hamiltonian [40],

$$\begin{aligned} G^{\left( \alpha \right) }\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a} ,x_{0a}\right) =\left( -\imath \right) \int _{0}^{\infty }d\lambda \left\langle \textbf{x}_{b},x_{b0}\right| \exp \left( i\lambda \hat{H}^{\left( \alpha \right) }\right) \left| \textbf{x}_{a},x_{a0}\right\rangle _{\alpha }. \end{aligned}$$
(12)

The global representation of the Green function can be easily shown that

$$\begin{aligned} S^{\left( \alpha \right) }\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a} ,x_{0a}\right) =\left( {\gamma }^{\mu }\hat{\Pi }_{\mu } -m \right) _{b}G^{\left( \alpha \right) }\left( \textbf{x}_{b},x_{0b} ,\textbf{x}_{a},x_{0a}\right) , \end{aligned}$$
(13)

where \(\lambda\) is the bosonic proper time and the Hamiltonian \(\hat{H}^{\left( \alpha \right) }\) gives a bosonic type operator for the \({\gamma }-\)matrices

$$\begin{aligned} \hat{H}^{\left( \alpha \right) }=\left( {\gamma }^{\mu }\hat{\Pi }_{\mu }+\text {m}\right) \left( {\gamma }^{\mu }\hat{\Pi }_{\mu }\text {-m }\right) . \end{aligned}$$
(14)

Under considerations of Eqs. (1), (2) and (3), the Hamiltonian operator expression is given by:

$$\begin{aligned}{} & {} \hat{H}^{\left( \alpha \right) }=\hat{p}_{0}^{2}-\varvec{\hat{P}}^{2} +2\imath \gamma ^{1}\gamma ^{2}\left( \alpha (\hat{X}_{2}\hat{P}_{1}-\hat{X} _{1}\hat{P}_{2})+m\omega (1+\alpha \hat{\textbf{X}}^{2})\right) \nonumber \\{} & {} \quad -2m\omega (\hat{P}_{1}\hat{X}_{2}-\hat{P}_{2}\hat{X}_{1})-m^{2}\omega ^{2} \hat{\textbf{X}}^{2}-m^{2}. \end{aligned}$$
(15)

Then, by taking into account the properties of the following exponential matrix, we can simplify it as:

$$\begin{aligned} \exp \left( -\lambda \gamma ^{1}\gamma ^{2}\hat{h}\left( \hat{X}_{i},\hat{P} _{i}\right) \right) =\cos \left( \lambda \hat{h}\left( \hat{X}_{i},\hat{P}_{i}\right) \right) -\gamma ^{1}\gamma ^{2}\sin \left( \lambda \hat{h}\left( \hat{X}_{i},\hat{P}_{i}\right) \right) , \end{aligned}$$
(16)

with \(\hat{h}(\hat{X}_{i},\hat{P}_{i})=2(\alpha \hat{L}_{3}+m\omega (1+\alpha \varvec{\hat{x}}^{2}))\) and \(\hat{L}_{3}=\hat{X}_{2}\hat{P}_{1} -\hat{X}_{1}\hat{P}_{2}.\) Thus, the result of Eq. (16) is done in cooperation with the properties of Dirac’s matrices \((\gamma ^{1}\gamma ^{2})^{2}=-1.\) Hence, Eq. (16) becomes

$$\begin{aligned} \exp \left( -\lambda \gamma ^{1}\gamma ^{2}\hat{h}\left( \hat{X}_{i},\hat{P} _{i}\right) \right) =\frac{1}{2}\sum _{s=\pm 1}\left[ 1+\imath s\gamma ^{1}\gamma ^{2}\right] \exp \left( -\imath s\lambda \hat{h}\left( \hat{X} _{i},\hat{P}_{i}\right) \right) . \end{aligned}$$
(17)

The two spin states are described by the parameter s, where \(s=+1\) for spin “up” and \(s=-1\) for spin “down”. Specifically, the above equation can be written

$$\begin{aligned} \exp \left( -\lambda \gamma ^{1}\gamma ^{2}\hat{h}\left( \hat{X}_{i},\hat{P} _{i}\right) \right) =\sum _{s=\pm 1}\mathcal {X}_{s}\mathcal {X}_{s}^{+} \exp \left( -\imath s\lambda \hat{h}\left( \hat{X}_{i},\hat{P}_{i}\right) \right) , \end{aligned}$$
(18)

where \(\mathcal {X}_{s}\mathcal {X}_{s}^{+}=(1+\imath s\gamma ^{1}\gamma ^{2} )/2\), and \(\mathcal {X}_{s}^{+}=\frac{1}{2}(1+s,1-s)\).

As a result, Eq. (12) can be represented as,

$$\begin{aligned} G^{\left( \alpha \right) }\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a} ,x_{0a}\right) =-\imath \sum _{s=\pm 1}\mathcal {X}_{s}\mathcal {X}_{s}^{+} \int _{0}^{\infty }d\lambda \left\langle \textbf{x}_{b},x_{0b}\right| \exp \left( -\imath \lambda \mathcal {\hat{H}}^{s}\right) \left| \textbf{x}_{a},x_{0a}\right\rangle _{\alpha }, \end{aligned}$$
(19)

with

$$\begin{aligned} \mathcal {\hat{H}}^{s}=\hat{p}_{0}^{2}-\varvec{\hat{P}}^{2}-2m\omega (\hat{P}_{1}\hat{X}_{2}-\hat{P}_{2}\hat{X}_{1})-m^{2}\omega ^{2}\hat{\textbf{X}} ^{2}-m^{2}+s\hat{h}\left( \hat{X}_{i},\hat{P}_{i}\right) . \end{aligned}$$
(20)

In order to obtain the path integral formalism of the Green function \(G^{\left( \alpha \right) }\left( \textbf{x}_{b},x_{0b},\textbf{x} _{a},x_{0a}\right)\), we insert N times, the identities of Eqs. (6) and (8) between each pair of infinitesimal operator \(\exp (\frac{-i\varepsilon }{\hbar }\hat{H}^{(\alpha )}).\) Then, to eliminate all the operators in the EUP framework (\(\hat{X}_{i}^{2},\hat{P}_{i}^{2}\) and \(\hat{P}_{i}\hat{X}_{j}\)) we inject these operators in the projection relation given in Eq. (7). After these stages, the expression \(G^{\left( \alpha \right) }\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right)\) is transformed into the following path integral

$$\begin{aligned} G^{\left( \alpha \right) }\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a} ,x_{0a}\right) =\sum _{s=\mp 1}\mathcal {X}_{s}\mathcal {X}_{s}^{+} \mathcal {G}^{s}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) , \end{aligned}$$
(21)

with

$$\begin{aligned}{} & {} \mathcal {G}^{s}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) =\left( -\imath \right) \lim _{N\rightarrow \infty }\int _{0}^{\infty } d\lambda \prod \limits _{k=1}^{N}\int \frac{d^{2}x_{k}}{\left( 1+\alpha \textbf{x}_{{k}}^{2}\right) }dx_{0k}\prod \limits _{k=1}^{N+1}\left[ \left( 1+\alpha \textbf{x}_{{k}}^{2}\right) \int \frac{dp_{0k}}{2\pi }e^{\imath p_{0k}\Delta x_{0k}}\frac{d^{2}p_{k}}{(2\pi )^{2}}\right] \nonumber \\{} & {} \quad \times \exp \left\{ \imath \varepsilon \sum _{k=0}^{N+1}\left[ p_{0k} ^{2}-(1+\alpha \textbf{x}_{k}^{2})\textbf{p}_{k}^{2}-m^{2}-6\imath \alpha (1+\alpha \textbf{x}_{k}^{2})\left( \textbf{x}_{k}\cdot \textbf{p} _{k}\right) +8\alpha ^{2}\textbf{x}_{k}^{2}+4\alpha -\left( m\omega \right) ^{2}\textbf{x}_{k}^{2}\right. \right. \nonumber \\{} & {} \quad \left. \left. +2m\omega (1+\alpha \textbf{x}_{k}^{2})(p_{1k}x_{2k} -p_{2k}x_{1k})-\frac{\left( \textbf{p}_{k}\cdot \Delta \textbf{x}_{k}\right) }{\varepsilon }+2s(1+\alpha \textbf{x}_{k}^{2})\left( -\alpha (p_{1k} x_{2k}-p_{2k}x_{1k})+m\omega \right) \right] \right\} , \end{aligned}$$
(22)

where \(p_{k}\) is the \(k-\)component of momentum and \(x^{\mu }=\left( x_{0},\text { }x,\text { }y\right)\) satisfy the boundary conditions

$$\begin{aligned} \textbf{x}_{k=0}=\textbf{x}_{a}\equiv \left( x_{a},y_{a}\right) ,\text { }x_{0k=0}=x_{0a},\text { }\textbf{x}_{N+1}=\textbf{x}_{b}\equiv \left( x_{b},y_{b}\right) ,\text { }x_{0N+1}=x_{0b}. \end{aligned}$$
(23)

Now shifting the following momenta coordinates

$$\begin{aligned} \textbf{p}=\textbf{p}-3\imath \frac{\alpha \textbf{x}}{1+\alpha \textbf{x}^{2}}, \end{aligned}$$
(24)

Eq. (22) yields this equivalence

$$\begin{aligned}{} & {} \mathcal {G}^{s}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) =\left( -\imath \right) \lim _{N\rightarrow \infty }\int _{0}^{\infty } d\lambda \prod \limits _{k=1}^{N}\left[ \int \frac{d^{2}x_{k}}{1+\alpha \textbf{x}_{k}^{2}}dx_{0k}\right] \prod \limits _{k=1}^{N+1}\left[ \frac{dp_{0k}}{2\pi }e^{\imath p_{0k}\Delta x_{0k}}\left( 1+\alpha \textbf{x}_{k}^{2}\right) \int \frac{d^{2}p_{k}}{(2\pi )^{2}}\right] \nonumber \\{} & {} \quad \times \exp \left\{ \imath \varepsilon \sum _{k=0}^{N+1}\left[ p_{0k} ^{2}-(1+\alpha \textbf{x}_{k}^{2})\textbf{p}_{k}^{2}-m^{2}+\frac{3i\alpha \textbf{x}_{k}\Delta \textbf{x}_{k}}{1+\alpha \textbf{x}_{k}^{2}}-\alpha ^{2}\textbf{x}_{k}^{2}+4\alpha -\left( m\omega \right) ^{2}\textbf{x}_{k} ^{2}\right. \right. \nonumber \\{} & {} \quad \left. \left. +2m\omega (1+\alpha \textbf{x}_{k}^{2})(p_{1k}x_{2k} -p_{2k}x_{1k})-\frac{\textbf{p}_{k}\Delta \textbf{x}_{k}}{\varepsilon }+2s(1+\alpha \textbf{x}_{k}^{2})\left( -\alpha (p_{1k}x_{2k}-p_{2k} x_{1k})+m\omega \right) \right] \right\} . \end{aligned}$$
(25)

After Gaussian integrations over \(p_{k}\) and \(x_{0k}\), the above Green function will be transformed to the Lagrangian path integral representation as follows:

$$\begin{aligned}{} & {} \mathcal {G}^{s}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) =\left( -\imath \right) \lim _{N\rightarrow \infty }\int _{0}^{\infty } d\lambda \int \frac{dp_{0}}{2\pi }e^{\imath p_{0}(x_{0b}-x_{0a})}e^{\imath \lambda (p_{0b}^{2}+4\alpha -m^{2})}\prod \limits _{k=1}^{N}\int \frac{dx_{k} dy_{k}}{1+\alpha \textbf{x}_{k}^{2}}\nonumber \\{} & {} \quad \times \exp \left\{ \imath \sum _{k=1}^{N+1}\left[ \frac{(\Delta \textbf{x} _{k})^{2}}{4\varepsilon (1+\alpha \textbf{x}_{k}^{2})^{2}}+3\imath \alpha \frac{\left( \textbf{x}_{k}\cdot \Delta \textbf{x}_{k}\right) }{(1+\alpha \textbf{x}_{k}^{2})}-(s\alpha -m\omega )\frac{x_{k}\Delta y_{k}-y_{k}\Delta x_{k}}{1+\alpha \textbf{x}_{k}^{2}}+2\varepsilon m\omega s\right] \right\} . \end{aligned}$$
(26)

Equation (26) represents the global Green function in the framework of EUP writing in Cartesian coordinates. As we showed in Introduction to this paper, we cannot find exact solutions to our problem in this representation of the existence of EUP. So in the next section, we will successfully complete the calculations if we use 2D spherical coordinates.

3 Green function in polar coordinates

As we know, symmetries play a preponderant role in the preservation of the physical grandeur of the system, which generally requires us to seek the best way of taking them into account. In consequence, let us develop the above path integrals Eq. (26) in the relative polar coordinates (r,  \(\theta )\). Therefore, let us introduce two dimensions spherical coordinates for position variables \(\textbf{x}\) defined by

$$\begin{aligned} x=r\cos \theta ,\text { \ }y=r\sin \theta , \end{aligned}$$
(27)

where \(0\le \theta <2\pi\) and \(r=\sqrt{\textbf{x}^{2}}=\sqrt{x^{2}+y^{2}},\) \(\tan \theta =y/x.\) This leads to the transformation over measure term, kinetic term and the rest action terms

$$\begin{aligned}{} & {} \prod \limits _{k=1}^{N}\left[ \int \frac{dx_{k}dy_{k}}{1+\alpha \textbf{x} _{k}^{2}}\right] =\prod \limits _{k=1}^{N}\left[ \int \frac{r_{k}dr_{k} }{1+\alpha r_{k}^{2}}d\theta _{k}\right] ,\nonumber \\{} & {} \quad (\Delta \textbf{x}_{k})^{2}=r_{k}^{2}+r_{k-1}^{2}-2r_{k}r_{k-1}\cos (\Delta \theta _{k}),\nonumber \\{} & {} \quad x_{k}\Delta y_{k}-y_{k}\Delta x_{k}=r_{k}r_{k-1}\sin (\Delta \theta _{k}),\nonumber \\{} & {} \quad \textbf{x}_{k}\cdot \Delta \textbf{x}_{k}=r_{k}\Delta r_{k}+r_{k}r_{k-1} (\Delta \theta _{k})^{2}/2. \end{aligned}$$
(28)

The value of correction \((\Delta \theta _{k})^{2}\) can be extracted from the kinetic term and gives us \((\Delta \theta _{k})^{2}\backsimeq \varepsilon (1+\alpha r_{k}^{2})^{2}.\) Thus, the expression of the Green function \(\mathcal {G}^{s}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right)\) in polar coordinates will be simplified as

$$\begin{aligned}{} & {} \mathcal {G}^{s}\left( r_{b},\theta _{b},x_{0b};r_{a},\theta _{a},x_{0a}\right) =\left( -\imath \right) \lim _{N\rightarrow \infty }\int _{0}^{\infty } d\lambda \int \frac{dp_{0}}{2\pi }e^{\imath p_{0}(x_{0b}-x_{0a})}e^{\imath \lambda (p_{0b}^{2}+4\alpha -m^{2})}\prod \limits _{k=1}^{N}\left[ \int \frac{r_{k}dr_{k}}{1+\alpha r_{k}^{2}}\int d\theta _{k}\right] \nonumber \\{} & {} \quad \times \exp \left\{ \imath \sum _{k=1}^{N+1}\left[ \frac{r_{k}^{2}+r_{k-1} ^{2}-2r_{k}r_{k-1}\cos (\Delta \theta _{k})}{4\varepsilon (1+\alpha r_{k}^{2} )^{2}}+\imath \frac{3r_{k}\alpha \Delta r_{k}}{1+\alpha r_{k}^{2}}\right. \right. \nonumber \\{} & {} \quad \left. \left. -3\alpha \varepsilon (1+\alpha r_{k}^{2})+2\varepsilon sm\omega -(s\alpha -m\omega )\frac{r_{k}r_{k-1}\sin (\Delta \theta _{k})}{1+\alpha r_{k}^{2}}\right] \right\} . \end{aligned}$$
(29)

The third term in kinetic energy together with the last term in the procedure indicates the possibility of an angle shift according to the following relation:

$$\begin{aligned} \Delta \theta _{k}\rightarrow \Delta \theta _{k}-2\varepsilon (s\alpha -m\omega )(1+\alpha r_{k}^{2}). \end{aligned}$$
(30)

After this step to activate the path integral over angle \(\theta (t_{k})\), we will use the well-known relation [41],

$$\begin{aligned} e^{a\cos \theta }=\sum _{\ell =-\infty }^{+\infty }e^{\imath \ell \theta }I_{\ell }\left( a\right) , \end{aligned}$$
(31)

where \(I_{\ell }\left( a\right)\) are the modified Bessel functions and after straightforward calculations, Eq. (29) can be written as

$$\begin{aligned}{} & {} \mathcal {G}^{s}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) =\left( -\imath \right) \lim _{N\rightarrow \infty }\int _{0}^{\infty } d\lambda \int \frac{dp_{0}}{2\pi }e^{\imath p_{0}(x_{0b}-x_{0a})}e^{\imath \lambda (p_{0}^{2}+4\alpha -m^{2})}\nonumber \\{} & {} \quad \times \prod \limits _{k=1}^{N}\left[ \int \frac{r_{k}dr_{k}}{\left( 1+\alpha r_{k}^{2}\right) }\right] {\prod \limits _{n=1}^{N+1}}\left[ \frac{\pi }{\imath \varepsilon (1+\alpha r_{k}^{2})}\sum _{\ell _{k}=-\infty }^{+\infty }I_{\ell _{k}}\left( \tfrac{-\imath r_{k}r_{k-1}}{2\varepsilon (1+\alpha r_{k}^{2})^{2}}\right) \right] \nonumber \\{} & {} \quad \times \prod \limits _{k=1}^{N}\left[ \int d\theta _{k}\right] \prod _{k=1} ^{N+1}\left[ e^{\imath \ell _{k}(\Delta \theta _{k}-2(s\alpha -m\omega )\varepsilon (1+\alpha r_{k}^{2}))}\right] \exp \left\{ \imath \sum _{k=1}^{\infty }\left[ \frac{r_{k}^{2}+r_{k-1}^{2}}{4\varepsilon (1+\alpha r_{k}^{2})^{2}}\right. \right. \nonumber \\{} & {} \quad \left. \left. +\frac{3r_{k}\Delta r_{k}}{1+\alpha r_{k}^{2}}+3\alpha \imath \varepsilon (1+\alpha r_{k}^{2})-\imath \varepsilon r_{k}r_{k-1} (s\alpha -m\omega )^{2}+2\imath \varepsilon sm\omega \right] \right\} . \end{aligned}$$
(32)

The modified Bessel function \(I_{\ell }\) is related to the Bessel function by

$$\begin{aligned} I_{\ell }(a)=e^{a}\left( \frac{1}{2\pi a}\right) ^{1/2}{\tilde{I}_{\ell }}(a), \end{aligned}$$
(33)

the Bessel function has the following asymptotic behavior

$$\begin{aligned} \lim _{|a|\rightarrow +\infty }\tilde{I}_{\nu }(a)=\exp \left( \frac{-\nu ^{2} +1/4}{2a}\right) . \end{aligned}$$
(34)

The \(N-\)integrations over the \(\theta _{k}\)-variables can now be performed and produce the N symbols of \(\delta -\)Kronecker

$$\begin{aligned} \prod \limits _{k=1}^{N}\int _{0}^{2\pi }d\theta _{k}\prod _{k=1}^{N+1}\left[ \sum _{\ell _{k}=-\infty }^{+\infty }e^{i\ell _{k}(\Delta \theta _{k})}\right] =\left( \prod _{k=1}^{N}2\pi \delta _{\ell _{k},\ell _{k-1}}\right) \prod _{k=1}^{N+1}e^{i\ell _{k}(\theta _{k}-\theta _{k-1})}. \end{aligned}$$
(35)

Now, we define the radial Green function that depends on the azimuthal quantum numbers \(\ell\):

$$\begin{aligned} \mathcal {G}^{s}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) =\frac{1}{2\pi \sqrt{r_{a}r_{b}}}\sum _{\ell =-\infty }^{+\infty }\mathcal {G} _{\ell }^{s}(r_{b},x_{0b},r_{a},x_{0a})e^{\imath \ell (\theta _{b}-\theta _{a})}, \end{aligned}$$
(36)

where \(\mathcal {G}_{\ell }^{s}(r_{b},x_{0b},r_{a},x_{0a})\) is obviously given by the radial path integrals

$$\begin{aligned}{} & {} \mathcal {G}_{\ell }^{s}(r_{b},x_{0b},r_{a},x_{0a})=-\imath \lim _{N\rightarrow \infty }\int _{0}^{\infty }d\lambda \int \frac{dp_{0}}{2\pi }e^{\imath p_{0} (x_{0b}-x_{0a})}e^{\imath \lambda (p_{0}^{2}-m^{2}+4\alpha )}\left( 4\pi \imath \varepsilon \right) ^{-\frac{N+1}{2}}\nonumber \\{} & {} \quad \times {\prod \limits _{k=1}^{N}}\left[ \int \frac{dr_{k}}{1+\alpha r_{{k}}^{2} }\right] \exp \left( \imath {\sum _{k=0}^{N+1}}\left[ \frac{(\Delta r_{k} )^{2}}{4\varepsilon (1+\alpha r_{k}^{2})^{2}}+\imath \frac{3r_{k}\Delta r_{k} }{1+\alpha r_{k}^{2}}-3\varepsilon \alpha (1+\alpha r_{k}^{2})\right. \right. \nonumber \\{} & {} \quad \left. \left. -2\varepsilon \ell (s\alpha -m\omega )(1+\alpha r_{k} ^{2})-\varepsilon (s\alpha -m\omega )^{2}r_{k}r_{k-1}+2\varepsilon sm\omega -\varepsilon (\ell ^{2}-1/4)\frac{(1+\alpha r_{k}^{2})^{2}}{r_{k}r_{k-1} }\right] \right) . \end{aligned}$$
(37)

It is noticeable that the above propagator does not correspond to what we are accustomed to in the ’Feynman evolution operator’, because there are deformations on the measure term \(\left( dr_{k}/\left( 1+\alpha r_{k} ^{2}\right) \right)\), the action term \(\left( \imath (\Delta r_{k} )^{2}/\left[ 4\varepsilon (1+\alpha r_{k}^{2})^{2}\right] \right)\) and the factor term \(\left( -3r_{k}\Delta r_{k}/\left( 1+\alpha r_{k}^{2}\right) \right)\). In order to restore the local Feynman propagator, we must apply the following coordinate transformation (\(r=g\left( \eta \right)\))

$$\begin{aligned} \frac{dg\left( \eta \right) }{d\eta }=1+\alpha r^{2}. \end{aligned}$$
(38)

From Refs. [42, 43], we can evaluate these corrections through two steps calculations. The first is to write this propagator at the \(\alpha -\)point discretization interval (\(\bar{r}_{k}^{_{\left( \alpha \right) }}=\alpha r_{k}+\left( 1-\alpha \right) r_{k-1}\)). While in the second step, to recover the usual kinetic term \((\frac{\imath }{\hbar }\frac{m}{2\varepsilon }\left( \Delta \eta _{k}\right) ^{2})\), we use the coordinate transformation method which is defined by (\(\sqrt{\alpha }r=\tan (\sqrt{\alpha }\eta )\)). As a result, from the condition (38), the total quantum correction \(C_{q}^{T}\) reads

$$\begin{aligned} C_{q}^{T}=\imath \varepsilon \alpha \left( 3\tan ^{2}(\sqrt{\alpha } \eta )-2\right) . \end{aligned}$$
(39)

This leads to following the explicit result

$$\begin{aligned}{} & {} \mathcal {G}_{\ell }^{s}(r_{b}(\eta _{b}),x_{0b},r_{a}(\eta _{a}),x_{0a})=\left( -\imath \right) \lim _{N\rightarrow \infty }\int _{0}^{\infty }d\lambda \int dp_{0}e^{\imath p_{0}(x_{0b}-x_{0a})}e^{\imath \lambda \left( -m^{2}+p_{0} ^{2}+m^{2}\omega ^{2}/\alpha \right) }\nonumber \\{} & {} \quad \times \mathcal {K}_{\ell }^{s}(\eta _{a},\eta _{b},\lambda ), \end{aligned}$$
(40)

the kernel propagator \(\mathcal {K}_{\ell }^{s}(\eta _{a},\eta _{b},\lambda )\) is exactly the path integral for a particle moving in Poschl–Teller (PT) potential written as [39],

$$\begin{aligned} \mathcal {K}_{\ell }^{s}(\eta _{a},\eta _{b},\lambda )&=\lim _{N\longrightarrow \infty }\prod _{k=1}^{{N}}\left[ \int d\eta _{k}\right] \left( \frac{M}{2\pi \imath \hbar \varepsilon }\right) ^{\frac{N+1}{2}}\exp \left\{ \frac{\imath }{\hbar }\sum _{k=1}^{N+1}\left[ \tfrac{M\left( \Delta \eta _{k}\right) ^{2}}{2\varepsilon }-\frac{\varepsilon \hbar ^{2}}{2M}\left[ \tfrac{\left( \rho _{s}^{2}-1/4\right) }{\cos ^{2}(\sqrt{\alpha }\eta _{k})}+\tfrac{\left( \kappa ^{2}-1/4\right) }{\sin ^{2}(\sqrt{\alpha }\eta _{k})}\right] \right] \right\} \nonumber \\&=\sum _{n=0}^{\infty }\Psi _{n,s}^{*}(\eta _{b})\Psi _{n,s}(\eta _{a} )\exp \left( -\imath \lambda \alpha (\rho _{s}+\kappa +2n+1)^{2}\right) , \end{aligned}$$
(41)

where

$$\begin{aligned}{} {} \Psi _{n,s}(\eta )=&\left[ 2\sqrt{\alpha }(\rho _{s}+\kappa +2n+1)\frac{n!\Gamma (\rho _{s}+\kappa +n+1)}{\Gamma (\rho _{s}+n+1)\Gamma (\kappa +n+1)}\right] ^{\frac{1}{2}}\nonumber \\{} & {} \times (\sin \sqrt{\alpha }\eta )^{\kappa +1/2}(\cos \sqrt{\alpha }\eta )^{\rho _{s}+1/2}P_{n}^{(\kappa ,\rho _{s})}(\cos (2\sqrt{\alpha }\eta )), \end{aligned}$$
(42)

with \(P_{n}^{(\alpha ,\beta )}(x)\) are the Jacobi polynomials, and (M,  \(\rho _{s},\) \(\kappa )\) are given by:

$$\begin{aligned} M=\tfrac{1}{2},\text { }\kappa =|\ell |,\text { }\rho _{s}=\pm \left( \frac{m\omega }{\alpha }-s-\ell \right) . \end{aligned}$$
(43)

Through the condition of the extended uncertainty principle given in Introduction of this paper, the values \(\rho _{+}=\frac{m\omega }{\alpha } -1-\ell ,\) \(\rho _{-}=\frac{m\omega }{\alpha }+1-\ell\) are accepted, and the other negative values are rejected. So it will be \(\rho _{-s}=\rho _{s}+2s\). The integration over \(\lambda\) and \(p_{0}\) can be computed by using the residue theorem,

$$\begin{aligned} \int \frac{dp_{0}}{2\pi }\frac{e^{\imath p_{0}(x_{0b}-x_{0a})}}{p_{0} ^{2}-(E_{n,\ell ,s}^{(\alpha )})^{2}}=-\imath \sum _{\epsilon =\pm 1}\Theta (\epsilon T)\frac{e^{-\imath \epsilon E_{n,\ell ,s}^{(\alpha )}(x_{0b}-x_{0a})}}{2E_{n,\ell ,s}^{(\alpha )}}, \end{aligned}$$
(44)

with \(E_{n,\ell ,s}^{(\alpha )}\) is given as

$$\begin{aligned} E_{n,\ell ,s}^{(\alpha )}=\sqrt{m^{2}-\frac{m^{2}\omega ^{2}}{\alpha } +\alpha \left( \frac{m\omega }{\alpha }-s-\ell +\arrowvert \ell \arrowvert +2n+1\right) ^{2}}, \end{aligned}$$
(45)

\(\Theta (x)\) is the Heaviside function.

For an arbitrary function f(x), we have

$$\begin{aligned} \sum _{\epsilon =\pm 1}f(\epsilon )\Theta (\epsilon T)=f\left( s\right) \Theta (sT)+f(-s)\Theta (-sT). \end{aligned}$$
(46)

Thus, the Green function of the 2D Dirac oscillator in the EUP background becomes as

$$\begin{aligned}{} & {} G^{\left( \alpha \right) }\left( \eta _{b},x_{0b},\eta _{a},x_{0a}\right) =-\frac{e^{\imath \ell (\theta _{b}-\theta _{a})}}{\sqrt{u_{a}u_{b}/v_{a}v_{b}} }\sum _{s=\pm 1}\sum _{\ell =-\infty }^{+\infty }\sum _{n=0}^{\infty }\frac{\sqrt{\alpha }(\rho _{s}+|\ell |+2n+1)}{2\pi E_{n,\ell ,s}^{(\alpha )}}\nonumber \\{} & {} \quad \times \frac{n!\Gamma (\rho _{s}+|\ell |+n+1)}{\Gamma (\rho _{s}+n+1)\Gamma (|\ell |+n+1)}\left\{ \Theta (-sT)e^{\imath sE_{n,\ell ,s}^{(\alpha )} (x_{0b}-x_{0a})}(u_{b})^{|\ell |+1/2}(v_{b})^{\rho _{s}+1/2}(u_{a})^{|\ell |+1/2}(v_{a})^{\rho _{s}+1/2}\right. \nonumber \\{} & {} \quad \left. \times P_{n}^{(|\ell |,\rho _{s})}(1-2u_{b}^{2})P_{n}^{(|\ell |,\rho _{s})}(1-2u_{a}^{2})\mathcal {X}_{s}\mathcal {X}_{s}^{+}+\Theta (sT)e^{-\imath sE_{n,\ell ,s}^{(\alpha )}(x_{0b}-x_{0a})}(u_{b})^{|\ell |+1/2}(v_{b})^{\rho _{s}+1/2}\right. \nonumber \\{} & {} \quad \left. \times (u_{a})^{|\ell |+1/2}(v_{a})^{\rho _{s}+1/2}P_{n}^{(|\ell |,\rho _{s})}(1-2u_{b}^{2})P_{n}^{(|\ell |,\rho _{s})}(1-2u_{a}^{2} )\mathcal {X}_{s}\mathcal {X}_{s}^{+}\right\} , \end{aligned}$$
(47)

where \(u=\sin (\sqrt{\alpha }\eta )\) and \(v=\cos (\sqrt{\alpha }\eta )\).

Moreover, to unify the expression of energy between the terms \(\Theta (sT)\) and \(\Theta (-sT\) ), we make the following change (\(s\rightarrow -s\)) in the terms that multiplied by \(\Theta (-sT),\) these lead to,

$$\begin{aligned} n\rightarrow n-s,\text { }\ell \rightarrow \ell +s,\rho _{s}\rightarrow \rho _{s}+s. \end{aligned}$$
(48)

Also, we have the Jacobi polynomials verify the corresponding property [44],

$$\begin{aligned} P_{n}^{(\alpha ,\beta )}(-x)=(-1)^{n}P_{n}^{(\beta ,\alpha )}(x). \end{aligned}$$
(49)

Therefore, the global representation of the Green function becomes

$$\begin{aligned}{} & {} G^{\left( \alpha \right) }\left( \eta _{b},x_{0b},\eta _{a},x_{0a}\right) =-e^{\imath \ell (\theta _{b}-\theta _{a})}\sum _{\ell =-\infty }^{+\infty }\sum _{n=0}^{\infty }\sum _{s=\pm 1}\frac{\sqrt{\alpha }(\rho _{s}+|\ell |+2n+1)}{2\pi E_{n,\ell ,s}^{(\alpha )}}\nonumber \\{} & {} \quad \times \frac{n!\Gamma (\rho _{s}+|\ell |+n+1)}{\Gamma (\rho _{s}+n+1)\Gamma (|\ell |+n+1)}\Theta (sT)e^{-\imath sE_{n,\ell ,s}^{(\alpha )}(x_{0b}-x_{0a} )}\left\{ F(\eta _{b})F(\eta _{a})\mathcal {X}_{s}\mathcal {X}_{s}^{+}+J(\eta _{b})J(\eta _{a})\mathcal {X}_{-s}\mathcal {X}_{-s}^{+}\right\} , \end{aligned}$$
(50)

where the functions \(F(\eta )\) and \(J(\eta )\) have the following formulas:

$$\begin{aligned}{} & {} F(\eta )=(-1)^{n}(u)^{|\ell |}(v)^{\rho _{s}+1}P_{n}^{(|\ell |,\rho _{s})} (1-2u^{2}),\nonumber \\{} & {} \quad J(\eta )=(-1)^{n}(u)^{|\ell |+s}(v)^{\rho _{s}+s+1}P_{n-s}^{(|\ell |+s,\rho _{s}+s)}(1-2u^{2}). \end{aligned}$$
(51)

4 Wave functions and energy spectrum

In order to extract the spectral energies and the corresponding spinorial wave functions for the \((2+1)-\)dimensional Dirac oscillator in the context of EUP, we act the operator (\(\gamma ^{\mu }\hat{\Pi }_{\mu }+m\))\(_{b}\) on the Green function given in Eq. (47). Before that, we use the following relationships

$$\begin{aligned} \gamma ^{0}\mathcal {X}_{s}=s\mathcal {X}_{s},\text { }\gamma ^{1}\mathcal {X} _{s}=\imath \sigma _{2}\mathcal {X}_{s}=-s\mathcal {X}_{-s},\text { }\gamma ^{2}\mathcal {X}_{s}=-\imath \sigma _{1}\mathcal {X}_{s}=-\imath \mathcal {X}_{-s}. \end{aligned}$$
(52)

As a consequence, the action of the operator \((\gamma ^{\mu }\hat{\Pi }_{\mu }+m)_{b}\) on \(\mathcal {X}_{s}\mathcal {X}_{s}^{+}\) is given by:

$$\begin{aligned} \left( \gamma ^{\mu }\hat{\Pi }_{\mu }+m\right) _{b}\mathcal {X}_{s} \mathcal {X}_{s}^{+}&=\left( s\imath \partial _{t_{b}}+m\right) \mathcal {X}_{s}\mathcal {X}_{s}^{+}-s\left( \hat{P}_{1b}-\imath m\omega {\gamma }^{0}\hat{X}_{1b}\right) \mathcal {X}_{-s}\mathcal {X}_{s} ^{+}\nonumber \\&-\imath \left( \hat{P}_{2b}-\imath m\omega {\gamma }^{0}\hat{X} _{2b}\right) \mathcal {X}_{-s}\mathcal {X}_{s}^{+}, \end{aligned}$$
(53)

where (\(\hat{P}_{ib}=\imath (1+\alpha \textbf{x}_{b}^{2})\partial _{ib},\) \(\hat{X}_{ib}=x_{ib}\)). Therefore, the Green function becomes

$$\begin{aligned}{} & {} S^{(\alpha )}\left( z_{b},x_{0b},z_{a},x_{0a}\right) =-\sum _{\ell =-\infty }^{+\infty }\sum _{n=0}^{\infty }\sum _{s=\pm 1}\Theta (sT)e^{-\imath sE_{n,\ell ,s}^{(\alpha )}(x_{0b}-x_{0a})}\nonumber \\{} & {} \quad \times \left\{ \frac{\alpha (\rho _{s}+|\ell |+2n+1)}{2\pi E_{n,\ell ,s} ^{(\alpha )}}\frac{n!\Gamma (\rho _{s}+|\ell |+n+1)}{\Gamma (\rho _{s} +n+1)\Gamma (|\ell |+n+1)}e^{\imath \ell (\theta _{b}-\theta _{a})}\left( (E_{n,\ell ,s}^{(\alpha )}+m)F(z_{b})F(z_{a})\mathcal {X}_{s}\mathcal {X}_{s} ^{+}\right. \right. \nonumber \\{} & {} \quad \left. \left. -\imath se^{\imath s\theta _{b}}\sqrt{\alpha }\left[ \frac{|\ell |\left( 1-z_{b}\right) }{2}P_{n}^{(\rho _{s},\sigma )} (z_{b})-\left( \rho _{s}+1-\frac{sm\omega }{\alpha }\right) \left( \frac{1+z_{b}}{2}\right) P_{n}^{(\rho _{s},\sigma )}(z_{b})-s\ell P_{n} ^{(\rho _{s},\sigma )}(z_{b})\right. \right. \right. \nonumber \\{} & {} \quad \left. \left. \left. +(1+z_{b})(1-z_{b})\frac{dP_{n}^{(\rho _{s},|\ell |)}\left( z_{b}\right) }{dz_{b}}\right] \left( \frac{1+z_{b}}{2}\right) ^{\frac{|\ell |-1}{2}}\left( \frac{1-z_{b}}{2}\right) ^{\frac{\rho _{s}}{2} }F(z_{a})\mathcal {X}_{-s}\mathcal {X}_{s}^{+}\right) \right. \nonumber \\{} & {} \quad \left. +\frac{\alpha (\rho _{s}+|\ell |+2n+1)}{2\pi E_{n,\ell ,s}^{(\alpha )} }\frac{(n-s)!\Gamma (\rho _{s}+|\ell |+n+1+s)}{\Gamma (\rho _{s}+n+1)\Gamma (|\ell |+n+1)}e^{\imath (\ell +s)(\theta _{b}-\theta _{a})}\right. \nonumber \\{} & {} \quad \left. \times \left( (-E_{n,\ell ,s}^{(\alpha )}+m)J(z_{b})J(z_{a} )\mathcal {X}_{-s}\mathcal {X}_{-s}^{+}+\imath se^{-\imath s\theta _{b}} \sqrt{\alpha }\left\{ (|\ell |+s)\frac{1-z_{b}}{2}P_{n-s}^{(\rho _{s} +s,\sigma +s)}(z_{b})\right. \right. \right. \nonumber \\{} & {} \quad \left. \left. -\left( \rho _{s}-s+1+\frac{sm\omega }{\alpha }\right) \left( \frac{1+z_{b}}{2}\right) P_{n-s}^{(\rho _{s}+s,\sigma +s)}(z_{b})+s\ell P_{n-s}^{(\rho _{s}+s,\sigma +s)}(z_{b})\right. \right. \nonumber \\{} & {} \quad \left. \left. \left. +(1+z_{b})(1-z_{b})\frac{dP_{n-s}^{(\rho _{s} +s,|\ell |+s)}\left( z_{b}\right) }{dz_{b}}\right\} \left( \frac{1+z_{b} }{2}\right) ^{\frac{|\ell |+s-1}{2}}\left( \frac{1-z_{b}}{2}\right) ^{\frac{\rho _{s}+s}{2}}J(z_{a})\mathcal {X}_{s}\mathcal {X}_{-s}^{+}\right) \right\} . \end{aligned}$$
(54)

Here \(z=1-2\cos ^{2}(\sqrt{\alpha }\eta )\). We will only focus on \(\ell >0\), that means \(|\ell |=\ell\).

The Jacobi polynomials have the following properties [45, 46]

$$\begin{aligned} \frac{dP_{n}^{\left( \rho _{s},\ell \right) }\left( z\right) }{dz}=\frac{1}{2}\frac{\Gamma \left( n+\ell +\rho _{s}+2\right) }{\Gamma \left( n+\ell +\rho _{s}+1\right) }P_{n-1}^{\left( \rho _{s}+1,\ell +s\right) }\left( z\right) , \end{aligned}$$
(55)

and

$$\begin{aligned}{} & {} \left( 1-z\right) ^{\rho _{s}}\left( 1+z\right) ^{\ell }\frac{d}{dz} P_{n}^{\left( \rho _{s},\ell \right) }\left( z\right) =-2\left( n+1\right) \left( 1-z\right) ^{\rho _{s}-1}\left( 1+z\right) ^{\ell -1}P_{n+1}^{\left( \rho _{s}-1,\ell -1\right) }\left( z\right) \nonumber \\{} & {} \quad -\left( \rho _{s}\left( 1-z\right) ^{\rho _{s}-1}\left( 1+z\right) ^{\alpha }-\ell \left( 1-z\right) ^{\rho _{s}}\left( 1+z\right) ^{\ell -1}\right) P_{n}^{\left( \rho _{s},\ell \right) }\left( z\right) . \end{aligned}$$
(56)

On other hand, from the expression of \(E_{n,\ell ,s}(\alpha )\), we get

$$\begin{aligned} \sqrt{\alpha }=\frac{\sqrt{E_{n,\ell ,s}^{(\alpha )}-m}\sqrt{E_{n,\ell ,s}^{(\alpha )}+m}}{\sqrt{2(\rho _{s}+\ell )(1-s)+4n(\rho _{s}+\ell +n+1)} }. \end{aligned}$$
(57)

Equations (55), (56) and (57) can simplify the Green function expression obtained in Eq. (54), where it will transform into the following form,

$$\begin{aligned}{} & {} S^{(\alpha )}\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) =-\sum _{\ell =-\infty }^{+\infty }\sum _{n=0}^{\infty }\sum _{s=\pm 1}\Theta (sT)e^{-\imath sE_{n,\ell ,s}^{(\alpha )}(t_{b}-t_{a})}\nonumber \\{} & {} \quad \times \left\{ \tfrac{\alpha (\rho _{s}+\ell +2n+1)}{E_{n,\ell ,s}^{(\alpha )} }\tfrac{n!\Gamma (\rho _{s}+\ell +n+1)}{\Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}\frac{e^{\imath \ell (\theta _{b}-\theta _{a})}}{2\pi }(E_{n,\ell ,s} ^{(\alpha )}+m)F(z_{b})F(z_{a})\mathcal {X}_{s}\mathcal {X}_{s}^{+}\right. \nonumber \\{} & {} \quad \left. -\imath \frac{e^{\imath (\ell +s)\theta _{b}}e^{-\imath \ell \theta _{a}} }{2\pi }\sqrt{\tfrac{\alpha (E_{n,\ell ,s}^{(\alpha )}-m)}{E_{n,\ell ,s}^{(\alpha )}}\tfrac{(n-s)!(\rho _{s}+\ell +2n+1)}{\Gamma (\ell +n+1)}\tfrac{\Gamma (\rho _{s}+\ell +n+1+s)}{\Gamma (\rho _{s}+n+1)}}J(z_{b})\right. \nonumber \\{} & {} \quad \left. \times \sqrt{\tfrac{\alpha (E_{n,\ell ,s}^{(\alpha )}+m)}{E_{n,\ell ,s}^{(\alpha )}}\tfrac{(\rho _{s}+\ell +2n+1)n!\Gamma (\rho _{s}+\ell +n+1)}{\Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}}F(z_{a})\mathcal {X}_{-s}\mathcal {X} _{s}^{+}\right. \nonumber \\{} & {} \quad \left. +\frac{e^{\imath (\ell +s)(\theta _{b}-\theta _{a})}}{2\pi }\tfrac{\alpha (\rho _{s}+\ell +2n+1)}{E_{n,\ell ,s}^{(\alpha )}}\tfrac{(n-s)!\Gamma (\rho _{s}+\ell +n+1+s)}{\Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}(-E_{n,\ell ,s}^{(\alpha )}+m)J(z_{b})J(z_{a})\mathcal {X}_{-s}\mathcal {X}_{-s}^{+}\right. \nonumber \\{} & {} \quad \left. +e^{\imath \ell \theta _{b}}\sqrt{\tfrac{E_{n,\ell ,s}^{(\alpha )}+m}{2\pi E_{n,\ell ,s}^{(\alpha )}}\tfrac{\alpha (\rho _{s}+\ell +2n+1)n!\Gamma (\rho _{s}+\ell +n+1)}{\Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}}F(z_{b})(-\imath )e^{-\imath (\ell +s)\theta _{a}}\right. \nonumber \\{} & {} \quad \left. \left. \times \sqrt{\tfrac{E_{n,\ell ,s}^{(\alpha )}-m}{2\pi E_{n,\ell ,s}^{(\alpha )}}\tfrac{\alpha (\rho _{s}+\ell +2n+1)n!\Gamma (\rho _{s}+\ell +n+1+s)}{\Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}}J(z_{a})\mathcal {X} _{s}\mathcal {X}_{-s}^{+}\right. \right\} . \end{aligned}$$
(58)

The above propagator \(S^{(\alpha )}\left( \eta _{b},x_{0b},\eta _{a},x_{0a}\right)\) can also be organized to the next format

$$\begin{aligned}{} & {} S^{(\alpha )}\left( \eta _{b},x_{0b},\eta _{a},x_{0a}\right) =-\sum _{n=0}^{+\infty }\sum _{\ell =-\infty }^{+\infty }\sum _{s=\pm 1}\Theta (sT)e^{-\imath sE_{n,\ell ,s}\left( x_{0b}-x_{0a}\right) }\nonumber \\{} & {} \quad \times \sqrt{\alpha }\left[ e^{\imath \ell \theta _{b}}\sqrt{\frac{(\rho _{s} +\ell +2n+1)n!\Gamma (\rho _{s}+\ell +n+1)}{2\pi \Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}+m}{E_{n,\ell ,s}^{(\alpha )}} }F(z_{b})\mathcal {X}_{s}\right. \nonumber \\{} & {} \quad \left. -\imath e^{\imath (\ell +s)\theta _{b}}\sqrt{\frac{(\rho _{s} +\ell +2n+1)(n-s)!\Gamma (\rho _{s}+\ell +n+1+s)}{2\pi \Gamma (\rho _{s} +n+1)\Gamma (\ell +n+1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}-m}{E_{n,\ell ,s}^{(\alpha )}}}J(z_{b})\mathcal {X}_{-s}\right] \nonumber \\{} & {} \quad \times \sqrt{\alpha }\left[ e^{-\imath \ell \theta _{a}}\sqrt{\frac{(\rho _{s} +\ell +2n+1)n!\Gamma (\rho _{s}+\ell +n+1)}{2\pi \Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}+m}{E_{n,\ell ,s}^{(\alpha )}} }F(z_{a})\mathcal {X}_{s}^{+}\right. \nonumber \\{} & {} \quad \left. -\imath e^{-\imath (\ell +s)\theta _{a}}\sqrt{\frac{(\rho _{s} +\ell +2n+1)(n-s)!\Gamma (\rho _{s}+\ell +n+1+s)}{2\pi \Gamma (\rho _{s} +n+1)\Gamma (\ell +n+1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}-m}{E_{n,\ell ,s}^{(\alpha )}}}J(z_{a})\mathcal {X}_{-s}^{+}\right] . \end{aligned}$$
(59)

In Eq. (59), we have two types of propagation, one with positive energy (\(+E_{n,\ell ,s}^{(\alpha )}\)) propagating to the future and the other with negative energy (\(-E_{n,\ell ,s}^{(\alpha )}\)) propagating to the past. We can write the propagator corresponding to \((2+1)-\)dimensional DO under the presence of EUP as

$$\begin{aligned}{} & {} S^{\alpha }\left( \textbf{x}_{b},x_{0b},\textbf{x}_{a},x_{0a}\right) =-\sum _{n=0}^{\infty }\sum _{\ell =-\infty }^{\infty }\sum _{s=\mp 1}s\Psi _{n,\ell ,s}(r,\theta )\Psi _{n,\ell ,s}^{\dagger }(r,\theta )e^{-\imath sE_{n,\ell ,s}(x_{0b}-x_{0a})}\nonumber \\{} & {} \quad \times \sigma ^{3}\Theta (s(t_{b}-t_{a})), \end{aligned}$$
(60)

and hence the normalized wave functions for the deformed 2D Dirac oscillator under the effect of EUP with \(\ell >0\) take the form

$$\begin{aligned}{} & {} \Psi _{n,\ell ,s}(r,\theta )=e^{\imath \ell \theta }\sqrt{\frac{\alpha (\rho _{s} +\ell +2n+1)n!\Gamma (\rho _{s}+\ell +n+1)}{2\pi \Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}+m}{E_{n,\ell ,s}^{(\alpha )}} }\sin ^{\ell }(\sqrt{\alpha }\eta )\cos ^{\rho _{s}+1}(\sqrt{\alpha }\eta )\nonumber \\{} & {} \quad \times P_{n}^{(\rho _{s},\ell )}\left( 1-2\cos ^{2}(\sqrt{\alpha }\eta )\right) \mathcal {X}_{s}-\imath e^{\imath (\ell +s)\theta }\sqrt{\frac{\alpha (\rho _{s}+\ell +2n+1)(n-s)!\Gamma (\rho _{s}+\ell +n+1+s)}{2\pi \Gamma (\rho _{s}+n+1)\Gamma (\ell +n+1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}-m}{E_{n,\ell ,s}^{(\alpha )}}}\nonumber \\{} & {} \quad \times \sin ^{\ell +s}(\sqrt{\alpha }\eta )\cos ^{\rho _{s}+s+1}(\sqrt{\alpha } \eta )P_{n-s}^{(\rho _{s}+s,\ell +s)}\left( 1-2\cos ^{2}(\sqrt{\alpha } \eta )\right) \mathcal {X}_{-s}. \end{aligned}$$
(61)

To fall back on the old variables, we use the following relations \(\cos (\sqrt{\alpha }\eta )=\sqrt{1/\left( 1+\alpha r^{2}\right) },\) \(\sin (\sqrt{\alpha }\eta )=\sqrt{\alpha r^{2}/\left( 1+\alpha r^{2}\right) }\).

Thus, the exact eigenenergies of a 2D Dirac oscillator under the presence of EUP can easily be deduced,

$$\begin{aligned} E_{n,\ell ,s}^{(\alpha )}=\pm \sqrt{m^{2}-\frac{m^{2}\omega ^{2}}{\alpha } +\alpha \left( \frac{m\omega }{\alpha }-s-\ell +\arrowvert \ell \arrowvert +2n+1\right) ^{2}}. \end{aligned}$$
(62)

By expanding the energy levels (62) to the first order of \(\alpha\), we get

$$\begin{aligned} E_{n,\ell ,s}^{(\alpha )}\simeq E_{n,\ell ,s}^{(\alpha =0)}+\alpha E_{n,\ell ,s}^{\left( 1\right) }, \end{aligned}$$
(63)

with

$$\begin{aligned} E_{n,\ell ,s}^{(\alpha =0)}=\pm \sqrt{m^{2}+2m\omega \left( 2n+1+\left| \ell \right| -\ell -s\right) }, \end{aligned}$$
(64)

and

$$\begin{aligned} E_{n,\ell ,s}^{\left( 1\right) }=\frac{1}{2E_{n,\ell ,s}^{(\alpha =0)}}\left( \left| \ell \right| -\ell -s+(2n+1)\right) ^{2}. \end{aligned}$$
(65)

The first term in Eq. (63) represents the energy spectrum of the ordinary (2+1)-dimensional DO and the second term is the first correction in the EUP framework. We note that the modification of the Heisenberg algebra makes the energies depend on \(n^{2}\). For the positive values of \(\ell\), there are infinite degeneracies of the usual 2D Dirac oscillator energies. Similarly, in the context of EUP (i.e., \(\alpha \ne 0)\), the degeneracies still exist. Therefore, the framework of EUP does not affect the degeneracies. Also, the deformation \(\alpha -\)parameter does not break the symmetry of the energy spectrum under the transformations \(s\rightarrow -s\) and \(n\rightarrow n-s\).

For \(\omega =0\), we can reduce (63) to

$$\begin{aligned} E_{n,\ell ,s}(\alpha )\backsimeq \pm \frac{\alpha }{2m}\left( \arrowvert \ell \arrowvert -\ell -s+(2n+1)\right) ^{2}\pm m. \end{aligned}$$
(66)

Moreover, when \(\ell <0\), we can easily remark that the effect of EUP on the 2D free systems, with spin down \(s=-1\), creates a rotation with a constant moment of inertia due to the \(\ell ^{2}-\)dependent energy spectrum plus the anharmonicity of vibrations and harmonic vibration. However, for spin up \(s=+1\), a rotation with a constant moment and confinement phenomenon appear due to the \(\ell ^{2}\) and \(n^{2}\) terms. If \(\ell >0\), the energy spectrum (66) describes the anharmonic and harmonic oscillators for particles with spin down, i.e., \(s=-1\), but for up-spin particles, the confinement phenomenon appears only in the EUP correction. In other words, the coefficient \(\alpha -\)deformation keeps the energies dependent on n,  \(\ell\) and spin values, even when there is no oscillation \(\left( \omega =0\right) ,\) where for a free fermion, the usual energy spectrum takes only two constants values \(\left( \pm m\right)\).

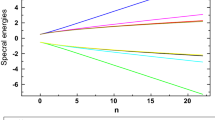
In the natural units \(\left( \hbar =c=1\right)\), we calculate the usual energy eigenvalues of DO and the correction caused by EUP for a single electron by means of Eqs. (64) and (65), for \(\alpha =10^{-77}\)MeV\(^{2}\), \(m=0.5\)MeV and \(m\omega =1\) MeV\(^{2}\) by considering the case \(s=+1\). The explicit values of the energy spectrum for different values of n and \(\ell\) are shown in table 1. Remarkably that the ground energy values in table 1 are not affected by the extended uncertainty principle. We can see from the table that for \(\ell >0,\) the energy levels for DO in the EUP background are independent of \(\ell\), whereas for the negative values of \(\ell\), the energies depend on \(\ell\). We also see that the positive energy spectrum of the EUP effect is larger than the energy of usual quantum mechanics (HUP), but for negative values, the EUP effect makes the energies smaller. The absolute values of the ordinary energies and the corrected ones are increasing with n for the same values of \(\ell\). If we fix the values of n, we can notice that the energy eigenvalues decrease with the negative values of \(\ell\).

We can indicate that the corrections of eigenvalues of energy are of the \(10^{-77}\) and \(10^{-78}\) orders, which means that the effect of EUP cannot be detected by current experimental means.

Table 1 The ordinary energy eigenvalues and the corrected ones of the 2D Dirac oscillator (in MeV) for a single electron at different values of n and \(\ell\) with \(s=+1\)
Full size table

The difference between the energy levels in (62) is constant for large values of n

$$\begin{aligned} \bigg |\lim _{n\rightarrow \infty }\Delta E_{n,\ell ,s}^{(\alpha )}\bigg |=\bigg |\lim _{n\rightarrow \infty }\left( E_{n+1,\ell ,s}^{(\alpha )}-E_{n,\ell ,s}^{(\alpha )}\right) \bigg |=2\sqrt{\alpha }. \end{aligned}$$
(67)

We can easily notice that the energy level spacing of the DO in two dimensions is equal to zero in absence of EUP. Similar results were obtained for one-dimensional DO on anti-de Sitter space [8] and in the presence of minimal lengths [30]. This means that in ordinary space, the energy levels become continuous for large values of n and the deformation coefficient keeps energy levels separate.

In the following, we will discuss two special cases of this system:

4.1 The Ordinary 2D Dirac Oscillator

From Eq. (61), the ordinary case of the spinorial wave functions for the 2D Dirac oscillator can be found within the framework of HUP (i.e., \(\alpha \rightarrow 0\)), wherefore, let us use the following limits [45]

$$\begin{aligned}{} {} \lim _{\alpha \rightarrow 0}\left( 1+\alpha r^{2}\right) ^{\frac{m\omega }{2\alpha }}&=e^{-\frac{m\omega r^{2}}{2}},\nonumber \\{} {} \quad \lim _{\rho _{s}\rightarrow +\infty }P_{n}^{(\rho _{s},\ell )}\left( \frac{2x}{\rho _{s}}-1\right) &=(-1)^{n}\lim _{\rho \rightarrow +\infty }P_{n}^{(\ell ,\rho _{s})}\left( 1-\frac{2x}{\rho _{s}}\right) =(-1)^{n}L_{n}^{\ell }(x),\nonumber \\{} {} \quad \lim _{\alpha \rightarrow +\infty }\frac{\Gamma (\alpha +\mu )}{\Gamma (\alpha )}e^{-\mu \ln (\alpha )}&=1. \end{aligned}$$
(68)

Here \(L_{k}^{\gamma }(x)\) are Laguerre polynomials. In this case, the variable x and the \(\alpha -\)parameter are given by

$$\begin{aligned} x=m\omega r^{2}, \alpha =\rho _{s}+n+1. \end{aligned}$$
(69)

Therefore, in the limit \(\alpha \rightarrow 0\), the spinorial wave functions become

$$\begin{aligned}{} & {} \lim _{\alpha \rightarrow 0}\Psi _{n,\ell ,s}(r,\theta )=(-1)^{n}e^{\imath \ell \theta }\sqrt{\frac{m\omega n!}{2\pi \Gamma (n+\ell +1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha =0)}+m}{E_{n,\ell ,s}^{(\alpha =0)}}}\left( \sqrt{m\omega }r\right) ^{\ell }e^{\frac{-m\omega r^{2}}{2}}L_{n}^{\ell }(m\omega r^{2})\mathcal {X} _{s}\nonumber \\{} & {} \quad -(-1)^{n}\imath e^{\imath (\ell +s)\theta }\sqrt{\frac{m\omega (n-s)!}{2\pi \Gamma (n+\ell +1)}}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha =0)}-m}{E_{n,\ell ,s}^{(\alpha =0)}}}\left( \sqrt{m\omega }r\right) ^{\ell +s}e^{\frac{-m\omega r^{2}}{2}}L_{n-s}^{\ell +s}(m\omega r^{2})\mathcal {X}_{-s}, \end{aligned}$$
(70)

with \(E_{n,\ell ,s}^{(\alpha =0)}\) are the spectral energies for the Dirac oscillator in two dimensions and in the context of HUP

$$\begin{aligned} E_{n,\ell ,s}^{(\alpha =0)}=\pm \sqrt{m^{2}+2m\omega \left( 2n+1+\left| \ell \right| -\ell -s\right) }, \end{aligned}$$
(71)

The authors in Ref. [47], have obtained the same formula of the usual eigenenergies for 2D Dirac oscillator (71) but with a different frequency because they studied the Dirac oscillator in the presence of magnetic field. So in the absence of a magnetic field, the result in Eq. (71) and the result obtained in Ref. [47] are the same.

4.2 The Non-Relativistic limit

The non-relativistic limit is obtained by setting \(E_{n,\ell ,s}^{(\alpha )}=m+E_{NR}\), where the rest mass m is much greater than any other energy (i.e., \(E_{NR}<<m)\). Thus, the non-relativistic energy of DO in the deformation space (EUP) is

$$\begin{aligned}{} & {} E_{NR}\simeq \omega (2n+1+|\ell |)-\omega \ell -\omega s\nonumber \\{} & {} \quad +\frac{\alpha }{2m}\left( \arrowvert \ell \arrowvert -\ell -s+(2n+1)\right) ^{2}. \end{aligned}$$
(72)

The familiar 2D harmonic oscillator has been shown together with spin and angular momentum, respectively; this result is consistent with [48]. The last term is the correction due to the modification of the Heisenberg algebra of the non-relativistic oscillator energy. In the non-relativistic limit, the normalized wave functions with spin 1/2 are given by

$$\begin{aligned}{} {} \Psi _{NR,n,\ell ,s}(r,\theta )&=e^{\imath \ell \theta }\sqrt{\frac{\alpha (\rho _{s}+|\ell |+2n+1)n!\Gamma (\rho _{s}+|\ell |+n+1)}{\pi \Gamma (\rho _{s} +n+1)\Gamma (|\ell |+n+1)}}\left( \frac{\alpha r^{2}}{1+\alpha r^{2}}\right) ^{\frac{|\ell |}{2}}\left( \frac{1}{1+\alpha r^{2}}\right) ^{\frac{\rho _{s}+1}{2}}\nonumber \\{} {} &\qquad \times P_{n}^{(\rho _{s},|\ell |)}\left( \frac{\alpha r^{2}-1}{\alpha r^{2} +1}\right) \mathcal {X}_{s}, \end{aligned}$$
(73)

where we have used the following limits [35]

$$\begin{aligned}{} & {} \lim _{m>>}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}+m}{E_{n,\ell ,s}^{(\alpha )}} }=\sqrt{2},\nonumber \\{} & {} \quad \lim _{m>>}\sqrt{\frac{E_{n,\ell ,s}^{(\alpha )}-m}{E_{n,\ell ,s}^{(\alpha )}}}=0. \end{aligned}$$
(74)

5 Thermodynamic Functions

Now, let us study the thermodynamic properties of a single electron interacting with the Dirac oscillator in the modified algebra (2). Before we proceed further to find all the thermodynamic properties, we must first find the partition function for this question. Indeed, we have

$$\begin{aligned} Z=\sum _{n=0}^{\infty }e^{-\bar{\beta }E_{n}}, \end{aligned}$$
(75)

where \(\bar{\beta }=1/(k_{B}T)\), \(k_{B}\) is the Boltzmann constant, T is the temperature of the system and \(E_{n}\) is the energy spectrum which is defined in Eq. (63). In particular, we will focus on the case of positive energy, because for the negative energy the sum (75) diverges. Also, we take \(s=+1\) and \(\ell =0,\) Eq. (75) reduces to

$$\begin{aligned} Z=\sum _{n=0}^{\infty }\exp \left[ -a\sqrt{1+bn}-\frac{4n^{2}\bar{\beta }\alpha }{2m\sqrt{1+bn}}\right] . \end{aligned}$$
(76)

In the first order of \(\alpha\), we get the following \(Z-\)partition function

$$\begin{aligned}{} & {} Z(T,\alpha )=Z(\bar{\beta },\alpha =0)+\alpha Z^{(1)}(\bar{\beta })\nonumber \\{} & {} \quad =\sum _{n=0}^{\infty }\exp \left[ -a\sqrt{1+bn}\right] -\alpha \bar{\beta } \sum _{n=0}^{\infty }\frac{4n^{2}\exp \left[ -a\sqrt{1+bn}\right] }{2m\sqrt{1+bn}}, \end{aligned}$$
(77)

with \(a=\bar{\beta }m\) and \(b=4\omega /m\). We can, however, evaluate the sums in (77) by using the Euler–Maclaurin summation formula

$$\begin{aligned} \sum _{n=0}^{\infty }f(n)=\frac{1}{2}f(0)+\int _{0}^{\infty }f(x)dx-\sum _{k=1}\frac{B_{2k}}{(2k-1)!}f^{(2k-1)}(0), \end{aligned}$$
(78)

where \(B_{2p}\) are the Bernoulli numbers and \(f^{(2k-1)}(0)\) is the derivative of order \((2k-1)\) at \(x=0\)

$$\begin{aligned}{} {} f(0)&=e^{-\bar{\beta }m},\nonumber \\{} {} \quad f^{(1)}(0)&=-2\bar{\beta }\omega e^{-\bar{\beta }m},\nonumber \\{} {} \quad f^{(3)}(0)&=-\dfrac{8\bar{\beta }\omega ^{3}e^{-\bar{\beta }m}}{m^{2}}\left[ \bar{\beta }^{2}m^{2}+3\bar{\beta }m+3\right] +24\alpha \bar{\beta }\frac{\omega }{m^{2}}\left( \bar{\beta }m+1\right) e^{-\bar{\beta }m}. \end{aligned}$$
(79)

The integral over x in Eq. (77) is given by

$$\begin{aligned} \int _{0}^{\infty }f(x)dx=\dfrac{e^{-\bar{\beta }m}\left( \bar{\beta }m+1\right) }{2\bar{\beta }^{2}m\omega }-\frac{\alpha e^{-\bar{\beta }m}}{2\bar{\beta } ^{4}m^{3}\omega ^{3}}\left\{ \bar{\beta }^{2}m^{2}+3\bar{\beta }m+3\right\} . \end{aligned}$$
(80)

At high temperatures, we can neglect the terms with \(\bar{\beta }^{n}\) and the terms without \(\bar{\beta }\). Consequently, the partition function to the first order in \(\alpha\) can then be obtained by

$$\begin{aligned} Z(T,\alpha )=\dfrac{T^{2}}{2m\omega }-\frac{\alpha }{2m^{3}\omega ^{3}}\left\{ 3T^{4}-\frac{m^{2}T^{2}}{2}\right\} . \end{aligned}$$
(81)

Note that \(k_{B}=1\) in natural units. The first term in Eq. (81) represents the partition function for the two-dimensional Dirac oscillator in the context of HUP. While the other terms are the contribution of the space deformation caused by the presence of the EUP. From (81), we conclude that with the smallest momentum uncertainty should verify the following constraint

$$\begin{aligned} (\Delta P_{i})_{min}\leqslant \dfrac{m\omega }{\sqrt{12T^{2}-2m^{2}}}. \end{aligned}$$
(82)

After we succeed in obtaining the expression for the first-order partition function of \(\alpha -\)perturbation, all related thermodynamic functions can be obtained. The Helmholtz free energy of the 2D Dirac oscillator in EUP context and for high temperature is written as

$$\begin{aligned}{} {} F(T,\alpha )&=-T\ln (Z)\nonumber \\{} {} \quad &=-2T\ln \left( \frac{T}{2m\omega }\right) +\frac{\alpha }{m^{2}\omega ^{2} }\left\{ 3T^{3}-\frac{m^{2}T}{2}\right\} . \end{aligned}$$
(83)

The relation between mean energy and partition function is

$$\begin{aligned} \bar{E}(T,\alpha )=-\frac{\partial \ln (Z)}{\partial \bar{\beta }}=2T-\frac{6\alpha T^{3}}{m^{2}\omega ^{2}}. \end{aligned}$$
(84)

For the heat capacity, we have

$$\begin{aligned} C(T,\alpha )=\dfrac{\partial \bar{E}}{\partial T}=2-\frac{18\alpha T^{2}}{m^{2}\omega ^{2}}. \end{aligned}$$
(85)

In the limit \(\alpha =0\), the heat capacity in the usual Heisenberg algebra is constant \(C=2\). Otherwise, we can see that the heat capacity varies with the temperature under the modification of the standard Heisenberg algebra. The expression of heat capacity (85) makes a stronger constraint of the smallest momentum uncertainty

$$\begin{aligned} (\Delta P_{i})_{min}\leqslant \dfrac{m\omega }{6T}, \end{aligned}$$
(86)

this constraint leads to an interesting result, which is \((\omega /T)-\)dependent minimum momentum uncertainty measurement. In Ref. [30], the author has obtained a similar result for the system of the one-dimensional Dirac oscillator in the context of GUP, where he found that the minimal length is proportional to the inverse of temperature. However, the minimum length obtained in this reference is independent of the \(\omega -\)frequency, unlike the minimum momentum uncertainty that we got in Eq. (86).

The last term for thermodynamic functions is entropy, which we can get

$$\begin{aligned}{} {} S(T,\alpha )&=k_{B}\ln (Z)-k_{B}\bar{\beta }\frac{\partial \ln (Z)}{\partial \bar{\beta }}\nonumber \\{} {} \quad &=2+2\ln \left( \frac{T}{2m\omega }\right) -\frac{9T^{2}\alpha }{m^{2}\omega ^{2}}. \end{aligned}$$
(87)

We can extract the effect of EUP on thermodynamic functions by plotting the difference between these functions in the presence of deformation (EUP) and its absence (HUP):

$$\begin{aligned}{} {} \Delta Z(T)&=Z(T,\alpha )-Z(T,\alpha =0),\nonumber \\{} {} \quad \Delta F(T)&=F(T,\alpha )-F(T,\alpha =0),\nonumber \\{} {} \quad \Delta \bar{E}(T)&=\bar{E}(T,\alpha )-\bar{E}(T,\alpha =0),\nonumber \\{} {} \quad \Delta C(T)&=C(T,\alpha )-C(T,\alpha =0),\nonumber \\{} {} \quad \Delta S(T)&=S(T,\alpha )-S(T,\alpha =0). \end{aligned}$$
(88)

These differences are plotted in Figs. (1, 2, 3, 4 and 5), as functions of temperature \(\left( T\right) ,\) with \(\alpha =10^{-77}\)MeV\(^{-2}\), \(m=0.5\) MeV and \(m\omega =1\) MeV\(^{2}\). We can easily see that the effect of EUP on partition function, Helmholtz free energy, mean energy, heat capacity and entropy increases with temperature. A similar observation was obtained in the case of the effect of EUP in one-dimensional Dirac oscillator [8]. The increasing effect of the extended uncertainty principle on the thermodynamic properties with temperature for the “Dirac oscillator” system is different from what is known about the effect of the extended uncertainty principle on these properties, where the EUP impact decreases with increasing temperatures in the cosmological framework [49, 50]. In Fig. 1, we can observe that EUP causes a decrease in the partition function, and the absolute value of the variation of \(\Delta Z(T)\) is growing relatively quickly with temperature, where

$$\begin{aligned} \bigg \arrowvert \Delta Z(T=10^{11}\text {MeV})-\Delta Z(T=10^{12}\text {MeV} )\bigg \arrowvert \simeq 1.5\times 10^{-29}. \end{aligned}$$

The variations \(\Delta F(T)\) with temperature are shown in Fig. 2; we can note that the EUP makes the Helmholtz increase. In other words, the EUP causes an increase in the useful work we can extract from this system at a constant temperature. The value of \(\Delta F(T)\) increases at an average rate with temperature,

$$\begin{aligned} \bigg \arrowvert \Delta F(T=10^{11}\text {MeV})-\Delta F(T=10^{12}\text {MeV} )\bigg \arrowvert \simeq 3\times 10^{-41}\text {MeV}. \end{aligned}$$

Fig. 3 shows that the EUP makes the mean energy smaller with increasing temperature. The value of \(\Delta \bar{E}(T)\) increases at an average rate with temperature,

$$\begin{aligned} \bigg \arrowvert \Delta \bar{E}(T=10^{11}\text {MeV})-\Delta \bar{E}(T=10^{12} \text {MeV})\bigg \arrowvert \simeq 7\times 10^{-41}\text {MeV}. \end{aligned}$$

In addition, Fig. 4 shows the variation of the EUP effect on heat capacity with temperature. As we can see, the EUP causes a decrease in the heat capacity with temperature, which means that in the high-temperature regime, the necessary amount of heat to produce a unit change in temperature decreases with temperature under the effect of EUP. Unlike the familiar Dirac oscillator where this amount is constant in the high-temperature regime, the absolute value of \(\Delta C(T)\) increases slowly with increasing temperature:

$$\begin{aligned} \bigg \arrowvert \Delta C(T=10^{11}\text {MeV})-\Delta C(T=10^{12}\text {MeV} )\bigg \arrowvert \simeq 2\times 10^{-52}. \end{aligned}$$

Finally, we present the effect of EUP on entropy function in Fig. 5. According to this figure, the EUP makes the values of entropy smaller with temperature. The absolute value of \(\Delta S(T)\) increases slowly with increasing temperature:

$$\begin{aligned} \bigg \arrowvert \Delta S(T=10^{11}\text {MeV})-\Delta S(T=10^{12}\text {MeV} )\bigg \arrowvert \simeq 10^{-52}. \end{aligned}$$

As we saw in the effect of the EUP on the eigenvalues of energy, its effect on thermodynamic functions is also too small to be detected by current experimental means. However, the EUP effect could be very important in the early universe [2]. In Ref. [21], the author shows that using the effective mass approach, the two-dimensional Dirac oscillator can be considered as a description of the thermodynamic properties of graphene under a uniform magnetic field. Therefore, our results can be used to describe the graphene in the presence of a uniform magnetic field in the EUP background.

Fig. 1
figure 1

The first correction of partition function for the DO as a function of temperature T

Full size image
Fig. 2
figure 2

The first correction of Helmholtz free energy for the DO as a function of temperature T

Full size image
Fig. 3
figure 3

The first correction of mean energy for the DO as a function of temperature T

Full size image
Fig. 4
figure 4

The first correction of heat capacity for the DO as a function of temperature T

Full size image
Fig. 5
figure 5

The first correction of entropy for the DO as a function of temperature T

Full size image

6 Conclusion

In this paper, we studied the 2D Dirac oscillator in the position space representation and in the presence of the extended uncertainty principle. The exact corresponding casual Green function has been calculated, and then, the eigenfunctions as well as the appropriate energy values have been extracted from them. We have shown that the effect of EUP makes the energies depend on n and \(\ell\) even in the absence of oscillation, where the harmonic oscillator, anharmonicity vibration and confinement phenomenons appear. In addition, we found that the energy level spacing becomes constant for large values of n and the deformation parameter \(\alpha\) keeps the energy levels separate. Moreover, the symmetry of energy levels under the transformations \(s\rightarrow -s,\) \(n\rightarrow n-s\) is not affected by the EUP. Finally, in the regime of high temperatures, the thermodynamic quantities such as Helmholtz free energy, mean energy, heat capacity and entropy of 2D DO have been determined using an Euler–Maclaurin formulation. By calculating these quantities under the effect of EUP, we get an interesting conclusion that the smallest uncertainty in momentum measurements is dependent on the frequency and temperature of the system, this dependence is absent in ordinary quantum mechanics. By plotting the EUP terms of thermodynamic functions with temperature T, we have shown the influence of the deformation parameter \(\alpha\) on them. For instance, the useful work we can extract from the 2D DO system increases under the effect of EUP. However, these effects cannot be detected by current experimental means.