1 Introduction

Surface plasmon polaritons (SPPs) have attracted the attention of researchers since the twentieth century. When electromagnetic waves propagate alongside the metal-dielectric interface at frequencies ranging from visible to infrared, SPPs can appear in specific circumstances. SPPs are surface waves with extreme spatial confinement that include collective electron oscillations. SPPs were originally detected in 1902 by an American physicist named Robert Wood [1]. Later, it was discovered that the long-range Coulomb interaction between valence electrons in metals causes collective plasma oscillations, which were named plasmons [2]. The word polariton was commonly used to describe the associated oscillation of bound electrons and light within transparent materials [3]. Ritchie theoretically described surface plasmons [4] and discovered that anomalous characteristics found in metal gratings are caused by simulation of surface plasmon resonances [5]. Powel and Swan conducted multiple tests on electron energy losses in 1959, demonstrating the presence of these collective excitations [6]. Stern and Ferrell used the term surface plasmons to describe the quanta of these oscillations [7]. Scientists examined surface plasmons in metallic films in the second half of the twentieth century and discovered that surface plasmons in thin and thick films may couple to light using diffraction grating [8].

We would like to emphasize that from the SPP dispersion relation, \(k_{spp}=\frac{\omega }{c}\sqrt{\frac{\epsilon _d \epsilon _m}{\epsilon _d+\epsilon _m}}\) [9] (where \(\epsilon _m\) and \(\epsilon _d\) are relative permittivity of metal and dielectric, respectively), it is evident that the momentum of a photon is smaller than that of SPP. However, momentum must be conserved in order for SPP to be excited. As a result, a coupler is necessary to impart extra momentum to a photon. Various coupling strategies have been developed for this purpose. Otto [10] and Kretschmann [11] propose the use of prisms as couplers. They considered to use a prism as a coupler to enhance the momentum of incident light. This technique uses the frustrated total internal reflection (FTIR) phenomenon and has been used for a variety of purposes. At the same time, gold and silver nanoparticles were studied, and research into their plasmonic characteristics resulted in remarkable advancement [12]. Eventually, the term SPP was introduced by Cunningham and his co-workers [13].

Quantum coherence is essential to the majority of atom optical phenomenon. For the incident weak coherent electromagnetic field, EIT occurs when another strong coherent electromagnetic field renders a previously opaque material transparent. EIT was first conducted theoretically by Boller et. al. [14], while Lukin and his co-workers conducted the first experiment to conduct the theory [15]. Additionally, EIT may control the optical characteristics of many atomic systems, resulting in zero absorption and sharp dispersion within a small range. For example, it may be used to create ultra-slow light or store optical pulses in a number of different processes that include atom optics or solid-state systems. An EIT-based approach may also amplify nonlinear effects and be used to analyze SPP in the quantum mechanical realm [16]. In a recent study, researchers provided an EIT-based model where it was indicated that coupler-free excitation of SPP may be accomplished if \(\epsilon _{d}\) of the quantum medium is smaller than 1 [17]. For sharp SPR, the losses should be minimal since the momentum match happened at a certain incidence angle \(\theta _p\).

In recent years, numerous forms of quantum optical nonlinear phenomena based on quantum coherence and interference in semiconductor QDs have also seen much studied. These phenomena include Kerr nonlinearity [18], optical switching [19], enhanced index of refraction [20], EIT [21], and other unique phenomena. This is mostly due to the fact that the processes that take place in QDs have a number of potentially important applications in the areas of solid-state optoelectronics and quantum information technology. Furthermore, systems based on intersubband transitions in QDs have a variety of unique advantages over atomic systems. Additionally, compared to atomic systems, devices based on intersubband transitions in QDs have a number of advantageous features. These advantages consist of the extremely large electric dipole moments generated by the low effective electron mass, the high nonlinear optical coefficients, the capability to customize transition energies, dipoles, symmetries, and the incredibly high degree of design flexibility in terms of materials and structural dimensions.

It has been reported recently that in a metal semiconductor waveguide optical gain observed by a propagating mode, known as modal gain, is usually distinct from material gain, which defines the inherent quality of a gain material. The confinement factor is the ratio of the modal gain to the material gain [22]. Furthermore, it was reported that power confinement factor is more than unity for highly directed plasmonic mode. However, the energy confinement factor is always less than unity. The less than unity criterion is fulfilled when the real component of metal permittivity is negative [23]. More recently, the idea of confinement factor is examined for a metal–semiconductor-metal waveguide near to the surface plasmon resonance, with QDs semiconductor as the active area [24]. When the waveguide Fermi energy was taken into account, it was claimed that substantial net modal gains were attained. This implied that the increase came from the material gain rather than the confinement factor [24].

In this paper, we investigate coupler-free excitation of lossless SPPs by considering a three-layer structure where the bottom layer consists of ladder-type QDs system. Our model is mainly used to examine how SPPs are generated at the metal–semiconductor interface, and is built on the quantum coherence phenomenon in QDs. One of the most important benefits of our system is that it is far more practical than its atomic analog due to its flexible structure, tunable quantum-interference effect, and wide range of adjustable parameters. Due to the incoherent pump field and control field’s intensity strength, it is possible to achieve an improved refractive index without absorbing light. As a result, in these systems, SPP’s features may be manipulated. SPPs may be used in a variety of devices, including photodetectors, sensors, polarizers, microscopy, lithography, and many more [25,26,27,28,29].

2 Model and equations

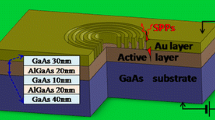
Figure 1 depicts the suggested model for the coupler-free SPR. We assume a system that consists of three layers: a bottom layer of QDs, a middle layer of metal film, and a transparent top layer that may be air or vacuum. The corresponding relative permittivity of these layers is \(\epsilon _t\), \(\epsilon _m\) and \(\epsilon _d\). In fact, the bottom layer is a quantum medium made up of ladder-type QDs, whose permittivity may be coherently adjusted under EIT circumstances. According to Fig. 1, three electromagnetic fields are incident at the top layer–metal interface: a weak probe field at angle \(\theta _{p}\), a strong control field at angle \(\theta _c\) and incoherent pump field at angle \(\theta _{in}\) as shown in Fig. 1. Because of the quantum nature of EIT, SPP may be excited at the metal semiconductor interface by the probe field in the presence of control fields.

Fig. 1
figure 1

(Color online) A three-layer SPR system with a transparent top layer, a thin metal film in the middle, and a semiconductor quantum medium made up of quantum dots at the bottom. The arrangement of the QDs energy levels is shown by the encircle

Full size image

The configuration of QDs energy levels is shown by the encircle in Fig. 1. The incoherent pump field has a rate \(\Lambda\) and is applied to transition \(|1\rangle \longrightarrow |3\rangle\), a control beam with Rabi frequency \(\Omega _{c}\) applied to transition \(|2\rangle \longrightarrow |3\rangle\) and a monitoring light beam with Rabi frequency \(\Omega _{p}\) is applied to transition \(|1\rangle \longrightarrow |2\rangle\). The interaction picture Hamiltonian of the system under consideration is represented by

$$\begin{aligned} H_I= & {} -\hbar \Delta _p|2\rangle \langle 2|-\hbar (\Delta _p+\Delta _{c})|3\rangle \langle 3|-\hbar (\Omega _{p}|2\rangle \langle 1|\nonumber \\{} & {} \quad +\Omega _{c}|3\rangle \langle 2|+\Omega _{p}^{*}|1\rangle \langle 2|+\Omega _{c}^{*}|2\rangle \langle 3|) \end{aligned}$$
(1)

where \(\Delta _{c}=\omega _{c}-\omega _{32}\) and \(\Delta _{p}=\omega _{p}-\omega _{21}\) are the two optical field’s intersubband transition detunings. The Rabi frequency of the corresponding transitions is \(\Omega _{c}=\frac{\mu _{32}E_{c}}{2\hbar }\) and \(\Omega _{p}=\frac{\mu _{21}E_{p}}{2\hbar }\). \(\omega _{21}\) and \(\omega _{32}\) are resonant frequencies associating with the corresponding transition \(|2\rangle \longrightarrow |1\rangle\) and \(|3\rangle \longrightarrow |2\rangle\), respectively. By adopting the standard approach using Liouville equation, we obtain following rate equations for the corresponding density matrix elements

$$\begin{aligned} \dot{\rho }_{12}= &\; {} i\Omega _{p}^{*}\rho _{22}-i\Omega _{p}^{*}\rho _{11}-i\Omega _{c}\rho _{13}-(i\Delta _{p}+\frac{\gamma _{21}+\Lambda }{2})\rho _{12},\nonumber \\ \dot{\rho }_{13}= &\; {} -i\Omega _{c}^{*}\rho _{12}+i\Omega _{p}\rho _{23}-[i(\Delta _{p}+\Delta _{c})+\frac{\gamma _{32}+\gamma _{31}+2\Lambda }{2}]\rho _{13},\nonumber \\ \dot{\rho }_{23}= &\; {} i\Omega _{p}\rho _{13}-i\Omega _{c}^{*}\rho _{22}+i\Omega _{c}^{*}\rho _{33}-(i\Delta _{c}+\frac{\gamma _{21}+\gamma _{31}+\gamma _{32}+\Lambda }{2})\rho _{23},\nonumber \\ \dot{\rho }_{11}= &\; {} i\Omega _{p}\rho _{21}-i\Omega _{p}^{*}\rho _{12}+\Lambda \left( \rho _{33}-\rho _{11}\right) +\gamma _{21}\rho _{22}+\gamma _{31}\rho _{33},\nonumber \\ \dot{\rho }_{22}= &\; {} i\Omega _{c}^{*}\rho _{32}-i\Omega _{c}\rho _{23}+i\Omega _{p}\rho _{12}-i\Omega _{p}^{*}\rho _{21}+\gamma _{32}\rho _{33}-\gamma _{21}\rho _{22},\nonumber \\ \dot{\rho }_{33}= &\; {} i\Omega _{c}\rho _{23}-i\Omega _{c}^{*}\rho _{32}+\Lambda (\rho _{11}-\rho _{33})-\gamma _{32}\rho _{33}-\gamma _{31}\rho _{33}, \end{aligned}$$
(2)

where \(\rho _{mn}=\rho _{nm}^{*}\) are interaction density operator between states \(|m\rangle\) and \(|n\rangle\). Also, \(\gamma _{mn}\) is spontaneous damping from \(|m\rangle\) to \(|n\rangle\), respectively. Under steady state conditions and in the limit of a weak probe field, these equations have the following answer:

$$\begin{aligned} \rho _{11}= &\; {} 1-\frac{(\gamma _{21}+\gamma _{32})\lambda }{\gamma _{21}\gamma _{31}+\gamma _{21}\gamma _{32}+2\gamma _{21}\Lambda +\gamma _{32}\Lambda }, \end{aligned}$$
(3)
$$\begin{aligned} \rho _{22}= &\; {} \frac{\gamma _{32}\Lambda }{\gamma _{21}\gamma _{31}+\gamma _{21}\gamma _{32}+2\gamma _{21}\Lambda +\gamma _{32}\Lambda }, \end{aligned}$$
(4)
$$\begin{aligned} \rho _{33}= &\; {} \frac{\gamma _{21}\Lambda }{\gamma _{21}\gamma _{31}+\gamma _{21}\gamma _{32}+2\gamma _{21}\Lambda +\gamma _{32}\Lambda }, \end{aligned}$$
(5)
$$\begin{aligned} \rho _{12}= &\; {} \frac{i\Omega _{p}\left( \rho _{22}-\rho _{11}\right) +A}{i\Delta _{p}+B+C}, \end{aligned}$$
(6)

where we have defined

$$\begin{aligned} A= &\; {} \frac{i\Omega _{c}^{2}\Omega _{p}\left( \rho _{33}-\rho _{22}\right) }{\left[ i\left( \Delta _{p}+\Delta _{c}\right) +\frac{\gamma _{21}+\gamma _{31}+2\Lambda }{2}\right] \left(i\Delta _{c}+\frac{\gamma _{21}+\gamma _{31}+\gamma _{32}+\Lambda }{2}\right)}, \end{aligned}$$
(7)
$$\begin{aligned} B= &\; {} \frac{\gamma _{21}+\Lambda }{2}, \end{aligned}$$
(8)
$$\begin{aligned} C= &\; {} \frac{\Omega _{c}^{2}}{i(\Delta _{p}+\Delta _{c})+\frac{\gamma _{21}+\gamma _{31}+2\Lambda }{2}}. \end{aligned}$$
(9)

The optical susceptibility of the probe transition is provided for a weak probe field by

$$\begin{aligned} \begin{aligned} \chi =\frac{N|\mu _{12}|^2\rho _{21}}{2\hbar \epsilon _0 \Omega _{p}}, \end{aligned} \end{aligned}$$
(10)

where \(\epsilon _{0}\) is the permitivity of free space and N is the quantum dot’s number density. The permittivity of the QDs is related to susceptibility by [30, 31]

$$\begin{aligned} \epsilon _d = 1+\frac{\chi }{1-\frac{1}{3}\chi }. \end{aligned}$$
(11)

Excitation of SPPs can be identified by the reflection and transmission spectrum. For three-layer structure, the reflection coefficient is given by [32]

$$\begin{aligned} r_{tms}=\frac{r_{tm}+r_{ms}exp(2i k_{mx} q)}{1+r_{tm} r_{ms} exp(2i k_{mx} q)}, \end{aligned}$$
(12)

where q is the thickness of the metallic film and \(r_{tm}\) and \(r_{ms}\) are reflection coefficients for a single interface. In the case of TM-polarized light, two-layer reflection coefficient for the top medium–metal interface is given by

$$\begin{aligned} r_{tm} = \frac{\epsilon _m k_{tx} -\epsilon _t k_{mx}}{\epsilon _m k_{tx} +\epsilon _t k_{mx}}, \end{aligned}$$
(13)

and for metal–semiconductor interface,

$$\begin{aligned} r_{ms}=\frac{\epsilon _d k_{mx}-\epsilon _m k_{sx}}{\epsilon _d k_{mx}+\epsilon _m k_{sx}}, \end{aligned}$$
(14)

where \(\epsilon _{t} (\epsilon _{m})\) is the permittivity of air (metal) and \(k_{jx}\) represents the normal wave vectors and can be expressed as

$$\begin{aligned} k_{jx}=\sqrt{k_0^2\epsilon _j-k_z^2}, \end{aligned}$$
(15)

where \(j\,=\,t,m,s\) is used to represent top medium, metal, and semiconductor medium, respectively, and \(k_z\) is in-plane component of wave vector related to top-medium refractive index \(n_t\) and probe field angle of incidence \(\theta _p\) and can be written as

$$\begin{aligned} k_z = k_0 n_t \text {sin}\theta _p, \end{aligned}$$
(16)

where \(k_0\,=\,\frac{\omega _p}{c}\) is free space wave vector of incident probe beam.

In a similar way, the transmission coefficient is given by

$$\begin{aligned} t_{tms}\,=\,\frac{t_{tm}t_{ms}exp(ik_{mx}q)}{1+r_{tm} r_{ms}exp(2ik_{mx}q)}, \end{aligned}$$
(17)

where \(t_{ij}\) is transmission coefficient. This two-layer transmission coefficient is related to the corresponding two-layer reflection coefficient by

$$\begin{aligned} t_{ij} = 1+r_{ij}. \end{aligned}$$
(18)

The reflectivity R is determined by \(R=|r_{tms}|^2\) and transmission T can be calculated as \(T=|t_{tms}|^2.\) Transmission is also known as the electric field intensity’s field enhancement factor, and for SPPs, it may be higher than 1. This is because permittivity of QDs has been considered to be less than unity, resulting in SPP being less than the wave vector of light in free space. As a result, with a suitable angle of incidence, the in-plane component of the photon wave vector coincides with the SPP wave vector, resulting in SPP enhancement. Because SPPs have significant spatial confinement, the energy density can be enhanced as a result of its confined distribution along the interface [17].

Due to the assumption that input light is TM-polarized and that magnetic fields only have y-components, the magnetic field’s enhancement of field factor is defined as \(T=|\frac{H_y (m/s)}{H_y (t/m)}|^2\), where \(H_y (t/m)\) denotes the magnetic field amplitude at the top medium–metal interface. Similar to this, the definition of the field enhancement factor for an electric field is \(T_{el}=|\frac{\textbf{E} (m/s)}{\textbf{E} (t/m)}|^2\), where \(\textbf{E} (t/m)\) are electric fields at top medium–metal interfaces and \(\textbf{E} (m/s)\) denotes the electric fields at the metal–semiconductor. The electric field enhancement factor for a TM-mode is related to magnetic field enhancement factor by [32]

$$\begin{aligned} T_{en}=\frac{\epsilon _t}{\epsilon _d} |t_{tms}|^2. \end{aligned}$$
(19)

Using Eqs. (12)–(19), reflectivity and field enhancement of incident probe field can be calculated.

3 Results

This section contains an analysis of the model we suggested for coupler-free SPP excitation. First we analyze the excitation of SPP at the air-metal interface. The wave vector of SPP is defined as \(k_{\text {spp}}=k_{0}\sqrt{\frac{\epsilon _{t}\epsilon _{m}}{\epsilon _{t}+\epsilon _{m}}}\) [32]. As the permittivity of air is \(\epsilon _{t}=1\) and that of metal is \(\epsilon _{m}<1\), so \(k_{0}<k_{\text {spp}}\). The resonance condition Eq. (16) becomes \(k_{\text {spp}}>k_0 \text {sin}\theta _p\) (here \(n_t=1\) for air); therefore, SPP cannot be excited directly by light due to momentum mismatch (\(\hbar k_{spp}> \hbar k_{0}\)). Usually, a coupler of refractive index \(n_c\) is needed to increase the wave vector of light from \(k_{0}\) to \(n_{c}k_{0}\) and hence the momentum of light increases to \(n_{c} \hbar k_{0}\). Next, we consider the excitation of SPP at the metal-QD interface in our propose model as shown in Fig. 1. The wavenumber of SPP can be written as \(k_{\text {spp}}=k_{0}\sqrt{\frac{\epsilon _{m}\epsilon _{d}}{\epsilon _{m}+\epsilon _{d}}}\). If permittivity of the QD \(\epsilon _{d}<1\), then \(k_{\text {spp}}<k_{0}\) and resonance condition \(k_{\text {spp}}=k_0 \text {sin}\theta _p\) can be satisfied for a specific angle \(\theta _p\). Hence we can excite SPP via QD without using any coupler.

We start our discussion by considering Rabi frequency of control field \(\Omega _{c}=8\,\mu\)eV. We plot the real (blue curve) and imaginary (purple curve) part of permittivity \(\epsilon _{d}\) versus the detuning of probe field \(\Delta _{p}\) as shown in Fig. 2a. Also we set the incoherent pumping \(\Lambda =5\mu\)eV. Other parameters are \(\gamma _{21}=1.6\mu\)eV, \(\gamma _{31}=3.2\mu\)eV, \(\gamma _{32}=0\), \(\Delta _c=0\). The imaginary part of the permittivity illustrates the transparency window in the vicinity of resonance, i.e., at \(\Delta _p=0\) and real part shows the normal dispersion. So our system behave as standard EIT behavior. Figure 2b shows reflectivity spectrum R (blue curve) and enhancement of field \(T_{en}\) (green curve) for monitoring field versus detuning of monitoring field \(\Delta _{p}\).

Fig. 2
figure 2

(Color online) a, c Real (blue curve) and imaginary (purple curve) part of permittivity \(\epsilon _d\) and b, d spectrum of the reflectivity R (blue curve), and field enhancement \(T_{en}\) (green curve) of probe field as a function of detuning of monitoring field \(\Delta _{p}\) for a, b \(\Omega _c=8\,\mu\)eV, c, d \(\Omega _c=10\, \mu\)eV. Other parameters are \(\Lambda =5\,\mu\)eV, \(\gamma _{21}=1.6\), \(\gamma _{31}=3.2\,\mu\)eV, \(\gamma _{32}=0\), \(\Delta _c=0\), \(n_t=1\), \(\epsilon _t=1\), \(\epsilon _m=-21.74+1.744i\), \(\theta _p=85.3^{\circ }\), \(\lambda _0=795\,\)nm and \(q=45\,\)nm

Full size image

The other parameters are \(n_t=1\), \(\epsilon _t=1\), \(\epsilon _m=-21.74+1.744i\), \(\theta _p =85.3^{\circ }\), \(\lambda _0=795\) nm and \(q=45\) nm. The remaining parameters are same as in Fig. 2a. In this case, the field enhancement factor \(T_{en}\) is not prominent due to losses (Im\([\epsilon _d]\ne 0\)) present in the system as shown in Fig. 2b. To compensate the losses, we increase intensity of pump field \(\Omega _{c}\) between state \(\left| 2\right\rangle\) and \(\left| 3\right\rangle\). Figure 2c shows the effect of intensity of Rabi frequency of pump field \(\Omega _{c}\) on the imaginary part of permittivity \(\epsilon _d\). The absorption decreases as we increase the strength of control field and at \(\Omega _{c}\approx 10\mu\)eV, the absorption becomes zero and there is gain in a system (Im\([\epsilon _d]<0\)) with real part showing the steep normal dispersion. In Fig. 2d, we see the effect of intensity of control field on enhancement \(T_{en}\) and reflectivity R. We observe significantly sharp field enhancement \(T_{en}\) and zero reflectivity R at \(\Lambda \approx 5\mu\)eV and \(\Omega _c=10\mu\)eV, where the system becomes lossless. The SPR condition \(k_{\text {spp}}=k_0 \text {sin}\theta _p\) can be met at \(\Delta _p=-6.4\mu\)eV and \(\theta _p=85.3^{\circ }\), where Re\([\epsilon _d]<1\) and Im\([\epsilon _d]<<1\). It should be noted that excited SPP radiates into the top layer and absorbs in the metal. The energy from the gain medium is transferred to the SPPs which is then radiated into the reflected wave. The details can be found in Ref. [33].

Figure 3 depicts the behavior of reflectivity R and field enhancement \(T_{en}\) as a function of probe field, angle of incidence \(\theta _p\) at fixed detuning \(\Delta _p=-6.4\mu\)eV for three different situations (a) \(\Omega _{c}=8\mu\)eV, (b) \(\Omega _{c}=9\mu\)eV and (b) \(\Omega _{c}=10\mu\)eV. Also the incoherent pumping \(\Lambda =5\mu\)eV. We observe dips and peaks in the reflectivity and field enhancement spectra, respectively, at certain angles of incidence called resonance angles.

Fig. 3
figure 3

(Color online) Angle spectra of reflectivity R (blue curve) and field enhancement \(T_{en}\) (purple curve) for a \(\Omega _c=8\mu\)eV, Xi’an Jiaotong University \(\Omega _c=9\mu\)eV and c \(\Omega _c=10\mu\)eV at \(\Delta _p=-6.4\mu\)eV. Other parameters are same as given in Fig. 2

Full size image

The angle spectra in both cases are symmetric about \(\theta _p=0\). But an important feature to note is that when amplitude of Rabi frequency is \(\Omega _{c}=8\mu\)eV, see Fig. 3a, there is small field enhancement at resonance which means that SPR effect is weak. This suggests that control field strength of \(8\mu\)eV cannot lead to sharp SPR. The small increment of control field strength to \(9\mu\)eV leads to increase the field enhancement see Fig. 3b. As soon as we increase the strength of control field while keeping all other parameters same, angle spectra are greatly modified and we observe highly sharp SPR with significantly large field enhancement as shown in Fig. 3c. Thus, the pump field strengthens the EIT effect of the control field at \(\Delta _p=-6.4\mu\)eV by compensating the losses in the SPR system.

Figure 4 shows plot of reflectivity R and field enhancement \(T_{en}\) against the metal thickness. Other parameters are the same as given in Fig. 3. SPPs undergo absorption (internal) losses \(\Gamma _{a}\) and radiation losses \(\Gamma _{r}\) owing to SPP leaking into the top medium because of the lossy nature of the metal. In Ref. [32], there is a detailed discussion of absorption and radiation losses. Radiation losses are substantially influenced by the metal layer thickness. As a result, the thickness of the metal coating is also important in the excitation of SPPs. Figure 4 shows how metal thickness q affects reflectivity R and field enhancement \(T_{en}\). The coupling strength between light and electron plasma oscillations is also affected by the thickness of the metal sheet. The coupling strength reduces as the tunneling distance of the incident probe field increases with thickness. We investigate here three coupling regimes depending on thickness. The first regime is over-coupling, and initially at small thickness values, reflectivity R is near to 1, and field enhancement has smaller value. In this regime, radiation losses \(\Gamma _{r}\) caused by SPP tunneling into the upper layer are larger than absorption losses \(\Gamma _{a}\). As we increase the metal thickness, the field enhancement gradually increases. At \(q=44\) nm, we obtain ideal coupling between light and electron plasma oscillations, and reflectivity R is absolutely zero, and field enhancement \(T_{en}\) is maximum, as illustrated in Fig. 4. When SPP radiation losses match absorption losses (\(\Gamma _{r}=\Gamma _{a}\)), the coupling strength is optimal. The destructive interaction of emitting radiation and the reflected component of incoming beam results in zero reflectivity. The coupling strength is less at greater thickness, and radiation losses \(\Gamma _{r}\) are smaller than absorption losses \(\Gamma _{a}\). As a consequence, reflectivity R increases, but field enhancement \(T_{en}\) decreases, see Fig. 4.

Fig. 4
figure 4

(Color online) Plot of reflectivity R (blue curve) and field enhancement \(T_{en}\) (green curve) against the metal thickness. Other parameters are the same as given in Fig. 3

Full size image

Figure 5 shows the reflection at different thicknesses q of the metal film. The thickness of metal film also effects the coupling strength between light and plasma oscillations of the electrons. The blue line represents optimal coupling that leads to sharp SPR resonance. The red line illustrates the weak coupling. In this case, dip in reflectivity R, therefore, it is difficult to observe SPR resonance. The orange line depicts over-coupling where dip and peak are quite broad. Thus, SPR resonance is not much sharp. Moreover, in Fig. 6 the field enhancement \(T_{en}\) spectrum has been shown at different thickness q of metal film. The blue line represents optimal coupling that leads to sharp SPR resonance. The red line illustrates the weak coupling. In this case, the field enhancement \(T_{en}\) is weak as compare to optical coupling. The orange line depicts over-coupling where field enhancement is very small in comparison to optimal coupling, therefore, it is difficult to observe SPR resonance.

Fig. 5
figure 5

(Color online) Angle spectra of reflectivity R at different thicknesses q of the metal film. \(q=44\) nm(black curve), \(q=70\) nm (green curve) and \(q=20\) nm (red curve). Other parameters are the same as given in Fig. 4

Full size image
Fig. 6
figure 6

(Color online) Angle spectra of field enhancement \(T_{en}\) at different thicknesses q of the metal film. \(q=44\) nm (black curve), \(q=70\) nm (green curve) and \(q=20\) nm (red curve). Other parameters are the same as given in Fig. 4

Full size image

4 Conclusion

In this paper, we have proposed a model for the coupler-free excitation of gain-assisted lossless SPPs using QDs with ladder-type configuration that exhibit EIT. SPPs are excited along the metal–semiconductor interface when Re\(\left[ \epsilon _d\right] < 1\). This condition can only be satisfied for probe field having small negative detunings where Im\(\left[ \epsilon _d\right]<< 1\) and SPR condition is also satisfied. When the strength of control field is \(\Omega _{c}=8\mu\)eV and in the absence of incoherent pumping, SPR effects are hardly noticeable, as shown by our analysis of the angle spectra of reflection and field enhancement. The increase in strength of control field and in the presence of incoherent pump field we obtain amplification in our system which causes the high excitation of SPPs. Thus, by applying the incoherent pumping and properly adjusting parameters, loss-free excitation of SPP can be achieved. The SPR system based on amplification in EIT for QDs has been shown to be very sensitive to probe detuning and metal film thickness. By slightly varying system parameters, SPR resonance is highly influenced. SPP based on QDs is more practical owing to the remarkable features. In conclusion, SPP can be efficiently excited along with the metal–semiconductor interface in the visible range.