1 Introduction

Rock fractures widely exist in natural rocks and strongly control the hydro-mechanical behavior of fractured rocks [1,2,3]. The fluid flow through rock fractures affects many subsurface processes and reservoirs, such as ground water contaminant and remediation [4, 5], hydrocarbon production [6, 7], geothermal extraction [8], and subsurface waste storage [9,10,11]. Rock fractures are typically rough in the nature, and the void space confined by two rough fracture walls is of complex 3D geometric morphology [12, 13]. Both fracture roughness and irregular geometric configuration of void space disturb the velocity distribution of fluid flow to be distinctly different from the parabolic flow profile of that through two smooth parallel plates [14,15,16,17,18]. To date, the linear fluid flow regime through rock fractures under the strong viscous and negligible inertial effects has been well understood [19, 20]. However, there are still many knowledge gaps regarding the nonlinear fluid flow regime under the paramount and pronounced inertial effect, where understanding the roles of fracture roughness and void space geometric morphology on the nonlinear fluid flow through 3D rock fractures is important.

The rock fractures are conventionally simplified to a pair of smooth parallel plates with a fixed aperture. The laminar fluid flow through two smooth parallel plates conforms to the well-known cubic law, where the volumetric flow rate is proportional to the cube of fracture aperture at a specific fluid pressure gradient [21, 22]. The cubic law facilitates the fluid flow calculation for laminar flow through rock fractures. However, using the cubic law to solve the fluid flow in natural rock fractures could give rise to considerable errors due to fracture aperture variation and flow pathway tortuosity [1, 23,24,25,26]. In addition, the nonlinear flow could occur at the elevated flow velocity [20, 27], where the cubic law no longer holds. The nonlinear fluid flow through tight rock fractures can be further divided into pre-linear and post-linear flow, that is, the initial pre-linear flow regime at extremely slow flow rates due to fluid slippage effect of the fracture wall and the post-linear flow regime at high flow rates due to dominant inertial effect [19, 28]. The present study only focuses on the post-linear flow and denotes it as the nonlinear flow here.

The nonlinear flow behavior of fluid flow through rock fractures has been studied extensively by theoretical derivation [29, 30], laboratory experiment [31, 32] and numerical modeling [33, 34]. Several factors triggering the nonlinear flow behavior in rough rock fractures have been identified, such as fluid pressure gradient [35, 36], fracture roughness [1, 20], fracture aperture [16, 37], mechanical shearing process [38, 39] and normal stress [12]. Intrinsically, the mechanism of the nonlinear flow regime was ascribed to coupled viscous and inertial effects, pure inertial effect and turbulence [19, 20, 27, 40]. However, the mechanism of nonlinear flow induced by different factors varies.

Fracture roughness plays an important role in the nonlinear deviation of fluid flow from linear Darcy’s law [17, 23, 41]. Generally, the fracture roughness complicates the fluid flow behavior [3, 42, 43]. However, this influence is scale-dependent [44,45,46], hinged on fracture void space geometry and related to the opening of the rock fractures as well [16, 47, 48]. In addition, fluid flow behaviors in many geological media have a scale effect [49,50,51]. For fluid flow through porous soil, the heterogeneity manifests its effect mainly through the shape and size of the pores and canaliculi at the smaller scales for soil samples, while it is mainly ascribed to the tortuosity and the interconnection of the paths and canaliculi at the major scales [51]. For fluid flow through rock fractures, the primary waviness of a fracture mostly controls the pressure field and the fluid flow paths, whereas the secondary roughness determines the nonlinear flow behaviors of the fluid flow [45]. The variation of the effect of fracture roughness on fluid flow leaves gaps in our understanding of fluid flow through rock fractures, and further investigation is required.

The mechanical normal compaction and tangential shearing are another factors deviating the linear fluid flow through rock fractures to be nonlinear [52,53,54]. When rough rock fracture is subjected to normal stress, rock fracture closes, resulting in the decrease in fracture aperture and the increase in contact area [55,56,57,58,59]. Additionally, normal compaction can cause the brittle damage of eminent asperities and smooth the fracture surfaces [60]. During shearing over rock fracture surfaces, the relative sliding between two rough fracture walls eventually enlarges the aperture and generally decreases the contact area after experiencing a short shear compaction stage [61,62,63]. Also, the shearing-off of fracture asperities can produce clogging flow [37, 64, 65]. The effects of normal compaction and tangential shearing of rock fractures on the fluid flow through rough rock fractures are complex. However, it can be attributed to the change of fracture surface roughness and the geometry configuration of void space between two confined fracture walls.

A single rock fracture consists of two rough fracture surfaces. The void space is formed between two rough fracture surfaces. For the mated rock fractures with no dislocation or shearing along rock fracture surfaces, the confined boundary of void space tends to show the matched waviness with fracture surface roughness [20, 28]. However, for the non-mated rock fractures, which may experience dislocation or shear dilation, the dislocation and the shearing-off of asperities make the two fracture walls mismatched, producing complex geometric morphology of void space [52, 60]. The void space provides the overall pathway for fluid flow through rock fractures, and the mismatched fracture surface morphology of each fracture wall influences the fluid flow process differently. The investigation of the role of geometric configuration of void space in fluid flow is important to properly understand the nonlinear deviation mechanism [66, 67]. Even though many research efforts have been made on the fluid flow regime through rock fractures, most previous studies mainly analyzed the influence of one or several factors separately, such as the fracture surface roughness, contact area, and the distribution of fracture aperture [28, 57, 68], and the effect of the geometric configuration of fracture void space on the nonlinear flow has not been well investigated.

Aiming at the aforementioned issues, the primary motivation of this study is to evaluate the influence of fracture surface roughness and geometric morphology of void space on nonlinear flow behaviors. Mated and non-mated 3D rough rock fracture models were generated using the ten sets of rough rock fracture profiles of a wide range of fracture roughness. Fluid flow through rock fractures was simulated by solving the Navier–Stokes (N–S) equations under a wide range of hydraulic gradients. The effect of fracture surface roughness and void space morphology on fluid flow in rough rock fractures is characterized by the statistical roughness parameters and fractal dimension. The evolution of flow velocity, fluid pressure distribution and the tortuosity of flow pathways in fractures were examined. Finally, some empirical models relating the statistical roughness parameters and fractal dimension with indexes characterizing nonlinear flow behavior were proposed in rough rock fractures.

2 Material and methods

2.1 Rock fracture model development

2.1.1 Rock fracture preparation and digitization

3D geometric models of rock fractures are required for numerical modeling of fluid flow. Here, the rough rock fractures were prepared in the laboratory by splitting the intact cylindrical sandstone samples into two halves using splitting wedges by referring to Barton’s rock fracture profiles [28, 69]. Then, the rock fracture surface was measured using a noncontact three-dimensional optical scanner (Cronos Dual, Open Technologies, Inc., Italy). The optical scanner has an accuracy of ± 0.02 mm in the elevation direction and ± 0.1 mm in the horizontal direction of fracture surfaces. Based on measured data, the fracture surface was digitized and is shown in Fig. 1. The digitized rock fracture surfaces were used as the parent surfaces to establish the 3D numerical fracture models. A total of ten rock fracture samples of a wide range of surface roughness were prepared and numbered from Fr1 to Fr10.

Fig. 1
figure 1

Digitized fracture surfaces in units of mm: a–j corresponding to samples Fr1–Fr10, respectively

Full size image

2.1.2 Rough fracture model establishment

The rough fracture models are established based on the digitized rock fracture surfaces as illustrated in Fig. 2. To generate the mated rock fracture samples, each rock fracture surface of an approximate length of 100 mm and a width of 50 mm is duplicated and then uplifted vertically by different distances. The mated rock fracture models (50 mm × 100 mm) were labeled in a manner of Fri-k, where the subscript i = 1–10 corresponding to ten sets of digitized rock fracture profiles, and k = 0.2, 0.4, 0.6, 0.8, 1.0 corresponding to uplift distances in the unit of mm, respectively. The non-mated rock fracture models were established by dislocating the upper and lower fracture surfaces along the horizontal length direction (x-direction). The dislocating distances of 0.5 mm and 1.0 mm were considered, and the uplift distance was fixed at 0.6 mm. The non-mated rock fracture models (50 mm × 99.5 (99.0) mm) were denoted in a manner of Fri-k-d with i = 1–10, k = 0.6 and d = 0.5 and 1.0, respectively. Note that the dislocated distance is to obtain the rock fractures of irregular geometric configuration in the fracture volumetric space, rather than the shearing process of rock fractures.

Fig. 2
figure 2

a Schematic of uplift and dislocation of fracture surface; b boundary conditions; c aperture distribution in non-mated fractures

Full size image

2.2 Numerical model

2.2.1 Governing equations and numerical methods

The fluid flow in rock fractures is governed by the well-known Navier–Stokes (N–S) equations, which is derived based on Newton’s second law and satisfies the law of momentum conservation. For the steady state, isothermal and incompressible Newtonian flow, the N–S equations and the continuity equation can be written as follows [22, 70]:

$$\rho ({\varvec{U}} \cdot \nabla ){\varvec{U}} = \mu \nabla^{2} {\varvec{U}} - \nabla P + {\varvec{F}}$$
(1)
$$\nabla \cdot {\varvec{U}} = 0$$
(2)

where ρ is the fluid density, U is the flow velocity vector, μ is the fluid viscosity, F is the body force vector, and ∇P is the pressure gradient. In Eq. (1), the term (μ·∇2U) represents the viscous force, while the term (U·∇)U represents the force component from the inertial effect caused by the change in the magnitude and direction of the fluid flow velocity, which renders the N–S equations to be nonlinear.

The N–S equations describe the fluid flow behavior well, but the nonlinearity makes the numerical computation inefficient. For simplicity, linear Darcy’s law has been developed to describe the laminar flow at the low flow velocity. The Forchheimer equation has been widely used to describe the nonlinear flow in porous and fractured media [16, 20, 30]:

$$- \nabla P = aQ + bQ^{2}$$
(3)
$$a = \frac{\mu }{{k_{0} A}} = \frac{12\mu }{{we_{h}^{3} }}$$
(4a)
$$b = \frac{\beta \rho }{{A^{{2}} }} = \frac{\beta \rho }{{w^{{2}} e_{h}^{2} }}$$
(4b)

where a is the linear term coefficient, b is the nonlinear term coefficient, Q is the volumetric flow rate, w is the fracture width normal to the flow direction, eh is the hydraulic aperture, A is the cross section area equal to ehw, and k0 is the intrinsic permeability of the rock fractures. Both coefficients a and b are related to the fluid properties and the geometric characteristics of rock fracture [16]. β is called the non-Darcy coefficient, which depends on the geometry of the fluid flow domain and the fluid inertial effect [71]. For β = 0, Forchheimer equation reduces to the linear Darcy’s law, where the inertial effect of fluid flow is negligible.

The Reynolds number Re, defined as the ratio of inertial force to viscous force, has been used to characterize the nonlinear flow in porous and fractured media [31]:

$${\text{Re}} = \frac{{\rho ve_{h} }}{\mu } = \frac{\rho Q}{{\mu w}}$$
(5)

where v is the flow velocity. According to Eq. (5), the Reynolds number increases with flow velocity. When the Reynolds number exceeds a critical value, the fluid flow transitions from linear to nonlinear flow, and the Reynolds number at the transition point is called the critical Reynolds number, which has a wide range from 1 to 2300 for rock fracture flow [27, 61]. A non-Darcy effect factor E is also employed to describe the onset of transition from linear to nonlinear flow based on Forchheimer equation (Eq. (3)) [72]:

$$E = \frac{{bQ^{2} }}{{aQ + bQ^{2} }}$$
(6)

E is the ratio of pressure gradient dissipated by the nonlinear effect to the total pressure gradient [19]. For engineering purposes, E = 0.1 has been generally proposed as a threshold [60, 72] of nonlinear effect that cannot be neglected. Combining Eqs. (4), (5) and (6), the critical Reynolds number Rec can be expressed as [16, 61]:

$${\text{Re}}_{\text{c}} = \frac{a\rho E}{{b\mu w(1 - E)}} = \frac{12E}{{\beta e_{h} (1 - E)}}$$
(7)

The Navier–Stokes equations are higher-order partial differential equations and describe the motion of viscous fluid well. However, analytical solutions to these equations do not exist. Numerical methods, such as the finite difference method (FDM), finite volume method (FVM), finite element method (FEM) and Lattice Boltzmann method (LBM), are used in computation [34, 41, 44, 45]. In the present study, the COMSOL Multiphysics was used to solve the Navier–Stokes and the continuity equations (Eqs. (1) and (2)), which has been extensively employed for multi-physics computations in the fields of rock mechanics and hydrology [18, 36, 62]. It has superior capability in dealing with problems associated with fluid dynamics, such as directly solving macroscopic flow quantities and allowing straightforward sequential coupling of different physical fields [73]. In computation, water is used as the fluid. Its density and dynamic viscosity are set to 1 × 103 kg/m3 and 1 × 10−3 Pa s, respectively.

2.2.2 Initial and boundary conditions

Once the fracture geometry model establishment is completed, it is straightforward to apply the required initial and boundary conditions for computational fluid dynamic analysis in COMSOL Multiphysics™. For all generated rock fracture models, the initial and boundary conditions were set as the same for comparison. A series of constant fluid pressures ranging from 1 to 2000 Pa was applied to the inlet of fractures, and the outlet pressure was set as zero, i.e., P = 0. The rest boundaries of the fractures were set as no fluid flow condition, and the upper and lower fracture walls were set as the no-slip boundary conditions, i.e., U = 0 m/s, as shown in Fig. 2b. Compared to the fluid pressure gradient, the hydraulic gradient due to fluid gravity is negligible. The free tetrahedral mesh element was used in all rock fractures based on its flexibility for irregular geometry and small apertures in specific locations. The maximum element size is 0.338 cm, and the minimum element is 0.0145 cm. The mesh diagram of the discretization of the fracture is shown in Fig. 2.

3 Rock fracture characterization

3.1 Fracture surface roughness characterization

The statistical parameters have been used to evaluate the rock fracture morphology, which can be directly calculated using the data coordinates of the asperity of fracture surface. The widely used statistical parameters include the root mean square of the height of the profile Rq, the peak asperity height Rz in the amplitude parameters; the root mean square of the first derivative of the profile Z2 and the standard deviation of the roughness angle σi in the textural parameters [74]

$$R_{q} = \left[ {\frac{1}{N}\sum\limits_{i = 1}^{N} {(z_{i} - z_{a} )^{2} } } \right]^{1/2}$$
(8)
$$R_{z} = z_{\max } - z_{\min }$$
(9)
$$Z_{2} = \left[ {\frac{1}{N - 1}\sum\limits_{i = 1}^{N - 1} {\frac{{(z_{i + 1} - z_{i} )^{2} }}{{(x_{i + 1} - x_{i} )^{2} }}} } \right]^{1/2}$$
(10)
$$\sigma_{i} = \tan^{ - 1} \left[ {\frac{1}{L}\int_{x = 0}^{x = L} {\left( {\left| {\frac{{{\text{d}}z}}{{{\text{d}}x}}} \right| - \tan \theta } \right)^{2} {\text{d}}x} } \right]^{1/2}$$
(11)
$$\theta = \frac{1}{L}\int_{x = 0}^{x = L} {\tan^{ - 1} \left| {\frac{{{\text{d}}z}}{{{\text{d}}x}}} \right|} {\text{d}}x$$
(12)

where L is the projected length of fracture profile, zi is the asperity height at point i, N is the number of sampling points, za is the distance of profile from the mean elevation line, zmax is the maximum asperity height, zmin is the minimum asperity height, (xi, zi) and (xi+1, zi+1) are the coordinate of adjacent points on the fracture profile, dz is the increment of z of the profile, dx is the increment of x of the profile, and θ is the average roughness angle of the profile.

In addition, the JRC was also calculated by an empirical equation [75]:

$${\text{JRC}} = 32.2 + 32.47\log Z_{2}$$
(13)

For calculation of statistical roughness parameters and JRC, nine equally spaced fracture profiles were extracted from each rock fracture surface along the direction parallel to the flow direction. Table 1 lists the averaged roughness parameters and JRC over the nine profiles. The fracture surface of Fr2 has the largest JRC to be 17.0. In contrast, the surface morphology of Fr1 is relatively smooth with a JRC of 7.6.

Table 1 The roughness parameters and JRC of different fracture surfaces
Full size table

3.2 Fracture void space characterization

The fracture void space was formed between the confined upper and lower fracture walls as shown in Fig. 3. The geometry of fracture void space exhibits self-similar characteristics, which can be quantified by the fractal dimension [76]. The triangular prism surface area method (TP) is an effective method to evaluate the fractal dimension in Euclidean space based on the measurement of the fracture surface area at different grid sizes [77, 78] and is used in the present study. The fractal dimension calculated with TP method can mirror the heterogeneity of the fracture geometry morphology. For a square grid with a side length of δ on the horizontal plane, its four corners correspond to four points on the fracture surface in the elevation direction forming an element as shown in Fig. 4. The elevation at the center of the grid cell (h0) is determined by the elevations of the adjacent four points. Four triangles are formed by connecting each corner elevation with the center elevation. Therefore, the total area of an element with grid cell-sized of δ × δ is equal to the sum of the areas of four triangles:

$$S_{i, j} = S_{1} + S_{2} + S_{3} + S_{4}$$
(14)
Fig. 3
figure 3

Schematic of the fracture void space geometry (a two-dimensional section)

Full size image
Fig. 4
figure 4

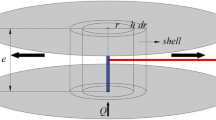
Schematic diagram of the triangular prism surface area method (modified after Clarke [77]). δ is the grid size, S1, S2, S3 and S4 represent the areas of four triangles; (i, j), (i, j + 1), (i + 1, j) and (i + 1, j + 1) are, respectively, the coordinates of the four points of the prism, h(0) denotes the elevation at the center of the grid cell, and h(i, j), h(i, j + 1), h(i + 1, j) and h(i + 1, j + 1) are the elevations of the four points, respectively

Full size image

Taking the area of triangle S1 as an example, the calculation method is as follows:

$$S_{1} = \sqrt {l_{1} (l_{1} - a_{1} )(l_{1} - b_{1} )(l_{1} - c_{1} )}$$
(15)

where

$$\begin{aligned} l_{1} & = \frac{1}{2}(a_{1} + b_{1} + c_{1} ), \\ a_{1} & = \sqrt {[h(i,j) - h(i,j + 1)]^{2} + \delta^{2} } \\ b_{1} & = \sqrt {[h(i,j) - h_{0} ]^{2} + \left( {\frac{\sqrt 2 }{2}\delta } \right)^{2} } \\ c_{1} & = \sqrt {[h(i,j + {1}) - h_{0} ]^{2} + \left( {\frac{\sqrt 2 }{2}\delta } \right)^{2} } \\ \end{aligned}$$
(16)
$$h_{0} = \frac{1}{4}[h(i,j) + h(i,j+ 1) + h(i + 1,j) + h(i + 1,j + 1)]$$
(17)

Similarly, the areas of the other three triangles (S2, S3 and S4) can be calculated. The total area of the fracture surface can be obtained by:

$$S(\delta ) = \sum\limits_{i,j = 1}^{N(\delta )} {S_{i,j} }$$
(18)

where N(δ) is the number of total grid cells with δ × δ in dimension. If the dimension δ changes, the measured area of the fracture surface also change, and their functional relationship can be described by [77]:

$$S(\delta ) = \chi (\delta^{2} )^{2 - D}$$
(19)

where D is the fractal dimension of fracture surface, and χ is a coefficient. However, Eq. (19) cannot be directly used to calculate D. By transformation, D can be expressed in a logarithmic form:

$$\ln(S(\delta )) = (2 - D)\ln (\delta^{2} ) + \ln (\chi )$$
(20)

Therefore, the fractal dimension D of the fracture void space morphology can be obtained by linear regression analysis.

Based on analysis above, the fracture void space is mainly determined by the elevation of the upper and lower fracture walls. Figure 5 shows the void space morphology of rock fractures dislocated by 0.5 mm. When the rock fractures were dislocated by 0.5 mm, a negligible amount of contact area (less than 0.5%) was developed in every individual rock fracture. The surface areas (S(δ)) of fracture void space morphology are calculated through TP with each grid size (δ) ranging from 0.1 to 0.8 mm, i.e., δ = 0.1 mm, 0.2 mm, 0.4 mm, 0.6 mm, 0.8 mm in the present study.

Fig. 5
figure 5

The morphology of void space of the non-mated fracture models dislocated by 0.5 mm: a–j corresponding to fracture models Fr1-0.6-0.5 to Fr10-0.6-0.5, respectively (all dimensions are in units of mm)

Full size image

Figure 6 shows the relationship between fracture surface area (S(δ)) and the square of grid size (δ), where the fractal dimension (D) is calculated based on the slope of the regression line using Eq. (20). This method has also been used by other researchers to characterize the fracture surface morphology [77,78,79,80,81]. Table 2 lists the fractal dimension (D) of the morphology of fracture void space, which varies from 2.01 to 2.35. The maximum of D is 2.3519 for the rock fracture model Fr10-0.6-0.5, while the minimum of D is 2.0126 for the rock fracture model Fr1-0.6-0.5. Even though the surface roughness of the parent fracture surfaces forming fracture models Fr1-0.6-0.5 and Fr2-0.6-0.5 differs very much (JRC = 7.6 for Fr1, JRC = 17.0 for Fr2), their fractal dimension D values are close and small in magnitude. This indicates that the two rock fracture models have good similarity in void space morphology. It also shows the heterogeneity of the fracture void space morphology of a rock fracture with relatively large surface roughness is not necessarily large after dislocation. In addition, the root mean square of the height of the profile (Rq) and the standard deviation of the roughness angle (σi) of the fracture void space morphology were also calculated to verify the suitability of the fractal dimension. The Rq and σi of void space morphology of the non-mated fracture models above were calculated at 0.5 mm sampling interval using Eqs. (8) and (11) and are listed in Table 2. Obviously, the Rq and σi increase with the increase of D. Figure 7 shows linear relationships exist between D and σi, and between D and Rq, with correlation coefficients of 0.87 and 0.9836, respectively. Therefore, the fractal dimension D calculated by the TP method is capable of characterizing the fracture void space morphology.

Fig. 6
figure 6

Logarithmic relationship between fracture surface area (S(δ)) and the square of grid size (δ) estimated by the triangular prism surface area method

Full size image
Table 2 Fractal dimension and roughness parameters of the void space morphology of the fracture models Fr(1–10)-0.6-0.5
Full size table
Fig. 7
figure 7

Correlation analysis between fractal dimension D of fracture void space morphology and statistical parameters Rq and σi, respectively

Full size image

4 Results and discussion

4.1 Fluid flow characteristics

4.1.1 Flow velocity distribution

Figure 8 shows the sliced contour of principal velocities of water flow through mated and non-mated rock fractures along the x- and y-directions, in which \(U = \sqrt {u_{x}^{2} + u_{y}^{2} + u_{z}^{2} }\). Figure 8a–d shows the velocity fields for water flow through mated rock fractures of Fr3-0.6, Fr3-1.0, Fr8-0.6 and Fr8-1.0 under the inlet pressure of 1000 Pa. Comparing the results of the rock fractures Fr3-0.6 and Fr3-1.0, fluid flow velocity increased significantly with the increase in fracture aperture. In addition, the flow velocity distribution in rock fracture Fr3-1.0 was more homogeneous than that of rock fracture Fr3-0.6 (Fig. 8a, b), which indicates that the narrowing of the fluid flow channel in rough rock fractures increases the tortuosity of flow. Similar results can also be observed in rock fractures Fr8-0.6 and Fr8-1.0 (Fig. 8c, d). Comparing rock fracture Fr3-0.6 (JRC = 10.1) with Fr8-0.6 (JRC = 14.1), the flow velocity distribution of rock fracture Fr8-0.6 was more heterogeneous and significantly channelized than that of rock fracture Fr3-0.6 as shown in Fig. 8a, c. Also, the low-velocity flow zones of rock fracture Fr8-0.6 concentrated more significantly around relatively large surface undulations (e.g., peaks or valleys), where the flow tortuosity increased due to fracture roughness. Therefore, the larger the fracture roughness, the more the inhomogeneity of the flow velocity distribution for rock fractures of equivalent fracture aperture. In addition, the difference of the homogeneity of the flow velocity distribution between the rock fractures of Fr3-1.0 and Fr8-1.0 is lower than that of between the rock fractures of Fr3-0.6 and Fr8-0.6 (Fig. 8a–d), illustrating that the influence of fracture roughness on fluid flow in rock fractures weakens with the aperture increase.

Fig. 8
figure 8

Three-dimensional principal velocity field for mated and non-mated fractures under the inlet pressure of 1000 Pa. Mated fracture models: a Fr3-0.6, b Fr3-1.0, c Fr8-0.6, and d Fr8-1.0; non-mated fracture models: e Fr3-0.6-0.5, f Fr3-0.6-1.0, g Fr8-0.6-0.5, and h Fr8-0.6-1.0

Full size image

Figure 8e–h shows the principal velocity field of water flow through non-mated fracture models of Fr3-0.6-0.5, Fr3-0.6-1.0, Fr8-0.6-0.5 and Fr8-0.6-1.0 under the inlet pressure of 1000 Pa. In Fig. 8e, f, the flow velocity distribution in rock fracture Fr3-0.6-1.0 was channelized and distorted more significantly than that of the rock fracture Fr3-0.6-0.5. This is ascribed to that the fracture surface dislocation results in the heterogeneity increase of the fracture void space morphology and the appearance of contact areas at some locations. This led to the principal velocity field of fluid flow through the non-mated rock fractures to be more complex (Fig. 8c, h). The low-velocity flow zones (blue-colored areas) increased due to the decrease in local aperture. For non-mated rock fractures, not only the flow tortuosity increased, but also eddy flow occurred around the contact spots. This locally developed eddy flow affects the overall fluid flow behavior through rock fractures by intensifying the inertial effect and further leads to more pressure head loss, facilitating the nonlinear fluid flow deviation.

4.1.2 Streamline distribution

Figure 9 shows the streamline distribution of different rock fractures. As shown in Fig. 9a, b, e, f, the streamlines of mated rock fractures were generally homogenous along the principal flow direction, in spite of small-scale tortuosity. In contrast, significant heterogeneity of streamline distribution with considerable channeling phenomenon was observed in the non-mated rock fractures as shown in Fig. 9c, d, g, h.

Fig. 9
figure 9

Top view of the streamlines of flow in the 3D rough fractures under the inlet pressure of 1000 Pa. Fractures models: a Fr3-0.6, b Fr3-1.0, c Fr3-0.6-0.5, d Fr3-0.6-1.0, e Fr8-0.5, f Fr8-1.0, g Fr8-0.6-0.5, and h Fr8-0.6-1.0

Full size image

Figure 9a, b shows the streamline distribution of rock fracture Fr3-1.0 was more homogenous than that of rock fracture Fr3-0.6, demonstrating that the flow tortuosity decreased with the increase in fracture aperture. The streamlines of rock fracture model Fr8-0.6 were more tortuous than that of Fr3-0.6 as shown in Fig. 9a, e. Therefore, the flow pathways become more tortuous with the increase in fracture roughness for the mated rock fractures of equivalent fracture aperture.

Complex channeling flow occurred and preferential flow pathways appeared in the non-mated rock fractures, such as Fr3-0.6-1.0 and Fr8-0.6-1.0. Also, the eddy flow was observed around the contact asperities as shown in Fig. 9d, h. The presence of the eddy flow reduces the effective flow channel and enhances the energy dissipation [44, 82]. With the increase in dislocation distance, the streamlines were channelized more significantly as plotted in Fig. 9c, d, which is mainly due to the increase in the contact asperities and the morphology heterogeneity of fracture void space. Moreover, the irregular geometry of the fracture void space impacts the flow behavior more significantly than surface roughness in open rock fractures.

The streamline distribution of rock fractures can be a measure for the tortuous degree of flow pathways and reflect the flow resistance too. When the fluid flows through the mated rock fractures with equivalent aperture distribution, the fluid flow is insignificantly obstructed, demonstrating low flow resistance. For the non-mated rock fractures, the dislocation of upper and lower halves of rough rock fractures results in mismatched morphology between two confined walls of fracture void space, inducing high flow resistance and energy loss. Also, the eddy flow occurred around the contact asperities, increasing the inertial effect of fluid flow and promoting nonlinear flow in rough rock fractures.

4.1.3 Fluid pressure distribution

Figure 10 shows fluid pressure distribution of water flow through mated and non-mated rock fractures under the inlet pressure of 1000 Pa. The fluid pressure exhibits a non-uniform distribution within the fractures due to fracture surface roughness, contact area and the irregular configuration of fracture void space. The distribution of fluid pressure fields has not been significantly changed with the increase in fracture aperture as plotted in Fig. 10a, b (corresponding to rock fractures Fr3-0.6 and Fr3-1.0). Similarly, the difference in the fluid pressure distribution in the rock fractures caused by the difference of fracture roughness is not obvious. However, the non-uniformity of fluid pressure distribution slightly increased with the heterogeneity of fracture void space as shown in Fig. 10c, h (corresponding to rock fracture models Fr8-0.6 and Fr8-0.6-1.0), despite the identical surface roughness of two rock fracture models.

Fig. 10
figure 10

Fluid pressure field for mated and non-mated fractures under the inlet pressure of 1000 Pa. Mated fracture models: a Fr3-0.6, b Fr3-1.0, c Fr8-0.6, and d Fr8-1.0; non-mated fracture models: e Fr3-0.6-0.5, f Fr3-0.6-1.0, g Fr8-0.6-0.5, and h Fr8-0.6-1.0

Full size image

To further explore the evolution of fluid pressure, the fluid pressure variation along the monitoring lines parallel to the x-axis and y-axis direction was quantified. Figure 11b, c shows the variation of the normalized fluid pressure of rock fractures Fr8-0.6 and Fr8-0.6-0.5 along the monitoring profile Y = 25 mm under the inlet pressure of 1000 Pa. The fluid pressure is normalized as the ratio of the monitored inner fluid pressure P to the constant inlet pressure Pinlet. It can be observed that the fluid pressure along the fluid flow direction decreased slightly in a nonlinear manner. Moreover, the degree of non-linearity increased significantly for the dislocated fracture. Figure 11d, e shows the variation of the monitored inner fluid pressure along the monitoring line X = 50 mm under the inlet pressure of 1000 Pa. Constrained by fracture surface roughness and geometric heterogeneity of fracture void space morphology, fluid pressure fluctuated significantly along the direction perpendicular to the flow direction. This is distinctly different from the general assumption of equal pressure gradient.

Fig. 11
figure 11

a Locations of the monitoring lines parallel with the X-axis and Y-axis, respectively, in the middle of the mated fracture model Fr8-0.6 and the non-mated fracture model Fr8-0.6-0.5 and Y = 25 mm and X = 50 mm, respectively, b, c the variation in the normalized fluid pressure along the profile Y = 25 mm in Fr8-0.6 and Fr8-0.6-0.5, respectively, under the inlet pressure of 1000 Pa, d, e the variation in fluid pressure along the profile X = 50 mm in Fr8-0.6 and Fr8-0.6-0.5, respectively, under the inlet pressure of 1000 Pa

Full size image

4.2 The nonlinear fluid flow behavior

4.2.1 The nonlinear relationship between fluid pressure and flow rate


Figure 12 shows the relationship between the pressure gradient (∇P) and the volumetric flow rate (Q) for the mated and non-mated rock fractures under different inlet fluid pressures. With the increase in pressure gradient, the nonlinear flow occurred. The best-fitting with the Forchheimer equation shows R2 exceeds 0.99 for each case. Also, the slopes of both linear and nonlinear portions became steeper with the decrease in fracture aperture for mated fractures as shown in Fig. 12a–j, indicating the flow resistance increased with the decrease in fracture aperture. However, the slopes of both linear and nonlinear portions were fairly close for most mated rock fractures of the same aperture, illustrating that the effect of the surface roughness on flow resistance is not as significant as that of fracture aperture in the mated rock fractures without contact area. The slopes of both linear and nonlinear portions among different non-mated fractures are not equal, despite these fracture models having the same initial aperture (Fig. 12k). This is mainly due to the combined effect of the surface roughness and the mismatched geometry of the fracture void space. In addition, comparing the curves of ∇P versus Q of the mated and non-mated fractures of the same initial mechanical aperture and fracture surface roughness, the discharge of the mated rock fractures was significantly larger than that of the non-mated rock fractures under the same hydraulic gradient as plotted in Fig. 13. This is mainly ascribed to the decrease in the effective aperture, as the mismatched configuration of fracture void space increases the flow resistance of the non-mated rock fractures.

Fig. 12
figure 12

The relation of pressure gradient (∇P) against numerical-obtained volumetric flow rate (Q) using Forchheimer equation, a–j correspond to the models of mated fractures Fr1–Fr10, respectively, (k) non-mated fracture models Fr(1–10)-0.6-0.5 (solid lines refer to the fitting curves using the Forchheimer equation, k represents mechanical aperture)

Full size image
Fig. 13
figure 13

Comparison of pressure gradient (∇P) against volumetric flow rate (Q) changes in different fracture models, a–j correspond to mated fracture models Fr(1–10)-0.6 and non-mated fracture models Fr(1–10)-0.5-0.6, respectively

Full size image

Figure 14 shows the variation of coefficients a and b for the mated rock fractures with the aperture of 0.6 mm and the non-mated fractures with the aperture of 0.6 mm and dislocation distance of 0.5 mm. Although the mated and non-mated rock fractures have the same initial mechanical aperture, both a and b are variable due to the difference of fracture roughness and geometric morphology of void space. Due to the mismatch of two confined fracture surfaces, the change of a and b is more significant in the non-mated rock fractures, indicating that the pressure loss in the non-mated rock fractures is more than that of mated fractures due to the complex geometric morphology of fracture void space. Therefore, the irregular geometry of the fracture void space enhances the inertial effect of fluid flow, facilitating nonlinear flow.

Fig. 14
figure 14

Comparison of linear coefficient a and nonlinear coefficient b in Forchheimer equation for mated and non-mated fractures with initial aperture of 0.6 mm

Full size image

4.2.2 The nonlinear coefficient b and the critical Reynolds number in mated fracture

According to Eq. (4b), the nonlinear coefficient b is determined by the non-Darcy coefficient (β) and fracture aperture under the circumstance of constant fluid properties. Note that β mainly depends on the geometry of the fluid flow domain [20, 71] and the fracture aperture is also related to fracture roughness [83]. Louis [84] established the relationship between the non-Darcy coefficient (β) and the hydraulic aperture eh and the peak asperity Rz of the fracture surface:

$$\beta = \frac{1}{{8e_{h} }}\left( {\log c - \log \frac{{R_{z} }}{{2e_{h} }}} \right)^{ - 2}$$
(21)

where c is a coefficient dependent on the surface roughness index, defined as the ratio of the peak asperity height of the fracture surface to the hydraulic aperture \(\left( {\frac{{R_{z} }}{{e_{h} }}} \right)\). Since then, several quantitative models have been proposed for b or β [20, 57, 60, 71, 85]. In the established conceptual models, the peak asperity height is commonly used to characterize the geometric attributes of fracture surface, which is a representative roughness parameter and easy to estimate. Nevertheless, Rz mainly reflects the maximum fluctuation of the asperity on the fracture surface, and it could not reflect the whole information of the asperity distribution. Moreover, the texture characteristics of the asperity have significant influence on fluid flow through rough rock fractures. For example, a larger inclination angle of fracture surface asperity could bring more violent nonlinear flow and result in the eddy flow [86]. Motivated by Eq. (21), a power-law relation for the nonlinear coefficient b based on Eq. (4b), containing the amplitude parameter Rz and textural parameter Z2 of fracture surface roughness, is proposed here:

$$b = m\frac{1}{{e_{h} }}\frac{\rho }{{w^{2} e_{h}^{2} }}\left( {\frac{{R_{z} \times Z_{2} }}{{e_{h} }}} \right)^{n} = m\frac{\rho }{{w^{2} e_{h}^{3} }}(Z_{2} )^{n} \left( {\frac{{R_{z} }}{{e_{h} }}} \right)^{n}$$
(22)

where m and n are regression coefficients. The roughness parameter Z2 was used to describe the influence of the asperity inclination angle of the fracture surface on the nonlinear flow. In Eq. (22), the influence of both amplitude and texture characteristics of the asperity distribution on fracture surface on the nonlinear fluid flow regime was quantified. Here, the roughness parameters directly representing the inclination angle of the asperity, such as the average roughness angle of the profile θ and the standard deviation of the roughness angle (σi), are not considered. One reason is that θ and σi are in unit of degrees, and it is inconvenient to eliminate this angle dimension in the proposed model. The other reason is that Z2, as a dimensionless roughness parameter, can characterize the fracture surface roughness well, and meanwhile, it has a close mathematical relationship with the angle parameter [74]. Figure 15 shows the variation in σi and θ with respect to Z2 for different rough rock fracture surfaces. It can be clearly seen that the two parameters have a strong linear correlation for the same fracture surface (R2 > 0.98).

Fig. 15
figure 15

Correlation analysis between Z2 and σi and θ, respectively

Full size image

Figure 16 shows the best-fitting curves with respect to the coefficient b against the hydraulic aperture eh for the mated rock fractures, where the hydraulic aperture eh can be calculated using Eq. (4a) (\(e_{h} = (12\mu /a/w)^{1/3}\)). Based on the proposed Eq. (22) for the mated rock fractures, the regression coefficients m and n were calculated, which falls in a range of 0.0498–0.3568 and − 0.8872 to − 0.4502, respectively. In addition, the coefficient of determination R2 is greater than 0.99, validating the proposed equation in characterizing the effect of fracture surface roughness on the nonlinear flow in rough rock fractures.

Fig. 16
figure 16

The nonlinear factor b as a function of the hydraulic aperture using Eq. (22), a–j corresponding to the mated fractures Fr1–Fr10, respectively

Full size image

Furthermore, the critical Reynolds number Rec to identify the onset of transition from linear to nonlinear fluid flow can be determined by substituting Eqs. (22) and (4a) into Eq. (7):

$${\text{Re}}_{{\text{c}}} = \frac{{12Ee_{h}^{n} }}{{m(1 - E)(R_{z} \times Z_{2} )^{n} }}$$
(23)

By substituting the regression coefficients m and n of Eq. (22) into Eq. (23), and taking E = 0.1 [19, 72], the critical Reynolds number for the onset of the nonlinear fluid flow can be calculated for rough rock fractures. The measured results of Rec are determined using Eq. (7) for comparison. Figure 17 shows the measured and predicted values of the critical Reynolds number Rec in terms of the hydraulic aperture eh for the mated rock fractures. It can be seen that the predicted Rec is in a good agreement with the measured ones. Figure 17 also shows that the critical Reynolds number Rec decreased with the increase in hydraulic aperture.

Fig. 17
figure 17

Comparison of the theoretical results of Rec versus eh with the models predictions by Eq. (22) for mated fractures

Full size image

4.2.3 The nonlinear coefficient b and the critical Reynolds number in non-mated fractures

The empirical equation can predict the nonlinear coefficient b in the Forchheimer equation based on fracture surface roughness parameters Z2, Rz and the hydraulic aperture eh for the fluid flow through mated rock fractures. However, the mismatch of two confined fracture walls in the non-mated rock fractures makes the geometric morphology of void space complex. As analyzed previously, the morphology of fracture void space can be characterized by the fractal dimension D. Figure 18 shows the variation of the nonlinear coefficient b with respect to the fractal dimension D of fracture void space morphology. Clearly, b is not uniquely dependent on D. An extended power-law relationship for b is proposed for the non-mated rock fractures:

$$b = m_{1} \frac{1}{{e_{h} }}\frac{\rho }{{w^{2} e_{h}^{2} }}\left( {\frac{{R_{z} \times Z_{2} }}{{e_{h} }}} \right)^{{n_{1} }} D^{p} = m_{1} \frac{\rho }{{w^{2} e_{h}^{3} }}\left( {\frac{{R_{z} \times Z_{2} }}{{e_{h} }}} \right)^{{n_{1} }} D^{p}$$
(24)

where m1, n1 and p are dimensionless coefficients.

Fig. 18
figure 18

The variation in the nonlinear coefficient (b) against the fractal dimension (D) for non-mated fractures

Full size image

Figure 19 shows the relationship between b and the variables Z2, Rz, eh and D. Using the Levenberg–Marquardt optimization algorithm, the dimensionless coefficients in Eq. (24) are determined, where m1 = 1.087e−4, n1 =  − 0.6592 and p = 8.969 with the coefficient of determination R2 = 0.6826.

Fig. 19
figure 19

Regression analysis of the nonlinear coefficient (b) as a function of the fractal dimension D of fracture void space morphology and roughness parameter Z2 and Rz of fracture surface by Eq. (24) for non-mated fractures

Full size image

Combining Eqs. (4a), 7 and (24), the critical Reynolds number equation can be calculated:

$${\text{Re}}_{{\text{c}}} = \frac{{12Ee_{h}^{{n_{1} }} }}{{m_{1} (1 - E)(R_{z} \times Z_{2} )^{{n_{1} }} D^{p} }}$$
(25)

Substituting the regression coefficients m1, n1 and p into Eq. (25), and taking E = 0.1, the critical Reynolds number for the onset of nonlinear fluid flow was calculated non-mated rough rock fractures falling in a range from 7.1 to 69.0. Figure 20 shows the comparison of the measured and predicted values of the critical Reynolds number Rec calculated by Eqs. (7) and (25) in terms of the fractal dimension. It can be seen that the predicted Rec agrees well with the measured ones. Figure 20 also shows that the critical Reynolds number Rec generally decreased with the increase in fractal dimension D of fracture void space morphology, even though the variation in Rec is also influenced by fracture aperture and the magnitude of the total inertial effect [3, 87, 88]. Nonetheless, it could be expected that the larger the fractal dimension D is, the smaller the critical Reynolds number Rec for the onset of nonlinear fluid flow in rock fractures while remaining other factors invariable. This indicates that the onset of nonlinear fluid flow in rock fractures of mismatched void space morphology is much earlier than that of mated ones.

Fig. 20
figure 20

Comparison of the theoretical results of Rec versus D with the models predictions by Eq. (25) for non-mated fractures

Full size image

5 Conclusions

The influence of fracture roughness and void space morphology on the nonlinear fluid flow through rough rock fractures was investigated by conducting fluid dynamic computation. The mated and non-mated rough-walled fracture models were established based on digitized sandstone fractures with a wide range of fracture roughness.

The fractal dimension D with the triangular prism surface area method was used to characterize to the morphology of fracture void space, which shows a positive correlation with either the root mean square of the height of the fracture void space morphology or the standard deviation of roughness angle. The fluid dynamic computation shows that fracture surface roughness and void space morphology significantly affect the nonlinear flow. The heterogeneity of fluid flow increased with fracture roughness, resulting in the tortuous flow pathways. Nevertheless, such influence of fracture roughness on the flow behavior is gradually weakened with the increase in aperture. After the rock fracture is dislocated, the preferential flow path becomes significant and eddy flow occurred obviously, promoting the nonlinear flow. The Forchheimer equation describes the nonlinear fluid flow through mated and non-mated rock fractures well. In contrast, the linear coefficient a and nonlinear coefficient b of Forchheimer equation for fluid flow through non-mated fractures are generally greater than those of mated ones, even though with the same initial mechanical aperture and surface roughness.

For mated rock fractures, a power-law relationship was proposed to quantify the nonlinear coefficient b in terms of fracture peak asperity Rz, the first derivative of the profile Z2 and fracture aperture eh, and then, the critical Reynolds number for the onset of nonlinear fluid flow was derived. To further describe the influence of fracture void space morphology on the nonlinear fluid flow through non-mated rock fractures, an extended power-law model was proposed by quantifying b in terms of fracture roughness parameters Rz, Z2, aperture eh and fractal dimension of void space D, and the critical Reynolds number to demark the onset of nonlinear flow was subsequently derived. The predicted critical Reynolds number agrees well with that of fluid dynamic computation for both mated and non-mated rock fractures, validating the proposed power-law and extended power-law relationships. Our research also shows that the critical Reynolds number for the onset of nonlinear flow generally decreased with the increase in fractal dimension D of fracture void space morphology.

This study aims to analyze the role of fracture geometry (including fracture roughness and void space morphology) in nonlinear fluid flow through a single rock fracture, and the proposed empirical formula allows a more reliable quantitative prediction for evaluating the nonlinear fluid flow in rock fractures. The findings can also be expected to promote an understanding of the role of fracture geometry in nonlinear flow within rough fractures. Given the primary interest of this research, the scaling effect of the characteristic parameters describing hydraulic behavior in rock fractures is not considered during quantitative analysis and will be performed in the near future.