1 Introduction

We extend the robust inverse scattering transformation method to investigate the derivation of the various exact solution formulae for an integrable fifth-order mKdV (modified Korteweg-de Vries) equation introduced by Ito in [1]

$$\begin{aligned} u_t+30u^4u_x+10u_x^3+40uu_xu_{xx}+10u^2u_{xxx}+u_{xxxxx}=0, \end{aligned}$$
(1.1)

where \(u=u(x,t)\) is a real function. This equation is the second member from the mKdV hierarchy, and its many integrable properties and exact solutions have been studied, such as the Bäcklund transformation and N-soliton solution [1], periodic wave solutions [2], one-pole soliton and breather on a nonzero constant background [3], rogue periodic waves [4], multi-breathers and double-pole solution in bilinear form [5]. Moreover, the long-time asymptotic behavior of solutions for Cauchy or half-line problem has been considered in [6,7,8,9] based on the nonlinear steepest descent method of Deift and Zhou [10].

It is well known that the standard inverse scattering transform provides a powerful approach to discover soliton solutions of some integrable evolution equations with initial value problems. In particular, each initial datum from an appropriate function space can generate a set of scattering data, consisting of poles and norming constants encoding solitons, as well as a reflection coefficient encoding radiation. The multiple-pole soliton is a reflectionless solution with scattering data consisting of a complex-conjugate pair of poles order \(N\ge 2\), which have very different qualitative behavior than standard solitons. Moreover, the construction of rational solutions for integrable nonlinear equations also has been becoming a topic of continued interesting in the description of rogue waves, which are known as large-amplitude spatiotemporally localized disturbances of a uniform background state and can cause damage to ships and fixed structures such as oil drilling platforms. Although multiple-pole solitons and rogue wave solutions have been studied in the above-mentioned literature; however, to the best of our knowledge, none of these solutions have been found directly as the solution of a Cauchy problem of (1.1) via an inverse scattering transform in the form of an associated matrix RH (Riemann–Hilbert) problem. Thus, in present paper, we aim to derive the multiple-pole soliton and rational solutions of Eq. (1.1) by means of the robust inverse scattering transform method. The so-called robust inverse scattering transform was recently introduced by Bilman and Miller in [11] to recapture the rogue wave solutions for the focusing NLS (nonlinear Schrödinger) equation. The key element of this approach is to modify the usual RH problem and combine it with the Darboux transformation. Once getting a representation formula for the rogue wave solution in terms of the solution of the RH problem, one immediately can use the nonlinear steepest descent method of Deift–Zhou [10] to analyze the properties of the solution in the limit of infinite order. In particular, for the focusing NLS equation with initial data satisfying nonzero constant background at infinity, the authors [12] studied the fundamental rogue wave solutions in the limit of large order. Under the zero boundary condition, the large-order asymptotics for multiple-pole solitons of focusing NLS equation was analyzed in [13, 14]. Moreover, it is interesting to note that the robust inverse scattering transforms for the Hirota and generalized NLS equation were performed in [15,16,17], wherein various exact solutions such as breathers and rogons have been derived. Thus, from a mathematical viewpoint, as a potential application, our results will provide a direct way to study asymptotic properties of these multiple-pole soliton and rational solutions such as their behaviors in the limit of high order. On the other hand, from the physical viewpoints, the multiple-pole soliton will play an important role to disclose the formation of very high waves [18], and the rational solutions for the fifth-order mKdV Eq. (1.1) plays the role of rogue waves and can present different descriptions in hydrodynamics from that in the NLS equation. Besides, it is noted that these rational solutions may appear in the electromagnetic waves in quantized films, internal waves in stratified flows [19] and so on. Finally, these solutions will undoubtedly be useful and will give insight in modeling nonlinear wave processes in various other physical systems.

To achieve our goal, we study the Cauchy problem of Eq. (1.1) by specifying an initial condition u(x, 0) which satisfies the nonzero boundary conditions at infinity, i.e.,

$$\begin{aligned} \lim _{x\rightarrow \pm \infty }u(x,0)=c, \end{aligned}$$
(1.2)

where \(c\ne 0\) is a real constant. Obviously, \(u(x,t)\equiv c\) is an exact solution of (1.1). According to [3], we learn that the Lax pair system of Eq. (1.1) with the background field \(u=u_{bg}(x,t)\equiv c\) admits a fundamental solution:

$$\begin{aligned} \begin{aligned} \Psi _{bg}(x,t;z)&={\mathcal {E}}(z)\text {e}^{\text {i}\theta (x,t;z)\sigma _3},\ {\mathcal {E}}(z)=\begin{pmatrix} 1 &{}~ \frac{\text {i}(\rho (z)-z)}{c}\\ \frac{\text {i}(\rho (z)-z)}{c} &{}~ 1 \end{pmatrix},\ \rho (z)=\sqrt{z^2+c^2},\\ \theta (x,t;z)&=\rho (z)[x+(-16 z^4+8 c^2z^2-6 c^4)t],\ \sigma _3=\begin{pmatrix} 1 &{} 0\\ 0 &{} -1 \end{pmatrix}. \end{aligned} \end{aligned}$$
(1.3)

Denote \({\Gamma }\doteq {\mathbb {R}}\cup \text {i}[-c,c]\). Define the scattering matrix s(z) determined by the initial value u(x, 0) for \(z\in {\Gamma }\setminus \{\pm \text {i}c\}\) by

$$\begin{aligned} s(z)=\begin{pmatrix} A(z) &{}~ -\overline{B(\bar{z})}\\ B(z) &{}~ \overline{A(\bar{z})}\\ \end{pmatrix}. \end{aligned}$$
(1.4)

Then, the solution u(x, t) of this initial-value problem can be solved in terms of the solution of the following RH problem:

Riemann–Hilbert Problem 1. Find an analytic function m(x, t; z) on \({\mathbb {C}}\setminus {\Gamma }\) with the following properties:

\(\bullet\) The jump condition: For each \(z\in {\Gamma }\), the continuous boundary values \(m_{\pm }(x,t;z)=\lim _{\varepsilon \uparrow 0}m(x,t;z\pm \text {i}\varepsilon )\) satisfy the jump relation

$$\begin{aligned} m_+(x,t;z)=m_-(x,t;z)J(x,t;z), \end{aligned}$$
(1.5)

with the jump matrix J(x, t; z) defined by

$$\begin{aligned} J(x,t;z)=\left\{ \begin{aligned}&\begin{pmatrix} \frac{1}{d(z)}(1+|r(z)|^2) ~&{} r(z)\text {e}^{2\text {i}\theta (x,t;z)}\\ \overline{r(z)}\text {e}^{-2\text {i}\theta (x,t;z)}~ &{} d(z) \end{pmatrix},\qquad \qquad \qquad z\in {\mathbb {R}}\setminus \{0\},\\&\begin{pmatrix} -\frac{\rho (z)-z}{\text {i}c}r(z)\text {e}^{2\text {i}\theta (x,t;z)} &{}~ \frac{2\rho (z)}{\text {i}c}\\ \frac{c}{2\text {i}\rho (z)}(1+r(z)\overline{r(\bar{z})}) &{} -\frac{\rho (z)+z}{\text {i}c}\overline{r(\bar{z})}\text {e}^{-2\text {i}\theta (x,t;z)} \end{pmatrix},\quad \ \ \ z\in \text {i}(0,c),\\&\begin{pmatrix} \frac{\rho (z)+z}{\text {i}c}r(z)\text {e}^{2\text {i}\theta (x,t;z)} &{}~ \frac{c}{2\text {i}\rho (z)}(1+r(z)\overline{r(\bar{z})})\\ \frac{2\rho (z)}{\text {i}c} ~&{} \frac{\rho (z)-z}{\text {i}c}\overline{r(\bar{z})}\text {e}^{-2\text {i}\theta (x,t;z)} \\ \end{pmatrix},\quad \quad \ \ z\in \text {i}(-c,0), \end{aligned} \right. \end{aligned}$$
(1.6)

where \(r(z)=-\frac{\overline{B(\bar{z})}}{A(z)},~d(z)=\frac{2\rho (z)}{\rho (z)+z}.\)

\(\bullet\) The residue conditions: m(x, t; z) has simple poles \(z_j\in {\mathbb {C}}_-\setminus \text {i}[-c,c]\) with \(A(z_j)=0\) at which the residue conditions are the following:

$$\begin{aligned} \begin{aligned} \underset{z=z_j}{\mathrm{Res}}m(x,t;z)=&\lim _{z\rightarrow z_j}\frac{m(x,t;z)}{d(z)} \begin{pmatrix} 0 &{} C_j\text {e}^{2\text {i}\theta (x,t;z)}\\ 0 &{} 0 \end{pmatrix},\\ \underset{z=\bar{z}_j}{\mathrm{Res}}m(x,t;z)=&\lim _{z\rightarrow \bar{z}_j}\frac{m(x,t;z)}{d(z)}\begin{pmatrix} 0 &{} 0\\ -\bar{C}_j\text {e}^{-2\text {i}\theta (x,t;z)} &{} 0 \end{pmatrix}, \end{aligned} \end{aligned}$$
(1.7)

where

$$\begin{aligned} C_j=\frac{c_j}{\dot{A}(z_j)},\ \dot{A}(z_j)=\frac{\text {d}}{\text {d}z}A(z_j)\ne 0 \end{aligned}$$
(1.8)

with some nonzero constants \(c_j\).

\(\bullet\) The normalization condition: \(m(x,t;z)\rightarrow I\) as \(z\rightarrow \infty .\)

The solution u(x, t) of the fifth-order-modified KdV Eq. (1.1) can be formulated in terms of the solution of the RH problem 1 as follows:

$$\begin{aligned} u(x,t)=-2\text {i}\lim _{z\rightarrow \infty }(z m(x,t;z))_{12}. \end{aligned}$$
(1.9)

In the following, we will formulate the robust inverse scattering transform for the Cauchy problem of Eq. (1.1). In particular, set

$$\begin{aligned} \Psi ^{BC}(x,t;z)=m(x,t;z)\text {e}^{\text {i}\theta (x,t;z)\sigma _3}. \end{aligned}$$
(1.10)

It follows from [11] that the spectral function A(z) cannot have zeros for sufficiently large |z| while \(\Delta u(\cdot ,0):=u(\cdot ,0)-c\in L^{1}({\mathbb {R}})\), and \((\Delta u(\cdot ,0))_x\in L^1({\mathbb {R}})\). Thus, one can define \(D_0\subset {\mathbb {C}}\) to be an open disk centered at origin of sufficiently large radius \(\varrho >0\) to contain all the singularities of \(\Psi ^{BC}(x,t;z)\). We now define a simultaneous fundamental solution for the Lax pair of fifth-order mKdV Eq. (1.1) as follows for \(z\in {\mathbb {C}}\setminus \Sigma\):

$$\begin{aligned} \Psi (x,t;z)= \left\{ \begin{aligned}&\Psi ^{in}(x,t;z),\quad \,\, z\in D_0,\\&\Psi ^{BC}(x,t;z),\quad \text {otherwise}, \end{aligned} \right. \end{aligned}$$
(1.11)

where \(\Sigma =\Sigma _+\cup \Sigma _-\cup (-\infty ,-\varrho ]\cup [\varrho ,\infty )\), \(\Sigma _+=\partial D_0\cap {\mathbb {C}}_+\), \(\Sigma _-=\partial D_0\cap {\mathbb {C}}_-\). The function \(\Psi ^{in}(x,t;z)\), \((x,t)\in D\) is a simultaneous fundamental solution of the Lax pair with the initial condition \(\Psi ^{in}(0,0;z)=I\), where \(D\subseteq {\mathbb {R}}^2\) is a simply-connected domain the contains the point (0, 0). Furthermore, for \((x,t)\in D\), \(\Psi ^{in}(x,t;z)\) is an entire function of z and \(\det [\Psi ^{in}(x,t;z)]=1\), \(\Psi ^{in}(x,t;z)=\sigma _2\overline{\Psi ^{in}(x,t;\bar{z})}\sigma _2\). It is easy to check that

$$\begin{aligned} \Psi (x,t;z)=\sigma _2\overline{\Psi (x,t;\bar{z})}\sigma _2,\, z\in {\mathbb {C}}\setminus \Sigma ,\, \sigma _2=\begin{pmatrix} 0 &{} -\text {i}\\ \text {i}&{} 0 \end{pmatrix}. \end{aligned}$$
(1.12)

Let \((-\infty ,-\varrho ],~[\varrho ,\infty )\) to be oriented left-to-right while \(\Sigma _+\) and \(\Sigma _-\) are oriented clockwise. Then, the function n(x, t; z) defined by

$$\begin{aligned} n(x,t;z)=\Psi (x,t;z)\text {e}^{-\text {i}\theta (x,t;z)\sigma _3},\ z\in {\mathbb {C}}\setminus (\Sigma \cup \text {i}[-c,c]), \end{aligned}$$
(1.13)

satisfies the following Riemann–Hilbert problem:

Riemann–Hilbert Problem 2. Find a \(2\times 2\) analytic matrix-valued function n(x, t; z) on \(z\in {\mathbb {C}}\setminus (\Sigma \cup \text {i}[-c,c])\) with the following properties:

  • The jump condition: For each \(z\in \Sigma \cup \text {i}[-c,c]\), n(x, t; z) satisfies the jump relations

    $$\begin{aligned} n_+(x,t;z)= \left\{ \begin{aligned}&n_-(x,t;z)\text {e}^{\text {i}\theta (x,t;z)\sigma _3}v(z)\text {e}^{-\text {i}\theta (x,t;z)\sigma _3},\quad \quad z\in \Sigma ,\\&n_-(x,t;z)\text {e}^{-2\text {i}\rho _+(z)[x+(-16z^4+8c^2z^2-6c^4)t]\sigma _3}, \,\,\, z\in \text {i}[-c,c], \end{aligned}\right. \end{aligned}$$
    (1.14)

    where

    $$\begin{aligned} v(z)= \left\{ \begin{aligned}&\begin{pmatrix} \frac{\psi _1^+(0,0;z)}{\overline{A(\bar{z})}d(z)}~&\psi ^-_2(0,0;z) \end{pmatrix},\quad \ z\in \Sigma _+,\\&\begin{pmatrix} \psi ^-_1(0,0;z), \frac{\psi ^+_2(0,0;z)}{A(z)d(z)} \end{pmatrix},\qquad z\in \Sigma _-,\\&\begin{pmatrix} \frac{1}{d(z)}(1+|r(z)|^2) ~&{} r(z)\\ \overline{r(z)} ~&{} d(z) \end{pmatrix},\,\,\,\ z\in (-\infty ,-\varrho ]\cup [\varrho ,\infty ), \end{aligned}\right. \end{aligned}$$
    (1.15)

    and \(\psi ^\pm (x,t;z)\) are the Jost solutions of the Lax pair to (1.1).

  • The normalization condition: \(n(x,t;z)\rightarrow I\) as \(z\rightarrow \infty .\)

The solution u(x, t) of the fifth-order mKdV Eq. (1.1) can be obtained by

$$\begin{aligned} u(x,t)=-2\text {i}\lim _{z\rightarrow \infty }(z n(x,t;z))_{12}. \end{aligned}$$
(1.16)

2 Darboux transformation

In this section, we describe the Darboux transformation in the setting of the robust inverse scattering transform. Specifically, we introduce the following Gauge transformation

$$\begin{aligned} \tilde{\Psi }(x,t;z)= \left\{ \begin{aligned}&\mathbf {T}(x,t;z)\Psi (x,t;z)\mathbf {T}^{-1}(0,0;z),\quad z\in D_0,\\&\mathbf {T}(x,t;z)\Psi (x,t;z),\qquad \qquad \quad \,\,\,\text {elsewhere}, \end{aligned}\right. \end{aligned}$$
(2.1)

where for any point \(\zeta \in D_0\),

$$\begin{aligned} \mathbf {T}(x,t;z)=I+\frac{\mathbf {H}(x,t)}{z-\zeta } +\frac{\sigma _2\overline{\mathbf {H}(x,t)}\sigma _2}{z-\bar{\zeta }} \end{aligned}$$
(2.2)

and

$$\begin{aligned} \mathbf {H}(x,t)=\frac{4\beta ^2(1-\overline{\omega (x,t)})\mathbf {n}(x,t)\mathbf {n}^{T}(x,t)\sigma _2 +2\text {i}\beta Z(x,t)\sigma _2\overline{\mathbf {n}(x,t)}\mathbf {n}^{T}(x,t)\sigma _2}{4\beta ^2|1-\omega (x,t)|^2+Z(x,t)^2} \end{aligned}$$
(2.3)

with \(\beta =\mathrm Im\zeta\), \(\mathbf {n}(x,t)=\Psi (x,t;\zeta )\mathbf {d}\), \(Z(x,t)=\mathbf {n}^\dag (x,t)\mathbf {n}(x,t)\), \(\omega (x,t)=\mathbf {n}^T(x,t)\sigma _2\dot{\mathbf {n}}(x,t)\) (\(\dot{\mathbf {n}}(x,t):=\dot{\Psi }(x,t;\zeta )\mathbf {d}\)), and \(\mathbf {d}=\begin{pmatrix} d_1&d_2 \end{pmatrix}^T\) being a nonzero complex-valued constant vector. Then, the function

$$\begin{aligned} \tilde{n}(x,t;z)=\tilde{\Psi }(x,t;z)\text {e}^{-\text {i}\theta (x,t;z)\sigma _3} \end{aligned}$$
(2.4)

satisfies the conditions of RH problem 2 in which only change is that for \(z\in \Sigma _+\cup \Sigma _-\), and the corresponding jump matrix v(z) is replaced by

$$\begin{aligned} \tilde{v}(z)=\left\{ \begin{aligned}&\mathbf {T}(0,0;z)v(z),\qquad z\in \Sigma _+,\\&v(z)\mathbf {T}^{-1}(0,0;z),\quad \ z\in \Sigma _-. \end{aligned}\right. \end{aligned}$$
(2.5)

It then follows from [11] that \(\tilde{\Psi }(x,t;z)\) simultaneously satisfies Lax pair equations of the fifth-order mKdV Eq. (1.1) in which u(x, t) is replaced by a modified potential \(\tilde{u}(x,t)\) given by

$$\begin{aligned} \tilde{u}(x,t)=-2\text {i}\lim _{z\rightarrow \infty }(z \tilde{n}(x,t;z))_{12}=u(x,t)-2\text {i}(\mathbf {H}_{12}(x,t)-\overline{\mathbf {H}_{21}(x,t)}). \end{aligned}$$
(2.6)

Hence \(\tilde{u}(x,t)\) is also a solution of Eq. (1.1).

Remark 2.1

The transform matrix \(\mathbf {T}(x,t;z)\) also can be chosen as a limiting case \(\epsilon \rightarrow 0\) for setting \(\mathbf {d}\) in the form \(\epsilon ^{-1}\mathbf {d}_\infty\) for a fixed vector \({\textbf{d}}_{\infty } \in {\mathbb{C}}^{2} { \setminus }\{ {\mathbf{0}}\}\) and \(\epsilon \in {\mathbb {C}}\). Then,

$$\begin{aligned} \mathbf {T}_\infty (x,t;z)=\lim _{\epsilon \rightarrow 0}\mathbf {T}(x,t;z)|_{\mathbf {d} =\epsilon ^{-1}\mathbf {d}_\infty }=I+\frac{\mathbf {H}_\infty (x,t)}{z-\zeta } +\frac{\sigma _2\overline{\mathbf {H}_\infty (x,t)}\sigma _2}{z-\bar{\zeta }}, \end{aligned}$$
(2.7)

where

$$\begin{aligned} \mathbf {H}_\infty (x,t):=\lim _{\epsilon \rightarrow 0}\mathbf {H}(x,t) =\frac{-4\beta ^2\overline{\omega _\infty (x,t)}\mathbf {n}_\infty (x,t)\mathbf {n}_\infty ^{T}(x,t)\sigma _2 +2\text {i}\beta Z_\infty (x,t)\sigma _2\overline{\mathbf {n}_\infty (x,t)}\mathbf {n}_\infty ^{T}(x,t)\sigma _2}{4\beta ^2|\omega _\infty (x,t)|^2+Z_\infty (x,t)^2}. \end{aligned}$$
(2.8)

3 Periodic solutions for Eq. (1.1)

We now choose an arbitrary point \(\zeta \in {\mathbb {C}}\setminus {\mathbb {R}}\) such that \(\zeta \in D_0\) and \(\mathbf {d}\in {\mathbb {C}}^2\setminus \{\mathbf {0}\}\), and let

$$\begin{aligned} \begin{aligned} \Psi _{bg}^{in}(x,t;z)=&\Psi _{bg}(x,t;z)\Psi _{bg}^{-1}(0,0;z) ={\mathcal {E}}(z)\text {e}^{\text {i}\theta (x,t;z)\sigma _3}{\mathcal {E}}^{-1}(z)\\ =&\cos (\theta )I+\frac{\sin (\theta )}{\theta }[x+(-16 z^4+8c^2z^2-6 c^4)t] \begin{pmatrix} \text {i}z &{} c\\ -c &{} -\text {i}z \end{pmatrix}. \end{aligned} \end{aligned}$$
(3.1)

Thus, we have

$$\begin{aligned} \mathbf {n}(x,t)=\text {i}\zeta \phi (\zeta )\sigma _3\mathbf {d}+\text {i}c\phi (\zeta )\sigma _2\mathbf {d}+\varphi (\zeta )\mathbf {d}, \end{aligned}$$
(3.2)

where

$$\begin{aligned} \phi (\zeta )=\frac{\sin (\theta (\zeta ))}{\rho (\zeta )},\quad \varphi (\zeta )=\cos (\theta (\zeta )). \end{aligned}$$
(3.3)

Differentiating with respect to \(\zeta\) yields

$$\begin{aligned} \mathbf {\dot{n}}(x,t)=\text {i}\phi (\zeta )\sigma _3\mathbf {d}+\text {i}\zeta \dot{\phi }(\zeta )\sigma _3\mathbf {d} +\text {i}c\dot{\phi }(\zeta )\sigma _2\mathbf {d}+\dot{\varphi }(\zeta )\mathbf {d}. \end{aligned}$$
(3.4)

We compute \(Z(x,t)=\mathbf {n}^\dag (x,t)\mathbf {n}(x,t)\) as

$$\begin{aligned} \begin{aligned} Z(x,t)=&[(c^2+|\zeta |^2)|\phi (\zeta )|^2+|\varphi (\zeta )|^2]\mathbf {d}^\dag \mathbf {d} -2\beta c|\phi (\zeta )|^2\mathbf {d}^\dag \sigma _1\mathbf {d}\\&-2\mathrm{Im}\{\zeta \phi (\zeta )\overline{\varphi (\zeta )}\}\mathbf {d}^\dag \sigma _3 \mathbf {d}-2c\mathrm{Im}\{\phi (\zeta )\overline{\varphi (\zeta )}\}\mathbf {d}^\dag \sigma _2\mathbf {d},\,\sigma _1 =\begin{pmatrix} 0 &{} 1\\ 1 &{} 0 \end{pmatrix} \end{aligned} \end{aligned}$$
(3.5)

and \(\omega (x,t)=\mathbf {n}^T(x,t)\sigma _2\dot{\mathbf {n}}(x,t)\) as

$$\begin{aligned} \omega (x,t)=c\phi ^2(\zeta )\mathbf {d}^T\sigma _3\mathbf {d} -\phi (\zeta )\varphi (\zeta )\mathbf {d}^T\sigma _1\mathbf {d}+ \mathbf {d}^T[\text {i}c I-\zeta \sigma _1] \mathbf {d}[\dot{\phi }(\zeta )\varphi (\zeta )-\phi (\zeta )\dot{\varphi }(\zeta )]. \end{aligned}$$
(3.6)

Finally, we find

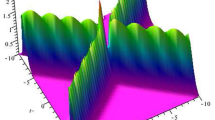
$$\begin{aligned} \tilde{u}(x,t)=c+\frac{8\beta ^2(1-\omega (x,t))\overline{n_2(x,t)^{2}} -8\beta ^2(1-\overline{\omega (x,t)})n_1(x,t)^2 -8\beta Z(x,t)n_1(x,t)\overline{n_2(x,t)}}{4\beta ^2|1-\omega (x,t)|^2+Z(x,t)^2}. \end{aligned}$$
(3.7)

Suppose that \(c=1\), \(\zeta =\text {i}/2\). Taking \(\mathbf {d}=(1~1)^T\) then the solution (3.7) obtained from the Darboux transformation exhibits periodic in x, see Fig. 1. It can be seen that the “width” of this solution changes periodically in the x-direction rather than exhibiting exponential decay to the background c, this solution corresponds to the so-called Akhmediev breather solution in the literature [20].

Fig. 1
figure 1

A special solution presented by (3.7) with the parameter selections \(c=1\), \(\zeta =\text {i}/2\), \(d_1=1,~d_2=1\): Three-dimensional plot (left) and density plot (right)

Full size image

4 Rational solutions for Eq. (1.1)

Now we construct the rational solutions of fifth-order mKdV Eq. (1.1). Take \(\zeta =\text {i}c\). By Taylor expansion, we then have

$$\begin{aligned} \phi (\zeta )=&x-30 c^4t,\quad \varphi (\zeta )=1,\nonumber \\ \dot{\phi }(\zeta )=&80\text {i}c^3t-\frac{1}{3}\text {i}c(x-30 c^4t)^3,\quad \dot{\varphi }(\zeta )=-\text {i}c(x-30 c^4t)^2. \end{aligned}$$
(4.1)

Thus, one can get

$$\begin{aligned} \begin{aligned} \mathbf {n}(x,t)=&\begin{pmatrix} d_1+c(x-30 c^4t)(d_2-d_1)\\ d_2+c(x-30 c^4t)(d_2-d_1)\end{pmatrix},\\ \dot{\mathbf {n}}(x,t)=&\begin{pmatrix} \text {i}(x-30 c^4t)d_1-\text {i}c(x-30 c^4t)^2d_1+c[80\text {i}c^3t-\frac{1}{3}\text {i}c(x-30 c^4t)^3](d_2-d_1)\\ -\text {i}(x-30 c^4t)d_2-\text {i}c(x-30 c^4t)^2d_2+c[80\text {i}c^3t-\frac{1}{3}\text {i}c(x-30 c^4t)^3](d_2-d_1)\end{pmatrix}. \end{aligned} \end{aligned}$$
(4.2)

If \(d_2-d_1=0\), namely, \(d_1=d_2=\gamma\), then

$$\begin{aligned} \begin{aligned} \mathbf {n}(x,t)=&\begin{pmatrix} \gamma \\ \gamma \end{pmatrix},\quad \dot{\mathbf {n}}(x,t)=\text {i}(x-30c^4t)\gamma \begin{pmatrix} 1-c(x-30c^4t)\\ -1-c(x-30c^4t)\end{pmatrix},\\ Z(x,t)=&\mathbf {n}^\dag (x,t)\mathbf {n}(x,t)=2|\gamma |^2,\quad \omega (x,t) =\mathbf {n}^T(x,t)\sigma _2\dot{\mathbf {n}}(x,t)=-2\gamma ^2(x-30c^4t). \end{aligned} \end{aligned}$$

Using these formulae in (3.7) then yields the first-order rational solution of Eq. (1.1)

$$\begin{aligned} \tilde{u}(x,t)=c-\frac{4\text {i}c^2\text {Im}\gamma ^2+4c|\gamma |^4}{|\gamma |^4+c^2\bigg (4|\gamma |^4(x-30c^4t)^2 +4\text {Re}\gamma ^2(x-30c^4t)+1\bigg )}. \end{aligned}$$
(4.3)

Particularly, if we use the limiting case \(\mathbf {H}_\infty (x,t)\) in (2.8) with \(\mathbf {d}_\infty =\begin{pmatrix} \gamma \\ \gamma \end{pmatrix}\) and choose \(c=-1\), \(\gamma =1\), one can get

$$\begin{aligned} \tilde{u}(x,t)=-1+\frac{4}{1+4(x-30t)^2}, \end{aligned}$$
(4.4)

which is consistent with the first-order bright rational solution formula (28) of the fifth-order mKdV Eq. (1.1) derived in [4] through the Darboux transformation method.

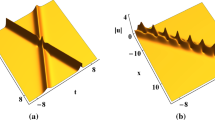
If \(d_2-d_1\ne 0\), for \(\zeta =\text {i}c\), we consider the limiting case in which the parameter is given by \(\mathbf {d}_\infty =\begin{pmatrix} -1&1 \end{pmatrix}^T\). The corresponding solution is plotted in Fig. 2 which is a second-order rational solution of fifth-order mKdV Eq. (1.1). In this circumstance, it is shown that the second-order rational solution exhibits a doubly localized high-peak structure which can be seen as a collision of a dark soliton and a bright soliton.

Fig. 2
figure 2

The second-order rational solution of fifth-order mKdV Eq. (1.1) for \(c=-1\) with \(\mathbf {d}_\infty =(-1 ~ 1)^T\)

Full size image

Finally, the high-order rational solutions can be obtained by the iteration of the Darboux transformation applied to the background eigenvector matrix \(\Psi _{bg}(x,t;z)\). Let \(\mathbf {T}_o^{[n]}(x,t;z)\) and \(\mathbf {T}_e^{[n]}(x,t;z)\) denote the Gauge transformation matrices calculated by (2.7) for \(\zeta =\text {i}c\), \(\mathbf {d}_\infty =\begin{pmatrix} 1\\ 1 \end{pmatrix}\) to \(\Psi _{o}^{[n]}(x,t;z)\) and \(\mathbf {d}_\infty =\begin{pmatrix} -1\\ 1 \end{pmatrix}\) to \(\Psi _{e}^{[n]}(x,t;z)\), respectively. Suppose that \(\Psi _{o/e}^{[n-1]}(x,t;z)\) is known, the n-fold \(\Psi _{o/e}^{[n]}(x,t;z)\) can be obtained as follows

$$\begin{aligned} \Psi _{o/e}^{[n]}(x,t;z)= \left\{ \begin{aligned}&\mathbf {T}_{o/e}^{[n-1]}(x,t;z)\Psi _{o/e}^{[n-1]}(x,t;z) \left( \mathbf {T}_{o/e}^{[n-1]}(0,0;z)\right) ^{-1},\,\,\,\, z\in D_0,\\&\mathbf {T}_{o/e}^{[n-1]}(x,t;z)\Psi _{o/e}^{[n-1]}(x,t;z),\qquad \qquad \qquad \qquad \text {elsewhere}. \end{aligned}\right. \end{aligned}$$
(4.5)

Then we can get the high-order rational solutions of the fifth-order mKdV Eq. (1.1) as follows:

$$\begin{aligned} \begin{aligned} u^{[2n-1]}(x,t)&=u^{[2n-3]}(x,t)-2\text {i}\left( \mathbf {H}^{[n-1]}_{o12}(x,t) -\overline{\mathbf {H}^{[n-1]}_{o21}(x,t)}\right) ,\\ u^{[2n]}(x,t)&=u^{[2n-2]}(x,t)-2\text {i}\left( \mathbf {H}^{[n-1]}_{e12}(x,t) -\overline{\mathbf {H}^{[n-1]}_{e21}(x,t)}\right) . \end{aligned} \end{aligned}$$
(4.6)

5 Multiple-pole soliton for Eq. (1.1)

Letting \(c=0\), we apply the Darboux transform with data \(\{\zeta ,\mathbf {d}\}\) to the trivial solution \(u^{[0]}=0\), then we can obtain a second-order pole soliton \(u^{[2]}(x,t;\mathbf {d})\). In this case, the background eigenfunction reads

$$\begin{aligned} \Psi ^{[0]}(x,t;z)=\text {e}^{\text {i}(zx-16z^5t)\sigma _3}. \end{aligned}$$
(5.1)

Then, for \(\zeta =\alpha +\text {i}\beta\), we have

$$\begin{aligned} \begin{aligned} \mathbf {n}^{[0]}(x,t)&=\Psi ^{[0]}(x,t;\zeta )\mathbf {d}=\begin{pmatrix} d_1\text {e}^{\text {i}(\zeta x-16\zeta ^5t)}\\ d_2\text {e}^{-\text {i}(\zeta x-16\zeta ^5t)} \end{pmatrix},\\ Z^{[0]}(x,t)&=\mathbf {n}^{[0]}(x,t)^\dag \mathbf {n}^{[0]}(x,t)=|d_1|^2\text {e}^{-2\beta x +32\beta t(5\alpha ^4+\beta ^4-10\alpha ^2\beta ^2)}+|d_2|^2\text {e}^{2\beta x-32\beta t(5\alpha ^4+\beta ^4-10\alpha ^2\beta ^2)},\\ \omega ^{[0]}(x,t)&=[\mathbf {n}^{[0]}]^T(x,t)\sigma _2\dot{\mathbf {n}}^{[0]}(x,t) =-2d_1d_2(x-80\zeta ^4t). \end{aligned} \end{aligned}$$
(5.2)

Hence, define

$$\begin{aligned} \mathbf {T}^{[0]}(x,t;z)=I+\frac{\mathbf {H}^{[0]}(x,t)}{z-\zeta } +\frac{\sigma _2\overline{\mathbf {H}^{[0]}(x,t)}\sigma _2}{z-\bar{\zeta }}, \end{aligned}$$
(5.3)

wherein

$$\begin{aligned} \mathbf {H}^{[0]}(x,t)=\frac{-4\beta ^2\overline{\omega ^{[0]}(x,t)} \mathbf {n}^{[0]}(x,t)\mathbf {n}^{[0]}(x,t)^{T}\sigma _2 +2\text {i}\beta Z^{[0]}(x,t)\sigma _2\overline{\mathbf {n}^{[0]}(x,t)} \mathbf {n}^{[0]}(x,t)^{T}\sigma _2}{4\beta ^2|\omega ^{[0]}(x,t)|^2+Z^{[0]}(x,t)^2}. \end{aligned}$$
(5.4)

It then follows from (2.6) that we obtain an explicit formula for second-order pole soliton solution \(u^{[2]}(x,t)\)

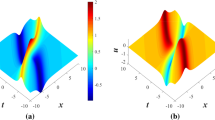
$$\begin{aligned} u^{[2]}(x,t)=\frac{-8\beta ^2\omega ^{[0]}(x,t))\overline{n^{[0]}_2(x,t)^{2}} +8\beta ^2\overline{\omega ^{[0]}(x,t)}n^{[0]}_1(x,t)^2 -8\beta Z^{[0]}(x,t)n^{[0]}_1(x,t)\overline{n^{[0]}_2(x,t)}}{4\beta ^2|\omega ^{[0]}(x,t)|^2+Z^{[0]}(x,t)^2}. \end{aligned}$$
(5.5)

For the explanation of this pole-count, we refer the readers to see Remark 2 in [13] for details. A second-pole soliton solution (5.5) is described in Fig. 3 with parameter selections \(\zeta =-1/2\text {i}\), \(d_1=1,~d_2=2\). We can see that as \(t\rightarrow -\infty ,\) the solution consists of two single solitons which are far apart and moving toward each other. When they collide, they interact strongly. But when \(t\rightarrow \infty\), these solitons re-emerge out of interactions without any change of shape and velocity (see Fig. 3a), indeed, after the interaction, each soliton acquires a position shift and a phase shift (see Fig. 3 (b)).

Fig. 3
figure 3

A special second-pole soliton presented by (5.5) with the parameter selections \(\alpha =0\), \(\beta =-1/2\), \(d_1=1,~d_2=2\): Three-dimensional plot (left) and density plot (right)

Full size image

6 Conclusions

In this work, based on matrix Riemann–Hilbert problem and Darboux transformation, we have constructed the explicit periodic and rational solutions for the fifth-order mKdV Eq. (1.1) with a nonzero constant initial condition by means of the robust inverse scattering transform method. In particular, the multiple-pole solitons also have been obtained by starting from the zero background. Some figures were presented to discuss the dynamic behavior of these solutions. As a by-product, our results will be valuable to analyze the infinite-order behavior of soliton solutions as in [12,13,14]. Of course, the idea used in this paper can also be extended to study the robust inverse scattering transform and solutions for other integrable nonlinear wave equations. Moreover, we will further study the large order and infinite order soliton or rogue wave for the fifth-order mKdV equation via the Deift–Zhou method in another literature.