1 Introduction

At the high-energy regime, the QCD theory of strong interactions can be determined as a many-body theory of partons within the so-called Color Glass Condensate (CGC) approach. It consists of a weakly coupled, albeit non-perturbative, QCD system, due to a large number of partons. The theory has been applied to study phenomena at many existing and upcoming high-energy collider facilities. The CGC has been proposed as a new state of matter, characterized by gluon saturation and by a saturation scale, \(Q_s\), growing with energy and has been applied to study the Deep Inelastic Scattering (DIS) of lepton scattering off hadronic targets [1,2,3,4]. During the collision, one can represent the hadron as a collection of constituents, partons, which are nearly on-shell excitations carrying some fraction x of the total hadron longitudinal momentum, where x encodes the empirical Bjorken variable \(x_{Bj}\). The inclusive cross sections in DIS can be expressed in terms of the Lorentz invariants, such as x which corresponds, at lowest order in perturbation theory, to the longitudinal momentum fraction carried by a parton in the hadron, the virtual photon four-momentum squared \(q^{2}= -Q^{2} < 0\) exchanged between the electron and the hadron, and the center-of-mass energy squared s.

In this setup, the differential configurational entropy (DCE) techniques predict the crucial points that help to understand the massive experimental data obtained by different collaborative groups [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. At high-energy regimes, the interesting and important information about various aspects of the reaction, for example, the total hadron-hadron or photon-hadron cross sections, can be derived by applying the nuclear DCE approach to nuclear systems at extreme conditions [22,23,24,25]. During short time of investigation, the comprehensive studies have been accumulated, in which such approach has been successfully used to describe the mechanism of the nuclear reactions at high-energies [26,27,28,29,30,31,32,33], glueballs [34], charmonium and bottomonium [35], the quark-gluon plasma [36], baryons [37], and also using the AdS/QCD model approach [38]. The main details and theory of the CE concept itself based on Shannon’s information entropy can be found in Refs. [39,40,41,42,43,44,45]. We can also mention other works, where the critical points of the CE have been used to explain the phenomena of AdS black holes and their quantum portrait as Bose–Einstein graviton condensates, also emulating magnetic structures [46,47,48,49,50,51]. The measure of the minimum values of CE, or the critical points, carries all information content about the stability of the complex nuclear systems. In the framework of the CGC, the nuclear DCE critical points have been deeply studied by computing the inelastic hadron cross sections [6, 23, 38, 52,53,54]. It is possible to compute the nuclear DCE when the cross section plays the role of a localized function that is related to the probability of the reaction product for any nuclear spatial configuration. Hence, one can estimate the critical points of the DCE via the Fourier transform of the cross section and subsequent calculation of the related modal fraction [6, 23, 53, 54].

Recently, the inner composition of hadrons, as well as the quark-gluon pairing, caused a lot of interest because of the numerous experimentally investigated scattering processes which have been done at high-energy regimes, for instance, with the data taken at LHC. Within the framework of QCD, using the factorization theorem, one can decompose the cross section at high energies into the hard and the soft components. While the perturbation method of QCD allows estimating the hard part of the cross section, it is not so straightforward to calculate the soft part due to its not perturbative origin. So, it is just possible to try to use some phenomenological approach, as the parton distribution functions (PDFs) parametrization, which is represented by the Bjorken scaling variable x and the energy scale \(Q^2\). At the high-energy regime of hadrons, the nonperturbative approach is one of the most convenient methods to calculate the process cross section within QCD. In such a context, the holographic QCD and the AdS/CFT correspondence have been used to examine the high-energy scattering reactions. One should suggest the Pomeron exchange (or a multi-gluon exchange) at the small x range to be able to characterize the whole dynamics of the partons. In Refs. [55,56,57], the deep analysis based on gauge/string duality to the small-angle scattering in QCD, was implemented by Brower, Polchinski, Strassler, and Tan (BPST), which comes after the analysis of the deep inelastic scattering within the holographic framework in Refs. [58, 59]. Results in holography for such processes were in Ref. [60] and, for the nuclear structure functions, in Refs. [61, 62].

This method assumes the contribution of the Pomeron exchange to the cross sections, which can be caused by a kernel in AdS space. Hence, it is possible to use the BPST kernel approach to calculate the total hadronic cross sections for various scattering processes at a high-energy regime. It is worth remembering that the masses of the participants in the hadron-hadron scattering process are the only variables in the AdS/CFT nonperturbative scale. In the AdS space within the BPST approach, the estimation of the total hadronic cross sections implies the BPST Pomeron exchange kernel and two density distributions. In the AdS/QCD approach the density distributions are characterized by the gravitational form factors [63]. For a non-excited state of hadron, one can use the hard-wall model to describe its behavior. Such a model is valid for the AdS geometry in the bulk background in the QCD scale, with a cutoff in the infrared region (IR). This setup was successfully used to describe the recent data of proton-proton total cross sections at the TeV scale provided by the TOTEM collaboration at LHC [64,65,66,67,68,69,70] as well as the other pp [71,72,73] and \({\bar{p}}p\) data [74,75,76] at high-energy scattering processes for which the Pomeron exchange gives a reasonable estimation.

In the case of fixed model parameters based on the given experimental data, the cross section for hadron scattering reaction can be easily calculated with the assumption of hadron normalizable mode and its normalized density distribution. Hence, we do not need to use any other parameters and get a universal description of any high-energy process within the Pomeron exchange approximation.

We use the DCE paradigm to investigate the pion-nucleon, nucleon-nucleon, and pion-pion cross section using the Pomeron exchange kernel and gravitational form factors. Section 2 is devoted to the Pomeron exchange model in the framework of holographic QCD for high-energy hadronic interactions. In Sect. 3, we present the main results of the analysis using the DCE approach and the concept of the critical points based on the experimentally determined hadron-hadron cross sections. The summary and outlook are given in Sect. 4.

2 Total hadron-hadron cross sections within the holographic QCD

Let us briefly represent the model description in the framework of the BPST Pomeron exchange kernel, which allows computing the hadron scattering total cross section (\(\chi \)). In the context of a conformal field theory with SU(N) symmetry, with large-N, one usually adds a massive probe, whose influence on the dynamics is subleading in 1/N, encompassing the massive quark in its fundamental representation of the Lorentz group. Therefore \(2\rightarrow 2\) high-energy scatterings can be considered in this setup, with states that are neutral with regard to gauge fields and are associated to the probe, such as massive quarkonium states, at fixed Mandelstam variables s, t [57]. The string description of this scattering process depends, besides s, t, on the bulk location z representing the energy scale in the dual QCD, wherein the scattering takes place. One considers suitable ranges of \(z, z'\), respectively denoting coordinates in AdS for incident and target particles, and the impact parameter b where the eikonal regime holds, for \(b= x_\perp -x'_\perp \) denoting the distance in the two Minkowski space transverse coordinates. In AdS/CFT, high-energy scattering processes can be realized to take place in a 3-dimensional (transverse) AdS\({}_3\), in addition to the usual 2-dimensional impact parameter space \({\varvec{b}}\), there is also the AdS radial direction z. One usually splits the scattering amplitude \(A_{2\rightarrow 2}(s,t)\) into the region where the eikonal approximation is valid, called the eikonal region, and into a complementary region where the eikonal regime does not hold. The contribution of the eikonal region to the amplitude reads [56, 57, 77]

$$\begin{aligned} {{{\mathcal {A}}}} (s, t) = 2 i s \int d^2 b e^{i {\varvec{k_\perp }} \cdot {\varvec{b}}} \int dzdz' P_{13}(z) P_{24}(z') \left[ 1-e^{i \chi (s, {\varvec{b}}, z, z')} \right] . \end{aligned}$$
(1)

In Eq. (1), \(k_\perp \) denotes the Fourier transform of the magnitude of the transverse momentum, \(p_\perp \), in the position space, whereas \(P_{13}(z)\) and \(P_{24}(z')\) are the density distributions of the two hadrons in the AdS space. The scattering has initial states indexed by 1, 2 and final states 3, 4. The wave functions \(\Phi _i\) for the scattered states appear pairwise, and are evaluated at z for the right-moving states and at \(z'\) for the left-moving states, given by

$$\begin{aligned} P_{13}(z)= & {} \left( \frac{z}{R}\right) ^2\sqrt{g(z)} \Phi _1(z) \Phi _3(z), \end{aligned}$$
(2)
$$\begin{aligned} P_{24}(z')= & {} \left( \frac{z}{R}\right) ^2\sqrt{g(z')} \Phi _2(z') \Phi _4(z'). \end{aligned}$$
(3)

They are normalized according to the following conditions:

$$\begin{aligned} \int dz\sqrt{g(z)}\left( \frac{z}{R}\right) ^2 \phi _i(z)\phi _j(z) =\delta _{ij} \end{aligned}$$
(4)

The eikonal kernel, \(\chi \), is then a function of \(b, z, z'\) as well as s and is related to a BPST Pomeron kernel [55,56,57], by

$$\begin{aligned} \chi (s,b,z,z')=\frac{g_{0}^{2}}{2{s}}\left( \frac{R^{2}}{zz'}\right) ^2K({s},b,z,z'). \end{aligned}$$
(5)

In fact, it emulates the eikonal approximation for graviton scattering in AdS\({}_5\) space, where here \(\chi \) is proportional to the Pomeron exchange kernel instead of the graviton propagator projected onto AdS\({}_3\). Denoting by \(\kappa _5\) the gravitational coupling constant in the AdS\({}_5\) bulk, the dimensionless coupling \(g_0^2= \kappa _5^2/R^3\sim 1/N^2\) is usually employed [57]. In the conformal limit, the Pomeron kernel can be expressed as a straightforward closed form, and the eikonal kernel becomes a function of two conformal invariants, consisting of a longitudinal boost \(\tau \) and a variable \(\xi \) relating to the chordal distance in transverse AdS\({}_3\), given by [55, 56]

$$\begin{aligned} \tau= & {} \log \left( \frac{\rho zz's}{2}\right) , \end{aligned}$$
(6)
$$\begin{aligned} \xi= & {} \sinh ^{-1}\left( \frac{b^{2}+(z-z')^{2}}{2zz'}\right) , \end{aligned}$$
(7)

where the parameter

$$\begin{aligned} \rho = \frac{2}{\sqrt{\lambda }}, \end{aligned}$$
(8)

where \(\lambda = g^2_{YM} N_c\) being the ’t Hooft coupling. The parameter \(\rho \) was evinced as the effective Pomeron intercept \(j_0\approxeq 2-\rho \) in Ref. [77] for the computation of two-body amplitudes with exchanging BPST Pomeron. It can be also derived in the pure AdS/CFT context [55, 78], being the \(\lambda ^{-1/2}\)-dependence, in Eq. (8), also proposed in Ref. [59]. In addition, this can be inferred when the weak-coupling perturbative sum to the strong coupling limit is taken into account [79, 80]. The BFKL Pomeron intercept and the range of \(\lambda \) were estimated in Ref. [77], in the context within data at HERA, also devising a phenomenological interface between the weak- and strong-coupling regime. The parameter \(\rho \) will be shown to play a relevant role in the context of the DCE.

Taking into account the optical theorem, in the single-Pomeron exchange model the total cross section can be expressed as [63]

$$\begin{aligned} \sigma (s) = 2 \int d^2b \int dzdz' P_{13} (z) P_{24} (z') \Im \chi (s,{\varvec{b}},z,z'). \end{aligned}$$
(9)

In the conformal limit, the imaginary part of the BPST Pomeron kernel, \(\Im K (s,b,z,z')\) can be written with the aid of Eq. (5), as [55]

$$\begin{aligned} \!\!\!\!\Im \; \chi (s,b,z,z') = \frac{g_{0}^{2} }{16\pi ^{3/2} }\sqrt{{\rho }}e^{(1-\rho )\tau }\frac{\xi {\tau ^{-\frac{3}{2}}}}{\sinh \xi }{\exp \left( \frac{-\xi ^{2}}{\rho \tau }\right) }, \end{aligned}$$
(10)

where \(\tau \) and \(\xi \) are given by (6) and (7) respectively. The final expression for the total hadron-hadron cross section can be written as [63]

$$\begin{aligned}&\sigma (s) = \frac{g_0^2 \rho ^{3/2}}{8 \sqrt{\pi }} \int dzdz' P_{13} (z) P_{24}(z') (zz') \Im [\chi _{c}(s,z,z')], \end{aligned}$$
(11)
$$\begin{aligned}&\Im [\chi _c(s,z,z') ] \equiv \frac{1}{\sqrt{\tau }} \exp \left[ {(1\!-\!\rho )\tau \!-\!\frac{1}{\rho \tau }\log ^2\left( \frac{z}{z'}\right) }\right] , \end{aligned}$$
(12)

where \({\Im } [\chi _{c}(s,z,z')]\) is the imaginary part of the scattering amplitude and \(\tau = \log (\rho z z' s/2)\) with \(g_0^2\) and \(\rho \) are the overall factor and the slope of the total cross section, respectively. It should be mentioned that in the nucleon-nucleon scattering the main value that describes the process is the nucleon mass (\(m_N \sim 1\) GeV). This fact supports the idea the leading role of the low energy dynamics with a strong coupling in QCD. It means that one can use the modified BPST kernel with the same functional form as the conformal kernel in the following form,

$$\begin{aligned}&\Im [\chi _{mod} (s, z, z')]= \Im [\chi _c (s, z, z') ]\nonumber \\&\quad + {\mathcal {F}} (s, z, z') \Im {[}\chi _c (s, z, z_0 z_0' / z') ], \end{aligned}$$
(13)

where

$$\begin{aligned} {\mathcal {F}} (s, z, z')&= 1 - 2 \sqrt{\rho \pi \tau } e^{\eta ^2} \text{ erfc }(\eta ), \end{aligned}$$
(14)
$$\begin{aligned} \eta&= -\frac{1}{\sqrt{\rho \tau }}\left( \log \left( \frac{z z'}{z_0 z_0'} \right) + \rho \tau \right) , \end{aligned}$$
(15)

with the coordinates cut-off parameters, \(z_0\) and \(z'_0\), in QCD scale, fixed by hadron masses.

The density distributions, \(P_{13}(z)\) and \(P_{24}(z')\), of the interacting hadrons in Eq. (1), can be additionally described by the gravitational form factors. Such form factors can be received from the bottom-up AdS/QCD models using the hadron-Pomeron-hadron 3-point functions. As the nucleon can be expressed as a solution to the 5-dimensional Dirac equation [63], the density distribution of the nucleon is expressed with the left-handed and right-handed components of the Dirac field (\(\psi _L\) and \(\psi _R\)) via the Bessel function in the following form:

$$\begin{aligned}&P_N (z) = \frac{1}{2z^{3}} \left[ \psi _L^2 (z) + \psi _R^2 (z) \right] , \end{aligned}$$
(16)
$$\begin{aligned}&\psi _L (z) = \frac{\sqrt{2} z^2 J_2 (m_N z)}{z_0^N J_2 (m_N z_0^N)}, \ \psi _R (z) = \frac{\sqrt{2} z^2 J_1 (m_N z)}{z_0^N J_2 (m_N z_0^N)}, \end{aligned}$$
(17)

The fixed cut-off parameter (\(z_0^N=4.081\) keV) obeys the conditions of the normalization \(J_1 (m_N z_0^N) = 0\) with \(m_p\) and \(m_n\) being the proton and neutron physical masses, respectively. The pion wave function \(\Psi \) is extracted from the bottom-up AdS/QCD model motion equation of mesons [63]. Hence, we can present the density distribution of the pion in the form of the Bessel function as the following:

$$\begin{aligned}&P_\pi (z) = \frac{ \left[ \Psi '(z) \right] ^2 }{4 \pi ^2 f_\pi ^2 z} + \frac{\sigma ^2 z^6 \Psi (z)^2 }{ f_\pi ^2 z^3 }, \end{aligned}$$
(18)

where the prime denotes the derivative with respective to z and the pion wave function reads

$$\begin{aligned}&\Psi \left( z \right) = z\Gamma \left( \frac{2}{3} \right) \left( {\frac{\alpha }{2}} \right) ^{1/3} \Biggl [ I_{ - 1/3} \left( {\alpha z^3 } \right) - I_{1/3} \left( {\alpha z^3 } \right) \frac{{I_{2/3} \left( {\alpha (z_0^\pi )^3 } \right) }}{{I_{ - 2/3} \left( {\alpha (z_0^\pi )^3 } \right) }} \Biggr ] \end{aligned}$$
(19)

with \(z_0^\pi = 3.105 \;\mathrm{keV}\) and \(\alpha = \frac{2 \pi }{3} \sigma \), for \(\sigma = (332\) MeV\()^3\), and \(f_\pi \) is the pion decay constant. The cutoff parameter, \(z_0^\pi \), encodes the mass of \(\rho \) meson (\(m_\rho \)) by the zeroes of the zeroth order Bessel function as \(J_0 (m_\rho z_0^\pi ) = 0\).

3 Configurational entropy via the BPST Pomeron exchange kernel

To determine the density distribution, one does not need any additional adjustable parameters. Within the BPST Pomeron exchange kernel approach, the only two parameters that should be extracted from the experiments are \(g_0^2\) and \(\rho \) (see Eq. (12)). During our analysis, we use the experimental data of TOTEM collaboration at LHC [63], as well as the recent hadron-hadron collision data which are given in the Particle Data Group within the energy range \(10^2< \sqrt{s} < 10^5\) GeV. As the check point values for the two adjustable parameters have been used the data from Ref. [63], \(g_0^2 = 6.27 \times 10^2\) and \(\rho = 0.824\).

We use the Pomeron exchange kernel to calculate the total hadron-hadron scattering cross sections at a high-energy range. As the using adjustable parameters of the model do not depend on the intrinsic properties of hadrons, one can assume the Pomeron exchange approach is a universal tool to describe the process at high energies. This fact is supporting also by the chosen normalizable modes of both the nucleon and the pion. In this way, one can easily compute the cross section for the incident pion, if the parameters for the nucleon-nucleon interaction are already fixed, and do not include other adjustable parameters. Besides, the scale of the scattering processes at high energies is characterized by the constant masses of the participated hadrons. Therefore, in such a case, we also have the same conditions for all three processes under study. which leads to the constant value for the total cross-section ratios among them. In this paper, we use the normalized structure factor for the collective coordinates, which have been obtained by the Fourier function decomposition into the number of weighted components for the total hadron-hadron cross sections [31]. The cross section for any collision, as the probability of the nuclear reaction, is governed by the modal fraction of the CE, and, consequently, contains all the needed information. On the other hand, the limit number of the critical points that can be determined using the Shannon entropy and the configurational entropy concepts, totally characterize an isolated localized nuclear system [39, 41].

If one considers as the localized integrable function the reaction cross section, it is possible to calculate the associated DCE, through the energy-weighted correlation function, which is the Fourier transform of the total cross section, given by:

$$\begin{aligned} \sigma _{}({k,\rho })=\frac{1}{2\pi }\! \int _{{\mathbb {R}}}\sigma _{} (s,\rho )\, e^{ikz} d z, \end{aligned}$$
(20)

where \(\sigma _{}(s,\rho )\) is defined by Eq. (9).

Then, the modal fraction of DCE can be determined as:

$$\begin{aligned} f_{\sigma _{}({k,\rho })}=\frac{\vert \sigma _{}({k,\rho }) \vert ^2}{\int _{{\mathbb {R}}}\vert \sigma _{}({k,\rho })\vert ^2 dk}. \end{aligned}$$
(21)

The set of the critical points is determined through the suitable expression for the DCE [39]:

$$\begin{aligned} \mathrm{DCE}(a,b) = - \int _{{\mathbb {R}}} f_{\sigma _{}({k,\rho })} \log f_{\sigma _{}({k,\rho })}d k. \end{aligned}$$
(22)

And finally, one obtains the CE critical points just by applying Eqs. (20 - 22) employing the total hadronic cross section.

Fig. 1
figure 1

DCE \(\times \) \(\rho \). Minimum: \(\rho = 0.814\), DCE = 164.72 nat (Natural unit of information)

Full size image

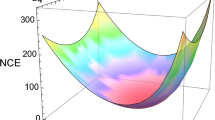
In Fig. 1 one can see the results of the DCE versus \(\rho \) calculations for the total hadron-hadron scattering cross sections at a high-energy regime, using Eqs. (20 – 22), and the related Eq. (11) – defining the cross section — and Eqs. (12, 13). Figure 1 shows the predominance of the quantum states with the slope of the total cross section \(\rho = 0.814\), corresponding to the nuclear DCE = 164.72 nat, with the corresponding global minimum of the nuclear configurational entropy at such point. The symbol nat means the natural unit of information, consisting of a unit of information, based on natural logarithms and powers of e, rather than powers of 2 and base 2 logarithms, which define the Shannon. This unit is also known by its unit symbol, the nat. One nat is the information content of an event when the probability of that event occurring is 1/e.

One can see that the differential configurational entropy curve tends to grow on both sides from the observed global minimum, although with different signs when one looks at the second derivative of the nuclear DCE with respect to \(\rho \), in Fig. 1. The result of our calculation for hadron-hadron interactions at high energies fits well with the value of parameter \(\rho =0.824\) obtained in Ref. [63], within 1.1%. The critical point of the nuclear DCE indicates the natural choice of the total hadron cross section for the parameter, which controls the energy dependence of the cross sections and confirms the earlier received experimental data with high enough precision. At \(\rho = 0.814\), the nuclear system stays at its most stable configuration. According to the results of Refs. [63] and Eq. (8), one can estimate the ’t Hooft coupling \(\lambda = 2.203\). In the case here derived, still using Eq. (8), for \(\rho =0.814\) the ’t Hooft coupling reads \(\lambda = 2.217\). As pointed out in Ref. [77], the BFKL Pomeron intercept, computed to second order, crosses the BPST intercept accurately in the range as the data provided by data at HERA data. According to these values, the ’t Hooft coupling attains relatively large values of \(\lambda \approxeq 10\), which may characterize the strong-coupling regime. The precise value defining the interface between the weak- and the strong-coupling is loose, as Ref. [81] considers the strong-coupling regime in the range \(\lambda \approxeq 10\).

Such minimum has been computed through Shannon’s information entropy approximation [40] and contains all information about the mechanism of the reactions. The fitting procedure of adjustable parameters for the experimentally determined total hadron-hadron cross sections clearly shows the conditions for the configurational stability of the excited nuclear system at high-energies. The stability of any localized nuclear configuration is characterized by the set of limited number degrees of freedom, which determine the most dominant state(s) after reaching the thermodynamic equilibrium of the system. And our results once again confirm this fact. Of course, each case of the reaction requires special and deeper investigation using the comprehensive results obtained via the recent studies in this area [20, 21, 82,83,84].

4 Conclusions

The total cross sections for three hadron-hadron scattering reactions at a high-energy regime have been studied within the Pomeron exchange kernel model of holographic QCD [85, 86]. This model allowed us to calculate the total hadron cross sections using the expression for the density distributions for the nucleon and for pion, which are expressed by the gravitational form factors in the framework of bottom-up AdS/QCD models. The model conditions imply complete independence from the observed s quantity because of the energy dependence of the cross section controlled by the BPST kernel. In the considering hadron energy range (\(10^2< \sqrt{s} < 10^5\) GeV) the total scattering cross sections are in satisfactory agreement with the data from Ref. [63]. We can conclude based on the results of this paper that the BPST Pomeron exchange kernel is a convenient tool in the investigation of high-energy hadron interactions with nonperturbative gluonic dynamics. We applied the nuclear DCE approach and estimated its global minimum, which characterizes the critical and stable point of the hadron-hadron reactions. The calculation of the total scattering cross section within the BPST Pomeron exchange kernel determined the natural choice for the excited nuclear configuration. We found the satisfactory agreement of the calculated parameters with those predicted by [63], within 1.1%. The stability of the nuclear system can be completely determined by the critical point of the nuclear DCE. Hence, all the available information can be reached through the systematic study of the DCE approach. One of the advantages of employing DCE-based methods is that computational tools are more straightforward when one compares to other approaches regarding AdS/QCD and lattice QCD as well. Besides, since the DCE is equivalent to the information chaoticity carried by a message, in the context of Shannon’s information entropy, one can shed additional light on high-energy hadron-hadron scattering processes. In high-energy fundamental collisions, chaos in QCD gauge dynamics may set in, and only particles in final states can be measured. The chaotic profile of high-energy hadron-hadron scattering processes can be then quantified by the loss of information at the end of the scattering processes. This quantitative aspect was here shown to be encompassed by the DCE. This additional interpretation complies with other results in the literature, regarding chaos in QCD and holography (see, e.g., Refs. [87,88,89,90,91,92]).