1 Introduction

Unlike usual solids, another group of materials can be addressed whose main feature is to promote negative Poisson’s ratio at least in one lateral direction [1,2,3,4]. These materials, known as metamaterials (or auxetic materials), are therefore able to be compacted or expanded in the plane that their Poisson’s ratio is negative in it if they are subjected to mono-directional compress or stretch, respectively. This interesting feature can avoid from material’s shrinkage [5]. Thanks to this specific property, auxetic materials can provide better indentation resistance, bending stiffness, acoustic properties, and vibration manipulation compared with conventional ones [6]. Auxeticity can be achieved by different types of lattice geometries [7]. Depending on the geometrical features of the unit cell employed for construction of the auxetic materials, expressions for the Poisson’s ratio and modulus can be obtained with our knowledge from classical mechanics (e.g., see [8,9,10]). It is reported that by using forming techniques, it will be possible to observe auxeticity in one loading mode which leads to achieving auxetic materials under bare stretch or compact [11].

Employment of auxetic composites in the design of critical devices can satisfy a large number of engineering demands. Following this concept, it was shown that it is possible to tailor the properties of honeycomb composites so that out-of-plane auxeticity will appear [12]. Based on a rotation-assisted forming of a heterogeneity in a matrix, negative Poisson’s ratio in the designed auxetic composite was gathered in [13]. In addition, experiments revealed that it is possible to manipulate the Young’s modulus and fracture strain of a laminated composite by forming it in graded lattices so that both honeycomb and auxetic patterns exist together [14]. Furthermore, numerical simulations have shown that it is possible to attain sandwich panels with better energy absorption if an auxetic core is hired in the composition of the system i.e., subjected to blast load [15]. Another investigation showed that utilization of either hollow or solid bars in a foam matrix can be led to construction of an auxetic composite which is able to provide an enhancement of about 81% in the fracture strain of the original specimen under compression [16]. Besides, it was proven that combination of rhombic configuration with re-entrant lattice leads to generation of a new class of auxetic composites which will be able to promote better resistance from themselves against buckling-mode stimulations [17]. Using the concept introduced in [16], it was conceived that auxetic composites are better candidates for the goal of being subjected to a low-velocity impactor in the mid-range strains thanks to their better energy absorption [18].

In the recent years, the attention of researchers was attracted by mechanical behaviors of continuous systems either entirely or partially made from auxetic materials. For instance, the first-order shear deformation theory (FSDT) of rectangular plates was employed in [19] to survey the nonlinear transient responses of multilayered plates with an auxetic core. In another study, a zigzag plate theorem was implemented for the purpose of analyzing time-dependent deflection of sandwich plates made from a metamaterial core which is surrounded by three-phase nanocomposites (composites containing nanosize reinforcements) [20]. The nonlinear dynamic and energy analyses of multilayered plates including an auxetic core were fulfilled by using the nonlinear expansion of the kinematic relations of higher-order shear deformation theory (HSDT) of Reddy in [21]. In a mixed experimental–numerical study, functionally graded (FG) distribution of three-dimensional (3D) auxetic lattices was employed to simulate and manufacture metamaterial plates whose nonlinear oscillation response was monitored [22]. Furthermore, it was demonstrated that if a gradual change in the auxeticity angle of metamaterial structures is made, it will be possible to tailor the fracture behaviors of the composite structures [23]. Lately, the well-known FSDT was utilized in [24] to probe nonlinear vibrations in bi-directionally stiffened doubly-curved panels consisting of porous metamaterials.

On the other hand, nanosize elements like carbon nanotube (CNT), graphene, and its derivatives (e.g., graphene oxide (GO) and graphene platelet (GPL)) have been widely used in the design and analysis of structural elements due to their extraordinary stiffness and strength [25]. Graphene promotes temperature-dependent properties [26] and investigation of its elastic features requires nonlinear frameworks [27]. So, lots of studies can be mentioned whose main concern is the investigation of either static or dynamic behaviors of nanocomposite structures. The nonlinear deflection responses of moderately thick beams made from GPL-reinforced (GPLR) nanocomposites were tracked in [28] by the means of FSDT. Both critical buckling resistance and postbuckling path of the multilayered beams made from GPLR nanocomposites were surveyed in [29] by the means of Timoshenko beam model. In another study, effect of temperature rise on the buckling performance of GO-reinforced (GOR) nanocomposite plates was studied [30]. Besides, the modal analysis of GOR nanocomposite beams was accomplished in the framework of HSDT while the influence of existence of a magnetic field in the environment on the system’s dynamic response was captured [31]. In addition, a finite element (FE)-based study was carried out in [32] to probe the variations of natural frequency in three-phase nanocomposite beams with respect to the shear deformation effects on the system’s mechanical behavior. A 3D solution for vibration and bending problems in GPLR nanocomposite annular plates was introduced in [33] with the aid of the fundamentals of elasticity. In the framework of an analytical investigation, the influence of existence of pores in the GPLR nanocomposites on the postbuckling path of the beams containing an initial deflection was considered in [34]. Furthermore, HSDT of curved beams was implemented in [35] to survey bending and buckling responses of porous nanocomposites reinforced via GPLs. Both mechanical and thermal vibration characteristics of GOR rectangular plates were monitored in the context of analytical attempts in [36] and [37], respectively. By using experimental datasets achieved from dynamic mechanical analysis (DMA) of GOR nanocomposites, the modulus of such nanomaterials was expressed in terms of local temperature in [38] with the aid of a machine learning (ML)-based method. Afterward, the obtained modulus was used for extracting the buckling load in nanocomposite beams. By considering the influence of CNT agglomerates on the material properties of three-phase nanocomposites, buckling load and postbuckling path of nanocomposite beams were approximated in [39] and [40], respectively. With the aid of an efficient FE solution, the nonlinear bending characteristics of porous GPLR nanocomposite curved beams were studied in [41] while the impacts of shear strain and stress on the derivation of the governing equations are included. In the framework of HSDT, smart electrically-actuated stability in multilayered plates consisting of graphene-reinforced nanocomposite plies was investigated in detail [42]. In another study concerned with the effect of existence of pores in the nanocomposites’ microstructure on the mechanical behavior of the continua, nonlinear bending features of GPLR plates with any desired geometry were analyzed [43]. In another effort, thermo-elastic buckling of three-phase nanocomposite beams and elastic buckling of plates made from the same nanomaterial were monitored by the means of Galerkin’s analytical method in [44] and [45, 46], respectively. In one of the other attempts in this area, the method of the power series expansion of the displacement field components was utilized in [47] for the goal of probing the thermo-mechanical buckling load and natural frequency variations in GPLR nanocomposite plates. Recently, dynamic responses of three-phase nanocomposite plates were reported in Refs. [48, 49] in the framework of HSDT of rectangular plates.

Once ultra-stiff nanocomposites are merged with metamaterials, lightweight meta-nanocomposites will be achieved. Regarding the specific capabilities of each one, it is easy to imagine that how useful can the attained material be for the design of structural elements. To this reason, recently, initial attempts in this area have begun. According to the Reddy’s HSDT of thick plates, nonlinear free vibration behaviors of multilayered meta-nanocomposite structures reinforced with CNTs were monitored in [50]. In the framework of the same kinematic theory for cylindrical shells, the postbuckling paths of metal-hosted meta-nanocomposite cylindrical panels reinforced via graphene sheets embedded on a stiff medium were analyzed in [51]. In addition, the impact of local temperature on the approximation of the postbuckling path of rectangular multilayered plates made from graphene-reinforced auxetic nanocomposites was included in [52]. With the aid of the Reddy plate hypothesis, the reaction of both auxetic and non-auxetic CNTR nanocomposite structures to a low-velocity impact excitation was examined in detail [53]. Furthermore, the effects of initial deflection of the cylindrical shells on the postbuckling path of such multilayered structures consisting of auxetic CNTR materials were taken into account in the framework of an analytical investigation in [54] while the thermal loading effects are considered. Recently, both elastic and thermal postbuckling paths of auxetic graphene-reinforced nanocomposite sandwich cylinders were probed by the means of Reddy’s shell theorem in [55] and [56], respectively.

Based on the conducted review on the literature, it is obvious that although auxetic nanocomposites are excellent candidates for design of structural components subjected to compressive stimulations, no research article can be found addressing buckling behaviors of meta-nanocomposite beams. To fill in the above crucial gap, present paper is organized to examine the postbuckling responses of auxetic CNTR nanocomposites. To present more reliable data, the negative influence of existence of aggregated bundles of CNTs in the microstructure of the meta-nanocomposite on the beam’s postbuckling load is covered, too. In the following parts of present text, the problem will be described and formulated as well. First, equivalent properties of the meta-nanocomposite will be extracted. Then, it will be explained how to derive the governing equation of the problem based on Euler–Bernoulli theory for slender beams. Thereafter, Galerkin’s powerful analytical method will be hired to solve the problem for beams with simply supported (S) and clamped (C) ends. Finally, illustrative case studies will be provided for reference.

2 Theory and formulations

2.1 Problem description

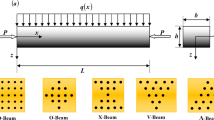
In this study, auxetic CNTR nanocomposite beams of length L with rectangular cross-section of width b and thickness h are considered. In this work, it will be assumed that width and thickness of the beam’s cross-section are identical and thickness is fixed on \(h = 2\,\,{\text{mm}}\). The beam-type structure is assumed to be long enough so that it falls in the scope of thin structures. In addition to the structural features, it must be denoted that the nanocomposite material is formed via re-entrant lattice model whose schematic view is depicted in Fig. 1. The degree of auxeticity in the meta-nanocomposite will be tailored by changing the angle θ, also known as auxeticity angle. It is worth regarding that parameters t, l, and e stand for thickness, inclined length, and vertical length of the cell rib of the re-entrant lattice, respectively.

Fig. 1
figure 1

Illustration of the auxetic lattice utilized in this work

Full size image

2.2 Homogenization method

Essence of heterogeneities in the composition of some of the materials cannot be ignored. To this end, some complicated mathematical methods have been developed to carry out the homogenization process [57,58,59,60]. Herein, a backward process will be presented to derive the material properties of meta-nanocomposite. The following method describes the Young’s modulus as a function of the structure’s thickness. Please keep this in mind that the independent variable addressing the thickness direction is z. As the first step, consider the equivalent Young’s modulus of the polymer nanocomposite (PNC) to be \(E_{{{\text{PNC}}}}\). If the nanomaterial is arranged like an auxetic lattice, the equivalent longitudinal modulus of the auxetic nanocomposite can be reached by [19]:

$$ E_{{{\text{eff}}}} = E_{{{\text{PNC}}}} \left( {{t \mathord{\left/ {\vphantom {t l}} \right. \kern-\nulldelimiterspace} l}} \right)^{3} \frac{\cos \theta }{{\left( {{e \mathord{\left/ {\vphantom {e l}} \right. \kern-\nulldelimiterspace} l} + \sin \theta } \right)\sin^{2} \theta }} $$
(1)

Now we will be about to find the Young’s modulus of the CNTR nanocomposite. To this purpose, the Eshelby-Mori–Tanaka method will be employed to account for the side effects of nanofillers’ entanglement on the modulus prediction in nanocomposites. Based on this method, the Young’s modulus of the CNTR nanocomposite can be extracted using the following expression [32]:

$$ E_{{{\text{PNC}}}} = \frac{9K(z)G(z)}{{3K(z) + G(z)}} $$
(2)

where \(K(z)\) and \(G(z)\) indicate on the bulk and shear moduli of the nanomaterial, respectively. They can be expressed in the following form [32]:

$$ K(z) = K_{{{\text{out}}}} \left( {1 + \frac{{\mu \left( {\frac{{K_{{{\text{in}}}} }}{{K_{{{\text{out}}}} }} - 1} \right)}}{{1 + \left( {1 - \mu } \right)\left( {\frac{{K_{{{\text{in}}}} }}{{K_{{{\text{out}}}} }} - 1} \right)\frac{{1 + \nu_{{{\text{out}}}} }}{{3\left( {1 - \nu_{{{\text{out}}}} } \right)}}}}} \right) $$
(3)
$$ G(z) = G_{{{\text{out}}}} \left( {1 + \frac{{\mu \left( {\frac{{G_{{{\text{in}}}} }}{{G_{{{\text{out}}}} }} - 1} \right)}}{{1 + \left( {1 - \mu } \right)\left( {\frac{{G_{{{\text{in}}}} }}{{G_{{{\text{out}}}} }} - 1} \right)\frac{{8 - 10\nu_{{{\text{out}}}} }}{{15\left( {1 - \nu_{{{\text{out}}}} } \right)}}}}} \right) $$
(4)

In the above relations, subscripts “in” and “out” denote the regions inside and outside of the clusters, respectively. Based on the utilized micromechanical scheme, the bulk moduli in these states can be obtained via [32]:

$$ \begin{gathered} K_{{{\text{in}}}} (z) = K_{m} + \frac{{V_{r} \eta \left( {\delta_{r} - 3K_{m} \alpha_{r} } \right)}}{{3\left( {\mu - V_{r} \eta + V_{r} \eta \alpha_{r} } \right)}}, \hfill \\ K_{{{\text{out}}}} (z) = K_{m} + \frac{{V_{r} \left( {1 - \eta } \right)\left( {\delta_{r} - 3K_{m} \alpha_{r} } \right)}}{{3\left( {1 - \mu - V_{r} \left( {1 - \eta } \right) + V_{r} \left( {1 - \eta } \right)\alpha_{r} } \right)}} \hfill \\ \end{gathered} $$
(5)

In addition, the value of shear moduli in the regions inside and outside of the clusters can be calculated as follows [32]:

$$ \begin{gathered} G_{{{\text{in}}}} (z) = G_{m} + \frac{{V_{r} \eta \left( {\eta_{r} - 2G_{m} \beta_{r} } \right)}}{{2\left( {\mu - V_{r} \eta + V_{r} \eta \beta_{r} } \right)}}, \hfill \\ G_{{{\text{out}}}} (z) = G_{m} + \frac{{V_{r} \left( {1 - \eta } \right)\left( {\eta_{r} - 2G_{m} \beta_{r} } \right)}}{{3\left( {1 - \mu - V_{r} \left( {1 - \eta } \right) + V_{r} \left( {1 - \eta } \right)\beta_{r} } \right)}} \hfill \\ \end{gathered} $$
(6)

In Eqs. (5) and (6), \(\alpha_{r}\), \(\beta_{r}\), \(\delta_{r}\), and \(\eta_{r}\) are stiff parameters whose definition can be found in Appendix. In the above relations, η and µ are called agglomeration parameters controlling the distribution of the nanofillers in the microstructure of the nanomaterial. The parameter η is the volume fraction of the CNTs inside the clusters; while, µ is the volume fraction of the clusters. It must be kept in mind that these parameters must obey from the mathematical constraint \(\mu \le \eta\) [32].

Besides, the Poisson’s ratio in the outside zone can be expressed as below:

$$ \nu_{{{\text{out}}}} = \frac{{3K_{{{\text{out}}}} - 2G_{{{\text{out}}}} }}{{6K_{{{\text{out}}}} + 2G_{{{\text{out}}}} }} $$
(7)

It is worth regarding that the volume fraction of the reinforcing nanofillers that was shown with \(V_{r}\) in Eqs. (5) and (6) can be gathered by the means of following definition [32]:

$$ V_{r} (z) = \left[ {\frac{{\rho_{r} }}{{w_{r} \rho_{m} }} - \frac{{\rho_{r} }}{{\rho_{m} }} + 1} \right]^{ - 1} \left( {\frac{z}{h} + \frac{1}{2}} \right)^{p} $$
(8)

where \(\rho_{m}\) and \(\rho_{r}\) are the mass densities corresponding with matrix and reinforcing phase, respectively. Also, p is the gradient index that is responsible for the geometry-dependent control of the nanomaterial’s modulus. In the above definition, the mass fraction of the nanofillers can be expressed as below [32]:

$$ w_{r} = \frac{{M_{r} }}{{M_{r} + M_{m} }} $$
(9)

2.3 Equations of motion

In order to formulate the problem, we need to use a kinematic beam theory in this section. Because of the main assumption of thin being of the structure, the effects of shear deformation of the structure on its mechanical behavior can be ignored and classical theories can be trusted [61, 62]. Based on this reality, the Euler–Bernoulli beam theory is implemented in the present work. According to this theorem, the displacement field of the beam can be considered to be like [40]:

$$ \begin{gathered} u_{x} (x,z) = u(x) - \left( {z - z^{*} } \right)\frac{\partial w(x)}{{\partial x}}, \hfill \\ u_{y} (x,z) = 0, \hfill \\ u_{z} (x,z) = w(x) \hfill \\ \end{gathered} $$
(10)

where \(u(x)\) and \(w(x)\) stand for the axial displacement and flexural deflection of the beam’s neutral axis, respectively. In this study, the exact position of the system’s neutral axis, i.e.; shown in the above definition via \(z^{*}\), will be considered. The exact position of the neutral axis of a beam consisting of auxetic nanocomposites can be calculated using the below relation:

$$ z^{*} = \frac{{\int_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{h/2} {zE_{{{\text{eff}}}} {\text{d}}z} }}{{\int_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{h/2} {E_{{{\text{eff}}}} {\text{d}}z} }} $$
(11)

Now, the displacement field introduced in Eq. (10) must be employed to derive a relation describing the system’s normal strain with regard to the impacts of von Kármán-type geometrical nonlinearity on the beam’s strain. Therefore, the normal strain in the longitudinal direction can be written as follows [40]:

$$ \varepsilon_{xx} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - \left( {z - z^{*} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(12)

The first two terms of the above relation indicate on the axial stretch and the last term reveals the curvature of the beam. In order to find the equations of motion, the principle of virtual work will be used in this study. This principle states that the variation of the total energy of any desired continuous system must be set to zero. Mathematical statement of this principle is [25]:

$$ \delta U = 0 $$
(13)

in which U is the strain energy of the beam. Based on the stress–strain relationship in linearly elastic solids and with the aid of the strain–displacement relation expressed in Eq. (12), the variation of the strain energy can be expressed as [40]:

$$ \delta U = \int\limits_{0}^{L} {\left\{ {N\left[ {\frac{\partial \delta u}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial \delta w}{{\partial x}}} \right] - M\frac{{\partial^{2} \delta w}}{{\partial x^{2} }}} \right\}{\text{d}}x} $$
(14)

In the above definition, the axial force and bending moment can be written as follows:

$$ \left[ \begin{gathered} N \hfill \\ M \hfill \\ \end{gathered} \right] = \int\limits_{A} {\left[ \begin{gathered} 1 \\ z - z^{*} \\ \end{gathered} \right]\sigma_{xx} {\text{d}}A} $$
(15)

Now if Eq. (14) is substituted in Eq. (13) and the coefficients of \(\delta u\) and \(\delta w\) are assumed to be zero, the below Euler–Lagrange equations can be obtained:

$$ \frac{\partial N}{{\partial x}} = 0 $$
(16)
$$ \frac{\partial }{\partial x}\left\{ {N\frac{\partial w}{{\partial x}}} \right\} - \frac{{\partial^{2} M}}{{\partial x^{2} }} = 0 $$
(17)

2.4 Governing equation

In the previous section, the motion equations were extracted. Now, it is required to find expressions for the axial force and bending moment in terms of the components of beam’s displacement field to find the final equation describing the problem. Remembering the Hook’s law in the linearly elastic solids, the following 1D relation for the auxetic nanocomposite beam can be written [25]:

$$ \sigma_{xx} = E_{{{\text{eff}}}} \varepsilon_{xx} $$
(18)

If the above relation is integrated over the beam’s cross-section and the definitions of axial force and bending moment are considered, one can reach to:

$$ N = A_{xx} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] $$
(19)
$$ M = - D_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(20)

In the above relations, \(A_{xx}\) and \(D_{xx}\) are extensional and bending rigidities, respectively. It is worth mentioning that the coupling stretching-bending rigidity of the beam will be zero because the precise location of the neutral axis is captured. The extensional and bending rigidities of the beam can be computed via:

$$ \left[ \begin{gathered} A_{xx} \hfill \\ D_{xx} \hfill \\ \end{gathered} \right] = \int\limits_{A} {\left[ \begin{gathered} 1 \\ \left( {z - z^{*} } \right)^{2} \\ \end{gathered} \right]E_{{{\text{eff}}}} {\text{d}}A} $$
(21)

Now, with respect to the first motion equation presented in Eq. (16), it can be concluded that the axial force possesses a constant value, i.e., \(N = {\text{cte}}\). Hence, Eq. (17) can be re-written in the following form:

$$ N\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{\partial^{2} M}}{{\partial x^{2} }} = 0 $$
(22)

If Eqs. (19) and (20) are inserted into Eq. (22), the below relation will be attained

$$ A_{xx} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right]\frac{{\partial^{2} w}}{{\partial x^{2} }} + D_{xx} \frac{{\partial^{4} w}}{{\partial x^{4} }} = 0 $$
(23)

The above relation describes the motion of the continua. If the constant value of the axial force is assumed to be e.g., c, it gives:

$$ \frac{\partial u}{{\partial x}} = \frac{c}{{A_{xx} }} - \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} \to u(x) = \frac{cx}{{A_{xx} }} - \frac{1}{2}\int_{0}^{x} {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} {\text{d}}x} + d $$
(24)

where d is an integer which must be determined using the boundary conditions (BCs) at the ends of the beam. In this study, the structure is assumed to be simply supported via immovable supports. According to this assumption, it can be revealed that:

$$ u(0) = 0 \to d = 0 $$
(25)
$$ u(L) = - \frac{{P_{b} L}}{{A_{xx} }} \to c = \frac{{A_{xx} }}{2L}\int_{0}^{L} {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} {\text{d}}x} - P_{b} $$
(26)

Now the decoupled governing equation of the problem can be extracted easily by inserting Eq. (24) into Eq. (23). Doing so, we have:

$$ \frac{{A_{xx} }}{2L}\int_{0}^{L} {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} dx} \frac{{\partial^{2} w}}{{\partial x^{2} }} - P_{b} \frac{{\partial^{2} w}}{{\partial x^{2} }} + D_{xx} \frac{{\partial^{4} w}}{{\partial x^{4} }} = 0 $$
(27)

3 Solution method

To date, many different methods have been employed by researchers to solve static [63,64,65,66,67,68] and dynamic [69,70,71,72,73,74,75] problems of continuous systems. In this work, the Galerkin’s analytical method will be used in order to derive the nonlinear buckling load of the meta-nanocomposite beam for both S–S and C–C BCs. Based on this method, the bending deflection of the beam can be considered to be like:

$$ w(x) = \sum\limits_{m = 1}^{\infty } {W_{m} X_{m} (x)} $$
(28)

In the above definition, \(W_{m}\) stands for the amplitude of the beam’s deformation and \(X_{m} (x)\) is the eigen function i.e., responsible for satisfying the essential BCs of the problem in the longitudinal direction. According to the constraints caused by each of the considered sets of BCs on ends of the structure, the following functions are recommended for S–S and C–C beams [40]:

$$ \begin{gathered} {\text{S - S}}\,\,{\text{Beam:}}\,\,\,\,\,X_{m} (x) = \sin \left( {\frac{m\pi x}{L}} \right) \hfill \\ {\text{C - C}}\,\,{\text{Beam:}}\,\,\,\,\,X_{m} (x) = \sin^{2} \left( {\frac{m\pi x}{L}} \right) \hfill \\ \end{gathered} $$
(29)

By substituting for the bending deflection from Eq. (28) in the governing equation of the problem, i.e., Eq. (27), and considering the orthogonality of the natural modes of the continuous system, one can write the below identity:

$$ K_{L} W_{m} + K_{NL} W_{m}^{3} - P_{b} W_{m} = 0 $$
(30)

where

$$ K_{L} = D_{xx} r_{40} ,\,\,\,\,\,\,\,\,\,\,K_{NL} = \frac{{A_{xx} }}{2L}r_{11} r_{20} $$
(31)

In the above definitions, \(r_{ij}\)’s are BC-based integrals which can be calculated via following formula:

$$ r_{ij} = \int_{0}^{L} {X_{m}^{(i)} (x)X_{m}^{(j)} (x)dx} $$
(32)

in which \(X_{m}^{(i)} (x)\) denotes the ith derivative of the eigen function \(X_{m} (x)\) with respect to x. By solving Eq. (30) for \(P_{b}\), the nonlinear buckling load of the meta-nanocomposite beam can be obtained easily.

4 Results and discussion

In this part of this manuscript, numerical examples will be presented and discussed to see how can the nonlinear buckling load of the beam be influenced by changes in the properties of the auxetic nanocomposite. In these studies, the slenderness ratio of the beam is fixed on \({L \mathord{\left/ {\vphantom {L h}} \right. \kern-\nulldelimiterspace} h} = 100\) in order to satisfy the assumption of thin being of the structure. If other values are not reported, the thickness-to-inclined length and vertical-to-inclined length, and auxeticity angle of re-entrant cell rib are assumed to be 0.01, 4, and − 45°, respectively. The material properties used for the epoxy matrix and CNTs can be found by referring to Table 1. It must be noticed that in future studies, the following nondimensional form of the nonlinear buckling load is tracked:

$$ P_{cr} = \frac{{P_{b} L^{2} }}{{E_{m} h^{3} }} $$
(33)
Table 1 Material properties of polymer matrix [32] and CNT [76]
Full size table

In the first step, the accuracy of the provided material is examined by comparing the postbuckling path of GPLR nanocomposite beams with those previously generated in Ref. [29]. In this comparison, the GPLs are assumed to be uniformly distributed in the polymeric matrix and their weight fraction is fixed on 0.3%. According to Fig. 2, it can be simply realized that the results of our study are very close to those reported in [29]. It must be mentioned that small differences between our data and those reported in [29] are caused by the fact that the slenderness ratio of the beam is \({L \mathord{\left/ {\vphantom {L h}} \right. \kern-\nulldelimiterspace} h} = 10\). In this case, the structure is thick and therefore, the mechanical response is highly affected by shear deformation. Due to the fact that in the following case studies we use slenderness ratios of as big as a hundred, the provided data can be trusted confidently.

Fig. 2
figure 2

Comparison of the postbuckling paths of fully simply supported PNC beams reinforced via GPLs with those reported in Ref. [29] (WGPL = 0.3%, L/h = 10)

Full size image

In Fig. 3, the influences of gradient index p and auxeticity angle θ on the Young’s modulus of the meta-nanocomposite are highlighted. Based on this illustration, it can be easily perceived that a rise in the gradient index leads to a reduction in the Young’s modulus of the auxetic nanocomposite in any arbitrary thickness. This trend shows that it is better to consider high gradient indices in the theoretical estimations to provide a safer structure which is able to resist against compressive excitations with a higher safety factor. In addition, it is well observed that assigning bigger values (in magnitude) to the auxeticity angle results in a decrease in the total stiffness of the meta-nanomaterial. Therefore, it is not recommended to design CNTR auxetic lattices with big auxeticity angles.

Fig. 3
figure 3

Through-the-thickness variation of the Young’s modulus of the auxetic PNC for (a) p = 0.5, (b) p = 1.0, and (c) p = 5.0 whenever different values are assigned to the auxeticity angle (η = 1, µ = 0.4, wr = 0.1)

Full size image

Figure 4 is dedicated to the investigation of the impacts of agglomeration parameter η and auxeticity angle θ on the nonlinear buckling load of meta-nanocomposite beams. According to this figure, the auxetic nanocomposite beam will fail under weaker buckling stimulations if a big value is assigned to the volume fraction of the CNTs inside the clusters. The physical reason of this issue is the negative effect of the agglomeration of the CNTs on the stiffness of the meta-nanocomposite. In other words, the stiffness-enhancement mechanism will be influenced by the agglomeration phenomenon as the volume fraction of the CNTs inside the clusters is increased. In reverse, it can be seen that by choosing an auxetic lattice with in magnitude smaller θ, the postbuckling endurance of the meta-nanocomposite beam will be aggrandized at any agglomeration parameter η. The major reason of this trend is the positive effect of utilization of lower auxeticity angles on the Young’s modulus of the meta-nanocomposite. This influence can be quantitatively seen by referring to Fig. 3. In addition to these outcomes, this figure shows that beams with clamped ends can resist against buckling-mode failure rather than those containing simple supports. The reason of higher resistance of C–C beams against compression is the greater structural stiffness of the clamped BC in comparison with simply supported one. It is noteworthy that this trend will be valid in Figs. 5, 6, 7, and 8, too. Therefore, the physical justification of this issue will not be repeated again.

Fig. 4
figure 4

Variation of the nonlinear buckling load of (a) S–S and (b) C–C auxetic PNC beams versus auxeticity angle while different values are assigned to the volume fraction of the CNTs inside the clusters (W = h, µ = 0.4, wr = 0.1, p = 5)

Full size image
Fig. 5
figure 5

Variation of the nonlinear buckling load of (a) S–S and (b) C–C auxetic PNC beams versus vertical-to-inclined length of the cell rib while different values are assigned to the volume fraction of the clusters (W = h, η = 1, wr = 0.1, p = 5, θ = − 45)

Full size image
Fig. 6
figure 6

Variation of the nonlinear buckling load of (a) S–S and (b) C–C auxetic PNC beams versus vertical-to-inclined length of the cell rib while different values are assigned to the mass fraction of the CNTs (W = h, η = 1, µ = 0.4, p = 5, θ = − 45)

Full size image
Fig. 7
figure 7

Variation of the nonlinear buckling load of (a) S–S and (b) C–C auxetic PNC beams versus thickness-to-inclined length of the cell rib while different values are assigned to the gradient index (W = h, η = 1, µ = 0.4, wr = 0.1, θ = − 45)

Full size image
Fig. 8
figure 8

Postbuckling path of (a) S–S and (b) C–C auxetic PNC beams while different patterns of nanofillers’ agglomeration are considered (µ = 0.4, wr = 0.1, p = 5, θ =   −  45, t/l = 0.01, e/l = 4)

Full size image

Concentrating on the influence of the other parameter of agglomeration (µ) on the static stability of the meta-nanocomposite beam, Fig. 5 is plotted. Based on this figure, it can be realized that bigger axial compression is required for the beam to reach to the postbuckling state if high values are assigned to the volume fraction of the clusters. This trend can be justified by considering the fact that by increasing the agglomeration parameter µ the stiffness of the meta-nanocomposite will be affected by the aggregation phenomenon lesser. So, a rise in µ makes the auxetic nanocomposite stiffer. Besides, this figure reflects the impact of the vertical-to-inclined length of the re-entrant lattice on the postbuckling performance of the continuous system as well. It is clear that as the vertical-to-inclined length grows, the auxetic nanocomposite system will be weaker against buckling-mode stimulations. This trend is originated from softening influence of adding e/l on the equivalent Young’s modulus of the meta-nanocomposite. Hence, it is natural to observe such a decrease in the nonlinear buckling load of the continua. Again, it is shown that clamped beams are better alternatives to resist against axial compression.

Like Fig. 5, the variation of nonlinear buckling load of the meta-nanocomposite beams against vertical-to-inclined length of the cell rib is drawn in Fig. 6 while the mass fraction of the CNTs is varied. This figure reveals the positive influence of the CNTs’ mass fraction on the postbuckling load of the beam. In other words, implementation of a higher content of the CNTs in the composition of the auxetic nanocomposite results in having stiffer meta-nanocomposite. Remembering the direct relationship between buckling load and stiffness, this trend can be justified simply. Also, it is demonstrated that using from wider re-entrant cell ribs leads to lower resistance of the meta-nanocomposite beam against compressive excitations. The physical reason of this issue can be found by referring to former paragraph. Plus, it is obvious that C–C beams possess greater buckling resistance compared to S–S ones.

Furthermore, the influences of thickness of the re-entrant cell rib and gradient index on the nonlinear buckling load of the auxetic nanocomposite beam are covered in Fig. 7. This illustration demonstrates that the continua will be more powerful against buckling-mode failure if the thickness-to-inclined length of the cell rib is increased. In this condition, a higher content of the meta-nanocomposite will be hired and due to this issue, the auxetic beam will be stiffer. Therefore, it is not strange to observe such a hardening behavior thanks to the direct relation between buckling load and stiffness. In addition, it is demonstrated that the nonlinear buckling load of the beam in any desired BC will be reduced by assigning a bigger value to the gradient index. This trend can be justified by recalling the negative influence of the gradient index on the effective modulus of the meta-nanocomposite in any arbitrary thickness (see Fig. 3).

Finally, effect of the agglomeration pattern on the postbuckling path of the auxetic nanocomposite beams is depicted in Fig. 8. In this figure, two cases are considered. In the first one, some of the CNTs are entangled in the clusters (partial agglomeration); whereas, all of the nanofillers are aggregated in the latter case (full agglomeration). It can be easily inferred that the postbuckling path of the meta-nanocomposite beam will be shifted downward once the full agglomeration pattern is utilized instead of partial one. The physical reason of this issue is the worst effect of the full agglomeration case on the stiffness of the meta-nanocomposite in comparison with the partial agglomeration one. In other words, if all of the CNTs are entangled in the clusters, the stiffness of the nanomaterial will be more affected in negative manner. Hence, the observed trend is completely justified. Another time, it is certified that higher compressive excitations can be applied on the auxetic nanocomposite beam if clamped support is utilized instead of simple one.

5 Conclusions

The main objective of this work was to see the variation of the nonlinear buckling load of the meta-nanocomposite thin beams. To this end, a bi-step micromechanical scheme was employed to extract the equivalent modulus of the auxetic CNTR nanocomposite with respect to the effect of the agglomeration of the CNTs on the modulus estimation. Afterward, the classical theory of thin beams was hired to formulate the problem. After solving the problem with the aid of the Galerkin’s analytical method, the postbuckling load of the beam was attained. According to this comprehensive study, the following highlights can be mentioned:

  • If the effects of existence of CNT agglomerates are ignored in static design, buckling-mode failure takes place in compressive excitations smaller than those predicted theoretically.

  • The postbuckling load of the meta-nanocomposite can be enhanced by using thicker cell ribs.

  • It is recommended to use small auxeticity angles for the goal of improving the resistance of the auxetic nanocomposite structure against buckling load.

  • Too wide auxetic lattice is not proper once it is purposed to design a meta-nanocomposite structure so that it is able to endure compressive excitations.