1 Introduction

One of the most popular models of dark matter and dark energy are scalar field models where dark matter and dark energy are identified by scalar fields. Because of the homogeneity and the isotropy of the universe, these fields at cosmological scales are taken to depend only on time. The situation becomes fathomable if the corresponding scalar fields form Bose–Einstein condensates at cosmological scales. Therefore, there are many studies that study Bose–Einstein condensation of such scalar fields and their collapse at different cosmological and astronomical backgrounds. Along the same lines, we had studied a model where initially only a scalar field \(\chi \) is present and then it is converted to another scalar field \(\phi \) through a \(\phi ^2\chi \) interaction term in the background of a Robertson-Walker metric [1]. We had shown that the evolution of \(\phi \) is toward condensation provided \(\phi \) particles are heavier than \(\chi \) particles. In this study, we consider a similar setting in the background of a Reissner–Nordstrøm black hole and investigate the effect of geometry and the field content on the tendency of the system toward formation of a condensate. To be more specific, we assume that initially there is a homogeneous distribution of a diluted \(\chi \) field in the presence of a Reissner–Nordstrøm black hole [2], and it transforms to a \(\phi \) field, by time, through a \(\chi ^*\chi \phi ^*\phi \) interaction term. We consider sufficiently early times of the process (so that the energy density of \(\chi \) reaches a considerable value through superradiance [3], while the energy densities of the scalar fields do not reach sufficiently high values that change the geometry appreciably). First, we study the motion of the scalar particles in the radial direction at the level of test particles. To this end, we mainly study the problem in the corresponding 1+1-dimensional subspace of the 3+1-dimensional space because we are mainly interested in the behaviors of the fields in the radial direction. Then, we find an approximate solution of the scalar field equations in 3+1 dimensions in closed form. We find that this solution has a soliton-like wave profile as expected from the analysis at the level of test particles.

In the next section, first, we review some basic well-known facts about the Reissner–Nordstrøm metric that are essential for the derivation of our results and provide the basic equations to be used in the next section. In Sect. 3 we introduce a wave-like particular solution for the wave profile of charged scalar fields around a Reissner–Nordstrøm black hole, and we discuss the phenomenological viability of this solution. Finally, in Sect. 4 we conclude, and some technical details are derived in appendices.

2 Framework

The Reissner–Nordstrøm metric is

$$\begin{aligned} ds^2\,=\,-f\,dt^2\,+\,f^{-1}dr^2\,+\, r^2\left( d\theta ^2\,+\,\sin ^2{\theta }\,d\varphi ^2\right) , \end{aligned}$$
(1)

where

$$\begin{aligned} f=\left( 1\,-\,\frac{2M}{r}\,+\,\frac{Q^2}{r^2}\right) . \end{aligned}$$
(2)

Here M, Q are the mass and the charge of the black hole, respectively. It describes a static black hole of mass M and charge Q. One may either take the charge Q to be a local U(1) charge other than electric charge, or one may take it to be a residual electric charge \(Q\,\ll \,M\) (that may be due to much longer mean free path of an electron compared to nucleon in a hot baryonic plasma in a star, so the gravitational capture of some of the electrons by nearby astronomical objects before its collapse to form a black hole).

2.1 Motion in radial direction

Consider the following 1+1-dimensional subspace of (1)

$$\begin{aligned} ds^2\,=\,-f\,dt^2\,+\,f^{-1}dr^2. \end{aligned}$$
(3)

The Lagrangian for a test particle of mass m in the space given by (3) is

$$\begin{aligned} L\,=\,m\frac{ds}{d\tau }\,=\,m\sqrt{-f{\dot{t}}^2\,+\,f^{-1}{\dot{r}}^2}, \end{aligned}$$
(4)

where \({\dot{t}}=\frac{dt}{d\tau }\), \({\dot{r}}=\frac{dr}{d\tau }\) with \(d\tau =\sqrt{-ds^2}\). The Lagrange equation for the coordinate t results in conservation of h, i.e., the total energy (including the potential energy) per unit mass of a test particle, namely

$$\begin{aligned} h\,=\,f\,{\dot{t}}\,=\,\frac{1}{m}\frac{\partial \,L}{\partial \,{\dot{t}}}\,=\,C\,=\,\text{ constant }, \end{aligned}$$
(5)

where we have used

$$\begin{aligned} \left( -f{\dot{t}}^2+f^{-1}{\dot{r}}^2\right) \,=\,-1 \end{aligned}$$
(6)

for massive particles. Equation (6) in combination with (5) results in

$$\begin{aligned} {\dot{r}}^2\,=\,C^2\,-\,\left( 1\,-\,\frac{2M}{r}\,+\,\frac{Q^2}{r^2}\right) . \end{aligned}$$
(7)

As \(r\,\rightarrow \,\infty \), (7) becomes

$$\begin{aligned} {\dot{r}}_\infty ^2\,=\,C^2\,-\,1. \end{aligned}$$
(8)

It is well known that charged particles of charge q (of the same charge as the black hole) with low enough energies \(\omega \) with \(0\,<\,\omega \,<q\frac{Q}{r_+}\) (where \(r_+=M+\sqrt{M^2-Q^2}\) is the radius of the event horizon) can be scattered by Reissner–Nordstrøm black holes. Moreover the scalar fields obeying the condition \(m\,<\,\omega \,<\,q\frac{Q}{r_+}\) experience superradiance after being scattered [4]. Therefore one may consider scalar fields \(\chi \) with mass \(m_\chi \) and total energy \(m_\chi \,C_\chi \) that fall to the black hole from large distance that may be approximated by infinity. Further one may consider another field \(\phi \) with \(m_\phi \,>\,m_\chi \) and a quartic interaction term \(\chi ^*\chi \phi ^*\phi \) that results in \(\chi \chi \,\rightarrow \,\phi \phi \) processes. Then, by conservation of energy (in the center of mass frame) we have \(m_\chi \,C_\chi \,=\,m_\phi \,C_\phi \), i.e., \(C_\phi \,=\,C_\chi \frac{m_\chi }{m_\phi }\). On the other hand, Eq. (8) implies that when the particle can barely reach infinity, i.e., when \({\dot{r}}_\infty ^2\,=\,0\), \(C^2\,=\,1\), and in general for a particle that can reach infinity \(C^2\,\ge \,1\), and for a particle that cannot reach infinity for \(C^2\,<\,1\) (if the particle is reflected by the black hole). These two results together imply that \(\phi \) particles that are scattered by the black hole can reach only a finite distance from the black hole (which is the greater root of \((1-C^2)r_0^2-2Mr_0+Q^2=0\) for \(C\,<\,1\), \(Q\,<\,M\), that may be found by equating \({\dot{r}}\) in (7) to zero, the other root being inside the event horizon ) if \(m_\chi \,<\,m_\phi \). In other words there will be belt of \(\phi \) particles with zero or almost zero momenta around the black hole. This provides a suitable condition for formation of Bose–Einstein condensation. (In fact this explains why we do not consider the simpler case of a Schwarzschild black hole instead of a Reissner–Nordstrøm black hole. In the case of a Schwarzschild black hole there will be no scattering from the horizon, so there will be no \(\chi \chi \,\rightarrow \,\phi \phi \) processes that are essential for the formation a belt of zero momenta scalar particles around the black hole that promotes formation of condensation.). The conclusions that are derived above at the level of test particles above will be studied at the level of field theory in the following paragraphs.

2.2 The field equations for the scalars

We consider the following action for \(\chi \) and \(\phi \) particles

$$\begin{aligned} S= & {} \int \;d^4x\,\sqrt{-g}\, \Bigg \{-g^{\mu \nu }\left[ D_\mu \phi \,\left( D_\nu \phi \right) ^*\,+\, D_\mu \chi \,\left( D_\nu \chi \right) ^*\right] \,-\,m_\phi ^2\left| \phi \right| ^2\, \nonumber \\&-\, m_\chi ^2\left| \chi \right| ^2\,-\,\lambda \,\phi ^*\phi \chi ^*\chi \Bigg \}, \end{aligned}$$
(9)

where \(D_\mu \,=\,\partial _\mu \,+\,iq\,A_\mu \) with q being the electric charge of the scalar field and \(A_\mu \,=\,\left( \frac{Q}{r}, 0, 0, 0\right) \) denoting the electric field of the black hole. We let both \(\chi \) and \(\phi \) have the same charge q. In (9) we have neglected the effect of electromagnetic interactions between the scalar particles since the coupling constant of electromagnetic interactions is small, and the density of the scalar particles is taken to be small.

If the coupling term in (9) is negligible with respect to the others, then the field equation for \(\phi \) is

$$\begin{aligned} D_\mu \,D^\mu \,\phi \,-\,m_\phi ^2\,\phi \,=\,0. \end{aligned}$$
(10)

The corresponding equation for \(\chi \) may be obtained by replacing \(\phi \) in (10) by \(\chi \). Equation (10) and the corresponding equation for \(\chi \) are supplemented by the following equation obtained in Sect. 2.1.

$$\begin{aligned} C_\phi \,=\,C_\chi \frac{m_\chi }{m_\phi }. \end{aligned}$$
(11)

In other words, although the coupling constant \(\lambda \) is taken to be very small so that the interaction term may be neglected with respect to the other terms in the field equations to obtain approximate solutions, the effect of the interaction is still imposed by imposing Eq. (11). Note that, by (11), \(C_\phi \,\ll \,C_\chi \) if \(m_\chi \,\ll \,m_\phi \) which implies that one expects \(\phi \) to be much more localized than \(\chi \) as discussed in Sect. 2.1.

Using the ansatz [4]

$$\begin{aligned} \phi _\omega \left( t,r,\theta ,\varphi \right) \,=\, \sum _{l,m}e^{-i\omega \,t}Y_l^m\left( \theta ,\varphi \right) \frac{\psi _\omega \left( r\right) }{r} \end{aligned}$$
(12)

(10) reduces to

$$\begin{aligned} f^2\frac{d^2}{dr^2}\psi _\omega +ff^\prime \frac{d}{dr} \psi _\omega +\left[ \left( \omega -\frac{qQ}{r}\right) ^2-V\right] \psi _\omega \,=\,0, \end{aligned}$$
(13)

where \(\prime \) denotes derivative with respect to r, and

$$\begin{aligned} V= f\left( \frac{l(l+1)}{r^2}+\frac{f^\prime }{r}+m_\phi ^2\right) . \end{aligned}$$
(14)

We seek an approximate solution of (13) for

$$\begin{aligned} \frac{f^\prime }{r}= \frac{2}{r^2}\left( \frac{M}{r}-\frac{Q^2}{r^2}\right) \,\ll \,m_\chi ^2. \end{aligned}$$
(15)

In the next section we will show that (15) is satisfied for a wide range of \(m_\chi ^2\) provided that r is not close to \(r_+\). Note that (15) implies a similar relation for \(m_\phi ^2\) since \(m_\chi \,<\,m_\phi \). For (15) (where \(m_\chi ^2\) is replaced by \(m_\phi ^2\)) and \(l\,=\,0\) (i.e., for the motion that depends on r), (13) reduces to

$$\begin{aligned} \frac{d^2\psi _\omega }{dr_*^2}\,+\,\left[ \left( \omega -\frac{qQ}{r}\right) ^2\,-\,{\tilde{m}}_\phi ^2\right] \,\psi _\omega \,=\,0, \end{aligned}$$
(16)

where \(dr_*\,=\,f^{-1}dr\), \({\tilde{m}}_\phi ^2\,=\,f\,m_\phi ^2\). In fact, (16) is similar to the corresponding exact 1+1-dimensional field equation (see “Appendix” A). Equation (16) may be also expressed as

$$\begin{aligned} \frac{d^2\psi _\omega }{dr_*^2}\,+\,\left[ \omega ^2\, -\,m_\phi ^2\,-\,\frac{2(qQ\omega -m_\phi ^2M)}{r}\,+\,\frac{q^2Q^2-m_\phi ^2Q^2}{r^2} \right] \,\psi _\omega \,=\,0. \end{aligned}$$
(17)

3 A special solution

3.1 Derivation

In the hope of obtaining a wave-like solution for (17) we consider a following type of solution

$$\begin{aligned} \psi _\omega =e^{isr_*}g(r_*), \end{aligned}$$
(18)

where \(s^2=\omega ^2-m^2\). Equation (16), after using (18), becomes

$$\begin{aligned} \frac{g^{\prime \prime }}{g}+2is\frac{g^{\prime }}{g} -\frac{2(qQ\omega -m^2M)}{r}+\frac{(q^2-m^2)Q^2}{r^2}=0, \end{aligned}$$
(19)

where \(\prime \) denotes the derivative with respect to \(r_*\).

We try the following choice

$$\begin{aligned} \frac{g^{\prime }}{g}&=\frac{\alpha _1}{r}+\frac{\beta _1}{r^2}+\frac{\gamma _1}{r^3}, \end{aligned}$$
(20)
$$\begin{aligned} \frac{g^{\prime \prime }}{g}&=\frac{\alpha _2}{r}+\frac{\beta _2}{r^2}+\frac{\gamma _2}{r^3}, \end{aligned}$$
(21)

where \(\alpha _1\), \(\beta _1\), \(\gamma _1\), \(\alpha _2\), \(\beta _2\), \(\gamma _2\) are some functions whose explicit forms will be derived below. Hence, if such a solution exists, then (18) becomes

$$\begin{aligned} \psi _\omega =e^{isr_*}\,\exp {\left[ \int {\frac{\alpha _1\,r}{r^2-2Mr+Q^2}dr} +\int {\frac{\beta _1}{r^2-2Mr+Q^2}dr}+\int {\frac{\gamma _1}{r^3-2Mr^2+Q^2r}dr}\right] }. \end{aligned}$$
(22)

We note this equation for reference later in the next subsection.

(20) and (21) solve (19) if (see Appendix B)

$$\begin{aligned} \alpha _1= & {} \frac{9}{5}-\frac{9}{20}\bigg (\frac{M}{Q}\bigg )^2 \,, \ \ \ \ \ \ \beta _1=-\frac{9}{2}M \,, \ \ \ \ \ \ \gamma _1=3Q^2\,, \end{aligned}$$
(23)
$$\begin{aligned} \alpha _2= & {} 0 \,, \ \ \ \ \ \ \beta _2=\bigg [\frac{9}{5}-\frac{9}{20}\bigg (\frac{M}{Q}\bigg )^2\bigg ] \bigg [\frac{4}{5}-\frac{9}{20}\bigg (\frac{M}{Q}\bigg )^2\bigg ] \,, \ \ \ \ \ \ \gamma _2=2\bigg [\frac{-18}{5}+\frac{63}{40} \bigg (\frac{M}{Q}\bigg )^2 \bigg ]M. \nonumber \\ \end{aligned}$$
(24)

Inserting (23) and (24) into (19) and using \(s^2=\omega ^2-m^2\), we get three equations for three unknown quantities \(\omega \), q, m for a given M and Q:

$$\begin{aligned}&(m^2-\omega ^2)-\frac{M^2}{9Q^4}\bigg (\frac{18}{5}-\frac{63}{40}\frac{M^2}{Q^2} \bigg )^2=0, \end{aligned}$$
(25)
$$\begin{aligned}&-\frac{3M^2}{Q^2}\bigg (\frac{18}{5}-\frac{63}{40}\frac{M^2}{Q^2}\bigg )+\bigg (\frac{9}{5}-\frac{9}{20}\frac{M^2}{Q^2} \bigg ) \bigg ( \frac{4}{5}-\frac{9}{20}\frac{M^2}{Q^2} \bigg ) +(q^2-m^2)Q^2=0, \end{aligned}$$
(26)
$$\begin{aligned}&\frac{2M}{3Q^2}\bigg (\frac{18}{5}-\frac{63}{40}\frac{M^2}{Q^2}\bigg )\bigg (\frac{9}{5}-\frac{9}{20}\frac{M^2}{Q^2}\bigg )-2(qQ\omega -m^2M)=0, \end{aligned}$$
(27)

where (11) is also imposed. The apparent independence of (25) of the charges and the masses of \(\chi \) and \(\phi \) may seem to imply independence of the form of the wave profile of the charges and the masses of \(\chi \) and \(\phi \) which may be misleading because the M and Q values in (25) are indirectly related to m and q through (26) and (27). Equation (25) implies that \(\omega \,=\) \(\,m_\chi \,C_\chi \,=\) \(\,m_\phi \,C_\phi \) \(\,\le \,m_\chi \,\ll \,m_\phi \) (i.e., s is imaginary or zero). In other words, the particles \(\chi \) and \(\phi \) are either gravitationally bound or they have barely sufficient energy to come from infinity, which is in agreement with our assumptions about the \(\chi \) and \(\phi \) particles. Localization of the wave profile of \(\phi \) will be discussed in the following paragraphs. Although we neglect the effect of the interaction term in the field equations to get an approximate solution, we, in fact, impose the effect of interaction by imposing condition (11). Note that we have \(\omega _\chi \,\le \,m_\chi \) and \(m_\chi \,\ll \,m_\phi \) by assumption, while we need (11), i.e., \(\omega _\phi \,=\,\omega _\chi \) to obtain \(\omega _\phi \,\le \,m_\chi \,\ll \,m_\phi \) to make (25) self-consistent. In other words, requirement of reality of \(\omega \) and (11) guarantees consistency of (25) and vice versa. In fact, one may simply assume the condition \(\omega \,\ll \,m_\phi \) for localization of the wave profile of \(\phi \) instead of introducing the interaction between \(\chi \) and \(\phi \) (with \(\omega \,=\) \(\,m_\chi \,C_\chi \,=\) \(\,m_\phi \,C_\phi \) \(\,\le \,m_\chi \,\ll \,m_\phi \)), while such an approach would be wholly ad hoc.

Equation (22), after using (25) and (23), becomes

$$\begin{aligned} \psi _\omega= & {} \exp \Bigg \{ \left( \frac{\pm \,3 M\left( 7 M^2-16 Q^2\right) }{40 Q^4 \sqrt{Q^2-M^2}}\right) (\left( 2 M^2-Q^2\right) \tan ^{-1}\left( \frac{r-M}{\sqrt{Q^2-M^2}}\right) \nonumber \\&+\left( Q^2-2 M^2\right) \tan ^{-1}\left( \frac{\text {r}_0-M}{\sqrt{Q^2-M^2}}\right) \nonumber \\&+\sqrt{Q^2-M^2} \left( M \log \left( -2 M r+Q^2+r^2\right) -M \log \left( -2 M \text {r}_0+Q^2+\text {r}_0^2\right) +r-\text {r}_0\right) \} \nonumber \\&\times \,[\,\exp \{\left( -\frac{9 \left( M^2-4 Q^2\right) }{40 Q^2 \sqrt{Q^2-M^2}}\right) (2 M \tan ^{-1}\left( \frac{r-M}{\sqrt{Q^2-M^2}}\right) -2 M \tan ^{-1}\left( \frac{\text {r}_0-M}{\sqrt{Q^2-M^2}}\right) \nonumber \\&+\sqrt{Q^2-M^2} \left( \log \left( -2 M r+Q^2+r^2\right) -\log \left( -2 M \text {r}_0+Q^2+\text {r}_0^2\right) \right) )\} \nonumber \\&-\frac{9M}{2\sqrt{Q^2-M^2}}\left( \tan ^{-1}\left( \frac{r-M}{\sqrt{Q^2-M^2}}\right) - \tan ^{-1}\left( \frac{\text {r}_0-M}{\sqrt{Q^2-M^2}}\right) \right) \nonumber \\&+\frac{6M}{2\sqrt{Q^2-M^2}}\left( -\tan ^{-1}\left( \frac{M-r}{\sqrt{Q^2-M^2}}\right) + \tan ^{-1}\left( \frac{M-\text {r}_0}{\sqrt{Q^2-M^2}}\right) \right) \nonumber \\&+3\sqrt{Q^2-M^2} (-\log \left( -2 M r+Q^2+r^2\right) +\log \left( -2 M \text {r}_0+Q^2+\text {r}_0^2\right) \nonumber \\&+2 \log (r)-2 \log (\text {r}_0))]. \end{aligned}$$
(28)

Depending on the relative values of M and Q, the exponential function in (28) is either an increasing or decreasing real exponential in r. We discard the case of increasing real exponential functions because that case would correspond to an unphysical situation. We will discuss the implications of (28) in the next subsection.

Equations (25), (26), (27) may be solved for m, \(\omega \), and q. The solutions (that are obtained by Mathematica) are given below.

$$\begin{aligned} m_{1,2}^2= & {} \frac{9}{\left[ (3200\, Q^{16} \left( Q^2-M^2\right) \right] }\Bigg \{ 133\, M^6 Q^{10} + 124\, M^4 Q^{12} - 1104\, M^2 Q^{14} + 256\, Q^{16} \nonumber \\&\pm \;Q^{10}\,[182329\, M^{12} - 1244936\, M^{10} Q^2 + 3281072\, M^8 Q^4 - 4249216\, M^6 Q^6 \nonumber \\&+ 2552064\, M^4 Q^8 - 237568\, M^2 Q^{10} + 65536\, Q^{12}]^\frac{1}{2}\Bigg \}, \end{aligned}$$
(29)
$$\begin{aligned} \omega _{1,2}= & {} \mp \,\frac{3}{40 \,\sqrt{2}\,Q^8\left( Q^2-M^2\right) ^\frac{1}{2}}\Bigg \{98 M^8 Q^8-413 M^6 Q^{10}+1084 M^4 Q^{12}-1616 M^2 Q^{14} \nonumber \\&+256\,Q^{16}+Q^{10} [182329 M^{12}-1244936 M^{10} Q^2+3281072 M^8 Q^4 \nonumber \\&-4249216 M^6 Q^6+2552064 M^4 Q^8 -237568 M^2 Q^{10}+65536 Q^{12}]^\frac{1}{2}\Bigg \}^\frac{1}{2}, \end{aligned}$$
(30)
$$\begin{aligned} w_{3,4}= & {} \mp \,\frac{3}{40 \,\sqrt{2}\,Q^8\,\sqrt{\left( Q^2-M^2\right) }}\Bigg \{-98 M^8 Q^8+413 M^6 Q^{10}-1084 M^4 Q^{12}\nonumber \\&+1616 M^2 Q^{14} -256\,Q^{16}+Q^{10} [182329 M^{12}-1244936 M^{10} Q^2 \nonumber \\&+3281072 M^8 Q^4-4249216 M^6 Q^6 +2552064 M^4 Q^8-237568 M^2 Q^{10}\nonumber \\&+65536 Q^{12}]^\frac{1}{2}\Bigg \}^\frac{1}{2}, \end{aligned}$$
(31)
$$\begin{aligned} q_{1,2}= & {} \mp \,\left[ \frac{3}{80 \sqrt{2} Q^{17}\, \sqrt{\left( Q^2-M^2\right) }\left( 49 M^7-182 M^5 Q^2-8 M^3 Q^4+384 M Q^6\right) }\right] \nonumber \\&\times \,\Bigg \{[49 M^6 Q^{10}-1100 M^4 Q^{12}+2384 M^2 Q^{14}-256 Q^{16}+Q^{10}[182329 M^{12} \nonumber \\&-1244936 M^{10} Q^2 +3281072 M^8 Q^4-4249216 M^6 Q^6 + 2552064 M^4 Q^8 \nonumber \\&-237568 M^2 Q^{10}+65536 Q^{12}]^\frac{1}{2}] \times \,[98 M^8 Q^8-413 M^6 Q^{10}+1084 M^4 Q^{12} \nonumber \\&-1616 M^2 Q^{14}++256 Q^{16} + Q^{10}[182329 M^{12}-1244936 M^{10} Q^2\nonumber \\&+3281072 M^8 Q^4 -4249216 M^6 Q^6 +2552064 M^4 Q^8-237568 M^2 Q^{10}\nonumber \\&+65536 Q^{12}]^\frac{1}{2}]^\frac{1}{2} \Bigg \}, \end{aligned}$$
(32)
$$\begin{aligned} q_{3,4}= & {} \pm \, \left[ \frac{3}{80 \sqrt{2}\, Q^{17}\, \left( 49 M^7-182 M^5 Q^2-8 M^3 Q^4+384 M Q^6\right) \sqrt{\left( M^2-Q^2\right) }}\right] \nonumber \\&\times \,\Bigg \{[-98 M^8 Q^8+413 M^6 Q^{10}-1084 M^4 Q^{12}+1616 M^2 Q^{14}-256 Q^{16} \nonumber \\&+Q^{10}\,[182329 M^{12}-1244936 M^{10} Q^2+3281072 M^8 Q^4-4249216 M^6 Q^6\nonumber \\&+2552064 M^4 Q^8 -237568 M^2 Q^{10}+65536 Q^{12}]^\frac{1}{2}]^\frac{1}{2} [-49 M^6 Q^{10}\nonumber \\&+1100 M^4 Q^{12} -2384 M^2 Q^{14} +256 Q^{16}+Q^{10} [182329 M^{12}-1244936 M^{10} Q^2\nonumber \\&+3281072 M^8 Q^4-4249216 M^6 Q^6 +2552064 M^4 Q^8-237568 M^2 Q^{10}\nonumber \\&+65536 Q^{12}]^\frac{1}{2}]\Bigg \}. \end{aligned}$$
(33)

3.2 Viability of the solution

To check the viability of the solution, it is more suitable to express \(r_*\) in (16) or (17) in terms of multiples of M or the mass of the sun (\(M_\circ \)). Then, for example, (16) may be expressed as (see Appendix C)

$$\begin{aligned} \frac{d^2\psi _\omega }{d{\overline{r}}_*^2}+\bigg [\big ({\overline{\omega }}-\frac{{\overline{q}}{\overline{Q}}}{{\overline{r}}}\big )^2-{\overline{m}}_\phi ^2\left( 1-\frac{2{\overline{M}}}{{\overline{r}}} + \frac{{\overline{Q}}^2}{{\overline{r}}^2}\right) \bigg ]\psi _\omega =0. \end{aligned}$$
(34)

Here

$$\begin{aligned} {\overline{r}}_*&=\frac{c^2}{GM_\circ }r_*,~~ {\overline{r}}=\frac{c^2}{GM_\circ }r, \end{aligned}$$
(35)
$$\begin{aligned} {\overline{\omega }}=\omega \frac{GM_\circ }{c^3}&=\bigg (\frac{\omega }{s^{-1}}\bigg )5\times 10^{-6}, \end{aligned}$$
(36)
$$\begin{aligned} {\overline{m}}&=m\frac{GM_\circ }{\hbar c} =\bigg ( \frac{m}{kg}\bigg )\,4.5\times 10^{45}, \end{aligned}$$
(37)
$$\begin{aligned} {\overline{M}}&=\frac{M}{M_\circ }=\bigg (\frac{M}{kg}\bigg )2\times 10^{-30}, \end{aligned}$$
(38)
$$\begin{aligned} {\overline{Q}}&=\frac{Q\sqrt{k}}{M_\circ \sqrt{G}}=\bigg (\frac{Q}{C}\bigg )5,7\times 10^{-21}, \end{aligned}$$
(39)
$$\begin{aligned} {\overline{q}}=q\frac{M_\circ \sqrt{Gk}}{\hbar c}&=\bigg (\frac{q}{C}\bigg ) 4,8 \times 10^{55}, \end{aligned}$$
(40)

where k is the Coulomb’s constant and we have explicitly written G, c, \(\hbar \), k (that we had set to 1) to see the phenomenological contents of these quantities.

\({\bar{m}}_1^2\) and \({\bar{m}}_2^2\) should be positive real numbers. This condition restricts possible values of \({\bar{Q}}\) for a given value of \({\bar{M}}\). To this end, first we determine the roots of \({\bar{m}}_{1,2}^2=0\) in the equation obtained from (29) by replacing the quantities in (29) by their barred forms. We find the real roots of (29) as \({\bar{Q}}_{1,2}=\pm \,\frac{\sqrt{7}{\bar{M}}}{4}\). Then, we plot \({\bar{m}}_{1,2}^2\) versus \({\bar{Q}}\) graphs for various values of \({\bar{M}}\). We find that \({\bar{m}}_{1}^2\) is real and positive in the intervals \({\bar{Q}}\,<\,-\frac{\sqrt{7}{\bar{M}}}{4}\) and \({\bar{Q}}\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\). On the other hand, \({\bar{m}}_{2}^2\) is real and positive in the intervals \(-\frac{{\bar{M}}}{2} \sqrt{\frac{1}{2} \left( \sqrt{697}-23\right) }\,<\,{\bar{Q}}\,<\,\frac{{\bar{M}}}{2} \sqrt{\frac{1}{2} \left( \sqrt{697}-23\right) }\) and \(\frac{\sqrt{7}{\bar{M}}}{4}\,<\,{\bar{Q}}\,<\,{\bar{M}}\), \(-{\bar{M}}\,<\,{\bar{Q}}\,<\,-\frac{\sqrt{7}{\bar{M}}}{4}\).

We have also checked the consistency of the formulation by solving Eqs. (25), (26), (27) (where all quantities are replaced by their barred forms) for \({\bar{m}}^2\), \({\bar{\omega }}\), \({\bar{Q}}\) for \({\bar{q}}=0\). We have found that the corresponding \({\bar{Q}}\) and \({\bar{M}}\) satisfy \({\bar{Q}}=\pm \frac{{\bar{M}}}{4} \sqrt{\frac{1}{10} \left( 299+\sqrt{52681}\right) }\)) (which corresponds to the case \({\bar{m}}={\bar{m}}_{2}\)). As expected from the discussion in the preceding paragraph we find that it gives \({\bar{q}}=0\) for \({\bar{m}}_{2}^2\,<\,0\). Therefore, we conclude that there are no physical solutions for \(q=0\). In other words, the solution described in the paper is realized only for \(q\,\ne \,0\).

Next, we discuss the order of the values of \({\bar{m}}^2\) and \({\bar{q}}\) for the phenomenologically viable intervals of \({\bar{Q}}\) discussed above. There are four relevant sets of parameters, namely, \(\Bigg \{\) \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\), \({\bar{m}}_1^2\), \({\bar{\omega }}_1\), \({\bar{q}}_1\) \(\Bigg \}\), \(\Bigg \{\) \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\), \({\bar{m}}_1^2\), \(-{\bar{\omega }}_1\), \(-{\bar{q}}_1\) \(\Bigg \}\), \(\Bigg \{\) \(|{\bar{Q}}|\,<\,\frac{{\bar{M}}}{2} \sqrt{\frac{1}{2} \left( \sqrt{697}-23\right) }\) or \(\frac{\sqrt{7}{\bar{M}}}{4}\,<\,|{\bar{Q}}|\,<\,{\bar{M}}\), \({\bar{m}}_2^2\), \({\bar{\omega }}_3\), \({\bar{q}}_3\) \(\Bigg \}\), \(\Bigg \{\) \(|{\bar{Q}}|\,<\,\frac{{\bar{M}}}{2} \sqrt{\frac{1}{2} \left( \sqrt{697}-23\right) }\) or \(\frac{\sqrt{7}{\bar{M}}}{4}\,<\,|{\bar{Q}}|\,<\,{\bar{M}}\), \({\bar{m}}_2^2\), \(-{\bar{\omega }}_3\), \(-{\bar{q}}_3\) \( \Bigg \}\) where the subindices are the ones in (29)–(33). We have used a Mathematica code to try values of \({\bar{M}}\) (as multiples of the mass of the Sun) and different values of \({\bar{Q}}\) to find the corresponding values of \({\bar{q}}_i\), \({\bar{m}}_i\). We observe that (the positive) \({\bar{m}}_1^2\) values go to their maximum values (that decrease with increasing \({\bar{M}}\) and which are about 1 for \({\bar{M}}=1\)) as \({\bar{Q}}\,\rightarrow \,\pm {\bar{M}}\) and go to zero as \({\bar{Q}}\,\rightarrow \,\pm \frac{\sqrt{7}{\bar{M}}}{4}\), and take intermediate values in between. This implies that the value of \({\bar{m}}_1^2\) cannot exceed 1 that corresponds to a mass of order of \(10^{-45}\,kg\), i.e., of the order of \(10^{-9}\,eV/c^2\). On the other hand (the positive) \({\bar{m}}_2^2\) values go to plus infinity as \({\bar{Q}}\,\rightarrow \,0\) or as \({\bar{Q}}\,\rightarrow \,^-{\bar{M}}\) or as \({\bar{Q}}\,\rightarrow \,-^+{\bar{M}}\), while they tend to zero as \({\bar{Q}}\,\rightarrow \,\pm \,\frac{{\bar{M}}}{2} \sqrt{\frac{1}{2} \left( \sqrt{697}-23\right) }\) and take all intermediate values in between. Note that positive real values of \({\bar{m}}_2^2\) are only possible for \(|{\bar{Q}}|\,<\,{\bar{M}}\), i.e., for black holes. Once the values \({\bar{m}}_i\) are determined, the values of \({\bar{\omega }}_i\) may be determined by (25). In agreement with the range of \({\bar{Q}}\) for positive values \({\bar{m}}_1^2\), \({\bar{q}}_{1,2}\) have nontrivial values for \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\), and they go to ± infinity as \({\bar{Q}}\,\rightarrow \,\pm \,\frac{\sqrt{7}{\bar{M}}}{4}\) and go to zero as \({\bar{Q}}\,\rightarrow \,\pm \,\infty \) and \({\bar{Q}}\,\rightarrow \,\pm \,\frac{{\bar{M}}}{4}\sqrt{\frac{1}{10} \left( 299-\sqrt{52681}\right) }\), and take intermediate values (smaller than of order of 1) in between. Hence, the relevant set of parameters are \(\{\) \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\), \({\bar{m}}_1^2\), \(\pm {\bar{\omega }}_1\), \(\pm {\bar{q}}_1\) \(\}\) and \(\{\) \({\bar{M}}\,>\,|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\), \({\bar{m}}_3^2\), \(\pm {\bar{\omega }}_3\), \(\pm {\bar{q}}_3\) \(\}\). To summarize, this analysis gives two main results. The first result is that the allowed values of \({\bar{m}}^2\) are smaller than \(10^{-9}\,eV/c^2\). The second result is that Q and q in this study cannot be the usual electric charge in the light of the condition \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\) derived above and in the light of absence of observation of astronomical compact object with a significant value of an electric charge. This scenario is possible if we take q and Q as electric charges of a dark U(1) force [5]. Another result of the above analysis is that the solutions with \(| {\bar{Q}}|\,<\,\frac{\sqrt{7}{\bar{M}}}{4}\) are unphysical.

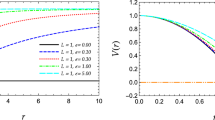
Now we check if one may find the wave profiles that are expected from a test particle treatment, i.e., if there exist wave profiles that peak about some values of r as discussed in the first part of the preceding section. Given the complicated form of (28) it is difficult to deduce simple general rules for the behavior of \(\psi _\omega \). We have plotted \(\psi _\omega \) plots for various values of its parameters by using a Mathematica code. We have found mainly two types of behaviors for \(|\psi _\omega |\), namely, exponentially increasing with increasing r, exponentially decreasing with increasing r with a local peak. We discard the exponentially increasing ones since they are unphysical. Some examples of the physically relevant cases for the physically relevant set (that is discussed above) \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\) are shown in Figs. 1, 2. We find that the corresponding \({\bar{M}}=10\) and \({\bar{Q}}=7\), \({\bar{Q}}=17\) result in \(-{\bar{\omega }}_1=0.0219237\), \(-{\bar{\omega }}_1=0.0550123\), and it seems that all \(\pm {\bar{\omega }}_1\) for \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\) are real, while all \(\pm {\bar{\omega }}_1\) for \(|{\bar{Q}}|\,<\,\frac{\sqrt{7}{\bar{M}}}{4}\) are imaginary (so, the corresponding solutions are unstable). Moreover, we find that \(\frac{{\bar{\omega }}_1^2}{{\bar{m}}_1^2}\,<\,1\) for \({\bar{M}}=10\) and \({\bar{Q}}=7,17\), while \(\frac{{\bar{\omega }}_1^2}{{\bar{m}}_1^2}\,>\,1\) for \({\bar{M}}=10\) and \({\bar{Q}}=6\), and it seems that \(\frac{{\bar{\omega }}_1^2}{{\bar{m}}_1^2}\,<\,1\) for all \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\), while \(\frac{{\bar{\omega }}_1^2}{{\bar{m}}_1^2}\,>\,1\) for all \(|{\bar{Q}}|\,<\,\frac{\sqrt{7}{\bar{M}}}{4}\). Both Figs. 1 and 2 are examples of scalar field profiles with \(\frac{\omega }{m}\,<\,1\) (as for \(\phi \) particles). The existence of the wave profiles of the form of Figs. 1, 2 is consistent with the accumulation of the scalar particles at some distance from the black hole that is suggested by the test particle behavior predicted in the first part of the preceding section. We observe that \(\frac{\omega }{m}\,>\,1\) always correspond to imaginary \(\omega \)’s, so the corresponding solutions are unstable. It is also observed that for some M, Q pairs the absolute value of \(\psi _\omega \) peaks at some values of Q, for example, as in Fig. 3.

Fig. 1
figure 1

\(|\psi _\omega |\) versus \({\bar{r}}\) graph for \({\bar{M}}=10\), \({\bar{Q}}=17\), \({\bar{r}}_0=20\)

Full size image
Fig. 2
figure 2

\(|\psi _\omega |\) versus \({\bar{r}}\) graph for \({\bar{M}}=10\), \({\bar{Q}}=7\), \({\bar{r}}_0=20\)

Full size image
Fig. 3
figure 3

\(|\psi _\omega |\) versus \({\bar{Q}}\) graph for \({\bar{M}}=10\), \({\bar{r}}=20\), \({\bar{r}}_0=30\)

Full size image

We notice that the \(\frac{f^\prime }{r}\) term is negligible with respect to \(m_\chi ^2\) for phenomenologically viable values of the parameters as can be seen below

$$\begin{aligned} \frac{f^\prime }{{\bar{r}}}= \frac{2}{{\bar{r}}^2}\left( \frac{{\bar{M}}}{{\bar{r}}}-\frac{{\bar{Q}}^2}{{\bar{r}}^2}\right) , \end{aligned}$$
(41)

where we have replaced r, M, Q by their barred forms and using (35)–(40). We find that for values of r greater than \(r_+\), \({\bar{r}}\) is at least at the order of \(\frac{M}{M_\circ }\), \({\bar{M}}\) is \(\frac{M}{M_\circ }\), \({\bar{Q}}\) for black hole solutions is at most in the order of \(\frac{M}{M_\circ }\). Therefore, \(\frac{f^\prime }{r}\) is at most in the order of 1 and for most values of r it is much smaller than 1. It is evident from (37) that \({\bar{m}}\,>\,1\) for \(mc^2\,>\,10^{-9}eV\). This, in turn, implies that one may get good information about \(\psi _\omega \) in the 3+1-dimensional case for \(l=0\) (i.e., for radial motion) by studying \(\psi _\omega \) given in this study provided that either \(mc^2\,\gg \,10^{-9}eV\) or \({\bar{r}}\,\gg \,1\). There may be also situations where \(mc^2\,>\,10^{-9}eV\) and \({\bar{r}}\,>\,2\) and \(\psi _\omega \) for \(l=0\) is a good approximation to (13). On the other hand, we have found above that the phenomenologically viable values of particle masses in this setup satisfy \(mc^2\,<\,10^{-9}eV\). However, the phenomenologically relevant interval \(\Bigg \{\) \(|{\bar{Q}}|\,>\,\frac{\sqrt{7}{\bar{M}}}{4}\), \({\bar{m}}_1^2\), \(\pm {\bar{\omega }}_1\), \(\pm {\bar{q}}_1\) \(\Bigg \}\) obtained above includes the case where \(|{\bar{Q}}|\sim \,{\bar{M}}\). Note that for small values of \({\bar{r}}\) outside the horizon \(r_+\), we have \(\frac{{\bar{M}}}{{\bar{r}}}\,\simeq \,1\). The case \(|{\bar{Q}}|\sim \,{\bar{M}}\) may make \(\frac{f^\prime }{r}\) negligible with respect to \(m_\chi ^2\) even for \(mc^2\,<\,10^{-9}eV\) for most of the values of \({\bar{r}}\) since the \(\left( \frac{{\bar{M}}}{{\bar{r}}}-\frac{{\bar{Q}}^2}{{\bar{r}}^2}\right) \) term ensures \(\frac{f^\prime }{{\bar{r}}}\sim \,0\) for small values of \({\bar{r}}\) that are in the order of 1, while the \(\frac{2}{{\bar{r}}^2}\) term ensures \(\frac{f^\prime }{{\bar{r}}}\sim \,0\) for large values of \({\bar{r}}\).

We have found that the \(\phi \) and \(\chi \) fields and the black hole must have dark electric charges. In this study we have considered small energy densities of the \(\phi \) and \(\chi \) fields so that they do not change the geometry of the space. Therefore, it is quite difficult to detect these dark matter candidates. On the other hand, we do not expect a radical change in the form of the geometry even when the energy density of the fields is increased provided we are at a sufficiently large distance from the black hole so that (15) is satisfied and the spherical shape of the wave profile is preserved, i.e., \(l=0\). In that case the geometry of the compact object will be still described by the Reissner–Nordstrøm metric. In such a situation, the presence of the scalar fields charged with a dark electric charge around a Reissner–Nordstrøm black hole (charged with the same dark electric charge) can be detected by the gravitational effect of these field(s), e.g., through their effect on the rotation curve(s) of their galax(ies) (while such an analysis will have additional, nontrivial points to be addressed). All these points need a separate and detailed analysis. To reach a definite and rigorous conclusion for the effect of non-negligible energy densities of the scalar fields, all these points must be considered in rigorous, separate detailed future studies. In fact, the question of galaxy rotation curves in the context of Bose–Einstein condensate dark matter that consists of a self-gravitating scalar dark matter gas cloud is discussed in the literature [6, 7]. There are also studies in the literature that consider the source of gravitational as a point source [8], while they do not discuss the predictions for galaxy rotations curves. Most of these studies are nonrelativistic, while there are also studies in the context of general relativity [6, 9]. [6] studies the problem through postulation of a mass density for the scalar field. On the other hand, [9] studies problem in the context of charged black holes including Reissner–Nordstrøm black hole, while scalar field is taken to be neutral. This paper also finds a localized solution of the scalar field, while the explicit form of the solution is derived only at the limits \(r_*\,\rightarrow \,\pm \infty \). In other words, there are studies in literature that have similar research interest as the present paper. The present study still has some novel aspects such as being a model of two interacting scalars that result in Eq. (11) (which may be considered as the mechanism behind the Bose–Einstein condensation in this context), and the solution given in Sect. 3 being a new analytical solution.

\(\phi \) and/or \(\chi \) particles discussed here may be taken as the only source or as one of the sources of dark matter in the universe. Given the mysterious nature of the source and the nature of dark matter, the possibility of this mechanism being the only source of dark matter cannot be wholly excluded. For example, a scenario where \(\chi \) particles (that are nonrelativistic at very large distances away from the black hole) may serve as the component of dark matter at cosmological scales, while \(\phi \) particles may be considered as the component of dark matter at galactic scales. The viability of such a scenario may be studied in future. Another related nontrivial point is that a fixed pair of M, Q results in a fixed pair of m, q by (29–33). In other words, for fixed values of \(m_\phi \), \(q_\phi \) the number of M, Q pairs is finite. At first glance, this seems to suggest that the solitonic-like scalar dark matter behavior discussed in this paper may exist only in very specific cases, so this mechanism cannot be considered as a significant source of dark matter in the universe. Such a reasoning may be misleading in the light of the following observations. Real black holes are expected to evolve in mass and charge by accretion, so they take different values through their evolution. As the black hole evolves by swallowing \(\chi \) and \(\phi \) particles, the change in the charge of the black hole evolves in proportional to the number of the swallowed particles (since charge is an additive quantum number), while the change in the mass of the black hole in general is smaller than the number of particles times their masses because of the gravitational potential between them. At the initial times of the accretion the effect of the gravitational potential between the particles may be neglected since the number density of the scalar particles is small at that time. Hence, one expects \(\frac{\Delta \,Q}{\Delta \,M}\,\simeq \,\frac{q}{m}\) at initial times, while \(\frac{\Delta \,Q}{\Delta \,M}\,>\,\frac{q}{m}\) at later times. Therefore, \(\frac{Q}{M}\) may start from a smaller value and evolve into a pair of Q and M that corresponds to formation of the solitonic solution discussed in this paper. To illustrate the argument, for example, we consider a black hole that initially has \({\bar{M}}=10\), \({\bar{Q}}=5\), and assume that it accredits by swallowing \(\phi \) and \(\chi \) particles. Let m satisfy the bound obtained above, i.e., \(mc^2\,<\,10^{-9}\,eV\). At later times \(\frac{\Delta \,{\bar{Q}}}{\Delta \,{\bar{M}}}\,\simeq \,\frac{{\bar{q}}}{{\bar{m}}}\,>\,10^{18}\) for \(q=e\) being the charge of a proton, and \(\frac{\Delta \,{\bar{Q}}}{\Delta \,{\bar{M}}}\,\simeq \,\frac{{\bar{q}}}{{\bar{m}}}\,>\,1\) for a millicharged particle [10] with \(q=10^{-18}e\), respectively. \(\Delta \,{\bar{M}}\) starts from zero and grows by time. When \(\Delta \,{\bar{M}}\) reaches \(\Delta {\bar{M}}\,=\,2\times \,10^{-18}\) for \(q=e\), then \(\frac{{\bar{Q}}+\Delta {\bar{Q}}}{{\bar{M}}+\Delta {\bar{M}}}\,>\,\frac{5+2}{10}=0.7\) which is in the physically relevant range obtained above, while \(\frac{{\bar{Q}}}{{\bar{M}}}=0.5\) is outside the physically relevant interval. In a similar way, when \(\Delta \,{\bar{M}}\) reaches \(\Delta {\bar{M}}\,=\,6\) for \(q=10^{-18}e\) , then \(\frac{{\bar{Q}}+\Delta {\bar{Q}}}{{\bar{M}}+\Delta {\bar{M}}}\,>\,\frac{5+6}{16}=0.6875\) which is in the physically relevant range obtained above, while \(\frac{{\bar{Q}}}{{\bar{M}}}=0.5\) is outside physically relevant interval. At even later times, accretion may change the M and Q values further so that the new values do not correspond to the solitonic solution, so the localized wave profile may begin to decay. However, at that time the energy density of the \(\phi \) particles around the black hole may become non-negligible so that at different distances from the black hole, the effective mass and charge of the black hole take different values. This implies that, at late times, always there will be a radial distance where the black hole’s mass and charge will satisfy the condition necessary for formation of the solitonic solution. This together with the gravitational force between the \(\phi \) particles tends to counteract dispersion of the wave profile. However, to reach a definite conclusion on this point, separate detailed technical studies on this issue are needed. Moreover, one may let \(C_\chi \) take values in an interval about \(C_\chi =1\), i.e., one may take \(\omega \) be in an interval about \(\omega =m_\chi \) instead of taking a sharp value. Hence, there will be more chance that a value of \((m_\phi ^2-\omega ^2)\) in the interval satisfies (25) for a given set of M, Q. In the light of these considerations, given the novelties of the solution and the mechanism discussed here, in our opinion, this new mechanism and the solution deserve detailed further studies that explore their all aspects and potential through future studies.

4 Conclusion

In this study we have considered the problem of evolution of a heavier scalar field \(\phi \) that is produced from a lighter homogeneously distributed scalar field \(\chi \) through a \(\chi ^*\chi \phi ^*\phi \) interaction term in the background of a Reissner–Nordstrøm black hole. To see the situation better, first, we have studied the problem at a wholly classical setting at the level of test particles. We have observed that \(\phi \) particles tend to accumulate at some distance from the black hole which provides a suitable condition for condensation. Then, we have considered the problem at the framework of field theory. We have found approximate solitonic-like solutions for the scalar fields where the heavier \(\phi \) particles seem to be more localized compared to the lighter \(\chi \) particles. This wave profile seems to suggest suitable conditions for condensation as in the case of the wholly classical treatment. We have also discussed the phenomenological viability of this model. The requirement of phenomenological viability of the model suggests that the black hole and the scalar particles should have a dark U(1) charge rather than the usual electromagnetic charge to sustain the soliton-like configuration studied in this study in a realistic framework. Note that we have argued that the \(\phi \) field is produced from \(\chi \) field through \(\chi ^*\chi \phi ^*\phi \) interactions, while we have neglected interactions between the \(\phi \) and \(\chi \) as we have obtained the wave profiles of the solutions. Although this approach may be considered as a sufficiently good approximation for small coupling constant \(\lambda \), a separate study in future where this interaction is not neglected in the derivation of the wave profile would be useful to understand all aspects of the problem.

The prospect of studying the extensions of this model along the lines mentioned above seems promising. It is a well-known fact that, in view of rotation curves of spiral galaxies and other astronomical data, there should be a localized distribution of dark matter around the centers of these galaxies. Moreover, almost all large galaxies contain supermassive black holes at their centers. Therefore, the model discussed in this study has the potential to describe such localized distributions of dark matter after the model is extended to the case of non-negligible energy density for the \(\phi \) fields provided that (at least some of) the supermassive black holes may be identified by the type of black holes discussed in this study. It will be interesting to study these points in detail in future.