Study of charged generalized polytropes with complexity factor

Abstract

The objective of this manuscript is to study the generalized polytropes in the presence of charge with the help of complexity factor. For this purpose, spherical symmetry and generalized relativistic polytropic equation of state will be used in two cases: (i) for mass density $(\mu _{o})$ and (ii) for energy density $(\mu )$, along with charge. These two cases will give two sets of differential equations, and they will be solved by mean of complexity factor. The solutions of these sets will be discussed graphically under different values of charge and parameters.

1 Introduction

The role of polytropes is very important in study of cosmological objects. Many researchers in mathematics and astrophysics have shown keen interest in the study of polytropes. Chandrasekhar [1] was the first who gave the basic idea of polytropes in Newtonian physics. Tooper [2] discussed the solution of field equations in general relativity for compressible fluid in gravitational equilibrium by using the polytropic equation of state (PEoS). He [3] also studied the solutions of relativistic hydrostatic equations using spherical symmetry for compressible fluid which obeyed the pressure–energy density relation. Kaplan and Lupanov [4] found an exact relation of density and mass using polytropic sphere. Kaufmann [5] obtained a radius–mass relation by using different values of polytropic index n for static polytropic sphere. Occhionero [6] gave the satisfactory description of effects of rotation on equilibrium structure of polytropes for n$\geqslant 2$. Kovetz [7] made some corrections in work of Chandrasekhar [1] about the theory of polytropes and confirmed some numerical results.

Horedt [8] observed that model became unstable for spherical and cylindrical polytropic index n greater than 3. Sharma[9] used Pade (2, 2) approximation to find the analytical solution for Einstein field equations with PEoS for spherical static geometry. Abramowicz[10] established the general form of Lane–Emden equation (LEe) for planer, cylindrical and spherical polytropes. Horedt [11] also used the gamma function to study the physical properties like acceleration, mass, mean density and gravitational potential. Pandey [12] used PEoS to discuss the spherical structure. Zhang and Wang [13] proved that self-gravitating polytropes are satisfied by the hydrostatic equilibrium equation.

Herrera [14] studied the relativistic polytropes by using effective variables. Herrera and Barreto [15] used PEoS to establish a generalized structure for anisotropic Newtonian stars. They [16] also developed a general formalism for polytropic models with anisotropic pressure and used Tolman mass to explain some features of these models. Herrera et al. [17] made use of conformally flat condition to reduce the parameters in an polytropic sphere and established a modified form of LEe. Herrera et al. [18] analyzed the stability of polytropes by applying the cracking technique.

The physical quantity, charge plays an important role in the study of astrophysical objects. Among the researchers, the study of charge in general relativity is always considered to be of great interest. Bonner [19] found that gravitational collapse can be delayed due to electric repulsion in spherical compact objects . Bondi [20] used Minkowski coordinates to give a detail explanation of contraction in isotropic radiating compact object. Bekenstein [21] gave the idea of hydrostatic equilibrium for gravitational collapse in charged compact object. Ray et al. [22] found that $10^{20}$ coulomb amount of charge can be held by a compact object with high density. Takisa and Maharaj [23] analyzed the models of polytropic sphere with charge. Sharif and Sadiq [24] studied the effects of charge on anisotropic polytropes.

The generalized polytropes (GPs) are defined by generalized polytropic equation of state (GPEoS) given as [25]

$$\begin{aligned} P_{\mathrm{r}}=\alpha _{1}\mu _{o} + K\mu ^{\gamma }_{o}=\alpha _{1}\mu _{o}+K\mu _{o}^{1+\frac{1}{n}}, \end{aligned}$$

(1)

where $\alpha _{1}$, $P_{\mathrm{r}}$, n, K and $\gamma$ are called linear coefficient constant, radial pressure, polytropic index, polytropic constant and polytropic exponent, respectively.

This GPEoS consists of two components

• i) Linear component, $\alpha _{1}\mu _{o}$ and

• ii) Polytropic component, $K\mu ^{\gamma }_{o}=K\mu _{o}^{1+\frac{1}{n}}$

if $\mu _{o}$ is changed by $\mu$, then Eq. (1) takes the form

$$\begin{aligned} P_{\mathrm{r}}=\alpha _{1}\mu + K\mu ^{1+\frac{1}{n}}. \end{aligned}$$

(2)

Azam et al. [25, 26] studied the polytropes with charge, using the GPEoS in the domain of general relativity, and gave the frameworks of anisotropic spherical and cylindrical polytropes. Azam and Mardan [27] carried out the stability analysis of charged polytropic models with GPEoS by using cracking technique.

Herrera [28] presented a new definition of complexity factor (CF) for a self-gravitating system. For this purpose, he used the orthogonal splitting of curvature tensor into structure scalars and named one of them as CF. After this, he gave zero value to that scalar in the context of general relativity and called it as vanishing CF. Sharif and Iqra [29] used the idea of CF on static spherical system to discuss the charge on the system. Khan et al. [30] made use of CF to give a framework for generalized spherical polytropes.

The outline of this work is as follows. In Sect. 2, we will use the spherical symmetry for the development of field equations and Tolman–Oppenheimer–Volkoff (TOV) equation. Section 3 will be devoted to discuss curvature and the Weyl tensors. In this section, mass function for gravitating object will also be studied. Orthogonal splitting of curvature tensor and CF will be discussed in Sects. 4 and  5. We will present charged GPs and energy conditions in Sect. 6. In Sect. 7, we will analyze the graphs of charged GPs with CF. In the last Sect. 8, we will conclude our discussion.

2 Einstein field equations

Consider a fluid distribution which is static spherically symmetric and the line element as

$$\begin{aligned} ds^2=e^{\nu }dt^{2}-e^{\lambda }dr^{2}-r^{2} d\theta ^{2}-r^{2}\sin ^{2}\theta d\phi ^{2}, \end{aligned}$$

(3)

where $\nu =\nu (r)$, $\lambda =\lambda (r)$ and coordinates are: $x^{0}=t, x^{1}=r, x^{2}=\theta , x^{3}=\phi$. The energy–momentum tensor is defined by

$$\begin{aligned} T_{\mu \nu }=(\mu +P_{\perp })u_{\mu }u_{\nu }-P_{\perp } g_{\mu \nu }+(P_{r}-P_{\perp })s_{\mu }s_{\nu }, \end{aligned}$$

(4)

here $P_{\perp }$ represents the tangential pressure, $u_{\mu }=(\frac{1}{e^{\frac{\nu }{2}}},0,0,0)$ ,$s_{\mu }=(0,\frac{1}{e^{\frac{\lambda }{2}}},0,0)$ are called four velocity and four vector, respectively, with properties $s^{\mu }u_{\mu }=0,\quad s^{\mu }s_{\mu }=-1,\quad u^{\mu }u_{\mu }=1.$

The electromagnetic tensor is defined by

$$\begin{aligned} \Gamma ^{i}_{j}=\frac{1}{4\pi }\left( -F^{i}_{\mu }F^{\mu }_{j} +\frac{1}{4}F^{\mu \nu }F_{\mu \nu }g^{i}_{j}\right) , \end{aligned}$$

where $F_{ij}$ is the Maxwell field tensor defined by $F_{ij}=\varphi _{j,i}-\varphi _{i,j}$ and $\varphi _{j}$ is four potential given by $\varphi _{i}=\varphi \delta ^{0}_{i}.$

The Maxwell field equations in terms of four-vector are

$$\begin{aligned} F^{ij}_{;j}=\phi _{o}J^{i}, \quad F_{[ij;k]}=0, \end{aligned}$$

where $\phi _{o}$ is the magnetic permeability and $J^{i}$ is the four current defined by $J^{i}=\sigma u^{i}$, where $\sigma$ is the charge density. The Maxwell field equation for metric (5), given as

$$\begin{aligned} \varphi ^{''}+\left( \frac{2}{r}-\frac{\nu ^{'}}{2}-\frac{\lambda ^{'}}{2}\right) \varphi ^{'}=4\pi \sigma e^{\frac{\nu +\lambda }{2}}. \end{aligned}$$

The above equation implies that

$$\begin{aligned} \varphi ^{'}=\frac{q(r)e^{\frac{\nu +\lambda }{2}}}{r}, \end{aligned}$$

where $q(r)=4\pi \int _{0}^{r}\sigma e^{\frac{\lambda }{2}}\overline{r} d\overline{r}$ denotes the total charge inside the sphere.

The field equations are

$$\begin{aligned} \mu= & {} -\frac{1}{8\pi }\left[ -\frac{1}{r^{2}}+e^{-\lambda } \left( \frac{1}{r^{2}}-\frac{\lambda '}{r}\right) -\frac{q^{2}}{r^{4}}\right] , \end{aligned}$$

(5)

$$\begin{aligned} P_{r}= & {} -\frac{1}{8\pi }\left[ \frac{1}{r^{2}}-e^{-\lambda }\left( \frac{1}{r^{2}}-\frac{\nu '}{r}\right) -\frac{q^{2}}{r^{4}}\right] , \end{aligned}$$

(6)

$$\begin{aligned} P_{\perp }= & {} \frac{1}{8\pi }\Big [\frac{1}{4e^{\lambda }}\left( \nu '^{2}-\lambda '\nu '+2\frac{\nu '-\lambda '}{r}+2\nu ''\right) \Big ]-\frac{q^{2}}{8\pi r^{4}}, \end{aligned}$$

(7)

where $`/'$ shows the differentiation w. r. t. $`r'$. Solving Eqs. (5–7) simultaneously to obtain generalized TOV equation, given as

$$\begin{aligned} P^{'}_{r}=-\frac{\nu ^{'}}{2}(\mu +P_{r})+\frac{2[(P_{\bot }-P_{r})+\frac{q q^{'}}{8\pi r^{3}}]}{r}, \end{aligned}$$

(8)

where

$$\begin{aligned} \nu '=2\frac{rm+4\pi P_{r}r^{3}-q^{2}}{r(r^{2}-2m+q^{2})}, \end{aligned}$$

(9)

then Eq. (8) becomes

$$\begin{aligned} P'_{r}=-\frac{rm+4\pi P_{r}r^{3}-q^{2}}{r(r^{2}-2m+q^{2})}(\mu +P_{r})+ \frac{2[(P_{\bot }-P_{r})+\frac{q q^{'}}{8\pi r^{3}}]}{r}, \end{aligned}$$

(10)

here m is given by

$$\begin{aligned} 1-e^{-\lambda }=\frac{2m}{r}-\frac{q^{2}}{r^{2}}, \end{aligned}$$

(11)

which implies

$$\begin{aligned} m=4\pi \int ^{r}_{0}\overline{r}^{2}\mu d\overline{r}+\int _{0}^{r}\frac{qq'}{\overline{r}}d\overline{r}. \end{aligned}$$

(12)

We can calculate the four acceleration, $a^{a}=u^{\alpha }_{,\beta }u^{\beta }$, as

$$\begin{aligned} a_{1}=-\frac{\nu '}{2}. \end{aligned}$$

(13)

It is more suitable to take the energy–momentum tensor as

$$\begin{aligned} T_{\nu }^{\mu }=\mu u^{\mu }u_{\nu }-Ph_{\nu }^{\mu }+\Delta _{\nu }^{\mu }+\Gamma ^{\mu }_{\nu }, \end{aligned}$$

(14)

with

$$\begin{aligned} \Delta _{\nu }^{\mu }= & {} \Delta (s^{\mu }s_{\nu }+\frac{1}{3}h_{\nu }^{\mu });\quad P = \frac{P_{r}+2P_{\perp }}{3},\nonumber \\ \Delta= & {} P_{r}-P_{\perp };\quad h_{\nu }^{\mu }=\delta _{\nu }^{\mu }-u^{\mu }u_{\nu }. \end{aligned}$$

(15)

We consider Reissner–Nordstrom space time for the exterior geometry

$$\begin{aligned} ds^{2}=\alpha _{2}dt^{2}-\alpha _{2}^{-1}dr^{2}-r^{2}d \theta ^{2}-r^{2}\sin ^{2}\theta d\phi ^{2}, \end{aligned}$$

(16)

where $\alpha _{2}=1-\frac{2M}{r}+\frac{Q^{2}}{r_{2}}$. The necessary and sufficient conditions for the smooth matching of two metrics Eqs. (3, 16) on the boundary $r=r_{\Sigma }=$constant, are $e^{\nu _{\Sigma }}=\alpha _{2}$, $e^{-\lambda _{\Sigma }}=\alpha _{2}$ and $P_{\Sigma }=0$. Here, Q and M are the total charge and total mass in the exterior boundary.

3 The curvature and the Weyl tensor

The curvature tensor can be written in terms of the Ricci scalar R, the Ricci tensor $R_{\alpha }^{\beta }$ and the Weyl tensor $C^{\rho }_{\alpha \beta \mu }$ as

$$\begin{aligned} R^{\rho }_{\alpha \beta \mu }=&C^{\rho }_{\alpha \beta \mu }+\frac{1}{2} R^{\rho }_{\beta g\alpha \mu }-\frac{1}{2}R_{\alpha \beta } \delta _{\mu }^{\rho }+\frac{1}{2}R_{\alpha \mu }\delta _{\beta }^{\rho }\nonumber \\&-\frac{1}{2}R_{\mu }^{\mu } g_{\alpha \beta }-\frac{1}{6} R(\delta _{\beta }^{\rho } g_{\alpha \mu }-g_{\alpha \beta }\delta _{\mu }^{\rho }). \end{aligned}$$

(17)

For spherical symmetric fluid distribution, the magnetic part of Weyl tensor vanishes and its electric part $(E_{\alpha \beta }=C_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta })$ can be expressed as

$$\begin{aligned} C_{\mu \nu 8\pi \lambda }=(g_{\mu \nu \alpha \beta }g_{\kappa \lambda \gamma \delta }- \eta _{\mu \nu \alpha \beta }\eta _{\kappa \lambda \gamma \delta })u^{\alpha } u^{\gamma }E^{\beta \delta }, \end{aligned}$$

(18)

with $g_{\mu \nu \alpha \beta }=g_{\mu \alpha }g_{\nu \alpha }$ and $\eta _{\mu \nu \alpha \beta }$. Note that

$$\begin{aligned} E_{\alpha \beta }=E\left( s_{\alpha }s_{\beta }+\frac{1}{3}h_{\alpha \beta }\right) , \end{aligned}$$

(19)

with

$$\begin{aligned} E=-\frac{1}{4r^{2}e^{\lambda }}[2-2e^{\lambda }-\frac{r^{2}}{2} (\lambda '\nu '-\nu ^{'2})+r^{2}\nu ''+r(\lambda '-\nu ')], \end{aligned}$$

(20)

satisfying

$$\begin{aligned} E_{\alpha }^{\alpha }=0,\quad E_{\alpha \gamma }=E_{(\alpha \gamma )}, \quad E_{\alpha \gamma }u^{\gamma }=0. \end{aligned}$$

(21)

From Eqs. (5–7, 17, 19) and Eqs. (11) or (12) we have

$$\begin{aligned} m=\frac{4\pi }{3}r^{3}(P_{\perp }-P_{r}+\mu )+\frac{r^{3}E}{3} +\frac{8\pi q^{2}}{3r}, \end{aligned}$$

(22)

then

$$\begin{aligned} E=-\frac{4\pi }{r^{3}}\int _{0}^{r}\overline{r}^{3}\mu 'd \overline{r}+4\pi (P_{r}-P_\perp )-8\pi \frac{q^{2}}{r^{4}}+\frac{3}{r^{3}}\int _{0}^{r} \frac{qq'}{\overline{r}}d\overline{r}. \end{aligned}$$

(23)

Using Eq. (23) into Eq. (22), we have

$$\begin{aligned} m(r)=\frac{4\pi }{3}r^{3}\mu -\frac{4\pi }{3}\int _{0}^{r} \overline{r}^{3}\mu 'd\overline{r}+\int _{0}^{r} \frac{qq'}{\overline{r}}d\overline{r}. \end{aligned}$$

(24)

Equation (23) relates the Weyl tensor with the physical properties of the self-gravitating fluid distribution, namely density in homogeneity and the anisotropy in pressure with total charge. Equation (24) expresses the corresponding mass function.

4 The orthogonal splitting of the curvature tensor

Now, we make use of orthogonal splitting of curvature tensor [31] and derived the structure scalars through which CF is defined [28]. Orthogonal splitting curvature tensor gives the following tensors [32, 33].

$$\begin{aligned} Y_{\alpha \beta }= & {} R_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$

(25)

$$\begin{aligned} X_{\alpha \beta }= & {} ^{*}R^{*}_{\alpha \gamma \beta \delta }u^{\gamma }u^{\delta }=\frac{1}{2}\eta _{\alpha \gamma }^{\epsilon \mu }R^{*}_{\epsilon \mu \beta \delta }u^{\gamma }u^{\delta }, \end{aligned}$$

(26)

where $*$ denotes the dual tensor, i.e., $R^{*}_{\alpha \beta \gamma \delta }=\frac{1}{2}\eta _{\epsilon \mu \gamma \delta }\; R_{\alpha \beta }^{\epsilon \mu }$. From field equations and Eq. (17), we may have

$$\begin{aligned} R_{\beta \delta }^{\alpha \gamma }=C^{\alpha \gamma }_{\beta \delta }+28\pi T_{[\beta ^{\delta }\delta ]}^{[\alpha \gamma ]}+8\pi T\left( \dfrac{1}{3}\delta ^{\alpha \gamma }_{[\beta ^{\delta }\delta ]} -\delta _{[\beta ^{\delta }\delta ]}^{[\alpha \gamma ]}\right) , \end{aligned}$$

(27)

Using Eq. (14) into Eq. (27)

$$\begin{aligned} R_{\beta \delta }^{\alpha \gamma }=R_{(I)\beta \delta }^{\alpha \gamma } +\beta _{(II)\beta \delta }^{\alpha \gamma }+R_{(III)\beta \delta }^{\alpha \gamma }, \end{aligned}$$

(28)

where

$$\begin{aligned} R_{(I)\beta \delta }^{\alpha \gamma }= & {} 16\pi \mu u^{[\alpha \gamma ]}u_{[\beta ^{\delta }\delta ]}-28\pi Ph^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]}+8(\mu -3P)(\dfrac{1}{3}\delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]})-\delta ^{[\alpha \gamma ]_{[\beta ^{\delta }\delta ]}}, \end{aligned}$$

(29)

$$\begin{aligned} R_{(II)\beta \delta }^{\alpha \gamma }= & {} 16\pi \Delta ^{[\alpha \gamma ]}_{[\beta ^{\delta }\delta ]}, \end{aligned}$$

(30)

$$\begin{aligned} R_{(III)\beta \delta }^{\alpha \gamma }= & {} 4u^{[\alpha \gamma ]}u_{[\beta ^{E}\delta ]}-\epsilon ^{\alpha \gamma }_{\mu }\epsilon _{\beta \delta \nu }E^{\mu \nu }=0, \end{aligned}$$

(31)

with

$$\begin{aligned} \epsilon _{\alpha \gamma \beta }=u^{\mu }\eta _{\mu \alpha \gamma \beta }, \quad \epsilon _{\alpha \gamma \beta }u^{\beta }=0, \end{aligned}$$

(32)

Now, the tensors in Eqs. (25) and (26) can be expressed as [29].

$$\begin{aligned} Y_{\alpha \beta }= & {} Y_{TF}(\frac{1}{3}h_{\alpha \beta } +s_{\alpha }s_{\beta })+\frac{1}{3}Y_{T}h_{\alpha \beta }, \end{aligned}$$

(33)

$$\begin{aligned} X_{\alpha \beta }= & {} X_{TF}(\frac{1}{3}h_{\alpha \beta }+s_{\alpha }s_{\beta })+\frac{1}{3}X_{T}h_{\alpha \beta }. \end{aligned}$$

(34)

After using the field equations, we have

$$\begin{aligned} X_{T}= & {} \frac{q^{2}}{r^{4}}+8\pi \mu , \end{aligned}$$

(35)

$$\begin{aligned} X_{TF}= & {} \frac{q^{2}}{r^{4}}+4\pi \Delta _{\alpha \beta } -E, \end{aligned}$$

(36)

$$\begin{aligned} X_{TF}= & {} \frac{4\pi }{r^3} \int _{0}^{r}\overline{r}{^3}\mu 'd\overline{r}+(8\pi -\frac{1}{2})\frac{q^{2}}{r^{4}}, \end{aligned}$$

(37)

$$\begin{aligned} Y_{T}= & {} 4\pi (\mu +3P_{r}-2\Delta )+\frac{q^{2}}{r^{4}}, \end{aligned}$$

(38)

$$\begin{aligned} Y_{TF}= & {} 4\pi \Delta +E+\frac{q^{2}}{r^{4}}, \end{aligned}$$

(39)

or using Eq. (23)

$$\begin{aligned} Y_{TF}=8\pi \Delta -\frac{4\pi }{r^3}\int _{0}^{r} \overline{r}^3\mu 'd\overline{r}+(\frac{5}{2}-8\pi )\frac{q^{2}}{r^{4}}. \end{aligned}$$

(40)

From Eq. (37) and Eq. (40)

$$\begin{aligned} \frac{2q^{2}}{r^{4}}+8\pi \Delta =X_{TF}+Y_{TF}. \end{aligned}$$

(41)

5 Complexity factor and fluid distribution

We have already known that the factor $Y_{TF}$ is defined as CF by Herrera in [28]. There are many elements due to which complexity is produced in the system, for example, pressure anisotropy, density inhomogeneity, viscosity, heat dissipation and charge. In the absence of the above-mentioned elements, a system having homogeneous energy density and isotropic pressure is the simplest system with vanishing complexity. However, the sources of complexity in our fluid distribution are charge, anisotropic pressure and inhomogeneous energy density. The scalar $Y_{TF}$ in Eq. (40) contains all the terms (elements) due to which complexity produced in the system; therefore, the scalar $Y_{TF}$ is termed as CF [29].

The field Eqs. (5–7) form a set of three differential equations, having five unknowns $(\lambda ,\nu ,\mu ,P_{\perp },P_{r})$. Using the condition $Y_{TF}=0$, we still need one more condition to solve set of differential equations. For this purpose Eq. (40), vanishing CF condition will give

$$\begin{aligned} \Delta = \frac{1}{2r^3}\int _{0}^{r}\overline{r}^3 \mu 'd\overline{r}+\left( 1-\frac{5}{16\pi }\right) \frac{q^{2}}{r^{4}}. \end{aligned}$$

(42)

6 Relativistic generalized polytropes

Consider GPEoS for anisotropic fluid [25] as

Case 1

$$\begin{aligned} P_{r}=\alpha _{1}\mu _{o}+K\mu _{o}^{1+\frac{1}{n}}, \end{aligned}$$

(43)

the mass density $\mu _{o}$ related to total energy density $\mu$ [17] as

$$\begin{aligned} \mu =\mu _{o}+nP_{r}. \end{aligned}$$

(44)

Let us consider the following assumptions

$$\begin{aligned} r= & {} \frac{\xi }{A}, \quad \alpha =\frac{P_{rc}}{\mu _{c}} ,\quad A^{2}=\frac{4\pi \mu _{c}}{(1+n)\alpha }. \end{aligned}$$

(45)

$$\begin{aligned} \psi _{o}= & {} \frac{\mu _{o}}{\mu _{oc}},\quad v(\xi )= \frac{m(r)A^{3}}{4\pi \mu _{c}}. \end{aligned}$$

(46)

Then, TOV Eq. (9) becomes

$$\begin{aligned} \nonumber&-\Big [(\alpha ^2 (n+1) \xi (\xi -2 \alpha (n+1) v)+4 \pi P_{rc}q^2) (4 \pi P_{rc}^2qq' \nonumber \\&\quad -\big [\alpha ^3 \big . (n+1)^2 \xi ^3 (\xi P_{rc} \psi _{o}^n \psi _{o}' ((n+1) \psi _{o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n) +\alpha _{1} n (1-\alpha n))\nonumber \\&\quad -2 \alpha \Delta \psi _{o})\big ]\big / \big [\psi _{o}\big ])][(n+1)^2 \xi ^3]+\alpha ^3P_{rc} \psi _{o}^n ((n+1) \psi _{o}(\alpha -\alpha _{1}\nonumber \\&\quad +\alpha \alpha _{1} n)-(\alpha n-1) (\alpha _{1}+\alpha _{1} n+1)) (\alpha ^3 (n+1)^2 \xi (-v-\xi ^3 \psi _{o}^n(\alpha _{1}\nonumber \\&\quad +\psi _{o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n)+\alpha \alpha _{1} (-n)))+4 \pi P_{rc}q^2)\Big ]\Big /\Big [4 \pi \alpha ^4P_{rc}\Big ]=0, \end{aligned}$$

(47)

where $`/'$ shows the differentiation w. r. t. $\xi$. From Eq. (5) and Eq. (11), we have

$$\begin{aligned} m'=4\pi r^{2}\mu +\frac{qq'}{r}, \end{aligned}$$

(48)

or from Eqs. (45, 46) we have

$$\begin{aligned} \dfrac{dv}{d\xi }=\xi ^2 \psi _ {o}^n (n \psi _ {o} (\alpha -\alpha _{1}+\alpha \alpha _{1} n)-(\alpha n-1) (\alpha _{1} n+1))+\frac{4 \pi P_{rc} q q'}{\alpha ^3 (n+1)^2 \xi }. \end{aligned}$$

(49)

The boundary of surface of sphere is defined by $\xi =\xi _{n}$ such that $\psi _{o}(\xi _{n})=0$ and the following boundary conditions are applied

$$\begin{aligned} v(\xi =0)=0\quad and \quad \psi _{o}(\xi =0)=1 . \end{aligned}$$

(50)

Equations (47, 49) both give the LEe for GPEoS in this case

$$\begin{aligned}&-\Big [-n P_{rc} \alpha ^3 ((n \alpha -1) (n \alpha _{1}+\alpha _{1}+1)-(n+1) (\beta _{1}) \psi _{o}) ((n+1)^2 \xi (\nonumber \\&\quad -\xi ^3 (-n \alpha \alpha _{1}+\alpha _{1}+(\beta _{1}) \psi _{o}) \psi _{o}^n-v ) \alpha ^3+4 \pi P_{rc} q^2){\psi _{o}}' \psi _{o}^{n-1}+(n+1) \nonumber \\&\quad P_{rc} \alpha ^3 (\beta _{1}) ((n+1)^2 \xi (-\xi ^3 (-n \alpha \alpha _{1}+\alpha _{1}+(\beta _{1}) \psi _{o}) \psi _{o}^n-v ) \alpha ^3+4 \pi P_{rc} q^2)\nonumber \\&\quad {\psi _{o}}' \psi _{o}^n+P_{rc} \alpha ^3 ((n \alpha -1) (n \alpha _{1}+\alpha _{1}+1)-(1+n) (\beta _{1}) \psi _{o}) (\big [(1+n)^2 \alpha ^3 (\xi ^3\nonumber \\&\quad (\psi _{o} ((4+n) (\beta _{1}) \psi _{o}-(n \alpha -1) ((n+4) \alpha _{1}+1))+\xi (n (1-n \alpha ) \alpha _{1}+(1+n)\nonumber \\&\quad \beta _{1} \psi _{o}) {\psi _{o}}') \psi _{o}^n+v \psi _{o})\big ]\big /\big [\psi _{o}\big ]-4 \pi P_{rc} q q') \psi _{o}^n-\big [3 (\xi (n+1) (\xi -2 (1+n) \nonumber \\&\quad v \alpha ) \alpha ^2+4 \pi P_{rc} q^2) ((n+1)^2 \alpha ^3 (2 \alpha \Delta \psi _{o}-P_{rc} \xi \psi _{o}^n ((1-n \alpha )n \alpha _{1}+(n+1)\nonumber \\&\quad (\beta _{1}) \psi _{o}) {\psi _{o}}') \xi ^3+4 q \pi P_{rc}^2 \psi _{o} q')\big ]\big /\big [(n+1)^2 \xi ^4 \psi _{o}\big ]+\big [2 \alpha ^2(\xi +(n+1) \alpha \nonumber \\&\quad (-\xi ^3 (n (\beta _{1}) \psi _{o}-(-1+n \alpha ) (1+n \alpha _{1})) \psi _{o}^n-v )) ((1+n)^2 \alpha ^3 (2 \alpha \Delta \psi _{o}-P_{rc} \xi \nonumber \\&\quad \psi _{o}^n (n (1-n \alpha ) \alpha _{1}+(1+n) \beta _{1} \psi _{o}) {\psi _{o}}') \xi ^3+4 \pi P_{rc}^2 q q' \psi _{o} )\big ]\big /\big [(1+n) \xi ^3\nonumber \\&\quad \psi _{o}\big ]+\big [(\xi (1+n) (\xi -2 (1+n) v \alpha ) \alpha ^2+4 \pi P_{rc} q^2) ((n-1) n (n+1)^2 \nonumber \\&\quad P_{rc} \alpha ^3 (n \alpha -1) \alpha _{1} \xi ^4{\psi _{o}}'^2 \psi _{o}^n-n (n+1)^2 P_{rc} \alpha ^3 \xi ^3 ((n+1) (\beta _{1}) \xi {\psi _{o}}'^2\nonumber \\&\quad -4 (n \alpha -1) \alpha _{1} {\psi _{o}}'+(1-n \alpha ) \alpha _{1} \xi {\psi _{o}}'') \psi _{o}^{n+1}-(n+1)^3 P_{rc} \alpha ^3 (\beta _{1})\nonumber \\&\quad \xi ^3 (4 {\psi _{o}}'+\xi {\psi _{o}}'') \psi _{o}^{n+2}+2 (3 (n+1)^2 \Delta \xi ^2 \alpha ^4+2 \pi P_{rc}^2 (q'^2+q q'')) \psi _{o}^2)\big ]\nonumber \\&\quad \big /\big [(n+1)^2 \xi ^3 \psi _{o}^2\Big ]\Big /\Big [4 \pi P_{rc} \alpha ^4\Big ]=0, \end{aligned}$$

(51)

where $\beta _{1}=n \alpha _{1} \alpha +\alpha -\alpha _{1}$.

Case 2

We can also consider [25]

$$\begin{aligned} P_{r}=\alpha _{1}\mu +K\mu ^{1+\frac{1}{n}}, \end{aligned}$$

(52)

in this case mass density $\mu _{o}$ is put back by energy density $\mu$ in Eq. (44), and they are connected as [15]

$$\begin{aligned} \mu =\frac{(-1)^{n}\mu _{o}}{(K\mu _{o}^{1/n}-1)^{n}}. \end{aligned}$$

(53)

Taking $\psi ^{n}=\frac{\mu }{\mu }_{o}$ we obtain TOV equation as

$$\begin{aligned}&-\frac{1}{4 \pi \alpha ^4 P_{rc}}(\big [(\alpha ^2 (1+n) \xi (\xi -2 \alpha (1+n) \nu )+4 \pi P_{rc} q^2) (\big [\alpha ^3 (n+1)^2 \xi ^3\nonumber \\&\quad (2 \alpha \Delta \psi +\xi P_{rc} \psi ^n \psi ' ((n+1) ({\alpha _{1}}-\alpha ) \psi -{\alpha _{1}} n))\big ]\big /\big [\psi \big ]+4 \pi P_{rc}^2 q q')\big ]\nonumber \\&\quad \big /\big [(n+1)^2 \xi ^3\big ]+\alpha ^3 P_{rc} \psi ^n ((\alpha -{\alpha _{1}}) \psi +{\alpha _{1}}+1) (\alpha ^3 (n+1)^2 \xi (-\nu \nonumber \\&\quad -\xi ^3 \psi ^n((\alpha -{\alpha _{1}}) \psi +{\alpha _{1}}))+4 \pi P_{rc} q^2)=0, \end{aligned}$$

(54)

and from Eq. (48) we have

$$\begin{aligned} \frac{dv}{d\xi }=\xi ^{2}\psi ^{n}+\frac{4 \pi P_{rc} q q'}{\alpha ^3 (n+1)^2 \xi }. \end{aligned}$$

(55)

Equations (54, 55) together give the generalized LEe

$$\begin{aligned}&-\big [4 \alpha ^6 \Delta (n+1) \xi -\alpha ^3 \psi ^{n-2} (\psi ^2 (4 \pi (n+1) \xi {P_{rc}}^2 (\alpha -{\alpha _1}) q^2 \psi ''\nonumber \\&+\alpha ^2 (n+1)^2 \xi ^2 (4 \alpha ^2 \Delta \xi +{P_{rc}} (\alpha -{\alpha _1}) (\xi \psi ''+3 \psi '))-4 \pi ({\alpha _1}\nonumber \\&-1) {P_{rc}}^2 q q')+{\alpha _1} (n-1) n \xi {P_{rc}} \psi '^2 (\alpha ^2 (n+1) \xi ^2+4 \pi {P_{rc}} q^2) \nonumber \\&+n {P_{rc}} \psi ({\alpha _1} \xi \psi '' (\alpha ^2 (n+1) \xi ^2+4 \pi {P_{rc}} q^2)+\psi ' (\alpha ^2 (n+1) \xi ^2 (3 {\alpha _1}\nonumber \\&+(n+1) \xi (\alpha -{\alpha _1}) \psi ')+4 \pi {P_{rc}} q^2 ((n+1) \xi (\alpha -{\alpha _1}) \psi '-1)))\nonumber \\&+4 \pi {P_{rc}}^2 ({\alpha _1}-\alpha ) \psi ^3 q q')+\big [4 \pi {P_{rc}}^2 (\alpha ^2 (n+1) \xi ^3 q'^2+\alpha ^2 (n+1) \xi ^2 \nonumber \\&q (\xi q''-q')+4 \pi \xi {P_{rc}} q^2 q'^2+4 \pi {P_{rc}} q^3 (\xi q''-3 q'))\big ]\big /\big [(n+1)^2 \xi ^4\big ]\nonumber \\&+\alpha ^3 v (-4 \alpha ^4 \Delta (n+1)^2+\alpha ^3 (-(n+1)^2) {P_{rc}} \psi ^{n-2} ((\alpha -{\alpha _1}) \psi ^3+\psi ^2\nonumber \\&({\alpha _1}-(n+1) \xi (\alpha -{\alpha _1}) (2 \xi \psi ''+3 \psi ')+1)+n \xi \psi (\psi ' (-3 {\alpha _1}+2 (n+1)\nonumber \\&\xi ({\alpha _1}-\alpha ) \psi '+1)-2 {\alpha _1} \xi \psi '')-2 {\alpha _1} (n-1) n \xi ^2 \psi '^2)-\big [8 \pi {P_{rc}}^2 (\xi q'^2\nonumber \\&+q (\xi q''-2 q'))\big ]\big /\big [\xi ^3\big ])-\alpha ^6 (n+1)^2 \xi ^3 {P_{rc}} \psi ^{2 n-1} (\psi (({\alpha _1}-\alpha ) \psi -{\alpha _1}\nonumber \\&-1) (4 ({\alpha _1}-\alpha ) \psi -4 {\alpha _1}-1)+\xi \psi ' ((\alpha -{\alpha _1}) \psi (2 {\alpha _1}+2 (n+1) (\alpha \nonumber \\&-{\alpha _1}) \psi +4 {\alpha _1} n-1)+2 {\alpha _1}^2 n))\big ]\big /\big [4 \pi \alpha ^4 {P_{rc}}\big ]=0. \end{aligned}$$

(56)

All models must satisfy the energy conditions [24].

$$\begin{aligned} \mu +\frac{q^{2}}{8\pi r^{4}}>0,\quad \frac{P_{r}}{\mu }\le 1+\frac{q^{2}}{4\pi r^{4}}, \quad \frac{P_{\perp }}{\mu }\le 1. \end{aligned}$$

(57)

In case 1, conditions (57) get to be as

$$\begin{aligned} \nonumber&n\alpha +n\alpha _{1}(n\alpha -1)<1+\frac{2\pi \mu _{c}\psi _{o}^{-n}}{\alpha ^{2}(n+1)^{2}\xi ^{4}},\,\alpha \psi _{o}+\alpha _{1}(1-n\alpha )(1-\psi _{o})\nonumber \\&\quad \le (1-n\alpha )(n\alpha _{1}+1)+\psi _{o}n(\alpha -\alpha _{1}+n\alpha \alpha _{1})+\frac{2\pi \mu _{c}\psi _{o}^{-n}}{\alpha ^{2}(n+1)^{2}\xi ^{4}},\nonumber \\&\quad 2(n\alpha -1)(n\alpha _{1}+1)+(1-n\alpha )+\frac{3v}{\xi ^{3}\psi _{o}^{n}}+\frac{8\pi q\mu _{c}\psi _{o}^{-n}}{\xi ^{2}(1+n)}\nonumber \\&\quad \left[ \frac{q'}{\xi }-\frac{2q}{(1+n)\alpha ^{2}}\right] \le [2n(n\alpha \alpha _{1}-1)+\alpha (n-1)+1]\psi _{o}, \end{aligned}$$

(58)

and in case 2 these conditions (57) become as

$$\begin{aligned} \nonumber&\mu +\frac{2q^{2}\pi \mu _{c}^{2}}{\xi ^{4}\alpha ^{2}(n+1)^{2}}>0,\quad \alpha _{1}+(\alpha -\alpha _{1})\psi \le 1+\frac{4\pi \mu \psi ^{-n}}{(1+n)^{2}\alpha ^{2}\xi ^{4}},\nonumber \\&\quad [\alpha _{1}(1-n\alpha )-2]+[\alpha -\alpha _{1}(1-n\alpha )]\psi +\frac{3v}{\xi ^{3}\psi ^{n}}+\frac{8\pi q\mu _{c}\psi ^{-n}}{\xi ^{2}(1+n)}\nonumber \\&\quad \left[ \frac{q'}{\xi }-\frac{2q}{(1+n)\alpha ^{2}}\right] \le 0. \end{aligned}$$

(59)

7 Complexity factor with relativistic generalized polytropes

7.1 Case No.1

Using Eqs. (45, 46) with $Y_{TF}=0$, we have

$$\begin{aligned}&\Big [2 \xi \Delta '+6 \Delta +{\mu _{c}} (-n) \xi {\psi _{o}}^{n-1} {\psi _{o}}' ((n+1) {\psi _{o}} (\alpha -{\alpha _{1}}\alpha {\alpha _{1}} n)+\alpha {\alpha _{1}} n)\nonumber \\&+\alpha {\alpha _{1}} n)-(\alpha n-1) ({\alpha _{1}} n+1))+\big [4 \pi {\mu _{c}}^2 (\frac{2-16 \pi }{(n+1)^2}+\frac{3}{(n+1)^2}) q q'\big ]\nonumber \\&\big /\big [\alpha ^2 \xi ^3\big ]+\big [{4 \pi (8 \pi -1) {\mu _{c}}^2 q^2}\big ]\big /\big [{\alpha ^2 (n+1)^2 \xi ^4}\big ]\Big ]\big /\Big [{\mu _{c}} n\Big ]=0. \end{aligned}$$

(60)

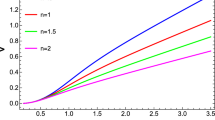
Now, Eqs. (47, 49, 60) make a set of differential equations involving three variables v, $\psi _{o}$ and $\Delta$ depending on charge and parameters n, $\alpha$, $\alpha _{1}$. This set of differential equations is numerically solved, and the solution is explained graphically. Figures (1, 2, 3) depict the curves of v, $\psi _{o}$ and $\Delta$.

Fig. 1

Graphs between $\xi$ and v for $\alpha _{1}=.5$, $n=1$, $\alpha =.58$ and $q = .2\,M_{\odot }$ (graph a); $q = .4\,M_{\odot }$ (graph b); $q = .6\,M_{\odot }$ (graph c) and $q = .7\,M_{\odot }$ (graph d)

Fig. 2

Graphs between $\xi$ and $\psi _{o}$; for $\alpha _{1}=.5$, $n=1$, $\alpha =.58$ and $q = .2\,M_{\odot }$ (graph a); $q = .4\,M_{\odot }$(graph b); $q = .6\,M_{\odot }$ (graph c) and $q = .7\,M_{\odot }$ (graph d)

Fig. 3

Graphs between $\xi$ and $\Delta$; for $\alpha _{1}=.5$, $n=1$, $\alpha =.58$ and $q = .2\,M_{\odot }$ (graph a); $q = .4 \,M_{\odot }$ (graph b); $q = .6\,M_{\odot }$ (graph c) and $q = .7\,M_{\odot }$ (graph d)

7.2 Case No.2

For case 2, we shall read the complexity factor as

$$\begin{aligned}&\Big [\xi ^4 (2 \xi \Delta '+6 \Delta -{\mu _{c}} n \xi \psi ^{n-1} \psi ')+\big [4 \pi {\mu _{c}}^2 (\frac{2-16 \pi }{(n+1)^2}+\frac{3}{(n+1)^2}) \xi q q'\big ]\nonumber \\&\big /\big [\alpha ^2\big ]+\big [4 \pi (8 \pi -1) {\mu _{c}}^2 q^2\big ]\big /\big [\alpha ^2 (n+1)^2\big ]\Big ] \Big /\Big [{\mu _{c}} n \xi ^4\Big ]=0. \end{aligned}$$

(61)

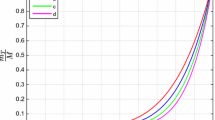
Equations (54, 55, 61) constitute a set of differential equations involving three variables $\Delta$, v and $\psi$ depending on charge and parameters $\alpha _{1}$, $\alpha$ and n. This set of differential equations is solved numerically, and the solution is explained through graphs in Figs. (4, 5, 6).

Fig. 4

Graphs between $\xi$ and v; for $\alpha _{1}=.5$, $n=1$, $\alpha =0.5$ and $q=0.2\,M_{\odot }$ (graph a); $q=0.25\,M_{\odot }$ (graph b); $q=0.3\,M_{\odot }$ (graph c) and $q=0.39\,M_{\odot }$ (graph d)

Fig. 5

Graphs between $\xi$ and $\psi$; for $\alpha _{1}=.5$, $n=1$, $\alpha =0.5$ and $q=0.2\,M_{\odot }$ (graph a); $q=0.25\,M_{\odot }$ (graph b); $q=0.3\,M_{\odot }$ (graph c) and $q=0.39\,M_{\odot }$ (graph d)

Fig. 6

Graphs between $\xi$ and $\Delta$; for $\alpha _{1}=.5$, $n=1$, $\alpha =0.5$ and $q=0.2\,M_{\odot }$ (graph a); $q=0.25\,M_{\odot }$ (graph b); $q=0.3\,M_{\odot }$ (graph c) and $q=0.39\,M_{\odot }$ (graph d)

8 Summary

In this study, we have discussed the charged polytropes with GPEoS with help of vanishing CF. In this regard, anisotropic inner fluid distribution with spherical static symmetry is used for compact object. We developed the Einstein field equations and calculated the mass function. The structure scalars in the context of charge have been studied, and CF is obtained. We have developed charged generalized LEe under the assumption of Eqs. (45, 46) to discussed the physical properties of relativistic GPs. These relativistic GPs have been studied into two cases, and these cases are (1) mass density and (2) energy density. The energy conditions for these two cases have also been developed under the assumption of Eqs. (45, 46) in the context of electromagnetic field. These two cases led us to the two sets of differential equations. The vanishing CF is discussed and used to solve the two sets of differential equations.

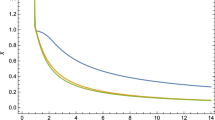
Figures (1, 2, 3) show the behavior of variables involve in the solution of differential equations for case (1). These figures illustrate the response of v, $\psi _{o}$ and $\Delta$ against distinct value of parameters and charge. The graphs in Fig. 1 show that v is zero at center and gradually increases, attaining a maximum value and then it shows a downward trend. Figure 2 depicts that $\psi _{o}$ has maximum value near center and decreases with the increase of radius till it becomes zero at surface boundary. In Fig. 3, $\Delta$ which is the measure of anisotropy shows the same behavior as shown by the $\psi _{o}$, but the graphs of $\Delta$ are less curved than $\psi _{o}$.

In case (2), graphs in Figs. (4, 5, 6) behave in the same pattern for v, $\psi$ and $\Delta$ against distinct values of $\xi$. They have zero value from $\xi =0$ to $\xi =2.5$ and then show a sudden increase.

In [30], behavior of variables v, $\psi _{o}$ and $\Delta$ was discussed for anisotropic spherical symmetrical fluid distribution with the help of complexity factor. In the present work, we have studied same variables with the addition of charge under the same procedure as discussed in [30]. We observed that addition of charge changed the orientation of graphs of v, $\psi _{o}$ and $\Delta$. For example, graphs of v in the present work are concave down, while in [30] concave up, but in both studies graphs of v are increasing. In case of $\psi _{o}$, graphs of the present paper and [30] are entirely different, i.e., charge completely changes the behavior of $\psi _{o}$. When we compare the graphs of $\Delta$ with the graphs of [30] we see that in both cases the values of $\Delta$ are maximum near the center and then become zero at boundary surface, but in the present work there is sudden decrease in the value of $\Delta$, whereas in [30] value of $\Delta$ decreases gradually.

In case 2, the graphs of v, $\psi$ and $\Delta$ in both papers (present and [30]) behave almost in the same pattern except that values of these variables show an abrupt increase at boundary surface, whereas they show gradually increase toward the boundary surface in [30].

It is also noticeable that when we take value of $\alpha =10^{-10}$ as in [30], graphs of all the variables show ambiguous behavior, so in the present work we have to choose the value of $\alpha =0.58$. So the presence of charge accelerates the spin rate of compact object.