Effect of zero mass flux condition on heat and mass transfer analysis of nanofluid flow inside a cavity with magnetic field

Abstract

The present paper examines steady natural convection of Buongiorno’s model nanofluid flow in a square cavity with enhanced mass flux boundary condition numerically. The impact of magnetic field, Brownian motion, radiation and thermophoresis is also considered in this analysis. The governing equations are represented in terms of stream function, temperature and concentration which are solved by utilizing finite difference method of second-order accuracy. The results are presented in the form of streamlines, temperature lines, concentration lines, local Nusselt number and Sherwood number for various values of influenced parameters, such as, Rayleigh number $\left( {100 \le {\text{Ra}} \le 10^{3} } \right)$, Magnetic parameter $\left( {0.1 \le {\text{M}} \le 0.5} \right)$, Buoyancy ratio parameter $\left( {0.1 \le {\text{Nr}} \le 1.0} \right)$, Radiation number $\left( {0.1 \le {\text{R}} \le 1.0} \right)$, Brownian motion number $\left( {0.1 \le {\text{Nb}} \le 0.7} \right)$, Thermophoresis number $\left( {0.1 \le {\text{Nt}} \le 1.0} \right)$ and Lewis number $\left( {10 \le {\text{Le}} \le 20} \right)$ are represented through graphs. The outcomes indicate that noticeable intensification in rate of heat transfer is perceived after suspending nanoparticles. Furthermore, increasing the values of both thermophoresis and Brownian motion parameters augments the values of Nusselt number inside the cavity.

1 Introduction

In recent day’s majority of the research community are working on nanofluids as it is more extensive area and its gigantic range of significances in transportation, cooling of electronic devises, biomedicine, food, heat exchangers, double windowpane, etc. Most of the research works suggest that the incident of nanoparticles in base fluids intensifies the rate of heat transfer due to its higher thermal conductivity. To amplify the general fluids thermal conductivity, such as, engine oils, ethylene glycol, kerosene and water we have to suspend different types of nanoparticles, like, Graphene, gold, alumina, silica, silver, copper, carbon nanotubes, etc., to the base fluids. Numbers of research articles are recognized in literature survey which deals the enrichment of base fluids thermal conductivity by adding various types of nanoparticles [1,2,3,4,5,6,7,8,9,10].

Natural convection nanofluid flow, heat and mass transfer within an enclosure has gained much research interest in engineering systems, science and technology due to its variety of significances in design of nuclear reactors, technology of lubrication, solar collectors operating systems, ventilation of houses, energy stock filling systems, heat exchangers, high performance building insulation, cooling of containment buildings, etc. In all above applications the model is constructed in terms of natural convection inside a cavity of several geometries. Noghrehabadi et al. [11] presented finite volume method to analyze isotherms and streamlines distributions of ${\text{CuO}}{-}{\text{Water}}$ based nanofluid flow within a closed chamber by considering double heat sink/source and detected intensification in heat transfer rate with growing values of Rayleigh number. Elshehabey and Ahmed [12] discussed the impact of thermophoresis and Brownian motion on nanoparticle volume fraction contours, isotherms and streamlines distributions of Buongiorno’s model MHD nanofluid flow inside a lid-driven cavity and perceived deterioration in nanofluid flow as magnetic parameter values rises. Sheremet et al. [13] studied mass and heat transfer analysis of nanofluid flow inside an open porous cavity with left wall has wavy surface and right wall has flat surface and noticed that with up surging values of wavy surface parameter the values of Nusselt number elevates. Sheremet et al. [14, 15] analyzed Buongiorno’s model natural convection MHD flow, heat transfer characteristics of nanofluid inside an enclosure. Ghalambaz et al. [16] presented finite element solution to investigate mass and heat transfer behavior of Buongiorno’s model nanofluid flow inside a square porous cavity with radiation and Eckert number and perceived that the rate of heat transfer up surges with intensifying values of Lewis number. Kefayati and Tang [17] perceived entropy generation of nanofluid flow, mass and heat transfer analysis within a cavity under the impact of thermophoresis and magnetic field and detected diminutions in entropy generations with elevating values of power-low index parameter. Kefayati and Che Sidik [18] studied non-Newtonian nanofluid entropy generation flow, heat transfer analysis inside an inclined cavity and noticed that with augmenting values of buoyancy ratio parameter the total entropy generation is intensifies. Chandra Sekhar et al. [19] discussed the impact of heat sink/source and radiation parameter on isoconcentrations, isotherms and streamlines distributions of Buongiorno’s model nanofluid inside a porous cavity. The resulting equations are solved by using finite element method and found that the values of Nusselt number are highly influenced with thermophoresis. Khalili et al. [20] professed ${\text{water}}{-}{\text{Al}}_{2} {\text{O}}_{3}$ nanofluid natural convection heat transport inside an enclosure experimentally and identified that the nanoparticle volume fraction augments from 18 to 28.74% with Rayleigh number. Selimefendigil and Öztop [21] examined heat transport and flow of ${\text{water}}{-}{\text{Al}}_{2} {\text{O}}_{3}$ based nanofluid within a trapezoidal lid-driven cavity by taking inclined magnetic field into the account in which the resultant equations are solved with finite element method. Bondareva et al. [22] investigated the impact of thermophoresis and Brownian motion on distributions of isotherms and streamlines of nanofluid inside trapezoidal open cavity and identified homogeneous distribution of nanoparticles with respect to Rayleigh number. Raizah et al. [23] scrutinized that the velocity of nanofluid and heat transfer rates deteriorates with augmenting power-low index parameter in their work on heat transfer of nanofluid within open shallow inclined porous cavity. Yu et al. [24] studied mixed convection mass and heat transfer of nanofluid flow inside a lid-driven inclined cavity with two side walls of the cavity are heated sinusoidally. Astanina et al. [25] examined the influence of volume fraction ${\text{CuO}}$ nanoparticles on isoconcentrations, isotherms and fluid lines scatterings of nanofluid within an enclosure and found that the strength of the fluid is depending on location of the heater. Mehryan et al. [26] scrutinized Buongiorno’s model nanofluid isotherms, isoconcentrations and fluid flow behavior inside a porous cavity which is contained an internal heater. Sun et al. [27] presented heat transfer and flow analysis of ${\text{water}}{-}{\text{Al}}_{2} {\text{O}}_{3}$ based non-Newtonian nanofluid in a Rayleigh–Benard cavity. Balla et al. [28] premeditated mass and heat transfer of bioconvection flow within a porous cavity saturated by nanofluid and oxytactic microorganism and determined that with rising values of thermophoresis parameter the heat transfer rate of the nanofluid elevates inside the cavity. Alsabery et al. [29] examined the influence of thickness of triangular wall on heat transport of MHD nanofluid flow within a lid-driven enclosure and detected increment in the migration of nanoparticles inside the cavity with intensifying values of thermophoresis parameter. Alsabery et al. [30] pondered that at 3% volume fraction of nanoparticles the fluid heat transport rate is excellent in their work on mixed convection of nanofluid flow inside an enclosure with wavy vertical walls saturated by rotating cylinder. Ghalambaz et al. [31] premeditated flow and heat transfer behavior of nanofluid within an inclined enclosure saturated by porous medium filled with phase change materials and detected that the nanofluid has performed excellent rate of heat transfer at inclination angle of the cavity is 42°. Ghalambaz et al. [32] noticed 80% decline in rates of heat transfer of nanofluid when the inclination angle of the cavity is − 75° in their work on fluid flow analysis in inclined cavity filled with mesoporous silica particles. Izadi et al. [33] studied the impact of two magnetic sources location inside the cavity filled with ferro-magneto phase change material and detected that the rate melting process is higher when the magnetic sources pair is at the vicinity of the cold wall. Gorla et al. [34] presented the impact of volume fraction of copper nanoparticles on isotherms and streamlines scatterings inside a lid-driven enclosure with heat source. Chamkha et al. [35] perceived the heat transfer and fluid behavior of hybrid nanofluid made up of ${\text{water}} - {\text{Al}}_{2} {\text{O}}_{3} - {\text{Cu}}$ within a square partly heated enclosure with heat absorption/generation and predicted that the rate of heat transfer of hybrid nanofluid is lesser than heat transfer of ${\text{water}} - {\text{Cu}}$ nanofluid and higher than ${\text{water}} - {\text{Al}}_{2} {\text{O}}_{3}$ nanofluid. Rashad et al. [36] discussed MHD nanofluid heat transfer analysis inside a cavity containing irregular cold obstacles and filled with ${\text{water}} - {\text{Al}}_{2} {\text{O}}_{3}$ based nanofluid and the results are illustrated in terms of isotherms and streamlines. Armaghani et al. [37] described that the Nusselt number values amplify with rising values of Rayleigh number in their work on isotherms and fluid lines analysis of nanofluid inside an I-shaped cavity. Azizul et al. [38] discussed ${\text{water}} - {\text{Alumina}}$ nanofluid performance inside a cavity containing solid cylinder with upper wall of the cavity has wavy shape and found that the properties of inner solid cylinder and borders wavy shape are highly influencing the rate of heat transfer. Sheremet et al. [39] presented isotherms and fluid lines behavior of ${\text{water}} - {\text{Al}}_{2} {\text{O}}_{3} /{\text{SiO}}_{2}$ based hybrid nanofluid inside a cavity. Shulepova et al. [40] presented the impact of internal solid block and adiabatic fin on heat transport phenomena of ${\text{water}} - {\text{alumina}}$ nanofluid within a cavity and determined that the rate of heat transfer is highly influenced by solid block location inside the cavity. Very recently, several authors [30, 41,42,43,44,45] presented flow and heat transfer analysis of nanofluid inside different enclosures filled with nano-encapsulated phase change materials.

After vigilant scrutiny of formerly published papers and to the best of authors information no studies have been reported to scrutinize the effect of enhanced zero mass flux boundary condition on isoconcentrations, isotherms and streamlines behavior of Buongiorno’s model nanofluid flow in an enclosure with magnetic field and thermal radiation. Hence we have made an attempt to examine this problem in this paper.

2 Mathematical formulations

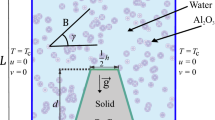
In the current study we have considered natural convection, laminar, two-dimensional, steady square chamber filled with magneto-hydrodynamic nanofluid by taking enhanced zero mass flux condition with the dimensional Cartesian coordinates $\bar{x}$, $\bar{y}$ and the length of the cavity is ${\text{L}}$ as shown in Fig. 1. Brownian motion, thermal radiation, magnetic field, Lewis number and thermophoresis are also taken into the account. The top and bottom horizontal walls of the cavity are both assumed to be thermally insulated. However, the left and right vertical walls of the cavity are kept isothermally at a constant temperature differences with $T_{\text{h}}$ is the temperature of left vertical wall and is assumed to be higher than the temperature of right vertical wall $T_{\text{c}}$. It is also considered that the properties of nanofluid are independent of volume fraction of nanoparticles and temperature. Under Darcy–Boussinesq approximations and by employing the reference work of Sheremet et al. [47] the governing equations take the following form:

Fig. 1

Physical model of the problem and coordinate system

$$ \frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} \bar{\psi }}}{{\partial \bar{y}^{2} }} = \frac{{\left( {1 - C_{0} } \right)\rho_{f } g \bar{K} \beta }}{\mu } \frac{\partial T}{{\partial \bar{x}}} + \frac{{\left( {\rho_{p} - \rho_{f} } \right) g\bar{K}}}{\mu } \frac{\partial C}{{\partial \bar{x}}} - \frac{{\sigma_{f} B_{0}^{2} }}{{\rho_{f } }}\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} $$

(1)

$$ \begin{aligned} & \frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} \frac{\partial T}{{\partial \bar{x}}} - \frac{{\partial \bar{\psi }}}{{\partial \bar{x}}} \frac{\partial T}{{\partial \bar{y}}} = \alpha_{m} \left( {\frac{{\partial^{2} T}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }}} \right) \\ & \quad + \tau \left[ {D_{B} \left( {\frac{\partial C}{{\partial \bar{x}}} \frac{\partial T}{{\partial \bar{x}}} + \frac{\partial C}{{\partial \bar{y}}} \frac{\partial T}{{\partial \bar{y}}}} \right) + \left( {\frac{{D_{T} }}{{T_{c} }}} \right)\left[ {\left( {\frac{\partial T}{{\partial \bar{x}}}} \right)^{2} + \left( {\frac{\partial T}{{\partial \bar{y}}}} \right)^{2} } \right]} \right] \\ & \quad - \frac{1}{{\rho c_{p} }}\left( {\frac{{\partial q_{rx} }}{{\partial \bar{x}}} + \frac{{\partial q_{ry} }}{{\partial \bar{y}}}} \right) \\ \end{aligned} $$

(2)

$$ \frac{1}{\in }\left( {\frac{{\partial \bar{\psi }}}{{\partial \bar{y}}} \frac{\partial C}{{\partial \bar{x}}} - \frac{{\partial \bar{\psi }}}{{\partial \bar{x}}} \frac{\partial C}{{\partial \bar{y}}}} \right) = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} C}}{{\partial \bar{y}^{2} }}} \right) + \left( {\frac{{D_{T} }}{{T_{c} }}} \right)\left[ {\frac{{\partial^{2} T}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }}} \right] $$

(3)

Here, $\psi$ is the stream function, T is the temperature and C is the concentration, ρ is the density, μ is viscosity, $\bar{x}$ and $\bar{y}$ are the coordinates of the system.

We now introduce the following non-dimensional variables as

$$ x = \frac{{\bar{x}}}{\text{L}},\quad y = \frac{{\bar{y}}}{\text{L}},\quad \psi = \frac{{\bar{\psi }}}{\text{L}},\quad \theta = \frac{{T - T_{\text{c}} }}{{T_{\text{h}} - T_{\text{c}} }},\quad \phi = \frac{C}{{C_{0} }}. $$

(4)

The radiative heat flux $q_{rx}$ and $q_{ry}$ (using Rosseland approximation) is defined as

$$ q_{rx} = - \frac{{4\sigma^{*} }}{{3K^{*} }}\frac{{\partial T^{4} }}{\partial x},\quad q_{ry} = - \frac{{4\sigma^{*} }}{{3K^{*} }}\frac{{\partial T^{4} }}{\partial y} $$

(5)

We assume that the temperature variances inside the flow are such that the term $T^{4}$ can be represented as linear function of temperature, so, it has Taylor series expansion. After neglecting higher-order terms from the Taylor series expansion of $T^{4}$ about $T_{\infty }$, we get

$$ T^{4} \cong 4T_{\text{c}}^{3} T - 3T_{\text{c}}^{4} . $$

(6)

Thus substituting Eq. (6) in Eq. (5), we get

$$ q_{rx} = - \frac{{16T_{c}^{3} \sigma^{*} }}{{3\beta_{r} }}\frac{\partial T}{\partial x},\quad q_{ry} = - \frac{{16T_{c}^{3} \sigma^{*} }}{{3\beta_{r} }}\frac{\partial T}{\partial y}. $$

(7)

Using Eq. (4) and (7), the governing Eqs. (1)–(3) take the form

$$ \frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }} = - {\text{Ra}} \frac{\partial \theta }{\partial x} + {\text{Ra}}.{\text{Nr}}\frac{\partial \phi }{\partial x} - M^{2} \frac{\partial \psi }{\partial y} $$

(8)

$$ \frac{\partial \psi }{\partial y} \frac{\partial \theta }{\partial x} - \frac{\partial \psi }{\partial x} \frac{\partial \theta }{\partial y} = \left( {1 + {\text{R}}} \right)\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) + \left[ {{\text{Nb}}\left( {\frac{\partial \phi }{\partial x} \frac{\partial \theta }{\partial x} + \frac{\partial \phi }{\partial y} \frac{\partial \theta }{\partial y}} \right) + {\text{Nt}}\left[ {\left( {\frac{\partial \theta }{\partial x}} \right)^{2} + \left( {\frac{\partial \theta }{\partial x}} \right)^{2} } \right]} \right] $$

(9)

$$ \frac{1}{\in }\left( {\frac{\partial \psi }{\partial y} \frac{\partial \phi }{\partial x} - \frac{\partial \psi }{\partial x} \frac{\partial \phi }{\partial y}} \right) = \frac{1}{\text{Le}}\left( {\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi }}{{\partial y^{2} }}} \right) + \frac{1}{\text{Le}}\frac{\text{Nt}}{\hbox{Nb}}\left[ {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right] $$

(10)

Here, Ra is Rayleigh number, Nr is buoyancy parameter, M is magnetic parameter, R is radiation parameter, Nb is Brownian motion parameter, Nt is thermophoresis parameter and Le is Lewis number.

With related boundary conditions

$$ \psi = 0,\quad \theta = 1,\quad {\text{Nb}}\frac{\partial \phi }{\partial x} + {\text{Nt}}\frac{\partial \theta }{\partial x} = 0\quad {\text{at}}\,x = 0. $$

(11)

$$ \psi = 0,\quad \theta = 0,\quad {\text{Nb}}\frac{\partial \phi }{\partial x} + {\text{Nt}}\frac{\partial \theta }{\partial x} = = 0\,{\text{at}}\quad x = 1. $$

(12)

$$ \psi = 0,\quad \frac{\partial \theta }{\partial y} = 0,\quad \frac{\partial \phi }{\partial y} = 0\,{\text{at}}\quad y = 0. $$

(13)

$$ \psi = 0,\quad \frac{\partial \theta }{\partial y} = 0,\quad \frac{\partial \phi }{\partial y} = 0\,{\text{at}}\quad y = 1. $$

(14)

The non-dimensional parameters are defined as

$$ \begin{aligned} {\text{Ra}} & = \frac{{\left( {1 - C_{0} } \right)\rho_{{{\text{f}} }} g \bar{K} \beta \Delta T L}}{{\mu \alpha_{\text{m}} }} ,\quad {\text{Nr}} = \frac{{\left( {\rho_{\text{p}} - \rho_{\text{f}} } \right) \Delta C}}{{\rho_{{{\text{f}} }} \beta \Delta T \left( {1 - C_{0} } \right)}} ,\quad {\text{Nb}} = \frac{{\tau D_{\text{T}} \Delta C}}{{\alpha_{\text{m}} }} ,\quad {\text{Nt}} = \frac{{\tau D_{\text{T}} \Delta T}}{{ T_{\text{c}} \alpha_{\text{m}} }}, \\ {\text{Le}} & = \frac{{\alpha_{\text{m}} }}{{\varepsilon D_{\text{B}} }},\quad M = B_{0} L\sqrt {\frac{\sigma }{\mu }} ,R = \frac{{16T_{\text{c}}^{3} \sigma^{*} }}{{3\beta_{r} }}. \\ \end{aligned} $$

The local Nusselt and Sherwood numbers are defined as

$$ {\text{Nu}}_{1} = - \left( {\frac{\partial \theta }{\partial x}} \right)_{x = 0} ,\,{\text{Sh}}_{1} = - \left( {\frac{\partial \phi }{\partial x}} \right)_{x = 0} . $$

(15)

The average Nusselt and Sherwood numbers are defined as

$$ \overline{{{\text{Nu}}_{1} }} = \mathop \int \limits_{0}^{1} {\text{Nu}}\,{\text{d}}y,\,\overline{{{\text{Sh}}_{1} }} = \mathop \int \limits_{0}^{1} {\text{Sh}}\,{\text{d}}y. $$

(16)

3 Numerical method of solution

Finite difference method of second-order accuracy [46,47,48] is employed to solve the non-dimensional partial differential Eqs. (8)–(10) together with boundary conditions (11)–(14). Central difference scheme is used for the numerical approximation of diffusion term and to approximate convective term we have used second-order up-wind scheme. The successive relaxation method is instigated to find the solution of corresponding linear algebraic equations. Based on the computing experiments we have chosen the relaxation parameter optimum value. We have terminated the computation after getting concentration, temperature and stream function residuals less than $10^{ - 10}$.

Grid sensitivity analysis is conducted to obtain the grid independent solution to investigate the steady state natural convection heat and mass transport in square cavity filled with nanofluid with thermal radiation at ${\text{Ra}} = 100, {\text{M}} = 0.5,{\text{Nb}} = 0.1, {\text{Nt}} = 0.1, {\text{Nr}} = 0.1, {\text{Le}} = 1.0, {\text{R}} = 0.1$. Five cases of non-uniform grid in a square cavity are verified: a grid of $50 \times 50$ points, $100 \times 100$ points, $150 \times 150$ points, $200 \times 200$ points and $300 \times 300$ points.

The uniform grid of $100 \times 100$ points is selected for this analysis based on conducted verifications, and an increase in mesh nodes leads to growth in computational time. The validity of present numerical code with the existing works is made and finds good agreement which is shown in Table 1. Table 2 displays the impact of mesh parameter on average Nusselt number inside the cavity.

Table 1 Comparisons of average Nusselt number at hot wall with the results available in literature

Table 2 Variations of the average Nusselt number at the hot wall with the uniform grid

4 Results and discussion

In this section, we have examined the effect of zero mass flux condition on streamlines, isotherms and isoconcentrations of MHD nanofluid flow inside a chamber with thermal radiation is analyzed. The numerical results for the distributions of isoconcentrations, isotherms and streamlines are presented by utilizing finite difference method for various values of influenced parameters, such as, Rayleigh number, magnetic parameter, Brownian motion number, buoyancy ratio parameter, Lewis number, thermophoresis number and radiation number and are plotted through graphs from Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 and 22.

Fig. 2

Streamlines for fixed ${\text{M}} = 0.5,{\text{Nr}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1, {\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 3

Isotherms for fixed ${\text{M}} = 0.5,{\text{Nr}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1, {\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 4

Isoconcentrations for fixed ${\text{M}} = 0.5,{\text{Nr}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1, {\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 5

Streamlines for fixed ${\text{Ra}} = 500,{\text{Nr}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1, {\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 6

Isotherms for fixed ${\text{Ra}} = 500,{\text{Nr}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1, {\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 7

Isoconcentrations for fixed ${\text{Ra}} = 500,{\text{Nr}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1, {\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 8

Streamlines for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 9

Isotherms for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 10

Isoconcentrations for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{R}} = 0.1$

Fig. 11

Streamlines for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 12

Isotherms for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 13

Isoconcentrations for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 14

Streamlines for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 15

Isotherms for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 16

Isoconcentrations for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nt}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 17

Streamlines for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nb}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 18

Isotherms for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nb}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 19

Isoconcentrations for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nb}} = 0.1,{\text{Le}} = 10,{\text{Nr}} = 0.1$

Fig. 20

Streamlines for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 10,{\text{Nr}} = 0.1$

Fig. 21

Isotherms for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 10,{\text{Nr}} = 0.1$

Fig. 22

Isoconcentrations for fixed ${\text{M}} = 0.5,{\text{Ra}} = 500,{\text{R}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 10,{\text{Nr}} = 0.1$

Figures 2, 3 and 4 reveal the effect of Rayleigh number $\left( {\text{Ra}} \right)$ on stream lines, temperature lines and concentration lines inside the cavity with fixed values of ${\text{M}} = 0.5,{\text{Nr}} = 0.1,{\text{Nb}} = 0.1,{\text{Nt}} = 0.1, {\text{Le}} = 10,{\text{R}} = 0.1$. It is seen from Fig. 2 that the fluid circulates in a clockwise vortex with a single core formed in the center of the cavity and the size of the core augments as the value of (Ra) rises from $10^{2} {-} 10^{3}$. Warming the left vertical wall of the cavity intensifies fluid motion in the cavity as a result fluid moves from hot wall to cold wall and the lines having descendent nature at the cold wall and then again having ascendant nature at the hot wall by developing a rotating cell inside the cavity. This is because of temperature differences between hot and cold walls. With the elevating values of $\left( {\text{Ra}} \right)$ the streamlines intensity and the length of the cell increase because of higher buoyancy forces. The patterns of isotherms are almost vertical shape near the bottom of left hot wall as well as near the top of right cold wall due to conduction heat transport; however, the shape of isotherms is almost horizontal in the middle of the cavity due to convection heat transfer as shown in Fig. 3 with rising values of $\left( {\text{Ra}} \right)$. The contours of isoconcentrations reveal a noticeable inhomogeneity, owing to thermophoresis effect, inside the cavity with rising values of $\left( {\text{Ra}} \right)$ as shown in Fig. 4.

Figures 5, 6 and 7 portray the distributions of streamlines, temperature lines and isoconcentrations with diverse values of magnetic parameter $\left( {\text{M}} \right)$ inside the cavity. Irrespective of the $\left( {\text{M}} \right)$ value one major convective cell core is formed inside the cavity which is rotating in clockwise direction. Furthermore, the shape and size of the recirculation cell is highly wedged by the presence of external magnetic field and the values of $\left( {\text{M}} \right)$ rises as shown Fig. 5. The diminution in the size of the recirculation cell core is because of the presence of external forces, and these forces reduce the convection currents as a result the length of the cell is attenuates. The conduction heat transport changes the pattern of temperature lines inside the cavity which are almost vertical at the corners of left and right walls, while, the have horizontal shape at the middle of the cavity as shown in Fig. 6. Furthermore, the curvature of the isotherms deteriorates within the cavity with up surging values of $\left( {\text{M}} \right)$. It observed from Fig. 7 that an increase in $\left( {\text{M}} \right)$ causes almost non-homogeneous distribution of isoconcentrations inside the cavity. This is due to the fact that higher the values of $\left( {\text{M}} \right)$ rises the dispersion of nanoparticles in the nanofluid. So, that there exist bigger non-homogeneity behavior of isoconcentrations inside the cavity.

The distributions of streamlines, isotherms and isoconcentrations with dissimilar rising values of buoyancy ratio parameter $\left( {\text{Nr}} \right)$ are depicted from Figs. 8, 9 and 10. The scatterings of streamlines form a clockwise rotating circulation cell of elliptical shape in the middle of the cavity and most of these lines appear near the hot and cold walls with high intensity with $\left( {\text{Nr}} \right)$. Additionally, the length and shape of recirculation cell elevate with growing values of $\left( {\text{Nr}} \right)$ which is shown in Fig. 8. Figure 9 depicts that the curvature of isotherms intensifies inside the cavity with rising values of $\left( {\text{Nr}} \right)$. Because of the buoyancy convective forces the temperature lines are almost vertical near the hot and cold walls, whereas, in the middle of the cavity they flatten horizontally. The distributions of isoconcentrations divulge that with rise in $\left( {\text{Nr}} \right)$ leads to the spreading of nanoparticles within the cavity and these scatterings are normally considered as non-homogeneous (Fig. 10).

The impact of radiation parameter $\left( {\text{R}} \right)$ on profiles of streamlines, isotherms and isoconcentrations is depicted from Figs. 11, 12 and 13 with in the cavity. It is perceived that a single recirculation cell is formed within the cavity and size of the cell augments with rising values of $\left( {\text{R}} \right)$ from 0.1 to 1.0 as shown in Fig. 11. The vortex velocity and rotation of fluid are both augments, because of elevation of heat conduction, in the middle of cavity as the values of $\left( {\text{R}} \right)$ rises. The curvature of the isotherms deteriorates with in the cavity as the values of $\left( {\text{R}} \right)$ intensifies (Fig. 12). In the case of radiative heat transport heat can be transferred from hot wall to cold wall by nanoparticles and these particles have better emitting heat transfer capabilities. The isoconcentrations which are related to distribution of volume fraction of nanoparticles inside the cavity is depicted in Fig. 13. Irrespective of the values of $\left( {\text{R}} \right)$ the spreading of nanoparticles is non-homogeneous and is from the reality that the impact of thermophoresis intensifies in the fluid area because of the heat conduction as a result the scatterings of nanoparticles have non-homogeneous nature.

Figures 14, 15 and 16 illustrate the impact of Brownian motion $\left( {\text{Nb}} \right)$ on streamlines, temperature lines and isoconcentrations distributions of nanofluid inside the cavity. Figure 14 reveals that high strength streamlines occur inside the nanofluid layer with single recirculation cell is formed in clockwise direction. Furthermore, there is intensification in the strength and size of circulation cell with rising values of $\left( {\text{Nb}} \right)$. The temperature lines pattern is almost horizontal in the middle of the cavity and there is nominal reduction in curvature of these lines due to the enhancement in $\left( {\text{Nb}} \right)$ as shown in Fig. 15. The nanoparticles aggregate in the entire cavity leads a non-homogeneous nature with rising values of $\left( {\text{Nb}} \right)$.

The distributions of streamlines, temperature lines and Isoconcentrations with diverse values of thermophoresis parameter $\left( {\text{Nt}} \right)$ are depicted in Figs. 17, 18 and 19 with in the cavity. It is perceived from Fig. 17 that due to the influence of temperature variations between left hot wall and right cold wall there exist one recirculate convection cell core is presented with in the cavity and the size and length of the core intensifies with rising values of $\left( {\text{Nt}} \right)$. At the fluid-solid border these fluid lines appear like ascending flows and they appear like descending flow in the middle of the cavity. Heat conduction is the dominating heat transport mechanism when the value of $\left( {\text{Nt}} \right)$ is high. As the values of $\left( {\text{Nt}} \right)$ rises the circulation intensity of the nanofluid raises as a result the isotherms are parallel to the vertical walls and in the center of the cavity these lines are parallel to the horizontal lines as shown in Fig. 18. Furthermore, the bent ness of these lines intensifies with higher values of $\left( {\text{Nt}} \right)$. The distribution of nanoparticles (Isoconcentrations) inside the cavity is depicted in Fig. 19. It divulges that non-homogeneous distribution of nanoparticles is perceived within the cavity which is mainly because of thermophoresis effect. This effect raises the rate of conduction within the cavity as a result concentration of nanofluid elongated horizontally.

Figures 20, 21 and 22 determine the scatterings of fluid lines, temperature lines and isoconcentrations with dissimilar values of Lewis number $\left( {\text{Le}} \right)$. Lesser strength recirculation cell is formed inside the cavity with lower $\left( {\text{Le}} \right)$ values as shown in Fig. 20. This means the impact of $\left( {\text{Le}} \right)$ on streamlines is nominal. It also perceived from Fig. 21 that as ${\text{Le }} = 10, 15$ there is no change in the behavior of isotherms, however, as ${\text{Le}} = 20$ the curvature of temperature lines is augmented. Elongated non-homogeneous distribution of nanoparticles in the entire cavity is perceived with rising values of $\left( {\text{Le}} \right)$ as shown in Fig. 22.

Impact of $\left( {\text{Ra}} \right)$ on non-dimensional average Nusselt number at the fluid-solid border is portrayed in Fig. 23. The profiles of rate of heat transfer augments inside the cavity with rising values of $\left( {\text{Ra}} \right)$ and is because of the fact that heat transfer intensifies as $\left( {\text{Ra}} \right)$ values rises. However, the dimensionless mass transfer rates deteriorate with intensifying values of $\left( {\text{Ra}} \right)$ and is depicted in Fig. 24. It is noticed from Fig. 25 that the values of rates of heat transfer diminish with augmenting values of $\left( {\text{M}} \right)$, however, values of Sherwood number enhance inside the cavity region with $\left( {\text{M}} \right)$ and is shown in Fig. 26. It is clear from Fig. 27 that the average Nusselt number values deteriorate with rising values of $\left( {\text{Nr}} \right)$. This is from the reality that the thickness of thermal boundary layer worsens with growing values of $\left( {\text{Nr}} \right)$ as a result the values of Nusselt number diminish. The values of non-dimensional mass transfer rates elevate with intensifying values of $\left( {\text{Nr}} \right)$ and are portrayed in Fig. 28. The scatterings of Nusselt number elevate in the cavity region with rising values of $\left( {\text{R}} \right)$ as shown in Fig. 29 and is from the reality that thermal radiation enhances heat conduction of the nanofluid as a result heat transfer rates augments. However, Sherwood number scatterings worsen with intensifying values of $\left( {\text{R}} \right)$ and are depicted in Fig. 30. Figure 31 presents the variations in average Nusselt number for diverse values of $\left( {\text{Nb}} \right)$. Generally, as Brownian motion rises the convection heat transfer augments as a result the scatterings of average Nusselt number elevates. However, the distributions of non-dimensional rates of mass transfer attenuate with increasing values of $\left( {\text{Nb}} \right)$ and are presented in Fig. 32. Both heat and mass transfer rates augment with intensifying values of $\left( {\text{Nt}} \right)$ and is from the reality that higher the values of $\left( {\text{Nt}} \right)$ leads to elevation in the thickness of thermal and solutal boundary layer (Figs. 33, 34). The impact of $\left( {\text{Le}} \right)$ on the average Nusselt number at the left hot wall is portrayed in Fig. 35. Nominal heat transfer enhancement is noticed with rising values of (Le). However, the Sherwood number scatterings deteriorate in the cavity with rising values of (Le) as depicted in Fig. 36.

Fig. 23

Impact of $\left( {\text{Ra}} \right)$ on Nusselt number at hot wall

Fig. 24

Impact of $\left( {\text{Ra}} \right)$ on Sherwood number at hot wall

Fig. 25

Impact of $\left( {\text{M}} \right)$ on Nusselt number at hot wall

Fig. 26

Impact of $\left( {\text{M}} \right)$ on Sherwood number at hot wall

Fig. 27

Impact of $\left( {\text{Nr}} \right)$ on Nusselt number at hot wall

Fig. 28

Impact of $\left( {\text{Nr}} \right)$ on Sherwood number at hot wall

Fig. 29

Impact of $\left( {\text{R}} \right)$ on Nusselt number

Fig. 30

Impact of $\left( {\text{R}} \right)$ on Sherwood number

Fig. 31

Impact of $\left( {\text{Nb}} \right)$ on Nusselt number at hot wall

Fig. 32

Impact of $\left( {\text{Nb}} \right)$ on Sherwood number at hot wall

Fig. 33

Impact of $\left( {\text{Nt}} \right)$ on Nusselt number at hot wall

Fig. 34

Impact of $\left( {\text{Nt}} \right)$ on Sherwood number at hot wall

Fig. 35

Impact of $\left( {\text{Le}} \right)$ on Nusselt number

Fig. 36

Impact of $\left( {\text{Le}} \right)$ on Sherwood number

5 Conclusion

Finite difference solution is presented to analyze the distributions of streamlines, temperature lines and isoconcentrations of Buongiorno’s model nanofluid flow inside a square cavity with diverse values of pertinent parameters. Magnetic field, thermophoresis, thermal radiation and Brownian motion are considered in this analysis. The significant findings of this research are as follows.

• (i) The non-dimensional rates of heat transfer augments inside the cavity with $\left( {\text{M}} \right)$.

• (ii) Streamlines are highly effected with $\left( {\text{R}} \right)$ and a single recirculation cell is formed with in the cavity.

• (iii) It is ascertained that the rate of heat transport intensifies with rising $\left( {\text{Ra}} \right)$ values.

• (iv) The curvature of isotherms elevates within the cavity as the values of $\left( {\text{Nt}} \right)$ rises.

• (v) Isotherms are almost horizontal in the middle of the cavity and there is nominal reduction in curvature of these lines with rising $\left( {\text{Nb}} \right)$ values.

• (vi) Sherwood number scatterings deteriorate in the cavity with rising values of (Le).