Investigation on free vibration and transient response of functionally graded graphene platelets reinforced cylindrical shell resting on elastic foundation

Abstract

This paper is concerned with the free vibration and transient response of graphene platelets reinforced functionally graded (GPL-FG) cylindrical shell resting on elastic foundation by utilizing the Chebyshev–Lagrangian approach. The boundary constraints are realized by setting reasonable values of stiffness of the artificial virtual springs. According to FSDT, the analysis model of GPL-FG cylindrical shell is established. Then, the displacement fields are expanded in terms of the Chebyshev–Lagrangian approach. Based on the work above, Rayleigh–Ritz energy method is employed to solve the unknown coefficients of Chebyshev expansions with purpose to indicate the dynamic characteristics of the analysis model. In addition, the Rayleigh damping coefficients are taken into account to investigate the transient response results from the external excitation. A series of numerical results show the rapid convergence and precision of the present method by comparison with results obtained by the published papers and FEM. Ultimately, the analysis about the effects of parameters and factors on free vibration and transient response are discussed, including geometry and material properties, boundary conditions, stiffness of elastic foundation, loading types and Rayleigh damping coefficients.

Graphic abstract

1 Introduction

Functionally graded (FG) cylindrical shells have been developed to take advantages of good dynamic behaviors, including mechanical, thermal and electrical properties in many engineering, particularly in space and marine industries which generally work in complicated environments [1]. FG cylindrical shells are generally made of mixtures composed of ceramics and metals to obtain a functional performance with gradually variable properties in one or more spatial directions. It is of most significance to promote the behavior of vibrations and response of FG cylindrical shells in case of free vibration and forced vibration, which separately result from single point excitation force and external dynamic loads. For one thing, excellent performance of FG cylindrical shells demands suitable structural design, lightweight materials, strong flexural and stretching strength, exceptional stability and so on. For another, research of FG cylindrical shells has attracted increasing attention under the influence of the rapidly expanding demands for high structural performance in extreme high temperature environment and high-speed industries [2, 3]. Catania et al. [4] made damping oriented design of thin-walled mechanical components by means of multi-layer coating technology. Demir [5] studied the free vibration and damping behaviors of multilayered symmetric sandwich beams and single layered beams made of FGMs by experiments and numerical simulation. Based on the Reuss model and Hashin–shtrickman equation, Yu et al. [6] investigated the damping efficiency of the coating system.

Reddy et al. [7,8,9] made sets of researches on the vibration of functionally graded cylindrical shells composed of stainless steel and nickel under various boundary conditions and loadings. On the one hand, the frequency characteristics of the functionally graded cylindrical shells share good agreement with those of homogeneous isotropic cylindrical shells. On the other hand, the natural frequency relates to various volume fractions and combination form of the materials. In addition, results showed that the natural frequencies and dynamic instability sections can be reasonable regulated by manipulating the power law index. Najafizadeh and Isvandzibaei [10] analyzed vibration of the natural frequency of functionally graded cylindrical shells corresponding to several boundary edges and ring support. Shah et al. [11] observed the frequency of thin functionally graded cylindrical shells, in which the exponent of material distribution varies in the shell radial direction. Iqbal [12] investigated the vibration characteristics of functionally graded circular cylindrical shells by means of the wave propagation approach. Based on the theory of discrete singular convolution technique, the study about vibration of functionally graded cylindrical shell was conducted [13], and the results are close to those obtained by previous researches.

However, FG cylindrical shells are surrounded by elastic foundations in some engineering applications. Typically, the Winker and Pasternak models are introduced to define the relationships between structural elements and elastic foundation [14, 15]. Sofiyev et al. [16,17,18,19] studied the vibrations and buckling of cylindrical shells resting on elastic medium by utilizing different methods. Shen [20] introduced the multi-scale approach to analyze the nonlinear behaviors caused by combined loadings of nanocomposite cylindrical panel which is surrounded by elastic medium. As a consequence, based on a multi-scale approach, the nonlinear vibration behavior of functionally graded graphene-reinforced composite laminated cylindrical panels surrounded by elastic medium in thermal environment was observed [21]. Introducing the first-order shear shell deformation theory [22] and von Kármán nonlinear theory into study [23], Sheng et al. [24] presented a study of nonlinear vibration characteristics of FG cylindrical shell surrounded by an elastic medium under the loading coupled by the transverse and thermal loadings Paliwal et al. [1] took advantage of the membrane theory to investigate the free vibrations of thin circular cylindrical shell with elastic foundation. Shah et al. [25] analyzed the vibrations of functionally graded shells based on Winkler and Pasternak elastic foundations with the wave propagation method. Subsequently, vibrational characteristics of fluid-filled functionally graded cylindrical shells based on Winkler and Pasternak elastic foundations are studied by Shah et al. [26]. Conclusions can be drawn that the frequency of the fluid-filled functionally graded cylindrical shell is much less than those of empty functionally graded cylindrical shell, and the Pasternak foundation makes more influence than Winkler modulus on the frequency of functionally graded cylindrical shell. The Rayleigh–Ritz approach was introduced to observe the behavior of vibration of functionally graded circular cylindrical shell, which is reinforced with ring-stiffeners made of various materials [27]. Asgari [28] studied the free vibration of thick hollow cylinder which based on three-dimensional mode shapes and made of 2D-functionally graded materials.

Since metal foams have properties of low density, superb bending stiffness and strength, and excellent energy absorption [29], they are regarded as core materials in industrial applications, known as aircraft wing structures. It is noted that the geometries and directions of the internal pores can be tailored to meet different design of mass density and size [30, 31], making negative effects on the stiffness and strength of structures. In order to decrease the mass density and improve the stiffness and strength of the FG cylindrical as well, the technologies of graphene platelet (GPL) and carbon nanotube (CNT) have been developed [32].

Since isolated by Novoselov et al. [33], graphene has been considered as an ideal material in engineering practice requiring high mechanical, thermal and electrical properties [34] because of its high aspect ratio, large specific surface area and relatively low cost [35]. Dong et al. [36, 37] study the vibration of functionally graded cylindrical shell reinforced by the graphene platelet with an analytical solution. Jie et al. [38] analyzed the effects of multiple parameters on the elastic buckling and free vibration responses of plates made of porous nanocomposite, where the porosity coefficient, graphene platelets weight fraction, plate thickness ratio and the graphene platelets shape ratios are taken into account. Song et al. [39,40,41] presented a series of studies about functionally graded shells reinforced by graphene based on FSDT and Navier solution, including the buckling, bending and vibration analyses. Shen et al. [42] observed the behaviors of nonlinear vibration of graphene-reinforced composite laminated structures in thermal environment. More recently, Blooyiyan [43] proposed an analytical approach to investigate the postbuckling of functionally graded graphene platelet-reinforced polymer composite cylindrical shells in the framework of Donnell shell theory. Meanwhile, Ansari et al. [44] developed a semi-analytical analysis of postbuckling of polymer nanocomposite cylindrical shells which are reinforced with functionally graded graphene platelets. On basis of first-order shear deformation theory, the modified Halpin–Tsai micromechanics mode was employed by Shahgholian-Ghahfarokhi et al. [45] in analysis of the torsional buckling of porous nanocomposite cylindrical shell which is reinforced with GPL.

In summary, although enormous investigations of vibration and response of FG cylindrical shells have been done, comprehensive analyses of GPL-FG cylindrical shell surrounded by elastic foundations are still scare. Based on the above discussion, the core interest of this paper is to observe the vibrations and transient response of GPL-FG cylindrical shells, including the effects of the componential material and boundary conditions as well as elastic foundation parameters. In the second chapters, the theoretical model is established, and the motion equations of GPL-FG cylindrical shell are obtained according to the first-order shear deformation shell theory. Then, the vibrations and transient response of GPL-FG cylindrical shell are presented and analyzed in details. Finally, some relevant conclusions on basis the aforementioned work are obtained.

2 Theoretical analysis

2.1 Establishment of the model

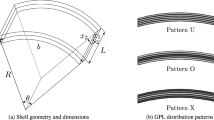
In order to analyze the transient responses and vibrations of GPL-FG cylindrical shells on the elastic foundation, a model is established as shown in Fig. 1. An orthogonal coordinate system (x, v, z) is established in the middle surface, where the length, thickness, angel and radii are denoted with L, h, $\theta$ and r, respectively. Position of one point in the middle surface is related to the coordinates x and $\theta$. The elastic foundation can be specified with K_r and K_g, which separately represent the Winkler foundation stiffness and the shear layer stiffness of the elastic foundations. The porous distributions of the GPL-FG cylindrical shells can be induced with four types. As shown in Fig. 2a, types 1, 2, 3 porosity distributions are the non-uniform porosity distribution, while type 4 porosity distribution is the uniform porosity distribution. The $E_{ \hbox{max} }$ ($\rho_{ \hbox{max} }$) denotes the maximum values of Young’s modulus (mass density) under the same weight fraction along with the thickness, while $E_{ \hbox{min} }$ ($\rho_{ \hbox{min} }$) resulting from the various porosity distributions represents the minimum values.

Fig. 1

The geometry model of the GPL-FG cylindrical shell resting on an elastic foundation: a geometry model; b boundary constraints

Fig. 2

The distributions of porosity: a P1 symmetric porosity (soft–stiff–soft); b P2 symmetric porosity (soft–stiff–soft); c P3 non-symmetric porosity, d P4 Uniform porosity

As for the porous cylindrical shell with type 1 distribution, the Young’s modulus, mass density and Poisson’s ratio are given as:

$$ E(z) = E_{c} \left[ {1 - e_{0} \lambda^{i} (z)} \right] $$

(1.a)

$$ \rho (z) = \rho_{c} \left[ {1 - e_{m} \lambda^{i} (z)} \right] $$

(1.b)

$$ v(z) = v_{c} \left[ {1 - e_{m} \lambda^{i} (z)} \right] $$

(1.c)

where $e_{0}$ denotes porosity coefficient used to explain the dimension and density of the internal pores. E_c and $\rho_{c}$ are equivalent to the E_max and $\rho_{ \hbox{max} }$, representing the maximum Young’s modulus, mass density of the cylindrical shell, $e_{0}$ is selected to be zero, in other words; Poisson’s ratio is denoted with $v(z)$ and $v_{c}$ arises without pores; According to Ref. [46], Poisson’s ratio is given as Eq. (2). $e_{m}$ can be express by Eq. (3) based on the closed-cell Gaussian random field model [47].

$$ v(z) = 0.342v_{c} \left[ {1 - e_{m} P_{i} (z)} \right]^{2} + (0.562v_{c} - 0.221)\left[ {1 - e_{m} P_{i} (z)} \right] + 0.132v_{c} + 0.221 $$

(2)

$$ e_{m} = \frac{{1.121\left[ {1 - {}^{2.3}\sqrt {1 - e_{0} P_{i} (z)} } \right]}}{{\lambda^{i} (z)}} $$

(3)

where P_i (i = 1, 2, 3, 4) corresponds to the porosity distributions P1, P2, P3 and P4. It should be noted that the total mass of the cylindrical shell is independent of the various porosity distributions. The specific forms and relations with each other are given as:

$$ P_{i} = \left\{ {\begin{array}{*{20}l} {\cos \left( {\frac{\pi z}{h}} \right)} \hfill & {(i = 1)} \hfill \\ {{\rm X}_{2} \left( {1 - \cos \frac{\pi z}{h}} \right)} \hfill & {(i = 2)} \hfill \\ {{\rm X}_{3} \cos \left( {\frac{\pi z}{2h} + \frac{\pi }{4}} \right)} \hfill & {(i = 3)} \hfill \\ {{\rm X}_{4} } \hfill & {(i = 4)} \hfill \\ \end{array} } \right. $$

(4)

$$ \int_{{\frac{ - h}{2}}}^{{\frac{h}{2}}} {\left[ {1 - e_{m} \lambda^{1} } \right]} {\text{d}}z = \left\{ \begin{aligned} \int_{{\frac{ - h}{2}}}^{{\frac{h}{2}}} {\left[ {1 - 1.121\left( {1 - \left( {1 - e_{0} \lambda^{2} } \right)^{{\frac{1}{2.3}}} } \right)} \right]} {\text{d}}z \hfill \\ \int_{{\frac{ - h}{2}}}^{{\frac{h}{2}}} {\left[ {1 - 1.121\left( {1 - \left( {1 - e_{0} \lambda^{3} } \right)^{{\frac{1}{2.3}}} } \right)} \right]} {\text{d}}z \hfill \\ \int_{{\frac{ - h}{2}}}^{{\frac{h}{2}}} {\left[ {1 - 1.121\left( {1 - \left( {1 - e_{0} \lambda^{4} } \right)^{{\frac{1}{2.3}}} } \right)} \right]} {\text{d}}z \hfill \\ \end{aligned} \right. $$

(5)

On the basis of the Halpin–Tsai micromechanics model, the Young’s modulus E_c can be calculated with Eq. (6). In order to obtain the values of the mass density and Poisson’s ratio of the cylindrical shells, the rule of the general rule is employed.

$$ E_{c} = E_{m} \left[ {\frac{3}{8}\left( {\frac{{1 + \gamma_{L} \chi_{L} P_{\text{GPL}} }}{{1 - \gamma_{L} P_{\text{GPL}} }}} \right) + \frac{5}{8}\left( {\frac{{1 + \gamma_{B} \chi_{B} P_{\text{GPL}} }}{{1 - \chi_{B} P_{\text{GPL}} }}} \right)} \right] $$

(6)

$$ \rho_{c} = \rho_{\text{GPL}} P_{\text{GPL}} + \rho_{M} (1 - P_{\text{GPL}} ) $$

(7)

$$ v_{c} = v_{\text{GPL}} P_{\text{GPL}} + v_{M} (1 - P_{\text{GPL}} ) $$

(8)

where $E_{\text{GPL}}$ and $E_{m}$ are the Young’s modulus of the GPL and matrix; $v_{\text{GPL}}$ and $v_{m}$ are the Poisson’s ratio of the GPL and matrix; $\rho_{\text{GPL}}$ and $\rho_{m}$ represent the mass density of the GPL and matrix; the parameter $P_{\text{GPL}}$ is used to explain the rules of conversion of the volume fraction of GPL along with the thickness of the shell shown in Fig. 3. $\chi_{L}$ and $\chi_{B}$ are defined by the length L_GPL, the width r_GPL, and the thickness h_GPL, the specific equations are given as follows.

Fig. 3

Schematic of the types of porosity distribution and corresponding dispersion patterns of the volume fraction of the GPL-FG cylindrical shell: a pattern G1 (symmetric distribution); b pattern G2 (symmetric distribution); c pattern G3 (non-symmetric distribution); d pattern G4 (uniform distribution)

$$ \chi_{L} = 2\frac{{L_{\text{GPL}} }}{{h_{\text{GPL}} }},\quad \chi_{B} = 2\frac{{r_{\text{GPL}} }}{{h_{\text{GPL}} }} $$

(9.a)

$$ \gamma_{L} = \frac{{E_{\text{GPL}} - E_{m} }}{{E_{\text{GPL}} - \chi_{L} E_{m} }},\quad \gamma_{L} = \frac{{E_{\text{GPL}} - E_{m} }}{{E_{\text{GPL}} - \chi_{B} E_{m} }} $$

(9.b)

$$ V_{\text{GPL}} = P_{j}^{i} \lambda_{j} $$

(10)

where $\lambda_{j}$ (j = 1, 2, 3, 4) correlating to GPL pattern G1, G2, G3 and G4 can be obtained by

$$ \lambda_{j} = \left\{ {\begin{array}{*{20}l} {1 - \cos \frac{\pi z}{h}} \hfill & {\left( {j = 1} \right)} \hfill \\ \lambda \hfill & {\left( {j = 3} \right)} \hfill \\ {1 - \cos \left( {\frac{\pi z}{2h} + \frac{\pi }{4}} \right)} \hfill & {\left( {j = 2} \right)} \hfill \\ \end{array} } \right. $$

(11)

Setting the extreme values of GPL volume fraction as $P_{j}^{i}$, it can be obtained by Eq. (12). It is noted that the subscripts i are equal to type i distributions, and the subscripts j represent the GPL patterns G1, G2, G3 and G4.

$$ P_{j}^{i} = \frac{{\kappa_{\text{GPL}} \rho_{m} \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left[ {1 - o_{m} \lambda^{i} (z)} \right]} {\text{d}}z}}{{\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\lambda_{j} } \left[ {1 - o_{m} \lambda^{i} (z)} \right]{\text{d}}z \cdot \left[ {\kappa_{\text{GPL}} \rho_{m} + \rho_{\text{GPL}} - \kappa_{\text{GPL}} \rho_{\text{GPL}} } \right]}} $$

(12)

2.2 Constitutive relation and energy equation

Based on the first-order shear deformation theory, the displacement field in the middle surface of the established model can be given as follows:

$$ {\mathbf{U}} = \left[ {\begin{array}{*{20}c} U \\ V \\ W \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & z & 0 \\ 0 & 1 & 0 & 0 & z \\ 0 & 0 & 1 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} u \\ v \\ w \\ {\phi_{x} } \\ {\phi_{\theta } } \\ \end{array} } \right] = {\mathbf{CD}} $$

(13)

$$ {\mathbf{D}} = \left[ {u,v,w,\phi_{x} ,\phi_{y} } \right]^{\text{T}} $$

where U, V, W express the displacement components of the cylindrical shell at any point in x, θ and z axial directions, respectively; u, v and w are the displacements in the middle surface of the shell; $\phi_{x}$ and $\phi_{\theta }$ separately represent the transverse normal rotations about the x and θ axes.

According to the Donnell’s shell theory, the strains components of the cylindrical shell can be expressed as:

$$ {\varvec{\upvarepsilon}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ {l_{x} } \\ {l_{\theta } } \\ {l_{x\theta } } \\ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{xz} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{\partial }{\partial x}} & 0 & {\frac{\partial }{r\partial \theta }} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{\partial }{r\partial \theta }} & {\frac{\partial }{\partial x}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\frac{\partial }{r\partial \theta }} & {\frac{\partial }{\partial x}} \\ 0 & 0 & 0 & {\frac{\partial }{\partial x}} & 0 & {\frac{\partial }{r\partial \theta }} & 0 & 1 \\ 0 & 0 & 0 & 0 & {\frac{\partial }{r\partial \theta }} & {\frac{\partial }{\partial x}} & 1 & 0 \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} u \\ v \\ w \\ {\phi_{x} } \\ {\phi_{\theta } } \\ \end{array} } \right] = {\mathbf{ID}} $$

(14)

where $\varepsilon_{x}$, $\varepsilon_{\theta }$, $\gamma_{x\theta }$ are the strains components corresponding to the displacement components u, v, w; $\gamma_{xz}$ and $\gamma_{\theta z}$ represent strains components corresponding to the transverse normal rotations $\phi_{x}$ and $\phi_{\theta }$; $l_{x}$, $l_{\theta }$, $l_{x\theta }$ are the changes of curvatures. They are given in terms of equations:

Then, the force and moment resultants are expressed as

$$ {\mathbf{N}} = \left[ {\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ {Q_{x} } \\ {Q_{\theta } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 & 0 & 0 \\ {A_{12} } & {A_{22} } & 0 & {B_{12} } & {B_{22} } & 0 & 0 & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } & 0 & 0 \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 & 0 & 0 \\ {B_{12} } & {B_{22} } & 0 & {D_{12} } & {D_{22} } & 0 & 0 & 0 \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {k_{s} A_{44} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {k_{s} A_{55} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ {l_{x} } \\ {l_{\theta } } \\ {l_{x\theta } } \\ {\gamma_{xz} } \\ {\gamma_{\theta z} } \\ \end{array} } \right] = {\mathbf{A}}\boldsymbol\varepsilon$$

(15)

where $N_{x}$, $N_{\theta }$ and $N_{x\theta }$ are the normal and shear resultants; $M_{x}$, $M_{\theta }$ and $M_{x\theta }$ denote the bending and twisting resultants; $Q_{x}$ and $Q_{\theta }$ express the transverse shear force resultants; $k_{s}$ denotes the shear correction factor; $A_{ij} , \, B_{ij} , \, D_{ij}$ are the extensional, coupling and bending stiffness, can be obtained by

$$ \left( {A_{ij} , \, B_{ij} , \, D_{ij} } \right) = \int_{ - h/2}^{h/2} {\left[ {Q_{ij} \left( z \right)\left( {1, \, z, \, z^{2} } \right)} \right]} {\text{d}}z $$

(16)

where $Q_{ij}$ are the material stiffness, which can be defined by Eq. (16) since the local effective properties at one certain point are assumed to be isotropic.

$$ \begin{aligned} Q_{11} & = \frac{E}{{1 - v^{2} }},\quad Q_{22} = \frac{vE}{{1 - v^{2} }},\quad Q_{12} = \frac{vE}{{1 - v^{2} }} \\ Q_{66} & = \frac{E}{{2\left( {1 + v} \right)}},\quad Q_{44} = \frac{E}{{2\left( {1 + v} \right)}},\quad Q_{55} = \frac{E}{{2\left( {1 + v} \right)}} \\ \end{aligned} $$

(17)

2.3 Energy equation

In order to investigate the vibration of the functionally graded graphene-reinforced porous cylindrical shells based on elastic foundations, Rayleigh–Ritz energy method is employed to study the vibration of functionally graded graphene-reinforced porous cylindrical shells based on elastic foundations. The Lagrangian energy function for the laminated plate is expressed as

$$ L = T - U - U_{f} - V_{\text{spring}} - W_{\text{ext}} $$

(18)

where $T$ denotes the total kinetic energy of the GPL-FG cylindrical shell, U expresses the strain energy, $U_{f}$ represents the strain energy due to the elastic foundations, $V_{\text{spring}}$ is the potential energy stored by the uniform boundary springs. They can be expressed as

$$ T = \frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\left[ {\left( {\frac{{\partial {\mathbf{D}}^{T} }}{\partial t}} \right){\mathbf{m}}\left( {\frac{{\partial {\mathbf{D}}}}{\partial t}} \right)R} \right]{\text{d}}x{\text{d}}\theta } } $$

(19)

where the expression of matrix m is given by

$$ {\mathbf{m}} = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\rho \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 &\quad z &\quad 0 \\ 0 &\quad 1 &\quad 0 &\quad 0 &\quad z \\ 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 \\ z &\quad 0 &\quad 0 &\quad {z^{2} } &\quad 0 \\ 0 &\quad z &\quad 0 &\quad 0 &\quad {z^{2} } \\ \end{array} } \right]} \right)} {\text{d}}z $$

(20)

Then, the strain energy for the GPL-FG cylindrical shell

$$ U{ = }\frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {{\mathbf{N}}^{T} {\varvec{\upvarepsilon}}} } {\text{d}}\theta {\text{d}}x{ = }\frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\left( {{\mathbf{D}}^{T} {\mathbf{I}}^{T} {\mathbf{AID}}} \right)} } {\text{d}}\theta {\text{d}}x $$

(21)

$$ \begin{aligned} U_{f} & = \frac{r}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\left\{ {\left[ {\begin{array}{*{20}c} w & {\frac{\partial w}{\partial x}} & {\frac{\partial w}{\partial \theta }} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {K_{r} } & 0 & 0 \\ 0 & {K_{g} } & 0 \\ 0 & 0 & {K_{g} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} w & {\frac{\partial w}{\partial x}} & {\frac{\partial w}{\partial \theta }} \\ \end{array} } \right]^{T} } \right\}} } {\text{d}}\theta {\text{d}}x \\ \, & = \frac{r}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\left( {{\mathbf{w}}^{T} {\mathbf{K}}_{e} {\mathbf{w}}} \right){\text{d}}\theta {\text{d}}x} } \\ \end{aligned} $$

(22)

$$ {\mathbf{w}} = \left[ {\begin{array}{*{20}c} w & {\frac{\partial w}{\partial x}} & {\frac{\partial w}{\partial \theta }} \\ \end{array} } \right]^{T} $$

$$ V_{\text{spring}} = \frac{1}{2}\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\left. {{\mathbf{D}}^{{\mathbf{T}}} {\mathbf{kD}}} \right|_{x = 0} + \left. {{\mathbf{D}}^{{\mathbf{T}}} {\mathbf{kD}}} \right|_{x = L} } \right){\text{d}}z} } {\text{d}}\theta $$

(23)

$$ W_{\text{ext}} = \frac{ 1}{ 2}\int_{0}^{L} {\int_{0}^{ 2\pi } {\int_{{ - \frac{h}{ 2}}}^{{\frac{h}{ 2}}} {\left( {{\mathbf{F}}^{T} {\mathbf{D}}} \right)} } } {\text{d}}z{\text{d}}\theta {\text{d}}x $$

(24)

where $K_{r}$ is the Winkler foundation stiffness of the elastic foundation; $K_{g}$ is the shear layer stiffness of the elastic foundations; k and F represent the matrix of the boundary spring stiffness and the external force, respectively, which are given by

$$ {\mathbf{k}} = {\text{diag}}\left[ {k_{u} ,k_{\theta } ,k_{w} ,K_{x} ,K_{\theta } } \right] $$

(25)

$$ {\mathbf{F}} = \left[ {f_{u} ,f_{v} ,f_{w} ,m_{x} ,m_{\theta } } \right]^{T} $$

where $f_{u}$,$f_{v}$ and $f_{w}$ represent the distributed forces in the corresponding directions; $m_{x}$ and $m_{\theta }$ are the couples about the reference surface.

2.4 Admissible displacement functions

Appropriate admissible functions are regarded as a critical role in the procedure for calculating the vibrations and transient response of the GPL-FG cylindrical shells surrounded by the elastic medium. Since the functions of boundary constraints are achieved by introducing the artificial virtual springs [48,49,50], there is no need to fully meet the requirements of the natural boundary conditions. According to Eqs. (19)–(24), it can be concluded that linear independence and orthogonalization are necessary for the admissible displacement functions. In this paper, the main interest of investigation is to provide a solution to satisfy the requirements, and the Chebyshev–Lagrangian approach is employed.

The Chebyshev–Lagrangian approach is defined as

$$ T_{0} \left( x \right) = 1, \, T_{1} \left( x \right) = x, \, T_{m + 1} \left( x \right) = 2xT_{m} \left( x \right) - T_{m - 1} \left( x \right), \, \left( {m \ge 2} \right) $$

(26)

It is noted that the Chebyshev–Lagrangian approach is defined in the interval of $x \in \left[ { - 1,{ 1}} \right]$. Consequently, the coordinate of the GPL-FG cylindrical shell is supposed to be transform from [0, L] to [− 1, 1] by means of a linear transformation rule.

On the basis of the above analyses, the admissible displacement exponents $u, \, v, \, w, \, \phi_{x}$ and $\phi_{\theta }$ can be expand by means of Chebyshev polynomials as

$$ u = \sum\limits_{m = 0}^{{m_{p} }} {\sum\limits_{n = 0}^{N} {A_{mn} } } T_{m} (\varsigma )\cos (n\theta ) $$

(27.a)

$$ v = \sum\limits_{m = 0}^{{m_{p} }} {\sum\limits_{n = 0}^{N} {B_{mn} } } T_{m} (\varsigma )\sin (n\theta ) $$

(27.b)

$$ w = \sum\limits_{m = 0}^{{m_{p} }} {\sum\limits_{n = 0}^{N} {C_{mn} } } T_{m} (\varsigma )\cos \left( {n\theta } \right) $$

(27.c)

$$ \phi_{x} = \sum\limits_{m = 0}^{{m_{p} }} {\sum\limits_{n = 0}^{N} {D_{mn} } } T_{m} (\varsigma ){ \cos }\left( {n\theta } \right) $$

(27.d)

$$ \phi_{\theta } = \sum\limits_{m = 0}^{{m_{p} }} {\sum\limits_{n = 0}^{N} {E_{mn} } } T_{m} (\varsigma )\sin (n\theta ) $$

(27.e)

where A, B, C, D, E are the coefficients of the Chebyshev expansions; $T_{m}$ denotes the m order Chebyshev polynomials; n represents the circumferential wave number. Substituting Eqs. (19)–(26) into Eq. (27), set the partial derivatives of the Lagrangian with respect to the unknown coefficients to be zero, one can be obtained as

$$ \left( {K - {\text{w}}^{2} M} \right)G = F $$

(28)

where K and M separately denote the stiffness and mass matrix of the GPL-FG cylindrical shell; G is the coefficients vector of the displacement; F is the column vector containing the external force contributions.

As for the problems of free vibration FG cylindrical shells, the natural frequency and eigenvectors can be obtained with ease by setting the external loading F presented by Eq. (31) as zero. With regard to analysis about the transient response of the GPL-FG cylindrical shell, the Newmark integration method is applied to acquire the time domain solutions. Since the study and applications of the Newmark integration method are published in Refs. [51, 52], it is not repeated in this paper for sake of brevity.

3 Numerical results and discussion

In this section, numerical examples are carried out first to demonstrate the feasibility, validity, versatility and precision of the present method employed in this paper. Then, applications of the present method are conducted and numerical results are obtained. On the basis, various parameters are taken into account in analysis, the details are as follows:

Firstly, the convergence and precision of the present manner are verified by means of comparing several numerical results of free vibration obtained by the present method with those presented by previous thesis. Consequently, the present method is applied to investigate the free vibration of GPL-FG shell and analyze the influence of various parameters, for instance, geometry and material properties, boundary edges and stiffness of elastic foundation. Then, compare the numerical results with the present method to those obtained by FEM to validate the feasibility and correctness of the present method which is used to investigate the transient response of GPL-FG shell. Finally, based on the demonstration above, further study on transient response of the GPL-FG cylindrical is conducted. Where the parameters of elastic foundation, porosity distribution, porosity coefficient, GPL pattern, GPL weigh faction W_GPL and Rayleigh damping coefficient are considered, respectively. To start with, for the purpose of brevity and convenience, some non-dimensional parameters are defined as:

$$ \varOmega { = }\omega R\sqrt {\rho (1 - v^{2} )} $$

$$ K_{w} = \frac{{K_{r} D_{m} }}{{L^{4} }},\quad G_{p} = \frac{{K_{g} D_{m} }}{{L^{2} }} , $$

where $\varOmega$ represents the non-dimensional frequency parameter; K_w and G_p are non-dimensional parameters corresponding to K_r and K_g, respectively.

3.1 Convergence and correctness study

As a foundation of parametric study of GPL-FG cylindrical shell, the convergence and correctness should be validated first to ensure the feasibility of the present method. In order to confirm the validity and accuracy of the present manner for convergence of GPL-FG cylindrical shell, some applications are conducted and the results are compared to those with FEM. To begin with, Fig. 4 shows the influence of stiffness of boundary springs on frequency parameter Ω of GPL-FG cylindrical shell surrounded by elastic foundation. Where the porosity efficient e₀ and circumferential waves number n are set to be 0.2 and 1, respectively, the non-dimensional parameters of elastic foundation (K_w, G_p) are selected as (100, 100); the mass efficient of GPL W_GPL = 1%. It is noted that geometry and material parameters are used in Sects. 3.1 and 3.2, unless otherwise stated. The geometry parameters and material properties are chosen as: for cylindrical shell the radius R = 1 m, length L = 2 m, thickness h = 0.1 m, Young’s modulus E_m = 130 GPa, Poisson’s ratio v_m = 0.34; mass density $\rho_{m}$  = 8960 kg/m³; for GPL the length L_GPL = 2.5 um, width b_GPL = 1.5 um, thickness h_GPL = 1.5 nm, Young’s modulus E_GPL = 1.01 TPa, Poisson’s ratio v_GPL = 0.186, mass density $\rho_{\text{GPL}}$  = 1062.5 kg/m³. From Fig. 4, we can conclude that the frequency parameter Ω is in proportion to the axial half waves number m. It can also be found that variations of stiffness of k_u and k_w result in a remarkable influence on frequency parameter Ω of GPL-FG cylindrical shell; nevertheless, frequency parameter Ω varies in a very tiny degree with the K_x and $K_{\theta }$ varying from 10⁻⁸ to 10¹⁶. More concretely, the sudden changes of frequency parameter Ω arise in a large extent in case that stiffness of boundary springs apart from K_x and $K_{\theta }$ increase from 10⁸ to 10¹². Thus, it can be regarded as clamped boundary constraints in case that all the spring stiffnesses are set over 10¹²; elastic boundary constraints can be realized by resetting the spring stiffness varying from 10⁰ and 10⁸; in case that all the springs stiffness is less than 10⁰, the boundary constraints are considered to be free. As a consequence, various boundary constraints and corresponding springs stiffness employed in this paper are exhibited in Table 1.

Fig. 4

Effect of stiffness of boundary springs on frequency parameter Ω of FG cylindrical shell resting on an elastic foundation (n = 1; P1; G1; e₀ = 0.2; (K_w, G_p) = (100, 100), W_GPL = 1%)

Table 1 Boundary conditions and corresponding spring stiffness

Figure 5 expresses the convergence behavior of frequency parameter of GPL-FG cylindrical shells surrounded by elastic medium with respect to value of truncation number m_p. Where sets of axial half waves number m and circumferential waves number n are taken into account under four boundary edges, C–C, F–F, E¹–E¹ and E¹–C, specifically. The porosity efficient e₀, the non-dimensional parameters of elastic foundation (K_w, G_p) and the mass efficient of GPL are same as those employed in Fig. 4. As shown in Fig. 5, it is easily observed that frequency parameter becomes stable when the truncation number m_p is not less than 8; thus, m_p = 10 is abundant in calculation. As is well known, the more truncation m_p used into calculation benefits the accuracy of the Chebyshev orthogonal polynomials of first kind employed in this paper, but takes more at the same time. On the basis of aforementioned discussion, the truncation number m_p is chosen to be 10 to guarantee the stable results in this paper.

Fig. 5

Convergence behavior of frequency parameter Ω of GPL-FG cylindrical shells resting on an elastic foundation with various boundary conditions: a C–C; b F–F; c E¹–E¹ b; d E¹–C

In order to test the accuracy of the present method, numerical results are compared to those provided by Ref. [25] in Table 2. The natural frequency of FG cylindrical shell is obtained under the same circumstance as Ref. [25]; the number of axial half waves m is selected to be 1. Observed from Table 2, it is obvious that the frequency increases with increasing the circumferential number n in case of a certain power index p; in contrary, it decreases with increasing power index p when the circumferential number n is stable. Moreover, the results obtained by the present method share excellent agreement with those provided by Ref. [25]. For further validating the accuracy of the present method, Table 3 expresses the comparison of frequency of free vibration of FG cylindrical shell obtained by present method with those reported by Qu [51]. The material and geometry parameters are chosen from Ref. [51]; the axial half waves m is chosen to be 1. According to Table 3, the results provided by present formulation and Ref. [51] are in excellent agreement. At the beginning, the frequency of FG cylindrical shell reduces with augmenting the circumferential waves number n in the interval [1, 3] and then increases with the increment of n when n is over 3. Besides, the frequency obtained in case of the power index p = 5 is less than those obtained when the power index p is chosen to be 6, the phenomenon is consistent with the discussion above. Compared with Ref. [34], frequency parameter Ω of free vibration of GPL-FG cylindrical shell with various porosity coefficients is exhibited in Table 4. The geometry and properties are selected to be: R = 1; L/R = 5; h/R = 0.02. The GPL pattern is chosen to be G4, and GPL weigh faction W_GPL is set to be 1%. It is visible that porosity coefficient e₀ is in negative relation to frequency parameter Ω regardless of the type of porosity distributions. Because higher porosity coefficient e₀ indicates porosities of larger size and more number, reducing the stiffness and strength of the structure. It is should be noted that the most relative error between results with different methods in Table 4 merely catches up to 0.35%, further confirming the accuracy of the present method.

Table 2 Comparison of frequency parameter Ω of free vibration of FG cylindrical shell resting on elastic foundation (L/R = 20; h/R = 0.002; m = 1; K_r = 2 × 10⁷ N/m²; K_g = 3 × 10⁷ N/m²; P3 porosity distribution; S–S)

Table 3 Comparison of frequency of free vibration of FG cylindrical shell with different boundary cases (for the zirconia: E₁ = 168 GPa, μ = 0.3, ρ = 5700 kg/m⁻³, for the aluminum: E₂ = 70 GPa, μ = 0.3, ρ = 2707 kg/m³)

Table 4 Comparison of frequency parameter Ω of free vibration of GPL-FG cylindrical shell for different porosity coefficients (R = 1, L/R = 5, h/R = 0.02, S–S; G4; W_GPL = 1%)

3.2 Free vibration of GPL-FG cylindrical shell

In this subsection, some new results about frequency of free vibration of the GPL-FG cylindrical shell are presented to study the parameters.

Figure 6 shows the effect of porosity coefficient e₀ on frequency parameter of GPL-FG shell with various types of GPL pattern under S–S boundary conditions. Where four types of porosity distributions are taken into account; GPL weigh faction W_GPL = 1%; the non-dimensional parameters of elastic foundation (K_w, G_p) = (100, 100). It is concluded from Fig. 6 that frequency parameter Ω is influenced by different porosity distributions and GPL patterns. The errors of frequency parameter Ω of GPL-FG cylindrical shell with four kinds of GPL pattern are minimum in case of P1 porosity distribution. The tendency expressed in Fig. 6b is opposite to that in Fig. 6c, since P2 and P3 mean two inverse porosity distributions. In addition, the connection between porosity coefficient e₀ and frequency parameter Ω is harmonious with the aforementioned conclusion from Table 4.

Fig. 6

The effect of porosity coefficient e₀ on frequency parameter Ω of GPL-FG shell with various types of GPL pattern under S–S boundary conditions: a P1; b P2; c P3; d P4

Figure 7 exhibits the variations of frequency parameter of GPL-FG shell along with GPL weigh faction W_GPL with different GPL patterns under C–C boundary conditions. Where porosity distributions P1, P2, P3 and P4 are taken into consideration, and porosity coefficient and e₀, GPL weigh faction W_GPL, the non-dimensional parameters of elastic foundation (K_w, G_p) are chosen from Fig. 6. As shown in Fig. 7, higher GPL weigh faction W_GPL leads to fast increasing of frequency parameter Ω of GPL-FG cylindrical shell. The reason is that the stiffness of structure is improved along with increment of GPL weigh faction W_GPL due to excellent mechanical performance of graphene. On the other hand, porosity distributions and GPL patterns should not be ignored because they make influence on frequency parameter Ω. Figure 7a shows the largest frequency parameter Ω. The numerical relationships among frequency parameter Ω shown in Fig. 7b reverse compared with those shown in Fig. 7c, the conclusion is consistent with discussion about Fig. 6. The differences among frequency parameter Ω with different GPL patterns are minimum in Fig. 7d. Variation of frequency parameter Ω of GPL-FG shells surrounded by an elastic foundation with respect to elastic foundation parameters (K_w, G_p) is presented in Fig. 8. Where C–C, C–S, E¹–C and E¹–E¹ boundary conditions are taken into account. For one thing, it is obvious that the frequency parameter Ω is proportional to values of elastic foundation parameters K_w and G_p. For another, G_p makes major influence when the boundary conditions are selected as C–C, E¹–C and E¹–E¹, while K_w takes a more important role in case of C–S boundary constraints. This is one of the main conclusions in this paper.

Fig. 7

Variations of frequency parameter Ω of GPL-FG shell along with increment of GPL weigh faction with different GPL patterns: a P1; b P2; c P3; d P4 (C–C)

Fig. 8

Variation of frequency parameter Ω of GPL-FG shells surrounded by an elastic foundation with respect to (K_w, G_p): a C–C; b C–S; c E¹–E¹; d E¹–C

In order to comprehensively analyze the vibration of GPL-FG cylindrical shell, Tables 5 and 6 are presented to study the frequency parameter Ω of GPL-FG cylindrical shell resting on various elastic foundations with respect to four types of porosity distributions. In Table 5, three classical boundary conditions are taken into consideration, specifically, C–C, S–S and F–C. For sake of completeness, E¹–E¹, E¹–C, F–E¹ are included in analysis shown by Table 6. As shown in Tables 5 and 6, different non-dimensional elastic foundation parameters (K_w, G_p) make influence on frequency parameter Ω. In particular, the frequency parameter Ω varies in large extend with (K_w, G_p) varying from (0, 0) to (0, 100), meanwhile a little change occurs in case that non-dimensional elastic foundation parameters (K_w, G_p) vary from (0, 0) to (100, 0), thus illustrating that G_p makes more influence than K_w on frequency parameter Ω of GPL-FG cylindrical shell under these circumstances. Furthermore, the boundary conditions with stronger boundary springs stiffness correspond to the higher frequency parameter Ω of free vibration of the GPL-FG cylindrical shell. C–C boundary constraints provide the maximum values of frequency parameter Ω. Last but not least, on basis of the discussions above, it is concluded that the frequency parameter Ω of free vibration of GPL-FG cylindrical shell is related to porosity distributions. However, when GPL-FG cylindrical shell is under elastic boundary conditions, such as E¹–E¹ and F–E¹ which are presented by Table 6, the frequency parameter Ω is certain values as long as the elastic foundation parameters (K_w, G_p) are chosen to be (100, 100), regardless of the porosity distributions. Figure 9 shows mode shapes of free vibrations of GPL-FG cylindrical shell surrounded by various elastic foundations with sets of classical boundary conditions, corresponding the frequency parameter Ω with GPL pattern G1 exhibited in Table 5.

Table 5 Frequency parameter Ω of GPL-FG cylindrical shell resting on various elastic foundations objected to three classical boundary conditions with respect to different porosity distributions and GPL patterns. (e₀ = 0.2; W_GPL = 1%)

Table 6 Frequency parameter Ω of GPL-FG cylindrical shell resting on various elastic foundations objected to three elastic boundary conditions with respect to different porosity distributions and GPL patterns (e₀ = 0.2; W_GPL = 1%)

Fig. 9

Mode shape of GPL-FG cylindrical shell with P1 porosity distribution resting on elastic foundations

3.3 Transient response of GPL-FG cylindrical shell

As shown in Fig. 10, there are four types of loading employed in this paper: (a) Rectangular pulse; (b) triangular pulse; (c) half-sine pulse; (d) exponential pulse, which can be expressed as

Fig. 10

The sketch of load time domain curve: a rectangular pulse; b triangular pulse; c half-sine pulse; d exponential pulse

For rectangular pulse:

$$ f\left( t \right) = f_{e} \left( {H\left( t \right) - H\left( {t - t_{e} } \right)} \right) $$

For triangular pulse:

$$ f\left( t \right) = f_{e} \left( {1 - t/t_{e} } \right)\left( {H\left( t \right) - H\left( {t - T} \right)} \right) $$

For half-sine pulse:

$$ f\left( t \right) = f_{e} \sin \left( {\pi t/T} \right)H\left( t \right) - H\left( {t - T} \right) $$

Exponential pulse:

$$ f\left( t \right) = f_{e} e^{ - \xi t} $$

where $f_{e}$ is the amplitude of the applied impulse load; t_e is the pulse width; t is the time variable. The function H(t) is given by

$$ H\left( t \right) = \left\{ {\begin{array}{*{20}c} 1 & \quad {t \ge 0} \\ 0 & \quad {t{ < 0}} \\ \end{array} } \right. $$

In order to ensure the feasibility of the present method, work about accuracy and correctness should be conducted before investigation about transient response. Figures 11 and 12 are presented to demonstrate the feasibility of the present method by comparing results with those obtained by finite-element method (FEM). Where rectangular pulse loading, triangular pulse loading, half-sine pulse loading and exponential pulse loading are taken into account; the time for loading t_e is set to be 10 ms; and the total time for analysis t₀ is 20 ms. The analysis is conducted under the condition of S–S boundary constraints, and the non-dimensional parameters of elastic foundation (K_w, G_p) are chosen as (0, 0). In order to avoid contingency of results provided by present method, the observation points positions are separately positioned at (3, 0) and (2, 0) in the $x - \theta$ coordinate system in Figs. 11 and 12, while the position of point loadings is stably located at (1, 0). It can be observed that the curves of two methods are nearly coincident, which are visibly presented by Figs. 11 and 12, validating the feasibility and precision of the present manner in investigating the transient response of GPL-FG cylindrical shell. In this subsection, except the length of FG cylindrical shell L is selected to be 4 m, the other geometry and material parameters are chosen as same as those presented in Sect. 3.2.

Fig. 11

Comparison of transient response of GPL-FG cylindrical shell: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading [loading position is (1, 0); observation position is (3, 0); t₀ = 20 ms; t_e = 10 ms; S–S; P1 porosity distribution; G2 GPL pattern; W_GPL = 1%]

Fig. 12

Comparison of transient response of GPL-FG cylindrical shell: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading [loading position is (1, 0); observation position is (2, 0); t₀ = 20 ms; t_e = 10 ms; S–S; P1 porosity distribution; G2 GPL pattern; W_GPL = 1%]

With purpose to study the effect of various non-dimensional parameters (K_w, G_p) on transient response of GPL-FG cylindrical shell, Fig. 13 is presented by taking four groups of (K_w, G_p) into account. In order to avoid contingency, four GPL patterns are employed to analyze the transient response of GPL-FG cylindrical shell with C–C boundary edges. The point loading is located at (1, 0) in the $x - \theta$ coordinate system, and the observation position is (3, 0); total time for analysis t₀ = 20 ms; time for loading t_e = 10 ms; porosity e₀ = 0.2; GPL weigh faction W_GPL = 1%. By comparing the curves exhibited in components (a) and (c) of Fig. 13, it is discovered that the curves in component (a) are very similar to those in component (c). The fact occurs as well by comparing component (b) with (d) of Fig. 13. The phenomenon illustrates that G_p makes the major influence on transient response of GPL-FG shell with C–C boundary edges. On the other hand, the amplitude of displacement decreases in a large extent when G_p increase from 0 to 100. Conclusions obtained by Fig. 13 share agreements with the discussion about Table 5.

Fig. 13

Transient response of GPL-FG cylindrical shell resting on various elastic foundations with P4 porosity distribution: a (K_w, G_p) = (0, 0); b (K_w, G_p) = (0, 100); c (K_w, G_p) = (100, 0); d (K_w, G_p) = (100, 100) [t₀ = 20 ms; t_e = 1010 ms; ρ_m = 8960 kg/m³; e₀ = 0.2; W_GPL = 1%; position of observation point = (3, 0)]

Figure 14 shows the influence of various point loadings and porosity distributions on transient response of GPL-FG cylindrical shell. where loading and observation point are both located at (2, 0) in the $x - \theta$ coordinate system; the porosity coefficient e₀ is 0.2; GPL weigh faction W_GPL is 1%; GPL pattern is G4; the non-dimensional parameter (K_w, G_p) = (0, 100); the boundary conditions are set as SD-C; the total time for analysis t₀ is 40 ms, and the time for loading t_e is 4 ms. As shown in Fig. 14, the curves provided by triangular pulse loading are similar to those provide by half-sine pulse loading. Exponential pulse loading results in the most stable transient response and the minimum amplitude. Besides, displacements with GPL patterns P2 and P4 are always higher than the others, and the curves with P4 are least smooth. For sake of completeness, the surface loadings of four types are taken into consideration in Fig. 15. Where the loading area is defined with $x \in [2,3]$ and $\theta \in [0,\pi /3]$; and the other parameters are consistent with Fig. 14. On the one hand, different with Fig. 14, the minimum amplitude appears in case of rectangular pulse loading, while the maximum amplitude results from triangular pulse loading. On the other hand, similar to Fig. 14, it is found that the curves of transient response provided by exponential pulse loading are more unstable than the other three loadings. Moreover, by comparing Fig. 15 with Fig. 14, it is found that the amplitudes of displacement results from surface loadings are lower than those occur with point loadings while applying one certain loading for the same time.

Fig. 14

Transient responses of GPL-FG cylindrical shells resting on an elastic foundation under various point loadings: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading (SD–SD; e₀ = 0.2; W_GPL = 1%; (K_w, G_p) = (0, 100); loading position = (2, 0); observation point position = (3, 0))

Fig. 15

Transient responses of GPL-FG cylindrical shells resting on an elastic foundation under various surface loadings: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading [SD–SD; e₀ = 0.2; W_GPL = 1%; (K_w, G_p) = (0, 100); loading area is defined with $x \in [2,3]$ and $\theta \in [0,\pi /3]$; observation point position is (3, 0)]

Figures 16, 17, 18 and 19 express the transient responses of GPL-FG cylindrical shells resting on different elastic foundations under four kinds of point loadings. Where structures are surrounded by elastic foundation with the non-dimensional parameters (K_w, G_p) as (0, 0), (0, 100), (100, 0), (100, 100), respectively; the boundary conditions are chosen as S–S; the time for loading and analysis is 4 ms and 50 ms; position of loading and observation point is (2, 0) and (3, 0); porosity distribution is selected to be P3; porosity coefficient e₀ is 0.2; GPL weigh faction W_GPL is 1%. As seen in Fig. 16 and Fig. 18, compared with others, the amplitude of displacement provided by loading with G3 GPL pattern is largest; while the amplitude of displacement provided by loading with G1 GPL pattern is least. Furthermore, the tendency and amplitude of curves of transient responses shown in Fig. 16 are similar to those in Fig. 18; the phenomenon appears as well by comparing Fig. 17 with Fig. 19. As for the non-dimensional parameters of elastic foundation, the amplitudes of curves of displacements under the non-dimensional elastic parameter G_p = 100 are much less than those with G_p = 0; on contrary amplitudes and tendency of curves is nearly stable in case that the non-dimensional elastic parameter K_w varies from 0 to 100. In other words, the G_p takes a role of more significance than K_w in affecting the transient response of GPL-FG shell with S–S boundary conditions. Moreover, it is observed from Figs. 16, 17, 18 and 19 that the tendency of transient responses resulting from triangular pulse loading and half-sine pulse loading are similar to each other; and so do the remaining loadings. Therefore, a conclusion is obtained that the tendency of transient response is related to the form of loading rather than the parameters of elastic foundation.

Fig. 16

Transient responses of GPL-FG cylindrical shells resting on an elastic foundation under various point loadings: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading [S–S; e₀ = 0.2; W_GPL = 1%; (K_w, G_p) = (0, 100); loading position = (2,0); observation point position = (3, 0)]

Fig. 17

Transient responses of GPL-FG cylindrical shells resting on an elastic foundation under various point loadings: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading [S–S; e₀ = 0.2; W_GPL = 1%; (K_w, G_p) = (0, 100); loading position = (2,0); observation point position = (3,0)]

Fig. 18

Transient responses of GPL-FG cylindrical shells resting on an elastic foundation under various point loadings: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading [S–S; e₀ = 0.2; W_GPL = 1%; (K_w, G_p) = (100, 0); loading position = (2, 0); observation point position = (3, 0)]

Fig. 19

Transient responses of GPL-FG cylindrical shells resting on an elastic foundation under various point loadings: a rectangular pulse loading; b triangular pulse loading; c half-sine pulse loading; d exponential pulse loading [S–S; e₀ = 0.2; W_GPL = 1%; (K_w, G_p) = (100, 100); loading position = (2, 0); observation point position = (3, 0); t₀ = 50 ms; t_e = 4 ms]

Figure 20 shows variations of transient responses of GPL-FG cylindrical shell with respect to GPL weigh faction W_GPL. Where e₀ is chosen to be 0.2, 0.4, 0.6 and 0.8; the form of loading is selected as half-sine pulse loading; the structure is subjected to S–S boundary constraints surrounded by elastic foundation with non-dimensional parameters (K_w, G_p) = (100, 100); loading area is defined with $x \in [2, \, 3]$ and $\theta \in [0, \, \pi / 3]$; position of observation point is (2, 0); time for loading and analysis are 4 ms and 40 ms; GPL pattern is G4; the porosity distribution is chosen to be P1. As shown in Fig. 20, the amplitude of displacement increases in proportion to the GPL weigh faction W_GPL, meanwhile the corresponding frequency of displacement decreases on contrary since higher W_GPL improves the stiffness of GPL-FG shell. Besides, under circumstance of the same W_GPL, the amplitude of curves of transient response increases with the increment of porosity coefficient e₀. Because larger porosity coefficient indicates larger size and more amounts of porosity, reducing the stiffness and strength of GPL-FG shell.

Fig. 20

Transient responses of GPL-FG cylindrical shells resting on an elastic foundation with respect to e₀: a e₀ = 0.2; b e₀ = 0.4; c e₀ = 0.6; d e₀ = 0.8 (S–S; (K_w, G_p) = (100, 100); loading area is defined with $x \in [2,3]$ and $\theta \in [0,\pi /3]$; observation point position = (2, 0); t₀ = 40 ms; t_e = 4 ms)

The above study on GPL-FG shell in this paper is conducted ignoring the Rayleigh damping. For sake of comprehensiveness, application of Rayleigh damping is presented by Fig. 21 by setting the values of $\alpha$ and $\beta$. In particular, the influence of the Rayleigh damping coefficients on transient response can be investigated as long as we set the reasonable values of $\alpha$ and $\beta$. In this work, GPL-FG cylindrical shell resting on an elastic foundation is used to perform the transient response for analysis. Where the effects of $\alpha$ and $\beta$ are separately shown by Fig. 21a, b; the GPL-FG cylindrical shell is subjected to S–S boundary conditions with the non-dimensional foundational parameters (K_w, G_p) = (0, 100); the porosity distribution is chosen to be P1; the GPL pattern is G2 and GPL weigh faction W_GPL is 1%; time for loading and analysis are as: t₀ = 60 ms, t_e = 30 ms. As shown in Fig. 21, it is visibly seen that the transient vibration with Rayleigh damping coefficients is completely different from those without damping coefficient. Secondly, the mass damping coefficient $\alpha$ takes a role of little influence in transient response behavior of GPL-FG shell from Fig. 21a. However, on basis of Fig. 21b, it can be found that a small increment of stiffness damping coefficient $\beta$ brings in a huge difference on transient response. For one thing, the transient response is unstable when $\alpha$  = 0 and $\beta$  = 0. For another, with a small increment of $\beta$, the transient gradually becomes stable oscillations as its oscillations decay. Moreover, the weaker oscillation is related to the lager value of $\beta$, while the more time is required for transient response to get stable.

Fig. 21

Effect of Rayleigh damping coefficients on transient response of GPL-FG cylindrical shell with S–S boundary conditions: a mass damping coefficient α₀; b mass damping coefficient ₀ [e₀ = 0.2; (K_w, G_p) = (0, 100); P1; G2; W_GPL = 1%;point loading position is (1, 0); observation point position = (2, 0); t₀ = 60 ms; t_e = 30 ms]

4 Conclusions

In this paper, an analysis model is established for investigating the free vibration and transient response of GPL-FG cylindrical shell resting on elastic foundation with sets of boundary conditions. In the framework of FSDT, the shear deformation is taken into account and the displacement functions of the GPL-FG cylindrical shell are obtained. Employing the Chebyshev polynomial of first kind, the displacement fields are expanded. The feasibility and versatility of the present method are invalidated for free vibration and transient response of GPL-FG cylindrical shell by comparing series of numerical examples with the previous study. In order to further analyze the influence of the parameters of structure and conditions, series of novel results provided by the present method are given, and the corresponding conclusions can be summarized as follows:

• 1. The frequency parameter Ω decreases with increasing the porosity coefficient e₀ since the higher e₀ indicates porosities of larger size and more number, reducing the stiffness and strength of the structure. For this season, higher e₀ enlarges the displacement of transient response of GPL-FG cylindrical shell as well. In a word, even though higher porosity coefficient e₀ reduces the weight of structure, it does harm to strength and mechanical behaviors of GPL-FG cylindrical shell.

• 2. Higher GPL weigh faction W_GPL leads to increasing of frequency parameter Ω of free vibration and the amplitude of transient displacement of GPL-FG cylindrical shell on one hand, but reducing the frequency of transient response on the other hand. The reason is that the stiffness of structure is improved along with increment of GPL weigh faction W_GPL due to the excellent mechanical performance of graphene.

• 3. Inverse porosity distributions make the reverse influence on frequency parameter Ω. However, the frequency parameter Ω stays with a certain value when the elastic foundation parameters are set large enough and the values of boundary spring stiffness are small, regardless of the distributions.

• 4. The free vibration and transient response are also related to the non-dimensional parameters of elastic foundation (K_w, G_P). Generally, the non-dimensional parameter of elastic foundation G_P makes the major effect on frequency parameter Ω and amplitude of displacement of GPL-FG cylindrical shell resting on elastic foundation. But it reverses in case of C–S boundary conditions, K_w takes the role of more significance instead of G_P.

• 5. Various kinds of loadings perform sensitive to the tendency of transient response. Besides, the point loadings bring about larger displacements compared with surface loadings.

• 6. With the Rayleigh damping coefficients taken into consideration, the transient response is completely different from that ignoring the Rayleigh damping coefficients. Furthermore, it is found that a small increment of mass damping coefficient $\beta$ causes the great influence on the transient response, while the variation of $\alpha$ hardly makes effect on transient response.

Appendix

The specific expressions of the stiffness matrix K can be written as

$$ {\mathbf{K}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{ 1 , 1} } & {{\mathbf{K}}_{1,2} } & {{\mathbf{K}}_{1,3} } & {{\mathbf{K}}_{ 1 , 4} } & {{\mathbf{K}}_{1,5} } \\ {{\mathbf{K}}_{ 1 , 2}^{\text{T}} } & {{\mathbf{K}}_{2,2} } & {{\mathbf{K}}_{2,3} } & {{\mathbf{K}}_{ 2 , 4} } & {{\mathbf{K}}_{2,5} } \\ {{\mathbf{K}}_{ 1 , 3}^{\text{T}} } & {{\mathbf{K}}_{ 2 , 3}^{\text{T}} } & {{\mathbf{K}}_{3,3} } & {{\mathbf{K}}_{ 3 , 4} } & {{\mathbf{K}}_{3,5} } \\ {{\mathbf{K}}_{ 1 , 4}^{\text{T}} } & {{\mathbf{K}}_{ 2 , 4}^{\text{T}} } & {{\mathbf{K}}_{ 3 , 4}^{\text{T}} } & {{\mathbf{K}}_{ 4 , 4} } & {{\mathbf{K}}_{ 4 , 5} } \\ {{\mathbf{K}}_{ 1 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 2 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 3 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 4 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 5 , 5} } \\ \end{array} } \right] $$

$$ {\mathbf{K}}_{i.j} = {\mathbf{K}}_{i.j}^{u} + {\mathbf{K}}_{i.j}^{V} + {\mathbf{K}}_{i.j}^{f} $$

$$ {\mathbf{K}}_{1,1}^{\text{u}} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {\frac{4}{{L^{2} }}A_{11} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{u}}}}{\partial \varsigma } + A_{66} u_{,\theta } \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{u}}}}{\partial \theta } + \frac{4}{L}A_{16} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{u}}}}{\partial \varsigma }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{1,2}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {\frac{2}{L}A_{12} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{v}}}}{\partial \theta } + \frac{2}{L}A_{66} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \varsigma } + \frac{4}{{L^{2} }}A_{16} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{u}}}}{\partial \varsigma }{\text{ + A}}_{26} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{1,4}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {\frac{4}{{L^{2} }}B_{11} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + B_{66} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta } + \frac{2}{L}B_{16} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta }{ + }\frac{2}{L}{\text{B}}_{16} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{u}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{1,5}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left[ {\frac{2}{L}B_{12} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta } + \frac{2}{L}B_{66} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + \frac{4}{{L^{2} }}B_{16} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma }{\text{ + B}}_{26} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta }} \right]{\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{2,2}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {A_{22} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \theta } + \frac{4}{{L^{2} }}A_{66} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{v}}}}{\partial \varsigma } + \frac{4}{L}A_{26} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \varsigma }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{2,4}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {\frac{2}{L}B_{12} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + \frac{2}{L}B_{66} + B_{26} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta }{ + }\frac{4}{{L^{2} }}{\text{B}}_{16} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{2,5}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {B_{22} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta } + \frac{4}{{L^{2} }}B_{66} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + \frac{2}{L}B_{26} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma }{ + }\frac{2}{L}{\text{B}}_{26} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{v}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{3,3}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{44} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{w}}}}{\partial \theta } + \frac{4}{{L^{2} }}k_{s} A_{55} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{w}}}}{\partial \varsigma } + \frac{4}{L}k_{s} A_{45} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{w}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{3,4}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {\frac{2}{L}k_{s} A_{55} {\varvec{\upphi}}_{x}^{T} \frac{{\partial {\mathbf{w}}}}{\partial \varsigma } + k_{s} A_{45} {\varvec{\upphi}}_{x}^{T} \frac{{\partial {\mathbf{w}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{3,5}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{44} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \theta }{\varvec{\upphi}}_{\theta } + \frac{2}{L}k_{s} A_{45} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \varsigma }{\varvec{\upphi}}_{\theta } } \right){\text{d}}\theta } } {\text{d}}\varsigma $$

$$ {\mathbf{K}}_{4,4}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{55} {\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} + \frac{4}{{L^{2} }}D_{11} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + D_{66} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta } + \frac{4}{L}D_{16} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta }} \right){\text{d}}\theta } } {\text{d}}\varsigma $$

$$ {\mathbf{K}}_{4,5}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{45} {\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{\theta } + D_{66} \frac{2}{L}\frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + D_{16} \frac{4}{{L^{2} }}\frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + D_{26} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{5,5}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{44} {\varvec{\upphi}}_{\theta }^{T} {\varvec{\upphi}}_{\theta } + D_{22} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta } + \frac{4}{{L^{2} }}D_{66} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + \frac{4}{L}D_{26} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$

$$ {\mathbf{K}}_{1,1}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {k_{u} \left. {{\mathbf{u}}^{T} {\mathbf{u}}} \right|_{x = 0} + k_{u} \left. {{\mathbf{u}}^{T} {\mathbf{u}}} \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } \quad {\mathbf{K}}_{2,2}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {k_{\theta } \left. {{\mathbf{v}}^{T} {\mathbf{v}}} \right|_{x = 0} + k_{\theta } \left. {{\mathbf{v}}^{T} {\mathbf{v}}} \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$

$$ {\mathbf{K}}_{3,3}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {k_{w} \left. {{\mathbf{w}}^{T} {\mathbf{w}}} \right|_{x = 0} + k_{w} \left. {{\mathbf{w}}^{T} {\mathbf{w}}} \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$

$$ {\mathbf{K}}_{4,4}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {K_{x} \left. {{\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} } \right|_{x = 0} + K_{x} \left. {{\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} } \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$

$$ {\mathbf{K}}_{5,5}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {K_{\theta } \left. {{\varvec{\upphi}}_{\theta }^{T} {\varvec{\upphi}}_{\theta } } \right|_{x = 0} + K_{\theta } \left. {{\varvec{\upphi}}_{\theta }^{T} {\varvec{\upphi}}_{\theta } } \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$

$$ {\mathbf{K}}_{3,3}^{f} { = }\frac{\text{Lr}}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left[ {K_{r} w^{2} + K_{g} \left( {\frac{4}{{L^{2} }}\frac{{\partial w^{T} }}{\partial \varsigma }\frac{\partial w}{\partial \varsigma } + \frac{{\partial w^{T} }}{r\partial \theta }\frac{\partial w}{r\partial \theta }} \right)} \right]} } {\text{d}}\theta {\text{d}}\varsigma $$

The mass matrix M is given by

$$ {\mathbf{M}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{ 1 , 1} } & 0 & 0 & {{\mathbf{M}}_{ 1 , 4} } & 0 \\ 0 & {{\mathbf{M}}_{ 2 , 2} } & 0 & 0 & {{\mathbf{M}}_{ 2 , 5} } \\ 0 & 0 & {{\mathbf{M}}_{ 3 , 3} } & 0 & 0 \\ {{\mathbf{M}}_{ 1 , 4}^{\text{T}} } & 0 & 0 & {{\mathbf{M}}_{ 4 , 4} } & 0 \\ 0 & {{\mathbf{M}}_{ 2 , 5}^{\text{T}} } & 0 & 0 & {{\mathbf{M}}_{ 5 , 5} } \\ \end{array} } \right] $$

$$ {\mathbf{M}}_{1,1} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{0} {\mathbf{u}}^{T} {\mathbf{u}}_{0} d\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{2,2} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{0} {\mathbf{v}}^{T} {\mathbf{v}}d\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{3,3} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{0} {\mathbf{w}}^{T} {\mathbf{w}}{\text{d}}\varsigma {\text{d}}\theta } } $$

$$ {\mathbf{M}}_{1,4} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{1} {\mathbf{u}}^{T} {\varvec{\upphi}}_{x} {\text{d}}\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{1,5} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{1} {\mathbf{v}}^{T} {\varvec{\upphi}}_{y} d\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{4,4} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{2} {\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} {\text{d}}\varsigma {\text{d}}\theta } } $$

$$ {\mathbf{M}}_{5,5} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{2} {\varvec{\upphi}}_{y}^{T} {\varvec{\upphi}}_{y} {\text{d}}\varsigma {\text{d}}\theta } } $$

$$ \left( {I_{0} ,I_{1} ,I_{2} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left( z \right)\left( {1,\,z,\,z^{2} } \right){\text{d}}z} $$

$$ {\mathbf{G}} =\left[ {{\mathbf{A}}_{\text{mn}} ,{\mathbf{ B}}_{\text{mn}} , { }{\mathbf{C}}_{\text{mn}} {\mathbf{, D}}_{\text{mn}} ,{\mathbf{ E}}_{\text{mn}} } \right]^{\text{T}} $$