Bilinear form, solitons, breathers and lumps of a (3 + 1)-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt equation in ocean dynamics, fluid mechanics and plasma physics

Abstract

A $(3+1)$-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt equation in ocean dynamics, fluid mechanics and plasma physics is investigated in this paper. Bilinear form, soliton and breather solutions are derived via the Hirota method. Lump solutions are also obtained. Amplitudes of the solitons are proportional to the coefficient $h_1$, while inversely proportional to the coefficient $h_2$. Velocities of the solitons are proportional to the coefficients $h_1$, $h_3$, $h_4$, $h_5$ and $h_9$. Elastic and inelastic interactions between the solitons are graphically illustrated. Based on the two-soliton solutions, breathers and periodic line waves are presented. We find that the lumps propagate along the straight lines affected by $h_4$ and $h_9$. Both the amplitudes of the hump and valleys of the lump are proportional to $h_4$, while inversely proportional to $h_2$. It is also revealed that the amplitude of the hump of the lump is eight times as large as the amplitudes of the valleys of the lump. Graphical investigation indicates that the lump which consists of one hump and two valleys is localized in all directions and propagates stably.

1 Introduction

The higher-dimensional nonlinear evolution equations have been utilized to reveal the relevant mechanisms in such fields as fluid mechanics, plasma physics, condensed matter physics and fiber optics [1,2,3,4,5,6,7,8,9,10]. In this paper, we will investigate the following $(3+1)$-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt (KDKK) equation:

$$\begin{aligned} u_t+h_1u_{xxx}+h_2uu_x+h_3u_{xxxxx}+ & {} h_4\int u_{yy}\text {d}x+h_5u_{xxy}+h_6\left( u_x\int u_{y}\text {d}x+uu_y\right) \nonumber \\+ & {} h_7(u_xu_{xx}+uu_{xxx})+h_8u^2u_x+h_9u_z=0\,, \end{aligned}$$

(1)

where the subscripts denote the partial differentials, $u=u(x,y,z,t)$ is a real function of the variables x, y, z and t, the coefficients $h_i$’s $(i=1,2,\ldots ,9)$ are the real parameters. Special cases of Eq. (1) in ocean dynamics, fluid mechanics and plasma physics have been presented as follows:

• When $h_9=0$ and u is independent of z, Eq. (1) has been reduced to the $(2+1)$-dimensional generalized KDKK equation in ocean dynamics, fluid mechanics and plasma physics, where u denotes the amplitude of the relevant wave, x and y are the running coordinates, t is the time [11]. Bilinear formalism, N-soliton solutions and periodic wave solutions of this case have been constructed [11].

• When $h_1=0$, $h_2=0$, $h_3=1$, $h_4=-5$, $h_5=-5$, $h_6=-15$, $h_7=15$, $h_8=45$, $h_9=0$ and u is independent of z, Eq. (1) has been reduced to the $(2+1)$-dimensional B-type KP equation for the shallow water wave in a fluid or electrostatic wave potential in a plasma, where u is a wave amplitude function, x and y are the scaled space coordinates and t is the scaled time coordinate [12]. For this case, soliton solutions, Bäcklund transformation and Lax pair [12], traveling wave, rational and periodic solutions [13] have been derived.

• When $h_1=0$, $h_2=0$, $h_4=h_5$ and $h_6=-h_7$, Eq. (1) has been reduced to the $(3+1)$-dimensional generalized B-type KP equation for the weakly dispersive waves propagating in a fluid, where u presents the amplitude of the weakly dispersive wave in a fluid, x, y and z are the scaled spatial coordinates and t is the scaled temporal coordinate [14]. Lump, breather wave and rogue wave solutions under certain constraints of this case have been derived with the Hirota method [14].

• When $h_2=6h_1$, $h_6=4h_5$, $h_3=h_4=h_7=h_8=h_9=0$ and u is independent of z, Eq. (1) has been reduced to the ($2+1$)-dimensional generalized breaking soliton equation for the interaction of a Riemann wave propagating along the y-axis and a long wave propagating along the x-axis, where u denotes the amplitude or elevation of the Riemann wave [15]. For this case, bilinear form, Bäcklund transformation, Bell-polynomial expressions and Wronskian-type N-soliton solutions [15, 16], exact solutions via Darboux transformation [17], positon, negaton and complexiton solutions [18], symmetry groups, Lie point symmetry group and exact solutions [19], singularity structure analysis [20] have been obtained.

Nonlinear localized waves such as the solitons, breathers, lumps and rogue waves have attracted researchers’ attention [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. The concept of solitons has been introduced to characterize the solitary waves which maintain their velocities and amplitudes unchanged during the propagation and after the interaction [36, 37]. Breathers, a kind of the localized waves with oscillatory patterns, are periodic in space or time, while localized in time or space [38, 39]. Lumps, localized in all directions in space, have the meromorphic structures to guarantee their stability [29, 40].

To our knowledge, soliton, breather and lump solutions of Eq. (1) have not been reported. In Sect. 2, we will derive the bilinear form, one- and two-soliton solutions of Eq. (1) via the Hirota method [41]. Breather and lump solutions will also be obtained. In Sect. 3, propagation of the one soliton, breathers and lumps and interactions between the two solitons will be analyzed. Section 4 presents our conclusions.

2 Bilinear form, soliton and lump solutions of Eq. (1)

2.1 Bilinear form and soliton solutions of Eq. (1)

Via the transformation

$$\begin{aligned} u=12h_1h_2^{-1}(\ln f)_{xx}\,, \end{aligned}$$

(2)

under the coefficient constraints

$$\begin{aligned} 2h_1h_2^{-1}=5h_3h_7^{-1}=h_5h_6^{-1}=h_7h_8^{-1}\,, \end{aligned}$$

(3)

bilinear form of Eq. (1) is obtained as

$$\begin{aligned} \left( D_xD_t+h_1D_x^4+h_3D_x^6+h_4D_y^2+h_5D_x^3D_y+h_9D_xD_z\right) f\cdot f=0\,, \end{aligned}$$

(4)

where $f=f(x,y,z,t)$ is a real function, $D_{x}$, $D_{y}$, $D_{z}$ and $D_t$ are the bilinear derivative operators defined by [41]

$$\begin{aligned} \begin{aligned}&D_{x}^{n_1}D_{y}^{n_2}D_{z}^{n_3}D_{t}^{n_4} a(x,y,z,t)\cdot b(x,y,z,t)\equiv \left( \partial _x-\partial _{x^{'}}\right) ^{n_1}\,\left( \partial _y-\partial _{y^{'}}\right) ^{n_2}\,\\&\quad \left( \partial _z-\partial _{z^{'}}\right) ^{n_3}\, \left( \partial _t-\partial _{t^{'}}\right) ^{n_4}\,a(x,y,z,t)\,b(x^{'},y^{'},z^{'},t^{'}) \bigg |_{x^{'}=x,\,y^{'}=y,\,z^{'}=z,\,t^{'}=t}\,,\ \end{aligned} \end{aligned}$$

(5)

where a(x, y, z, t) and $b(x^{'},y^{'},z^{'},t^{'})$ are the differentiable functions, $x^{'}$, $y^{'}$, $z^{'}$ and $t^{'}$ are the independent variables, while $n_1$, $n_2$, $n_3$ and $n_4$ are the nonnegative integers.

Substituting the power series expansion of f with respect to a small parameter $\varepsilon$,

$$\begin{aligned} f=1+\varepsilon f_1+\varepsilon ^2 f_2+\varepsilon ^3 f_3+\cdot \cdot \cdot \,, \end{aligned}$$

(6)

into Bilinear Form (4) and equating the coefficients of the same power of $\varepsilon$ to zero, we can obtain the soliton solutions, where $f_k$’s $(k=1,2,3\ldots )$ are the real functions of x, y, z and t.

Truncating Expression (6) as

$$\begin{aligned} f=1+\varepsilon f_1\,, \end{aligned}$$

(7)

and without loss of generality, setting $\varepsilon =1$, we derive the one-soliton solutions of Eq. (1) as

$$\begin{aligned} u=12h_1h_2^{-1}[\ln (1+f_1)]_{xx}\,, \end{aligned}$$

(8)

where

$$\begin{aligned} f_1=e^{kx+ny+mz+\omega t+\delta }\,,\,\,\,\omega =-h_1k^3-h_3k^5-h_9m-h_5k^2n-h_4n^2k^{-1}\,, \end{aligned}$$

(9)

with k, n, m and $\delta$ being the real constants.

Truncating Expression (6) as

$$\begin{aligned} f=1+\varepsilon f_1+\varepsilon ^2 f_2\,, \end{aligned}$$

(10)

and without loss of generality, setting $\varepsilon =1$, we derive the two-soliton solutions of Eq. (1) as

$$\begin{aligned} u=12h_1h_2^{-1}[\ln (1+f_1+f_2)]_{xx}\,, \end{aligned}$$

(11)

where

$$\begin{aligned} \begin{aligned}&f_1=e^{\theta _1}+e^{\theta _2}\,,\,\,\,f_2=A_{12}e^{\theta _1+\theta _2}\,,\\&\theta _1=k_1x+n_1y+m_1z+\omega _1 t+\delta _1\,,\,\,\,\theta _2=k_2x+n_2y+m_2z+\omega _2 t+\delta _2\,,\\&\omega _j=-h_1k_j^3-h_3k_j^5-h_9m_j-h_5k_j^2n_j-h_4n_j^2k_j^{-1}\,,\,\,\,(j=1,2)\\&A_{12}=\frac{F_1}{F_2}\,,\\&F_1=k_2^2\{k_1^2(k_1-k_2)^2[3h_1+5h_3(k_1^2-k_1k_2+k_2^2)]+h_5k_1(k_1-k_2)(2k_1-k_2)n_1-h_4n_1^2\}\\&\qquad \quad +\,k_1k_2[h_5k_1(k_1-2k_2)(k_1-k_2)+2h_4n_1]n_2-h_4k_1^2n_2^2\,,\\&F_2=k_2^2\{k_1^2(k_1+k_2)^2[3h_1+5h_3(k_1^2+k_1k_2+k_2^2)]+h_5k_1(k_1+k_2)(2k_1+k_2)n_1-h_4n_1^2\}\\&\qquad \quad +\, k_1k_2[h_5k_1(k_1+2k_2)(k_1+k_2)+2h_4n_1]n_2-h_4k_1^2n_2^2\,, \end{aligned}\nonumber \\ \end{aligned}$$

(12)

with $k_j$’s, $n_j$’s, $m_j$’s and $\delta _j$’s being the real constants.

2.2 Lump solutions of Eq. (1)

To obtain the lump solutions of Eq. (1), we assume that

$$\begin{aligned} f=(a_1x+a_2y+a_3z+a_4t+a_5)^2+(a_6x+a_7y+a_8z+a_9t+a_{10})^2+a_{11}\,, \end{aligned}$$

(13)

where $a_\varrho$’s $(\varrho =1,2,\ldots ,11)$ are the real constants to be determined. Substituting Ansatz (13) into Bilinear Form (4), we obtain

$$\begin{aligned} \begin{aligned}&a_4=-\frac{a_1^2 a_3 h_9+a_1 h_4 \left( a_2^2-a_7^2\right) +a_6 (2 a_2 a_7 h_4+a_3 a_6 h_9)}{a_1^2+a_6^2}\,,\\&a_9=-\frac{a_1^2 a_8 h_9+2 a_1 a_2 a_7 h_4-a_2^2 a_6 h_4+a_6^2 a_8 h_9+a_6 a_7^2 h_4}{a_1^2+a_6^2}\,,\\&a_{11}=-\frac{3 \left( a_1^2+a_6^2\right) ^2 \left[ a_1^2 h_1+a_1 a_2 h_5+a_6 (a_6 h_1+a_7 h_5)\right] }{h_4 (a_2 a_6-a_1 a_7)^2}\,, \end{aligned} \end{aligned}$$

(14)

with the constraints

$$\begin{aligned}&a_1^2+a_6^2>0\,, \end{aligned}$$

(15a)

$$\begin{aligned}&a_2a_6-a_1a_7\ne 0\,, \end{aligned}$$

(15b)

$$\begin{aligned}&\frac{a_1^2 h_1+a_1 a_2 h_5+a_6 (a_6 h_1+a_7 h_5)}{h_4}<0\,. \end{aligned}$$

(15c)

Notice that Constraints (15a) and (15b) make the denominator of f nonzero, and Constraint (15c) insures that f is positive. Substituting Ansatz (13) and Expressions (14) into Transformation (2), we obtain the lump solutions of Eq. (1) as

$$\begin{aligned} u=\frac{12h_1[-(2a_1g+2a_6h)^2+2(a_1^2+a_6^2)(g^2+h^2+a_{11})]}{h_2(g^2+h^2+a_{11})^2}\,, \end{aligned}$$

(16)

where

$$\begin{aligned} \begin{aligned}&g=a_1x+a_2y+a_3z+a_4t+a_5\,,\\&h=a_6x+a_7y+a_8z+a_9t+a_{10}\,, \end{aligned} \end{aligned}$$

(17)

with $a_4$, $a_9$ and $a_{11}$ defined in Expressions (14).

3 Discussion

3.1 Discussion on the solitons

In this section, the propagations and interactions of the solitons, as well as the influences of the coefficients on the solitons, will be discussed.

Based on Solutions (8), the one-soliton solutions can be rewritten as

$$\begin{aligned} u=3h_1h_2^{-1}k^2\text {sech}^2\left[ \frac{1}{2}(kx+ny+mz+\omega t+\delta )\right] \,. \end{aligned}$$

(18)

Thus, the amplitude $\varDelta$ and the velocity components along the x, y and z directions $V_x$, $V_y$ and $V_z$ of the solitons are obtained as

$$\begin{aligned} \begin{aligned}&\varDelta =3k^2\left| \frac{h_1}{h_2}\right| \,,\\&V_x=\frac{h_1k^4+h_3k^6+h_9km+h_5k^3n+h_4n^2}{k^2}\,,\\&V_y=\frac{h_1k^4+h_3k^6+h_9km+h_5k^3n+h_4n^2}{km}\,,\\&V_z=\frac{h_1k^4+h_3k^6+h_9km+h_5k^3n+h_4n^2}{kn}\,. \end{aligned} \end{aligned}$$

(19)

From Expressions (19), we find that the amplitudes of the solitons are related to the coefficients $h_1$ and $h_2$: the amplitudes of the solitons are proportional to $h_1$, while inversely proportional to $h_2$. Velocities of the solitons are proportional to the coefficients $h_1$, $h_3$, $h_4$, $h_5$ and $h_9$.

With different choices of the parameters, we will study the interaction phenomena of the solitons via Two-Soliton Solutions (11). With the parameters $\frac{n_1}{k_1}=\frac{n_2}{k_2}$ and $\frac{m_1}{k_1}=\frac{m_2}{k_2}$, the parallel interactions between the two solitons are observed since the propagation directions of the two solitons are the same. The large-amplitude soliton moves faster than the small-amplitude one. As t increases, the large-amplitude soliton overtakes the small-amplitude one, as seen in Fig. 1. Oblique interaction occurs between the two solitons owing to different propagation directions, as seen in Fig. 2. Two solitons on the $x-y$ and $x-z$ planes propagate along the opposite directions in x-axis, as seen in Fig. 2a–f, while the two solitons on the $y-z$ plane propagate along the same direction in z-axis, as seen in Fig. 2g–i. Both the parallel interaction in Fig. 1 and oblique interaction in Fig. 2 are elastic: the amplitudes and the wave shapes of the solitons are invariant before and after the interactions except for phase shifts. When $A_{12}=0$, the inelastic interaction which is also known as the soliton resonance occurs, as seen in Fig. 3. It can be seen that the amplitudes of the two solitons have a linear superposition in the interaction region.

Fig. 1

Parallel interaction of the two solitons via Solutions (11) with $h_1=1$, $h_2=6$, $h_3=2$, $h_4=1$, $h_5=1$, $h_9=1$, $k_1=2$, $k_2=1.2$, $n_1=1.5$, $n_2=0.9$, $m_1=3$, $m_2=1.8$, $\delta _1=0$ and $\delta _2=0$

Fig. 2

Oblique interaction of the two solitons via Solutions (11) with $h_1=1$, $h_2=6$, $h_3=2$, $h_4=1$, $h_5=1$, $h_9=1$, $k_1=2$, $k_2=-1.2$, $n_1=2.4$, $n_2=1.8$, $m_1=3$, $m_2=0.9$, $\delta _1=0$ and $\delta _2=0$

Fig. 3

Inelastic interaction of the two solitons via Solutions (11) with $h_1=1$, $h_2=6$, $h_3=-\frac{29}{60}$, $h_4=1$, $h_5=1$, $h_9=1$, $k_1=1$, $k_2=2$, $n_1=2$, $n_2=3$, $m_1=1$, $m_2=3$, $\delta _1=0$ and $\delta _2=0$

Breather solutions can be obtained based on Two-Soliton Solutions (11) with $k_j$, $n_j$ and $m_j$ ($j=1,2$) being the complex constants. Taking $k_1=k_2^*=i k_{1I}$, $n_1=n_2^*=n_{1R}+i n_{1I}$, $m_1=m_2^*=i m_{1I}$ and $\delta _1=\delta _2=0$, we derive the breather solutions of Eq. (1) as

$$\begin{aligned} u=12h_1h_2^{-1}\left[ \ln \left( 1+e^{\theta _1}+e^{\theta _1^*}+A_{12}e^{\theta _1+\theta _1^*}\right) \right] _{xx}\,, \end{aligned}$$

(20)

where

$$\begin{aligned} \begin{aligned}&\theta _{1}=\theta _{1R}+i\theta _{1I}\,,\\&\theta _{1R}=n_{1R}y+\left( h_5 k_{1I}^2 n_{1R}-\frac{2h_4n_{1R}n_{1I}}{k_{1I}}\right) t\,,\\&\theta _{1I}=k_{1I}x+n_{1I}y+m_{1I}z+\left[ -k_{1I}^5h_3+ k_{1I}^3h_1+k_{1I}^2h_5n_{1I}-h_9m_{1I}+\frac{h_4\left( n_{1R}^2-n_{1I}^2\right) }{k_{1I}}\right] t\,,\\&A_{12}=1+\frac{15h_3k_{1I}^6-3h_1k_{1I}^4-3h_5n_{1I}k_{1I}^3}{h_4n_{1R}^2}\,, \end{aligned}\nonumber \\ \end{aligned}$$

(21)

with $k_{1I}$, $n_{1R}$, $n_{1I}$ and $m_{1I}$ as the real constants. Breathers are localized along the direction of $\theta _{1R}=0$ and periodic along the direction of $\theta _{1I}=0$. Since the coefficients of x and z are equal to zero in the expression of $\theta _{1R}$, the breathers are parallel to the x-axis on the $x-y$ plane and parallel to the z-axis on the $y-z$ plane. On the $x-z$ plane, the localized behavior only appears in the coordinate t and the breather is reduced to the periodic line wave which is also called the homoclinic orbit.

Based on Solutions (20), taking $k_1=i$, $k_2=-i$, $n_1=-1+2i$, $n_2=-1-2i$, $m_1=i$ and $m_2=-i$, the breathers and periodic line waves are illustrated in Fig. 4. Solutions (20) on the $x-y$ and $y-z$ planes lead to the breathers which propagate stably with t increasing, as seen in Fig. 4a–c and g–i. On the $x-z$ plane, Solutions (20) lead to the periodic line wave whose amplitude is varying with t changing. Periodic line wave arises from the constant background and then decays into the constant background, as seen in Fig. 4d–f.

Fig. 4

Breathers and periodic line waves via Solutions (11) with $h_1=1$, $h_2=6$, $h_3=2$, $h_4=1$, $h_5=1$, $h_9=1$, $k_1=i$, $k_2=-i$, $n_1=-1+2i$, $n_2=-1-2i$, $m_1=i$, $m_2=-i$, $\delta _1=0$ and $\delta _1=0$

3.2 Discussion on the lumps

In this part, we will analyze the propagation of the lumps and the influences of the coefficients on the lumps. We first analyze the lumps on the $x-y$ plane with $z=0$. Based on Lump Solutions (16), setting $u_x=u_y=0$, we derive

$$\begin{aligned} \begin{aligned} x&=\frac{a_1^2 \left[ a_{10} a_2+h_9 t (a_3 a_7-a_2 a_8)-a_5 a_7\right] -a_1 a_7 h_4 t \left( a_2^2+a_7^2\right) }{\left( a_1^2+a_6^2\right) (a_1 a_7-a_2 a_6)}\\&\quad +\,\frac{a_6 \left[ a_{10} a_2 a_6+t \left( a_2^3 h_4-a_2 a_6 a_8 h_9+a_2 a_7^2 h_4+a_3 a_6 a_7 h_9\right) -a_5 a_6 a_7\right] }{\left( a_1^2+a_6^2\right) (a_1 a_7-a_2 a_6)}\,,\\ y&=\frac{a_1^3 (a_8 h_9 t-a_{10})+a_1^2 (2 a_2 a_7 h_4 t-a_3 a_6 h_9 t+a_5 a_6)+a_1 a_6 t \left( -2 a_2^2 h_4+a_6 a_8 h_9+2 a_7^2 h_4\right) }{\left( a_1^2+a_6^2\right) (a_1 a_7-a_2 a_6)}\\&\quad +\,\frac{-a_1 a_{10} a_6^2+a_6^2 [a_5 a_6-t (2 a_2 a_7 h_4+a_3 a_6 h_9)]}{\left( a_1^2+a_6^2\right) (a_1 a_7-a_2 a_6)}\,. \end{aligned}\nonumber \\ \end{aligned}$$

(22)

Thus, we obtain that the lumps propagate on the $x-y$ plane along the straight lines as

$$\begin{aligned}&L_1:\,\,\,y=\frac{\varDelta _1x+\varDelta _2}{\varDelta _3}\,, \nonumber \\&\qquad \quad \varDelta _1=a_1^3 a_8 h_9+2 a_1^2 a_2 a_7 h_4-a_1^2 a_3 a_6 h_9-2 a_1 a_2^2 a_6 h_4+a_1 a_6^2 a_8 h_9\nonumber \\&\qquad \quad +\,2 a_1 a_6 a_7^2 h_4-2 a_2 a_6^2 a_7 h_4-a_3 a_6^3 h_9\,,\nonumber \\&\varDelta _2=-a_1^2 a_{10} a_3 h_9+a_1^2 a_5 a_8 h_9-a_1 a_{10} a_2^2 h_4+a_1 a_{10} a_7^2 h_4+2 a_1 a_2 a_5 a_7 h_4\nonumber \\&\qquad \quad -\,2 a_{10} a_2 a_6 a_7 h_4-a_{10} a_3 a_6^2 h_9-a_2^2 a_5 a_6 h_4+a_5 a_6^2 a_8 h_9+a_5 a_6 a_7^2 h_4\,,\nonumber \\&\varDelta _3=-a_1^2 a_2 a_8 h_9+a_1^2 a_3 a_7 h_9-a_1 a_2^2 a_7 h_4-a_1 a_7^3 h_4\nonumber \\&\qquad \quad +\,a_2^3 a_6 h_4-a_2 a_6^2 a_8 h_9+a_2 a_6 a_7^2 h_4+a_3 a_6^2 a_7 h_9\,. \end{aligned}$$

(23)

Similarly, we derive that the lumps propagate on the $x-z$ and $y-z$ planes along the straight lines as

$$\begin{aligned} \begin{aligned} L_2:\,\,\,z&=\frac{\varDelta _1x+\varDelta _2}{\varLambda _3}\,,\\ L_3:\,\,\,z&=\frac{-\varDelta _3y+\varDelta _2}{\varLambda _3}\,, \end{aligned} \end{aligned}$$

(24)

Fig. 5

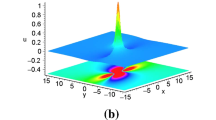
Lumps via Solutions (16) with $h_1=1$, $h_2=6$, $h_3=2$, $h_4=-3$, $h_5=1$, $h_9=2$, $a_1=1$, $a_2=2$, $a_3=2$, $a_5=1$, $a_6=3$, $a_7=-2$, $a_8=2$ and $a_{10}=-2$

with

$$\begin{aligned} \varLambda _3=a_1 a_2^2 a_8 h_4-2 a_1 a_2 a_3 a_7 h_4-a_1 a_7^2 a_8 h_4+a_2^2 a_3 a_6 h_4+2 a_2 a_6 a_7 a_8 h_4-a_3 a_6 a_7^2 h_4\,.\nonumber \\ \end{aligned}$$

(25)

Amplitudes of the hump and valleys of the lump are derived as

$$\begin{aligned} \begin{aligned} {\mathscr {A}}_1&=\left| -\frac{8 h_1 h_4 (a_2 a_6-a_1 a_7)^2}{h_2 \left( a_1^2+a_6^2\right) \left[ a_1^2 h_1+a_1 a_2 h_5+a_6 (a_6 h_1+a_7 h_5)\right] }\right| \,,\\ {\mathscr {A}}_2&=\left| \frac{h_1 h_4 (a_2 a_6-a_1 a_7)^2}{h_2 \left( a_1^2+a_6^2\right) \left[ a_1^2 h_1+a_1 a_2 h_5+a_6 (a_6 h_1+a_7 h_5)\right] }\right| \,. \end{aligned} \end{aligned}$$

(26)

From Expressions (23) and (24), we find that the lumps propagate along the straight lines which are affected by the coefficients $h_4$ and $h_9$. From Expressions (26), we find that the amplitudes of the lumps are proportional to the coefficient $h_4$, while inversely proportional to $h_2$. In addition, amplitude of the hump of the lump is eight times as large as the amplitudes of the valleys of the lump. As seen in Fig. 5, the lump which consists of one hump and two valleys is localized in all directions and propagates stably.

4 Conclusions

In this paper, we have investigated a $(3+1)$-dimensional generalized KDKK equation in ocean dynamics, fluid mechanics and plasma physics, i.e., Eq. (1). Bilinear Form (4) has been obtained, One-Soliton Solutions (8) and Two-Soliton Solutions (11) have been constructed via the Hirota method, and Lump Solutions (16) have also been derived. With certain values of the parameters $k_j$’s, $n_j$’s and $m_j$’s, breathers have been obtained based on the two-soliton solutions. Propagation of the solitons, breathers and lumps as well as the interactions between the solitons has been studied. Our results have been concluded as follows:

• (1) From Expressions (19), we have found that (i) the amplitudes of the solitons are proportional to the coefficient $h_1$, while inversely proportional to the coefficient $h_2$; (ii) the velocities of the solitons are proportional to the coefficients $h_1$, $h_3$, $h_4$, $h_5$ and $h_9$. Elastic interactions including the parallel interactions and oblique interactions have been illustrated. As seen in Fig. 1, the large-amplitude soliton has moved faster than the small-amplitude one, so that the large-amplitude soliton has overtaken the small-amplitude one with t increasing at the parallel interaction. Oblique interaction has been presented in Fig. 2. Inelastic interaction has been depicted in Fig. 3.

• (2) Based on Two-Soliton Solutions (11), with certain values of $k_j$’s, $n_j$’s and $m_j$’s, the breathers and periodic line waves have been obtained. On the $x-y$ and $y-z$ planes, Solutions (20) have led to the breathers, as seen in Fig. 4a–c and g–i. On the $x-z$ plane, Two-Soliton Solutions (20) have led to the periodic line waves, as seen in Fig. 4d–f.

• (3) Via Expressions (23) and (24), the lumps have been seen to propagate along the straight lines related to $h_4$ and $h_9$. Amplitudes of the lumps have been derived in Expressions (19), indicating that the amplitude of the hump of the lump is eight times as large as the amplitudes of the valleys of the lump. Both the amplitudes of the hump and valleys of the lump have been proportional to $h_4$, while inversely proportional to $h_2$. Graphical investigation has shown that the lump consists of one hump and two valleys and propagates stably, as seen in Fig. 5.