Small scale effects on transient vibrations of porous FG cylindrical nanoshells based on nonlocal strain gradient theory

Abstract

This research investigates transient vibrational characteristics of a porous functionally graded cylindrical nanoshell under different impulsive loadings with the use of nonlocal strain gradient theory (NSGT). Based on NSGT, two size parameters accounting for stiffness softening and hardening effects are incorporated in modeling of the nanoshell. Impulse forces have three forms of triangular, rectangular and sinusoidal. Two sorts of porosity distributions called even and uneven have been taken into account. Governing equations obtained for porous nanoshell have been solved through inverse Laplace transforms technique to derive dynamical deflections. It is shown that transient responses of a nanoshell are affected by the form and position of impulse loading, amount of porosities, porosities dispensation, nonlocal and strain gradient parameters.

1 Introduction

In recent studies about static and dynamic responses of nano-sized structural elements, the most complicated matter is using of non-classical continuum theories for their proper scale-dependent modelling. Theory of nonlocal elasticity having a size parameter has been repeatedly employed in investigations on nano-size structural components including nanobeam, nanoshell and nanoplate [1,2,3,4,5,6,7,8] which own possible application in sensors, nano-mechanical devices and systems [9]. Taking into account the size parameter in nonlocal theory yields devaluation in structure stiffness and vibrational frequency. Furthermore, several investigations showed increase of structure stiffness owing to the existence of strain gradient at small size [10]. So, recent researches on nano-scaled structures devoted non-local strain gradient theory containing two scale factors to discuss increase and reduction in stiffness of nano-scale structures [11,12,13,14,15,16,17,18,19].

New types of structural components such as beams, plates and shells are constructed from functionally graded materials which are often a combination of a ceramic phase together with a metal phase. The amount of these two phases determines the mechanical performance of the above mentioned structural components. Tang and Yang [20] studied nonlinear buckling and vibrational characteristics of fluid-conveying pips constructed from FG material. Tang et al. [21] examined the vibrational behavior of FG beams in which the material properties are graded in two directions. The producing methods of FG materials may lead to some defects, for instance pores/voids inside them. In recent years, it is indicated that vibration behaviors of FG structural components rely on the content of porosities and their dispersion models [22]. Free vibration behaviors of rotary FG beams having porosities have been investigated by Ebrahimi and Mokhtari [23] according to the improved rule of mixture of porous FG materials. Vibration behavior of a micro-size beam made of porous FG material has been investigated by Shafiei et al. [24]. Recently, Barati and Shahverdi [25] explored vibrational behaviors of a porous FG plate constructed from two piezoelectric materials. Atmane et al. [25] introduced a new shear deformation beam theory to examine vibration behavior of FG beams with porosities. Vibration characteristics of a porous FG nano-size beam in thermal environments have been analyzed by Mirjavadi et al. [26]. Also, Faleh et al. [27, 28] researched forced vibrations of porous metal foam and FG nanoscale shells accounting for small scale effects. Geometrically nonlinear vibrational response of porous FG nano-scale beam having an initial imperfection is studied by Li et al. [29].

Recently, many researches have been focused on static/dynamic analysis of nano-size shells according to non-local strain gradient elasticity. Among them, Mehralian et al. [30] studied free vibrations of carbon-based nanoshells based on NSGT via analytical method and also molecular dynamic simulation. Mohammadi et al. [31] researched the vibration response of a NSGT nano-size shell in the context of first-order shell model. Also, Barati [32] studied free vibration behavior of porous nanoshells with the use of NSGT and an analytical solution. Recently, Karami et al. [33] studied wave propagations in NSGT nanoshells via a variation approach.

Based on a survey in literature, one can conclude that many researches are relevant to free vibration study of nonlocal strain gradient nanoshells and their transient vibration due to exerted impulse loading has not been researched. Structure components including beams or shells might be exposed to abruptly applied loads leading to transient vibrations [34]. Within the time of loading, the structure might withstand large deflection and enormous vibrations. Thus, studying transient vibrations of cylindrical nanoshells subjected to impulsive loadings is crucial to realize their dynamical behaviors.

The present research deals with the analysis of transient characteristic of a FG porous nanoshell in exposure to different types of impulsive loadings. Pore dispersions have been supposed to be even and uneven within FG material. Based on NSGT, two size parameters accounting for stiffness softening and hardening effects incorporate in modeling of the nanoshell. Impulse forces have three forms of triangular, rectangular and sinusoidal. Governing equations of FG nanoshell have been solved through inverse Laplace transform method to derive dynamical deflections. It will be observed that transient responses of a nanoshell are affected by the type and position of impulse loading, porosity content, porosity dispersion type, nonlocal and strain gradient parameters as well as shell geometry.

2 Theories and formulations

2.1 Porosity-dependent properties of FG nanoshell

The volume fraction of porosities which highlights their portion in the FG material can be denoted by ξ. With the use of power-law FG model with material gradation parameter p, all of material properties including elastic moduli (E) and mass density ($\rho$) can be defined as functions of the portion of porosity [35, 36] (Table 1).

Table 1 Material properties for a FG material [3]

2.1.1 Even porosity distribution

$$ E(z) = \left( {E_{c} - E_{m} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{\;p} + E_{m} - \frac{\xi }{2}\left( {E_{c} + E_{m} } \right), $$

(1)

$$ \rho (z) = \left( {\rho_{c} - \rho_{m} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{\;p} + \rho_{m} - \frac{\xi }{2}\left( {\rho_{c} + \rho_{m} } \right). $$

(2)

2.1.2 Uneven porosity distribution

$$ E(z) = \left( {E_{c} - E_{m} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{\;p} + E_{m} - \frac{\xi }{2}\left( {E_{c} + E_{m} } \right)\left( {1 \, - \, \frac{2\left| z \right|}{h}} \right) , $$

(3)

$$ \rho (z) = \left( {\rho_{c} - \rho_{m} } \right)\left( {\frac{z}{h} + \frac{1}{2}} \right)^{\;p} + \rho_{m} - \frac{\xi }{2}\left( {\rho_{c} + \rho_{m} } \right)\left( {1 \, - \, \frac{2\left| z \right|}{h}} \right). $$

(4)

2.2 First-order shell model

In the context of first-order shell formulation, the three dimensional displacement field (u_x, u_y, u_z) has five variables which are axial (u), circumferential (v) and radial (w) displacements and also the rotations $\varphi_{x}$ and $\varphi_{\theta }$ as [31, 37]:

$$ u_{x} \left( {x,\theta ,z,t} \right) = u\left( {x,\theta ,t} \right) + z\varphi_{x} \left( {x,\theta ,t} \right), $$

(5)

$$ u_{y} \left( {x,\theta ,z,t} \right) = v\left( {x,\theta ,t} \right) + z\varphi_{\theta } \left( {x,\theta ,t} \right), $$

(6)

$$ u_{z} (x,\theta ,z,t) = w(x,\theta ,t). $$

(7)

Note that shear deformations play an important role in the structural analysis [38,39,40,41,42,43,44,45,46]. The strain field may be obtained with the help of Eqs. (5)–(7) as:

$$ \begin{aligned} \varepsilon_{xx} = & \frac{\partial u}{\partial x} + z\frac{{\partial \varphi_{x} }}{\partial x}, \\ \varepsilon_{\theta } = & \frac{1}{R}\left( {\frac{\partial v}{\partial \theta } + w + z\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right), \\ \gamma_{x\theta } = & \frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x} + \frac{z}{R}\frac{{\partial \varphi_{x} }}{\partial \theta } + z\frac{{\partial \varphi_{\theta } }}{\partial x}, \\ \gamma_{zx} = \,& \varphi_{x} + \frac{\partial w}{\partial x},\gamma_{z\theta } = \varphi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R}. \\ \end{aligned} $$

(8)

Based on the above formulation, five governing equations of a first-order shell model are established before as can be found in previous researches [31, 32]:

$$ \frac{{\partial N_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \varphi_{x} }}{{\partial t^{2} }}, $$

(9)

$$ \frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial N_{\theta \theta } }}{\partial \theta } + \frac{{Q_{z\theta } }}{R} = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial t^{2} }}, $$

(10)

$$ \frac{{\partial Q_{xz} }}{\partial x} + \frac{1}{R}\frac{{\partial Q_{z\theta } }}{\partial \theta } - \frac{{N_{\theta \theta } }}{R} = + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + q_{\text{dynamic}} , $$

(11)

$$ \frac{{\partial M_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial M_{x\theta } }}{\partial \theta } - Q_{xz} = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \varphi_{x} }}{{\partial t^{2} }}, $$

(12)

$$ \frac{{\partial M_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } - Q_{\theta z} = I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial t^{2} }}, $$

(13)

in which $q_{\text{dynamic}}$ is applied load $q_{\text{dynamic}} = f_{0} \delta (x - x_{0} )\varPhi (t)$ in which f₀ is load amplitude and x₀ is load location and

$$ (I_{0} ,I_{1} ,I_{2} ) = \int_{ - h/2}^{h/2} {(1,z,z^{2} )\rho } (z){\text{d}}z. $$

(14)

Also, in-plane normal N_ij, shear Q_ij forces and bending moment M_ij can be defined as:

$$ \{ N_{xx} ,N_{\theta \theta } ,N_{x\theta } \} = \int_{ - h/2}^{h/2} {\{ \sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } \} } {\text{d}}z, $$

(15)

$$ \{ M_{xx} ,M_{\theta \theta } ,M_{x\theta } \} = \int_{ - h/2}^{h/2} {\{ \sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } \} } z{\text{d}}z, $$

(16)

$$ \{ Q_{xz} ,Q_{z\theta } \} = \kappa_{s} \int_{ - h/2}^{h/2} {\{ \sigma_{xz} ,\sigma_{z\theta } \} } {\text{d}}z. $$

(17)

Here, σ_ij denotes the stresses and $\kappa_{s} = 5/6$ denotes the shear correction coefficient.

Based on NSGT with nonlocality coefficient ea and strain gradient coefficient l, the constitutive equation of a nano-scale shell may be introduced as [32]:

$$ [1 - (ea)^{2} \nabla^{2} ]\left\{ {\left. \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{x\theta } \hfill \\ \sigma_{xz} \hfill \\ \sigma_{z\theta } \hfill \\ \end{aligned} \right\}} \right. = [1 - l^{2} \nabla^{2} ]\frac{E(z)}{{1 - v^{2} }}\left( {\begin{array}{*{20}c} 1 & v & 0 & 0 & 0 \\ v & 1 & 0 & 0 & 0 \\ 0 & 0 & {(1 - v)/2} & 0 & 0 \\ 0 & 0 & 0 & {(1 - v)/2} & 0 \\ 0 & 0 & 0 & 0 & {(1 - v)/2} \\ \end{array} } \right)\left\{ {\left. \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \gamma_{xy} \hfill \\ \gamma_{xz} \hfill \\ \gamma_{z\theta } \hfill \\ \end{aligned} \right\}} \right.. $$

(18)

Here, strain gradient coefficient l is used to consider non-uniform strain field observed at small scales and also nonlocal coefficient ea is used to consider the nonlocality of the stress field due to atomic interaction. Based on a molecular dynamic (MD) simulation on a nonlocal strain gradient nanoshell [30], the range of the nonlocal parameter is 1–3.5 nm² and for the strain gradient parameter can be 0.1–0.4 nm². Inserting Eqs. (18) in Eqs. (15)–(17) yields the resultants as follows:

$$ [1 - (ea)^{2} \nabla^{2} ]N_{xx} = [1 - l^{2} \nabla^{2} ]\left[ {A_{11} \frac{\partial u}{\partial x} + B_{11} \frac{{\partial \varphi_{x} }}{\partial x} + \frac{{A_{12} }}{R}\left( {\frac{\partial v}{\partial \theta } + w} \right) + \frac{{B_{12} }}{R}\frac{{\partial \varphi_{\theta } }}{\partial \theta },} \right]\nonumber\\ $$

(19)

$$ [1 - (ea)^{2} \nabla^{2} ]M_{xx} = [1 - l^{2} \nabla^{2} ]\left[ {B_{11} \frac{\partial u}{\partial x} + D_{11} \frac{{\partial \varphi_{x} }}{\partial x} + \frac{{B_{12} }}{R}\left( {\frac{\partial v}{\partial \theta } + w} \right) + \frac{{D_{12} }}{R}\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right],\nonumber\\ $$

(20)

$$ [1 - (ea)^{2} \nabla^{2} ]N_{\theta \theta } = [1 - l^{2} \nabla^{2} ]\left[ {A_{12} \frac{\partial u}{\partial x} + B_{12} \frac{{\partial \varphi_{x} }}{\partial x} + \frac{{A_{11} }}{R}\left( {\frac{\partial v}{\partial \theta } + w} \right) + \frac{{B_{11} }}{R}\frac{{\partial \varphi_{\theta } }}{\partial \theta },} \right]\nonumber\\ $$

(21)

$$ [1 - (ea)^{2} \nabla^{2} ]M_{\theta \theta } = [1 - l^{2} \nabla^{2} ]\left[ {B_{12} \frac{\partial u}{\partial x} + D_{12} \frac{{\partial \varphi_{x} }}{\partial x} + \frac{{B_{11} }}{R}\left( {\frac{\partial v}{\partial \theta } + w} \right) + \frac{{D_{11} }}{R}\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right],\nonumber\\ $$

(22)

$$ [1 - (ea)^{2} \nabla^{2} ]N_{x\theta } = [1 - l^{2} \nabla^{2} ]\left[ {A_{66} \left( {\frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x}} \right) + B_{66} \left( {\frac{1}{R}\frac{{\partial \varphi_{x} }}{\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right)} \right], $$

(23)

$$ [1 - (ea)^{2} \nabla^{2} ]M_{x\theta } = [1 - l^{2} \nabla^{2} ]\left[ {B_{66} \left( {\frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x}} \right) + D_{66} \left( {\frac{1}{R}\frac{{\partial \varphi_{x} }}{\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right)} \right], $$

(24)

$$ [1 - (ea)^{2} \nabla^{2} ]Q_{xz} = [1 - l^{2} \nabla^{2} ]\tilde{A}_{66} \left( {\varphi_{x} + \frac{\partial w}{\partial x}} \right), $$

(25)

$$ [1 - (ea)^{2} \nabla^{2} ]Q_{\theta z} = \tilde{A}_{66} [1 - l^{2} \nabla^{2} ]\left( {\varphi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R}} \right), $$

(26)

in which:

$$ \begin{aligned} A_{11} = & \int_{ - h/2}^{h/2} {\frac{E(z)}{{1 - v^{2} }}\,} {\text{d}}z,B_{11} = \int_{ - h/2}^{h/2} {\frac{E(z)}{{1 - v^{2} }}z} {\text{d}}z,\;D_{11} = \int_{ - h/2}^{h/2} {\frac{{E(z)z^{2} }}{{1 - v^{2} }}\,} {\text{d}}z, \\ A_{12} = & \int_{ - h/2}^{h/2} {\frac{vE(z)}{{1 - v^{2} }}\,} {\text{d}}z,B_{12} = \int_{ - h/2}^{h/2} {\frac{vE(z)}{{1 - v^{2} }}z} {\text{d}}z,\;D_{12} = \int_{ - h/2}^{h/2} {\frac{{vE(z)z^{2} }}{{1 - v^{2} }}\,} {\text{d}}z, \\ A_{66} = & \int_{ - h/2}^{h/2} {\frac{E(z)}{2(1 + v)}\,} {\text{d}}z,\;B_{66} = \int_{ - h/2}^{h/2} {\frac{E(z)}{2(1 + v)}\,} z{\text{d}}z,\;D_{66} = \int_{ - h/2}^{h/2} {\frac{E(z)}{2(1 + v)}\,z^{2} } {\text{d}}z \\ \tilde{A}_{66} = & k_{s} \int_{ - h/2}^{h/2} {\frac{E(z)}{2(1 + v)}\,} {\text{d}}z, \\ \end{aligned} $$

(27)

Next, governing equations of the FGM nanoshell in the framework of NSGT might be established as follows by substituting Eqs. (19)–(26), into Eqs. (9)–(13):

$$\begin{aligned} [1 - l^{2} \nabla^{2}] & \left[A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + B_{11}\frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} +\frac{{A_{12} }}{R}\left( {\frac{{\partial^{2} v}}{\partial x\partial \theta } + \frac{\partial w}{\partial x}} \right) \right.\\ & \quad \left. + \frac{{B_{12} }}{R}\frac{{\partial^{2} \varphi_{\theta } }}{\partial x\partial \theta } + \frac{{A_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} u}}{{\partial \theta^{2}}} + \frac{{\partial^{2} v}}{\partial x\partial \theta }} \right) + \frac{{B_{66} }}{R}\left({\frac{1}{R}\frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2}}} + \frac{{\partial^{2} \varphi_{\theta } }}{\partial x \partial \theta }} \right) \right] \\ & \qquad\qquad + [1 - (ea)^{2} \nabla^{2}]\left[ { - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1}\frac{{\partial^{2} \varphi_{x} }}{{\partial t^{2} }}} \right] =0,\end{aligned} $$

(28)

$$\begin{aligned} [1 - l^{2} \nabla^{2}] & \left[A_{66} \left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } + \frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) + B_{66} \left( {\frac{1}{R}\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta } + \frac{{\partial^{2} \varphi_{\theta } }}{{\partial x^{2} }}} \right) + \frac{{A_{12} }}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } + \frac{{B_{12} }}{R}\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta }\right.\\ & \qquad\left. + \frac{{A_{11} }}{{R^{2} }}\left( {\frac{{\partial^{2} v}}{{\partial \theta^{2} }} + \frac{\partial w}{\partial \theta }} \right) + \frac{{B_{11} }}{{R^{2} }}\frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }} + \frac{{\tilde{A}_{66} }}{R}\left( {\varphi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R}} \right) \right] \\ & \qquad+ [1 - (ea)^{2} \nabla^{2} ]\left[ { - I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial t^{2} }}} \right] = 0,\end{aligned}$$

(29)

$$\begin{aligned} & [1 - l^{2} \nabla^{2}] \left[{\tilde{A}_{66} \left( {\frac{{\partial \varphi_{x} }}{\partial x} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{{\tilde{A}_{66} }}{R}\left( \frac{{\partial \varphi_{\theta } }}{\partial \theta } + \frac{1}{R}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{\partial v}{\partial \theta } \right)}\right. \\ & \quad \left. - \frac{{A_{12} }}{R}\frac{\partial u}{\partial x} - - \frac{{B_{12} }}{R}\frac{{\partial \varphi_{x} }}{\partial x} - \frac{{A_{11} }}{{R^{2} }}\left( {\frac{\partial v}{\partial \theta } + w} \right) - \frac{{B_{11} }}{{R^{2} }}\frac{{\partial \varphi_{\theta } }}{\partial \theta }]\right. \\ & \quad \left. + [1 - (ea)^{2} \nabla^{2} \right]\left[ { - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right] = [1 - (ea)^{2} \nabla^{2} ]q_{\text{dynamic}} , \end{aligned}$$

(30)

$$\begin{aligned} & [1 - l^{2} \nabla^{2} ] \left[ B_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + D_{11} \frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} + \frac{{B_{12} }}{R}\left( {\frac{{\partial^{2} v}}{\partial x\partial \theta } + \frac{\partial w}{\partial x}} \right) +\frac{{D_{12} }}{R}\frac{{\partial^{2} \varphi_{\theta } }}{\partial x\partial \theta } \right. \\ & \quad\left.+ \frac{{B_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial \theta }} \right) + \frac{{D_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} \varphi_{\theta } }}{\partial x\partial \theta }} \right) - \tilde{A}_{66} \left( {\varphi_{x} + \frac{\partial w}{\partial x}} \right) \right] \\ & \quad + [1 - (ea)^{2} \nabla^{2} ]\left[ { - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \varphi_{x} }}{{\partial t^{2} }}} \right] = 0, \end{aligned}$$

(31)

$$\begin{aligned} & [1 - l^{2} \nabla^{2} ] \left[ B_{66} \left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } + \frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) + D_{66} \left( {\frac{1}{R}\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta } + \frac{{\partial^{2} \varphi_{\theta } }}{{\partial x^{2} }}} \right) + \frac{{B_{12} }}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } \right.\\ & \quad\left. + \frac{{D_{12} }}{R}\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial \theta } + \frac{{B_{11} }}{{R^{2} }}\left( {\frac{{\partial^{2} v}}{{\partial \theta^{2} }} + \frac{\partial w}{\partial \theta }} \right) + \frac{{D_{11} }}{{R^{2} }}\frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }} - \tilde{A}_{66} \left( {\varphi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R}} \right)\right] \\ & \quad+ [1 - (ea)^{2} \nabla^{2} ]\left[ { - I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial t^{2} }}} \right] = 0.\end{aligned}$$

(32)

3 Solution technique

Since the transient vibration of the nanoshell is a time-dependent problem, the governing equations will be solved in Laplace domain. However, in the first step the equations have been discretized with the help of Galerkin’s method based on the following displacement assumptions:

$$ u = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {U_{mn} (t)\frac{{\partial F_{m} (x)}}{\partial x}} \cos \left( {n\theta } \right)} , $$

(33)

$$ v = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {V_{mn} (t)F_{m} (x)} \,\sin \left( {n\theta } \right)} , $$

(34)

$$ w = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {W_{mn} (t)F_{m} (x)} \,\cos \left( {n\theta } \right)} , $$

(35)

$$ \varphi_{x} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\varPhi_{mn} (t)\frac{{\partial F_{m} (x)}}{\partial x}} \,\cos \left( {n\theta } \right)} $$

(36)

$$ \varphi_{\theta } = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\varTheta_{mn} (t)F_{m} (x)} \,\sin \left( {n\theta } \right)} , $$

(37)

where $U_{mn}$, $V_{mn}$, $W_{mn}$, $\varPhi_{mn}$ and $\varTheta_{mn}$ are oscillation amplitude. Also, the function ${\text{F}}_{m} \left( x \right) = \sin \left( {\frac{m\pi }{L}x} \right)$ is an admissible function to satisfy simply supported boundary conditions:

$$ w = \frac{{\partial^{2} w_{{}} }}{{\partial x^{2} }} = \frac{{\partial^{4} w_{{}} }}{{\partial x^{4} }} = 0. $$

(38)

Next, a compact form of governing equations may be obtained by Replacing Eqs. (33)–(37) into Eqs. (28)–(32):

$$ [K]\left\{ \begin{array}{l} U_{mn} \hfill \\ V_{mn} \hfill \\ W_{mn} \hfill \\ \varPhi_{mn} \hfill \\ \varTheta_{mn} \hfill \\ \end{array} \right\} + [M]\left\{ \begin{array}{l} \ddot{U}_{mn} \hfill \\ \ddot{V}_{mn} \hfill \\ \ddot{W}_{mn} \hfill \\ \ddot{\varPhi }_{mn} \hfill \\ \ddot{\varTheta }_{mn} \hfill \\ \end{array} \right\} = \left\{ \begin{array}{l} 0 \hfill \\ 0 \hfill \\ F(t) \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} \right\}, $$

(39)

where the coefficients of [K] and [M] are presented in Appendix. Then, the time-dependent Eq. (39) is transformed into Laplace domain with initial zero condition as follows:

$$ [K]\left\{ {L[D_{mn} ]} \right\} + S^{2} [M]\left\{ {L[D_{mn} ]} \right\} = F(S) = \left\{ \begin{array}{l} 0 \hfill \\ 0 \hfill \\ L[F(t)] \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} \right\}, $$

(40)

where D_mn is the amplitude vector $D_{mn} = \{ U_{mn} ,V_{mn} ,W_{mn} ,\varPhi_{mn} ,\varTheta_{mn} \}$ and S is Laplace operator. Thus, the governing equations may be in Laplace domain. To obtain Eq. (40) from Eq. (39), some properties of Laplace transform technique must presented:

$$ L[\ddot{D}_{mn} ] = S^{2} L[D_{mn} ] - SD_{mn} (0) - \dot{D}_{mn} (0). $$

(41)

Next, implementation of inverse Laplace transform in Eq. (40) yields the time-dependent governing equation as:

$$ D_{mn} (t) = L^{ - 1} [F(S)([K] + S^{2} \{ M])^{ - 1} ]. $$

(42)

After solving the problem, the results will be presented based on normalized parameters as:

$$ t^{*} \, = \frac{t}{{t_{0} }},\,\,\bar{W} = W\frac{{100E_{c} I}}{{f_{0} L^{3} }},\,\,\lambda = \frac{l}{L}\,,\,\,\mu = \frac{ea}{L}\,. $$

(43)

4 Numerical results and discussions

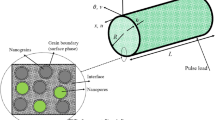
The present section focuses on transient vibration behavior of a nanoshell with graded porous material properties exposed to three types of impulse loadings based upon NSGT. Graphical results are presented for time response of the nanoshell for different porosity distributions, impulse loadings, load location, two small scale coefficients, and also radius-to-thickness ratio of the nanoshell. To validate the present formulation based on NSGT, vibration frequency of a nano-scale shell is compared with the data provided by Mehralian et al. [30] implementing analytical method and molecular dynamic simulation (MD). Results for this verification are presented in Table 2 for different values of nanoshell length based on obtained values of ea = 3.3–3.5 nm² and l = 0.1–0.4 nm² for nonlocal and strain gradient coefficients. In the following sentences, obtained new results and complete discussion related to transient vibration of a FG nanoshell will be presented. The geometry of FG nanoshell is shown in Fig. 1, while three types of applied pulse loads are introduced in Fig. 2. Another verification is provided in Fig. 3 for transient response of a cylindrical shell under linear impulse load based on the data provided in Ref. [47]. It can be concluded that the presented method in this article can accurately predict transient response of a shell under impulse loads.

Table 2 Verification of vibrational frequencies of a nano-scale shell

Fig. 1

Geometrical coordinates of a cylindrical shell

Fig. 2

Types of exerted pulse loads

Fig. 3

Validation of time response of the cylindrical shell due to linear pulse load (h = 1.2 mm, R = L = 0.2 m)

Affections of nonlocal and strain gradient coefficients on time responses of the FG nanoshell subjected to linear-type impulse loading are illustrated in Fig. 4. Radius-to-thickness ratio is assumed as R/h = 5 and material gradient index is p = 1. In the range of 0 < t* < 1 for the non-dimensional oscillation time, the FG nanoshell has transient oscillations because of exerted impulse loading. The transient oscillations will be removed by passing from t* = 1. This means than by passing from t* = 1, the nanoshell has free oscillations since the impulse loading is eliminated. This figure indicates that the free or transient vibrations of FG nanoshell rely on the magnitude of nonlocal and strain gradient coefficients. As a consequence, greater values for nonlocal parameter are corresponding to lager dynamic deflections due to stiffness-softening mechanism presented by nonlocal effects. However, stiffness-hardening mechanism due to strain gradients results in smaller deflections. So, the affections of nonlocality and strain gradient size-dependency on transient vibrations of nanoshells are opposite to each other.

Fig. 4

Time responses according to linear impulse loading and different nonlocality and strain gradient coefficients (R/h = 5, L/h = 50, ξ  = 0, p = 1)

Illustrated in Fig. 5 is the influence of pore volume fraction on time responses of the FG nanoshell with and without porosities subjected to three types of impulse loadings when R/h = 5, µ = 0.2 and λ = 0.1. This figure focuses on FG nanoshells having even porosity distribution. Based on rectangular impulse loading, a monotonic procedure may be seen during transient zone and when the load is abruptly deleted at t* = 1, free vibration happens. Also, by increase of t* based on triangular impulsive load, the transient region linearly (not abruptly) reaches to free vibration region. For every type of impulse loading, greater values of porosity amount lead to larger deflection during both transient and free oscillations. Such observation is due to the fact that the total stiffness of a nanoshell diminishes with the increase of porosity amount. Consequently, porosity content in the material structure should be controlled for a reliable design of FG structures subjected to dynamical loadings.

Fig. 5

Time responses according to various pore parameters and applied impulse loadings (p = 1, R/h = 5, L/h = 50, µ = 0.2, λ = 0.1)

Depicted in Fig. 6 is the impact of pore distribution type on transient/free vibrations of porous FG nanoshell subjected to a linearly varying impulse load. This figure focuses on FG nanoshells accounting for various material gradation indices (p) as well as pore distributions having the parameter ξ = 0.2. For the case of un-even type, pores have been produced in middle zone of the cross section, but they may vanish at corners for the case of even type. This issue highlights that the elastic moduli of a nanoshell with un-even pore type are smaller than that of even type. Hence, one can see from the figure that un-even type results in lower deflections than even type. Regardless of the type of porosity distribution, increasing in the values of material gradient index results in larger dynamic deflection in both transient and free vibration zones.

Fig. 6

Time responses according to linear impulse loading and different porosity distribution and material gradation (R/h = 5, L/h = 50, µ = 0.2, λ = 0.1, ξ = 0.2)

Plotted in Figs. 7 and 8 are, respectively, the influences of loading duration time (t₀) and load location (x₀) on transient/free vibrations of porous FG nanoshells subjected to different impulse loads. These figures deal with FGM nanoshells based on the material gradation p = 1 and also even porosity distribution. It is obvious that the vibrations number in transient region becomes higher as the magnitude of loading time becomes greater. Moreover, loading time have no effect on obtained deflections in the case of rectangular pulse load. As a deduction, it is possible to express that as loading time is lower the nanoshells pass from transient zone with fewer vibrations number. Another observation is that as the load moves away from the center point of the nanoshell, the dynamical deflections in transient region become lower. Thus, the maximum deflections occur when the impulse load is embedded at the center point of the nanoshell. Moreover, vibrations number in the transient zone remains constant with changing of loading position.

Fig. 7

Time responses based on various loading time and applied impulse loadings (R/h = 5, L/h = 50, µ = 0.2, λ = 0.1, p = 1, ξ = 0.2)

Fig. 8

Time responses according to various locations of applied impulse loading (R/h = 5, L/h = 50, µ = 0.2, λ = 0.1, ξ = 0.1)

Figure 9 illustrates the influence of radius-to-thickness ratio (R/h) on time response of a porous FG nanoshell exposed to various kinds of impulsive loads. In this figure, the nanoshell contains even pores based on the volume fraction of ξ = 0.2. One may observe that as the radius-to-thickness ratio growths, the dynamical deflection in both transient and free vibration regions becomes smaller. This is because of the increase in the stiffness of nanoshell. Thus, the geometry of nanoshell has a great affection on its transient response.

Fig. 9

Time responses based on a variety of radius-to-thickness ratios (L/h = 50, µ = 0.2, λ = 0.1, p = 1, ξ = 0.2)

5 Conclusions

The presented article focused on the transient vibration behavior of a nanoshell with graded porous material properties exposed to three types of impulse loadings based upon nonlocal strain gradient theory. Based on NSGT, two-scale parameters were included into the formulation to capture small size effects. The problem was solved based on inverse Laplace transform method to find dynamic deflections for three types of impulse loadings. It was reported that greater values for nonlocal parameter were corresponding to lager dynamic deflections due to stiffness-softening mechanism presented by nonlocal effects. Also, stiffness-hardening mechanism due to strain gradients led to smaller deflections. It was also concluded that greater values of porosity volume fraction led to greater deflections during both transient and free oscillations. But, the magnitude of dynamic deflection or oscillation amplitudes dependent on the type of porosity distribution. Even porosities led to larger deflections than uneven porosities. Moreover, the vibrations number in the transient zone remained constant with changing of loading position.

Appendix

$$ k_{1,1} = A_{11} \left( {\varPsi_{31} - l^{2} \left( {\varPsi_{51} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{31} } \right)} \right) - n^{2} \frac{{A_{66} }}{{R^{2} }}\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right), $$

(44)

$$\begin{aligned} & k_{2,1} = n\left( {\frac{{A_{12} }}{R} + \frac{{A_{66} }}{R}} \right)\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right),\\ & \qquad \;k_{1,2} = - n\left( {\frac{{A_{12} }}{R} + \frac{{A_{66} }}{R}} \right)\left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right),\end{aligned} $$

(45)

$$ k_{3,1} = + \frac{{A_{12} }}{R}\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right), \;k_{1,3} = - \frac{{A_{12} }}{R}\left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right), $$

(46)

$$ \begin{aligned} k_{4,1} = & + B_{11} \left( {\varPsi_{31} - l^{2} \left( {\varPsi_{51} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{31} } \right)} \right) - n^{2} \frac{{B_{66} }}{{R^{2} }}\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right), \\ k_{1,4} = & B_{11} \left( {\varPsi_{31} - l^{2} \left( {\varPsi_{51} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{31} } \right)} \right) - n^{2} \frac{{B_{66} }}{{R^{2} }}\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right), \\ \end{aligned} $$

(47)

$$ \begin{aligned} & k_{5,1} = n\left( {\frac{{B_{12} }}{R} + \frac{{B_{66} }}{R}} \right)\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right),\\ & \qquad \;k_{1,5} = - n\left( {\frac{{B_{66} }}{R} + \frac{{B_{12} }}{R}} \right)\left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right),\end{aligned} $$

(48)

$$\begin{aligned} & k_{2,2} = A_{66} \left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right) - n^{2} \frac{{A_{11} }}{{R^{2} }}\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right) \\ & \qquad - \frac{{\tilde{A}_{66} }}{{R^{2} }}\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right),\end{aligned} $$

(49)

$$\begin{aligned} & k_{3,2} = - n\left( {\frac{{A_{11} }}{{R^{2} }} + \frac{{\tilde{A}_{66} }}{{R^{2} }}} \right)\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right),\\ & \qquad \;k_{2,3} = - n\left( {\frac{{\tilde{A}_{66} }}{{R^{2} }} + \frac{{A_{11} }}{{R^{2} }}} \right)\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right),\end{aligned} $$

(50)

$$\begin{aligned} & k_{4,2} = - n\left( {\frac{{B_{12} }}{R} + \frac{{B_{66} }}{R}} \right)\left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right),\\ & \qquad \;k_{2,4} = + n\left( {\frac{{B_{12} }}{R} + \frac{{B_{66} }}{R}} \right)\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right),\end{aligned} $$

(51)

$$\begin{aligned} k_{5,2} &= B_{66} \left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right) - n^{2} \frac{{B_{11} }}{{R^{2} }}\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right)\\ & \quad + \frac{{\tilde{A}_{66} }}{R}\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right),} \right)\end{aligned} $$

(52)

$$\begin{aligned} k_{3,3} &= \tilde{A}_{66} \left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}}}}\varPsi_{20} } \right)} \right) - n^{2} \frac{{\tilde{A}_{66} }}{{R^{2} }}\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right) \\ & \quad- \frac{{A_{11} }}{{R^{2} }}\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right),\end{aligned}$$

(53)

$$\begin{aligned} & k_{4,3} = \left( {\tilde{A}_{66} - \frac{{B_{12} }}{R}} \right)\left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right),\\ & \qquad\;k_{3,4} = + \left( {\frac{{B_{12} }}{R} - \tilde{A}_{66} } \right)\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right),\end{aligned} $$

(54)

$$\begin{aligned} & k_{5,3} = n\left( { + \frac{{\tilde{A}_{66} }}{R} - \frac{{B_{11} }}{{R^{2} }}} \right)\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right),\\ & \qquad \;k_{3,5} = - n\left( { + \frac{{B_{11} }}{{R^{2} }} - \frac{{\tilde{A}_{66} }}{R}} \right)\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right),\end{aligned} $$

(55)

$$\begin{aligned} k_{4,4} & = + D_{11} \left( {\varPsi_{31} - l^{2} \left( {\varPsi_{51} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{31} } \right)} \right) - n^{2} \frac{{D_{66} }}{{R^{2} }}\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right)\\ &\quad - \tilde{A}_{66} \left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right),\end{aligned} $$

(56)

$$\begin{aligned} & k_{5,4} = + n\left( {\frac{{D_{12} }}{R} + \frac{{D_{66} }}{R}} \right)\left( {\varPsi_{11} - l^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right),\\ & \qquad\;k_{4,5} = - n\left( {\frac{{D_{66} }}{R} + \frac{{D_{12} }}{R}} \right)\left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right),\end{aligned} $$

(57)

$$\begin{aligned} k_{5,5}& = + D_{66} \left( {\varPsi_{20} - l^{2} \left( {\varPsi_{40} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{20} } \right)} \right) - n^{2} \frac{{D_{11} }}{{R^{2} }}\left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right)\\ & \quad - \tilde{A}_{66} \left( {\varPsi_{00} - l^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right),\end{aligned} $$

(58)

$$ m_{1,1} = + I_{0} \left( {\varPsi_{11} - ea^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right), $$

(59)

$$ m_{2,2} = m_{3,3} = m_{5,5} = + I_{0} \left( {\varPsi_{00} - ea^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right), $$

(60)

$$ m_{4,4} = + I_{2} \left( {\varPsi_{11} - ea^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right), $$

(61)

$$ m_{4,1} = + I_{1} \left( {\varPsi_{11} - ea^{2} \left( {\varPsi_{31} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{11} } \right)} \right),\;m_{5,2} = m_{2,5} = + I_{1} \left( {\varPsi_{00} - ea^{2} \left( {\varPsi_{20} - \frac{{n^{2} }}{{R^{{}} }}\varPsi_{00} } \right)} \right), $$

(62)

$$ Q_{\text{dynamic}} = Q_{n} \varPsi_{00} , $$

(63)

in which

$$ \varPsi_{00} = \int_{0}^{L} {F_{m} } F_{m} {\text{d}}x, $$

(64)

$$ \varPsi_{20} = \int_{0}^{L} {\frac{{{\text{d}}^{2} F_{m}^{{}} }}{{{\text{d}}x^{2} }}} F_{m} {\text{d}}x, $$

(65)

$$ \varPsi_{11} = \int_{0}^{L} {\frac{{{\text{d}}F_{m}^{{}} }}{{{\text{d}}x}}} \frac{{{\text{d}}F_{m}^{{}} }}{{{\text{d}}x}}{\text{d}}x, $$

(66)

$$ \varPsi_{31} = \int\limits_{0}^{L} {\frac{{{\text{d}}^{3} F_{m}^{{}} }}{{{\text{d}}x^{3} }}} \frac{{{\text{d}}F_{m}^{{}} }}{{{\text{d}}x}}{\text{d}}x, $$

(67)

$$ \varPsi_{40} = \int_{0}^{L} {\frac{{{\text{d}}^{4} F_{m}^{{}} }}{{{\text{d}}x^{4} }}} F_{m} {\text{d}}x, $$

(68)

$$ \varPsi_{51} = \int_{0}^{L} {\frac{{{\text{d}}^{5} F_{m}^{{}} }}{{{\text{d}}x^{5} }}} \frac{{{\text{d}}F_{m}^{{}} }}{{{\text{d}}x}}{\text{d}}x, $$

(69)