1 Introduction

Rearranging ion-atom collisions at intermediate and high impact energies received tremendous attention by theoreticians and experimentalists alike [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. One of such frequently studied encounters is single-electron transfer from hydrogenlike and heliumlike targets by heavy nuclei. This problem area is of notable fundamental interest in atomic physics due to the need to gain a fuller comprehension of few-body collisional dynamics. Among the results customarily provided by this research area, highly ranked are theoretical and measured total cross sections. The validity and overall usefulness of theoretical modelings for these collisions rest upon their performance in comparisons with the associated experimental data. Of especial relevance to all applications are the perturbative theories because they are by far more manageable in numerical computations than any of the various variants of the close-coupling methods.

The practical importance of the electron capture total cross section data bases is enhanced by their extensive usage in numerous and ever lasting applications within the versatile fields of heavy ion transport physics. These include plasma physics [18,19,20,21], thermonuclear fusion research [18,19,20,21,22,23], astrophysics [24, 25] and medical physics [26,27,28,29,30,31,32,33,34,35]. Herein, the most important are estimates of energy losses of heavy ions during their passage through matter. To this end, due to the complexity of the traversed media, the conventional procedures are based on various Monte Carlo simulations [36, 37]. Their reliability depends critically on the accuracy of the main input data, the atomic total cross sections for charge exchange, ionization and excitation.

There is an interplay between the capture and ionization channels depending on the impact energy. For slower projectiles, capture dominates. Ionization prevails for faster projectiles. Thus, while traversing the given medium, an initially fast projectile will lose its energy mainly through the ionization channel. However, at the end of its range, near the Bragg peak, an exhausted projectile will slow down so that the capture channel opens up and begins to yield the main contribution to the heavy ion energy losses.

The line shape of the Bragg peak is sharp and narrow. It usually covers a small size of about 1 mm for a typical pencil beam. The location of such a Bragg peak, for the given medium (tissue in radiotherapy), depends only on the type of the applied ion beam and on its initial energy. Thus, if a wider area of the deposited energy in the medium should be covered (as in tumor therapy by ions), the initial energy of the beam should be varied (tuned, modulated). Then, a sequence of the resulting Bragg peaks produced by several ion beams of different initial energies lines up next to each other. Their superposition produces a relatively flat energy deposition profile within the preassigned area (which can be a few centimeters for tumors irradiated by ions). Thus, the tumor should be scanned by several beams of different energies to have a relatively flat dose profile within the tumor borders. Such a line shape, which conforms with the given size of the treated tumor, is called the spread out Bragg peak (SOBP). In this way, the deposited dose is maximized in the tumor itself with practically no spillover beyond the range for protons (for heavier ions, there appears a fragmentation tail after the SOBP). Prior to the tumor, the entry doses from the multiple beams of varying initial energies are added together. Thus, while the SOBP profile signifies deposition of an optimal (maximum) dose in the tumor, it also enhances the dose level prior to the tumor [32,33,34].

The fact that ionization dominates over capture at high energies cannot be overstated. The reason is that the capture probability itself could be augmented if ionization is included as an intermediate channel. Such an anticipation is indeed materialized in computations when at least some of the continuum intermediate states of the active electron are taken into account in either one or both channels. This possibility has been explored in a number of distorted wave methods within their three- and four-body formalisms. Among these, the present main focus is on the four-body boundary-corrected continuum intermediate state (BCIS-4B) method applied specifically to single charge exchange in proton–helium collisions at intermediate and high energies (10–11000 keV).

To contextualize and expand the framework of this subject, also of practical interest (for atomic physics and beyond) is to see whether there is an energy region of the potential merit/advantage for using a four-body method instead of some of the three-body counterparts. In this regard, to expose the BCIS-4B method to a significant challenge, it is essential to juxtapose it to a theoretically well-founded theory, which is reasonably successful relative to measurements. Such a challenger is currently opted to be the three-body continuum distorted wave (CDW-3B) method [38], which has abundantly been documented as reliable at intermediate and high energies [1, 2, 6, 38,39,40,41,42,43].

In their three- or four-body versions, the main difference between the CDW and BCIS methods is in the manner in which the continuum intermediate states are included [1, 2, 6, 38,39,40,41,42,43,44,45,46,47,48]. In the CDW method, these states are incorporated both initially (entrance channel) and finally (exit channel), whereas in the BCIS method they appear only in one channel (entrance or exit). As emphasized, the electronic continuum intermediate states are important at higher energies. Nevertheless, if over-accounted, they could impact adversely on the capture probability at the lower part of the intermediate energies.

Such an over-account may arise from the interference effects of the two multiplied full Coulomb wave functions in the transition amplitude of, e.g., the CDW method. The BCIS method alleviates this over-account since its transition amplitude contains only one full Coulomb wave function for single charge exchange. Moreover, in the presently used prior cross sections from the BCIS method, the initial wave function of the whole system is normalized at all distances, while in the CDW method this is true only at the asymptotic inter-particle separations. However, the transition amplitudes in any distorted wave theory are given by some multi-dimensional integrals carried out over all the inter-particle distances and not just their asymptotic values.

The present applications of the BCIS-4B method exploits an analytical calculation of seven out of nine integrals in the transition amplitude \(T_{if}.\) Here, we are concerned with the state-selective and state-summed total cross sections for single-electron capture by protons from helium targets. Capture into a number of excited states of the newly formed hydrogen atom \(\textrm{H}(nlm)\) with \(1\le n\le 4\) is considered, including all the lm sub-levels. This is a new feature, which advantageously complements the earlier investigations in the BCIS-4B method [49, 50] that were restricted to formation of atomic hydrogen solely in the ground state, \(\textrm{H}(1s)\). Various state-resolved and state-summed cross sections are frequently needed in versatile applications within plasma physics [18,19,20,21], thermonuclear fusion program [18,19,20,21,22,23], astrophysics [24, 25] and medical physics [26,27,28,29,30,31]. This is a further motivation to report the results of our investigations in the present article.

Atomic units will be used throughout unless stated otherwise.

2 Theory

For heavy scattering aggregates under study, a general type of single-electron capture by a bare nucleus from a heliumlike atomic target is schematized as:

$$\begin{aligned} Z_\textrm{P}+(Z_\textrm{T};e_1,e_2)_{1s^2}\longrightarrow (Z_\textrm{P},e_1)_{nlm}+(Z_\textrm{T},e_2)_{1s}, \end{aligned}$$
(1)

where P and T are the projectile and target nuclei of charges \(Z_\textrm{P,T}\) and masses \(M_\textrm{P,T}\gg 1\), respectively. Electrons \(e_{1,2}\) in process (1) are in their bound states symbolized by the parentheses. Therein, the subscripts indicate the usual quantum numbers nlm or the spectroscopic notation of the states \(\{1s^2,\, 1s\}.\)

The target system \((Z_\textrm{T};e_1,e_2)_{1s^2}\) is in the ground state, \(1s^2.\) The newly formed hydrogenlike system \((Z_\textrm{P},e_1)_{nlm}\) is in any fixed nlm state. The target remainder \((Z_\textrm{T},e_2)_{1s}\) is in the ground state, 1s. The system \((Z_\textrm{T},e_2)_{n'l'm'}\), with an arbitrary set \(n'l'm'\) can also be formed by one-electron capture from \((Z_\textrm{T};e_1,e_2)_{1s^2}\) by \(Z_\textrm{P}\). This is not examined here since the total contribution of such a pathway to capture of electron \(e_1\) in process (1) does not surpass 5% [2, 51,52,53]. If electron \(e_2\) is captured, indices 1 and 2 should exchange their places. Either of the two target electrons can be captured with the same probability. Therefore, the final cross sections for capture of, e.g., electron \(e_1\) should be multiplied by 2.

The following nomenclature for process (1) is adopted (see Fig. 1). For electrons, \(\vec {x}_{k}\) and \(\vec {s}_{k}\) are the position vectors of \(e_{k}\, (k=1,2)\) relative to \(Z_\textrm{T}\) and \(Z_\textrm{P},\) respectively. For nuclei, \(\vec R\) is the vector directed from \(Z_\textrm{T}\) to \(Z_\textrm{P}\). In the entrance channel, \({\vec r}_i\) is the position vector of \(Z_\textrm{P}\) relative to \((Z_\textrm{T};e_1,e_2)_{1s^2}\). Likewise, in the exit channel, \({\vec r}_f\) is the position vector of \((Z_\textrm{T},e_2)_{1s}\) relative to \((Z_\textrm{P},e_1)_{nlm}\). The sets \(\{\varphi _i(\vec x_1,\vec x_2),\, E_i\}\) (entrance channel, \(i=1\,s^2\)) and \(\{\varphi _{nlm}(\vec s_1),\, E_n;\, \varphi _{1\,s}(\vec x_2),\,E'_{1\,s}\}\) (exit channel) represent the bound states and binding energies, respectively, where \(E_n=-Z_\textrm{P}^2/(2n^2)\) and \(E'_{1s}=-Z_\textrm{T}^2/2\).

Fig. 1
figure 1

Geometry for process (1) with all the relevant position vectors

Full size image

Taking the target to be at rest, the incident velocity vector \(\vec v\) is directed along the Z-axis in an arbitrary Galilean reference system XOYZ of coordinates. In this case, \(\vec R\) can be decomposed as \(\vec R=\vec \rho +\vec Z,\) where \(\vec \rho \) is the vectorial projection of \(\vec R\) in the scattering XOY-plane, so that \(\vec \rho \cdot \vec v=0.\) Vector \(\vec \rho \) should not be confused with the impact parameter from the semi-classical formalism. We are using the purely quantum-mechanical description of all the four particles (light and heavy) in process (1).

For a heavy particle collision, such as process (1), using the mass limits \(1/M_\textrm{P,T}\ll 1\), the prior transition amplitude \(T_{if}\) in the BCIS-4B method is defined by the matrix element [49, 50]:

$$\begin{aligned} T_{if}(\vec \eta \,)&=Z_\textrm{P}N^\star _\textrm{T}\nonumber \\&\quad \times \int \int \int \textrm{d}\vec s_1\textrm{d}\vec s_2\textrm{d}\vec R \,(\rho v)^{2i\nu _i} \varphi ^*_{nlm}(\vec s_1) \varphi ^*_{1s}(\vec x_2)\nonumber \\&\quad \times \left( \frac{2}{R}-\frac{1}{s_1}-\frac{1}{s_2}\right) \varphi _{i}(x_1, x_2) \,\textrm{e}^{i\alpha \cdot s_1+i\beta \cdot x_1} \nonumber \\&\quad \times {}_1 F_1(i\nu _\textrm{T},1,ivx_1+i v\cdot x_1) (vR+ v\cdot R)^{i\xi }, \end{aligned}$$
(2)
$$\begin{aligned} \vec \alpha&=\vec \eta -\gamma _+{\vec v},\, \vec \beta =-\vec \eta -\gamma _-{\vec v},\nonumber \\ \gamma _\pm&=\frac{1}{2}\mp \frac{\Delta E}{v^2},\,\Delta E=E_i-(E_n+E'_{1s}), \end{aligned}$$
(3)

where \(\nu _i=Z_\textrm{P}(Z_\textrm{T}-2)/v,\) \(\xi =Z_\textrm{P}/v\), and \(\vec \eta \) is the transverse momentum transfer \((\vec \eta \cdot \vec v=0)\). Here, \(N_\textrm{T}\) is the normalization constant of the customary full Coulomb wave function, \(N_\textrm{T}=\textrm{e}^{\pi \nu _\textrm{T}/2} \Gamma (1+i\nu _\textrm{T}),\) with the Sommerfeld parameter \(\nu _\textrm{T}=(Z_\textrm{T}-1)/v\). Symbols \(\Gamma \) and \({}_1F_1\) refer, respectively, to the standard gamma function and the Gauss confluent hypergeometric function (also known as the Kummer function).

For computations of total cross sections, the phase \((\rho v)^{2i\nu _i}\) gives no contribution [2] and it will hereafter be dropped from Eq. (2). As such, using a powerful method originally devised by Belkić in Ref. [3], seven out of nine integrals in \(T_{if}\) from Eq. (2) are calculated analytically in a closed form. The remaining two Feynman parametrization integrals are over the real variables in the intervals running from 0 to 1. Both remaining integrals are computed by the Gauss–Legendre numerical quadratures. The final expression for \(T_{if}(\vec \eta \,)\) does not depend on the angle of vector \(\vec \eta ,\) so that \(T_{if}(\vec \eta \,)=T_{if}(\eta \,)\).

The calculation of \(T_{if}(\vec \eta \,)\) is carried out using the two-parameter target wave function \(\varphi _{i}({\vec x}_1,{\vec x}_2)\) of Silverman et al. [54] which includes about 95% of radial electronic correlations:

$$\begin{aligned} \varphi _{i}(\vec x_1,\vec x_2)= N(\textrm{e}^{-\alpha _1 x_1-\alpha _2 x_2}+ \textrm{e}^{-\alpha _2 x_1-\alpha _1x_2}), \end{aligned}$$
(4)

where \(\alpha _1=2.183171\), \(\alpha _2=1.18853\), \(E_i=-2.8756614\), and N is the normalization constant \(N=[(\alpha _1\alpha _2)^{-3}+(\alpha _1/2+\alpha _2/2)^{-6}]^{-1/2}/(\pi \sqrt{2})\).

With the help of \(T_{if}(\vec \eta \,)\) from Eq. (2), leaving out the phase \((\rho v)^{2i\nu _i}\) as indicated, the total cross section \(Q_{if}\) for process (1) is given by:

$$\begin{aligned} Q_{if}(\pi a_0^2)=\frac{1}{2\pi ^2 v^2}\int \limits _0^\infty \eta \textrm{d}\eta \, |T_{if}(\eta \,)|^2, \end{aligned}$$
(5)

where \(a_0\) is the Bohr radius and \(\pi a^2_0=8.797\times 10^{-17}\,\mathrm{cm^2}.\) The integration over \(\eta \) is scaled to an interval from 0 to 1 to take advantage of the dominant contribution stemming from the forward direction of scattering of heavy particles [5]. The three remaining integrals in \(Q_{if}\), two of which are due \(T_{if}(\vec \eta )\), are performed by means of the Gauss–Legendre quadrature rule. The same optimal number of integration points for each of the three axes is chosen to secure the accuracy within the stabilized two decimal places in all the computed cross sections \(Q_{if}\).

Fig. 2
figure 2

Total cross sections \(Q_{1s,2s,2p}\) (\(\textrm{cm}^2\)) as a function of impact energy \(E(\textrm{keV})\) for formation of atomic hydrogen in one-electron capture by protons from \(\textrm{He}(1s^2)\). Theoretical methods: BCIS-4B, present results (full curve), CDW-3B [40] (dashed curve). Experimental data for \(Q_{2s}\): \(\square \) Hughes et al. [55], \(\circ \) Cline et al. [56]. Experimental data for \(Q_{2p}\): \(\square \) Hughes et al. [55], \(\circ \) Cline et al. [56], \(\vartriangle \) Hippler et al. [57], \(\triangledown \) Hippler et al. [58]

Full size image
Fig. 3
figure 3

Total cross sections \(Q_{3s,3p,3d}\) (\(\textrm{cm}^2\)) as a function of impact energy \(E(\textrm{keV})\) for formation of atomic hydrogen in one-electron capture by protons from \(\textrm{He}(1s^2)\). Theoretical methods: BCIS-4B present results (full curve), CDW-3B [40] (dashed curve). Experimental data for \(Q_{3s}\): \(\circ \) Ford et al. [59], \(\square \) Conrads et al. [60], \(\vartriangle \) Brower and Pipkin [61], \(\triangledown \) Cline et al. [56]. Experimental data for \(Q_{3p}\): \(\square \) Ford et al. [59], \(\vartriangle \) Brower and Pipkin [61], \(\circ \) Cline et al. [62]. Experimental data for \(Q_{3d}\): \(\vartriangle \) Ford et al. [59], \(\triangledown \) Brower and Pipkin [61], \(\circ \) Cline et al. [62], \(\square \) Edwards and Thomas [63]

Full size image
Fig. 4
figure 4

Total cross sections \(Q_{4s,4p,4d,4f}\) (\(\textrm{cm}^2\)) as a function of impact energy \(E(\textrm{keV})\) for formation of atomic hydrogen in one-electron capture by protons from \(\textrm{He}(1\,s^2)\). Theoretical methods: BCIS-4B present results (full curve), CDW-3B [40] (dashed curve). Experimental data: \(\circ \) Hughes et al. [64], \(\square \) Doughty et al. [65], \(\vartriangle \) Brower and Pipkin [61]

Full size image
Fig. 5
figure 5

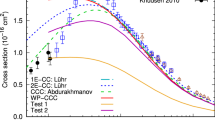
Total cross sections \(Q_{n=2,3,4}\) and \(Q_\mathrm{\Sigma }\) (\(\textrm{cm}^2\)) as a function of impact energy \(E(\textrm{keV})\) for formation of atomic hydrogen in one-electron capture by protons from \(\textrm{He}(1s^2)\). Theoretical methods: BCIS-4B present results (black full curve), CDW-3B [40] (dashed curve), TDDFT (\(\blacklozenge \), [14], blue full curve [15]), SDLA-Sic (\(\star \), [16]), BGM [11] (red full curve). Experimental data for \(Q_{n=2}\): \(\circ \) Andreev et al. [66], \(\bullet \) Il’in et al. [67]. Experimental data for \(Q_{n=3}\): \(\bullet \) Il’in et al. [67], \(\square \) Lenormand [68], \(\vartriangle \) Bobashev et al. [69]. Experimental data for \(Q_{n=4}\): \(\bullet \) Il’in et al. [67], \(\square \) Lenormand [68], \(\vartriangle \) Bobashev et al. [69]. Experimental data for \(Q_\mathrm{\Sigma }\): \(\blacktriangledown \) Berkner et al. [70], \(\blacksquare \) Welsh et al. [71], \(\vartriangle \) Scryber [72], \(\circ \) Williams [73], \(\blacktriangle \) Martin et al. [74], \(\square \) Horsdal-Pedersen et al. [75], \(\bullet \) Shah and Gilbody [76], \(\lozenge \) Shah et al. [77]

Full size image

3 Results and discussion

Here, the general process (1) is specified by considering one-electron capture by protons from the ground state of helium targets:

$$\begin{aligned} \mathrm{H^+}+\textrm{He}(1s^2)\longrightarrow & {} \textrm{H}(nlm)+\textrm{He}^+(1s), \end{aligned}$$
(6)
$$\begin{aligned} \mathrm{H^+}+\textrm{He}(1s^2)\longrightarrow & {} \textrm{H}(nl)+\textrm{He}^+(1s), \end{aligned}$$
(7)
$$\begin{aligned} \mathrm{H^+}+\textrm{He}(1s^2)\longrightarrow & {} \textrm{H}(n)+\textrm{He}^+(1s), \end{aligned}$$
(8)
$$\begin{aligned} \mathrm{H^+}+\textrm{He}(1s^2)\longrightarrow & {} \textrm{H}(\Sigma )+\textrm{He}^+(1s). \end{aligned}$$
(9)

Total cross sections for these processes are available from many measurements performed over a long period of time lasting for several decades [55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77]. The majority of the measured cross sections in these studies are in reasonably good mutual agreement. Such a circumstance represents a favorable testing ground for various theoretical methods. These experimental data are employed to evaluate the reliability of the BCIS-4B method. Also included in the comparisons are the associated results from the CDW-3B method [40].

The main part of the computations encompasses the state-selective cross sections \(Q_{nlm}\) for \(1\le n\le 4\) including all the lm sub-levels. From the obtained results for \(Q_{nlm}\), the state-summed cross sections \(Q_{nl}\) and \(Q_{n}\) are deduced:

$$\begin{aligned} Q_{nl}=\sum _{m=-l}^{l}Q_{nlm},\quad Q_{n}=\sum _{l=0}^{n-1}Q_{nl}. \end{aligned}$$
(10)

The cross sections \(Q_{\Sigma }\) summed over \(Q_{n}\, (n\le 3)\) are extracted by utilizing the Oppenheimer \(n^{-3}\) scaling rule [4, 78]:

$$\begin{aligned} Q_{\Sigma }=Q_1+Q_2+2.081Q_3. \end{aligned}$$
(11)

It was found that the Oppenheimer rule, coupled with the higher n-levels of \(\textrm{H}(n)\), does not appreciably change \(Q_{\Sigma }\) from the related values given by Eq. (11). We checked that, e.g., above 4000 keV, the cross sections \(Q_{\Sigma }=1.202Q_1\), \(Q_{\Sigma }=Q_1+1.616Q_2\) and \(Q_{\Sigma }=Q_1+Q_2+2.081Q_3\) are graphically indistinguishable from each other.

The detailed results covering \(Q_{nl},\) \(Q_{n}\) and \(Q_\mathrm{\Sigma }\) for processes (7)–(9) in the BCIS-4B and CDW-3B methods are listed in Tables 1 and 2 at proton energies \(10\, \textrm{keV}\le E\le 4000\, \textrm{keV}\). Further, in Figs. 2, 3, 4 and 5 for processes (7)–(9), the available experimental data are compared with the BCIS-4B (full curves) and CDW-3B (dashed curves) methods. Cross sections \(Q_{1s,2s,2p}\) are on Fig. 2, \(Q_{3s,3p,3d}\) on Fig. 3, \(Q_{4s,4p,4d,4f}\) on Fig. 4 and \(Q_{2,3,4,\mathrm{\Sigma }}\) on Fig. 5.

Regarding the spherically symmetric s-states (\(l=0\)) in process (7), cross sections \(Q_{1s}\) (Fig. 2a), \(Q_{2s}\) (Fig. 2b), \(Q_{3s}\) (Fig. 3a) and \(Q_{4s}\) (Fig. 4a) in the BCIS-4B and CDW-3B methods are seen to be in excellent mutual agreements above about 70 keV. Below 70 keV, there are considerable discrepancies between these two theories. Thus, cross sections \(Q_{ns}\) in the BCIS-4B method exhibit the well-delineated Massey peaks. Instead of this maximum, \(Q_{ns}\) from the CDW-3B method continues to rise with the decrease in impact energy. Importantly, accord between the BCIS-4B method and the experimental data on \(Q_{ns}\) above about \(50\, \textrm{keV}\) is very good for \(Q_{2s}\) (Fig. 2b) as well as for \(Q_{3s}\) (Fig. 3a) and nearly perfect for \(Q_{4s}\) (Fig. 4a).

As to the spherically asymmetric states (\(l\ge 1\)) in process (7), the comparisons of the BCIS-4B method with the experimental data show a high level of compatibility for \(Q_{2p}\) (Fig. 2c), \(Q_{3p}\) (Fig. 3b) and \(Q_{3d}\) (Fig. 3c) at energies as low as 10 or 25 keV, depending on the value of the angular momentum quantum number l. The single datum at \(240\, \textrm{keV}\) [59] is an outlier since it is at variance with all the other measured cross sections for \(Q_{3d}.\) Here too, the Massey peaks are seen in both the BCIS-4B method and measurements, but not in the CDW-3B method.

Moreover, the CDW-3B method for \(Q_{np}\) largely overestimates the experimental data throughout with the exception of merely three energies \(150\, \textrm{keV}\) for \(Q_{2p}\) (Fig. 2c), \(300\, \textrm{keV}\) for \(Q_{3p}\) (Fig. 3b) and \(240\, \textrm{keV}\) for \(Q_{3d}\) (Fig. 3c). Only the theoretical results are depicted for \(Q_{4p}\) (Fig. 4b), \(Q_{4d}\) (Fig. 4c) and \(Q_{4f}\) (Fig. 4d) since the related experimental data are unavailable. The CDW-3B method shows an increased extent of departures from the BCIS-4B method when passing from \(Q_{2p}\) (Fig. 2c) to \(Q_{3p,3d}\) (Fig. 3b,c) as well as from \(Q_{4p}\) (Fig. 4b) to \(Q_{4d}\) (Fig. 4c) and \(Q_{4f}\) (Fig. 4d).

For process (8), agreement between the BCIS-4B method and the experimental data is remarkably good for \(Q_{2}\) (Fig. 5a), \(Q_{3}\) (Fig. 5b) and \(Q_{4}\) (Fig. 5c) down to 10 or 20 keV, depending on the value of the principal quantum number n. On panels a–c of Fig. 5, the Massey peaks clearly emerge in the BCIS-4B method and measurements. Therein, however, there is no hint about this essential structure in the CDW-3B method. At impact energies above 70 keV, the BCIS-4B and CDW-3B methods are highly concordant.

Finally, Fig. 5d shows the cross sections for electron capture by protons from helium into any atomic hydrogen state \(\textrm{H}(\Sigma ),\) as in process (9). Herein, above about 80 keV, the BCIS-4B and CDW-3B methods cohere very well with each other. Moreover, the BCIS-4B method is in perfect agreement with all the experimental data from about 20 keV to the highest energy (10500 keV) considered in the measurement from Ref. [70]. This is gratifying since \(Q_{\Sigma }\) is seen in Fig. 5d to vary over some 11 orders of magnitude across a wide energy range which covers 3 orders of magnitude. Note that for \(Q_{\Sigma },\) the Massey peak is present in the BCIS-4B method, but absent from the CDW-3B method.

Also plotted in Fig. 5d are the results of the three non-perturbative formalisms, the ‘basis generator method’ (BGM) [11] at 10–6000 keV, the ‘time-dependent density functional theory’ (TDDFT) at 40–500 keV [14] as well as at 10–1000 keV [15] and the spin-dependent ‘local density approximation with the self-interaction correction’ (SLDA-Sic) [16]. At \(E\le 300\) keV, the two sets of the TDDFT results from Refs. [14, 15] agree very well with each other as well as with the BCIS-4B method. Moreover, at \(E\le 50\) keV, the TDDFT results [14, 15] are also in a very good accord with the SLDA-Sic findings [16]. However, the situation is notably changed at higher energies. Thus, above 400 and 1500 keV, the BGM [11] and TDDFT [15], respectively, deviate completely from the BCIS-4B method and, by implication, also from the experimental data. Divergence of the BGM [11] and TDDFT [15] at higher energies is caused by inaccurate computations of scattering integrals that oscillate heavily due to the presence of the electronic translation factors.

Besides the SDLA-Sic, also of interest is to consider the two related spin-independent variants with and without the self-interaction correction, the LDA-Sic [16] and LDA [17], respectively. According to Ref. [16], the results from the SLDA-Sic [16] lie between those from the LDA and LDA-Sic. As has been shown in Ref. [16], at 1–10 keV, the LDA and LDA-Sic predictions significantly differ from each other by a factor ranging from about 4 to 100, but they merge smoothly together at 30 and 50 keV. Among these three methods, the SLDA-Sic was found [16] to perform best in comparisons with the experimental data. The implication is that, within the LDA-based formalisms used at lower energies (\(E\le 10\) keV), it is advantageous to simultaneously include both the spin statistics and the self-interaction corrections.

Table 1 Cross sections for single-electron capture from a ground-state helium atom by an energetic proton
Full size table
Table 2 Cross sections for single-electron capture from a ground-state helium atom by an energetic proton
Full size table

The physical origin of the Massey peaks for cross sections \(Q_{nl}\), \(Q_n\) and \(Q_\Sigma \) at energies around about 30 keV is in the resonance nature of the electron capture process. Resonance, leading to the cross section maximum, occurs when the incident velocity v matches the orbital velocity \(v_e\) of the electron to be captured from the target by the projectile, \(v > av_e.\) Constant \(a>1\) is usually assessed empirically by comparing the given theory with measurements. For electron capture by a nucleus of charge \(Z_\textrm{P}\) from a hydrogenlike atomic target of nuclear charge \(Z_\textrm{T}\), we have \(v_e=Z_\textrm{T}/n.\)

Thus, the mentioned matching can be expressed as \(E(\mathrm{keV/amu})>25 (aZ_\textrm{T}/n)^2\), or equivalently, by \(E(\mathrm{keV/amu})>50 a^2|E_j|\, (j=i,f)\). In the CDW-3B method, the scaling factor a has been found empirically to be \(a\approx 1.6,\) according to which the lowest validity limit of this theory is \(E(\mathrm{keV/amu})\approx 80\,\textrm{max}\{|E_i|,|E_f|\}\) [2]. However, as the analyzed cross sections demonstrate, the lowest impact energy at which the BCIS-4B method is valid is at \(E(\mathrm{keV/amu})\approx 20b\,\textrm{max}\{|E_i|,|E_f|\},\) where constant b is either 1 or 1/2, depending on the nl-state in the formed atomic hydrogen \(\textrm{H}(nl).\)

4 Conclusions

This study is on single-electron capture from heliumlike atomic targets by heavy nuclei at intermediate and high impact energies with the illustrations on the \(\mathrm{H^++He}\) colliding system. For such rearrangement collisions, the distorted wave formalism of scattering theory is flexible as it offers a multitude of choices of distorted waves and distorting potentials. In this framework, a distorted wave is conceived as the product of an unperturbed channel state and a distorting factor. The distorting factor is usually the product of the two full Coulomb continuum wave functions, one for the active electron and the other for the heavy nuclei. The given electronic full Coulomb wave is placed on the nuclear charge around which the active electron is not in a bound state.

Thus, e.g., in the exit channel, the captured electron is bound to the scattered projectile nucleus, while the full Coulomb wave function of the same electron corresponds to the field of the target nucleus. This is the essence of a typical distorted wave methodology signifying that the active electron simultaneously resides in two Coulomb centers, the projectile and the target nuclei. For instance, the three-body continuum distorted wave (CDW-3B) method employs two electronic full Coulomb waves, one in the entrance and the other in the exit channels. The four-body boundary-corrected continuum intermediate state (BCIS-4B) method uses one electronic full Coulomb wave in either the entrance channel (for the post form) or in the exit channel (for the prior form of the perturbation interactions).

Both methods satisfy the correct boundary conditions in the entrance and exit channels. Regarding the Coulomb waves for the relative motion of heavy nuclei in the BCIS-4B and CDW-3B methods, they appear in both the entrance and exit channels, but their product does not contribute to any total cross section computed in the heavy mass limit. Overall, in this type of distorted wave methods, capture takes place in two steps. An electron is first ionized from the target and continues to move in the Coulomb field of the scattered projectile nucleus. Subsequently, capture of that electron occurs from its continuum intermediate states in either the target or projectile nucleus, depending on whether the prior or post form of the perturbation interaction potential is employed.

Such an intermediate ionization channel is very important for capture processes at high energies. The reason is that ionization dominates over capture precisely at high energies. Therefore, description of capture is expected to be substantially improved by inclusion of some of the intermediate ionization channels. This is indeed abundantly confirmed in the past literature by comparing the second-order perturbation theories with measurements. On the other hand, the computationally by far more demanding non-perturbative atomic basis set expansion methods either exclude altogether the genuine continuum intermediate states [9] or replace them by certain quasi-continuum (discretized positive-energy pseudostates) [10, 12]. These close-coupling methods have been applied to the \(\mathrm{H^+} \mathrm{+He}\) one-electron transfer problem at impact energies that did not exceed 1 MeV and, as such, unlike the BCIS-4B methods [46], were not reported to predict the Thomas peaks. For this particular collision, regarding, e.g., the state-summed total cross sections \(Q_{\Sigma }\), some among the non-perturbative formalisms, notably the BGM [11] and the TDDFT [15], have been found to strikingly deviate from the experimental data already above 1500 and 400 keV, respectively. By comparison, the BCIS-4B method is presently demonstrated to agree perfectly with the measured cross sections \(Q_{\Sigma }\) at the widest available interval of impact energies, 20–10500 MeV.

The present work deals with the three- and four-body formalisms implemented in the CDW-3B and BCIS-4B methods, respectively. Concerning various practical applications, comparisons between these two methods are important and useful. This is motivated by at least two reasons: (i) to evaluate the effect of the Coulomb wave distortions through two centers (in two channels) versus one center (in one channel) and (ii) to assess the potential advantages of the four-body over the three-body treatments of the same electron capture problem. For a systematic reliability assessment of the theoretical methods, these comparisons should be validated by the existing experimental data, whenever available.

The specific illustrative example is chosen to be single-electron capture by protons from helium targets at 10–11000 keV. The computations include the state-selective \(Q_{nlm}\) and state-summed total cross sections \(Q_{nl}\) (sum of \(Q_{nlm}\) over m), \(Q_n\) (sum of \(Q_{nl}\) over l) and \(Q_{\Sigma }\) (sum of \(Q_{n}\) over n). The principal quantum number n covers the range \(1\le n\le 4\) with all the sub-levels \((-l\le m\le l,\, 0\le l\le n-1\)). Cross sections for formation of atomic hydrogen in any bound state, \(\textrm{H}(\Sigma ),\) are computed using the obtained values of \(Q_{n}\) and the accompanying Oppenheimer \(n^{-3}\) scaling rule for the higher excited states.

The comprehensive cross sections from the BCIS-4B and CDW-3B methods are given in Tables 1 and 2 and four figures with 3 or 4 panels. Above about 70 keV, the BCIS-4B and CDW-3B methods are in a very tight proximity of the measured cross sections for formation of \(\textrm{H}(2s,3s,4s)\) and \(\textrm{H}(\mathrm \Sigma ).\) However, as to forming \(\textrm{H}(2p,3p,3d),\) the CDW-3B method is found to largely overestimate both the BCIS-4B method and the experimental data, particularly around the Massey peaks and at higher energies. For instance, the cross sections from the CDW-3B method incessantly increase with decrease in impact energy showing no indication whatsoever about the existence of the Massey peaks. In sharp contrast, the BCIS-4B method always predicts the Massey peaks at their theoretically expected and experimentally observed locations (about 30 keV/amu).

Crucially, the presented results for all the investigated total cross sections systematically show that the BCIS-4B method for formation of \(Q_{2s,2p,3s,3p,3d,4s},\) \(Q_{2,3,4}\) and \(Q_{\Sigma }\) is in excellent agreement with the associated experimental data at intermediate and high energies (above about 10 or 20 keV/amu). Thus far, no measurements have been reported on \(Q_{4p,4d,4f}\). It is remarkable that this perturbation theory successfully covers also the lower part of intermediate energies that are usually viewed as the prime applicability domain of the non-perturbative close-coupling-type methods.

Overall, within the perturbative theories, the expounded analysis establishes a definite superiority of the BCIS-4B method over the CDW-3B method, especially for formation of \(\textrm{H}(np,nd)\). Most importantly, the BCIS-4B method is demonstrated to be a very reliable theory capable of accurately describing the measured cross sections for electron capture by protons from helium targets. This method is valid in a wide domain from the lowest edge (20 keV) of intermediate up to very high energies, including the highest energy 10.5 MeV for which the experimental data exist. Such features are expected to find the most useful applications in plasma physics, thermonuclear fusion, astrophysics and medical physics.