Fully differential cross sections for single ionization of helium by proton impact

Abstract

We have studied the electron emission angular distributions for single ionization of helium atoms in their ground states induced by fast proton impact in coplanar geometry. We have employed the four-body formalism of distorted wave (DW-4B) approximation to calculate the fully differential cross sections (FDCS) of the ejected electron for several values of the momentum transfer and energies of the electrons ejected in the scattering plane. In this formalism, distortion in the exit channel related to the Coulomb continuum states of the scattered proton and the ejected electron in the field of residual target ion are included. In the entrance channel, the initial bound state wavefunction is distorted by the incoming proton and the corresponding wavefunction is related to the Coulomb continuum state of the active electron and the proton. The transition amplitude contains nine-dimensional integrals, and it is analytically reduced to two-dimensional integrals. These two-dimensional integrals can be calculated numerically. The influence of the target wavefunctions on the FDCS is also investigated using various bound-state wavefunctions for the helium atom. The obtained results using the DW-4B approximation have been compared with the recent measurements of Schulz et al. (Phys Rev A 73:062704, 2006), Gassert et al. (Phys Rev Lett 116:073201, 2016) and Chuluunbaatar et al. (Phys Rev A 99:062711, 2019) and with the other theoretical calculations. It is found that in the whole angular range clear discrepancies are found between the experimental data and the theoretical predictions at large momentum transfer and intermediate impact energy.

Graphic abstract

1 Introduction

In recent years, the study of atomic ionization induced by ion impact is of fundamental importance for atomic collision from both theoretical and experimental point of view because of the increasing need of such data, particularly in the fields of plasma physics, astrophysics, penetration of swift ions through matter, radiation material science, ion therapy [1,2,3] and short wavelength laser development. With the development of the experimental technique known as the cold target recoil ion momentum spectroscopy (COLTRIMS) [4], it is possible to determine the three-dimensional angular distributions for electron emission at different values of electron emission energy and momentum transfer which is known as the fully differential cross sections (FDCS). Such studies are the most sensitive tests for different theoretical models describing few-body dynamics in ionization processes. However, experimental data of FDCS are essential to guide different theoretical models such as the continuum distorted-wave-eikonal initial state (CDW-EIS) approximation [5,6,7,8], the first Born approximation (FBA) [8, 9], the nonperturbative coupled pseudo-state (CP) approximation [10, 11] and the distorted wave (DW) approximation [12]. Therefore, at present such field is enjoying renowned interest. In 2001, first Schulz et al. [13] measured the FDCS for single ionization of He by 100 MeV/amu $C^{6+}$ and compared with the first Born approximation (FBA). The measured FDCS was reproduced satisfactorily by the FBA approximation in the scattering plane although poor agreement was found in the perpendicular plane. The observed discrepancies have been attributed due to the absence of all interactions among the heavy colliding partners. Later, Schulz et al. [9] extended their work [13] by measuring the FDCS for 75 keV proton impact on helium atom. Their results were compared with various distorted-wave calculations along with the CDW-EIS approximation [14,15,16,17]. In this paper, we have investigated the single ionization of helium induced by proton impact with different incident energies in the framework of four-body distorted-wave (DW-4B) approximation.

Investigations on fully differential cross sections for single ionization of $\mathrm{He}$ by highly charged projectiles [18,19,20,21] have been reported where the strength of the interaction between the projectile and the target was much strong. These experimental measurements show a significant discrepancies with the theoretical results. However, ionization process for strong perturbation is more challenging to the theory. Recently, several theoretical groups [22, 23] have investigated the FDCS for single ionization of $\mathrm{He}$ by $Au^{q+}$ in the framework of more sophisticated three-body distorted wave (3DW) approximation. In this calculation, the final state is approximated by a product of three-Coulomb wave (3CW) which takes into account the distortion due to three-body mutual Coulombic interaction. This is a well-known theoretical model originally proposed by Brauner et al. [24] which is called BBK model. We found that this calculations show some promising structures and predict a strong peak in the forward direction of the FDCS spectra which had not been observed in previous theoretical calculations.

Another strong interaction in ion-atom collision also helps us to understand the details of the dynamics in ionization process which is important in carbon therapy. In this context, it is mentioned that Schulz et al. [13] and Madison et al. [25] have measured the FDCS for single ionization of helium by 100 MeV/amu $C^{6+}$. Later, Fischer et al. [26] have reported the measurements of FDCS for 2 MeV/amu $C^{6+}$ and 3.6 MeV/amu $\hbox {Au}^{q+}$ ($q=24,53$) impacted on $\mathrm{He}$. Subsequently, the simple FBA [10], the three-body distorted wave (3DW) [12, 25], the CDW-EIS [18, 27], the three-Coulomb wave (3CW) [28, 29] and the first-order Born-approximation with two Coulomb wave (FBA-2CW) [30] models have been employed to study this process.

Arthanayaka et al. [31] have done both experimental and theoretical investigation of FDCS for $p-\mathrm{He}$ collisions. The experimental data have been compared with the non-perturbative time-dependent model. They observed the projectile coherence effects and qualitatively reproduced by their calculations. An important role of coherence effect (both two-center and single-center) was first obtained from the measurements of FDCS for $p-H_{2}$ collision [32, 33]. Two-center interference is well known to us. But one-center interference is interpreted as interference between the first- and higher-order transition amplitudes. In this work, they clearly explained the one-center interference phenomena.

Theoretical cross sections of the ejected-electron angular distributions for 1 MeV $p-\mathrm{He}$ collisions at small values of momentum transfer and ejected-electron energy have been calculated by Chuluunbaatar et al. [34] in the scattering plane. In this study, three different calculations such as the first Born, second Born and the three-Coulomb (3C) model with different ground state wavefunctions of $\mathrm{He}$ have been presented and compared with the experiment [35]. They have shown the effect of electron–electron correlations in the ground state of the $\mathrm{He}$ atom on the absolute value of the recoil peak to binary peak. From this study, we found that both FBA and 3C calculations underestimate the experimental results [35] in the region of binary-peak position, whereas excellent agreement has been observed in the recoil peak position.

Later, Chuluunbaatar et al. [36] presented experimental data on FDCS for single ionization of $\mathrm{He}$ by 1 MeV proton impact and compared with various theoretical approaches. In this angular distribution, we find two slight peaks around $\theta _{\mathrm{e}}=0^\circ$ and $180^\circ$ in addition to recoil and binary peaks at small momentum transfer. It is observed the disagreement between different theoretical models (FBA and 3C) and experiment for electron emission energy and momentum transfer values away from the Bethe ridge [2]. All calculations were carried out using the Roothaan–Hartree–Fock (RHF) [37] ground-state wavefunction of the $\mathrm{He}$ atom. Recently, Abdurakhmanov et al. [38] have investigated the single ionization of helium by 0.5, 1 and 2 MeV proton impact in the scattering plane by means of the wave packet convergent close-coupling (WP-CCC) method in different kinematical regimes. The results thus obtained are in good agreement with the recent experimental findings [36]. This may be due to the coupling between channels and multiple scattering effects.

In the present theoretical investigation, we have mainly focused our attention on FDCS for single ionization of helium by proton impact with different energies using the DW-4B approximation. In this approximation, both the scattered projectile and the ejected electron are described by the Coulomb wave in the final state wavefunction. In initial channel, we take the Coulomb distortion between the active electron in the target and the projectile ion.

The paper is organized as follows. In Sect. 2, we summarize our theoretical model and evaluate the transition amplitudes for FDCS. In Sect. 3, the theoretical results are compared with the experimental data. Finally, the paper ends with concluding remarks in Sect. 4. Atomic units characterized by $\hbar =m_{\mathrm{e}}=e=4\pi \varepsilon _{0}=1$ are used throughout the paper unless stated otherwise.

2 Theory

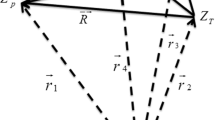
Let us consider the single ionization of a helium atom of nuclear charge $Z_{\mathrm{T}}$ and mass $M_{\mathrm{T}}$ by the collision of a projectile (P) of charge $Z_{\mathrm{P}}$ and mass $M_{\mathrm{P}}$, and the initial velocity vector $\vec {v}$. Here, a four-body collision is considered in which a target consists of two electrons $e_{1}$ and $e_{2}$. Let $\vec {r}_{1}$ and $\vec {r}_{2}$ ($\vec {s}_{1}$ and $\vec {s}_{2}$) be the position vectors of the electrons $e_{1}$ and $e_{2}$ relative to the target nucleus T (projectile P). In terms of these vectors, the inter-electron distance $\vec {r}_{{12}}$ is given by $r_{{12}}=|\vec {s}_{1}-\vec {s}_{2}|\equiv s_{{12}}=|\vec {r}_{1}-\vec {r}_{2}|$. Let, further $\vec {R}$ be the vector of the internuclear distance directed from T to P. In the entrance channel, it is convenient to introduce $\vec {r}_{i}$ as the relative vector of P with respect to the center of mass of $(Z_{T}; e_{1}, e_{2})$. Similarly, in the exit channel $\vec {r}_{f}$ denotes the position vector of the target nucleus with respect to the center of mass of $(Z_{P}; e_{1}, e_{2})$. In the center of mass system (CM), the prior form of the transition amplitude in the DW-4B method may be written as:

$$\begin{aligned} T_{{if}}^{(-)}=\,{<}\psi _{{f}}^{-}|V_{{i}}|\varPhi _{{i}}^{+}{>}, \end{aligned}$$

(1)

where $V_{i}$ is the perturbation potential in the initial channel. The form of $V_{i}$ is given by

$$\begin{aligned} V_{i}=Z_{\mathrm{P}}\bigg (\frac{Z_{\mathrm{T}}}{R}-\frac{1}{s_{1}}-\frac{1}{s_{2}}\bigg ). \end{aligned}$$

(2)

Here, the initial state $\varPhi _{{i}}^{+}$ is represented by a product of a Coulomb distortion for the incoming projectile and a wavefunction of helium atom in ground state. So the wavefunction $\varPhi _{i}^{+}$ is given by

$$\begin{aligned} \varPhi _{{i}}^{+}(\vec {r}_{1},\vec {r}_{2},\vec {r}_{i})=(2\pi )^{-\frac{3}{2}}\exp (i\vec {k_{i}}.\vec {r}_{i})\chi _{i}^{+}\phi _{i}(\vec {r}_{1},\vec {r}_{2}), \end{aligned}$$

(3)

where $\vec {k_{i}}$ is the momentum of the incident projectile with respect to the target center of mass. $\chi _{i}^{+}$ is the Coulomb distortion of the initial bound state due to the incoming projectile. Therefore, $\chi _{i}^{+}$ reads

$$\begin{aligned} \chi _{i}^{+}=\mathrm{e}^{\frac{\pi }{2}\alpha _{pe}}\varGamma (1+i\alpha _{pe}){_{{1}}}F{_{{1}}}\{i\alpha _{pe};1;(vs_{1}+\vec {v}.\vec {s_{1}})\}, \end{aligned}$$

(4)

where $\alpha _{pe}=\frac{Z_{\mathrm{P}}}{v}$.

Here, v is the projectile velocity. In the present calculation, we have taken two types of helium ground-state wavefunction $\phi _{i}(\vec {r}_{1},\vec {r}_{2})$ such as:

• (i) one-parameter uncorrelated Hylleraas wavefunction [39] :

  $$\begin{aligned} \phi _{i}(\vec {r_{1}},\vec {r_{2}})=\left( \frac{\gamma ^{3}}{\pi }\right) \mathrm{e}^{-\gamma (r_{1}+r_{2})}, \end{aligned}$$

  (5)

  where $\gamma$ is the effective charge $\gamma =Z_{T}-Z_{S}$, with the parameter $Z_{S}$ being the inner Slater screening ($Z_{S}=0.3125$). The corresponding binding energy $\epsilon _{i}=-\,2.8476$ a.u.,

• (ii) 20-parameter Hylleraas wave function [40]: this wavefunction contains both radial and angular correlation,

  and

• (iii) the highly correlated four-parameter Byron and Joachain wavefunction [41]:

  $$\begin{aligned} \phi _{i}(\vec {r}_{{1}},\vec {r}_{{2}}){=}\frac{1}{4\pi }(Ae^{-\alpha r_{1}}+Be^{-\beta r_{2}})(Ae^{-\alpha r_{2}}+Be^{-\beta r_{1}}), \end{aligned}$$

  (6)

where $A = 2.60505$, $B=2.081144$, $\alpha =1.41$, $\beta =2.61$ and binding energy $\epsilon _{i}=-\,2.86167$ a.u. The ground-state wavefunction of helium [40] includes radial correlations but no angular correlations. The final state wavefunction $\psi _{f}^{-}$ is approximated as a product of two Coulomb distorted wavefunctions $\chi _{f}^{-}\, (2CW)$ and the hydrogen-like wavefunction ($\mathrm{He}^{+}$). Therefore, the form of $\psi _{f}^{-}$ may be written as:

$$\begin{aligned} \psi _{f}^{-}=\chi _{f}^{-}(2CW)\phi _{{\mathrm{He}^{+}}}(\vec {r}_{2}). \end{aligned}$$

(7)

After single ionization, the electron $e_{2}$ remains bound to the target and is described by a hydrogen-like wavefunction with $Z_{T}=2$, i.e., $\phi _{{\mathrm{He}^{+}}}(\vec {r}_{2})=(\frac{2^{3}}{\pi })^{1/2}\mathrm{e}^{-2r_{2}}$. In the present approximation, both the scattered projectile ion and the ejected electron are described by the Coulomb wave $\chi _{f}^{-}(2CW)$ which takes the following form as:

$$\begin{aligned} \chi _{f}^{-}(2CW)&=C\exp (i\vec {k}_{\mathrm{p}}.\vec {R}+i\vec {k}_{\mathrm{e}}.\vec {r}_{1}){_{{1}}} \nonumber \\&\quad F{_{{1}}}[i\alpha _{PT};1;-i(\vec {k}_{\mathrm{p}}.\vec {R}+k_{\mathrm{p}}R)] {_{{1}}} \nonumber \\&\quad F{_{{1}}}[-i\alpha _{\mathrm{Te}};1;-i(\vec {k}_{\mathrm{e}}.\vec {r}_{1}+k_{\mathrm{e}}r_{1})], \end{aligned}$$

(8)

where $\alpha _{\mathrm{Te}}=\frac{Z_{\mathrm{T}}^{e}}{k_{\mathrm{e}}}$, $\alpha _{PT}=\frac{Z_{\mathrm{P}}Z_{\mathrm{T}}^{e}}{k_{\mathrm{P}}}$, $C=(2\pi )^{-3}\mathrm{e}^{\frac{\pi }{2} (\alpha _{\mathrm{Te}}-\alpha _{PT})}\varGamma (1-i\alpha _{PT})\varGamma (1+i\alpha _{\mathrm{Te}})$. Here, $Z_{\mathrm{T}}^{e}$ refers to the effective charge of the residual target seen by the scattered projectile and the emitted electron. $k_{\mathrm{e}}$ ($k_{\mathrm{p}}$) is the final relative momentum of the ionized electron (projectile) with respect to the residual target ion. To determine the FDCS, we have to find out the $T_{\mathrm{if}}^{(-)}$, which is transformed as:

$$\begin{aligned} \begin{aligned} T_{\mathrm{if}}^{(-)}=&C^{\prime }(2\pi )^{-\frac{9}{2}}(4\pi )^{-1}Z_{P}(\frac{2^{3}}{\pi })^{\frac{1}{2}}\\&\sum ^{N}_{{i=1}}c_{i}\int \int \int \mathrm{d}\vec {r}_{1} \mathrm{d}\vec {r}_{2} \mathrm{d}\vec {R} \mathrm{e}^{i\vec {q}.\vec {R}-i\vec {k}_{\mathrm{e}}.\vec {r}_{1}}\\&\bigg (\frac{Z_{\mathrm{T}}^{e}}{R}-\frac{1}{|\vec {r}_{2}-\vec {R}|}-\frac{1}{s_{1}}\bigg ) \\&\mathrm{e}^{-(2+\beta (\alpha ))r_{2}}\mathrm{e}^{-\alpha (\beta )r_{1}}F_{CW}, \end{aligned} \end{aligned}$$

(9)

with

$$\begin{aligned} \begin{aligned}&F_{CW}={_{{1}}}F{_{{1}}}[-i\alpha _{{PT}};1;i(\vec {k}_{\mathrm{P}}.\vec {R}+k_{\mathrm{P}}R)]{_{{1}}}\\&F{_{{1}}}[i\alpha _{\mathrm{Te}};1;i(\vec {k}_{\mathrm{e}}.\vec {r}_{1}+k_{\mathrm{e}}r_{1})]{_{{1}}}\\&F{_{{1}}}[i\alpha _{\mathrm{Pe}};1;i(\vec {v}.\vec {s}_{1}+vs_{1})] \end{aligned} \end{aligned}$$

(10)

and $C^{\prime }=\mathrm{e}^{\frac{\pi }{2}(\alpha _{\mathrm{Te}}+\alpha _{\mathrm{Pe}}-\alpha _{PT})}\varGamma (1+i\alpha _{PT})\varGamma (1-i\alpha _{\mathrm{Te}})\varGamma (1+i\alpha _{\mathrm{Pe}})$.

Here, $c_{i}$ is the coefficient used in the ground-state wavefunction of $\mathrm{He}$ [39,40,41]. Here, $\vec {q}=\vec {k}_{i}-\vec {k}_{\mathrm{P}}$ is the projectile momentum transfer. We can easily separate out the integral over $r_{2}$ using the integral identities,

$$\begin{aligned} \int \mathrm{e}^{-\beta _{2}r_{2}}\mathrm{d}\vec {r}_{2}=\frac{8\pi }{\beta _{2}^{3}}, \end{aligned}$$

(11)

and

$$\begin{aligned} \int \frac{\mathrm{e}^{-\beta _{2}r_{2}}}{|\vec {r}_{2}-\vec {R}|} \mathrm{d}\vec {r}_{2}=\frac{8\pi }{\beta _{2}^{3}}\bigg [\frac{1}{R}-\frac{\beta _{2}}{2}\mathrm{e}^{-\beta _{2}R}-\frac{1}{R}\mathrm{e}^{-\beta _{2}R}\bigg ], \end{aligned}$$

(12)

where $\beta _{2}=2+\beta (\alpha )$. Using Eqs. (11) and (12), Eq. (9) may be written as:

$$\begin{aligned} \begin{aligned} T_{\mathrm{if}}^{(-)}&=\frac{8\pi N^{\prime }}{\beta _{2}^{3}}Z_{\mathrm{P}}\bigg [Z_{T}^{e}\frac{\partial ^{2}}{\partial \lambda _{i}\partial \alpha _{i}}|_{{\beta _{2}\rightarrow 0^{+},\lambda _{i} \rightarrow 0^{+}}}\\&\quad -\frac{\partial ^{2}}{\partial \beta \partial \alpha _{i}}|_{{\beta _{2}\rightarrow 0^{+},\lambda _{i}\rightarrow 0^{+}}}\\&\quad -\frac{\partial ^{2}}{\partial \lambda _{i}\partial \alpha _{i}}|_{{\beta _{2}\rightarrow 0^{+},\lambda _{i}\rightarrow 0^{+}}} \\&\quad -\frac{\beta _{2}}{2}\frac{\partial ^{3}}{\partial \beta \partial \lambda _{i}\partial \alpha _{i}}|_{{\beta _{2}\ne 0,\lambda _{i}\rightarrow 0^{+}}}\\&\quad +\frac{\partial ^{2}}{\partial \lambda _{i}\partial \alpha _{i}}|_{{\beta _{2}\ne 0,\lambda _{i}\rightarrow 0^{+}}}\bigg ]I, \end{aligned} \end{aligned}$$

(13)

where I is given by

$$\begin{aligned} I=\int \int \frac{\mathrm{d}\vec {r}_{1}\mathrm{d}\vec {R}}{r_{1}s_{1}R}\mathrm{e}^{i\vec {q}.\vec {R}-i\vec {k}_{\mathrm{e}}.\vec {r}_{1}-\alpha _{i}r_{1}-\lambda _{i}s_{1}-\beta _{2}R}\times F_{CW}. \end{aligned}$$

(14)

The contour integral representation of the confluent hypergeometric function by Nordsieck [42] may be written as:

$$\begin{aligned} {_{{1}}}F{_{{1}}}(i\alpha ;1;z)=\frac{1}{2\pi i}\oint _{\varGamma }^{(0+,1+)}P(\alpha ,t)\mathrm{e}^{zt}\mathrm{d}t, \end{aligned}$$

(15)

where $P(\alpha ,t)=t^{i\alpha -1}(t-1)^{-i\alpha }$, $P(\alpha ,t)$ is single valued and analytic over the contour $\varGamma$ enclosing 0–1 once anticlockwise, and here is a branch cut from 0 to 1. Applying this representation, we may express Eq. (14) as:

$$\begin{aligned} I= & {} \frac{1}{(2\pi i)^{3}}\oint _{\varGamma _{1}}\oint _{\varGamma _{2}}\oint _{\varGamma _{3}}\mathrm{d}t_{1}\mathrm{d}t_{2}\mathrm{d}t_{3}\nonumber \\&t_{1}^{i\alpha _{\mathrm{Te}}-1}(t_{1}-1)^{-i\alpha _{\mathrm{Te}}} t_{2}^{-i\alpha _{{PT}}-1}(t_{2}-1)^{i\alpha _{{PT}}}\nonumber \\&t_{3}^{i\alpha _{\mathrm{Pe}}-1}(t_{3}-1)^{-i\alpha _{\mathrm{Pe}}}I_{C}, \end{aligned}$$

(16)

where

$$\begin{aligned} I_{C}=\int \int \int \frac{\mathrm{d}\vec {r}_{1}\mathrm{d}\vec {R}}{r_{1}s_{1}R}\mathrm{e}^{i\vec {q}.\vec {R}-i\vec {k}_{\mathrm{e}}.\vec {r}_{1}-\beta _{1}r_{1}-\lambda _{1}s_{1}-\xi R}, \end{aligned}$$

(17)

with $\beta _{1}=\alpha -ik_{\mathrm{e}}t_{1}$, $\lambda _{1}=\lambda _{i}-ivt_{3}$, $\xi =\beta _{2}-ik_{\mathrm{P}}t_{2}$. After performing the integration, $I_{C}$ becomes

$$\begin{aligned} I_{C}=16\pi ^{2}\int _{0}^{\infty }[As^{2}+2Bs+C]^{-1}\mathrm{d}s. \end{aligned}$$

(18)

Here, the parameters A, B and C are now

$$\begin{aligned} \begin{aligned} A&=|\vec {q}_{1}-\vec {q}_{2}|^{2}+(\lambda _{1}+\xi )^{2}, \\ B&=\beta _{1}A+\xi (q_{1}^{2}+\lambda _{1}^{2}+\beta _{1}^{2})+\lambda _{1}(q_{2}^{2}+\epsilon ^{2}+\beta _{1}^{2}),\\ C&=[q_{1}^{2}+(\lambda _{1}+\beta _{1})^{2}][q_{2}^{2}+(\beta _{1}+\xi )^{2}], \end{aligned} \end{aligned}$$

(19)

with $q_{1}=\vec {k}_{\mathrm{e}}(1-t_{1})-\vec {v}t_{3}$, $q_{2}=\vec {k}_{\mathrm{e}}(1-t_{1})-\vec {q}-\vec {k}_{\mathrm{P}}t_{2}$. Applying Cauchy’s residue theorem, finally we obtain

$$\begin{aligned} I= & {} \frac{16\pi ^{2}}{2\pi i}\oint _{\varGamma _{1}}\mathrm{d}t_{1}t_{1}^{(i\alpha _{\mathrm{Te}}-1)} (t_{1}-1)^{-i\alpha _{\mathrm{Te}}}\nonumber \\&\int _{0}^{\infty }\mathrm{d}s A^{i\alpha _{\mathrm{Pe}}-1}(1+B/A)^{i\alpha _{{PT}}}(A+C)^{i\alpha _{\mathrm{Pe}}}{_{{2}}}\nonumber \\&F{_{{1}}}\{-i\alpha _{{PT}};i\alpha _{\mathrm{Pe}};1;z\}, \end{aligned}$$

(20)

where $z=\frac{BC-AD}{(A+B)(A+C)}$.

Fig. 1

Fully differential cross sections for single ionization of $\mathrm{He}$ by 75 keV proton impact in the scattering plane. The ejected electron energy is 5.4 eV and the transverse momentum transfers $(q_{\mathrm{t}})$ are a 0.13 a.u., b 0.41 a.u., c 0.73 a.u. and d 1.38 a.u., respectively. The filled circles are the experimental data from [9]; the red short dotted line is the CDW-EIS [17]; the blue dashed line is the FBA-2CW [44]; and the full line is the present DW-4B model obtained by using the four-parameter Byron and Joachain wavefunction [41]. The black dashed and green dash-dotted lines represent the present calculation obtained from one-parameter [39] and 20-parameter Hylleraas wavefunction [40] for $\mathrm{He}$. The arrow in each graph indicates the direction of the momentum transfer

Here, A, B, C and D are the functions of the integration variables $(s, t_{1}$), $\vec {v}$, $\vec {k}_{\mathrm{p}}$, $\vec {k}_{i}$, $\vec {q}$, $\alpha$ and $\beta$. ${_{{2}}}F{_{{1}}}(a,b;c;z)$ stands for the Gaussian hypergeometric function.

The contour integration $t_{1}$ in Eq. (20) has been transformed into one-dimensional real integral [43] ranging from 0 to 1. Therefore, Eq. (20) may be written as:

$$\begin{aligned} \begin{aligned} I&= \frac{1}{2\pi i}\oint _{\varGamma _{1}}\mathrm{d}t_{1}t_{1}^{i\alpha _{\mathrm{Te}}-1}(t_{1}-1)^{-i\alpha _{\mathrm{Te}}}V(0,t_{1}) \\&=\left( \frac{1-\mathrm{e}^{2\pi \alpha _{\mathrm{Te}}}}{2\pi i}\right) \int _{0}^{1}\mathrm{d}t_{1}\left( \frac{1-t_{1}}{t_{1}}\right) ^{-i\alpha _{\mathrm{Te}}}f(t_{1})+V(0)\mathrm{e}^{2\pi \alpha _{\mathrm{Te}}}, \end{aligned} \end{aligned}$$

(21)

where $f(t_{1})=\frac{V(t_{1})-V(0)}{t_{1}}$. Thus, a two-dimensional integration of variables $t_{1}$ and s is reached and can be evaluated numerically by the Gauss–Legendre quadrature method to evaluate the transition amplitude.

In the center-of-mass (C.M.) frame, the FDCS corresponding to the transition amplitude $T_{{if}}^{(-)}$, in the projectile solid angle ($\Omega _{\mathrm{p}}$), ejected electron solid angle ($\Omega _{\mathrm{e}}$) and electron energy ($E_{\mathrm{e}}$), respectively, is given by

$$\begin{aligned} \frac{d^{3}\sigma }{\mathrm{d}E_{\mathrm{e}}\mathrm{d}\Omega _{\mathrm{e}}\mathrm{d}\Omega _{\mathrm{p}}}=(2\pi )^{4}N_{\mathrm{e}}\mu _{\mathrm{Te}}\mu _{\mathrm{PA}}^{2}\frac{k_{P}k_{\mathrm{e}}}{k_{i}}|T_{{if}}|^{2}, \end{aligned}$$

(22)

where $N_{\mathrm{e}}$ is the number of the initial equivalent electrons in the atomic shell. The reduced mass of the ionized electron-residual ion sub-system is $\mu _{\mathrm{Te}}$, and the reduced mass of the projectile-target atomic system is $\mu _{\mathrm{PA}}$.

3 Results and discussion

In this section, we present the numerical results for the FDCS as a function of ejected electron scattering angle ($\theta _{\mathrm{e}}$) at different values of the momentum transfer $(\mathbf{q })$ and the ejected-electron energies ($E_{\mathrm{e}}$) in the scattering plane. The calculations have been done within the framework of four-body distorted-wave model (DW-4B) and have been compared with the available experimental data. The corresponding results are displayed in Fig. 1a–d for 75 keV and Figs. 2, 3 and 4 for 1 MeV proton impact. Figure 5a, b presents our calculations for the comparison of the FDCS for single ionization of $\mathrm{He}$ between 0.5 and 1 MeV proton impact. The scattering plane is the plane containing both the initial and final momentum vectors of the incoming projectile ion. It is assumed that the scattering plane lies in the xz plane, where the x-axis is defined by the transverse component of the momentum vector $q_{\mathrm{t}}$ and the z-axis is the initial projectile beam axis. Therefore, we have $\mathbf{k }_{i}=(0, 0, k_{i})$, $\mathbf{k }_{\mathrm{p}}=(k_{\mathrm{p}}\sin {\theta _{\mathrm{p}}}, 0, k_{\mathrm{p}}\cos {\theta _{\mathrm{p}}})$ and $\mathbf{q }=(k_{\mathrm{p}}\sin {\theta _{\mathrm{p}}}, 0, k_{\mathrm{p}}\cos {\theta _{\mathrm{p}}}-k_{i})$. Here, $\theta _{\mathrm{p}}$ is the projectile scattering angle. Also in the scattering plane, the momentum vector of the ejected electron is $\mathbf{k }_{\mathrm{e}}=(k_{\mathrm{e}}\sin {\theta _{\mathrm{e}}}, 0, k_{\mathrm{e}}\cos {\theta _{\mathrm{e}}})$, where $\theta _{\mathrm{e}}$ is the polar angle of the ejected electron relative to the initial projectile beam direction (the z-axis). In Figs. 1, 2, 3 and 4, our DW-4B results are compared with the absolute experimental results and the theoretical (CDW-EIS, PWSBA, FBA-2CW and 3C) results. However, numerical values of the FDCS for single ionization of He by proton impact may be obtained on request.

Fig. 2

Fully differential cross sections (FDCS) for ionization of $\mathrm{He}$ by 1 MeV protons in the scattering plane as a function of electron emission polar angle for the electron emission energy $E_{\mathrm{e}}=6.5$ eV and momentum transfer $q= 0.75$ a.u. The present DW-4B results (shown by full curve) obtained by Byron and Joachain wavefunction [41] and dashed curve obtained from Hylleraas wavefunction [39] for ground state of $\mathrm{He}$; PWSBA results (red dotted curve) [34]. Filled circle represents the experimental results [35]

Fig. 3

Fully differential cross sections (FDCS) for single ionization of $\mathrm{He}$ by 1 MeV proton impact in the scattering plane as a function of the polar angle of the ejected electron for the electron emission energies and momentum transfers. The present DW-4B results (full curve for $q=0.5$ a.u., black dash-dotted curve for $q=1.0$ a.u. and black dotted curve for $q=1.75$ a.u.). The results are obtained by using four-parameter Byron and Joachain wavefunction [41]. 3C results [36] (red full curve for $q=0.5$ a.u., red dash-dotted curve for $q=1.0$ a.u. and red dotted curve for $q=1.75$ a.u.); the present DW-4B results from one-parameter Hylleraas wavefunction [39] (green full curve for $q=0.5$ a.u., green dash-dotted curve for $q=1.0$ a.u. and green dotted curve for $q=1.75$ a.u.). Filled circle, square and triangle represent the experimental data [36] for $q=0.5,1.0$ and 1.75 a.u., respectively

Fig. 4

Same as in Fig. 3 except electron emission energy $E_{\mathrm{e}}=20$ eV

Fig. 5

Fully differential cross sections (FDCS) for single ionization of $\mathrm{He}$ by 500 keV and 1 MeV proton impact in the scattering plane as a function of electron emission polar angle for momentum transfer, a $q= 0.5$ a.u., b $q= 1.0$ a.u. Full curve represents the projectile energy for 500 keV and dotted red curve for 1 MeV projectile energy

In Fig. 1a–d, we have displayed the present results obtained from our DW-4B calculations for single ionization of $\mathrm{He}$ by 75 keV proton impact. Calculations have been done at transverse momentum transfer ($q_{\mathrm{t}}$) of 0.13, 0.41, 0.73, and 1.38 a.u. and at ejected electron energy of 5.4 eV. These results are compared with the measurements of Schulz et al. [9] for the ejected electron polar angles ($\theta _{\mathrm{e}}$) varying from $-\,90^\circ$ to $240^\circ$ relative to the incident direction of the projectile. Figure 1a–d also includes the FBA-2CW [44] (blue dashed curve) and the most successful CDW-EIS [17] (red dotted curve) theories. The present calculations are performed using uncorrelated one-parameter [39] (dashed curve), correlated 20-parameter [40] (green dash dotted cure) and the highly correlated four-parameter Byron and Joachain wave function [41] (full curve) for helium atom in its ground state. The wavefunctions [40, 41] are highly correlated because it gives a correlation energy which is very close to the exact binding energy value. In Fig. 1a–d, the present results are in overall agreement with the experimental results of Schulz et al. [9] in the whole range of emission angle except in the region around binary peak at transverse momentum transfer ($q_{\mathrm{t}}$) of 0.73 and 1.38 a.u. The blue dashed curve shows the results of the FBA-2CW calculation of Ghanbari-Adivi and Eskandari [44], and the results are in good agreement with the present results as well as the experimental data [9] for ejected electron angles between $\theta _{\mathrm{e}} = -\,90^{\circ }$ and $\theta _{\mathrm{e}} = 30^{\circ }$ except the region of binary peak for all values of $q_{\mathrm{t}}$. In the backward scattering angular region (from $120^{\circ }$ to $270^{\circ }$), the FBA-2CW overestimates the present results. We find that the recoil peak is clearly observed in this model at small values of $q_{\mathrm{t}}$, whereas experimental data do not show this structure. In this model, the final state includes the two Coulomb waves for both the scattered projectile and the ejected electron. From this graph, we also find that the present results are compatible with those of the CDW-EIS, but for the large value of $q_{\mathrm{t}}=1.38$ a.u., our results show a better agreement with the measured data in the angular region between $-\,30^\circ$ and $120^\circ$. The CDW-EIS theory represents the projectile distortion in the initial state by an eikonal phase, and the final state is described by a two-center continuum wavefunction [45, 46]. However, the CDW-EIS is suitable to describe electron emission in the combined Coulomb fields of the projectile and the target. This theoretical approach was first proposed by Crothers and his group [47, 48] to analyze the total ionization cross sections for ion-atom collisions. Moreover, the CDW-EIS calculations of Gulyas et al. [17] contain nuclear–nuclear interactions which is the sum of three interaction terms such as projectile-target nucleus, projectile-passive electron and polarization due to the distortion of the core electron by the incident projectile. In the present calculation, the final-state wavefunction is approximated by a product of two Coulomb wave (2CW) where both the scattered projectile ion and the ejected electron are described by the Coulomb waves, whereas in the initial channel, the Coulomb distortion between the projected and the active electron is included. In each graph, the arrow indicates the direction of the momentum transfer. It is seen from the figure that all the curves show the strong peak structure which can be explained in terms of a binary interaction between the projectile and the ejected electron. This peak is called the ‘binary peak’. The angular location of the peak is given theoretically by the expression: $\theta _{q}=\cos ^{-1}(\frac{q_{z}}{q})$, where $q_{z}$ is the z-component of the momentum transfer $(q_{z}=k_{\mathrm{p}}\cos \theta _{\mathrm{p}}-k_{i})$. It is also observed that the binary peak occurs near the direction of momentum transfer and shifts toward the larger emission angle as $q_{\mathrm{t}}$ increases. It is mentioned that the present results do not show the same location of the binary peak with the values of the momentum transfer direction $(\theta _{q})$ obtained from $\theta _{q}=\cos ^{-1}{(\frac{q_{z}}{q})}$, whereas the CDW-EIS results [17] show almost the same location for corresponding values of $q_{\mathrm{t}}$. Generally, the binary peak is pointing in the forward direction and the recoil peak in the backward direction. It is known to us that the strong peak (binary peak) in the forward direction is attributed due to a post-collision interaction (PCI) between the projectile and the ionized electron. Since the projectile is a heavy particle so the projectile will drag the electron from the target along in the forward direction. For example, at $q_{\mathrm{t}}=0.41$ a.u. the theoretical value of $\theta _{q}$ is $34^\circ$ but the location of the binary peak in DW-4B and CDW-EIS calculations are $45^\circ$ and $32^\circ$. The same discrepancies are observed between the two models for other values of the transverse momentum transfer $q_{\mathrm{t}} = 0.13$, 0.73, and 1.38 a.u. The present calculations (see Fig. 1d) do not exhibit the double peak structure which is observed in the experimental data and the theoretical calculations of CDW-EIS around $-\,30^\circ$ and $60^\circ$. Here, we find the second peak (around $-\,30^\circ$) which is weaker than the binary peak (around $60^\circ$). The second peak is called recoil peak (RP). This small peak normally occurs in the vicinity of the $-\,q$ direction. Such peaks occur due to a two-step scattering process. First, the active electron in the target is kicked by the projectile in the direction of the projectile momentum transfer (q) and then is back scattered by the residual $\mathrm{He}^{+}$ in the opposite direction ($-\,\mathbf{q}$). The recoil peak is absent in our calculations for any values of the transverse momentum transfer. We also find from Fig. 1a–d that the calculated FDCS obtained from different static uncorrelated [39] and correlated wavefunctions [40, 41] are almost the same except around binary peak for all values of the transverse momentum transfer. Among one-parameter and 20-parameter Hylleraas function for ground-state helium, we find that the two sets of results are almost the same. Slightly better agreement is found in the region of binary peak for 20-parameter Hylleraas function [40]. Thus, the FDCS results for ionization around the binary peak are more sensitive for the static correlated wavefunctions of the He atom. Consequently, a suitable description of such correlated wavefunctions can improve the theoretical results. But the two sets of result obtained from the DW-4B calculations show the same location of the binary peak.

Similar results for 6.5 eV electron energy and 0.75 a.u. momentum transfer are shown in Fig. 2. The shape of angular distributions reproduced by the present calculations has acceptable agreement with the experimental results of Gassert et al. [35] and differs from the plane wave second Born approximation (PWSBA) [34] in the binary peak region. The PWSBA emphasizes the motion of the projectile by a plane wave for which the final-state wave function is expressed in powers of two Somerfield parameters $\alpha _{PT}$ (Eq. 8), $\alpha _{\mathrm{Pe}}$, where $\alpha _{\mathrm{Pe}}$ is related to the relative motion between the scattered projectile and the ejected electron. This correlated motion is not included in our calculation. As can be seen from Fig. 2, two distinct peaks of larger (binary peak) and smaller intensity (recoil peak) are observed at $75^{\circ }$ and $-\,90^{\circ }$, respectively. However, the two peaks occur in the direction of equal and opposite momentum transfer. The DW-4B cross sections using one-parameter wavefunction [39] (dashed curve) and four-parameter wavefunction [41] (full curve) appear to be close to each other except in the binary peak region. Therefore, in this region we can say that the ionization is an uncorrelated process, but in the angular region of binary peak, ionization is the correlated one.

Figures 3 and 4 show our theoretical results of the FDCS in the scattering plane in comparison with the experimental data [34] and theoretical calculations (3C and FBA) of Chuluunbaatar et al. [36] for the ejected electron energies $E_{\mathrm{e}}=2.5$ eV and 20 eV and three projectile scattering angles for 1 MeV $p-\mathrm{He}$ collision. The projectile scattering angles are given by the momentum transfer $q=0.5, 1$ and 1.75 a.u., respectively. We find that the DW-4B and 3C model show overall good agreement with the experiment in all cases. For all values of the momentum transfer, the recoil peak is clearly observed in the 3C model, whereas the present theory does not exhibit a distinct recoil peak specially for the large value of $q_{\mathrm{t}}=1.75$ a.u. at 2.5 eV electron emission energy (see in Fig. 3). This may be due to the effect of including the PCI in the 3C or sometimes called 3CW model, whereas the DW-4B model does not include the PCI. In the 3C or 3CW model, three Coulomb continuum functions have been employed for the description of the final-state wavefunctions. This 3C function is basically asymptotic, providing the correct-Dollard asymptotic behavior. The DW-4B results show the prominent binary peak only at small values of momentum transfer or small projectile scattering angle which gives the maximum contributions to the total cross sections. One can see that with increasing momentum transfer the position of the binary peak moves toward the larger ejection angles which is already observed in Fig. 1a–d. This is due to the change in the direction of the momentum transfer. At the same time, we find from Figs. 3 and 4 that the weak recoil peak is clearly visible as electron emission energy decreases. It is also observed that the absolute value of the binary peak decreases at $q=0.5$ a.u. when the electron energy changes from 2.5 to 20 eV, whereas at $q=1$ a.u. and $q=1.75$ a.u. there is no significant changes in magnitude.

Finally, Fig. 5a, b presents only our calculations for the FDCS in the scattering plane for single ionization of $\mathrm{He}$ by 0.5 and 1 MeV proton impact at momentum transfer $q=0.5$ and $q=1$ a.u. One can see that the difference ($\Delta \theta _{\mathrm{e}}$) in the position of the binary peak at two projectile energies decreases with increasing momentum transfer. It is obvious, because the position of the binary peak goes maximum to $90^\circ$. However, with increasing momentum transfer, it disappears. This structure was already shown by other group [38]. We also find from Fig. 5 that with increasing projectile energy, the location of the binary peak shifts toward higher ejection angles. The reason is already explained in the previous description. In comparison between intermediate-energy (75 keV, see in Fig. 1) and high-energy region (1.0 MeV, see in Figs. 3, 4), overall the FDCS results at high energy obtained by the DW-4B method show better agreement with the experiments than the FDCS at intermediate energy region. This may be due to the exclusion of Coulomb wave associated with the relative coordinate between the projectile and the active electron in the final channel. After single ionization, the three charged particles, i.e., the projectile, the active electron and the residual ion, are unbound. So there exists a correlated motion which forbid the free motion. However, the Coulomb wave associated with the coordinate ($\vec {s}_{1}$) in the final channel is needed for the improvement of the cross sections at intermediate impact energy. Moreover, at this energy region (75 keV) the electron capture is the dominant channel over the ionization. Therefore, the electron capture probability into the bound states as well as the continuum of the projectile cannot be neglected.

4 Conclusions

We have presented the DW-4B results for the single ionization of helium by 0.075, 0.5 and 1 MeV proton impact. The calculations are done using uncorrelated and correlated ground-state wavefunctions of helium atom. The FDCS has been calculated and compared with other theoretical results (CDW-EIS, PWSBA, FBA-2CW and 3C) as well as the available experimental findings. Overall satisfactory agreement with the recent experimental data is obtained at high impact energy for all considered kinematical regimes in the scattering plane. In the spectrum of angular distribution, the binary and the recoil peak is clearly visible at higher projectile energies. The position of the binary peak shifts toward larger ejection angles with increasing momentum transfer. The amount of separation between the binary peaks corresponding to two different projectile energies is comparatively small at 20 eV emission energy as the momentum transfer increases. It is also mentioned that a suitable correlated wavefunction for target atom shows a significant role on the ionization process near the binary peak region, while in the other angular region, the uncorrelated and correlated wavefunctions are insignificant for the same process. The present calculations are well reproduced by the higher-order calculations like 3C model and the CDW-EIS model. However, there are some advantages of the present theory in comparison with the others. In future, we plan further calculations in support of the ion-impact single ionization experiments for highly charged bare ion impact, particularly carbon ion as such ion beam is useful in radiation therapy.