Broadband multi-functional terahertz polarization converter based on graphene metasurface

Abstract

Based on graphene metasurface, this paper proposes a broadband multifunctional reflective polarization converter in the terahertz regime. This converter was formed of periodic unit cells, and each cell comprises two gold resonant ribbons, two-layer graphene sheets, a dielectric spacer, and a ground plane. The results demonstrated that the converter presented dynamical multiple polarization-manipulating functions, such as linear-to-circular conversion and linear-to-linear conversion, by varying the Fermi energy of the graphene. For example, in the frequency range from 0.92 to 1.47 THz, the ultra-broadband cross-polarization conversion was obtained with a Fermi energy of 0 eV, and in the range from 0.55 to 1.26 THz, the ultra-broadband linear-to-circular polarization conversion was achieved by varying the Fermi energy with a tunable relative bandwidth of 78.5%. Finally, the physical mechanisms were determined by analyzing the equivalent circuits and current distributions. This polarization converter has the potential for future applications in electronic measurements, photonic design, and other optoelectronic systems.

Graphic abstract

1 Introduction

Polarization is an important characteristic of electromagnetic waves, and the polarization manipulation can be implemented in many applications such as communication, sensing, and spectroscopy [1]. Nowadays, studies on the polarization manipulation of terahertz (THz) waves have increased rapidly with the development of terahertz technology. In general, the polarization state of THz waves is managed by the application of dichroic crystals or birefringent materials, which not only leads to a narrow response waveband because of the crystal properties, but also results in bulky THz systems [2]. Recently, as an alternative means of controlling THz wave polarization, metal-patterned metasurfaces provide a new route to enhance optical activity effects [3]. Owing to the lower profile and less absorption, metal-patterned metasurface-based THz polarization converters have been extensively studied [4,5,6]. For example, Liu et al. reported a THz broadband cross linear-to-linear (LTL) polarization converter made of a metasurface operating in the transmission mode [7]. Rajour Tanyi Ako et al. reported a broadband and wide-angle reflective LTL polarization converter for THz waves [8]. Gao et al. reported an ultrawideband reflective LTL polarization converter based on a double V-shaped metasurface [9]. Zang et al. reported a broadband THz linear-to-circular (LTC) polarization converter based on an ultrathin reflective metasurface [10]. However, the application of these designs is limited by the absence of tunability.

More recently, graphene, a two-dimensional allotrope of carbon, has become the focus of extensive research because of its interesting physical properties, such as high charge carrier mobility, anomalous quantum Hall effect, and tunable interband and intraband conductivities [11]. These properties make graphene a promising material in metasurface-based polarization converter applications to dynamically tune polarization. Yu et al. presented a reflective LTC and LTL broadband tunable polarization converter based on graphene metamaterial in the THz regime [12]. Chen et al. reported a wideband tunable cross polarization converter based on graphene metametarial with a hollow-carved “H” array in the THz regime [13]. Based on graphene metametarial, Ding et al. proposed a dual-frequency tunable THz cross polarization converter operating in the reflective mode [14]. However, these polarization converters present limitations in bandwidth and immobilization in the polarization conversion pattern [15,16,17,18,19,20].

Fig. 1

a $3\times 3$ unit structure diagram and b cross section of the proposed polarization converter

In this paper, a reflective tunable THz polarization converter based on graphene metasurface is proposed with ultra-wideband and multifunctional polarization conversion. The converter consists of a double gold resonant ribbon, two graphene sheets, a dielectric spacer, and a gold ground. It possesses wideband tunable polarization-manipulating functions in the THz region.

Fig. 2

a Reflection coefficients and CPCR for the proposed converter. b Frequency dependent CPCR for various $E_{F}$

2 Design and analysis

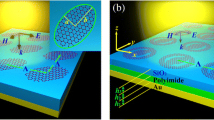
Figure 1a presents the $3\times 3$ unit structure diagram of the proposed graphene-based metasurface polarization converter. As observed in Fig. 1b, from top to bottom, there are two gold ribbons with a thickness of 200 nm, two graphene sheets separated by a silicon dioxide layer with a permittivity of 3.9 and thickness t of 100 nm, a layer of polyimide (dielectric material) with a permittivity of 3, loss tangent of 0.001 and thickness h of $44.6\,\upmu \hbox {m}$, and a gold ground plane. The specific parameters of the design are as follows: $p = 139\,\upmu \hbox {m}$, $w_{1} = 15\, \upmu \hbox {m}$, $w_{2}= 30\,\upmu \hbox {m}$, and $d= 15.6\,\upmu \hbox {m}$. The surface of conductivity $\sigma _{\mathrm{s}}$ of graphene, which is two-dimensional material, is defined by the Kubo formula [21] as follows:

$$\begin{aligned}&\sigma _{\mathrm{s}}=\sigma _{\mathrm{intra}}(\omega , \mu _{\mathrm{c}}, \varGamma , T)+ \sigma _{\mathrm{inter}}(\omega , \mu _{\mathrm{c}}, \varGamma , T)\nonumber \\&\sigma _{\mathrm{intra}}(\omega , \mu _{\mathrm{c}}, \varGamma , T)= -j\frac{e^{2}k_{\mathrm{B}}T}{\pi \hbar ^{2}(\omega -j2\varGamma )}\nonumber \\&\quad \left( \frac{\mu _{\mathrm{c}}}{k_{\mathrm{B}}T}+2\hbox {In}\left( e^{-\frac{\mu _{\mathrm{c}}}{k_{\mathrm{B}}T}}+1\right) \right) \nonumber \\&\sigma _{\mathrm{inter}}(\omega , \mu _{\mathrm{c}}, \varGamma , T)\cong -\frac{je^{2}}{4\pi \hbar }\hbox {In}\nonumber \\&\quad \left( \frac{2\big |\mu _{\mathrm{c}}\big |-(\omega -j2\varGamma \hbar )}{2\big |\mu _{\mathrm{c}}\big |+(\omega -j2\varGamma \hbar )}\right) \end{aligned}$$

(1)

where $\sigma _{\mathrm{intra}}$ and $\sigma _{\mathrm{inter}}$ are, respectively, the intraband term and the interband term, e, $\hbar$, $k_{\mathrm{B}}$, T, and $\mu _{\mathrm{c}}$, respectively, represent the electron charge, reduced Planck’s constant, Boltzmann’s constant, the temperature, and chemical potential. The collision frequency is defined as $\varGamma = 1/2\tau (\tau$ is the relaxation time), and the temperature T is assumed to be 300 K [21]. It should be noted that the parameters of the two layers of graphene are identical in the proposed design. Additionally, $\mu _{\mathrm{c}}$ has an approximate expression with $V_{g}$ and it can be expressed as:

$$\begin{aligned} \mu _{c}=E_{F}\thickapprox \hbar \nu _{f}\sqrt{\frac{\pi \varepsilon _{r}\varepsilon _{0}V_{g}}{et}} \end{aligned}$$

(2)

where $v_{f}$, $V_{g}$, $\varepsilon _{r}$ and $\varepsilon _{o}$ are, respectively, the Fermi velocity ($1.1\times 10^{6}\hbox { m/s}$ in graphene), the bias voltage, the permittivity of silicon dioxide and vacuum.

This design is modeled by the commercial software CST Microwave Studio. In the simulation, periodic boundary conditions are used in the x and y directions. The incident wave with u-polarization ($45^{\circ }$ relative$+x$-axis) propagates along the -z axis (i.e., the incident angle $\theta = 0^{\circ }$) and is defined as ${{\varvec{E}}}_{{{\varvec{i}}}}= E_{ui}\hbox {exp}$(jkz)${{\varvec{e}}}_{{{\varvec{u}}}}$. In general, the reflected wave, ${{\varvec{E}}}_{{{\varvec{r}}}}$, can be expressed as ${{\varvec{E}}}_{{{\varvec{r}}}} = E_{ur}{{\varvec{e}}}_{{{\varvec{u}}}}+ E_{vr}{{\varvec{e}}}_{{{\varvec{v}}}} = r_{uu}\hbox {exp}(j\varphi _{uu})E_{ui}{{\varvec{e}}}_{{{\varvec{u}}}}+ r_{vu}\hbox {exp}(j\varphi _{vu})E_{ui}{{\varvec{e}}}_{{{\varvec{v}}}}$, where $r_{uu}$ ($\varphi _{uu})$ and $r_{vu}$ ($\varphi _{vu})$ represent the reflection coefficient magnitudes (phases) of the u-to-u and u-to-v polarization conversions, respectively.

Fig. 3

Frequency dependent CPCR for various a relaxation time $\tau$, b incident angles $\theta$, c thicknesses h, d periodicities p, e widths $w_{1}$, and f distances d

Fig. 4

a AR for $E_{F} = 0, 0.2, 0.4$ and 1.0 eV, and b LTC PCE for various values of $E_{F}$ (the star-shaped symbols represent at the resonant frequencies for the chosen Fermi energies)

Due to the anisotropic characteristics of metasurfaces and the controllable property of graphene, $r_{uu}$ and $r_{vu}$ (or $\varphi _{uu}$ and $\varphi _{vu})$ are likely to be different. The polarization state of the reflected wave is determined by the amplitudes and phases of the co-polarized and cross-polarized waves undergoing multiple reflections, and there may be two types of polarization conversions: the cross-polarization conversion for $r_{vu}$ being much higher than $r_{uu}$ and the LTC polarization conversion for $r_{uu}\approx r_{vu}$ and $\Delta \varphi =\varphi _{vu}- \varphi _{uu} \approx \pm \uppi /2 + 2\hbox {n}\uppi$.

2.1 Cross-polarization conversion

To estimate the performance of the cross-polarization conversion, the cross-polarization conversion ratio (CPCR) [13, 22] can be defined as follows:

$$\begin{aligned} \hbox {CPCR}=\frac{r_{vu}^{2}}{r_{uu}^{2}+ r_{vu}^{2}} \end{aligned}$$

(3)

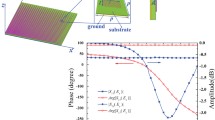
From (3), it can be observed that, for a CPCR close to 1 (i.e., $r_{vu}>> r_{uu})$, a high cross-polarization conversion is obtained. In the first simulation, for $\tau = 1$ ps and $\mu _{c} =0 \hbox {eV}$, $r_{uu}$, $r_{vu}$, the CPCR values of the proposed design are shown in Fig. 2a. In the frequency regime between 0.92 and 1.47 THz, $r_{vu}$ is greater than $r_{uu}$ and CPCR $\ge 0.9$, which indicates that an ultra-wideband cross polarization conversion is obtained. Moreover, two strong resonances are observed at 1.05 THz (CPCR $\approx$ 99.98%) and 1.42 THz (CPCR $\approx$ 99.61%), which are combined into an ultra-wideband cross-polarization conversion in the proposed design. Furthermore, the frequency dependent CPCR for various $E_{F}$ is shown in Fig. 2b. One can observe that, when $E_{F}= 0\hbox { eV}$, the widest bandwidth with the cross-polarization conversion can be obtained.

Further, the cross-polarization conversion was investigated depending on the relaxation time $\tau$ and incident angle $\theta$. As shown in Fig. 3a, despite the cross-polarization regime (CPCR $\ge$ 90%) exhibits a small red shift with a decreasing $\tau$ for $\theta = 0$, the proposed converter presents high cross-polarization conversion performance for different values of $\tau$. On the other hand, as shown in Fig. 3b, by varying $\theta$ with $\tau = 1\hbox { ps}$, the converter can still operate accurately with a large incident angle $\theta$ of $40^{\circ }$. The above results demonstrate that the proposed design can operate accurately for various $\tau$ and $\theta$.

Additionally, due to the effect of Fabry-Perot cavity, the thickness h and the surface structure of cavity have a great effect to the converter. Thus, the cross-polarization conversion with various geometrical parameters, such as h, p, $w_{1}$, and d, is explored with $\mu _{c}= 0\hbox { eV}$ (the dielectric-like property of the graphene), as shown in Fig. 3c–f. By increasing h, a red shift can be observed. Conversely, a slight red shift occurs by increasing p. Both bandwidths of the CPCR are becoming narrower, and an optimal thickness h of $44.6\, \upmu \hbox {m}$ and period p of $139\, \upmu \hbox {m}$ are achieved for the widest bandwidth and CPCR $\ge$ 0.9. By increasing $w_{1}$ and d, the bandwidth of the CPCR becomes wider and the optimal $w_{1}$ and d are $15\,\upmu \hbox {m}$ and $15.6\,\upmu \hbox {m}$, respectively. However, the continuous ultra-broadband performance is damaged by increasing the geometrical parameters.

2.2 LTC polarization conversion

In order to describe the LTC polarization conversion, the stokes parameters [4, 23] are introduced as follows:

$$\begin{aligned} I= & {} r_{uu}^{2} +r_{vu}^{2}, \end{aligned}$$

(4)

$$\begin{aligned} Q= & {} r_{uu}^{2} -r_{vu}^{2}, \end{aligned}$$

(5)

$$\begin{aligned} U= & {} 2r_{uu} r_{vu} \cos \Delta \varphi , \end{aligned}$$

(6)

$$\begin{aligned} V= & {} 2r_{uu} r_{vu} \sin \Delta \varphi . \end{aligned}$$

(7)

Table 1 Comparison between the relative bandwidth of reported polarization converters based on graphene and the present design

In which, $\hbox {sin}2\beta = V/I$ and $\beta$ is the ellipticity angle, the axial ratio (AR) is therefore introduced as AR $=$ 10lg(tan$\beta$) to estimate the character of the LTC polarization conversion. Further, $\Delta \varphi$ can be presented as $\Delta \varphi = \varphi _{vu}$ –$\varphi _{uu}$. Due to tunability of graphene, the tunable ultra-wideband LTC polarization conversion can be achieved, as illustrated in Fig. 4a. The Fermi energy varies from 0 to 1 eV, and the proposed design operates in an LTC polarization conversion with $\hbox {AR} < 3\hbox {dB}$ in the frequency range from 0.55 to 1.26 THz (i.e., a tunable relative bandwidth of 78.5%). It should be noted that, without the reconfiguration of the structure, the circular polarization reflective waves can be obtained at corresponding frequencies by controlling the specified Fermi energy with values of 0.73, 0.91, 1, and 1.1 THz for $E_{F} = 0\hbox { eV}$, 0.2 eV, 0.4 eV, and 1 eV, respectively. In addition, the proposed design presents a reconfigurable polarization pattern, i.e., this design can operate both in cross-polarization and LTC polarization conversions by tuning the Fermi energy in the frequency range from 0.92 to 1.26 THz.

The LTC polarization conversion efficiency (PCE), $\eta$, of the proposed converter is calculated by $\eta =| r_{vu}|^{2} + |r_{uu}|^{2}$ and shown in Fig. 4b. From 0.55 to 0.73 THz and from 1.1 to 1.26 THz, $\eta$ with $\hbox {AR} < 3\hbox {dB}$ is greater than 91.8% and 70% for $E_{F}= 0$ and 1.0 eV, respectively (as shown by the solid black line and the dark-yellow dash line). From 0.73 to 1.1 THz, by contrast, $\eta$ with $\hbox {AR} <3\hbox {dB}$ represents the LTC conversion efficiencies corresponding to the resonant frequencies by tuning the Fermi energy from 0 to 1 eV (as shown by the solid black line with dots). As observed in Fig. 4a, a high circular polarization conversion is achieved for $\eta \ge$ 81.8% in the frequency range from 0.73 to 1.1 THz by varying the Fermi energy. Additionally, by comparing with the other reported graphene-based THz polarization converters from the studies, the proposed design shows a larger bandwidth, as summarized in Table 1. In which, the tunable bandwidth indicates the continuous frequency regime with AR ($\le$ 3dB) or CPCR ($\ge$ 0.8). Tunable relative bandwidth is calculated by 2($f_{\mathrm{H}} - f_{\mathrm{L}}) / (f_{\mathrm{H}} + f_{\mathrm{L}})$. Here, $f_{\mathrm{H}}$ and $f_{\mathrm{L}}$ indicate upper limiting and lower limiting frequency, respectively. Obviously, this design exhibits a stronger polarization-manipulating function.

Fig. 5

Distributions of the surface current (a, b) on the gold ribbons at 1.05 THz with the excitation of the y-polarized wave and x-polarized wave at $E_{F} = 0$ (the blue arrows represent the directions of the surface current on the gold ribbons)

Fig. 6

Magnitudes of the reflection coefficients for the x-to-x, y-to-y, y-to-x, x-to-y polarization conversions and the corresponding phase difference $\Delta \varphi `$ with a $E_{F} = 0\hbox { eV}$ and b $E_{F}= 1$ eV

3 Physical mechanisms

To investigate the physical mechanisms of the polarization conversion, both the incident plane wave and the reflected wave are decomposed into two orthogonal parts. In general, the incident wave with a u-polarization (see Fig. 1a) can be expressed as ${{\varvec{E}}}_{{{\varvec{i}}}} = E_{ui}\hbox {exp}(\textit{jkz}){{\varvec{e}}}_{{{\varvec{u}}}} ={{\varvec{e}}}_{{{\varvec{x}}}}E_{ui}\hbox {exp}(\textit{jkz})/\surd 2 + {{\varvec{e}}}_{{{\varvec{y}}}}E_{ui}\hbox {exp}(\textit{jkz})/\surd 2$, and the reflected wave can be expressed as ${{\varvec{E}}}_{{{\varvec{r}}}}= E_{ui}\{ r_{xx}\hbox {exp}[j(-\textit{kz }+ \varphi _{xx})]+r_{xy}\hbox {exp}[j(-\textit{kz }+ \varphi _{xy})]\} {{\varvec{e}}}_{{{\varvec{x}}}}/\surd 2 + E_{ui}\{ r_{yx}\hbox {exp}[j(-\textit{kz }+ \varphi _{yx})] + r_{yy}\hbox {exp}[j(-\textit{kz }+ \varphi _{yy})]\} {{\varvec{e}}}_{{{\varvec{y}}}} / \surd 2$, where $r_{xx}$, $r_{yx}$, $\varphi _{xx}$, and $\varphi _{\mathrm{yx}}$ represent the magnitudes and phases of the reflection coefficients for the x-to-x and x-to-y polarization conversions, and $r_{xy}$, $r_{yy}$, $\varphi _{\mathrm{xy}}$, and $\varphi _{yy}$ are the magnitudes and phases of the reflection coefficients for the y-to-x and y-to-y polarization conversions, respectively. If $r_{xy}$ and $r_{yx}$ are close to 0, ${{\varvec{E}}}_{{{\varvec{r}}}} = r_{xx}E_{ui}\hbox {exp}[j(-\textit{kz} + \varphi _{xx})]{{\varvec{e}}}_{{{\varvec{x}}}} /\surd 2 + r_{yy}E_{ui}\hbox {exp}[j(-\textit{kz }+\varphi _{yy})]{{\varvec{e}}}_{{{\varvec{y}}}} / \surd 2$, and there are two special cases: 1) when $r_{yy} \cong r_{xx} = r$ and $\Delta \varphi `= \varphi _{yy}$– $\varphi _{xx} = \pm \uppi$, a cross-polarization reflected wave can be obtained; 2) when $r_{yy} \cong r_{xx} = r$ and $\Delta \varphi ` = \varphi _{yy}$ – $\varphi _{xx} = \pm \uppi /2 + 2\hbox {n}\uppi$, the reflected wave is polarized circularly [4, 27,28,29,30,31,32].

Fig. 7

Surface currents a, c across the metasurface and b, d on the gold ground and e the corresponding equivalent electric moments at 1.1 THz with $E_{F}=1\hbox { eV}$. In which, a, b and c, d are, respectively, for the x-polarized and y-polarized waves

3.1 Mechanisms of the cross-polarization conversion

From Fig. 2a, it can be deduced that the converter operating with a cross-polarization conversion with $E_{F} =0$ at 1.05 THz and 1.42 THz. Under the illumination of the plane wave with a y- and x-polarization, the surface currents across the metasurface at 1.05 THz are shown in Fig. 5. It can be observed in Fig. 5a that the strong currents are induced along the gold ribbons, which are equivalent to the inductance $L_{1}$ with the excitation of the y-polarized wave. Similarly, from Fig. 5b, the current distributions on the gold ribbons can be observed with the excitation of x-polarized wave, which are also equivalent to the inductance L [12, 28]. By contrast, the electric fields along the x-direction are distributed between the parallel adjacent gold ribbons, which indicate that the equivalent capacitance C is produced with the excitation of the x-polarized wave [28]. Therefore, the equivalent inductance $L_{1}$ can control the reflected y-polarized wave and series LC circuit can operate the reflected x-polarized wave. According to the circuit principle, the impedance in the y direction can be expressed as $Z_{1} = R +\textit{jwL}_{1}$, and the impedance in the x direction can be expressed as $Z_{2} =R' + j (wL - 1/wC)$, where, R and R‘ represent the loss resistances on the gold ribbons induced by the y-polarized reflected wave and x-polarized reflected wave, respectively. Because $L_{1}$ and L are related to $w_{1}$, C is related to $w_{1}$ and d, the condition $|Z_{1}| =| Z_{2}|$ ($r_{yy} \cong r_{xx})$ and phase difference ($\Delta \varphi ` \approx \pm \uppi )$ between $Z_{1}$ and $Z_{2}$ which cause the cross polarization conversion can be satisfied by optimizing $w_{1}$ and d. Moreover, it should be noted that, the distributions of the surface current and the electric field at 1.42 THz, although it is not shown in the results, are similar to those at 1.05 THz. The optimization of the proposed design can bring these two resonant frequencies closer and produce an ultra-wideband cross-polarization conversion, as shown in Fig. 6a. It should be noted that, at $E_{F}= 0$, the metallicity of graphene is weak [20], and there is no surface current along the graphene ribbons for the excitation of both the y-polarized and x-polarized waves.

Fig. 8

a $r_{xx}$, b $\varphi _{xx}$, c $r_{yy}$, d $\varphi _{yy}$, with various $E_{F}$

3.2 Mechanisms of the LTC polarization conversion

For $E_{F} = 1\hbox { eV}$, the magnitudes, phases, and the phase difference are shown in Fig. 6b. It can be observed that $r_{yx}$ and $r_{xy}$ are nearly equal to 0 (indicating the incident electric field produces a small cross-polarization reflective component), and $|r_{xx}$–$r_{yy}| <0.2$ in the frequency range from 0.95 to 1.26 THz. In other words, from 0.95 to 1.056 THz, $|r_{xx}$–$r_{yy}|< 0.06$ and $\Delta \varphi$‘ $\in$ ($54^{\circ }, 80^{\circ })$. By contrast, $\Delta \varphi$‘ $\in$ ($80^{\circ }, 100^{\circ }$) and is close to $\uppi /2$ or $-3\uppi /2$ in the frequency range from 1.056 to 1.26 THz, despite $|r_{xx}$–$r_{yy}|<0.2$. In particular, $\Delta \varphi `\approx \uppi /2$ at approximately 1.1 THz with $|r_{xx}$–$r_{yy}|\approx 0.06$. Finally, in the frequency range from 0.95 to 1.26 THz, $\hbox {AR} <3\hbox {dB}$ and the LTC polarization conversion has been achieved in the proposed design (indicated by the dark-yellow dash line in Fig. 4).

To determine the physical mechanisms of the LTC conversion at $E_{F}= 1\hbox { eV}$, it is assumed that the x-polarized and y-polarized incident waves excite the proposed design at 1.1 THz, respectively. The surface currents across the metasurface and on the gold ground are shown in Fig. 7. It can be observed that, under the excitation of the x-polarized wave, the current on the graphene layers is parallel to that on the ground, which is equivalent to the electric resonance and forms the equivalent electric dipole (${{\varvec{p}}}_{\mathbf{1 }}$) [4, 27]. Furthermore, the analogous current distributions are observed on the gold ribbons and the gold ground, the electric resonance is equivalent, and the equivalent electric dipole (${{\varvec{p}}}_{\mathbf{2 }}$) is formed [9, 33] under the excitation of the y-polarized wave, as shown in Fig. 7e. The electric moments ${{\varvec{p}}}_{\mathbf{1 }}$ and ${{\varvec{p}}}_{\mathbf{2 }}$ manipulate $r_{xx}$, $\varphi _{xx}$, and $r_{yy}$, $\varphi _{yy}$ of the reflected wave, respectively. By optimization, $r_{xx}$ approaches $r_{yy}$ and $\Delta \varphi$‘ $\approx \uppi /2$ at the neighbourhood of 1.1 THz (as indicated by the violet solid line in Fig. 8 (a, c) and Fig. 9). Thus, a circular polarization reflected wave is obtained. Due to the tunability of graphene, $E_{F}$ can be varied to manipulate the electric resonances, and a tunable ultra-wideband LTC polarization conversion can be obtained. Therefore, from 0.55 to 1.26 THz, $r_{xx}$, $r_{yy}$, and $\varphi _{yy}$ are stable (Fig. 8 (a, c, and d)). However, from the adjustment of the surface conductivity $\sigma _{\mathrm{s}}$ in (1), $\varphi _{xx}$ varies in a large range (Fig. 8b), which tunes the resonant frequencies of the circular polarization reflected wave to 0.73, 0.91, 1 and 1.1 THz at $E_{F}= 0, 0.2, 0.4$, and 1 eV, respectively.

Fig. 9

$\Delta \varphi$‘ with various $E_{F}$

4 Conclusions

Herein, a reflective multifunctional ultra-wideband converter was developed based on graphene metasurfaces. By varying the Fermi energy of graphene, the multifunctional polarization conversion, namely the LTL cross-polarization and the LTC polarization conversions, were obtained. At Fermi energy of 0 eV, an ultra-wideband LTL conversion was achieved from 0.92 THz to 1.47 THz. In addition, an ultra-wideband LTC conversion was obtained from 0.55 THz to 1.26 THz by varying the Fermi energy from 0 to 1 eV. The proposed converter can be used as the key component in applications such as photonics measurements, biosensors, and other THz systems.