Muon $g-2$ and W-mass in a framework of colored scalars: an LHC perspective

Abstract

A color octet isodoublet can have esoteric origins and it complies with minimal flavour violation. In this study, we take a scenario where the well known Type-X Two-Higgs doublet model is augmented with a color octet isodoublet. We shed light on how such a setup can predict the recently observed value for the W-boson mass. The two-loop Barr-Zee contributions to muon $g-2$ stemming from the colored scalars are evaluated. It is subsequently found that the parameter space compatible with the observed muon $g-2$ gets relaxed w.r.t. what it is in the pure Type-X 2HDM by virtue of the contribution from the colored scalars. The extended parameter region therefore successfully accounts for both the W-mass and muon $g-2$ anomalies simultaneously. Finally, a collider signature leading to a $\tau ^+ \tau ^- b \overline{b}$ final state is explored at the 14 TeV LHC using both cut-based and multivariate techniques. Such a signal can confirm the existence of both colorless as well colored scalars that are introduced by this framework.

1 Introduction

The particle spectrum of the Standard Model (SM) is deemed complete following the discovery of a Higgs boson [1, 2] at the Large Hadron Collider (LHC). Additionally, the interaction strengths of the Higgs with the SM fermions and gauge bosons are in good agreement with the SM predictions. Despite such triumph of the SM, some longstanding issues on both theoretical and experimental fronts have long been advocating additional dynamics beyond the SM (BSM). Such issues include a non-zero neutrino mass, the existence of dark matter (DM), the observed imbalance between matter and antimatter in the universe, and, the instability (or metastability) of the electroweak (EW) vacuum [3,4,5,6] in the SM. Interestingly, extensions of the SM Higgs sector can serve as powerful prototypes of BSM physics that can potentially solve the aforesaid issues.

Apart from the longstanding issues, some recent experimental observations have thrown fresh insight on as to what could be the nature of some hitherto additional dynamics beyond the SM. One example is the recently reported value of the mass of the W-boson by the CDF collaboration [7], that is deviated with respect to the SM prediction [8,9,10,11,12,13,14,15,16,17,18] by 7.2$\sigma$. That is,

$$\begin{aligned} M^{\text {CDF}}_W= & {} 80.4335~\text {GeV} \pm 6.4~\text {MeV} (stat)\nonumber \\{} & {} \quad \pm 6.9~\text {MeV} (sys). \end{aligned}$$

(1)

The origin of this deviation is suspected to be some New Physics (NP). The second experimental result is the reporting of an excess in the anomalous magnetic moment of the muon by FNAL [19, 20], thereby concurring with the earlier result by BNL [21]. The combined result is quoted as

$$\begin{aligned} \Delta a_\mu = (2.51 \pm 0.59) \times 10^{-9}. \end{aligned}$$

(2)

A Two-Higgs doublet model (2HDM) [22, 23] with a Type-X texture for Yukawa interactions has been long known to address the muon $g-2$ excess. The scalar sector of a 2HDM comprises the CP-even neutral scalars h, H, the CP-odd neutral scalar A, and a singly charged scalar $H^+$. Here, h denotes the SM-like Higgs with mass 125 GeV. The vacuum expectation values of two doublets are $v_1$ and $v_2$ with tan$\beta = \frac{v_2}{v_1}$. Demanding invariance under a $\mathbb {Z}_2$ symmetry with the aim of avoiding flavour changing neutral currents (FCNCs) leads to several variants of the 2HDM a particular kind of which is the Type-X. This variant features enhanced leptonic Yukawas with H and A and sizeable contributions to muon $g-2$ are introduced via two-loop Barr-Zee (BZ) amplitudes. A resolution of the anomaly thus becomes possible for a light A ($M_A \lesssim$ 100 GeV) and high tan$\beta$ ($> rsim 20$) [24,25,26,27,28,29,30,31]. The 2HDM framework can also accommodate $M_W^{\text {CDF}}$ [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. However, stringent constraints coming from lepton flavour universality in $\tau$ decays restricts large tan$\beta$. Also, recent LHC searches for $h \rightarrow AA \rightarrow 4\tau , 2\tau 2\mu$ [51] channels rules out a large $h \rightarrow A A$ branching ratio. Such experimental results restrict to a great extent the parameter space in the Type-X that leads to the observed $\Delta a_\mu$. A possible way to relax the parameter space is to introduce additional scalar degrees of freedom so that additional BZ amplitudes are induced.

An interesting extension of the SM involves a scalar multiplet transforming as (8,2,1/2) [52] under the SM gauge group. Such a scenario is motivated by minimal flavour violation (MFV). It assumes all breaking of the underlying approximate flavour symmetry of the SM is proportional to the up- or down-quark Yukawa matrices. And it has been shown in [52] that the only scalar representations under the SM gauge group complying with MFV are (1,2, 1/2 ) and (8,2, 1/2 ). The colored scalars emerging from the latter are the CP-even $S_R$, the CP-odd $S_I$ and the singly charged $S^+$. In addition, a color-octet can also stem from Grand Unification [53,54,55,56], topcolor models [57] and extra dimensional scenarios [58, 59]. Important phenomenological consequences of such a construct were studied in [60,61,62,63,64,65,66,67]. In fact, a scenario augmenting a 2HDM with a color-octet isodoublet has also been discussed in [68, 69]. The Type-I and Type-II variants were employed there. Important exclusion limits on such a framework were deduced in [70] and the radiatively generated $H^+ W^- Z(\gamma )$ vertex was studied in [71].

In this work, we extend the Type-X 2HDM by a color-octet iso doublet. Taking into account the various constraints on this setup, we first identify the parameter region that accounts for $M^{\text {CDF}}_W$. We subsequently demonstrate how the parameter space accommodating $\Delta a_\mu$ expands w.r.t. the pure Type-X on account of the additional BZ amplitudes stemming from the colored scalars. Thus, the given framework is shown to address the two anomalies simultaneously. We also propose the collider signal $p p \rightarrow S_R \rightarrow S_I A,~S_I \rightarrow b \overline{b},~A \rightarrow \tau ^+ \tau ^-$ for a hadron collider. Such a final state gives information about both the colorless and colored scalars involved in the cascade. In addition to the conventional cut-based methods, we plan to also use the more modern multivariate techniques for the analysis.

The study is organised as follows. We introduce the Type-X 2HDM plus color-octet framework in Sect. 2. In Sect. 3, we list the important constraints on this model from theory and experiments. The resolution of the W-mass and muon $g-2$ anomalies in detailed in Sect. 4. A detailed analysis of the proposed LHC signature is presented in Sect. 5 employing both cut-based as well as multivariate techniques. Finally, the study is concluded in Sect. 6. Various important formulae are given in the Appendix.

2 The type-X 2HDM + color octet framework

The scalar sector of the framework consists of two color-singlet $SU(2)_L$ scalar doublets $\Phi _{1,2}$ and one color-octet $SU(2)_L$ scalar S. The multiplets are parametrised as:

$$\begin{aligned}{} & {} \Phi _r = \begin{pmatrix} \phi _r^+ \\ \frac{1}{\sqrt{2}} (v_r + h_r + i z_r) \end{pmatrix}, (r = 1,2),~ \nonumber \\{} & {} S = \begin{pmatrix} S^+ \\ \frac{1}{\sqrt{2}} (S_R + i S_I) \end{pmatrix}. \end{aligned}$$

(3)

The electroweak gauge group $SU(2)_L \times U(1)_Y$ is spontaneously broken to $U(1)_Q$ when $\Phi _{1,2}$ receive a vacuum expectation values (VEV) $v_{1,2}$ with $v^2 = v_1^2 + v_2^2 = (246 ~\textrm{GeV})^2$. That the multiplet S receives no VEV averts a spontaneous breakdown of $SU(3)_c$.

The most generic scalar potential consistent with the gauge symmetry consists of a part containing the interactions among $\Phi _{1,2}$ only ($V_a(\Phi _{1},\Phi _{2})$), a part containing only S ($V_b(S)$) and a part containing the interactions among all $\Phi _{1,2},S$ ($V_c(\Phi _{1},\Phi _{2},S)$). The scalar potential therefore looks like [68]

$$\begin{aligned} V (\Phi _{1},\Phi _{2},S)= & {} V_a (\Phi _{1},\Phi _{2}) + V_b(S) + V_c(\Phi _{1},\Phi _{2},S),\nonumber \\ \end{aligned}$$

(4)

where,

$$\begin{aligned} V_a (\Phi _{1},\Phi _{2})= & {} m_{11}^2 \Phi _1^\dag \Phi _1 + m_{22}^2 \Phi _2^\dag \Phi _2 \nonumber \\{} & {} - m_{12}^2 \left( \Phi _1^\dag \Phi _2 + \Phi _2^\dag \Phi _1 \right) \nonumber \\{} & {} + \frac{\lambda _1}{2} \left( \Phi _1^\dag \Phi _1 \right) ^2 \nonumber \\{} & {} + \frac{\lambda _2}{2} \left( \Phi _2^\dag \Phi _2 \right) ^2 + \lambda _3 \left( \Phi _1^\dag \Phi _1 \right) \left( \Phi _2^\dag \Phi _2 \right) \nonumber \\{} & {} + \lambda _4 \left( \Phi _1^\dag \Phi _2 \right) \left( \Phi _2^\dag \Phi _1 \right) \nonumber \\{} & {} + \left[ \frac{\lambda _5}{2} \left( \Phi _1^\dag \Phi _2 \right) ^2 + \lambda _6 \left( \Phi _1^\dag \Phi _1 \right) \left( \Phi _1^\dag \Phi _2 \right) \nonumber \right. \\{} & {} \left. + \lambda _7 \left( \Phi _2^\dag \Phi _2 \right) \left( \Phi _1^\dag \Phi _2 \right) + \mathrm{H.c.}\right] , \end{aligned}$$

(5)

$$\begin{aligned} V_b(S)= & {} 2m_S^2 \textrm{Tr}S^{\dag i}S_i + \mu _1 \textrm{Tr}S^{\dag i}S_i S^{\dag j}S_j \nonumber \\{} & {} + \mu _2 \textrm{Tr} S^{\dag i}S_j S^{\dag j}S_i \nonumber \\{} & {} + \mu _3 \textrm{Tr} S^{\dag i}S_i \textrm{Tr}S^{\dag j} S_j\nonumber \\{} & {} + \mu _4 \textrm{Tr}S^{\dag i}S_j \textrm{Tr}S^{\dag j}S_i + \mu _5 \textrm{Tr}S_i S_j\textrm{Tr} S^{\dag i}S^{\dag j}\nonumber \\{} & {} + \mu _6 \textrm{Tr}S_i S_j S^{\dag j}S^{\dag i} , \end{aligned}$$

(6)

$$\begin{aligned} V_c(\Phi _{1},\Phi _{2},S)= & {} \nu _1 \Phi _1^{\dag i}\Phi _{1i}\textrm{Tr}S^{\dag j}S_j \nonumber \\{} & {} + \nu _2 \Phi _1^{\dag i}\Phi _{1j} \textrm{Tr}S^{\dag j}S_i\nonumber \\{} & {} + \left( \nu _3 \Phi _1^{\dag i}\Phi _1^{\dag j}\textrm{Tr}S_i S_j + \nu _4 \Phi _1^{\dag i}\textrm{Tr} S^{\dag j}S_j S_i \nonumber \right. \nonumber \\{} & {} \left. + \nu _5 \Phi _1^{\dag i}\textrm{Tr}S^{\dag j}S_i S_j + \mathrm{h.c.} \right) \nonumber \\{} & {} + \omega _1 \Phi _2^{\dag i}\Phi _{2i}\textrm{Tr}S^{\dag j}S_j+ \omega _2 \Phi _2^{\dag i}\Phi _{2j} \textrm{Tr}S^{\dag j}S_i\nonumber \\{} & {} + \left( \omega _3 \Phi _2^{\dag i}\Phi _2^{\dag j}\textrm{Tr}S_i S_j + \omega _4 \Phi _2^{\dag i}\textrm{Tr} S^{\dag j}S_j S_i \nonumber \right. \\{} & {} \left. + \omega _5 \Phi _2^{\dag i}\textrm{Tr}S^{\dag j}S_i S_j + \mathrm{h.c.} \right) \nonumber \\{} & {} + \kappa _1 \Phi _1^{\dag i}\Phi _{2i}\textrm{Tr}S^{\dag j}S_j\nonumber \\{} & {} + \kappa _2 \Phi _1^{\dag i}\Phi _{2j}\textrm{Tr}S^{\dag j}S_i + \kappa _3 \Phi _1^{\dag i}\Phi _2^{\dag j}\textrm{Tr}S_j S_i, + \mathrm{h.c.} \end{aligned}$$

(7)

Here, i, j denote the fundamental SU(2) indices. One can define $S_i = S_i^B T^B$ ($T^B$ being the SU(3) generators and $'B'$ being the SU(3) adjoint index) and the traces in Eqs. (6) and (7) are taken over the color indices. We mention here that we do not impose some ad-hoc discrete symmetry to restrict the scalar potential. Rather, we are guided purely by MFV [52]. One clearly identifies $V_a(\Phi _{1},\Phi _{2})$ with the generic scalar potential of two Higgs doublet model (2HDM). An important 2HDM parameter is $\tan \beta = \frac{v_2}{v_1}$. We take the VEVs and all model parameters to be real in order to avoid $\text {CP}$-violation. The scalar spectrum expectedly consists of both color-singlet as well as color-octet particles.

The color-singlet scalar mass spectrum comprising the $\text {CP}$-even h, H, a $\text {CP}$-odd A and a charged Higgs $H^+$, coincides with that of a 2HDM. Of these, h is identified with the discovered scalar with mass 125 GeV. The expressions of the physical masses belonging to the particles in the colorless counterpart in terms of the couplings and mixing angles $\beta$ and $\alpha$¹ could be found in [22]. On the other hand, the masses of the neutral ($S_R,S_I$) and charged mass eigenstate ($S^+$) of the color-octet can be expressed in terms of the quartic couplings $\omega _i, \kappa _i, \nu _i$ and mixing angle $\beta$ as [68]:

$$\begin{aligned} M_{S_R}^2= & {} m_S^2 + \frac{1}{4} v^2 \Big (\cos ^2 \beta (\nu _1 + \nu _2 + 2 \nu _3) \nonumber \\{} & {} +\sin 2 \beta (\kappa _1 + \kappa _2 + \kappa _3) + \sin ^2 \beta (\omega _1 + \omega _2 + 2 \omega _3)\Big ) , \nonumber \\ \end{aligned}$$

(8a)

$$\begin{aligned} M_{S_I}^2= & {} m_S^2 + \frac{1}{4} v^2 \Big (\cos ^2 \beta (\nu _1 + \nu _2 - 2 \nu _3) \nonumber \\{} & {} +\sin 2 \beta (\kappa _1 + \kappa _2 - \kappa _3)+ \sin ^2 \beta (\omega _1 + \omega _2 - 2 \omega _3)\Big ) , \nonumber \\ \end{aligned}$$

(8b)

$$\begin{aligned} M_{S^+}^2= & {} m_S^2 + \frac{1}{4} v^2 \Big (\nu _1 \cos ^2 \beta + \kappa _1 \sin 2 \beta + \omega _1 \sin ^2 \beta \Big ).\nonumber \\ \end{aligned}$$

(8c)

We take $S_I$ to be the lightest colored scalar in the analysis with the $S_R \rightarrow S_I Z$ decay in foresight. The Yukawa interactions in this framework are discussed next. For the interactions involving $\phi _1$ and $\phi _2$, we adopt the Type-X 2HDM Lagrangian. Here, the quarks get their masses from $\phi _2$ and the leptons, from $\phi _1$. That is,

$$\begin{aligned} -\mathcal {L}^{\text {2HDM}}_Y= & {} \Big [ y_u \overline{Q_L} \tilde{\phi }_2 u_R + y_d \overline{Q_L} \phi _2 d_R + y_\ell \overline{L_L} \phi _1 \ell _R \Big ]\nonumber \\{} & {} \quad + \text {h.c.} \end{aligned}$$

(9)

The lepton Yukawa interactions in terms of the physical scalars then becomes

$$\begin{aligned} \mathcal {L}^\text {2HDM}_Y= & {} \sum _{\ell =e,\mu ,\tau } \frac{m_\ell }{v} \bigg (\xi _\ell ^h h \overline{\ell } \ell + \xi _\ell ^H H \overline{\ell } \ell - i \xi _\ell ^A A \overline{\ell } \gamma _5 \ell \nonumber \\{} & {} + \Big [ \sqrt{2} \xi ^A_\ell H^+ \overline{\nu _\ell } P_R \ell + \text {h.c.} \Big ] \bigg ). \end{aligned}$$

(10)

The various $\xi _\ell$ factors are tabulated in the Appendix.

The Yukawa interactions of the colored scalars can be expressed as [52]

$$\begin{aligned} -\mathcal {L}^{\text {col. oct.}}_Y= & {} \sum _{p,q=1,2,3} \Big [Y^{pq}_u~\overline{Q_{Lp}} \tilde{S} u_{Rq} \nonumber \\{} & {} \quad + Y^{pq}_d~\overline{Q_{Lp}} S d_{Rq} + \text {h.c.} \Big ]. \end{aligned}$$

(11)

In compliance with MFV, we take $Y_{u}^{pq} = \eta _U \frac{\sqrt{2}m_{u}}{v} \delta ^{pq}$ and $Y_{d}^{pq} = \eta _D \frac{\sqrt{2}m_{d}}{v} \delta ^{pq}$. We refer to [52] for further details. The scaling constants $\eta _U$ and $\eta _D$ are complex in general. However, they are taken real in this study for simplicity.

3 Constraints applied

The 2HDM plus color octet setup is subject to various restrictions from theory and experiments. We discuss them below.

3.1 Theoretical constraints

A perturbative theory demands that the magnitudes of the scalar quartic couplings must be $\le 4\pi$. Next, tree-level unitarity demands that the $2 \rightarrow 2$ matrices constructed out of the tree-level scattering amplitudes involving the various scalar states of the model must have eigenvalues whose magnitudes are $\le 8\pi$. The following unitarity conditions can be derived for the present framework [68].

$$\begin{aligned}{} & {} \left[ \frac{3}{2} (\lambda _1 + \lambda _2) \pm \sqrt{\frac{9}{4} (\lambda _1 - \lambda _2)^2 + (2 \lambda _3 + \lambda _4)^2}\right] \le 8 \pi , \nonumber \\ \end{aligned}$$

(12a)

$$\begin{aligned}{} & {} \left[ \frac{1}{2} (\lambda _1 + \lambda _2) \pm \sqrt{\frac{1}{4} (\lambda _1 - \lambda _2)^2 + \lambda _4^2} \right] \le 8 \pi , \end{aligned}$$

(12b)

$$\begin{aligned}{} & {} \left[ \frac{1}{2} (\lambda _1 + \lambda _2) \pm \sqrt{\frac{1}{4} (\lambda _1 - \lambda _2)^2 + \lambda _5^2} \right] \le 8 \pi , \end{aligned}$$

(12c)

$$\begin{aligned}{} & {} (\lambda _3 + 2 \lambda _4 - 3 \lambda _5)\le 8 \pi , \end{aligned}$$

(12d)

$$\begin{aligned}{} & {} (\lambda _3 - \lambda _5)\le 8 \pi , \end{aligned}$$

(12e)

$$\begin{aligned}{} & {} (\lambda _3 + \lambda _4 )\le 8 \pi , \end{aligned}$$

(12f)

$$\begin{aligned}{} & {} (\lambda _3 + 2 \lambda _4 + 3 \lambda _5)\le 8 \pi , \end{aligned}$$

(12g)

$$\begin{aligned}{} & {} (\lambda _3 + \lambda _5)\le 8 \pi , \end{aligned}$$

(12h)

$$\begin{aligned}{} & {} |\nu _1| \le 2 \sqrt{2} \pi , ~ |\nu _2| \le 4 \sqrt{2} \pi , ~|\nu _3| \le 2 \sqrt{2} \pi , \end{aligned}$$

(12i)

$$\begin{aligned}{} & {} |\omega _1| \le 2 \sqrt{2} \pi , ~ |\omega _2| \le 4 \sqrt{2} \pi , ~|\omega _3| \le 2 \sqrt{2} \pi , \end{aligned}$$

(12j)

$$\begin{aligned}{} & {} |\kappa _1| \le 2 \pi , ~ |\kappa _2| \le 4 \pi , ~|\kappa _3| \le 4 \pi , \end{aligned}$$

(12k)

$$\begin{aligned}{} & {} |17 \mu _3 + 13 \mu _4 + 13 \mu _6| \le 16 \pi , \end{aligned}$$

(12l)

$$\begin{aligned}{} & {} |2 \mu _3 + 10 \mu _4 + 7 \mu _6| \le 32 \pi , \end{aligned}$$

(12m)

$$\begin{aligned}{} & {} |\nu _4 + \nu _5| \lesssim \frac{32 \pi }{\sqrt{15}}, \end{aligned}$$

(12n)

$$\begin{aligned}{} & {} |\omega _4 + \omega _5| \lesssim \frac{32 \pi }{\sqrt{15}} . \end{aligned}$$

(12o)

Thus, unitarity restricts the magnitudes of the quartic couplings of the model. Equations (12a)–(12h) correspond to the unitarity limit for a pure two-Higgs doublet scenario [72,73,74,75,76,77,78]. We refer to [68, 79] for more details. Finally, the conditions ensuring a bounded-from-below scalar potential in this model along different directions in the field space are [80]:

$$\begin{aligned}{} & {} \mu = \mu _1 + \mu _2 + \mu _6 + 2(\mu _3 + \mu _4 + \mu _5) > 0, \end{aligned}$$

(13a)

$$\begin{aligned}{} & {} \mu _1 + \mu _2 + \mu _3 + \mu _4 > 0, \end{aligned}$$

(13b)

$$\begin{aligned}{} & {} 14(\mu _1 + \mu _2) + 5\mu _6 + 24(\mu _3 + \mu _4) \nonumber \\{} & {} - 3|2(\mu _1 + \mu _2) - \mu _6| > 0, \end{aligned}$$

(13c)

$$\begin{aligned}{} & {} 5(\mu _1 + \mu _2 + \mu _6) + 6(2\mu _3 + \mu _4 + \mu _5) \nonumber \\{} & {} - |\mu _1 + \mu _2 + \mu _6| > 0, \end{aligned}$$

(13d)

$$\begin{aligned}{} & {} \lambda _1 \ge 0,~ \lambda _2 \ge 0,~ \lambda _3 \ge - \sqrt{\lambda _1 \lambda _2}, \end{aligned}$$

(13e)

$$\begin{aligned}{} & {} \lambda _3 + \lambda _4 - |\lambda _5| \ge - \sqrt{\lambda _1 \lambda _2}, \end{aligned}$$

(13f)

$$\begin{aligned}{} & {} \nu _1 \ge -2 \sqrt{\lambda _1 \mu }, \end{aligned}$$

(13g)

$$\begin{aligned}{} & {} \omega _1 \ge -2 \sqrt{\lambda _2 \mu }, \end{aligned}$$

(13h)

$$\begin{aligned}{} & {} \nu _1 + \nu _2 - 2 |\nu _3| \ge -2 \sqrt{\lambda _1 \mu }, \end{aligned}$$

(13i)

$$\begin{aligned}{} & {} \omega _1 + \omega _2 - 2 |\omega _3| \ge -2 \sqrt{\lambda _2 \mu }, \end{aligned}$$

(13j)

$$\begin{aligned}{} & {} \lambda _1 + \frac{\mu }{4} + \nu _1 + \nu _2 + 2\nu _3 - \frac{1}{\sqrt{3}}|\nu _4 + \nu _5| > 0, \end{aligned}$$

(13k)

$$\begin{aligned}{} & {} \lambda _2 + \frac{\mu }{4} + \omega _1 + \omega _2 + 2\omega _3 - \frac{1}{\sqrt{3}}|\omega _4 + \omega _5| > 0. \end{aligned}$$

(13l)

Among the above, Eqs. (13e) and (13f) correspond to the pure 2HDM. The rest of the conditions ensure positivity of the scalar potential in a hyperspace spanned by both colorless as well as colored fields.

3.2 Higgs signal strengths

The model also faces restrictions from signal strength measurements in different decay modes of the 125 GeV Higgs. The signal strength for the channel $p p \rightarrow h, ~h \rightarrow i$ is defined as

$$\begin{aligned} \mu _i = \frac{\sigma ^\mathrm{{theory}}(pp \rightarrow h)~ \mathrm{BR^{theory}}(h \rightarrow i)}{\sigma ^\mathrm{{exp}}(pp \rightarrow h)~ \mathrm{BR^{exp}}(h \rightarrow i)}. \end{aligned}$$

(14)

We take $g g \rightarrow h$ as the production process at the partonic level. The cross section for the same can be expressed as

$$\begin{aligned} \sigma (gg \rightarrow h) = \frac{\pi ^2}{8 M_h} \Gamma (h \rightarrow gg)~ \delta (\hat{s} - M_h^2) , \end{aligned}$$

(15)

$\sqrt{\hat{s}}$ being partonic centre-of-mass energy. Further, expressing the branching fractions in terms of the decay widths, one rewrites Eq. (14) as

$$\begin{aligned} \mu _i= & {} \frac{\Gamma ^\mathrm{{BSM}}_{h \rightarrow gg}}{\Gamma ^\mathrm{{SM}}_{h \rightarrow gg}} ~\frac{\Gamma _i^\mathrm{{BSM}}}{\Gamma _\mathrm{{tot}}^\mathrm{{BSM}}} ~\frac{\Gamma _\mathrm{{tot}}^\mathrm{{SM}}}{\Gamma _i^\mathrm{{SM}}}. \end{aligned}$$

(16)

The alignment limit i.e. $\alpha = \beta - \frac{\pi }{2}$ is strictly imposed throughout the analysis in which the $h \rightarrow WW,ZZ,\tau ^+\tau ^-$ decay widths at the leading order are identical to the corresponding SM values. Therefore, the signal strength in these channels deviates from the corresponding SM predictions on account of only the additional contribution to the $g g \rightarrow h$ amplitude coming from the colored scalars. This is not the case with the $h \rightarrow g g, \gamma \gamma$ signal strengths where additional one-loop contributions are induced by the scalar sector. We refer to [68, 69, 71] for relevant formulae on the decay widths for this framework.

The latest data on Higgs signal strengths for $g g \rightarrow h$ is summarised in Table 1. We combine the data using $\frac{1}{\sigma ^2} = \frac{1}{\sigma ^2_{\text {ATLAS}}} + \frac{1}{\sigma ^2_{\text {CMS}}}$ and $\frac{\mu }{\sigma ^2} = \frac{\mu _{\text {ATLAS}}}{\sigma ^2_{\text {ATLAS}}} + \frac{\mu _{\text {CMS}}}{\sigma ^2_{\text {CMS}}}$. The resulting data is used at 2$\sigma$ in our analysis.

Table 1 Latest limits on the h-signal strengths

3.3 Direct search

Searches for an $H^+$ in the $e^+ e^- \longrightarrow H^+ H^-$ channel at LEP [91] has led to a $M_{H^+} > 100$ GeV bound for all 2HDM Types. As for the Type-X, various exclusion limits are rather weak (compared to Type-II, for instance) owing to the suppressed Yukawa couplings of $H,A,H^+$ with the quarks [92]. We take $M_H$ = 150 GeV and $M_{H^+} \ge M_H$ to comply with the exclusion constraints. In foresight, we shall also adhere to $M_A > M_h/2$ to evade the limit on BR($h \rightarrow A A$) derived from BR($h_{125} \rightarrow AA \rightarrow 4\tau , 2\tau 2\mu$) [51].

We now discuss exclusion constraints on the color octet mass scale. Color-octet resonances have been searched for at the LHC in the $pp \rightarrow S \rightarrow j j$ [93,94,95,96] and $pp \rightarrow S \rightarrow t \overline{t}$ [97,98,99] channels. Reference [70] recasted the search of colored scalars at the LHC for the Manohar-Wise scenario. The lightest colored scalar was taken to be $S_R$ therein. Since the colored scalars have Yukawa interactions with the quarks, exclusion limits on the color octet mass scale can depend on the strength of such couplings. Reference [70] reported that no clear constraints were derived from the $p p \rightarrow S_R \rightarrow t \overline{t}$ channel. As for $p p \rightarrow S_R t \overline{t} \rightarrow t \overline{t} t \overline{t}$, a bound $M_R > rsim$ 1 TeV can be derived for $\eta _U \sim \mathcal {O}(1)$. This bound is therefore expected to relax upon lowering $\eta _U$. Another channel is $p p \rightarrow S^+ t \overline{b} \rightarrow t \overline{b} t \overline{b}$ that leads to a bound of 800 GeV irrespective of the value of $\eta _U$ and $\eta _D \ne 0$. These bounds should apply to $S_I$, the lightest scalar assumed in our case. We take $\eta _U \ll \eta _D$ = 1 and $M_{S_I}$ = 800 GeV throughout our numerical analysis in order to comply with the direct search constraints.

3.4 Lepton flavour universality

Enhanced Yukawa couplings of the $\tau$-lepton potentially modify the $\tau \rightarrow \ell \nu \overline{\nu }$ due to additional contributions stemming from the 2HDM scalars at both tree and loop-levels. This is particularly seen in the lepton-specific case for high $\tan \beta$. We refer to [29] for details where this has been studied extensively. Following [29], we have therefore restricted $\tan \beta < 60$ throughout the analysis to comply with lepton flavour universality.

4 The CDF II and muon $g-2$ excesses

This section discusses how the measured values of the W-mass and muon anomalous magnetic moment can be realised in the 2HDM + color octet setup. The W-mass predicted by a new physics framework can be expressed in terms of its contributions to the oblique parameters $\Delta S$, $\Delta T$ and $\Delta U$ as [100]

$$\begin{aligned} M^2_W= & {} M^2_{W,\text {SM}} \Bigg [1 + \frac{\alpha _{em}}{c^2_W - s^2_W} \Bigg ( -\frac{\Delta S}{2} + c^2_W \Delta T \nonumber \\{} & {} \quad + \frac{c^2_W - s^2_W}{4 s^2_W} \Delta U \Bigg ) \Bigg ] \end{aligned}$$

(17)

where $M_{W,\text {SM}}$ is the mass in absence of quantum corrections, and, $c_W$ and $\alpha _{em}$ respectively denote the cosine of the Weinberg angle and the fine-structure constant. We list below the contributions from the colorless and colored sectors to the T-parameter [101, 102] in the alignment limit.

$$\begin{aligned} \Delta T_{\text {2HDM}}= & {} \frac{1}{16 \pi s^2_W M^2_W}\Big [F(M^2_{H^+},\nonumber \\{} & {} M^2_{H}) + F(M^2_{H^+},M^2_{A}) - F(M^2_{H},M^2_{A})\Big ] , \nonumber \\ \Delta T_S= & {} \frac{N_S}{16 \pi s^2_W M^2_W}\Big [F(M^2_{S^+},M^2_{S_R}) + F(M^2_{S^+},\nonumber \\{} & {} M^2_{S_I}) - F(M^2_{S_R},M^2_{S_I})\Big ] , \end{aligned}$$

(18a)

where,

$$\begin{aligned} F(x,y)= & {} \frac{x+y}{2} - \frac{xy}{x-y}~\textrm{ln} \bigg (\frac{x}{y}\bigg )~~~ \textrm{for} ~~~x \ne y , \nonumber \\= & {} 0~~~ \textrm{for} ~~~ x = y. \end{aligned}$$

(19)

Similarly, the corresponding contributions to the S-parameter read

$$\begin{aligned} \Delta S_{\text {2HDM}}= & {} \frac{1}{2\pi } \Bigg [\frac{1}{6}\text {log}\Bigg (\frac{M^2_H}{M^2_{H^+}}\Bigg ) - \frac{5}{108} \frac{M^2_H M^2_A}{(M^2_A - M^2_H)^2}\nonumber \\{} & {} + \frac{1}{6}\frac{M^4_A(M^2_A - 3 M^2_H)}{(M^2_A - M^2_H)^3}\text {log}\Bigg (\frac{M^2_A}{M^2_{H}}\Bigg ) \Bigg ], \end{aligned}$$

(20a)

$$\begin{aligned} \Delta S_S= & {} \frac{N_S}{2\pi } \Bigg [\frac{1}{6}\text {log}\Bigg (\frac{M^2_{S_R}}{M^2_{S^+}}\Bigg ) \nonumber \\{} & {} - \frac{5}{108} \frac{M^2_{S_R} M^2_{S_I}}{(M^2_{S_I} - M^2_{S_R})^2} \nonumber \\{} & {} + \frac{1}{6}\frac{M^4_{S_I}(M^2_{S_I} - 3 M^2_{S_R})}{(M^2_{S_I} - M^2_{S_R})^3}\text {log}\Bigg (\frac{M^2_{S_I}}{M^2_{S_R}}\Bigg ) \Bigg ]. \end{aligned}$$

(20b)

The total oblique parameter in the present setup is given by the sum of the colorless and colored components, i.e., $\Delta S = \Delta S_{\text {2HDM}} + \Delta S_S$ and $\Delta T = \Delta T_{\text {2HDM}} + \Delta T_S$. The $M_W$ value reported by CDF II can be accommodated by the following ranges [103, 104] of $\Delta S$ and $\Delta T$ for $\Delta U=0$:

$$\begin{aligned} \Delta S = 0.15 \pm 0.08,~~\Delta S = 0.27 \pm 0.06,~~\rho _{ST} = 0.93. \nonumber \\ \end{aligned}$$

(21)

Fig. 1

Parameter points in the $M_{H^+} - M_H$ vs $M_{S^+} - M_{S_R}$ (top-left), $M_{H^+} - M_H$ vs $M_{S^+} - M_{S_I}$ (top-right), $M_{H^+} - M_A$ vs $M_{S^+} - M_{S_R}$ (bottom-left) and $M_{H^+} - M_A$ vs $M_{S^+} - M_{S_I}$ (bottom-right) planes compatible with the observed $M_W$ and the various constraints

In the above, $\rho _{ST}$ denotes the correlation coefficient. The impact of stipulated ranges for the oblique parameters is expected to get reflected in the scalar mass splittings. To test it, we fix $M_H$ = 150 GeV and $M_{S_I}$ = 800 GeV and make the variations 0 $< M_{H^+} - M_H <$ 300 GeV, $\frac{M_h}{2} < M_A<$ 200 GeV, 0 $< M_{S^+} - M_{S_I} <$ 100 GeV and 0 $< M_{S_R} - M_{S_I} <$ 100 GeV. The parameter points predicting $\Delta S$ and $\Delta T$ in the aforesaid ranges are plotted in the $M_{H^+} - M_H$ vs $M_{S^+} - M_{S_R}$, $M_{H^+} - M_H$ vs $M_{S^+} - M_{S_I}$, $M_{H^+} - M_A$ vs $M_{S^+} - M_{S_R}$ and $M_{H^+} - M_A$ vs $M_{S^+} - M_{S_I}$ planes in Fig. 1. An inspection of the figure immediately suggests that the (0, 0) point in each panel is excluded by the CDF data. This is expected on account of the fact that $M_{H/A} = M_{H^+}$ and $M_{S_R/S_I} = M_{S^+}$ respectively lead to $\Delta T_{\text {2HDM}}$ = 0 and $\Delta T_{S}$ = 0 for all $M_{A}$ and $M_{S_R}$ and a vanishing $\Delta T$ does not suffice to predict the observed $M_W$.

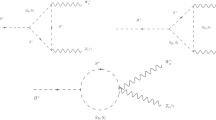
We now discuss muon $g-2$ in the given setup. Elaborate discussions on the purely Type-X contributions to $\Delta a_\mu$ are skipped here for brevity. We focus on the contribution coming from the colored scalars in this section. Since the color-octet does not couple to the leptons at the tree-level, it does not contribute to muon $g-2$ at one-loop. The color-octet sector contributes to the muon anomalous magnetic moment through the two-loop BZ amplitudes shown in Fig. 2. The diagram on the left panel is a two-loop topology involving an effective $\phi \gamma \gamma$ ($\phi =h,H$) vertex that is generated at one loop via $S^\pm$ running in the loop. The BZ amplitude can be expressed as

Fig. 2

Two loop BZ contributions to $\Delta a_\mu$ involving the color octet

$$\begin{aligned} {\Delta a_\mu }_{\{S^+,~\phi \gamma \gamma \}}^{\text {BZ}}= & {} \sum _{\phi = h,H} \frac{N_S\alpha M_\mu ^2}{8 \pi ^3 M_{\phi }^2}~ y_l^{\phi }~ \lambda _{\phi S^+ S^-}\mathcal {F}\left( \frac{M_{S^+}^2}{M_{\phi }^2}\right) . \nonumber \\ \end{aligned}$$

(22)

Similarly, the right panel diagram involves an $H^+ W^- \gamma$ vertex that is generated at one loop. The amplitudes stemming from $S_R$ and $S_I$ in the loops are given by

$$\begin{aligned} {\Delta a_\mu }_{\{S_R,~H^+ W^-\gamma \}}^{\text {BZ}}= & {} \frac{N_S \alpha M_\mu ^2 }{64 \pi ^3 s_w^2 (M_{H^+}^2 - M_W^2)} \zeta _l \nonumber \\{} & {} \times \lambda _{ H^+ S^- S_R} \int _{0}^{1} dx~x^2 (x-1) \nonumber \\{} & {} \times \left[ \mathcal {G}\left( \frac{M_{S^+}^2}{M_{H^+}^2},\frac{M_{S_R}^2}{M_{H^+}^2}\right) \nonumber \right. \\{} & {} \left. - \mathcal {G}\left( \frac{M_{S^+}^2}{M_W^2},\frac{M_{S_R}^2}{M_W^2}\right) \right] , \end{aligned}$$

(23a)

$$\begin{aligned} {\Delta a_\mu }_{\{S_I,~H^+ W^-\gamma \}}^{\text {BZ}}= & {} \frac{N_S\alpha M_\mu ^2 }{64 \pi ^3 s_w^2 (M_{H^+}^2 - M_W^2)} \zeta _l \nonumber \\{} & {} \times \lambda _{ H^+ S^- S_I} \int _{0}^{1} dx~x^2 (x-1) \nonumber \\{} & {} \times \left[ \mathcal {G}\left( \frac{M_{S^+}^2}{M_{H^+}^2},\frac{M_{S_I}^2}{M_{H^+}^2}\right) \nonumber \right. \\{} & {} \left. - \mathcal {G}\left( \frac{M_{S^+}^2}{M_W^2},\frac{M_{S_I}^2}{M_W^2}\right) \right] . \end{aligned}$$

(23b)

The subscripts in Eqs. (22), (23a) and (23b) refer to the circulating colored scalar and the one-loop effective vertex. The expressions for the trilinear couplings $\lambda _{\phi S^+ S^-},\lambda _{ H^+ S^- S_R},\lambda _{ H^+ S^- S_I}$ and the functions $\mathcal {F}(z)$ and $\mathcal {G}(z^a,z^b,x)$ are given in the Appendix. We intend to test the magnitudes of the three Barr-Zee contributions and choose tan$\beta$ = 50, $M_{H}$ = 100 GeV, $M_{H^+}$ = 250 GeV, $M_{S_I}$ = 800 GeV, $M_{S^+}$ = 805 GeV, 810 GeV, 820 GeV. The values taken for tan$\beta$ and $M_{S_I}$ are allowed by the lepton flavour universality and direct search constraints respectively. In addition, the $M_{H^+}-M_H$ and $M_{S^+}-M_{S_I}$ mass differences are thus compatible with $M_W^\text {CDF}$, as can be checked with Fig. 1. As for the values of the trilinear couplings at $\alpha = \beta - \frac{\pi }{2}$, one derives $\lambda _{H S^+ S^-} = -\frac{1}{2}\big ((\nu _1 - \omega _1)c_\beta s_\beta + \kappa _1 s_{2\beta }\big ) \simeq -\frac{\kappa _1}{2}$ for large tan$\beta$. Since $\kappa _1$ is a priori a free parameter of the theory, $|\lambda _{H S^+ S^-}|$ can be as large as 2$\pi$. It similarly follows that $|\lambda _{H^+ S^- S_R}|$ and $|\lambda _{H^+ S^- S_I}|$ $\lesssim \pi$.

Fig. 3

Variation of different BZ contributions involving colored scalars for $M_{S^+}$ = 805 GeV (top left), 810 GeV (top right) and 820 GeV (bottom). We have further taken $\lambda _{H S^+ S^-} = -2\pi$ and $\lambda _{H^+ S^- S_R}=\lambda _{H^+ S^- S_I} = -\pi$ in these plots. The $1\sigma$, $2\sigma$ and $3\sigma$ experimental bounds on $\Delta a_\mu$ are shown using horizontal lines in all the panels

We plot the individual BZ amplitudes in Fig. 3 versus $M_{S_R}$ for tan$\beta$ = 50, $\lambda _{H S^+ S^-} = -2\pi$ and $\lambda _{H^+ S^- S_R}=\lambda _{H^+ S^- S_I} = -\pi$. With such choices for the trilinear couplings, we find that they can be $\mathcal {O}(10^{-10})$ with the largest being ${\Delta a_\mu }_{\{S^+,~H \gamma \gamma \}}^{\text {BZ}}$². This sizeable magnitudes can be understood from the fact that the products $\lambda _{H S^+ S^-}\times \tan \beta$, $\lambda _{H^+ S^- S_R}\times \tan \beta$ and $\lambda _{H^+ S^- S_I}\times \tan \beta$ are $\mathcal {O}(100)$ numbers. Variations introduced by the said changes of $M_{S^+}$ are small and do not change the ball-park contributions to $\Delta a_\mu$.

Retaining the same values for the scalar masses as in Fig. 3, we perform the following scan over the rest of the parameters:

$$\begin{aligned} 20~\text {GeV}< M_A< 200~\text {GeV},~0< m_{12}< 100~\text {GeV}, \nonumber \\ 10< \tan \beta< 100,~|\omega _1|,|\kappa _1|,|\kappa _2|,|\kappa _3|, |\nu _1|,|\nu _2|,|\nu _3| < 2\pi . \nonumber \\ \end{aligned}$$

(24)

We elucidate a bit on the choice of the interval of $\Delta a_\mu$. A heavy colored mass scale $\sim$ 800 GeV tends to suppress the BZ contributions to $\Delta a_\mu$. However, this is compensated to some extent by the color factor $N_S = 8$, and, sizeable magnitudes of the scalar couplings. In view of such competing affects at play here, we impose the requirement of muon $g-2$ at the 3$\sigma$ limit. That is,

$$\begin{aligned} {7.4 \times 10^{-10}< \Delta a_\mu < 4.28 \times 10^{-9}.} \end{aligned}$$

(25)

In addition, the model is demanded to be consistent at 2$\sigma$ with $M_W^{\text {CDF}}$. Parameter points compatible with $\Delta a_\mu$ and $M_W^{\text {CDF}}$ and clearing the constraints discussed before are plotted in the $M_A-\tan \beta$ ($M_A-M_{S_R}$) plane in the left (right) panel of Fig. 4. One inspects in this figure that owing to the color-octet contributions, an A compliant with the observed $\Delta a_\mu$ can now be much heavier compared to what it is in the pure Type-X 2HDM. To elucidate, the enlarged parameter space now includes $M_A \lesssim 180$ GeV for a tan$\beta$ around 50 for the all three $M_{S^+}$ values taken. The lower bound $M_A > rsim 80$ GeV is noticed for $M_{S^+}$ = 805 GeV. This is a consequence of demanding $\Delta T$ and $\Delta S$ in the stated ranges (Eq. 21) so as to comply with the observed $M_W$. We remind that $S_I$ is taken to be the lightest colored scalar in this setup we also show the subregions where $M_{S_R} > M_{S_I} + M_A$ keeping in mind the $S_R \rightarrow S_I A$ decay. Such a requirement restricts $M_A \lesssim$ 140 GeV, 110 GeV and 85 GeV for $M_{S^+}$ = 805 GeV, 810 GeV and 820 GeV respectively.

Fig. 4

Parameter region in the $M_A$-tan$\beta$ plane (left panel) and $M_A$-$M_{S_R}$ plane (right panel) compatible with the CDF-II and muon $g-2$ excesses. The regions left to the vertical line ($M_A = \frac{M_h}{2}$ limit) $M_A$-tan$\beta$ plane are excluded by the latest data. Similarly, the regions left to the vertical line ($M_A = \frac{M_h}{2}$ limit) and below the horizontal line ($M_{S_I}$ = 800 GeV bound) in $M_A$-$M_{S_R}$ plane are excluded by the latest data

5 Collider analysis

Having validated the multi-dimensional parameter space through the theoretical and experimental constraints, in this section, we aim to analyse a possible signature of the colored scalars at the high-luminosity (HL) 14 TeV LHC. The signal topology allows for the single production of $S_R$ dominantly through gluon-gluon and quark fusion and then subsequent decay of $S_R$ into $S_I$ and A. Finally the colored scalar $S_I$ decays into two b-jets and A decays to $\tau ^+ \tau ^-$. The full cascade therefore is

$$\begin{aligned} p p \rightarrow S_R \rightarrow S_I A,~S_I \rightarrow b \overline{b},~A \rightarrow \tau ^+ \tau ^- . \end{aligned}$$

(26)

Depending on the visible decay products of the $\tau ^\pm$, there could be the following three possibilities:

• Both $\tau$ leptons in the final state decay leptonically leading to the final state with $\tau _\ell = \tau _e, \tau _\mu$. However, the efficiency of such a channel is poor and thus we refrain from presenting its analysis in this work.

• One of the two $\tau$s in the final state decays leptonically while the second decays hadronically. This semi-leptonic decay topology gives rise to final state. For convenience, this case will be denoted by “SL”.

• Both $\tau$ leptons decay hadronically³ and lead to a final state. This case is dubbed as “NoL” since there are no leptons in the final state.

Once again, we ensure that the $S_R \rightarrow S_I A$ decay remains kinematically open by enforcing $M_{S_R} > M_{S_I} + M_A$. Next, we choose five benchmark points (BP1-BP5) characterized by low, medium and high masses of A ranging from 66 GeV to 147 GeV. All the benchmarks are not only allowed by the theoretical and experimental constraints, but also can envisage the muon anomalous magnetic moment within the $3 \sigma$ band about the central value and address the W-mass anomaly simultaneously. For the chosen benchmarks, the masses of other scalars like $H^+, S^+$, the branching ratios of the processes $S_R \rightarrow S_I A, ~S_I \rightarrow b \overline{b},~ A \rightarrow \tau ^+ \tau ^-$ along with the corresponding values of $\Delta a_\mu$ and $(M_W^\textrm{CDF}- 80.000)$ are tabulated in Table 2. BR$(S_R \rightarrow S_I A)$ is $\sim 99\%$ for BP1 and BP2. Since the mass splitting $(M_{S_R}-M_{S_I})$ increases from BP3 to BP5, the $S_R \rightarrow S_I Z,~ S_R \rightarrow S^\pm W^\mp$ decay modes open up and BR$(S_R \rightarrow S_I A)$ drops appropriately. One additionally notes BR$(A \rightarrow \tau ^+ \tau ^-)$ $\sim 99 \%$ for all the BPs, an expected feature of the Type-X texture. It is added that the choice $\eta _D=1$ and $\eta _U \ll \eta _D$ ensures that $S_I \rightarrow b \overline{b}$ is the dominant decay mode.

Table 2 Benchmarks compatible with $M^{\text {CDF}}_W$ and the observed $\Delta a_\mu$

We discuss the relevant backgrounds next. The dominant contributors to the backgrounds are $p p \rightarrow Z \rightarrow \tau ^+ \tau ^- + jets, ~ p p \rightarrow t \overline{t} \rightarrow 1 \ell + jets,~ ~ p p \rightarrow t \overline{t} \rightarrow 2 \ell + jets$.⁴ The first background can mimic the final state of the signal if the light jets fake as b-jets. And the second background leads to a final state when one of the light jets is mis-tagged as a $\tau$-jet, two of the light jets fake as b-jets and one of the leptons is missed. That is, the second background then becomes identical to the SL signal in terms of the final state. In addition, sub-dominant backgrounds include $tW,~ WZ \rightarrow 2 \ell 2q$ and $WZ \rightarrow 3 \ell \nu + jets$. A complete set of the backgrounds is listed in Table 3.

The particle interactions relevant to the collider analysis are first implemented in FeynRules [105] and an Universal Feynrules Output (UFO) file is generated. Showering and hadronization are achieved through Pythia8 [107]. We use the default CMS detector simulation card included in Delphes$-$3.4.1 [108] to mimic a realistic detector environment. The anti-$k_t$ jet-clustering algorithm [109] is adopted for jet reconstruction. We now briefly describe our evaluation of the signal and background cross sections. The background cross sections at the leading order (LO) cross sections are computed using MG5aMC@NLO [106] and are subsequently multiplied with relevant k-factors to obtain the corresponding next-to-leading order (NLO) values. As for the signal, its cross section is straightforwardly estimated as $\sigma _{p p \rightarrow S_R} \times \text {BR}(S_R \rightarrow S_I A) \times \text {BR}(S_I \rightarrow b \overline{b}) \times \text {BR}(A \rightarrow \tau ^+ \tau ^-)$. In this study, we remain agnostic to a detailed computation of $\sigma _{p p \rightarrow S_R}$ which would involve parameters such as the scalar couplings $\mu _i$ that are not otherwise correlated with the rest of the analysis. Therefore, looking at the values of $M_{S_R}$ in the benchmarks, we choose a rather conservative $\sigma _{p p \rightarrow S_R}$ = 50 fb for all BP1-5 following the results in [70]. The signal and background cross sections are tabulated in Table 3. We must add that we have applied certain cuts while generating some of the backgrounds (mentioned in Table 3 and its footnote). For other backgrounds, we impose the similar cuts at the detector level to keep all the event samples at the same footing.

Table 3 Cross sections of the signal benchmark points and the relevant SM backgrounds

Table 4 Summary of acceptance cuts to select analysis level objects

Table 5 Event yields of the signal and SM background processes after the baseline selection (C0–C4) and after each successive selection cuts (C5–C8) of the cut based analysis at the 14 TeV LHC for $\mathcal{L}\,=\,3000\,\mathrm{fb^{-1}}$. Each row is divided into two subrows that contain the information of the SL (upper row) and NoL (lower row) channels, respectively

The subsequent discussion on the collider analysis is divided into the two following subsections that contain cut-based and multivariate analyses respectively.

5.1 Cut-based analysis

We first apply a few pre-selection cuts (C0–C4) on the events that are used as baseline selection criteria and then perform cut-based as well as multivariate analyses to estimate the signal sensitivity. We describe the baseline selection criteria in detail below.

• C0: A few basic selection criteria are applied to select $e, \mu , \tau$ and jets in the final state. We construct the following set of kinematic variables both for leptons and jets: (a) transverse momentum $p_T$, (b) pseudo-rapidity $\eta$, and (c) separation between i and j-th objects $\Delta R_{ij}\,=\,\sqrt{(\Delta \eta _{ij})^2 + (\Delta \Phi _{ij})^2}$, which is defined in terms of the azimuthal angular separation $(\Delta \Phi _{ij})$ and pseudo-rapidity difference $(\Delta \eta _{ij})$ between the same objects. The chosen threshold values of these variables are quoted in Table 4.

• C1: Next we ensure that the final state acquires correct lepton multiplicity. By lepton, here we mean $\mu$ and e only. In the final state, we demand one and zero leptons for the SL and NoL channels respectively.

• C2: As expected from the topology of the signals, we require two $\tau$-jets in the final state for the NoL channel. Similarly, for the SL channel, one $\tau$-jet is demanded.

• C3: Since the lepton + $\tau$-jet (two $\tau$-jets) originate from two oppositely charged $\tau$-leptons in the SL (NoL) channel, we demand that the decay products in both cases must have opposite charges.

• C4: Since the signals in both channels include two b-jets in the final state coming from $S_R$, we demand two b-jets in the final state for both channels.

Thus the baseline selection criteria are mainly aimed at selecting a desired final state in the event samples. As can be seen from Table 5, after applying the cuts C0–C4, the signal-to-background ratio for each benchmark turns out to be small at an integrated luminosity $\mathcal{L}\,=\,3000\,\mathrm{fb^{-1}}$. Thus, imposing only C0–C4 does not suffice to achieve a healthy signal significance⁵. However, certain kinematic variables seem to discern the signal more efficiently from the background, as can be seen in Figs. 5 and 6. We briefly describe these variables (C5–C9) and the corresponding cuts below.

Fig. 5

Distributions of some kinematic variables: a, b Distribution of leading b jet $p_T$, c, d distributions of sub-leading b jet $p_T$ for SL and NoL channels respectively

Fig. 6

Distributions of some kinematic variables: a, b $\Delta R$ between two b-jets c, d $\Delta R$ between the decay products of A for SL and NoL channels respectively

Fig. 7

Distributions of some kinematic variable: a, b $\sqrt{\hat{s}_{min}}$ for SL and NoL channels respectively

• C5: We have depicted the normalized distributions of the transverse momentum of the leading b-jet ($p_T^{b_1}$) for all benchmarks and dominant backgrounds for SL and NoL channels in Fig. 5a, b respectively. Since the b-jets originate from the decay of a heavy particle $S_I$ having mass 800 GeV, the corresponding distributions of $p_T^{b_1}$ for the signal are harder than that of the backgrounds. Thus we demand $p_T^{b_1} > 200$ GeV to eliminate the backgrounds to a large extent.

• C6: Similarly, for the sub leading b-jet, the distributions of $p_T^{b_2}$ are shown in Fig. 5c, d respectively for the SL and NoL channels. In this case, an efficient discrimination of the signal from the backgrounds entails $p_T^{b_2} > 100$ GeV.

• C7: The normalized distributions of $\Delta R_{b_1, b_2}$ corresponding to the SL and NoL channels are shown in Fig. 6a, b respectively. In both channels, two b-jets originate from the massive particle $S_I$ in case of the signal. Since $S_I$ is not boosted enough to keep it’s decay products collimated, the $\Delta R_{b_1, b_2}$ distribution peaks at a higher value for the signal than it does for the backgrounds. This prompts us to impose the lower cut $\Delta R_{b_1, b_2} > 2.0$.

• C8: Another important variable with a reasonable distinguishing power between the signal and backgrounds is $\Delta R_{\ell , \tau _h}$ ($\Delta R_{\tau _{h_1}, \tau _{h_2}}$) for the SL (NoL) channel. The corresponding distributions are shown in Fig. 6c, d for the SL and NoL channels respectively. The visible decay products of $\tau ^+ \tau ^-$ in the semi-leptonic and fully hadronic decay modes originate from a lighter pseudoscalar with mass $\sim$ 66–147 GeV. Thus the final state lepton and $\tau$-jet (two $\tau$-jets) in SL (NoL) channel become collimated, thereby setting $\Delta R_{\ell , \tau _h}$ ($\Delta R_{\tau _{h_1}, \tau _{h_2}}$) to a smaller value for signal compared to the backgrounds. Thus, we apply an upper cut: $\Delta R_{\ell , \tau _h}$ ($\Delta R_{\tau _{h_1}, \tau _{h_2}}$) $< 1.8$ to suppress the backgrounds.

• C9: Finally, we use the minimum parton level centre-of-mass energy ($\sqrt{\hat{s}_{min}}$) [113] which has the highest degree of discerning power between the signal and backgrounds. Basically, this is a global inclusive variable for determining the mass scale of any new physics in presence of missing energy at the final states. The signal- and background- distributions for both the channels are depicted in Fig. 7a, b. Since this variable is effective in eliminating the backgrounds to a great extent, the signal significance is expected to be sensitive to it. Thus, instead of giving a fixed lower cut on this variable, we try to tune $\sqrt{\hat{s}_{min}}$ over a suitable range to maximize the significance. Thus we do not include this cut (C9) in the cut-flow Table 5. And Table 6 shows the variation of the signal significances with various lower limits on $\sqrt{\hat{s}_{min}}$. For instance, the significance in case of BP2 increases by 20$\%$ (14.8$\%$) for the SL (NoL) channel after applying the stated cut on this variable.

In Table 5 we tabulate the signal (BP1–BP5) and background yields at $\mathcal {L}$ = 3000 fb$^{-1}$ after imposing the baseline selection cuts (C0–C4) and the more specific cuts (C5–C9). Looking at the signal significances in Table 6, one concludes that the NoL channel turns out to be more promising among the two at the 14 TeV HL-LHC. In the same table, we also turn on linear-in-background $5 \%$ systematic uncertainty and evaluate the reduced signal significances. Due to a huge background contribution, a $5\%$ systematic uncertainty on background affects the signal significance by a large margin. Therefore, this warrants a multivariate analysis using deep neural networks that we take up in the next section.

Table 6 Best cut on $\sqrt{\hat{s}_{min}}$ and corresponding signal and background yields for the five signal benchmark points. Each row is divided into two subrows that contain the information of the SL (upper row) and NoL (lower row) channels, respectively. Last two columns show the signal significance values at $\mathcal{L}\,=\,3000\,\mathrm{fb^{-1}}$ with and without a systematic uncertainty $(\theta )$ of 0$\%$ and 5$\%$, respectively

5.2 Multivariate analysis

We use deep neural network (DNN) [114] to perform the multivariate analysis (MVA). We follow a supervised learning technique to do a binary-classification. Before going to the details of DNN analysis, we shall present a brief outline of the basic work flow of a DNN.

A DNN has more than one hidden layer with multiple nodes or neurons fully connected to the nodes of the consecutive layers via different weights and biases. The input to each node of nth layer is the linear superposition of the outputs of all the nodes in $(n-1)$th layer. A nonlinear activation function is applied on the output of each node of all the layers except the input layer. The input layer is basically the first layer with the input features as nodes. The final layer is the output layer and the output is estimated in terms of probability which is a function of all the weights and biases of the network. The difference between the true output and the predicted one is referred as the loss function. The loss function is finally minimized using gradient descent method through back propagation technique to extract the best values of the model parameters. Those optimized weights and biases correspond to a suitable nonlinear boundary on the plane of the input features that can classify the signal and background events. Here a mini-batch gradient descent method is used where the loss is estimated using a batch of events and then the average loss per batch is used in the back propagation. A detailed description of a DNN can be found in [114].

Table 7 Input variables used for DNN

Here we follow a parametric deep neural network (p-DNN) [115] approach to deal with all the five signal benchmark points through a single network. A single p-DNN can include multiple signal benchmarks with different kinematics. Therefore, it is not required to train different networks for different benchmarks. One single network can take care of it. Also, any underlying configuration between two chosen signal benchmarks can be inferred more precisely with the help of parametric DNN. A detailed discussion of p-DNN can be found in [115]. The p-DNN algorithm uses a fixed parameter for a single benchmark and for our analysis, the parameter is $M_A$. For the background events, the value of $M_A$ is randomly selected from the five benchmark values. Next the p-DNN networks for signal and backgrounds are trained for the two analysis channels: SL and NoL.

We use $80\%$ of the whole dataset (i.e. signal and background combined), for training and to evaluate the performance of corresponding networks, we keep the remaining set for testing. We use 25 (26) input features for NoL (SL) channel mentioned in Table 7 and also include $M_A$ as one of the parameters. The importance of the features is estimated by the F-score using permutation invariance [116] method for both analysis channels.

We use a Residual Network (ResNet) [117] based DNN architecture for the classification task. Figure 8 demonstrates a schematic diagram of the networks. They are trained using Tensorflow and Keras. All the layers are basically “Dense” layers with multiple neurons that built the whole architecture in a sequential manner. All the hidden layers, except the input and output ones, are equipped with a skip connection which is the fundamental characteristic of a ResNet. It takes care of tiny or vanishing gradient values through the skip connections. Therefore, it enables a long network to train better.

Fig. 8

A schematic of the DNN architecture

We use Scaled Exponential Linear Units (SELUs) [118] as the activation function for all the nodes of hidden layers. SELU performs better than Exponential Linear Units (ELU) or Rectified Linear Unit (ReLU) because it can avoid the vanishing gradient problem and also it can take care of the internal normalization as well. For the output nodes, we use Sigmoid activation function to convert the network output to probability values. As shown in Fig. 8, after each hidden layer, a Batch Normalization (Batch_Norm) layer is added which determines the mean and variance of the input values to the activation layer per batch and then normalizes the vectors so that the output of each node, before activation, follows a standard normal distribution across each batch. It can also be used after the activation. The Batch_Norm makes a network faster and more stable. Then after applying activations, Dropout is used where a fraction of nodes are dropped off randomly at each iteration of training. Dropout helps to reduce the over-fitting of a network. Every details of the p-DNN especially the parameters and their corresponding values are shown in Table 8.

Table 8 Details of DNN parameters

The networks are trained in stochastic approach and therefore, with increasing the number of iteration, the loss is expected to decrease because the network tries to learn the nature of signal and background from the distributions of the input features. We observe similar behavior of the loss for two mutually exclusive datasets kept for training and validation purposes, which indicate the presence of negligible over-training as shown in Fig. 9. Based on that, we proceed to use respective networks to evaluate the signal significance for all the five benchmark points. We also consider a $5\%$ linear-in-background systematic uncertainty on the background contribution to see the effect in the signal significance values.

Fig. 9

Variation of loss for with the number of iteration over the whole dataset i.e. epochs

The p-DNN responses for both SL and NoL channels are shown in Fig. 10. All the SM backgrounds are merged into three groups: $t\overline{t}+$jets, $t\overline{t}(V)+$jets and $VV(V)+$Other processes. The respective contributions are scaled at $\mathcal{L}\,=\,3000~\mathrm{fb^{-1}}$ and then stacked together. The signal benchmark cross sections are scaled at $1~\textrm{pb}$ to see the nature of the reponse for signal benchmarks.

Fig. 10

Distributions of parametric DNN scores for all five signal benchmark points and all the SM backgrounds

Considering the actual signal cross sections, we iterate over the p-DNN responses to find the best score where the signal significance gets maximum. Unlike the cut based analysis, the best cut on p-DNN score does not ensure either very high number of backgrounds (B) or $B \ge 10 \times$ number of signal events (S). Therefore we use the log-formula to compute the significance:

$$\begin{aligned} \mathcal{S} = \sqrt{2\Bigg ((S + B)\textrm{ln}\Bigg (1 + \frac{S}{B}\Bigg ) - S\Bigg )} \end{aligned}$$

(27)

To observe the effect of uncertainty on the signal significance, we recompute the significance using

$$\begin{aligned}{} & {} \mathcal{S} =\nonumber \\{} & {} \sqrt{2\Bigg ((S+B)~\textrm{ln}\Bigg [\frac{(S+B)(B+\sigma _B^2)}{B^2+(S+B)\sigma _B^2}\Bigg ]-\frac{B^2}{\sigma _B^2}~\textrm{ln}\Bigg [1+\frac{\sigma _B^2 S}{B(B+\sigma _B^2)}\Bigg ]\Bigg )}\nonumber \\ \end{aligned}$$

(28)

Table 9 Best cut on DNN response and corresponding signal and background yields for the five signal benchmark points. Each row is divided into two subrows that contain the information of the SL (upper row) and NoL (lower row) channels respectively. Last two columns show the signal significance values at $\mathcal{L}\,=\,3000\,\mathrm{fb^{-1}}$ with and without a systematic uncertainty $(\theta )$ of 0$\%$ and 5$\%$, respectively

Table 9 shows the best possible cut on the p-DNN responses and the corresponding significance values for SL and NoL analysis channels. Comparing Table 6 and Table 9, one concludes that the analysis using DNN markedly improves the signal significance with respect to the cut-based analysis. For instance, the signal significance that folds in $5\%$ systematics is enhanced by a factor $\simeq$ 3.5–6.5 upon going from BP1 to BP5. To comment on the observability of the setup, the DNN predicts $> 5\sigma$ discovery potential for BP1 to BP4 even after incorporating 5$\%$ systematics. And this is despite the conservative value chosen for the $p p \rightarrow S_R$ production cross section. The cross section can increase upon incorporating NLO corrections and that entails an enhanced observability of the scenario.

We make a passing remark prior to closing this section. The computation of the BZ amplitudes that stem from colored scalars and the collider implications of this setup will remain largely unaltered even if the reported discrepancy in $M_W$ is no longer corroborated by future experiments. In such a case, maintaining $M_{S^+}-M_{S_I}$ and $M_{H^+}-M_H$ to appropriate non-zero values will no longer be necessary for this specific scalar sector, something we have adhered to in this study. For instance, choosing $M_{S^+} = M_{S_I}$ = 800 GeV and $M_{H^+} = M_H$ = 150 GeV would not change the collider analysis in any fashion since the signal we have analysed here does not involve charged scalars. And the $g-2$ amplitudes induced by the color-octet would increase only slightly given the small change in $M_{S^+}$. In all, the utility of the present study as an explanation of the observed $\Delta a_\mu$ and a robust investigation of a color-octet isodoublet at the LHC would still remain intact.

6 Summary and conclusions

The recently reported discrepancy between the measured value of $M_W$ and its SM prediction has stirred up fresh hopes of having observed BSM phenomena. At the same time, the lingering excess in the muon anomalous magnetic moment of the muon has also opened door to model building using BSM physics. In thus study, we have proposed a solution to the twin anomalies in the framework comprising both color-singlet as well as color-octet scalars. More precisely, the well-known Type-X 2HDM was augmented with the color octet isodoublet. Particular emphasis has been laid on the role of the colored scalars in this context. That is, a virtual contribution of the colored scalars to the oblique parameters aids to uplift the W-mass to the observed value. At the same time, two-loop Barr-Zee contributions induced by the colored scalars extend the parameter region compatible with muon $g-2$ with respect to what is seen for the pure Type-X 2HDM.

Table 10 Various Yukawa scale factors for the lepton-specific case

We have proposed the $p p \rightarrow S_R \rightarrow S_I A \rightarrow b \overline{b} \tau ^+ \tau ^-$ signal in this work to look for the various scalars involved, both colorless as well as colored. The final ensuing $b\overline{b}\tau \tau$ final state is attractive from the perspective of collider experiments. This signal has been analysed at the 14 TeV LHC using both cut-based as well as multivariate techniques, in particular, deep neural networks. We have found that the observability of the framework appreciably improves upon incorporating DNN. One must also note that the effect of systematics is also quite high in the statistical significances due to high amount of background contamination. Several sources of systematics are not taken care of, such as: jet to $\tau _h$ fake, lepton to jet fake, pdf error, several normalised and shape based scale factors templates etc. By proper implementation of all the experimental details, such signal topologies have the potential to unravel the presence of both colorless as well as color octer scalars at the HL-LHC.

Appendix

1.1 A. Yukawa scale factors

See Table 10.

1.2 B. Functions in the two-loop BZ amplitudes

$$\begin{aligned} \mathcal {F}^{(2)} (z)= & {} \frac{1}{2} \int _{0}^{1} dx \frac{x(1-x)}{z-x(1-x)} ~\textrm{ln} \left( \frac{z}{x(1-x)}\right) , \nonumber \\ \end{aligned}$$

(29a)

$$\begin{aligned} \mathcal {G}(z^a,z^b,x)= & {} \frac{\textrm{ln} \left( \frac{z^a x + z^b (1-x)}{x(1-x)}\right) }{x(1-x) - z^a x - z^b (1-x)}. \end{aligned}$$

(29b)