1 Introduction

Astronomical observation suggests that our universe is expanding and could be described by the de Sitter solution [1, 2] of the Einstein equations with a positive cosmological constant [3]. The term dark energy is normally associated with this cosmological constant, namely the energy contained in the space that is responsible for the expansion of our universe. To have a complete picture of dark energy is among the big mysteries in physics nowadays [4].

On the other hand, recent years can be considered as a golden era for black hole physics. The first image of black hole by Event Horizon Telescope collaboration [5] has revived the enthusiasm among black hole theorists and astronomers. The astronomical observation on the image of black hole confirms that black holes are really part of our universe, not just some mathematical objects that only exist in a theory of gravity. Realizing the relevance of the de Sitter solution in explaining our universe’s expansion and the fact that black holes do really exist out there lead us to the understanding that studies on the aspects of de Sitter black holes are important.

Unlike the case of asymptotically flat black holes, the spacetime of de Sitter black holes can contain more than two positive valued horizon radii. These are the inner and outer black hole horizons, and also the cosmological horizon. Moreover one can propose that each of these horizons associates to an entropy [6,7,8] that takes the form of a quarter horizon’s area. Consequently, the thermodynamic processes in the de Sitter black hole spacetime would be more complicated compared to the asymptotically flat case or even probably to the asymptotically anti-de Sitter counterpart [9]. For example, one can write down a distinguished first law of thermodynamics for each horizons in the spacetime and show that they can be related to each other [8]. A quite similar spirit can be found in [7], where there exist several first laws of thermodynamics including the one that corresponds to the inner horizon of the black hole. Moreover, the authors of [7] show that a single Gibbs free energy-like thermodynamic potential can capture the whole thermodynamics in the system. Some general approaches to compute the conserved charges that are related to the symmetries of horizons in de Sitter space can be found in literature [10, 11].

The proposal of Kerr/CFT correspondence conjectures that some physics related to rotating and charged black holes can be holographically understood by using some two dimensional conformal field theory (CFT\(_2\)) approaches. This includes the entropy of black hole and the scattering process near the horizon. The Kerr/CFT conjecture has been discussed in many cases and in several theories of gravity. In particular for the Einstein–Maxwell theory with cosmological constant, the Kerr/CFT correspondence has been examined in previous works [12,13,14,15]. In the discussions of Kerr/CFT correspondence in non-extremal case, one can establish the hidden conformal symmetry that associates to the test scalar wave equation in some limits [16]. It can be shown that there exists a local conformal invariance in the solution space of the wave equation which allows us to establish a CFT\(_2\) description on some aspects of the black hole. Explicitly, the CFT\(_2\) calculation can recover the results for the entropy counting and scattering process of the scalar fields. In early works of hidden conformal symmetry of Kerr/CFT correspondence, one assumes the invariance of central charge from the extremal state. Subsequently, some methods to compute the central charge that can apply to the non-extremal case are presented [17, 18]. Moreover, the author of [10] has presented a way to understand the entropy of de Sitter spacetime by using the Cardy formula, i.e. the formula that is also used in the standard Kerr/CFT approach to reproduce the Bekensteing–Hawking formula for black hole entropy [19, 20].

Then one can ask a question, what is the role of the cosmological horizon in the Kerr/CFT correspondence? Can we establish the hidden conformal symmetry that corresponds to it and perform a holographic calculation to reproduce its entropy? Note that for an observer in the visible region \(r_b \le r \le r_c\), which could be relevant for us, it is understood that the total accessible information is \(S_b+S_c\) where \(S_b\) and \(S_c\) are the entropy for black hole and cosmological horizon, respectively. Due to the similarities between the properties of black hole and cosmological horizons, one can guess that the cosmological horizon should possess some conformal invariance as well. It is one of our goals in this paper, namely to show the hidden conformal symmetry in the fashion of [16] that is related to the cosmological horizon, and in turn to use it in establishing a Kerr/CFT correspondence calculation to reproduce the entropy. This paper can also be viewed as an extension of the Kerr–de Sitter/CFT holography constructed in [12] where the thermodynamics aspects of the cosmological horizon are incorporated. Despite most of the calculations in this paper appear straightforward and closely follow those that are already exist in literature for the black hole horizon [6, 12, 13], to the best of our knowledge the analysis presented here is the first work that discusses the hidden conformal symmetry in the near region of cosmological horizon.

The organization of this paper is as follows. In the next section we provide a short review on Kerr–de Sitter spacetime. The hidden conformal symmetry is constructed in Sect. 3 by studying the radial part of the scalar wave with some constraints. The microscopic entropy calculation is performed in Sect. 4, whereas the supporting holographic scattering discussion is worked out in Sect. 5. Finally, we give some conclusions. In this paper we consider the natural units \(G = {\hbar } = k_B = c = 1\).

2 Kerr–de Sitter spacetime

The Kerr–de Sitter spacetimes are axially symmetric stationary type D solutions of the Einstein–Maxwell theory with a positive cosmological constant. Plebanski in [21] introduced a class of solutions containing the Kerr–de Sitter spacetimes, and later was generalized to a larger class of solutions with the acceleration parameter [22]. In a compact form, the line element Kerr–de Sitter solution can be written as [3, 23]

$$\begin{aligned} \mathrm{{d}}s^2= & {} - \frac{{\varDelta _r }}{{\rho ^2 }}\left( {\mathrm{{d}}t - \frac{\Sigma }{\Xi }\mathrm{{d}}\phi } \right) ^2 + \rho ^2 \left( {\frac{{\mathrm{{d}}r^2 }}{{\varDelta _r }} + \frac{{\mathrm{{d}}{\theta }^2 }}{{\varDelta _{\theta } }}} \right) \nonumber \\&+ \frac{{\varDelta _{\theta } \sin ^2\theta }}{{\rho ^2 }}\left( {a\mathrm{{d}}t - \frac{{\left( {r^2 + a^2 } \right) }}{\Xi }\mathrm{{d}}\phi } \right) ^2, \end{aligned}$$
(1)

where \(\rho ^2 = r^2 + a^2 \cos ^2\theta \), \(\Xi = 1 + a^2 l^{-2}\), \(\varDelta _{\theta } = 1 + a^2 l^{-2} \cos ^2\theta \), and

$$\begin{aligned} \varDelta _r = \left( r^2 +a^2\right) \left( 1-\frac{r^2}{l^2}\right) - 2Mr. \end{aligned}$$
(2)

The metric (1) solves the Einstein equations of motion with cosmological constant \(\varLambda = 3 l^{-2}\), i.e.

$$\begin{aligned} R_{\mu \nu } - \frac{1}{2}g_{\mu \nu } R + \varLambda g_{\mu \nu } = 0. \end{aligned}$$
(3)

Note that the presence of \(\Xi ^{-1}\) scale factor in \(g_{\phi \phi }\) component of the tensor metric (1) is to maintain the \(2\pi \) periodicity of \(\phi \) coordinate. In the equations above, m and a stand for the mass and rotational parameter, respectively.

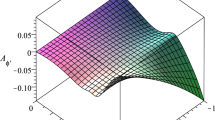
The horizons in Kerr–de Sitter spacetime are the roots of \(\varDelta _r =0\), where we can get three positive valued roots provided that the inequality

$$\begin{aligned}&\left\{ {\left( {l^2 - a^2 } \right) ^2 - 12l^2 a^2 }\right\} ^3 > \left\{ \left( {l^2 - a^2 } \right) ^3 \right. \nonumber \\&\quad \left. + 36l^2 \left( {l^2 - a^2 } \right) a^2 - 54m^2 l^2 \right\} ^2 \end{aligned}$$
(4)

is satisfied [8]. It is widely known that the coincidence of inner and outer black hole horizons is the extremal state of black hole. It is also possible for the outer black hole and cosmological horizons to coincide which is considered as the other type of extremality. To illustrate these extremalities, we provide the plots in Fig. 1 where we have set \(l=1\).

There are several approaches in discussing thermodynamics in Kerr–de Sitter spacetime. In this paper, we adopt the work by Sekiwa [8] which was inspired by the thermodynamics discussions by Teitelboim et al. [24, 25]. We define the physical parameters which associate to the black hole horizon and cosmological one separately. In defining the physical parameters that associate to the black hole horizon, namely

$$\begin{aligned} M_b =\frac{M}{{\Xi ^2 }},~~J_b = aM_b,~~\varLambda _b = \varLambda , \end{aligned}$$
(5)

the cosmological horizon is considered just as a boundary. On the other hand, to have the physical parameters

$$\begin{aligned} M_c =-\frac{M}{{\Xi ^2 }},~~J_c = aM_c = -a M_b,~~\varLambda _b = -\varLambda \end{aligned}$$
(6)

that are related to the cosmological horizon, then the black hole horizon is considered as just a boundary.

Fig. 1
figure 1

Plots for \(r_c=r_h\) and \(r_i = r_h\) in the case of \(l=1\). The solid line represents the extremal state of black hole, whereas the dashed one describes the extremal condition for the cosmological horizon

Full size image

The area of each horizons are given by

$$\begin{aligned} A_b =\frac{{4\pi \left( {r_b^2 + a^2 } \right) }}{\Xi },~~A_c = \frac{{4\pi \left( {r_c^2 + a^2 } \right) }}{\Xi }, \end{aligned}$$
(7)

where the corresponding entropy obey the quarter of area form, i.e.

$$\begin{aligned} S_b = \frac{A_b}{4},~~S_c = \frac{A_c}{4}. \end{aligned}$$
(8)

The Hawking temperature of each horizon can be obtained by imposing the Euclidean regularity that gives us

$$\begin{aligned} T_b = - \frac{{3r_b^4 + \left( {a^2 - l^2 } \right) r_b^2 + a^2 l^2 }}{{4\pi l^2 r_b \left( {r_b^2 + a^2 } \right) }}, \end{aligned}$$
(9)

and

$$\begin{aligned} T_c = \frac{{3r_c^4 + \left( {a^2 - l^2 } \right) r_c^2 + a^2 l^2 }}{{4\pi l^2 r_c \left( {r_c^2 + a^2 } \right) }}, \end{aligned}$$
(10)

whereas the relevant angular velocity related to each horizon are

$$\begin{aligned} \Omega _b = \frac{{a\Xi }}{{r_b^2 + a^2 }} - \frac{{a }}{{l^2 }},~~\Omega _c = \frac{{a\Xi }}{{r_c^2 + a^2 }} - \frac{{a }}{{l^2 }}. \end{aligned}$$
(11)

Furthermore, the total mass inside the horizons are given by

$$\begin{aligned} M_b^2 = \left( {\frac{\pi }{{S_b }} - \frac{1}{{l^2 }}} \right) J_b^2 + \frac{{S_b }}{{4\pi }}\left( {1 - \frac{{S_b }}{{\pi l^2 }}} \right) ^2 \end{aligned}$$
(12)

for the black hole horizon, and

$$\begin{aligned} M_c^2 =\left( {\frac{\pi }{{S_c }} - \frac{1}{{l^2 }}} \right) J_c^2 + \frac{{S_c }}{{4\pi }}\left( {1 - \frac{{S_c }}{{\pi l^2 }}} \right) ^2. \end{aligned}$$
(13)

Finally, from the last two equations, one can derive the first law of thermodynamics associated to each horizons as follows

$$\begin{aligned} \delta M_b = T_b \delta S_b + \Omega _b \delta J_b + \Theta _b \delta \varLambda _b, \end{aligned}$$
(14)

and

$$\begin{aligned} \delta M_c =T_c \delta S_c + \Omega _c \delta J_c + \Theta _c \delta \varLambda _c. \end{aligned}$$
(15)

The last term in both Eqs. (14) and (15) represent the change of vacuum energy, where

$$\begin{aligned} \Theta _b= - \frac{{a^2 l^2 m + r_b \left( {r_b^2 + a^2 } \right) \left( {l^2 + a^2 } \right) }}{{6l^2 \Xi ^2 }}, \end{aligned}$$
(16)

and

$$\begin{aligned} \Theta _c = - \frac{{a^2 l^2 m + r_c \left( {r_c^2 + a^2 } \right) \left( {l^2 + a^2 } \right) }}{{6l^2 \Xi ^2 }}, \end{aligned}$$
(17)

are the generalized volumes. Indeed, the last terms of Eqs. (14) and (15) can exist due to the consideration that cosmological constant is a dynamical parameter. However, it would contradict the view that it should be a constant in the Einstein equations. Otherwise, the Kerr–de Sitter spacetime metric would not take the form as written in Eq. (1). However, some works consider the semiclassical view where cosmological constant may slightly fluctuate [26] and it yields the change of total energy covered by a horizon as expressed in both Eqs. (14) and (15). Having this perspective in mind, the first laws of thermodynamics (14) and (15) can be accepted.

3 Hidden conformal symmetry

The hidden conformal symmetry that is related to the Kerr/CFT correspondence is revealed by exploring the near region and low frequency limits of the massless scalar field in spacetime. The wave equation \(\nabla _\mu \nabla ^\mu \Psi = 0\) in Kerr–de Sitter background can be expressed as

$$\begin{aligned}&\partial _r \left( {\varDelta _r \partial _r \Phi } \right) + \left( {\omega \left( {r^2 + a^2 } \right) - am\Xi } \right) ^2 \frac{\Phi }{{\varDelta _r }} \nonumber \\&\quad = \left( {\frac{{\left( {m\Xi } \right) ^2 }}{{\sin ^2 \theta }} + \left( {a\omega \sin \theta } \right) ^2 - 2m\omega a\Xi } \right) \frac{\Phi }{{\varDelta _\theta }}\nonumber \\&\qquad - \frac{{\partial _\theta \left( {\varDelta _\theta \sin \theta \partial _\theta \Phi } \right) }}{{\sin \theta }}, \end{aligned}$$
(18)

where \(\Psi \left( t,r,\theta ,\phi \right) = e^{-i\omega t + i m \phi } \Phi \left( r,\theta \right) \) and \(\Phi = R\left( r\right) \Theta \left( \theta \right) \). It turns out that Eq. (18) is separable and can be split into two equations, namely the radial equation

$$\begin{aligned}&\frac{\mathrm{d}}{{\mathrm{d}r}}\left( {\varDelta _r \frac{{\mathrm{d}R\left( r \right) }}{{\mathrm{d}r}}} \right) + \left\{ {\frac{{\left( {\omega \left( {r^2 + a^2 } \right) - am\Xi } \right) ^2 }}{{\varDelta _r }} } \right\} R\left( r \right) \nonumber \\&\quad = \lambda R \left( r\right) , \end{aligned}$$
(19)

and the angular one

$$\begin{aligned}&\frac{1}{{\sin \theta }}\frac{\mathrm{d}}{{\mathrm{d}\theta }}\left( {\varDelta _\theta \sin \theta \frac{{\mathrm{d}\Theta \left( \theta \right) }}{{\mathrm{d}\theta }}} \right) \nonumber \\&\quad - {\left( {\frac{{\left( {m\Xi } \right) ^2 }}{{\sin ^2 \theta }} + \left( {a\omega \sin \theta } \right) ^2 - 2m\omega a\Xi } \right) }\frac{\Theta \left( \theta \right) }{{\varDelta _\theta }} = -\lambda \Theta \left( \theta \right) .\nonumber \\ \end{aligned}$$
(20)

In the equations above, \(\lambda \) is the separation constant.

The proposal of hidden conformal symmetry [16] is based on the fact that the near region and low frequencies limit of radial equation (19) can be rewritten in terms of squared Casimir operator of \(SL\left( 2,R\right) \) symmetry group. Originally, the construction of low energy and near region limits of the radial part of an equation for a massless test scalar requires the expression of \(\varDelta _r\) in the second term of l.h.s. of Eq. (19) to be expressible as

$$\begin{aligned} \varDelta _r =\left( r-r_+\right) \left( r-r_-\right) , \end{aligned}$$
(21)

where \(r_+\) and \(r_-\) are the outer and inner horizons in the spacetime, respectively [16, 19]. However, the \(\varDelta _r\) function that appears in Eq. (19) is quartic in r instead of quadratic, and it requires a delicate treatment of the \(\varDelta _r\) function in order to reveal the hidden conformal symmetry from Eq. (19). The quartic property of \(\varDelta _r\) in Eq. (19) explains the existence of more than two horizons in the Kerr–de Sitter spacetime. A similar situation can also be found in the case of accelerating black hole [27], where the acceleration parameter contributes to some extra horizons in addition to the well known inner and outer ones in the Kerr black hole geometry.

To show the hidden conformal symmetry for Kerr–de Sitter black hole, an approximation for the \(\varDelta _r\) function in (19) is required so it has a quadratic form and can be factorized into the form \(\left[ \left( r-r_k\right) \left( r-r_k^*\right) \right] \) up to some constants [12, 13]. Here we use the subscript “k” to represent both horizons of our concern, i.e. \(k=b\) for black hole horizon and \(k=c\) for cosmological oneFootnote 1. The trick is a Taylor expansion for \(\varDelta _r\) near the horizon radius \(r_k\) up to the second order of \(\left( r-r_k\right) \), i.e.

$$\begin{aligned} \varDelta _r \simeq \left. {\varDelta _r } \right| _{r_k } + \left. {\frac{{\mathrm{{d}}\varDelta _r }}{{\mathrm{{d}}r}}} \right| _{r_k } \left( {r - r_k } \right) + \left. {\frac{1}{2}\frac{{\mathrm{{d}}^2 \varDelta _r }}{{\mathrm{{d}}r^2 }}} \right| _{r_k } \left( {r - r_k } \right) ^2,\nonumber \\ \end{aligned}$$
(22)

where the first term in r.h.s. of the above equation is obviously vanished. For the Kerr–de Sitter case, one can find an approximation for the \(\varDelta _r\) function as

$$\begin{aligned} \varDelta _r\simeq K_{k}\left( r-r_k\right) \left( r-r_k^*\right) , \end{aligned}$$
(23)

where

$$\begin{aligned} r_k^* = \frac{{3r_k^4 - a^2 l^2 }}{{r_k \left( {6r_k^2 + a^2 - l^2 } \right) }}, \end{aligned}$$
(24)

and \(K_k= -l^{-2}\left( {6r_k^2 + a^2 - l^2 } \right) \). Note that in obtaining (23), the second order in the Taylor expansion of \(\varDelta _r\) in Eq. (22) is needed and we have used the relation

$$\begin{aligned} M = \frac{\left( r_k^2+a^2\right) \left( l^2-r_k^2\right) }{2l^2 r_k}, \end{aligned}$$
(25)

that comes from \(\varDelta _r \left( r_k\right) =0\). Taking the \(l \rightarrow \infty \) limit for the metric (1) gives us the Kerr spacetime, and this limit yields \(r_k^*\) to be the inner horizon of the Kerr black hole.

Now let us study the hidden conformal symmetry associated to the massless scalar fields near horizon \(r_k\). Studies on scalar fields in de Sitter spacetime have been performed decades ago, for example those related to the field quantization [28, 29]. The scalar field under consideration should be well defined in the visible region \(r_h< r < r_c\) as information beyond the horizons cannot be accessed by an observer in this visible region. To reveal the hidden conformal symmetry in the corresponding radial part of Klein–Gordon equation for the test massless scalar field, one needs to impose the near region \(r\omega \ll 1\) and low frequency \(a\omega \ll 1\) limits [16, 19] for the field. Particularly for the Kerr–de Sitter spacetime, we also consider the near-horizon region constraint \(r_k \omega \ll 1\). Obviously, the near-horizon region condition for black hole horizon differs from that of the cosmological one. This implies that these two near regions are distinguished. If finally we can show that there exist a hidden conformal symmetry near the cosmological horizon, then the visible region \(r_h< r < r_c\) consists of two distinguished hidden conformal symmetries that associate to each boundary in this region.

The considerations above yields a simplified version of radial equation (19), namely

$$\begin{aligned}&\frac{\mathrm{{d}}}{{\mathrm{{d}}r}}\left\{ {\left( {r - r_{k} } \right) \left( {r - r_{k}^* } \right) \frac{{\mathrm{{d}}R\left( r \right) }}{{\mathrm{{d}}r}}} \right\} + \frac{{\left( {r_{k} - r_{k}^* } \right) C_1 R\left( r \right) }}{{\left( {r - r_{k} } \right) }}\nonumber \\&\quad + \frac{{\left( {r_{k} - r_{k}^* } \right) C_2 R\left( r \right) }}{{\left( {r - r_{k}^* } \right) }} = C_3 R\left( r \right) , \end{aligned}$$
(26)

where

$$\begin{aligned} C_1= & {} \frac{{\left( {am\Xi - \omega \left( {r_{k}^2 + a^2 } \right) } \right) ^2 }}{{K_{k}^2 \left( {r_{k} - r_{k}^* } \right) ^2 }}, \end{aligned}$$
(27)
$$\begin{aligned} C_2= & {} - \frac{{\left( {am\Xi - \omega \left( {r_{k}^{*2} + a^2 } \right) } \right) ^2 }}{{K_{k}^2 \left( {r_{k} - r_{k}^* } \right) ^2 }}, \end{aligned}$$
(28)

and

$$\begin{aligned} C_3 = \frac{\lambda }{{K_{k} }}. \end{aligned}$$
(29)

The solution to Eq. (26) can be expressed in term of the hypergeometric function

$$\begin{aligned} R\left( \zeta _k \right) = \left( \zeta _k\right) ^\alpha \left( {1 - \zeta _k } \right) ^\beta F\left( {c_1 ,c_2 ,c_3 ;\zeta _k } \right) \end{aligned}$$
(30)

where \(\zeta _k =\left( r-r_k^*\right) ^{-1} \left( r-r_k\right) \), \(i \alpha = \sqrt{C_1}\), \(2\beta = 1-\sqrt{1-4 C_3}\), \(c_3 = 1+2\alpha \), \(c_1 = \alpha + \beta - \sqrt{C_2}\), and \(c_2 = \alpha + \beta + \sqrt{C_2}\).

To show the hidden conformal symmetry that associates to the horizons in Kerr–de Sitter spacetime, let us first define the conformal coordinate \(\left\{ \omega _k^+,\omega _k^-,\omega _k^0\right\} \) whose relation to the Boyer–Lindquist type of coordinate that appear in the radial wave equation (19), i.e. \(\left( t,r,\phi \right) \), is given by

$$\begin{aligned} \omega _k^ += & {} \sqrt{\frac{{r - r_k }}{{r - r_k^* }}} \exp \left( {2\pi T_R^k \phi + 2n_R^k t} \right) , \end{aligned}$$
(31)
$$\begin{aligned} \omega _k^ += & {} \sqrt{\frac{{r - r_k }}{{r - r_k^* }}} \exp \left( {2\pi T_L^k \phi + 2n_L^k t} \right) , \end{aligned}$$
(32)
$$\begin{aligned} \omega _k^0= & {} \sqrt{\frac{{r_k - r_k^* }}{{r - r_k^* }}} \exp \left( {\pi \left( {T_R^k + T_L^k } \right) \phi + \left( {n_R^k + n_L^k } \right) t} \right) .\nonumber \\ \end{aligned}$$
(33)

Subsequently, we also define the operators

$$\begin{aligned} H_{k, + }= & {} i\partial _{k, + }, \end{aligned}$$
(34)
$$\begin{aligned} H_{k,0}= & {} i\left( {\omega _k^ + \partial _{k, + } + \frac{1}{2}\omega _k^0 \partial _{k,0} } \right) , \end{aligned}$$
(35)
$$\begin{aligned} H_{k, -}= & {} i\left( {\left( {\omega _k^ + } \right) ^2 \partial _{k, + } + \omega _k^ + \omega _k^0 \partial _{k,0} - \left( {\omega _k^0 } \right) ^2 \partial _{k, - } } \right) , \end{aligned}$$
(36)

and

$$\begin{aligned} {\bar{H}}_{k, +}= & {} i\partial _{k, - }, \end{aligned}$$
(37)
$$\begin{aligned} {\bar{H}}_{k,0}= & {} i\left( {\omega _k^ - \partial _{k, - } + \frac{1}{2}\omega _k^0 \partial _{k,0} } \right) , \end{aligned}$$
(38)
$$\begin{aligned} {\bar{H}}_{k, - }= & {} i\left( {\left( {\omega _k^ - } \right) ^2 \partial _{k, - } + \omega _k^ - \omega _k^0 \partial _{k,0} - \left( {\omega _k^0 } \right) ^2 \partial _{k, + } } \right) . \end{aligned}$$
(39)

In the equations above, we have used the notations

$$\begin{aligned} \partial _{k, + } = \frac{\partial }{{\partial \omega _k^ + }},~~\partial _{k, - } = \frac{\partial }{{\partial \omega _k^ - }},~~\partial _{k,0} = \frac{\partial }{{\partial \omega _k^0 }}. \end{aligned}$$
(40)

It can be verified that the operators above obey the \(SL\left( 2,R\right) \) Lie algebra that reads

$$\begin{aligned} \left[ {H_{k,0} ,H_{k, \pm } } \right] = \mp iH_{k, \pm },~~ \left[ {H_{k, + } ,H_{k, - } } \right] = 2iH_{k,0}, \end{aligned}$$
(41)

for the set of operators \(\left\{ H_{k,0},H_{k,+},H_{k,-}\right\} \), and

$$\begin{aligned} \left[ {{\bar{H}}_{k,0} ,{\bar{H}}_{k, \pm } } \right] = \mp i{\bar{H}}_{k, \pm },~~\left[ {{\bar{H}}_{k, + } ,{\bar{H}}_{k, - } } \right] = 2i{\bar{H}}_{k,0}, \end{aligned}$$
(42)

for the bar counterparts \(\left\{ {{\bar{H}}}_{k,0},{{\bar{H}}}_{k,+},{{\bar{H}}}_{k,-}\right\} \). Using the operators defined above, we can construct the quadratic Casimirs

$$\begin{aligned} {{\mathcal {H}}}_k^2 = - H_{k,0}^2 + \frac{1}{2}\left( {H_{k, + } H_{k, - } + H_{k, - } H_{k, + } } \right) , \end{aligned}$$
(43)

and

$$\begin{aligned} \bar{{\mathcal {H}}}_k^2 = - {\bar{H}}_{k,0}^2 + \frac{1}{2}\left( {{\bar{H}}_{k, + } {\bar{H}}_{k, - } + {\bar{H}}_{k, - } {\bar{H}}_{k, + } } \right) , \end{aligned}$$
(44)

and turn out to have the same expression in terms of conformal coordinate, namely

$$\begin{aligned} {{\mathcal {H}}}_k^2 = \bar{{\mathcal {H}}}_k^2 = \frac{1}{4}\left( {\left( {\omega _k^0 } \right) ^2 \partial _{k,0}^2 - \omega _k^0 \partial _{k,0} } \right) + \left( {\omega _k^0 } \right) ^2 \partial _{k, + } \partial _{k, - }\nonumber \\ \end{aligned}$$
(45)

Explicitly, in terms of \(\left( t,r,\phi \right) \) coordinates, the squared Casimir operator (45) can be expressed as

$$\begin{aligned} {{\mathcal {H}}}_k^2= & {} \left( {r - r_k } \right) \left( {r - r_k^* } \right) \frac{{\partial ^2 }}{{\partial r^2 }} + \left( {2r - r_k^* - r_k } \right) \frac{\partial }{{\partial r}} \nonumber \\&+ \frac{{\left( {r_k - r_k^* } \right) }}{{r - r_k^* }}\left( {\frac{{n_L^k - n_R^k }}{{4\pi {\Sigma ^k} }}\frac{\partial }{{\partial \phi }} - \frac{{T_L^k - T_R^k }}{{4{\Sigma ^k} }}\frac{\partial }{{\partial t}}} \right) ^2\nonumber \\&- \frac{{\left( {r_k - r_k^* } \right) }}{{r - r_k }}\left( {\frac{{n_L^k + n_R^k }}{{4\pi {\Sigma ^k} }}\frac{\partial }{{\partial \phi }} - \frac{{T_L^k + T_R^k }}{{4{\Sigma ^k} }}\frac{\partial }{{\partial t}}} \right) ^2, \end{aligned}$$
(46)

where \(\Sigma ^k= n^k_L T^k_R - n^k_R T^k_L\). Interestingly, the eigen equation for the Casimirs above,

$$\begin{aligned} {{\mathcal {H}}}_k^2 R\left( r\right) = \bar{{\mathcal {H}}}_k^2 R\left( r\right) = \lambda R\left( r\right) , \end{aligned}$$
(47)

can reproduce the radial equation (26) after matching the incorporated parameters as the followings,

$$\begin{aligned} n_R^k = 0,~~n_L^k = \frac{1}{{2\left( {r_k + r_k^* } \right) }}, \end{aligned}$$
(48)

and

$$\begin{aligned} T_R^k = \frac{{K_k \left( {r_k - r_k^* } \right) }}{{4\pi a\Xi }},~~T_L^k = \frac{{K_k \left( {r_k^2 + {r_k^*}^2 + 2a^2 } \right) }}{{4\pi a\Xi \left( {r_k + r_k^* } \right) }}, \end{aligned}$$
(49)

In this way, we have established the hidden conformal symmetries in the Kerr–de Sitter spacetime that exist in two near regions in the geometry, one is near the black hole and the other is near the cosmological horizon. However, the \(2\pi \) periodicity of \(\phi \) yields the spontaneous breaking of \(SL\left( 2,R\right) _L \times SL\left( 2,R\right) _L\) symmetry associated to the generators \(\left\{ H_{k,0},H_{k,+},H_{k,-},\right\} \) and \(\left\{ {{\bar{H}}}_{k,0},{{\bar{H}}}_{k,+},{{\bar{H}}}_{k,-},\right\} \) into the \(U\left( 1\right) _L \times U\left( 1\right) _R\) symmetry. Nevertheless, the two copies of \(U\left( 1\right) \) symmetries in the theory allow us to interpret \(T_L^k\) and \(T_R^k\) as the left and right temperatures in the dual CFT\(_2\) description. In the next section, the left and right temperatures in (49) will be used in the dual Cardy formula to reproduce the black hole entropy by assuming that the central charge is invariant to that in the extremal case [16, 19].

4 Microscopic entropy

To reproduce the entropy that is related to each horizon, we need the corresponding central charge that comes from some algebra between the appropriate diffeomorphism generators representing the symmetry of spacetime. For extremal black hole geometry, the central charge calculation in the context of Kerr/CFT holography was proposed in [20, 30]. The central charge obtained in these calculations is used in the dual Cardy entropy formula in two dimensional conformal field theory and it can reproduce the extremal entropy of a black hole. In the non-extremal consideration of Kerr/CFT correspondence [20], the central charge for Cardy formula is assumed to be invariant compared to the extremal case.

Interestingly, a more general approach was proposed in [10] where the entropies in a de Sitter black hole geometry were calculated by imposing the near extremal consideration. The author of [10] showed that one can obtain a central charge for each horizon by utilizing the Gibbons–Hawking–York counter term and the near horizon symmetries. This is in contrast to the approaches in [20, 30] where the extremality is required from the beginning. The author of [10] showed how to compute the total entropy that is relevant for an observer at \(r_b \le r \le r_c\) which is the sum of black hole and cosmological horizon entropies.

Nevertheless, here we can still adopt the method to compute the central charge as performed in [20] and for the case of Kerr–(anti) de Sitter has been worked out in [12]. The obtained central charge is assumed to be invariant as we shift from extremal to non-extremal state. In getting the central charge, let us consider the near-horizon geometry that applies to both black hole and cosmological horizons. To proceed, we also need to consider that \(r_k^* < r_k\). Following [12], the appropriate coordinate to study the near-horizon geometry is

$$\begin{aligned} r = \frac{{r_k + r_k^* }}{2} + \varepsilon {\bar{r}}_k {\tilde{r}},~t = {\tilde{t}}\frac{{{\bar{r}}_k }}{\varepsilon },~\phi = {\tilde{\phi }} + \Omega _k {\tilde{t}}\frac{{{\bar{r}}_k }}{\varepsilon }, \end{aligned}$$
(50)

where

$$\begin{aligned} r_k = r_k^* + \mu \varepsilon {\bar{r}}_k, \end{aligned}$$
(51)

and

$$\begin{aligned} {{\bar{r}}_k }^2 = \frac{r_k^2+a^2}{K_k}. \end{aligned}$$
(52)

Taking \(\varepsilon \rightarrow 0\) after performing the coordinate transformation above yields the corresponding near horizon of a near extremal system that can be read as

$$\begin{aligned} \mathrm{d}s^2= & {} \Gamma _k \left( \theta \right) \left\{ - \left( {{\tilde{r}}^2 - \frac{{\mu ^2 }}{4}} \right) \mathrm{d}{\tilde{t}}^2 + \left( {{\tilde{r}}^2 - \frac{{\mu ^2 }}{4}} \right) ^{ - 1} \mathrm{d}{\tilde{r}}^2 \right. \nonumber \\&\left. + \alpha _k \left( \theta \right) \mathrm{d}\theta ^2 \right\} + \gamma _k \left( \theta \right) \left( {\mathrm{d}{\tilde{\phi }} + {\tilde{f}}_k \mathrm{d}{\tilde{t}}^2 } \right) \end{aligned}$$
(53)

where

$$\begin{aligned} \Gamma _k \left( \theta \right)= & {} \frac{{\rho _k^2 {\bar{r}}_k ^2 }}{{r_k^2 + a^2 }}, \end{aligned}$$
(54)
$$\begin{aligned} \alpha _k \left( \theta \right)= & {} \frac{{r_k^2 + a^2 }}{{\varDelta _\theta {\bar{r}}_k ^2 }}, \end{aligned}$$
(55)
$$\begin{aligned} \gamma _k \left( \theta \right)= & {} \frac{{\varDelta _\theta \sin ^2 \theta \left( {r_k^2 + a^2 } \right) ^2 }}{{\rho _k^2 {\bar{r}}_k ^2 }}, \end{aligned}$$
(56)
$$\begin{aligned} {\tilde{f}}_k= & {} \frac{{ar_k^2 \Xi \left( {r_k + r_k^* } \right) }}{{\left( {r_k^2 + a^2 } \right) ^2 }}, \end{aligned}$$
(57)

\(\rho _k^2 = r_k^2 + a^2 \cos ^2 \theta \). The parameter \(\mu \) appearing in the equations above associates to the near extremality state under consideration. Taking \(\mu \rightarrow 0\) yields the discussions turn to the extremal case where \(r_k \rightarrow r_k^*\) in Eq. (51) and the metric (53) reduces to the near horizon extremal geometry [19]. The form of near horizon of near extremal geometry above falls into the general category studied in [31], hence the result for central charge

$$\begin{aligned} c_{L}^k = c_{R}^k = 3{\tilde{f}}_k\int \limits _0^\pi {\sqrt{\Gamma _k \left( \theta \right) \alpha _k \left( \theta \right) \gamma _k \left( \theta \right) } }, \end{aligned}$$
(58)

can apply and it gives

$$\begin{aligned} c_{L}^k = c_{R}^k = \frac{{6a\left( {r_k + r_k^* } \right) }}{{K_k }}. \end{aligned}$$
(59)

Using the result in (59) and temperatures (49), one can employ the Cardy formula to compute the horizon entropy microscopically, i.e.

$$\begin{aligned} S_{k,\mathrm{{Cardy}}} = \frac{{\pi ^2 }}{3}\left( {c_L^k T_L^k + c_R^k T_R^k } \right) . \end{aligned}$$
(60)

This Cardy formula recovers the entropy expressions for both horizons, namely

$$\begin{aligned} S_k = \frac{\pi }{\Xi }\left( {r_k^2 + a^2 } \right) , \end{aligned}$$
(61)

and this is in agreement with Eq. (8).

Then the corresponding conjugate charge can be determined from the first laws of thermodynamics (14) and (15), i.e.

$$\begin{aligned} \delta S_k = \frac{{\delta M_k - \Omega _k \delta J_k -\Theta _k \delta \varLambda _k}}{{T_H^k }} = \frac{{\delta E_L^k }}{{T_L^k }} + \frac{{\delta E_R^k }}{{T_R^k }}. \end{aligned}$$
(62)

Note that, in the last equation we have inserted a term representing the change of entropy due to the variation of cosmological constant. As we have mentioned previously, it is possible due to some quantum fluctuations [7, 8, 26, 32] and it can contribute to the change of total energy inside of a horizon. A particular example of work that considers cosmological constant as a thermodynamic black hole parameter is the one in [33] where the authors showed that coupling of the gravitational field to a completely antisymmetric third rank tensor field \(A_{\alpha \beta \gamma }\) can lead to Einstein equations with cosmological constant provided that the field equations for \(A_{\alpha \beta \gamma }\) are satisfied. In this consideration the cosmological constant will play a role similar to the mass parameter, namely another “hair” of black hole. Therefore, it is understood why the variation of cosmological constant can appear in the corresponding first law of horizon thermodynamics in a similar footing with the variation of mass parameter. Furthermore, recall that there also exists a perspective that dark energy can be related to the cosmological constant [4]. Therefore, the existence of the \(\Theta _k \delta \varLambda _k\) term in (62) is worth considering.

However, there is a subtlety in regard to the \(\Theta _k \delta \varLambda _k\) term in our first law of thermodynamics. In the case of charged and rotating black holes, there exists the term \(\Phi _b \delta Q\) in the first law of black hole thermodynamics that represents the change of electromagnetic energy in the system. As we define the conjugate charges based on the first law of thermodynamics [12], the term \(\delta Q\) can be associated with the probe’s charge q [19]. However, if we follow the usual prescription in establishing the conjugate charges in the hidden conformal symmetry [12, 13, 19], it seems that the term \(\Theta _k \delta \varLambda _k\) cannot be connected to any of the scalar probe properties as its counterpart.

This issue can be resolved as follows. First we can generalize the change in rotational work

$$\begin{aligned} \Omega _k ' \delta J_k ' = \Omega _k \delta J_k + \Theta _k \delta \varLambda _k, \end{aligned}$$
(63)

where \(\Theta _k \delta \varLambda _k\) can be considered as a correction that comes from the generalized volume in de Sitter geometry. Now, from Eq. (62), one can get the solutions

$$\begin{aligned} \delta E_L^k= & {} \frac{{r_k^2 + \left( {r_k^* } \right) ^2 + 2a^2 }}{{2a\Xi }}\delta M_k, \end{aligned}$$
(64)
$$\begin{aligned} \delta E_R^k= & {} \frac{{r_k^2 + \left( {r_k^* } \right) ^2 + 2a^2 }}{{2a\Xi }}\delta M_k - \delta J_k'. \end{aligned}$$
(65)

Furthermore, identifying

$$\begin{aligned} \delta M_k = \omega ,~~\delta J_k' = m, \end{aligned}$$
(66)

can give us

$$\begin{aligned} \omega _L^k = \frac{{r_k^2 + \left( {r_k^* } \right) ^2 + 2a^2 }}{{2a\Xi }}\omega , \end{aligned}$$
(67)

and

$$\begin{aligned} \omega _R^k = \frac{{r_k^2 + \left( {r_k^* } \right) ^2 + 2a^2 }}{{2a\Xi }}\omega - m. \end{aligned}$$
(68)

Accordingly, this leads to the conjugate charges \({\delta E}_L^k = \omega _L^k\) and \({\delta E}_R^k = \omega _R^k\), and we can see that the correction term \(\Theta _k \delta \varLambda _k\) has been accommodated in the quantum magnetic number m of the scalar probe.

Above we have shown how to compute both black hole and cosmological horizon entropies by using microscopic formulas. For an observer in the visible region, we propose that the relevant total entropy is

$$\begin{aligned} S_{\mathrm{total}} = S_b + S_c, \end{aligned}$$
(69)

where each of entropy in the r.h.s. of last equation can be computed by the results in (60) and (61). This total entropy in a de Sitter black hole has been computed in [10] where the author applies a formalism based on the Gibbons–Hawking–York surface counterterm and the near horizon symmetries [17, 18]. Explicitly, the total entropy of Kerr–de Sitter geometry is given by [10]

$$\begin{aligned} S_{\mathrm{total}} =\frac{A_h + A_c}{4}, \end{aligned}$$
(70)

which is in agreement to the proposal in Eq. (69).

5 Holographic scattering near horizon

To support the holographic entropy calculation in the previous section, let us show here that the scattering near the horizon can be reproduced by using a dual CFT\(_2\) formula as well. This is common in the hidden conformal symmetry of the Kerr/CFT discussions [19], where the starting point is the CFT\(_2\) two-point function

$$\begin{aligned} G\left( {t_+ ,t_- } \right) = \left\langle {{{\mathcal {O}}}^\dag \left( {t_+ ,t_- } \right) {{\mathcal {O}}}\left( {0,0} \right) } \right\rangle . \end{aligned}$$
(71)

In equation above, \({\mathcal {O}}\) is some operators that associate to the perturbation field in the spacetime, whereas \(t_+\) and \(t_-\) are the left and right moving coordinates in two dimensional worldsheet. Recall that in the previous section we discussed the scalar fields that reveal the hidden conformal symmetry at each horizon. The operator \({\mathcal {O}}\) being considered here is related to that scalar field.

Here let us also adopt the subscript “k” from the previous sections to allow the later outcome to apply for both black hole and cosmological horizon considerations. Hence we will have a distinct worldsheet that corresponds to each horizon, where the coordinates now are \(\left\{ t_+^k , t_-^k\right\} \). The conformal symmetry yields the two-point function (71) to have the form

$$\begin{aligned} G_k\left( {t_+^k ,t_-^k } \right)\sim & {} \left( { - 1} \right) ^{h^k_L + h^k_R } \left( {\frac{{\pi T^k_L }}{{\sinh \left( {\pi T^k_L t^k_+ } \right) }}} \right) ^{2h^k_L }\nonumber \\&\times \left( {\frac{{\pi T^k_R }}{{\sinh \left( {\pi T^k_R t^k_+ } \right) }}} \right) ^{2h^k_R }, \end{aligned}$$
(72)

where \(h^k_L\) and \(h^k_R\) are the conformal dimensions of operators \({{\mathcal {O}}}\), whereas \(T^k_L\) and \(T^k_R\) is the left and right temperature, respectively. Using the Fermi’s golden rule, the CFT absorption cross section can be defined as

$$\begin{aligned} \sigma _k\sim & {} \int dt^k_+ dt^k_- e^{ - i\left( {\omega _R^k t_R^k + \omega _L^k t_L^k } \right) } \left( G\left( {t_L^k - i\varepsilon ,t_R^k - i\varepsilon } \right) \right. \nonumber \\&\left. - G\left( {t_L^k + i\varepsilon ,t_R^k + i\varepsilon } \right) \right) . \end{aligned}$$
(73)

In momentum space, the cross section (73) reads

$$\begin{aligned} \sigma _k\sim & {} \left( {T_R^k } \right) ^{2h^k_R - 1} \left( {T_L^k } \right) ^{2h^k_L - 1} \sinh \left( {\frac{{\omega _L^k }}{{2T_L^k }} + \frac{{\omega _R^k }}{{2T_R^k }}} \right) \nonumber \\&\times \left| {\Gamma \left( {h_L + i\frac{{\omega _L^k }}{{2\pi T_L^k }}} \right) } \right| ^2 \left| {\Gamma \left( {h_R + i\frac{{\omega _R^k }}{{2\pi T_R^k }}} \right) } \right| ^2. \end{aligned}$$
(74)

The above result in (74) can be matched by the superradiant scattering formula near the horizons as we shall show in the following.

According to the coordinate transformation (50), the scalar wave function now can be expressed as

$$\begin{aligned} \Psi \left( {t,r,\theta ,\phi } \right) = e^{ - i\left( {\omega - m\Omega _k } \right) \frac{{{\tilde{r}}_k }}{\varepsilon }{\tilde{t}} + im{\tilde{\phi }} } \Phi \left( {r,\theta } \right) \end{aligned}$$
(75)

and we consider the near supperradiant bound where

$$\begin{aligned} \omega - m\Omega _k = {\tilde{\omega }} \frac{\varepsilon }{{{\tilde{r}}_k }} \end{aligned}$$
(76)

for a finite \({\tilde{\omega }}\) which yields the scalar wave can be read as \(\Psi = e^{ - i{\tilde{\omega }} {\tilde{t}} + im{\tilde{\phi }} } \Phi \left( {r,\theta } \right) \). In this near horizon coordinate, the radial equation (26) has the solution

$$\begin{aligned} R_k\left( {{\tilde{\zeta }} } \right) = \zeta ^{{\tilde{\alpha }}_k } \left( {1 - {\tilde{\zeta }} } \right) ^{{\tilde{\beta }}_k } F\left( {{\tilde{c}}_1 ,{\tilde{c}}_2 ,{\tilde{c}}_3 ,{\tilde{\zeta }} } \right) , \end{aligned}$$
(77)

where \({\tilde{\zeta }} = \left( {{\tilde{r}} - \mu /2} \right) \left( {{\tilde{r}} + \mu /2} \right) ^{ - 1} \), \(i {{\tilde{\alpha }}_k} = \sqrt{{\tilde{C}}_1}\), \(2{\tilde{\beta }}_k = 1-\sqrt{1-4 {\tilde{C}}_3}\), \({\tilde{c}}_3 = 1+2{\tilde{\alpha }}_k\), \({\tilde{c}}_1 = {\tilde{\alpha }}_k + {\tilde{\beta }}_k - \sqrt{{\tilde{C}}_2}\), and \({\tilde{c}}_2 = {\tilde{\alpha }}_k + {\tilde{\beta }}_k + \sqrt{{\tilde{C}}_2}\), with

$$\begin{aligned} {{\tilde{C}}}_1= & {} \frac{{\tilde{\omega }}^2}{\mu ^2}, \end{aligned}$$
(78)
$$\begin{aligned} {{\tilde{C}}}_2= & {} -\left( \frac{{\tilde{\omega }}}{\mu } - \frac{2r_k m \Omega _k}{K_k}\right) ^2, \end{aligned}$$
(79)

and

$$\begin{aligned} {{\tilde{C}}}_3 = - \frac{{\tilde{\lambda }}}{K_k}. \end{aligned}$$
(80)

The asymptotic behavior of solution (77) that satisfies the ingoing boundary condition at the horizon can be written as

$$\begin{aligned} R_k\left( {{\tilde{r}}} \right) \sim A_1 {\tilde{r}}^{h^k - 1} + A_2 {\tilde{r}}^{ - h^k}, \end{aligned}$$
(81)

where

$$\begin{aligned} A_1 = \frac{{\Gamma \left( {{\tilde{c}}_3 } \right) \Gamma \left( {2h - 1} \right) }}{{\Gamma \left( {{\tilde{c}}_3 - {\tilde{c}}_1 } \right) \Gamma \left( {{\tilde{c}}_3 - {\tilde{c}}_2 } \right) }}, \end{aligned}$$
(82)

and

$$\begin{aligned} A_2 = \frac{{\Gamma \left( {{\tilde{c}}_3 } \right) \Gamma \left( {1 - 2h} \right) }}{{\Gamma \left( {{\tilde{c}}_1 } \right) \Gamma \left( {{\tilde{c}}_2 } \right) }}, \end{aligned}$$
(83)

whereas the conformal weight \(h^k = h^k_L = h^k_R\) is given by

$$\begin{aligned} h^k = \frac{1}{2}\left( {1 + \sqrt{1 - 4{\tilde{C}}_3 } } \right) . \end{aligned}$$
(84)

Accordingly, the absorption cross-section of the scalar field can be obtained as

$$\begin{aligned} \sigma _{k} \sim \left| {A_1 } \right| ^{ - 2} = \frac{{\sinh \left( {2\pi {\tilde{\alpha }}_k } \right) \left| {\Gamma \left( {{\tilde{c}}_3 - {\tilde{c}}_1 } \right) } \right| ^2 \left| {\Gamma \left( {{\tilde{c}}_3 - {\tilde{c}}_2 } \right) } \right| ^2 }}{{2\pi {\tilde{\alpha }}_k \left| {\Gamma \left( {2h - 1} \right) } \right| ^2 }}\nonumber \\ \end{aligned}$$
(85)

The cross-section (85) matches the one from CFT in Eq. (74) if we identify the followings

$$\begin{aligned} T^k_L= & {} \frac{{K_k }}{{4\pi r_k \Omega _k }}, \end{aligned}$$
(86)
$$\begin{aligned} T^k_L= & {} \frac{{K_k {\bar{r}}_k }}{{4\pi a\Xi }}\mu \varepsilon , \end{aligned}$$
(87)
$$\begin{aligned} \omega ^k_L= & {} m, \end{aligned}$$
(88)

and

$$\begin{aligned} \omega ^k_R = \frac{{{\bar{r}}_k K_k }}{{a\Xi }}\left( {{\tilde{\omega }} - \frac{{\mu r_k m\Omega _k }}{{K_k }}} \right) \varepsilon . \end{aligned}$$
(89)

6 Conclusion

In this paper, we have extended the Kerr–de Sitter/CFT correspondence [12] to include the microscopic calculation for the cosmological horizon entropy. This is novel, despite most calculations are straightforward and following the ones available in literature for black hole horizon [12, 15]. To the best of our knowledge this is the first work that considers the hidden conformal symmetry in the near region of cosmological horizon and use the obtained symmetry to argue that one can compute the cosmological horizon entropy using the Kerr/CFT proposal. Our result shows that one can perform some holographic calculation in the fashion of [20] to reproduce the cosmological horizon entropy in the Kerr–de Sitter spacetime and it supports the previous work [10] where the author has shown that the entropy can be computed by using the Cardy formula as well from a different point of view. In this work we propose the total entropy that is relevant for an observer between the two largest horizons in Kerr–de Sitter spacetime is the sum of black hole and cosmological horizon entropies. The conformal symmetry that can be probed by a test scalar field in both near regions can really accessed by the observer.

In this work, we have considered that the cosmological constant that can slightly vary. Similar view in discussing spacetime thermodynamics can be found in literature [7, 8, 26]. Nevertheless, it leads to a delicate treatment in deriving the conjugate charges in Sect. 4. To have a consistent result, we have generalized the change of rotational energy in the corresponding first law of thermodynamics to include a contribution from the product of generalized volume and variation in \(\varLambda \). To the best of our knowledge, there is no previous work in discussing Kerr/CFT for de Sitter background which considers such variation in \(\varLambda \) and to incorporate that in the corresponding first law of thermodynamics.

For the future works, the analysis presented in this paper can be extended to some other cases. First, it is known there exist J and Q pictures in the hidden conformal symmetry for a rotating and charged black hole spacetime [13]. It would be interesting to show that these J and Q pictures can also be found in the case of Kerr–Newman–de Sitter spacetime where the thermodynamics aspects of the cosmological horizon are included in the discussion. Second, it is also interesting to check the hidden conformal symmetry that corresponds to the cosmological horizon in the spacetime solution that belongs to some other gravitational theories beyond Einstein–Maxwell.