1 Introduction

Due to their importance in the discovery of new physical properties, newly designed heterostructures such as quantum wells (QWs) are of great interest for the exploration of correlated electronic states in two-dimensional systems [1]. The advance in both theoretical and experimental tools have make it possible to growth nano-objects with different semiconductor materials and shapes. However, a huge number of theoretical and experimental research have been reported for GaAs and related ternary alloys thin-layered heterostructures [2,3,4,5,6] due to its well-known and spectacular structural, chemical and physical feathers such as a narrow band-gap of about 1.424 eV (at 300 K) and high electron mobility 9000 cm2/(V s) (at 300 K). This makes it a suitable semiconductor for such conventional optoelectronic applications like MESFET transistors, diode lasers, tunneling diodes, and photoelectric and solar cells as well [7,8,9,10]. Unlike, wide band-gap (WBG) semiconductor materials, especially nitride-based semiconductors such as GaN and \({\mathrm{In}}_{x}{\mathrm{Ga}}_{1-x}\mathrm{N}\) (\(x\) is the indium rate, which does not exceed 20% to avoid delocalization at the interfaces) offer interesting and an appropriate feathers [11, 12]. They allow smaller, faster, more reliable power electronic components with higher performance and efficiency than their counterpart’s silicon and GaAs-based devices due to their fascinated characteristics such as wide band-gap, relatively high mobility and high break voltage as well [13,14,15]. These abilities make them very attractive and competitive materials to reduce weight, volume, and life-cycle costs in a wide range of power and Terahertz applications.

In InGaN-based QWs, the transitions energies are in the Terahertz range (1–5 THz) where many applications are envisaged such as detectors, cascade lasers, negative differential resistance diodes (NDRD), plasma wave FETs, and many other sources of this type of radiation [16]. The electronic properties of these low-dimensional systems have been intensively investigated. They have been studied with various forms, shapes, and geometries considering single and multiple QWs heterostructures using different techniques and methods [17,18,19,20,21]. It has been proven that the compositions and applied electrical field on a QW heterostructures are powerful tools to tune electron quantum confinement, its effective mass, spatial dimensions, dielectric constants, and band gaps in such systems. These effects allow us to manipulate and govern the device’s electrical and optical properties for different applications [22, 23]. Furthermore, the electronic transitions between the donor-impurity ground state and the conduction intra-subband transitions in semiconductor QWs are also affected by varying the size, compositions, impurity position, and electric field effects [22, 23].

Recently, Maouhoubi et al. have investigated the effects of pressure, temperature, conduction band non-parabolicity, dielectric screening, and magnetic field on the both diamagnetic susceptibility and ionizing energy of a shallow donor impurity in a GaAs-based quantum disk (QDisk) [24, 25]. Solaimani has reported a theoretical investigation of donor impurity-related diamagnetic susceptibility and binding energy in quantum dots with various geometries and potentials considering the number of wells. He has found that spherical quantum dot (QD) systems are much more tunable than cylindrical ones [28]. Moreover, Iqraoun et al. have theoretically studied the binding energy, the diamagnetic response and the polarizability of a donor impurity in a quantum dot based on hexagonal GaN where they found that the Stark-shift binding energy, polarizability, dipole moment, and diamagnetic susceptibility vary greatly with electric field intensity [29]. Another work related to the same teamwork by EL-Bakkari et al. [29] where they have investigated the conduction band non-parabolicity and polaron influences on the diamagnetic susceptibility, binding energy, and polarizability of a shallow donor impurity located in an AlGaN quantum ring (QR). They have shown that the polarizability increases (decreases) with the applied electric field and it is nearly insensitive to the polaron effect for the strong confinement. Ina addition, by adopting the variational procedure, Morales et al. have examined the effects of both electric field and hydrostatic pressure on the donor-impurity-related polarizability and photoionization cross section in AlGaAs double asymmetric QWs are considering an electric field applied along the growth direction. They have concluded that the donor-impurity binding energy and polarizability in the investigated system can be tuned with respect to the applied external electric field and hydrostatic pressure [30]. Earlier in 2021, we have reported the effects of size, compositions, impurity’s position and temperature on a shallow donor-impurity ionization energy in double QWs system [31]. However, the purpose of this paper is to examine the electron probability, polarizability, diamagnetic susceptibility, and ionization energy of an on-center hydrogenic donor impurity in a modified InGaN- ∩-shaped quantum well (IPQW) under the influences of the electric field, confinement profile, and In-compositions. Our analysis method of choice is the finite element analysis, which is known for its accuracy and ability to incorporate boundary conditions and interface correlations, making it superior to conventional approaches like the Ritz-variational approach. The mesh grid and results were generated and analyzed using Python.

2 Theory and models

In this study, we have considered a Hydrogen-like donor impurity located at the center of ∩-shaped parabolic quantum well (IPQW) made out of GaN/InGaN/GaN heterostructure with a variable finite confinement potential. The barriers have been made of GaN while the well has been made of InGaN. The potential energy experienced by the electrons within the well can be approximated by a parabolic potential [32]. However, in some cases, the conduction band edge in the well can be lower than that in the surrounding material, resulting in an inverted potential profile. In this case, the potential energy well can be better described by an inverted parabolic potential.

The analytical form of the Hamiltonian is expressed in the presence of an electric field applied along the growth direction within the framework of the effective mass approach that describes particle (electron, hole) motion near band extremes (wave vector, K ~ 0) in the presence of slow varying weak perturbations, such as applied electric fields and without electron–phonon interaction. Effective mass theory is a theoretical framework used to describe the behavior of electrons in a solid, in which electrons are treated as having an effective mass that depends on the properties of the solid. This theory simplifies the complex interactions between electrons and the atomic lattice in a solid and allows an easier-to-understand description of electronic behavior and properties, such as conductivity and optical properties. Effective mass is generally derived from the curvature of energy bands in the solid and is generally used to predict a wide range of electronic properties and behaviors. It is given as follows [33]:

$$H=-\left(\frac{{\hbar}^{2}}{2}\overrightarrow{\nabla }\right)\left(\frac{1}{{m}^{*}\left(x\right)}\overrightarrow{\nabla }\right)+{V}_{c}\left(\alpha , z,x\right) -\frac{{e}^{2}}{{\varepsilon }_{r}^{*}\left(x\right)\left|\overrightarrow{r}-{\overrightarrow{r}}_{0}\right|}+e\gamma \left(z-{z}_{0}\right),$$
(1)

where \(\mathrm{\hslash }, {m}^{*}\), and \({\varepsilon }_{r}^{*}\) are, respectively, the Planck constant and the relative electron effective masses and dielectric constants of the semiconductor (i.e., GaN, InGaN). It is important to notice that we assume that \({\varepsilon }_{r}^{*}\) at the interfaces between GaN and InGaN materials is given as the square root of the product of the two dielectric constants of the two materials (\(\sqrt{{\varepsilon }_{b}^{*}\times {\varepsilon }_{w}^{*}}\)). \(\left|\overrightarrow{r}-{\overrightarrow{r}}_{0}\right|=\sqrt{{X}^{2}+{Y}^{2}+{\left(Z-{Z}_{0}\right)}^{2}}\) denotes the electron–impurity distance knowing that the impurity is located in the center of the system (i.e., \(\mathcal{L}=L+\frac{l}{2}\)). The symbols \(L\) and \(l\) are used to denote the thicknesses of the barriers and well, while γ represents the strength of the electric field. To gauge the impact of the electric field on the system under investigation, we employed a dimensionless parameter denoted by F. Specifically, in this study, F denotes the effective electric field strength was calculated as (\(F=\frac{e\gamma {a}^{*}}{{R}^{*}}\)), where \({a}^{*}\) and \({R}^{*}\) are relevant quantities. \({R}^{*}\) is the unit of energy and is known as the effective Rydberg; whereas, \({a}^{*}\) denotes the unit of length and is known as the effective Bohr radius. These quantities are given in the first paragraph of the discussion section.

The \({V}_{c} (\alpha ,z,x)\) is the ∩-shaped confinement parabolic quantum well (IPQW), it is given analytically as follows. It describes a specific mathematical expression that represents the potential energy of a confined system. This potential energy is denoted by \({V}_{c}\), and it is a function of three variables: α (a dimensionless parameter), \(z\) (growth direction), and \(x\) (In-composition within the well region). This function represents an ∩-shaped confinement parabolic quantum well (IPQW), which is a specific type of confinement potential commonly used in quantum mechanics. The mathematical expression for the \({V}_{c} \left(\alpha ,z,x\right)\) function is given analytically, this analytical form of the potential energy function is essential for solving quantum mechanical problems, such as finding the wave functions and energy levels of particles confined within the well and it is given as follows [34]:

$${V}_{c}\left(\alpha , z\right)=\left\{\begin{array}{ll}{V}_{0} & For \left\{\begin{array}{c}z<L\\ z>L+l\end{array}\right.\\ \frac{{V}_{0}}{{\alpha }^{2}}\left(1-\frac{4}{{l}^{2}}\right){\left[z-L-\frac{l}{2}\right]}^{2}& For L\le z\le L+l\\ \infty & Elsewhere\end{array} ,\right.$$
(2)

where \(\alpha \) is a dimensionless parameter that modifies the confinement potential profile (see Fig. 1), \({V}_{0},\) which is given as \({V}_{0}=0.7\Delta {E}_{\mathrm{g}}\) with \(\Delta {E}_{\mathrm{g}}={E}_{\mathrm{g}}^{\mathrm{GaN}}-{E}_{\mathrm{g}}^{\mathrm{InGaN}}\).

Fig. 1
figure 1

Schematic diagram of the conduction band of a single GaN/InGaN/GaN quantum well with an inverted modified potential (∩-shaped) showing the effect of the parameter \(\alpha \)

Full size image

According to the equation provided, \({V}_{0}\) will change as \(\alpha \) varies. Specifically, as \(\alpha \) increases, \({V}_{0}\) will decrease for values of \(z\) between \(L\) and \(L+l\) due to the decreasing term \({V}_{0}/{\alpha }^{2}\) in the equation. The magnitude of this decrease will depend on the term \(\left(1-\frac{4}{{l}^{2}}\right){\left[z-L-\frac{l}{2}\right]}^{2}\), which is a function of \(z\) and the length scale \(l\). For values of \(z\) outside the range of \(L \mathrm{to} L+l, {V}_{0}\) will remain constant at infinity (see Fig. 1).

The energy difference indium content dependence is given as follows (Vegard’s law),

$${E}_{\mathrm{g}}^{\mathrm{InGaN}}=x{E}_{\mathrm{g}}^{\mathrm{InN}}+\left(1-x\right){E}_{\mathrm{g}}^{\mathrm{GaN}}+3.8\left(1-x\right).$$
(3)

Energy band gaps of both GaN and InN semiconductor materials are equal to 3.51 and 0.70 eV, respectively [35].

Similarly, the effective masses and dielectric constants indium content dependence are given as follows [36],

$${\varepsilon }_{w,b}^{*}=\left\{\begin{array}{ll}{\varepsilon }_{\mathrm{GaN}}^{*}+6.4x, & \mathrm{ In the well}\\ {\varepsilon }_{\mathrm{GaN}}^{*}, & \mathrm{ Elsewhere}\end{array}\right.$$
(4)
$${m}_{w,b}^{*}=\left\{\begin{array}{ll}0.1{m}_{\mathrm{InN}}^{*}+0.9{m}_{\mathrm{GaN}}^{*}, & \mathrm{ In the well }\\ {m}_{\mathrm{GaN}}^{*}, & \mathrm{ Elsewhere}\end{array},\right.$$
(5)

where \(w\) \(\mathrm{and}\) \(b\) denote the well and barriers, consequently.

The electron effective mass is given as \({m}_{\mathrm{GaN}}^{*}=0.20{m}_{0}\) and \({m}_{\mathrm{InN}}^{*}=0.11{m}_{0}\) (where \({m}_{0}\) denotes the electron mass in vacuum) and the mean relative dielectric constants of GaN and InN consequently are \(9.8{\varepsilon }_{0}\) and \(10.5{\varepsilon }_{0}\) (where \({\varepsilon }_{0}\) is the permittivity of free space) [31, 32].

The Schrodinger equation has been solved numerically using the finite element method by applying the boundary conditions given below:

$${\left[\underset{n}{\to }.\underset{\nabla }{\to }\left(\frac{\psi }{{m}_{e,b}^{*}}\right)\right]}_{b}={\left[\underset{n}{\to }.\underset{\nabla }{\to }\left(\frac{\psi }{{m}_{e,w}^{*}}\right)\right]}_{w}.$$
(6)

The first and the second derivatives wave functions are given respectively by [38]:

$${\left.\frac{{\partial }^{2}\psi (z)}{{\partial z}^{2}}\right)}_{{z}_{k}}=\frac{{\psi }_{k+1}-2{\psi }_{k}+{\psi }_{k-1}}{{({z}_{k+1}-{z}_{k})}^{2}},$$
(7)
$${\left.\frac{\partial \psi \left(z\right)}{\partial z}\right)}_{{z}_{k}}=\frac{{\psi }_{k+1}-{\psi }_{k}}{{z}_{k+1}-{z}_{k}}.$$
(8)

To solve the one-dimensional Schrödinger equation, we used the finite element method (FEM), which is a powerful tool to solve complex mathematical problems involving partial differential equations. FEM discretizes the problem domain into smaller and simpler parts, allowing the use of matrix algebra to approximate the solution. Compared to other methods, such as variational and perturbative methods, FEM typically provides more accurate solutions for problems involving complex geometries or boundary conditions. Indeed, FEM can handle material nonlinearities and heterogeneities, and can provide high resolution solutions for localized phenomena. Various software packages in Python, including SciPy, NumPy, matplotlib, and Pylab, were utilized to analyze and interpret the results. This study has made the assumption that the focus is solely on the growth direction, specifically the Z-axis. Furthermore, a one-dimensional solution of the Schrodinger equation was utilized to characterize the electron's behavior within the systems. Thus, the mesh grid of \(3N+1\) points is considered for the studied system with \(N=50\) points. Each layer discretized by various discretization step. For the barriers, the step is \({h}_{b}=L/N;\) while for the well’s regions, it is given as \({h}_{w}=l/N\). Therefore, for \(0<k<N\), the mesh’s nodes of single QW are given, respectively, as follows, left barrier is \({z}_{k}=k*{h}_{b}\), in the well region is \({z}_{k}=L+k*{h}_{w}\) and in the right barrier is given as \({z}_{k}=L+l+k*{h}_{b}\).

2.1 Electron presence probability (EPP) within the well region

In this study, we also calculated the probability of the electron inside the well in the absence of the impurity, which had hardly ignored previously. This probability is measured as the partial probability (within the well) divided by the probability of the presence in the whole system. Once the wave function \(\psi (z)\) is obtained, the probability density \({|\psi (z)|}^{2}\) at any position \(z\) within the well can be calculated. The probability density \((P)\) represents the probability of finding the electron at a specific position. It is expressed as follows [39]:

$$P\left(z\right)= {\left|\psi \left(z\right)\right|}^{2}.$$
(9)

The total probability of finding the electron within the quantum well (well region) is obtained by integrating the probability density over the well region:

$${P}_{\mathrm{total}} = {\int }_{0}^{2L+l}{|{\psi }_{1s}(z)|}^{2} \mathrm{d}z\cong {|<{\psi }_{1\mathrm{s}}^{\mathrm{system}}|{\psi }_{1\mathrm{s}}^{\mathrm{system}}>|}^{2},$$
(10)
$${P}_{\mathrm{partial}} = {\int }_{L}^{L+l}{|{\psi }_{1s}(z)|}^{2} \mathrm{d}z\cong {|<{\psi }_{1\mathrm{s}}^{\mathrm{QW}}|{\psi }_{1\mathrm{s}}^{\mathrm{QW}}>|}^{2},$$
(11)
$$\mathrm{EPP}=\frac{{P}_{\mathrm{total}}}{{P}_{\mathrm{partial}}},$$
(12)

where \({\psi }_{1\mathrm{s}}^{\mathrm{QW}}\) and \({\psi }_{1\mathrm{s}}^{\mathrm{system}}\) are, respectively, the ground-state wave functions of the quantum well and the whole system.

2.2 Impurity ground-state binding energy of the system

Considering the correlation between electron and impurity, the ground-state binding energy is given by the difference of the ground-state electron energy without the impurity minus that in the presence of the impurity. It is given analytically by the following expression [40]:

$${E}_{b}={E}_{0}-{E}_{0}^{I},$$
(13)

where \({H}_{0}\) and \({H}_{I}\) represent the electron Hamiltonians without and with the impurity, respectively, while \({\psi }_{1\mathrm{s}}\) denotes the ground-state electron wave function of the system.

2.3 Diamagnetic susceptibility

In electromagnetism, the diamagnetic response is a measure of how much a semiconductor material will become polarized or magnetized under an external applied electric or magnetic field.

Analytically, the diamagnetic susceptibility (\({\chi }_{\mathrm{dia}}\)) of the hydrogenic donor impurity confined in a \(\mathrm{GaN}/{\mathrm{In}}_{x}{\mathrm{Ga}}_{1-x}\mathrm{N}\) IPQW in atomic units, is given by it is given as follows [41]:

$${\chi }_{\mathrm{dia}}=-\frac{{e}^{2}}{6{m}_{w}^{*}\left(x\right){\varepsilon }_{w}^{*2}\left(x\right){c}^{2}}<{r}^{2}>,$$
(14)

where \(<{r}^{2}>=\frac{<{\psi }_{1s}|{z}^{2}|{\psi }_{1s}>}{<{\psi }_{1s}|{\psi }_{1s}>},\) while \({m}_{w}^{*}\) and \({\varepsilon }_{w}^{*}\) are the electron effective mass and dielectric constant in the well region (InGaN), subsequently.

2.4 Polarizability formalism

An atomic or molecular structure that does not have a permanent dipole moment can acquire one under the action of an electric field. The response capability of a material to an electric field (\(\overrightarrow{E}\)), is expressed by the polarization vector \(\overrightarrow{P}\). For a weak external applied electric field, the relationship between the applied electric field and the polarization is linear; it is given analytically as follows:

$$\overrightarrow{P}=\Omega \overrightarrow{E},$$
(15)

where \(\Omega \) being the polarizability of a semiconductor material. Therefore, the obtained wave function can provide the impurity polarization in the investigated system (IPQW), which is given by the following expression [30]:

$$\Omega =-\frac{\mathrm{e}}{F}\left[<{\psi }_{1s}\left|z\right|{\psi }_{1s}{>}_{F\ne 0}-<{\psi }_{1s}\left|z\right|{\psi }_{1s}{>}_{F=0}\right].$$
(16)

3 Results and discussion

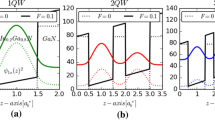
In this study, to simplify our calculations, we adopted the atomic effective units. The effective Rydberg is considered as a unit of energy while the effective Bohr radius is considered as a unit of length. The effective Bohr radius and Rydberg are given, respectively, by \({a}_{b}^{*}\left(=\frac{4\pi {\varepsilon }_{b}^{*}{\mathrm{\hslash }}^{2}}{{m}_{b}^{*}{e}^{2}}\approx 2.69\mathrm{ nm}\right)\), \({R}_{b}^{*}\left(=\frac{{m}_{b}^{*}{e}^{3}}{2(4\pi {\varepsilon }_{b}^{*}{\mathrm{\hslash })}^{2}}\approx 27.60\mathrm{ meV}\right)\) for \(L=1, l=2\), and \(x=0.1 (10\%)\). In the whole study, \(L\) and \(l\) denote the barriers and well widths, respectively; while \(x\) is the indium concentration within the well region (\({\mathrm{In}}_{x}{\mathrm{Ga}}_{1-x}N\)). Before commencing the discussion of our findings, it is important to notice that the quantum confinement potential profile depends on the dimensionless parameter \(\alpha \) (see Eq. 2). As it can be seen from Fig. 2a, for \(\alpha =10,\) the confinement potential is squared (black solid line); however, with \(\alpha =1,\) it is tuned to an inverted parabolic QW (red dotted line), which is quite similar to a double semi-triangular QW system.

Fig. 2
figure 2

The variation of the confinement potential and the ground-state electron probability density versus the z-axis without (a) and with (b) applied electric field (F) considering various confinement profiles in \(\mathrm{GaN}/{\mathrm{In}}_{0.2}{\mathrm{Ga}}_{0.8}\mathrm{N}/\mathrm{GaN}\) ∩-shaped QW

Full size image

Figure 2 depicts the schematic band structure and the lowest-state electron probability density with respect to the growth direction without and with applied electric field considering four different confinement profiles in \(\mathrm{GaN}/{\mathrm{In}}_{0.2}{\mathrm{Ga}}_{0.8}\mathrm{N}/\mathrm{GaN}\) ∩-shaped QW (IPQW) without impurity. It is evident from panel (a) that in the absence of and applied electric field and for \(\alpha =10\), both the confinement profile as well as the electron probability densities are symmetric in the well center. Moreover, regardless the electric field, the reduction of the parameter \(\alpha \) increases the parabolicity of the inverted well and then the electron becomes more localized near the well edges due to the improvement in the spatial confinement in the well center. Although, with an applied electric field different to zero (\(F\ne 0\)), both the confinement profile and the electron probability densities have changed. Regardless of the parameter \(\alpha \), it is clearly from panel (b) that the QW has been distorted and the ground-state probability density of electrons has become more localized in the left side of the well, which is expected. Because the electric field is applied along the direction of growth (positive direction), causing the elect to move in the opposite direction (negative direction).

The ground-state electron probability density (EPD) as a function of the z-axis with and on-center impurity in IPQW taking into account the effects of potential profile (a), electric field strength (F) (b), barriers width (c), and In-compositions (d) has been presented in Fig. 3. It is obvious from panels (a) and (d) that EPD is localized around the well center where the impurity is located. According to same panels, EPD increases with increasing both \(\alpha \) and \(x\) due to improvement in the quantum confinement under the increase of the compositions while the electron–impurity distance falls with respect to \(\alpha \), which improves the EPD. Whereas, panel (b) shows that EPD diminished and shifted toward the left side of the system with rising the applied electric field intensity as it was expected. This is explained by the fact that with increasing the electric field strength, the ground-state electron wave function is moved from the well center and then the electron–impurity distance enhances, which makes the electron less bounded; and therefore, the EPD can only drop. In addition, it can one clearly seen from panel (c) that EPD improved and moved with the displacement of the impurity in the system. The shift is explained by the fact that with increasing the barrier thickness (L), the impurity’s position change. For example, the impurity initially is located at the center of the system (i.e., \(\mathcal{L}= L+\mathrm{l}/2\)). However, for \(L=l=1\), the impurity’s position becomes located in \(\mathcal{L}=1.5{a}^{*}\) while for \(L=2l=2,\) it becomes located in \(\mathcal{L}=2.5{a}^{*};\) though, the greater the barriers are, the important the confinement become, which explains the enhancement in the EPD of the system.

Fig. 3
figure 3

Ground-state electron probability versus the growth direction with and on-center impurity in \(\mathrm{GaN}/\mathrm{InGaN}/\mathrm{GaN}\) ∩-shaped QW considering four effects: potential profile (a), electric field (b), barriers width (c), and In-fraction (d)

Full size image

Figure 4, we plots the ground-state electron’s presence probability within the well region (EPP) versus the growth direction with and on-center impurity in IPQW considering the influences of the potential profile (a), electric field (b), barriers width (c), and In-compositions (d). It is evident from all the panels (a, b, c, d) that EPP is significantly influenced by the QW’s size, potential shape, and compositions as well. It increases smoothly with increasing the well width, which is expected. Because, the wider the well is, the important electron localization within the well becomes. Moreover, it is improved with the augmentation of the parameter \(\alpha \) (a), and with respect to the vertical applied electric field (b), the compositions (d). The improvement of the EPP under the increase of \(\alpha \) and \(x\) is explained by the increase of the spatial quantum confinement while that caused by the electric field is due to the improvement of the localization of the electrons far from the impurity localized in the center of the well with higher electric field strengths. Although, it is noticed that the EPP is slightly reduced with increasing barrier width, which is expected because it must be opposed to the behavior of EPP with respect to the well width. The physical reason is that the larger the barriers are, the reduced the well becomes, and therefore, the spatial confinement becomes considerably important, which imposes the electron to tunnel through the barrier (potential barrier) to the GaN material. Consequently, its EPP within the well becomes weaker.

Fig. 4
figure 4

Ground-state electron presence probability within the well region versus the well thickness with and on-center impurity in \(\mathrm{GaN}/\mathrm{InGaN}/\mathrm{GaN}\) ∩-shaped QW considering four effects: potential profile (a), electric field (b), barriers width (c), and In-fraction (d)

Full size image

Now, it is crucial to state out that the impact of the above-mentioned parameters on both the electron EPD and EPP considering and on-center impurity, will definitely affect the ionization energy related to this donor impurity. Figure 5 depicts ground-state binding energy according to the well thickness for an on-center impurity in an IPQW considering the effects of potential profile (a), electric field (b), barriers width (c), and compositions (d). On the hand, it is obviously seen from all panels (a, b, c, d) that the donor-impurity binding energy (DIBE) drops quasi-exponentially with respect to the well thickness, which is expected and confirmed by many reported theoretical works in literature [36, 37]. On the other hand, it is noticed that DIBE diminishes with increasing \(\alpha , L\) and\(x\), panels (a), (c) and (d), respectively, due to the enhancement in the electron–impurity distance. Because the increase in \(\alpha \) and \(x\) makes the electron less attached to the impurity and then the DIBE should only drop. However, it is observed from panel (b) that DIBE enhanced with respect to the vertical applied electric field \((F)\) due to the reduction in the Columbian interaction with the increase of\(F\). Additionally, the effects of the electric field and confinement parabolicity are more pronounced for wider QWs, panels (a, b); whereas, DIBE seems to be insensitive to the compositions in thin and thick QWs except for \(0.25<l<1.5\), panels (d). This is due to the fact that in thin-layered QWs, the spatial confinement becomes stronger which makes it the most dominator effect in this region while for high indium ratio, the electron becomes less linked to the impurity, which explains the non-sensation of DIBE in this region. Moreover, it is remarked that regardless the other parameters, the barriers impact on DIBE is neglected in thick QWs with\(l>1\), panel (c). The results plotted in this figure regarding the effects the well/barriers widths and the compositions are in good conformity with those reported by Belaid et al. in Ref. [43]. However, the impact of electric field and the parabolicity can be approved by the results reported by Priester et al. [44] and Zhigang et al. [45], respectively.

Fig. 5
figure 5

Ground-state impurity-related binding energy versus the well thickness with on-center impurity in \(\mathrm{GaN}/\mathrm{InGaN}/\mathrm{GaN}\) ∩-shaped QW considering four effects: potential profile (a), electric field (b), barriers width (c), and In-fraction (d)

Full size image

In Fig. 6, we presented the variation of the ground-state impurity-related diamagnetic response (\({\chi }_{\mathrm{dia}}\)) with respect to the well thickness of on-center impurity in \(\mathrm{GaN}/\mathrm{InGaN}/\mathrm{GaN}\) IPQW considering the impacts of the potential profile (a), electric field (b), barriers width (c), and compositions (d). Regardless all the effects, it is noticed from all panels (a, b, c, d) that \({\chi }_{\mathrm{dia}}\) decreases as a function of the well thickness, which is expected. Because the spatial confinement diminishes, which leads to an improvement in the electron–impurity distance. In addition, it is remarked that \({\chi }_{\mathrm{dia}}\) enhanced with all the considered parameters except the barrier width effect. Panel (a) shows that \({\chi }_{\mathrm{dia}}\) improved due to reduction of the spatial quantum confinement with increasing the parameter \(\alpha \), which causes the improvement in the electron–impurity distance.

Fig. 6
figure 6

Ground-state impurity-related diamagnetic susceptibility versus the well thickness with on-center impurity in \(\mathrm{GaN}/\mathrm{InGaN}/\mathrm{GaN}\) ∩-shaped QW considering four effects: potential profile (a), electric field (b), barriers width (c), and In-fraction (d)

Full size image

Furthermore, panel (b) demonstrates that the \({\chi }_{\mathrm{dia}}\) decreases quasi-linearly; whereas, with the incorporation of a vertical applied electric field, the \({\chi }_{\mathrm{dia}}\) dropped smoothly to reach a stable value for \(l>1.\) It is also noticeable that \({\chi }_{\mathrm{dia}}\) becomes more sensitive to the applied electric field in thick QWs than in thin ones. This is because in thin-layered QWs, spatial confinement dominates over the electric field effect. However, panel (c) displays that \({\chi }_{\mathrm{dia}}\) falls with increasing the barrier’s width. This is due the fact that the greater the barriers are, the thinner the well becomes, which leads to the reduction in the electron–impurity distance. As a result, \({\chi }_{\mathrm{dia}}\) decreases. Though, from panel (d), it is evident that \({\chi }_{\mathrm{dia}}\) improved with increasing the indium compositions in the well region (\({\mathrm{In}}_{x}{\mathrm{Ga}}_{1-x}\mathrm{N}\)). Referred to Eq. 13, this is explained by the fact that with adding a small fraction of indium in the well, the electron effective mass and its relative dielectric constant diminish; and therefore, the \({\chi }_{\mathrm{dia}}\) can only drop. In addition, it is observed that the effects of the barriers thickness as well as that of the compositions is distinct compared to the other parameters. The results reported above have quite similar with previously reported works for a GaAs-based QD such as the work of Rezaei et al. [46] and it show a remarkable agreement with them as well.

In Fig. 6, we illustrate the impurity-related polarizability (IP) according to the well thickness with an on-center impurity in IPQW for two different influences: potential profile (a) and compositions (b). From the two plotted panels, it is clearly seen that IP diminished smoothly versus the well thickness in thin-layered QWs (\(l<1\)), while it is dropped faster for thicker QWs \(( l>1\)). The effects of those parameters is less marked in thin QWs because of the strong quantum confinement is this area, which means that the response to an external excitation such as electric field decreases with increasing the well width. Because the wider the QW is, the lower the spatial quantum confinement becomes and then the sensation to an excitation becomes significant. Furthermore, panel (a) shows that IP increases with increasing the parameter \(\alpha \) reduces the confinement and therefore, IP can only improves. Although, panel (b) demonstrates that IP augmented with increasing the ratio of the indium in the well region. The reason behind this behavior is that the more the indium fraction is, the important the electric field influence on the impurity becomes, which explains the improvement in the impurity polarizability of the system. These results are quite comparable with those reported by Morales et al. [47] (Fig. 7).

Fig. 7
figure 7

Impurity-related polarizability versus the well thickness with an on-center impurity in ∩ \(\mathrm{GaN}/\mathrm{InGaN}/\mathrm{GaN}\)-shaped QW considering two effects: potential profile (a) and In-fraction (b)

Full size image

4 Conclusions

To summarize, this article presents significant findings regarding the simultaneous impact of the electric field, potential parabolicity, compositions, and system geometry on the electron presence probability, donor-impurity-related binding energy, diamagnetic susceptibility, and polarizability. The eigenvalues and eigenvectors were computed numerically by solving the Schrodinger equation within the effective mass theory using finite element analysis. These parameters were found to have a significant impact on the physical properties studied. While there are no experimental studies similar to ours, we compared our theoretical results with those estimated in the literature and found a good level of agreement. The presented results make a significant contribution to the field of solid-state physics and condensed matter by providing a detailed understanding of the electronic properties of hydrogenic donor impurities in III-nitride-based materials with modified potential energy, which are essential for the development of high-performance optoelectronic devices such as solar cells, photodetectors, and lasers.