1 Introduction

Generally speaking, human behaviors can be commonly found in these two genres: anti-social behaviors and pro-social behaviors. Anti-social behavior damages others interest to maximize self-benefits, but pro-social behavior usually sacrifices self for others and bring maximization of population benefits [1,2,3,4]. While the internal competition and the selection of nature strongly gives impetus to evolution, and theoretically, anti-social behavior gains more benefits for existence, in realistic, pro-social behavior is ubiquitous from the bacterial communities to human society. With the rapid development of network science, evolutionary game theory based on complex network have made a great contribution to solve this puzzle [5,6,7]. Complex networks can be found in everywhere including human society, which is widespread investigated. In human society network, individuals occupy network nodes and interact along network links [8,9,10,11]. Prisoner’s dilemma game, in which individuals have two choices: cooperation (pro-social behavior) or defection (anti-social behavior), a deputy for pair interaction is commonly used.

Fig. 1
figure 1

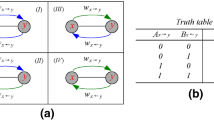
Strategy-updating rule of N and L. a Central player x whose type is N(represented in green) updates strategies of four directed links. b Central player x whose type is L (represented in orange) updates strategy (blue represents defection and white represents cooperation) to neighbor y whose type is N

Full size image

Obviously, mutual cooperation is more favorable for group but defect happens because of the incentive. It seems that cooperation will be replaced by defection unless there are some mechanisms, for example, kin selection, group selection, direct reciprocity, in-direct reciprocity, and network reciprocity proposed by Nowak and May [12, 13]. Inspired by the seminal work, many explorations about the underline mechanism have been put forward. For example, punishment [14, 15], reward [16, 17], aspiration [18,19,20,21], learning ability [22, 23] and coevolution [24,25,26]. Network topology, like small world network, scale-free network, multiple network is demonstrated playing an important role in cooperation evolution [27,28,29,30,31,32,33,34]. Public goods game, a typical multiplayer interaction and other model are also widely studied [35,36,37,38]. In addition to these theoretical researches, experiment about prisoner’s dilemma game conclude that repeated anonymous interactions will improve cooperation [39].

As mentioned above, most previous work based on the assumption that players take interactive identity [40] to all neighbors whatever their performance. However, it is impossible that humans can treat everyone around equally but independent because of individual diversity [41,42,43]. Actually, studies not only about interactive diversity [44, 45], but also other heterogeneous characteristics [45, 46] attract attention in recent decades. So how the cooperation dynamics will perform when two behaviors are mixed in population still needs detailed exploration.

Based on the palmary work [47], where individuals taking interactive identity (termed node player in this paper) adopt the most success neighbor’s strategy or keep unchanged if himself is the success one and found out that cooperation will be improved in a large range of the defection incentive, we introduced interactive diversity (termed link player) where individuals take different behaviors facing different neighbors. Based on this model, each player in network interact with neighbors with four directed edges, specially, node players adopt the same four. For link player, we assume individuals can update specific strategy not only from the neighbor interacting along directed link but also other neighbors. We proposed a measurement p to weight the learning willingness, which is a function of payoff. From the personal perspective, p describes one neighbor’s pro-social degree and regular a universal social norm: pro-social individual is recognized by society universally. A neighbor with higher degree of pro-social among surrounding, the more likely will be deemed as learning model. While human nature is sane, desperately imitating the behavior of the vulnerable will hardly happen. So pro-social degree only provides a reference that higher degree will abstract higher willingness to learn (also 1-p to learn from others), but whether prosocial strategy successfully spread depending on fitness, in our paper, pay-off.

The following part of this paper is organized as the follows. First, detailed description about our model with the strategy update rule for node players and link players is given. Then we give the results of Monte Carlo steps and detailed analyses. Finally, conclusion of the full work and outlook for future are conducted clearly.

Fig. 2
figure 2

The frequency of cooperation in \(\mathrm {b-w}\) space. From the left to right are the cooperation frequency of a all the players (\(N + L\)), b the node players (N) and c the link players (L), respectively. Red represents cooperation and blue represents defection

Full size image

2 Model

We consider evolutionary prisoners’ dilemma game (PDG) on a \(E\times E\) square a lattice with periodic boundary conditions PDG, a typical form for pair interaction game, concluding two players, each player has two choices: cooperation (C) or defection (D). Reward R for mutual cooperation and punishment P for mutual defection, and sucker’s payoff S for cooperation and temptation T for defection when strategies are different. These parameters strictly satisfy the relationships \(T>R>P>S\) and \(2R>T+S\) For simplify but without lose generality, we mainly focus on the weak PDG when \(R=1\), \(T=b\, \left( b>1 \right) \) and others are equal to zero [45] In this way, D will be a better choice for player to gain more payoff for self-stead of C which can create more group wealth. Under the framework of weak PDG, players in network occupying the vertexes can act as C or D, and interact with four nearest neighbors along the network links connecting nodes.

In this paper, initially, all players in lattice network will be randomly assigned as node (N) players and link (L) players with a certain probability, where the proportion of node participants is \(w(0\le w\le 1\)) Node players adopts the same strategy for all surrounding neighbors, while the link player adopts different strategies for different neighbors Then each directed network link will be assigned a strategy of C or D with equal probability (0.5) In each Monte Carlo steps (MCS), first, each player will interact with four neighbors and accumulate the game payoff \({\Pi }_{x}\). For simplicity, we calculate one of the players x’s payoff as the following formation:

$$\begin{aligned} \Pi _{x}=\sum \limits _{y\in \varOmega _{x}} \Pi _{xy} =\sum \limits _{y\in \varOmega _{x}} s_{x\rightarrow y}As_{y\rightarrow x}{}^\mathrm{T}, \end{aligned}$$
(1)

where \(\Pi _{xy}\) denotes the payoff of player x from interacting with one neighbor \(y, s_{x\rightarrow y}=(0,1\)) denotes that player x adopts a defection strategy to interact with y while \(s_{x\, \rightarrow y}=(1,0\)) denotes cooperation strategy, \(\Omega _{x}\) represents the set of neighbors of x, and the payoff matrix A is shown as

$$\begin{aligned} A=\begin{array}{ccc} \, &{} C &{} D\\ C &{} \mathrm {1} &{} \mathrm {0}\\ D &{} b &{} \mathrm {0}\\ \end{array}. \end{aligned}$$
(2)

Second, players update their strategies in different ways synchronously For N players, as shown in Fig. 1a, the focus player x will not change strategy if her \({\Pi }_{x}\) is not less than all her neighbors, otherwise she will accept the strategy of one of the most profitable neighbor out of four, which is the same as the model proposed by Nowak It is worth noticing, in our paper, N players and L players are mixed Regardless of the type of neighbor, N player will only imitate the corresponding strategy adopted by the selected neighbor against her when updating the strategy, which is called \(s_{y\rightarrow x}\) In other words, if N’s payoff is not greater than the neighbor’s payoff, her strategy to all four neighbors will be replaced by the directional link strategy, the owner of which has the highest payoff in the N player-centered group

We use \(s_{x_{i}}\) to represent the strategy of player x against neighbor \(y_{i}\) This strategy-update rule for player x whose type is N can be formatted as follows:

$$\begin{aligned} {s_{{x_i}}} = \left\{ {\begin{array}{ll} {s_{{x_i}}}\,&{}{{{{\Pi }}_x} \ge {\text {max}}\left\{ {{{{\Pi }}_y},{y_i} \in {{{\Omega }}_x}} \right\} } \\ {{s_{{y_i} \rightarrow x}}}&{}{{{{\Pi }}_x} < {\text {max}}\left\{ {{{{\Pi }}_y},{y_i} \in {{{\Omega }}_x}} \right\} } \end{array}} \right. . \end{aligned}$$
(3)

In particular, N-type players adopt the same strategy in the four directions. However, for L type players, as shown in Fig. 1b, the L-type player x learns the strategy of one of her neighbors \(y_{i}\) with the probability of \(p_{i}\, (0\ll p_{i}\ll 1\)) while x learns from the other three players with the probability of \(1-p_{i}\) This process only determines the learning object of x, but whether to learn a strategy will be further explained below.

Fig. 3
figure 3

The frequency of cooperation (\(\rho _\mathrm{C}\)) and various kinds of directed links (\(\rho _\mathrm{LINK}\)) in network. When \(b=1.04\), a the frequency of cooperation for all players (TC), for N (NC) and for L (LC), b the frequency of \(C{-}C\) links (CC) \(C{-}D\) links (CD), \(D{-}C\) links (DC) and \(D{-}D\) links (DD), c the frequency of \(C{-}C\) links (NNCC) \(C{-}D\) links (NNCD) \(D{-}C\) links (NNDC)and \(D{-}D\) links (NNDD) between N and N d the frequency of \(C{-}C\) links (LLCC) \(C{-}D\) links (LLCD) \(D{-}C\) links (LLDC)and \(D{-}D\) links (LLDD)between L and L e the frequency of \(C{-}C\) links (LNCC) \(C{-}D\) links (LNCD) \(D{-}C\) links (LNDC)and \(D{-}D\) links (LNDD)from L to N (f) the frequency of \(C{-}C\) links (NLCC) \(C{-}D\) links (NLCD) \(D{-}C\) links (NLDC)and \(D{-}D\) links (NLDD)from N to L

Full size image

Considering the realistic, we introduce the influence of payoff, therefore \(p_{i}\) is denoted as the liner function of payoff:

$$\begin{aligned} p_{i}=\frac{\Pi _{xy_{i}}}{\sum \nolimits _{y_{j}\in \Omega _{x}} \Pi _{xy_{j}} }. \end{aligned}$$
(4)

In this way, the more x obtains from neighbor \(y_{i}\) the more likely x will treat neighbor \(y_{i}\) as a learning role Conversely, the less x obtains from neighbor \(y_{i}\) the more likely x will chose to learn from other neighbors. The reason for this is in realistic, pro-social individuals always bring more income for others while selfish individuals damage others interests to maximize their own. Here, we empower players to measure the prosocial degree of their opponents as \(p_{i}\) from the point of themselves, large value of \(p_{i}\) means great willingness to deem \(y_{i}\) as a model to learn from But at the same time players also have possibility \({1-p}_{i}\) to be disturbed by other neighbors and decide to learn from. \(p_{i}\) plays more like a measurement role than social norm After determining learning object, x update her strategy \(s_{x\rightarrow y_{i}}\) to \(s_{y_{i}\rightarrow x}\) with probability f as Fermi function.

$$\begin{aligned} f=\frac{1}{1+\mathrm{exp}\, {((}\varPi _{x}-\varPi _{y_{i}})/K)}, \end{aligned}$$
(5)

where 1/K depicts the selection intensity in evolutionary game process and K is set equal to 0.1 in this paper following previous studies [46] Payoff of player x will be compared with \(y_{i}\)’s, it will be convenient for \(y_{i}\) extend strategy to x if the payoff gap is great. As we can see in the Fermi function, the spread of a strategy depending on its payoff, although we defined pro-social degree as the willingness to learn, actually, success affection on surrounding is based on self-fitness, namely, payoff. It consistent with the theory of Darwin. Pro-social may not create prevalent, but high fitness can. As mentioned before, L contains four unrelated strategies for each neighbor, so x duplicates the strategy-updating process four times.

Fig. 4
figure 4

The frequency of cooperation for different players and different directed links evolving with MCS From top to bottom, when \(w=0.1 , w=0.5\) and \(w=0.9\), the frequency of cooperation evolves with MCS for all players (TC), for N (NC) and for L (LC) in first column the frequency of \(C{-}C\) links (CC) \(C{-}D\) links (CD), \(D{-}C\) links (DC) and \(D{{-}}D\) links (DD)evolves with MCS in second column, the frequency of \(C{-}C\) links \(C{-}D\) links, \(D{-}C\) links and \(D{-}D\) links radiated from N (\(NCC,\, NCD,\, NDCNDD\)) evolves with MCS in third column, and the frequency of \(C{-}C\) links \(C{-}D\) links, \(D{-}C\) links and \(D{-}D\) links radiated from L (\(LCC,\, LCD,\, LDCLDD\)) evolves with MCS in the last column, respectively

Full size image

To avoid the finite size effects, the adopted system size in this paper various from \(E=100\) to 400. Then the results are obtained by incorporating the last 5000 steps of the full MCS with 50,000 steps. Each result is averaged over 10 independent simulation runs for each set of parameters to ensure the accuracy.

3 Results

First of all, we investigated the frequency of cooperation (\(\rho _\mathrm{C}\)) which is an intuitive reflection of result. As is depicted in Fig. 2, it is obviously that in the left part of (a), there is a basin of \(\rho _\mathrm{C}\) in the middle, in other words, when w is larger (for example, \(w=0.9\)) or smaller (for example, \(w=0.1\)) the frequency of cooperation is higher than w is middle (for example around 0.5) It is an interesting appearance since all N or all L approve cooperation (\(\rho _\mathrm{C}\) around 0.9), logically speaking, the alliance of N and L should have stronger endorsement to cooperation. However, we see the opposite results actually (\(\rho _\mathrm{C}=0.8\) when \(w=0.5\)). With the increase of b, this likelihood gradually disappears. When w is small which means in the network most nodes are occupied by L, color green exists in the most bottom part implying that the value of the temptation b has no notable effect on \(\rho _\mathrm{C}\). When w is large where N occupies the most network nodes, with the increase of \(b , \rho _\mathrm{C}\) shows a significant step down, obviously, temptation b strongly influence \(\rho _\mathrm{C}\). These two phenomena are widely observed in traditional pour L and N game results. Based on this, we can suppose that whatever the value of w, the percent of L and N in the network, the larger proportion accounted one always is the dominant one in the evolution process. This assumption can be confirmed in both (b) and (c) which shows when w is less than 0.5, L plays an important role in the network (we can see a large green piece in (c)) which is similar to the phenomenon in the bottom part of Fig. 2a, while with the increase of w (when w is larger than 0.5) N become decisive (we can see significant step down), which is similar to the top part of Fig. 2a.

Fig. 5
figure 5

Snapshots of strategies and players’ type in different steps. When \(b=1.04\) from top to bottom are \(w=0\), \(w=0.5\) and \(w=1\) We simulated on \(\mathrm{size}=100\times 100\) lattice and intercept a quarter of the full snapshots. Blue represents defection, light yellow represents cooperation, orange represents L and green represent N

Full size image
Fig. 6
figure 6

Snapshots of strategies and players’ type in different steps. When \(b=1.54\) from top to bottom are \(w=0\), \(w=0.5\) and \(w=1\) We simulated on \(L=100\) lattice and intercept a quarter of the full snapshots. Blue represents cooperation, light yellow represents defection, orange represents L and green represents N

Full size image

Given the phenomenon and conclusion obtained in Fig. 2, we mainly focused on the condition when b is small to study how N, L and different kinds of directed links perform and the internal characteristics of the cooperation basin. In Fig. 3, \(b=1.04\) frequency of cooperation for different players and different directed links are painted clearly. Obviously, in Fig. 3a, the frequency of cooperation for all players (TC) trends as a convex function first decreasing and then increasing, along with b increase from 1 to 2, as we can see in the left part of Fig. 2a, which can be deemed as N and L do not jointly support cooperation but works in their own way even disturb each other, thereby TC become less when N and L are mixed. As the cooperation of frequency for N(NC) and L(LC) monotonous reduction and increase exist with the increase of w respectively Both can be approximate as a liner function of w and the absolute slope of L is larger than N This demonstrate the proportion will affect the behavior of L more greatly than N Under the same proportion condition, L supports cooperation more strongly than N In Fig. 3b, all links of the frequency of \(C\mathrm {-}C\) directed links (CC) \(C\mathrm {-}D\) links (CD), \(D\mathrm {-}C\) links (DC) and \(D\mathrm {-}D\) links (DD) are depicted regardless of the player’s type. The tendency of CC is basically same as TC in Fig. 3a which decrease first and then increase. The gap between DD and DC (or CD) is dissymmetry which will be explained by Fig. 3c, d later. The \(C\mathrm {-}C\) links between N (NNCC) in Fig. 3c and L (LLCC) in Fig. 3e are monotonously increase and decrease like the tendency of NC and LC Also \(C\mathrm {-}C\) links are far higher than \(D-C\)(or \(C-D\)) links, which intimates big cooperation clusters emerge in the network. Besides this, the trend between DD and CD (DC) are not symmetry, for instance, when \(w=0.1\) the discriminant is larger than when \(w=0.9\). Namely, in Fig. 3c, d NNDD and LLDD show discriminate appearances, for instance, NNDD is similar to NNCD and NNDC on the contrary, disparity presents between LLDD and LLCD, LLDC \(C\mathrm {-}D\) links or \(D\mathrm {-}C\) links means the boundary of cooperation and defection, more boundary links existence than \(D\mathrm {-}D\) links in Fig. 3d may be the results of random separated small clusters instead of gathered big clusters, cause separated distribution of \(D\mathrm {-}D\) links will leads to more \(C\mathrm {-}D\) links or \(D\mathrm {-}C\) links if cooperation is near Moreover, equal quantity of \(D\mathrm {-}D\) links and \(C\mathrm {-}D\) links or \(D\mathrm {-}C\) links in Fig. 3c also attract our attention. The defection clusters in moderate scale may lead to the same quantity of inside \(D\mathrm {-}D\) links and adjacent DC (or CD) links. Strategy distribution will be showed in Fig. 5.

Based on the discussion before, when \(b=1.04\) with the increase of w, cooperation level changes like basin. Thence, Fig. 4 majorly depicted the time evolution when \(w=0.1 , w=0.5\) and \(w=0.9\), which represent the condition when w is small (almost network nodes are L), middle (N and L equally distribute) and large (almost network nodes are N) Comparing the top line and the bottom line where N and L both start from 10%, in Fig. 4a, NC dropped after the simulation start and finally turned to the cooperation level near 5% which means about half of N are defection, while in Fig. 4i, LC slightly dropped and eventually maintained the cooperation level near to initial 10% which means almost all L are cooperation Apparently, L maintain cooperation more outstanding than N in the same situation. Combine with the middle line, in Fig. 4e, N and L start from equal initial proportion (i.e. 0.5), L spunkily rise and present a high level of cooperation at the evolutionary stable state about 0.4 (nearly four fifth of the L is cooperation), and N drop as in Fig. 4i and back to a lower level of cooperation than L We can find explanation in the last three columns, DD links radiate from N decrease distinctly. NDD rapidly reach a peak as soon as the evolution begins, meanwhile NCC and NCD decrease, which leads to the cooperation level drop. From this, N is reputed as weak to against the invasion of defection and more likely to delivery defection to others. However, although LDD shows a upward trend at the beginning, this downward trend of LDC is more drastic than LCD, which leads to the cooperation level gently rise. In the light of this, N can resist defection invasion stubbornly. According to these, we can make a conclusion that N is more fragile with the irruption of defection, as the defection radiated from N is more than L, L behave better than N at supporting cooperation and avoiding defection, as the cooperation radiated from L is over N.

To figure out the reason how L present a better behavior when support cooperation and avoid defection in Fig. 4 and why N and L mix perform worse in Fig. 3, Fig. 5 shows the snapshots of strategies (blue represents cooperation, and light yellow represents defection) and type of players (orange represents L and green represent N) when \(w=0\) (only L in the network), \(w=0.5\) (N and L occupy equal proportion in the network) and \(w=1\) (only N in the network). By contrasting these three parameter conditions, we can review the evolutionary difference and interaction between N and L. For the top line, at the stable state, defection distributes separately in the network, while for the bottom line, defection forms distinct bar-like clusters with smooth border. It is also explained in Fig. 2 why LLDD is less than LLCD (LLDC), because LLDD disperses randomly in the network, so one LLDD will connect with more than one C and why NNDD is equal to NNCD (NNDC), because NNDD forms clusters but of small scale, so the internal NNDD and the boundary NNCD (NNDC) are similar in quantity. As for the middle line, when N and L are mixed together, isolated LLDD is attached with NNDD and sparse clusters with jagged border appear. The formation of these cluster is somewhere between only N and only L characteristic of both scatter and bar-like. From the holistic perspective, N and L interact with each other and bring out this shape. Zoom in one of the defection clusters, interestingly, N holds the most nodes and surround \(\, L\) inside. This point out the reason why the alliance of N and L perform worse. Although defection of N assembles clusters in the network, it is local and limited in size. When \(w=0.5\), defection of N with the help of separated and random defection distribution of L will form connected and strip-like defection collection, which will protect more defection staying safely.

In addition to this, Fig. 6 illustrates the distribution of cooperation and defection for N and L when \(b=1.54\). Clusters of defection are bigger in size, however, still with small cooperation clusters inside and not smooth on the boundary. One point needs to be noticed is that when \(b=1.54\), N sharply loses its advantages at improving cooperation and preventing from defection. Defection when \(w=0\) in Fig. 6 establishes relationships with each other and is no longer an isolated existence. In Fig. 6, when \(w=0.5\), defection is still characteristic of gathering as bar-shape clusters. As the result of these, when \(w=0.5\), defection will not be improved because of the interaction of N and L. Also, from the zoom of defection clusters \(w=1\) in Fig. 6, N and L equally occupied the nodes instead of N dominant.

4 Discussion

Here we mainly focus on the cooperation evolution process when both node players and link players are mixed in network. Node players who adopt the same strategy facing different neighbors, while link players take diversity strategies. According to this assumption, network links are directed and spread strategies along. We can reveal that when only one type of the players exists in the network, cooperation will be promoted. Even for link player, incentive has no obvious effect on cooperation. Although cooperation is maintained when link players or node players alone, the origin and the strategy distribution appear distinct difference. For link players, defection distributed randomly in the network without clusters, only connected defection links are easily found. Players in network have the ability to take different strategies for different opponents, so the boundary player will adopt cooperation to cooperation while defection to defection. Clusters are hard to develop within the evolution process. For node players, cooperation will form big clusters to resist the invasion of defection and defection occupy the node in small size clusters. The results are consisted with previous works, spatial structure facilitates the classify of strategy and favor cooperation clusters. By the way, defection clusters appear at the same time. When players are mixed in the network, defection clusters of node players and the connected defection links of link players will influence each other. Connected and widespread defection clusters are present, as the result of this, cooperation is damaged. Many experiments and theory have argued that heterogeneity will benefit cooperation, while in this paper, opposite conclusions, mixed population has no optimistic influence on cooperation. Besides the effect of mixed population, the parameter p we introduced plays a realistic role, which is a pro-social degree from a personal perspective. The more you bring for others, the more pro-social you are in their mind. As a consequence, this kind of individuals are commonly deemed as role model. At the same time, in the main part, we did not betray the evolution theory of Darwin, which claimed natural selection and the fittest survival. Strategy updating depends on the fitness, in this paper, payoff, as described in Fermi function. Players obtained greater payoff are more successfully transfer strategy to neighbors. p is a selected measurement, disable to decide the strategy propagation essentially. Combining p and Fermi function, our model is realistic and reflect human daily life. However, what we do in this paper is far from resolving social dilemma. For instance, human social network is far more complex than lattice, and interaction between individuals can be interfered by various factors. In future works, networks like scale-free will be considered. Also third part intervene or internal social norm will be discussed. Taking these into account can help further understanding of the cooperation evolution process and resolute realistic dilemma.