1 Introduction

The interaction of charged particles with external fields is a longstanding subject of interest in electromagnetic and hadron physics. J. Schwinger shared the Nobel prize in 1965 (with R. Feynman and S. Tomonaga) for ’fundamental work in quantum electrodynamics, with deep-ploughing consequences for the physics of elementary particles’. In a series of works he formulated a relativistic theory for the emission of a photon from electrons [1]. Since, the calculation of radiative corrections (RC) in scattering and annihilation reactions involving electron and proton is an important issue: any new experiment needs corrections matching the new features as kinematical conditions, resolution and acceptance of the setup. Radiative corrections may require involved calculations, and a careful analytical check of cancellation of divergent terms, in particular at high order of \(\alpha =e^2/(4\pi )=1/137\), the electromagnetic fine constant. The degree of development in \(\alpha \) depends on the required precision of the calculation that, in turns, depends on the precision of the measured physical observables.

Typical radiative effects in electron-proton scattering were small before the advent of high luminosity accelerators: calculations at first order in \(\alpha \) were sufficient to correct the measured quantities, generally affected by a precision of several percents. On the other hand, in electron-positron collider experiments, higher order corrections were found to be mandatory as the seeked precision on the observables was better than the percent. Calculations become very complicated and lengthy beyond the first order, due to the larger number of diagrams involved. A very efficient solution was developed in Ref. [2, 3], implementing the lepton structure function method (LSF). More recently, an effective field theory was developed in Ref. [4], triggered by the the precision reached by the proton radius and the proton form factor measurements.

Radiative corrections change not only the absolute value of the observables, but also their dependence on the relevant kinematical variables. Therefore, if the extraction of the physical information requires the knowledge of specific terms in a multi differential cross section, radiative corrections of few percent on the cross section may induce a much larger error on the observables, changing essentially the shape of the distributions. Typical examples are given by virtual Compton scattering [5] and elastic ep cross section, that is object of Sect. 2. A brief introduction on LSF is given in Sect. 3 together with its application to ep elastic scattering; in Sect. 4 ’hard two photon exchange’ is discussed both in terms of model independent statements and of a model calculation of charge asymmetry that is directly compared to recent experimental results in Sect. 5. The charge asymmetry in the annihilation region is briefly discussed in Sect. 6. Conclusions summarize the discussion and stress the importance of a precise calculation of radiative corrections in modern experiments.

2 Elastic electron proton scattering

An elegant formalism relates elastic ep cross section and electromagnetic proton form factors (FFs), under the assumption that the reaction occurs by exchanging one virtual photon of four momentum q [6]. The cross section is theoretically calculated at the order \(\alpha ^2\) (Born cross section) and depends on two kinematical variables (\(\epsilon ,Q^2\)) or (\(E,\theta _e\)), with \(\epsilon =[1+2(1+\tau )\tan ^2(\theta _e/2)]^{-1}\), \(\tau =Q^2/(4M^2)\) (M the proton mass, E the electron beam energy, and \(\theta _e\) the electron scattering angle in the proton rest frame) and on two electromagnetic FFs that are functions of the transferred momentum squared only, \(Q^2=-q^2\). The elastic ep cross section is usually measured by detecting both particles, in order to decrease the background. Note, however, that a precise measurement with good resolution of the full kinematics, i.e., angles and energies of the final particles, is not currently done.

The measured cross section needs to be corrected by the radiative emission from all charged particles in order to recover the Born cross section. Typically, experimental data on ep (in)elastic scattering were corrected at first order following [7,8,9], revised more recently in Refs. [10, 11].

Radiative corrections, being \(\epsilon \) and \(Q^2\) dependent, modify essentially the slope of the Rosenbluth plots [12, 13]. Usually, radiative corrections calculated at the first order (extra order of \(\alpha \) with respect to the Born contribution) are included as a multiplicative factor \(\delta (Q^2,\epsilon )\) to the measured cross section \(d\sigma ^{meas}\):

$$\begin{aligned} d\sigma ^{meas}(Q^2,\epsilon )= & {} d\sigma ^B(Q^2,\epsilon )(1+\delta ),\ \nonumber \\ \delta= & {} 1+\delta _{odd} +\delta _{even}, \end{aligned}$$
(1)

where \(\delta \) contains terms that are dependent (\(\delta _{odd}\)) or not (\(\delta _{even}\)), on the charge of the lepton, see Fig. 1. The error associated to this procedure is at few percent level.

The traditional method to access the electromagnetic proton structure was the Rosenbluth separation [6], i.e., the measurement of the unpolarized cross section in ep elastic scattering at the same \(Q^2\) for different angles. One defines a reduced cross section as

$$\begin{aligned} \sigma _{Born}(Q^2,\epsilon )= & {} \frac{\sigma _M}{\epsilon \rho (1+\tau )}\sigma _{\textrm{red}}(Q^2,\epsilon ), \nonumber \\~\sigma _{\textrm{red}}(Q^2,\epsilon )= & {} {\tau }G_M^2(Q^2)+\epsilon G_E^2(Q^2), \end{aligned}$$
(2)

where \(\sigma _M=\alpha ^2\cos ^2(\theta /2)/[4E^2\sin ^4(\theta /2)]\) is the Mott’s cross section and \(G_E\) and \(G_M\) are the electric and magnetic FFs. In the one photon approximation at fixed \(Q^2\), \(\sigma _{\textrm{red}} (\epsilon ,Q^2)\) is linear in the variable \(\epsilon \), with slope \(G_E^2\), and intercept \(\tau G_M^2\). The magnetic term is dominant at large \(Q^2\), as it is proportional to \(\tau \).

Fig. 1
figure 1

Scheme of decomposition of radiative corrections into charge odd and even terms

Full size image

It was suggested at the end of the 1960 years [14,15,16,17], that the scattering of longitudinally polarized electrons on a transversally polarized hydrogen target (or the measurement of the polarization of the outgoing proton in the transverse plane) leads to very precise measurements as the small electric FF does not contribute in square but as an interference term. Potentially, this method allows also to access the sign of FFs (what is especially important for the neutron electric FF).

The corresponding measurements where done only after the years 2000, when high luminosity, highly polarized electron beams, large angle spectrometers and proton polarimeters working in the GeV range became available (see [18] and References therein). Not only the determination of the FF ratio was more precise, as expected, but the data showed a decrease of the proton electric to magnetic FF ratio \(R=G_E/G_M\) with \(Q^2\), while earlier it was assumed constant as suggested by the unpolarized experiments.

A constant \(Q^2\) behavior of the ratio R is indeed expected in perturbative QCD (pQCD) as elastic FFs represent the probability that a proton remains a ground state proton after that one of its valence quarks has received a four momentum \(Q^2\) and transferred to the other two quarks. Scaling laws predict a \((1/Q^2)^2\) dependence of the amplitude of the process [19, 20] (corresponding to the exchange of two gluons, the minimum number of gluons needed for sharing the momentum among the three valence quarks). However, pQCD can not predict at which \(Q^2\) the perturbative regime applies.

The large (\(Q^2\)-increasing) difference between the R measurements in unpolarized and polarized ep elastic scattering, is a critical issue that has stimulated a large number of theoretical and experimental works.

The monotonic decrease of the ratio R is attributed to \(G_E\) because \(G_M\) is considered to be well determined by the Rosenbluth method [21]: the magnetic contribution to the unpolarized cross section is larger than 90% at \(Q^2\ge 3 \) GeV\(^2\). An extrapolation of the present data to large \(Q^2\) may even show a zero crossing of the ratio R for \(Q^2 \le 10 \) GeV\(^2\), what is unexpected and not consistent with most theoretical model (see, for a recent example, Ref. [22]). The extension of the recoil proton polarization measurements at large \(Q^2\) is planned at the Jefferson Laboratory in the next future [23].

Different explanations have been put forward, such as the importance of high order radiative corrections or the presence of a large contribution of the exchange of two photons. Simpler explanations have also been suggested: at large \(Q^2\), the small electric contribution would be hidden in the experimental error of the Rosenbluth fit, then its \(Q^2\) dependence is driven by the dominant magnetic term [24] (\(G_M\), as measured in unpolarized experiments, follows roughly a dipole behavior as predicted by pQCD). The slope of the Rosenbluth plot is largely affected by the (\(Q^2,\epsilon \))-dependent radiative corrections (the uncorrected slope becoming even negative for Q\(^2~>~2\) GeV\(^2\)) inducing a large correlation of the parameters from the Rosenbluth fit [12]. The issue of the approximations used in the past, when mainly first order radiative corrections [7, 8, 25] were considered, has been recently discussed in a series of articles [11, 26, 27] as well as in the review [28], whereas the role of higher order corrections was pointed out in [24, 29]. Moreover, to be compared with the results of the SLAC experiment [21], Ref. [26] included external bremstrahlung and ionization losses, and showed that the discrepancy with the polarization data was removed at moderate \(Q^2\). Note that precise first order calculations have to agree with LSF at the % level. The calculation from Ref. [26] was implemented in a MonteCarlo generator [10], conveniently used in subsequent experimental works, as [30].

3 Lepton structure functions applied to electron proton elastic scattering

The need to go beyond the lowest order of perturbation theory in present experiments at electron accelerators is justified at least by two characteristics: the large \(Q^2\) values and the high precision. Schematically, first order corrections are proportional to the product \(\ln (\Delta E/E)\ln (Q^2/m^2)\), where E is the beam energy and \(\Delta E \) is the maximum energy of the photon that escapes the detection. In modern experiments, E may be very large and the experimental resolution is very good, allowing to reduce \(\Delta E\). Already at \(Q^2\) = 5 GeV\(^2\), one currently has \(\ln (Q^2/m^2)\simeq 20\), m is the lepton mass. \(L=\ln (Q^2/m^2)\) is called ’the large logarithm’.

To calculate high order radiative corrections, one has to consider a large number of diagrams. A convenient method to resum the contributions at all orders, in the large logarithm limit, has been proposed in Refs. [2, 3], resulting in permille precision. The accuracy can be further improved calculating non-leading contributions as a K-factor.

Writing the cross section as for a Drell-Yan process, the structure functions of the electron play the role of probability distributions. LSF obey to the renormalization equations, with well known solutions. The cross section is obtained in the leading logarithmic approximation, i.e., taking correctly into account the terms of the order \([(\alpha / \pi ) L]^n\). This corresponds to collinear kinematics, where the photon is emitted in the direction of the electron. Knowing the value of radiative corrections in the lowest order of perturbation theory, the non-leading contributions, of order \((\alpha /\pi )[(\alpha /\pi )L]^n\), that are suppressed by a factor \((\alpha /\pi )\), are introduced in form of a K-factor.

The cross section for elastic scattering ep scattering, taking into account the contributions of higher orders of perturbation theory and the role of initial state photon emission, can be expressed in terms of LSF of the initial electron and of the fragmentation function of the scattered electron energy fraction :

$$\begin{aligned} d\sigma ^{LSF}(Q^2,\epsilon )= \int _{z_0}^1 dz {{{\mathcal {D}}}}(z,\beta ) d{{\tilde{\sigma }}}(Q^2_z,\epsilon _z)\left( 1+\frac{\alpha }{\pi }K \right) , \nonumber \\ \end{aligned}$$
(3)

with

$$\begin{aligned} d{{\tilde{\sigma }}}(Q^2_z,\epsilon _z)= \frac{d\sigma ^B(Q^2_z,\epsilon _z)}{[1-\Pi (Q^2_z)]^2}. \end{aligned}$$
(4)

The notation \(d\sigma \) stays for the double differential cross section \(d\sigma ^{LSF,B}= (d\sigma ^{LSF,B}/{d\Omega })\), for the radiatively corrected cross section (LSF) and the Born approximation (B), respectively.

In Eq. (3) the main role is played by the non singlet LSF:

$$\begin{aligned} {{{\mathcal {D}}}}(z,\beta )= & {} \frac{\beta }{2}\left[ \left( 1+\frac{3}{8}\beta \right) (1-z)^{\frac{\beta }{2}-1}- \frac{1}{2}(1+z)\right] \left( 1+O(\beta )\right) ,\nonumber \\ \beta= & {} \frac{2\alpha }{\pi }(L-1). \end{aligned}$$
(5)

The integration in Eq. (3) requires a careful treatment as \({{{\mathcal {D}}}}(z)\) has a singularity for \(z=1\). The method of integration of any function \(\Phi \) can be found in Appendix A of Ref. [29].

The Born cross section \(d{{\tilde{\sigma }}}(Q^2_z,\epsilon _z)\), corrected by the vacuum polarization, \(\Pi (Q^2_z)\), is calculated for a kinematics shifted by z. The z-dependent kinematical variables \(Q^2_z\), and \(\epsilon _z\), taking into account the change of the electron four momentum due to photon emission, are calculated after replacing the initial electron energy E by zE, where zE is the energy carried by the electron after emission of one or more collinear photons.

The lower limit of integration, \(z_0\), is related to the ’inelasticity’ cut, c, used to select the elastic data:

$$\begin{aligned} z_0=\frac{c}{\rho -c(\rho -1)}, \end{aligned}$$
(6)

where \(\rho \) is the recoil factor \(\rho =1+(E/M)(1-\cos \theta _e)\). In terms of \(\rho \), one can write \(Q^2={2E^2(1-\cos \theta _e)}/{\rho }\). The value of c depends on the kinematics, and it is usually taken around 3% in the comparison with the experimental values.

The vacuum polarization for a virtual photon with momentum q, is included as a factor \(1/[1-\Pi (Q^2)]\). The main contribution to this term arises from the polarization of electron-positron vacuum:

$$\begin{aligned} \Pi (Q^2)=\frac{\alpha }{3\pi }\left[ L-\frac{5}{3} \right] . \end{aligned}$$
(7)

The factor \(1+({\alpha }/{\pi })K\) in Eq. (3) has been calculated in detail for ep elastic scattering in Refs. [29, 31], where the K-term is the sum of five contributions:

$$\begin{aligned} K=K_e+K_p+K_{b}+K_h+K_o. \end{aligned}$$
(8)

  • \(K_e\) is related to non leading contributions arising from the photon emission in the electron line and from the electron self-energy. It can be written as [2, 3, 32]

    $$\begin{aligned}{} & {} K_e= -\displaystyle \frac{\pi ^2}{6} -\displaystyle \frac{1}{2} -\displaystyle \frac{1}{2}\ln ^2\rho +\text{ Li}_2(\cos ^2\theta _e/2), \ \nonumber \\ {}{} & {} \text{ Li}_2(z)=-\int _0^z \displaystyle \frac{dx}{x} \ln (1-x). \end{aligned}$$
    (9)

  • The second term, \(K_p\), refers to the emission from the proton line. The emission of virtual and soft photons by the proton is not associated with the large logarithm because of the large proton mass. Therefore the whole proton contribution can be included as a \(K_p\) factor:

    $$\begin{aligned} K_p= & {} \displaystyle \frac{Z^2}{\beta _p}\left\{ -\displaystyle \frac{1}{2}\ln ^2x-\ln x\ln [4(1+\tau )] +\ln x \right. \nonumber \\{} & {} \quad - (\ln x-\beta _p)\ln \left[ \displaystyle \frac{M^2}{4E^2(1-c)^2}\right] +\beta _p \nonumber \\{} & {} \quad \left. -\text{ Li}_2\left( {1-\displaystyle \frac{1}{x^2}}\right) +2\,\text{ Li}_2\left( {-\displaystyle \frac{1}{x}}\right) + \displaystyle \frac{\pi ^2}{6} \right\} ,\nonumber \\ \end{aligned}$$
    (10)

    with \(x=(\sqrt{1+\tau }+\sqrt{\tau })^2\), \(\beta _p=\sqrt{1-M^2/E'^2}\) the velocity and \(E'=E(1-1/\rho )+M\) the energy of the scattered proton. The largest value from Ref. [8] gives a \(K_p\) contribution to the K-factor almost constant in \(\epsilon \) and equal to \(-0.2\%\) for \(c=0.99\), \(E=21.5\) GeV, \(Q^2=31.3\) GeV\(^2\).

  • \(K_{b}\) represents the interference of electron and proton emission. More precisely the relevant part of the soft photon emission (i.e., the interference between the electron and proton soft photon emission), as well as the interference between the two and one virtual photon exchange amplitudes must be both included in the term \(K_{b}\). All these effects can be considered non-leading contributions of the order of unity.

  • Two additional contributions to the K-factor are \(K_{h}\) from hard photon emission and the C-odd contribution from the interference between electron and proton emission, \(K_{o}\), and are calculated in detail in Ref. [31].

Finally, in order to make a comparison with the existing calculations of radiative corrections, it is convenient to express the corrections calculated with the LSF method in the form of Eq. (1) where \( 1 + \delta \) becomes:

$$\begin{aligned} 1+ \delta= & {} \displaystyle \frac{1}{ [1-\Pi (Q^2) ] ^2} \Bigg \{ 1+\displaystyle \frac{\alpha }{2\pi }(L-1) \Big [ -\bigg ( 2\ln \bigg (\displaystyle \frac{1}{1-z_0}\bigg )-z_0-\displaystyle \frac{z_0^2}{2} \bigg )\nonumber \\{} & {} \quad + \int _{z_0}^1 dz\displaystyle \frac{1+z^2}{1-z} \bigg ( \displaystyle \frac{d{{\tilde{\sigma }}}^B(Q^2_z,\epsilon _z)}{ d{{\tilde{\sigma }}}^B(Q^2,\epsilon )}-1\bigg ) \Bigg ]+\displaystyle \frac{\alpha }{\pi } K.\Bigg \}. \end{aligned}$$
(11)

The application of the structure function method to ep elastic scattering can be found in Refs. [29, 32], and, including hard photon emission, in Ref. [33]. It has been shown that a precise calculation of radiative corrections can bring into agreement FF data from polarized [18] and unpolarized electron proton scattering [21], at least up to 3–4 GeV\(^2\). The calculations show that these corrections are consistent with the known experimental results:

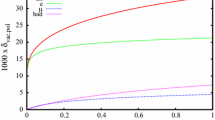
  • the \(\epsilon \) dependence of the LSF corrections is large : as one can see from Fig. 2, the slope of the Rosenbluth data [21], when corrected by LSF, is compatible to the slope expected from polarization experiments;

  • at large \(Q^2\), the corrections to the unpolarized cross section as well as to the individual longitudinal and transverse (polarized) cross sections are also large, but their \(\epsilon \)-dependence cancels in the ratio [29, 34].

  • the non-linearities in \(\epsilon \) for the Rosenbluth plots (see Fig.  2) as well as for the polarization ratio remain small [12, 29, 35] in agreement with the observation [34].

Fig. 2
figure 2

\(\epsilon \)-dependence of the reduced cross section at \(Q^2=5~\text{ GeV}^2\): the points are from Ref. [21] (red squares); data corrected by the SF method from Ref. [29] (black circles). The lines are from the dipole parametrization (solid red line), from the LSF calculation Ref. [29] (dashed black line) and from the polarization measurements (dot-dashed blue line) under the dipole assumption for \(G_M\). The LSF calculation corresponds to c-values around 3% (as reported in Table I of Ref. [33].)

Full size image

Of course, the application of these calculations to the experimental results is limited by the fact that one has to ’deconvolute’ the published results from the applied radiative corrections. This is a relatively easy procedure for the data before the year 2000, where the value of the multiplicative factor \(\delta \) was explicitly given in the publications for each kinematics. Since, radiative corrections for large acceptance spectrometers and detectors need to be embedded in the Monte-Carlo programs used in the analysis and merge in other corrections such as acceptance and background subtraction, in particular of the inelastic \(e p \pi ^0\) contribution.

The size and the kinematical dependence of the hard photon contribution depend strongly on the kinematical cuts due to the detection and a subtle cancellation may occur because the sign of soft plus virtual corrections is sometimes opposite to the hard photon correction.

Note that LSF are currently applied in experiments at \(e^+e^-\) colliders, that need a precision better than the percent.

4 Two photon exchange

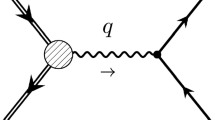
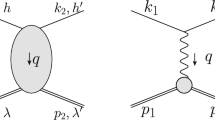
The underlying formalism that allows to extract the electromagnetic FFs from the unpolarized and polarized elastic ep cross section is based on the assumption that the interaction occurs through the exchange of a single photon of momentum \(Q^2\). The interference between one and two photon exchange is of the order of \(\alpha ^3\), therefore it must be introduced in first order radiative corrections. When one photon is ’soft’ and the second is ’hard’, this term cancels infrared divergences arising from initial and final state emission, but in principle one has to integrate over all momenta involved in the box diagrams. A complete calculation should take into account all proton inelastic states, the proton structure and off-mass shell effects, becoming strongly model dependent.

In the 70’s it was noted that two photon exchange could become important at large \(Q^2\) [36,37,38], when the transferred momentum is equally shared between the two photons: the suppression of \(\alpha \) may be compensated by the steep decreasing of the FFs with \(Q^2\). Therefore, it is expected that this effect increases with \(Q^2\) and with the hadron mass.

Such mechanism, if present, invalidates the formalism underlying the extraction of electromagnetic FFs in polarized and unpolarized electron scattering: instead of two real functions of \(Q^2\), elastic ep scattering is described by three amplitudes, generally of complex nature, functions of two kinematical variables. However, in Refs. [39,40,41] it has been shown that it is still possible to recover the electric and magnetic proton FFs, even in presence of two photon exchange, but this requires the measurement of three time-odd or five time-even polarization observables (including triple spin observables, that are expected to be small, of the order of \(\alpha \)) or the generalization of the Akhiezer-Rekalo recoil proton polarization method [14,15,16,17] with beams of longitudinally polarized electrons and positron in identical kinematical conditions.

A discrepancy between two sets of data in ed elastic scattering, from two different experiments at JLab-HallC [42] and JLab-HallA [43], might have been explained by the presence of two photon exchange: the data, differing by several percent, were taken at similar \(Q^2\) but not at the same energies and angles, therefore the presence of extra amplitudes would bias the results that were extracted under the assumption of one photon approximation. The reanalysis of Ref. [44] concluded that the problem was related instead to a systematic error of \(\simeq 0.3^{\circ }\) in the determination of the central angle of the Hall C spectrometer: the data show a systematic shift, not increasing with \(Q^2\). In spite of this finding, later on, two photon exchange was advocated to explain the discrepancy between proton FFs from polarized and non polarized experiments [45, 46]. Different models were further developed apparently solving, at least partially, this discrepancy [47,48,49,50]. However the same models give very divergent predictions for the \(\epsilon \)-dependence of the polarization ratio (see Fig. 2 of Ref. [18]). Only the structure function method, where non linearities are small, reproduces all experimental data.

The experimental search early in the 1970 years did not give any evidence of deviation from the one photon exchange expectations, in the limit of the errors. As for today, there is no experimental evidence of an enhancement of two photon exchange: the linearity of the Rosenbluth plot is confirmed [21, 51], as well as the \(\epsilon \)-independence of the polarization ratio [34]. Note that a deviation from the Born prediction of \(P_L\) and \(P_T\) separately [18] does not constitute a hint of the presence of two photon exchange: the corrections to these polarized observables taken separately have the same magnitude as to the unpolarized cross section and essentially cancel in the ratio [29].

A similar situation is found for the charge asymmetry in the electron over positron cross section ratio. Some models predicted a very large effect [52], starting at relatively small \(Q^2\). Such effect is not found in the data [53,54,55]. This issue is further discussed below. Indeed, the two photon contribution induces a non vanishing charge asymmetry in \(e^{\pm }p\) scattering, due to its C-odd character. By crossing symmetry, in the annihilation region the non linearities in the Rosenbluth fit translate into a forward-backward angular asymmetry. The comparison with the data does no allow to detect and quantify any of these effects.

5 Compared analysis of recent experiments

The charge asymmetry including soft and hard two photon contributions was calculated in Ref. [56]:

$$\begin{aligned} A_{odd}^K= & {} \frac{d\sigma ^{e+p}-d\sigma ^{e^-p}}{d\sigma ^{e+p}+d\sigma ^{e^-p}} =\frac{2\alpha }{\pi (1+\delta _{even})} \biggl [ \ln \frac{1}{\rho } \ln \frac{(2\Delta E)^2}{ME}\nonumber \\{} & {} \quad - \frac{5}{2}\ln ^2\rho + \ln x\ln \rho +\text{ Li}_2\left( 1-\frac{1}{\rho \tilde{x}}\right) -\text{ Li}_2\left( 1-\frac{\rho }{{{\tilde{x}}}}\right) \biggr ],\nonumber \\ {{\tilde{x}}}= & {} \frac{\sqrt{1+\tau }+\sqrt{\tau }}{\sqrt{1+\tau }-\sqrt{\tau }} \end{aligned}$$
(12)

The term containing \(\Delta E/E\) has a large \(\epsilon \) dependence and plays the largest role in the asymmetry when \(\Delta E\) is small. A deviation from unity of the ratio:

$$\begin{aligned} R^{meas}= \displaystyle \frac{d\sigma ^{meas} (e^+ p\rightarrow e^+p )}{d\sigma ^{meas} (e^- p\rightarrow e^-p )} =\frac{1+\delta _{even}-\delta _{2\gamma }-\delta _s}{1+\delta _{even}+\delta _{2\gamma }+\delta _s} \nonumber \\ \end{aligned}$$
(13)

is a clear signature of (soft and hard) C-odd contributions to the cross section.

After correcting the data for the contributions of the vertex-type corrections \(\delta _{even}\) and soft two-photon contributions \(\delta _s\), \(R^{meas}\) from Eq. (13) reduces to

$$\begin{aligned} R_{2\gamma }\simeq \frac{1-\delta _{2\gamma }}{1+\delta _{2\gamma }}, \end{aligned}$$
(14)

where \(\delta _{2\gamma }\) is the contribution of hard virtual two-photon exchange.

As radiative corrections may differ from one calculation to another by some finite expression (which depends on kinematical invariants), a difference of 1 or 2% in the asymmetry may be attributed to the applied radiative corrections. To be compared, the published data on \(R_ {2\gamma }\) have to be corrected for those radiative corrections that depend on the inelasticity cut c and contain the term proportional to \(\ln (\Delta E/E)\). In order to be less sensitive to model corrections, the following procedure is adopted in Ref. [57]: the C-odd correction applied to the experimental data is removed from the total C-odd contribution that is instead replaced by the calculation of Ref. [56]. This allows to proceed from \(R^{meas}\) to \(R_{2\gamma }\):

$$\begin{aligned} R_{2\gamma }^{K}=\frac{1-A^K_{odd}(1+\delta _{even})+\delta _{M}}{1+A^K_{odd}(1+\delta _{even})-\delta _{M}}, \end{aligned}$$
(15)

where the contributions ’odd’ and ’even’ are denoted according to Fig. 1, and the soft term, \(\delta _{M} \), can be calculated from Ref. [7] or from Ref. [8]. A constant value \(c=3\%\) is taken, as it is consistent with most experimental data. Note that the final result for the hard two photon contribution does not depend on this parameter.

As the ratio R depends on both variables \(\epsilon \) and \(Q^2\), the difference point by point between the experimental and the theoretical values can be calculated. The difference between the calculation from Eq. (12) and the data is plotted as a function of \(\epsilon \) and \(Q^2\) in Figs. 3 and 4, respectively, after removing the C-odd corrections as in Eq. (15) with \(\delta _M\) from Ref. [8]. The \(\epsilon \) and \(Q^2\) dependences show that the difference point by point between data and theory is in general in very good agreement, within the theoretical and experimental precisions, being smaller than a percent for most of the points. A larger difference appears for VEPP data. The different trend of these data has been possibly attributed to normalization issues. The same procedure with \(\delta _M\) taken from Ref. [7] leads to similar results.

Fig. 3
figure 3

Point to point difference between the calculation from Eq. (12), Ref. [56] and the data for the ratio R, with the corresponding linear fits as a function of \(\epsilon \) from OLYMPUS [54] (red circles and red solid line), CLAS [55] (green squares and green dashed line) and VEPP-3 [53] (blue triangles and blue dotted line), after removing the C-odd corrections as in Eq. (15) with \(\delta _M\) from Ref. [8]. The black dash-dotted line corresponds to the global linear fit

Full size image
Fig. 4
figure 4

Same as Fig. 3, but as a function of \(Q^2\)

Full size image

6 Asymmetry in the annihilation region

Model independent statements hold also in the annihilation region [58, 59]. Assuming crossing symmetry, time and parity invariance, the reactions \(e^+e^-\leftrightarrow p{{\bar{p}}}\) are described by the same electromagnetic FFs. However, in the time-like region of transferred momentum, FFs are of complex nature, even in case of one photon exchange. One can connect the crossed channels as the amplitudes are the same, but the kinematical variables act in different kinematical regions.

One can show [44] that the linearity of the Rosenbluth plot translates into a symmetrical angular distribution in \(\cos {{\tilde{\theta }}}\), where \({{\tilde{\theta }}}\) is the center of mass angle of one of the produced particle. A precise measurement of the angular distribution of one of the final hadrons allows to extract the moduli of the FFs. In principle this measurement is simpler than a Rosenbluth fit, because, having a \(4\pi \) detector, it requires only one setting of the collider. As a forward-backward asymmetry arises in presence of C-odd contributions, the sum (difference) of the cross section at corresponding angles cancels (enhances) the two photon exchange contribution. Due to the large transferred momenta that are involved above the physical threshold \(q^2>(2M)^2\) one expects that two photon effects are enhanced in the time-like region.

The study of both annihilation reactions related by time reversal is also very instructive as radiative corrections are in general different. The search of C-odd contributions to the annihilation cross section has been reported for the BaBar data [60] in Ref. [61]. No evidence was found in the limit of 2%, which is of the same of order of the interference between initial and final radiation emission.

The presence of two photon exchange in the future data from PANDA at FAIR has been simulated in Ref. [62] pointing out that a contribution \(\ge 5\% \) would be detectable.

7 Conclusions

The LSF method is a powerful tool to improve the precision of radiative corrections calculations. It includes high orders by convolution of the Born cross section with a universal function. While the lepton structure function is quite general, as it gives the probability to find an electron in the initial electron at a definite kinematics, the calculation of the K-factor, entering as a correction of order \(\alpha /\pi \), is specific to each process. Among the most discussed contributions to the K-factor, the exchange of two photons has been object of a large number of recent calculations and experiments. It has been advocated as a possible solution of the observed discrepancy among electromagnetic proton FFs extracted from polarized and unpolarized elastic ep scattering.

Symmetries of the strong and electromagnetic interaction allow to establish model independent requirements for scattering and annihilation reactions, on the basis of the C-odd nature of the two photon exchange contribution. The experimental observations both in space and in time like regions do not report evidence of a sizeable contribution of two photon exchange. Other explanations for this discrepancy are favored, as the relevance of high order radiative corrections or a careful reanalysis of the data including correlation and normalization issues [63]. Note that recent and precise calculations of first order radiative corrections [10, 11] do agree with the LSF method up to the K-factor.

The calculation of charge asymmetry in frame of the analytical model [56], shows that the radiatively corrected charge asymmetry does not exceed a 2% deviation form unity, with no indication of increase with \(Q^2\). The precision of first order calculations is by definition of the percent level, which explains that the difference among first order calculations may reach 2-3%. Let us note that a \(\ge \) 5% correction is required to solve the FFs discrepancy, accompanied by a nonlinear change in the \(\epsilon \)-slope of the Rosenbluth plot.

Some model independent indications of the non-relevance of two photon exchange in the FFs discrepancy are

  • \(\mu p\) elastic scattering can be calculated exactly, the tw-photon contribution is small and it is an upper limit of ep elastic scattering [64, 65];

  • concerning inelastic channels, calculations give opposite contributions for the \(\Delta \) [66], and other resonances [67]. Possible inelastic channels eventually cancel the small elastic contribution, what is expected from sum rules [56];

  • the loop integral is maximum when the two photons share the momentum transfer squared. It has been shown that such enhancement does not exceed a factor of \(2\alpha /\pi \) (see Figure 3 in Ref. [29]) .

As for today, there is no experimental evidence of an enhancement of two photon exchange: the linearity of the Rosenbluth plot is confirmed [21, 51], as well as the \(\epsilon \)-independence of the polarization ratio [34] and a negligible charge asymmetry in \(e^{\pm }p\) scattering [53,54,55].

However, a quantitative and precise measurement of the two photon exchange mechanism is important as a relevant contribution of such mechanism would imply to reconsider the analysis of a large number of experimental results.

Other C-odd contributions to the elastic ep reaction may arise due to Z-boson exchange. For moderate to large energies, but smaller than the Z-boson mass, \(\sqrt{t}/M_Z\ll 1\), the Z-boson exchange can be neglected. Its contribution can be evaluated to be of the order of \({{{\mathcal {A}}}}_Z\sim (t/M_Z)^2a_va_a\sim 10^{-6}\) where \(a_v\) and \(a_a\) are the vector and axial coupling constant of the Z boson with the electron [56].