Disappointing Survival Forecast for a Local Population of Androsace albana in a Random Environment

Abstract

A local population of Andropace albana, a short-lived perennial plant, has been monitored during 10 years on permanent plots laid down in an alpine lichen heath in 2009. We summarize the outcome of monitoring as a non-autonomous matrix model of stage-structured population dynamics. The model originates from a life cycle graph constructed earlier for the stages of ontogenesis and consists of 9 annual “projection” matrices that are calibrated in a unique way from the observation data. Five of the 9 matrices have their dominant eigenvalues greater than 1, i.e., give favorable forecasts for the local population survival, while the rest four have those values less than 1, i.e., give the negative forecasts. To make the resulting prediction, we apply an original concept of the pattern-geometric averaging of given nonnegative matrices and obtain the dominant eigenvalue, λ₁(G₉), of the average matrix G₉ markedly less than 1, indicating the population decline in the long term. The traditional method to forecast the local population is to estimate λ_S, the stochastic growth rate of the population in a random environment formed by a random choice from the same 9 annual matrices. Assuming the choice to be independent and equiprobable, we obtain the negative result as well, yet with higher quantitative values of λ_S. We associate these higher values with the artificial assumption of equal choice probability when forming the random sequence of annual matrices, each of which is indirectly reflecting the habitat conditions that have influenced the growth and development of plants during the year prior the calibration moment. This motivates the task to construct a more adequate model for choosing annual matrices, in which the probability of choice would be related to the dynamics of the real habitat factors for a given local population.

INTRODUCTION

The prognosis of local population survival is obtained from assessing its current state, and some quantitative indicators were proposed in the Russian literature to compare local populations. For instance, Δ, the age index; ω, the efficiency index, I_r, the renewal index, I_ag, the aging index (Zhukova, 1995; Glotov, 1998; Zhivotovsky, 2001) are all calculated from data on the population stage structure. However, the actual meaning of ‘age’ does not imply knowing the age in chronological units (years) and the corresponding index is determined by the ratio of young and senescing stages in the population structure. From known particular indices, botanists responsible for including species into the regional Red Books are trying to develop general indicators whose actual values would provide for judgments of the state of a local population, thus to formulate recommendations for making decisions on the inclusion of the species in the Red Book (see, e.g., Klinkova et al., 2011). For example, the vitalitet, an indicator of vitality (degree of prosperity or oppression), based on a strict quantitative assessment of one parameter in the individual plant structure (Zlobin, 1989a, 1989b, 1998), is included into the vitality index based on several parameters (Ishbirdin and Ishmuratova, 2004, 2009; Zlobin, 2009). Here, the way to divide measurements into discrete classes of vitalitet is arbitrary by the expert, as well as to give particular weights to different individual parameters when composing the total index. Similar elements of arbitrary expert decisions in the development of quantitative indicators are also characteristic of other indices as well (Ishbirdin and Ishmuratova, 2004, 2009; Zlobin, 2009). Indisputable positions such as the shift towards younger stages of ontogenesis in the structure of a growing population are taken into account in the indices by the expert method again. The choice of specific indicators from a very diverse set of existing indices also remains at the expert discretion. The question of whether such indices are capable of reflecting a changing trend in the local population dynamics with a sharp change in living conditions and giving a long-term forecast of the state remains outside the scope of the proposed approaches to calculating indices.

In world practice, matrix models of discrete-structured populations developed on the basis of certain (observable and/or measurable) trait of individuals: age, size, stage of development, etc., are long and fruitfully used to assess the state of local populations and to compare them (Caswell, 2001, and references therein). The classical Perron–Frobenius theorem for non-negative matrices (Gantmakher, 1967; Horn and Johnson, 1990) serves as a theoretical foundation for matrix population models, and an impressive set of characteristics of the local population has been developed on its basis, as well as methods to calculate them from the population projection matrix (PMP) L, the core of the matrix model (see textbook: Logofet and Ulanova, 2018), which transforms (“projects” in the unlucky, yet well-established, terminology) the vector, x(t), of the stage structure at the year of observation t into a similar vector of the year t + 1 according to the rule of linear algebra: x(t + 1) = Lx(t).

In particular, the dominant eigenvalue, λ₁(L), of the matrix L serves as a quantitative measure of how the local population is adapted to environmental conditions, and the value of this measure is specific in space and time, namely, it reflects the state of the population where and when the data are collected for calibrating the matrix L (On the ground …, 2013; Logofet et al., 2014, 2016, 2017a, 2017b). Therefore, on the one hand, the PMP is an effective tool for the comparative demography of species, and on the other hand, requirements are increasing for the calibration of PMP according to empirical data to be reliable (On the ground…, 2013; Logofet et al., 2014, 2016, 2017a, 2017b).

Matrix models become more and more popular in scientific and practical fields: the global COMPADRE/ COMADRE databases for plant and animal species contain already more than 7000 and about 2000 published models, respectively (COMPADRE, 2019; COMADRE, 2019).

Monitoring the status of local populations continues in time, and if we get more than one PMP, i.e., their time series (for example, a series of “annual” PMPs as in our projects), then the forecast of local population viability by means of the dominant eigenvalue λ₁(L) can both change quantitatively and qualitatively, from the population growth to decline (Logofet et al., 2017b, 2018a, 2018b, 2019). The ideology of long-term forecasting in this case is based on the concept of “environmental stochasticity” (Tuljapurkar, 1990; Caswell, 2001, Ch. 14). The essence of the concept is that each PMP is considered as a generalized characteristic of the environment and then the environment changing in a long series of years is equivalent to changing matrices in an equally long sequence, and “randomly changing environment” is equivalent to choosing a matrix randomly from the available set at every step of the sequence.

It was long been established mathematically (Oseledec, 1968; Cohen, 1976) that (under certain restrictions on the nature of randomness) such a sequence converges with probability 1 to a limit as t → ∞, i.e., at an infinitely large number of steps, and this limit determines a value, which was later called λ_S, the population stochastic growth rate (Tuljapurkar, 1986)— by analogy to (yet with a difference from) the asymptotic rateλ₁(L). If λ_S > 1, then the total population size increases exponentially with probability 1; if λ_S < 1, then it tends to zero (Tuljapurkar, 1986).

The elegant idea and a good term contributed to the further development of the theory in the directions motivated by the needs of practice: no one was going to take the infinite number of steps, and mathematical theory has proposed some estimates of λ_S based on certain assumptions about stochastic characteristics of the matrices to be chosen (Tuljapurkar, 1990; Caswell, 2001; current review in Sanz, 2019). In particular, if we consider the set of annual PPMs as a small random noise that additively changes some average matrix A, then the estimate of λ_S can be obtained from λ₁(A) (the dominant eigenvalue of the average matrix) and the variance of the probability distribution for the variations (Caswell, 2001), the average matrix then being the arithmetic mean of the given set of PPMs. However, significant changes in the annual matrices such as those that are observed in alpine short-lived perennials (Logofet et al., 2017b, 2018a, 2018b, 2019) make one doubt the fidelity of the low noise paradigm and look for a different paradigm of averaging the annual PPMs obtained as a result of long-term monitoring (Logofet et al., 2017b, 2018a, 2018b, 2019; Logofet, 2018).

An original concept of the pattern-geometric mean of given PPMs (Logofet et al., 2017b, 2018a, 2018b, 2019) proceeds from the logic to transform the population structure vector for the entire observation period—from the initial to the last moment—and imposes a natural requirement on the pattern of the average matrix: it must coincide with the pattern of the matrices to be averaged, i.e., correspond to the life cycle graph, a graphic expression of knowledge about the biology of the species and the mode of monitoring (Caswell, 2001; Logofet and Ulanova, 2018). This logic leads to formulating the mathematical problem of pattern-geometric averaging for given non-negative matrices, which can be solved by modern computer technology (for example, in the MatLab system), when the size of the matrices is small, for instance, 4 × 4 or 5 × 5, as for alpine short-lived perennials (Logofet et al., 2017b, 2018a, 2018b). The matrix G thus found summarizes the entire monitoring period with its dominant eigenvalue λ₁(G) and other characteristics.

Annual observations of the of the Androsace albana local population at constant sites have been ongoing since 2009 (Logofet et al., 2018b), and every next year adds a new matrix to the PPM set as a starting point in estimating the stochastic growth rate and in the problem of pattern-geometric averaging. This paper presents survival forecasts for the local population obtained by the two above methods. Both estimates turned out to be noticeably less than 1, which indicates population decline in the long term.

MATERIALS AND METHODS

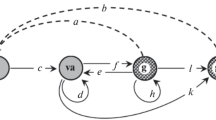
Object. In botanical literature, Androsace albana Stev. is often regarded as a herbaceous biennial tap-root monocarpic species (Shishkin and Bobrov, 1952; Shkhagapsoev, 1999). According to our data, A. albana manifests itself in the alpine lichen heaths as a herbaceous chamaephyte, summer-green, tap-root, monocarpic perennial. The species is included into the Red Data Book of the Krasnodar Krai: Plants and Fungi (Krasnaya kniga Krasnodarskogo..., 2007) and the The Red Data Book of the Republic of Adygea (Krasnaya kniga Respubliki Adygeya..., 2012) as a Category 3 rare species. The biology, ecology, and ontogenesis of the species were described earlier (Kazantseva, 2016; Logofet et al., 2018b), and a life cycle graph (LCG) was constructed (Fig. 1).

Fig. 1.

Life cycle graph of Androsace albana: pl, plantules; j, juvenile plants; im, immature plants; v, adult vegetative plants, and g, generative plants.

Along with consecutive transitions from stage to stage in 1 year, the following were also observed:

—delays in stages im and v explainable by the fact that the harsh conditions of the highlands force the plants to resort to the “space-holder strategy” (Körner, 2003), which means staying or growing in one place for as long as possible. Soil poorness results in some virginal plants accumulating resources for fruiting longer than one year (Rabotnov, 1950, 1978; Bender et al., 2000; Körner, 2003; Keller and Vittoz, 2014);

—accelerated transitions plim as a manifestation of polyvariant ontogeny in A. albana under the conditions of the alpine belt in S.-W. Caucasus.

There is only one reproductive event in the life cycle of monocarp plants, but the population recruitment may turn out to be at each of the three stages pl, j, or im, at the moment of next census. Accordingly, the parameters a, b and c have the meaning of the average (per generative plant) number of recruiting individuals found by the next census at the corresponding stage.

The local A. albana population under study is a normal complete population, i.e., it contains individuals of all stage statuses. In some years, its “age spectrum” in the terminology of Uranov (1975) can be recognized as left-handed; in others, the maximum shares occur at the stage of adult plants. In the (arithmetic) average over 10 years of observation: 48% of the population are seedlings and juvenile individuals, 50% are immature and adult virgin, and only 2% are generative.

Methods of study. The research is carried out in the Karachay-Cherkess Republic, the territory of Teberda State Biosphere Reserve, on permanent plots laid in 2009 in a lichen heath, on the Malaya Khatipara mountain at the altitude of 2800 m asl. (Logofet et al., 2018b). Two 1.25 × 0.25 m transects were laid, 5 plotsd of 0.25 × 0.25 m in size each. All individuals of A. albana were plotted on site plans with their serial numbers and labels of their ontogenetic states (stages). The next year, individuals recorded last year are given their last year numbers, and new individuals are assigned new ones; in all individuals, their ontogenetic state at the time of the current observation are determined. Monitoring is carried out every year at the end of August for 10 years, from 2009 to 2018; the previously published data series (Logofet et al., 2018b) has been expanded for another 2 years.

The data collected are of the “identified individuals” type (Caswell, 2011, p. 134), i.e., contain information about the stage of each individual A. albana plant from the moment it appears on the site and until flowering, with a 1-year time step. Therefore, along with the local population structure in each year of observation (Table 1), the events of transitions between stages are also known (Table 2). To date, the time series of data has been expanded to 2018 inclusive.

Table 1.   Structure of the local A. albana population by years according to observation data (expanding Table 1 from Logofet et al., 2018b)

Table 2.   Numbers of recruited individuals and transitions along the LCG arcs (Fig. 1) according to the census data (expanding Table 2 from Logofet et al., 2018b)

Matrix model and the calibration of matrices. In the matrix model, the population structure is described by the (column-)vector x(t) = [pl(t), j(t), im(t), v(t), g(t)]^T, whose components are the number of individuals found at the corresponding stages of ontogenesis in the year t of observation. Observable changes in vector x(t) through years (Table 1) are described by the basic model equation in the vector-matrix form:

$$x\left( {t + {\text{ }}1} \right) = L(t)x(t),\,\,\,\,~t = 0,1, \ldots ,8,$$

(1)

where L(t) is the population projection matrix of (PPM, Caswell, 2001) associated with the LCG (Logofet and Belova, 2007) that is shown in Fig. 1. All nine PPMs L(t) have the 5 × 5 size and the following pattern in common:

$$L = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&a \\ d&0&0&0&b \\ e&f&h&0&c \\ 0&0&k&l&0 \\ 0&0&0&m&0 \end{array}} \right];\,\,\,\,a,\,\,b,\,\, \ldots ,\,\,l,\,\,\,\,m \geqslant 0,$$

(2)

although some of the demographic parameters (vital rates) a, b, …, l, m may turn out to be zeros in some years due to the lack of corresponding transitions in the data (Table 2). When coupled with the changing population structure (Table 1), these data enable calibrating the PPM with absolute accuracy and accordance with Eq. (1) and the meaning of the parameters as the frequencies of the corresponding transition events recorded in the observations. Thus, whether the method is objective and reliable is only determined by the data themselves. This is a huge advantage of the matrix model, but it also poses a problem for long-term survival prediction when, as a result of calibration, the model turns out to be inhomogeneous in time (nonautonomous).

The forecast is obtained from the value λ₁(L), the dominant eigenvalue of the calibrated PPM L, which shows the asymptotic growth rate of the population: if L(t) = L remains constant in time, then the population structure x(t) converges as t → ∞ to an equilibrium, the eigenvector x* corresponding to λ₁(L); the dynamics x(t) ~ λ₁(L) ^tx*, i.e., tends to geometric growth (or decline) with the exponent λ₁(L) > 0 (Logofet, 1993; Caswell, 2001; Logofet and Ulanova, 2018). Therefore, the forecast for the local population survival is positive if λ₁(L) > 1, and negative if λ₁(L) < 1. In the nonautonomous model, the value of λ₁(L) changes along with the changing matrix L(t), leaving the final forecast uncertain.

Survival forecast through averaging the annual PPMs. To fix ontogenetic transitions and population recruitment, data from two consecutive censuses (at times t and t + 1) are necessary, and therefore the number of calibrated PPMs is always one less than the number of observation years (10 years of observations provide for 9 calibrated matrices L(t)). There is no reason to believe that they will turn out equal each other, and the practice of calibration do show differences not only quantitative, but also qualitative: in some years, the survival forecast changes to the opposite (Logofet et al., 2018a, 2018b, 2019). What is able to reflect the outcome of the entire monitoring period is a matrix, G, found as the pattern-geometric average of nonnegative matrices (Logofet, 2018).

The logic of pattern-geometric averaging is as follows: according to the calibrated model (1), the vector, x(0), the population structure at the initial moment of observation, t = 0, transforms to x(9), the structure vector at the last moment, t = 9, by successively multiplying x(0) with 9 annual PPMs L(t), i.e., (after renaming L(t) = L_t)

$$x(9) = {{L}_{8}} \cdot {{L}_{7}} \cdot {{L}_{6}} \cdot {{L}_{5}} \cdot {{L}_{4}} \cdot {{L}_{3}} \cdot {{L}_{2}} \cdot L \cdot {{L}_{0}} \cdot x(0).$$

(3)

The average matrix G should do exactly the same, hence

$${{G}^{9}} = {{L}_{8}} \cdot {{L}_{7}} \cdot {{L}_{6}} \cdot {{L}_{5}} \cdot {{L}_{4}} \cdot {{L}_{3}} \cdot {{L}_{2}} \cdot {{L}_{1}} \cdot {{L}_{0}}.$$

(4)

Equation (4) declares the geometric (or multiplicative) nature of averaging, while the pattern (2) common to all the matrices to be averaged requires the same of the average matrix G. Also, it is logical that all elements of the average matrix do not go beyond the boundaries of those to be averaged.

This logic leads to the mathematical problem of minimizing the approximation error in solving the matrix Eq. (4) (Appendix A). The position of the dominant eigenvalue, λ₁(G), of the average matrix G with respect to 1 enables us to conclude about the long-term fate of the local population basing on ten years: growth, if λ₁(G) >1, decline if λ₁(G) < 1, stabilization, if λ₁(G) = 1.

It is interesting to trace how this indicator changes when we add the matrix L(t) obtained in the next monitoring year, t + 1, to the previous PPMs to be averaged, the number of years varying from 2 to 9. The method itself remains the same, but only the number of factors changes in the product of annual PPMs in Eq. (4) and, accordingly, the power that matrix G is to be raised to.

Survival forecast through the stochastic growth rate. The stochastic growth rate of a population in a randomly changing environment is the value of λ_S defined by the following limit (Tuljapurkar, 1986, 1990; Caswell, 2001):

$$\mathop {\lim }\limits_{\tau \to \infty } \frac{1}{\tau }{\text{log}}N(\tau ) = \lim \frac{1}{\tau }{\text{log}}{{\left\| {{{L}_{{\tau - 1}}} \ldots {{L}_{0}}x(0)} \right\|}_{1}} = {\text{log}}{{\lambda }_{{\text{S}}}},$$

(5)

where L_τ–1 is the annual matrix chosen randomly from the available set of annual PPMs at the step τ = 1, 2, …; N(τ) denotes the total population size, and || … ||₁ the norm as the sum of vector components in absolute value.

In the simplest case, the random choice is of type i.i.d. (independent, identically distributed; etc.), i.e., the choice does not depend on the result at the previous step and the probability distribution of matrices remains the same. A value of λ_S with respect to 1 indicates an exponential increase or decrease in the total size, thus giving the forecast for the local population survival in the long term. We obtain the estimate of λ_S by the direct method, i.e., approximating the value of the limit (5) by a far enough (from the beginning), yet finite, member of the infinite sequence; finite realizations of random sequence (5) are obtained by the Monte Carlo method. Each of them gives, by chance, its own different estimate of λ_S, and therefore the result of applying the method is a range of estimates (from minimum to maximum) obtained on a finite set of realizations.

RESULTS

Retrospective data correction. Along with the ontogenetic transitions and the population recruitment at the 2017 → 2018 step, the last-year observations have recorded exiting out of secondary dormancy in the ontogenesis of A. albana: individuals who were considered dead due to severe drought for two consecutive years (2016–2017) have come to life and are continuing to grow. Thus, the previously fixed population structure has changed: in comparison with the previous data (Logofet et al., 2018b, Table 1), the components v(2016), im(2017), and v(2017) have received new values (Table 1). The pattern of transitions (Table 2) has changed accordingly, compared with the previous one (Logofet et al., 2018b, Table 2), and after it, the corresponding annual matrices L(t) have changed too.

Calibrated matricesL(t). The calculation of PPM elements is provided by Table 2, in which all the recruited plants and transitions between stages recorded in the observation data are calculated. We obtain the elements of the annual matrices L(t) (Table 3, 1st and 2nd columns) by dividing the corresponding cells of Table 2 by the size of the proper group.

Annual PPMs L(t) (Table 3), calibrated according to the observational data, gives an objective, yet indirect, picture of variations in the environmental conditions to which the local population is sensitive, and this picture convinces that the conditions have been quite crucial: the adaptation measure λ₁(L(t)) fell in some years to extremely low values, for example, below 0.4 in the interval 2014–2015 between censuses, while the recruitment sizes in 2015, 2017 were the smallest over the entire observation period in all three stages (Table 2). In that interval, the conditions for the young A. albana plants (seedlings, juveniles, immatures) survival, overwintering, and growth of adult individuals (vegetative and generative) were perhaps the most severe for the entire observation period. Were they repeated at least 2 years in a row, then the local population would have decreased to more than 0.42 × 100% = 16% of its size, if 3 years in a row, then to 0.43 × 100% ≈ 6%.

However, the next year, i.e. in the 2015–2016 interval, the conditions improved and, as a result of the retrospective 2016 data correction, the previous forecast for a decline, i.e., λ₁(2015) = 0.8382 (Logofet et al., 2018b, Table 3) has changed to a more favorable one: λ₁(2015) = 1.0679.

Along with λ₁, the adaptation measure, the annual PPMs offer also the corresponding eigenvector x* (4th column of Table 3), a steady-state structure that the population would have if these conditions remained unchanged for a long enough time. Among the steady-state structures for different years, there is no distinct tendency towards the left-sided “age spectrum”—even among growing populations the distribution is more likely to be two-humped, with the humps merging sometimes into a “plateau” over the juvenile and immature stages.

Whether the observed (relative) structure x(t + 1) is far from equilibrium can be seen from the measure of difference between these vectors according to Keyfitz (Keyfitz, 1968), the values of which are presented in the neighboring column of Table 3. Basically, they do not exceed 10–20% (with a maximum theoretical distance of 100% between two structures).

In general, the differences among the annual PPMs are very significant, with 4 out of 9 matrices giving a measure of adaptation λ_S(L) that is noticeably less than 1, the remaining 5 are markedly greater than 1. Does this predominance give a favorable forecast for the local population survival as a result of a 10-year monitoring? Simple “arithmetic” reasoning leaves this question open.

Pattern-geometric mean of the annual matrices. The matrix presented in the last row of Table 3 gives an approximate solution for the 9 matrices from this Table with acceptable approximation accuracy. Its pattern does obviously correspond to the LCG (Fig. 1), and the values of the transition and reproduction rates do not go beyond the boundaries defined by the corresponding elements of the matrices to have been averaged (Table 3).

There is a tendency clearly seen in the transitional part, T, of matrix G that occurred only in some annual matrices T(t): in each column, the positive elements decrease with increasing row number. In a unidirectional (i.e., without regression links) process (Fig. 1), this means that plants are more likely to delay development rather than move to the next stage and accelerated transitions (skipping one stage) are less likely than sequential ones.

Despite the values of λ₁(t) > 1 for 2010–2012, 2015, 2017, the tendency to decrease prevails in the local population over a 10-year observation period, which is expressed by the value of λ₁(G(8)) < 1. The pattern of the population steady-state structure (normalized dominant eigenvector y*) is rather likely two-humped than left-handed, with maxima in the juvenile and adult vegetative stages. Thus, it differs fundamentally from the structure obtained by arithmetic averaging (Table 1), adding another argument against the arithmetic mean in matrix models.

When the number, m (equal to t + 1), of the PPMs to be averaged increases successively from 2 to 9, certain regularities are observed in the averaging results. For instance, the averaging error decreases with increasing m; if the next L(t) added to the set of averaged PMPs has λ₁(L(t)) less than 1, then the average matrix G_m also decreases its λ₁; if the next L(t) has λ₁(L(t)) greater than that of the previous one, then the average G_m increases its λ₁, too. Thus, the sensitivity of the pattern-geometric mean to changes in the set of matrices to be averaged is logically correct, i.e., this method is well-grounded to predict survival. The pattern of the steady-state structures corresponding to the average matrices is two-humped (as after averaging 9 matrices), with maxima in the juvenile and adult vegetative stages. Their differences from the population structures observed at the current moment t + 1 are less than 8%, and they are extremely small for 7 and 9 annual matrices, less than 1% (Table 3, the far right column).

Table 3. The outcome of A. albana PPM calibration according to the 2009–2018 data and the pattern-geometric average (G_m) of the increasing number, m = t + 1, of matrices L(0), L(1), …, L(t), t = 1, …, 8

Estimation of the stochastic growth rate. The results of λ_S calculations are presented in Table 4 for four values of the length of the finite sequence with randomly chosen PPMs and three options for the number of random irealizatations of this sequence. The larger this number, the logically wider the range of λ_S estimates, while the growth of the matrix “product length” narrows the range naturally, illustrating the fundamental property of convergent sequences. The width of the range varies from 20 to 96 thousandths, revealing the hundredths to be a reliable significant figure. The range [0.956316, 0.958686], obtained from the longest sequence after the greatest number of realizations should be recognized as the most reliable.

Table 4.   Estimating the stochastic growth rate, λ_S, of the local A. albana population by the direct Monte Carlo method with an equally probable choice of 9 one-year PPMs (Table 3)

All the ranges of λ_S estimates are located to the left of 1, giving, like the method of pattern-geometric averaging (Table 3), a negative forecast of the of local population survival. However, the quantitative difference in the results of both methods is already observed in the second decimal place, which makes us think of the reasons for this discrepancy.

DISCUSSION

One of the possible reasons for such a noticeable quantitative difference between λ_S and λ₁(G₉) equal to 0.89264 could be seen in the averaging error, which arises objectively due to the lack of an exact solution of Eq. (4). To say the truth, rare cases are known where the exact solution does exist due to the digraph of transitions (e.g., between possible states in a Markov model of two-state dwarf-shrub community) being complete, i.e. having transitions form each state to any other and to itself (Logofet and Maslov, 2019). But such a completeness is principally impossible in the life cycle graph reflecting the course of ontogenesis, so that a nonzero error of averaging is objectively inevitable. But it was only about 0.01 (Table 3) while the minimal difference between the estimates of λ_S and λ₁(G₉) is about 0.06 (Table 4). The reasons for this discrepancy should apparently be deeper, and the concept of the pattern-geometric mean of non-negative matrices (Logofet, 2018) needs further mathematical study.

The transition to vegetation dormancy in the life cycle of alpine plants is a principally known phenomenon (Shefferson, 2009); however, it has been found for the first time in the studied A. albana population after 10 years of monitoring. The corresponding 2016–2017 data correction caused changes in the annual PPMs, the matrix L(2015) yielding even the qualitative change in the forecast: from the value of λ₁(L(2015)) < 1 (Logofet et al., 2018b, Table 3) to λ₁(L(2015)) > 1 after the data correction. However, despite this circumstance and some optimism caused by the favorable state of A. albana local population in 2018, the results summarizing the 10-year monitoring period predict the population decline by each of the methods applied. Both of them are sill open for criticism—if not in the ideological aspect, then at least in methodological one.

Pattern-geometric averaging is motivated by the logic of monitoring, but the corresponding mathematical problem of finding an approximate solution to the averaging equation is computationally difficult, and the approximation error is not yet amenable to theoretical estimates. This error varies from about 0.7 to 0.01 when averaged are from 2 to 9 A. albana PPMs, decreasing with an increase in the number of matrices to be averaged (Table 3). Still it seems to be acceptable for a qualitative prediction of survival.

In spite of the wide variety of theoretical approximations and estimates for λ_S, the stochastic growth rate (Caswell, 2001; Sanz, 2019), the direct estimation method should be considered the most reliable of all existing ones (because it is justified by the fundamental lemma of mathematical analysis about convergent sequences), if not for one weak point: in the absence of reliable information about the law of alternation of annual matrices in sequence (5), their random choice was taken equally probable at each step and independent of the choice at the previous step (i.i.d.).

Of course, i.i.d. is a caricature of reality, as far as changes in the habitat conditions crucial for the growth and development of plants follow their own laws. Their effect during the year from the moment of the previous census is indirectly reflected by a set of vital rates (matrix elements) calibrated according to the observation data at the current moment, i.e., by the corresponding annual PPM. Therefore, the first step towards reality was made in theoretical works (Cohen, 1976, 1977a, 1977b) with ergodicity theorems (in other words, suitability for modeling dynamics) for the age structure of a population if the random sequence of Leslie operators is governed by an ergodic Markov chain. Later, the class of operators was expanded to the PPM for a generalized staged structure (Tuljapurkar, 1986, 1990; Caswell, 2001), but the Markov chain remained homogeneous (in time) as before. Practical illustrations of the “governing” Markov chain still do not go beyond artificial constructions—from simple switching between “good” and “bad” PPMs in the simplest case (Sanz, 2019) to quite sophisticated (but still artificial, imposed by the author’s will) schemes pretending even to simulate the effects of global climate change on the random choice of annual matrices for a local population (Rees and Ellner, 2009; Ozgul et al., 2010; Williams et al., 2015). No attempt to connect the governing chain with changes in real environmental factors that determine seed germination and plant growth/development has come to our notice.

Meanwhile, the factors themselves certainly exist and have been noted by biologists of A. albana and other alpine species (Rabotnov, 1950, 1978; Grime, 1979, 2001; Serebryakova, 1985; Zhukova, 1986, 1995; Chambers, 1993; Bowers et al., 1995; Bender et al., 2000; Körner, 2003; Onipchenko, 2004, 2013; Adzhiev and Onipchenko, 2011; Keller and Vittoz, 2014). Presenting the course of changes in those factors over the years in the form of a Markov chain that would govern the changes of PPMs in the random sequence (5) is the task whose solution would make the direct method for estimating λ_S truly the most reliable.

CONCLUSIONS

The outcome of long monitoring of the stage structure in a population of a short-lived perennial species in permanent plots are reflected in a forecast of local population survival, which ensues from the corresponding nonautonomous matrix model. The data of 10 observation years make it possible to unambiguously calibrate 9 one-year PPMs, and an original concept of the pattern-geometric mean (G₉) leads to the prediction of local population survival as the dominant eigenvalue, λ₁(G₉), of the average matrix. The obtained value of λ₁(G₉) equals 0.89264, which is noticeably less than 1 and means population decline in the long run.

The survival forecast from the range, [0.956316, 0.958686], of estimates for λ_S, the stochastic growth rate of the population in a random environment (formed by a random choice from the same 9 matrices), turned out to be less pessimistic, yet for decline, too. However, the quite artificial assumption of the equal probability of choosing each of the 9 matrices to form the random environment undermines the belief in the quantitative value of this forecast. The challenge is therefore to develop a model of random choice adequate to the dynamics of changes in habitat conditions that affect the growth and development of the local population of this species.

The Problem to Average the Population Projection Matrices

Equation (4) to find the patter-geometric mean matrix G contains 5 × 5 matrices and 10 unknown parameters a, b, …, l, m. The product of nine PPMss on the right-hand side of the equation is a positive matrix, which means that the matrix equation is equivalent to a system of 25 nonlinear algebraic equations with respect to 10 unknowns, i.e., an overdetermined system. Such systems do not have any exact solution, and we are looking for the best approximate solution, i.e., such a set of parameter values that delivers a minimum to the quadratic sum of deviations from zero for all 25 elements of the matrix difference between the left- and right-hand sides of Eq. (4). Formally, we solve the following problem of bounded minimization:

$${{\min }_{\mathbb{B}}}\left\| {{{{\left[ {\begin{array}{*{20}{c}} 0&0&0&0&a \\ d&0&0&0&b \\ e&f&h&0&c \\ 0&0&k&l&0 \\ 0&0&0&m&0 \end{array}} \right]}}^{9}} - {{L}_{8}}{{L}_{7}} \ldots {{L}_{1}}{{L}_{0}}} \right\|,$$

(A1)

where ||…|| denotes the Euclidean norm, while the exact form of the product L₈·L₇·…·L₁·L₀ obtained by means of machine symbolic algebra is too cumbersome to publish.

In the constraint minimization problem (A1), the above parameters a, …, m are the variables whose set, $\mathbb{B}{\text{,}}$ of feasible values represent a parallelepiped in $\mathbb{R}_{ + }^{{10}},$ obtained from the following considerations. Being the elements of the average matrix, vector [a, …, m] = $g \in \mathbb{R}_{ + }^{{10}}$ should not go out of the ranges of their values in the matrices L_t (t = 0, 1, …, 8) to be averaged, i.e.,

$${\text{min}}L \leqslant g \leqslant {\text{max}}L.$$

(А2)

Here, vectors minL and maxL are composed of the corresponding entries to the positions a, …, m within the matrices L_t:

$${\text{min}}L = .{\text{min}}\{ {{L}_{0}},{{L}_{1}}, \ldots ,{{L}_{8}}\} ,$$

(A3)

$${\text{max}}L = .{\text{max}}\{ {{L}_{0}},{{L}_{1}}, \ldots ,{{L}_{8}}\} ,$$

(A4)

and the dot before the function name means its element-wise execution.

Strictly speaking, the substochasticity conditions of the transition part, T = G – F, for those columns that contain more than one nonzero elements (restrictions on single elements automatically follow from (A2)), i.e.,

$$d + e \leqslant 1,~\,\,\,\,h + k \leqslant 1,\,\,\,~l + m \leqslant 1$$

(А5)

should cut a polyhedron out of the parallelepiped $\mathbb{B}$. However, it is technically simpler to verify the substochasticity of T in the optimal solution obtained for $\mathbb{B}$.

We find the solution to problem (A1)–(A3), as well as to seven similar problems with the number, m = 2, 3, …, 8, of matrices to be averaged, using the library function fmincon (…) in the Matlab computing environment (MathWorks, 2018a). The difference norm from expression (A1) is calculated by the special user-created function, normGm_prodmL(g), of the vector argument $g \in \mathbb{R}_{ + }^{{10}},$ while the lower and upper bounds of the variables are given by conditions (A2), where the extrema are determined from the first m matrices L_t; the actual value of m is set directly in the function body.

The procedure of constraint minimization is launched by the Matlab line

$$\begin{gathered} \gg \left[ {g,FVAL} \right] = fmincon(@normGm\_prodmL, \\ g{\mathbf{0}},{\text{ }}\left[ {~} \right],\left[ {~} \right],\left[ {~} \right],\left[ {~} \right],{\text{min}}{\mathbf{L}},{\text{max}}{\mathbf{L}}) \\ \end{gathered} $$

(А6)

after choosing an algorithm and appropriately tuning the technical parameters of optimization with the optimtool options (MathWorks, 2019b); the notation “[], [],” means the absence of equality constraints and substantial inequalities of type (A5) in the formulation of the problem, vector $g0 \in \mathbb{R}_{ + }^{{10}}$ is the starting point of the solution search algorithm; the output argument (on the left-hand side of (A6)), $g \in \mathbb{R}_{ + }^{{10}}$, is a (local) solution found to the problem; FVAL is the corresponding minimum value of the function normGm_prodmL, the error of averaging in the Table 3.

As a result of (A6), we obtain some local minimum, while the global minimum (among several dozen local ones) is found by the GlobalSearch procedure (MathWorks, 2019c) with the technical “tolerance” settings (ibid.) at the level of 10^–12.