INTRODUCTION

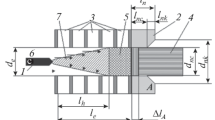
The laminar plasma jet is an extremely efficient tool in the modern plasma technologies. However, creation of a laminar arc plasma torches requires specific definition of conditions in the plasma flow stabilization zone providing stable formation of the laminar plasma jet at the plasma torch nozzle exit. Experimental studies [1] show that the discharge channel of the laminar plasma torch (Fig. 1) should include a stabilization zone domain providing the average (over the cross section) Reynolds number at the nozzle entrance no greater than 150.

Fig. 1.
figure 1

Structure of the electric arc laminar plasma torch: (1) cathode; (2) anode; (3) interelectrode inserts (discharge channel sections); (4) laminar plasma jet; (5) zone of the laminar jet stabilization; (6) gas flow in the discharge channel; (7) turbulent plasma flow domain; le is the discharge channel length; lh is the domain of gas heating by the arc; dnc is the diameter of the cylindrical part of the nozzle channel; dnk is the diameter of the outlet section of the conical part of the nozzle channel; Δla is the anode spot binding area; de is the diameter of the plasma torch discharge channel.

Full size image

In the present paper, we consider a method of universal characteristics of electric arc as a basis of the heat-exchange electric arc model (HEEAM) making it possible to calculate its temperature characteristics.

HEAT-EXCHANGE ELECTRIC ARC MODEL

At the laminar flow of plasma, the arc column with radius ra in fact totally fills the discharge column with diameter de and, owing to compression by the discharge walls, transfers into the stabilized arc mode. In that case, the coefficient of the arc compression by the walls,

$${{\delta }_{r}} = \frac{{2{{r}_{{\text{a}}}}}}{{{{d}_{e}}}},$$
(1)

exceeds 0.96.

In the arc compression layer, between the column and the discharge channel walls, the process of molecular thermal conductivity dominates over the convective heat transfer; thus, we can calculate the gas temperature in the near-wall arc compression layer from the condition

$${{p}_{\lambda }} = \frac{{2\pi }}{{\ln \left( {\frac{1}{{{{\delta }_{{\hat {e}}}}}}} \right)}}[S({{T}_{{{\text{sa}}}}}) - S({{T}_{{\text{w}}}})],$$
(2)

where pλ is the linear density of the heat flux on the column surface due to the thermal conductivity, Tsa is the isotherm of the arc column surface (for the plasma-producing air gas medium, Tsa = 5300–5700 K), Tw is the temperature of the discharge channel wall, and S(T) = \(\int_0^T {\lambda (T)dT} \) is a property of the thermal plasma mode.

Absence of convective dissipation of the electric field energy in the column volume is a condition for realization of the stabilized arc mode; thus, we can obtain a solution of the energy equation for the stabilized arc column

$$E_{{\text{c}}}^{2}\sigma (T(r)) = {{\sigma }_{\varepsilon }}(T(r)) - \frac{1}{r}\frac{d}{{dr}}\left[ {r\lambda (T(r))\frac{{dT(r)}}{{dr}}} \right],$$
(3)

where σ is the electrical conductivity, σε is the volume radiation density, λ is the thermal conductivity, T is the plasma temperature, r is the column radius, and Ec is the electric field strength of the cylindrical part of the column.

When simulating the arc heat transfer processes in the discharge channel of the laminar plasma torch, we assume that the plasma column is transparent to its own radiation [2]; then, we can consider the stabilized arc column as an optically thin body.

With allowance for the plasma transparency condition, we can apply the electric field superposition principle to the energy equation

$${{E}_{{\text{c}}}} = {{E}_{\lambda }} + {{E}_{\varepsilon }} = \frac{{{{p}_{\lambda }}}}{I} + \frac{{{{p}_{\varepsilon }}}}{I},$$
(4)

where I is the arc current, pλ is the linear heat flux density on the surface of the cylindrical column part due to the thermal conductivity process in the thermal plasma, and \({{p}_{\varepsilon }}\) = \(2\pi \int_0^{{{r}_{{\text{a}}}}} {{{\sigma }_{\varepsilon }}(T(r))dr} \) is the linear density of the column radiation intensity.

With the condition for determining the average plasma temperature and the expressions for the thermal conductivity and radiation characteristics of the stabilized arc plasma column with regard to the temperature profile for the relative radius \(\tilde {r}\) = r/ra, we can write

$$g = 2\pi r_{{\text{a}}}^{2}\int\limits_0^1 {\sigma (T(\tilde {r}))\tilde {r}d\tilde {r}} ,$$
(5)
$${{p}_{\varepsilon }} = 2\pi r_{{\text{a}}}^{2}\int\limits_0^1 {{{\sigma }_{\varepsilon }}(T(\tilde {r}))\tilde {r}d\tilde {r}} .$$
(6)

With allowance for the electric field superposition (4), we determine the temperature profile over the stabilized arc column cross section T(\(\tilde {r}\)) from the equation

$$E_{\lambda }^{2}\sigma (T(r)) = - \frac{1}{r}\frac{d}{{dr}}\left[ {r\lambda (T(r))\frac{{dT(r)}}{{dr}}} \right].$$
(7)

Using the property of the thermal plasma potential S(T), we rewrite the Eq. (7) as

$$\sigma (S(r))E_{\lambda }^{2} = - \frac{1}{r}\frac{d}{{dr}}\left[ {r\frac{{dS(r)}}{{dr}}} \right].$$
(8)

Under the condition of linearization of the thermal function σ(S) (Fig. 2), Eq. (8) has a tabular solution

$$S(\tilde {r}) = {{S}_{{{\text{sa}}}}} + ({{S}_{0}} - {{S}_{{{\text{sa}}}}}){{J}_{0}}(2.405\tilde {r}),$$
(9)

where J0 is the zero-order Bessel function.

Fig. 2.
figure 2

Linearization of the σ(S) thermal function for air plasma at atmospheric pressure.

Full size image

We can account for the nonlinearity of the thermal function σ(S) in the solution of Eq. (8) by using the calculation algorithm shown in Fig. 3 [3]. In that case, to determine the profile of the temperature distribution over the stabilized arc column cross section T(\(\tilde {r}\)), double integration is required with application of the method (proposed in [3]) of correction of the linear solution, Sj(\(\tilde {r}\)) = S(\(\tilde {r}\)), that assumes the equality of the areas F1 and F2. Thus, we can represent the procedure of double integration with corrections [3] as

$$\begin{gathered} \left. \begin{gathered} {{S}_{j}}(\tilde {r}) = {{S}_{{{\text{sa}}}}} + \frac{{{{p}_{\lambda }}}}{{7.843}}{{J}_{0}}(2.405\tilde {r}) \hfill \\ 2\int\limits_{{{S}_{{{\text{sa}}}}}}^{S(\tilde {r})} {\sigma (S)dS = ({{S}_{j}}(\tilde {r}) - {{S}_{{{\text{sa}}}}})\sigma ({{S}_{j}}(\tilde {r}))} \hfill \\ \end{gathered} \right\} \\ \Rightarrow \,\,S(\tilde {r}) \Rightarrow S(T) \Rightarrow T(\tilde {r}). \\ \end{gathered} $$
(10)
Fig. 3.
figure 3

Algorithm accounting for the nonlinearity of the thermal function σ(S).

Full size image

This procedure makes it possible to calculate the temperature profile of the arc column for the relative radius with allowance for the linear heat flux density, caused by the plasma thermal conductivity, on the column surface [2].

The obtained solution (10) makes it possible to form universal thermal arc characteristics depending only on the chemical composition of the plasma-producing gas and the linear heat flux density on the column surface pλ caused by the plasma thermal conductivity. Here, we have the universal characteristic of the arc conductivity

$$\tilde {g}({{p}_{\lambda }}) = 2\pi \int\limits_0^1 {\sigma (T(\tilde {r}))\tilde {r}d\tilde {r}\,\,\,{\text{[}}{{\text{S}} \mathord{\left/ {\vphantom {{\text{S}} {\text{m}}}} \right. \kern-0em} {\text{m}}}]} $$
(11)

and the universal characteristic of the arc radiation

$${{\tilde {p}}_{\varepsilon }}({{p}_{\lambda }}) = 2\pi \int\limits_0^1 {{{\sigma }_{\varepsilon }}} (T(\tilde {r}))\tilde {r}d\tilde {r}\,\,\,[{{{\text{kW}}} \mathord{\left/ {\vphantom {{{\text{kW}}} {{{{\text{m}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{m}}}^{{\text{3}}}}}}].$$
(12)

For the air medium, we can represent the calculated universal arc characteristics by approximating functions. At pλ ≤ 300 kW/m,

$${{\tilde {p}}_{\varepsilon }}({{p}_{\lambda }}) = \exp \left[ {\frac{{a + c{{p}_{\lambda }}}}{{1 + b{{p}_{\lambda }} + dp_{\lambda }^{2}}}} \right]\,\,\,[{{{\text{kW}}} \mathord{\left/ {\vphantom {{{\text{kW}}} {{{{\text{m}}}^{{\text{3}}}}]}}} \right. \kern-0em} {{{{\text{m}}}^{{\text{3}}}}]}},$$

where a = 0.033937309, b = 0.038198424, c = 0.63630613, and d = –2.6979283 × 10–6,

$${\text{and}}\,\,\,\,\tilde {g}({{p}_{\lambda }}) = \exp \left[ {\frac{{a + c{{p}_{\lambda }}}}{{1 + b{{p}_{\lambda }} + dp_{\lambda }^{2}}}} \right]\,\,\,[{{\text{S}} \mathord{\left/ {\vphantom {{\text{S}} {{\text{m}}]}}} \right. \kern-0em} {{\text{m}}]}},$$

where a = 0.035119868, b = 0.049630468, c = 0.50882931, and d = –1.036762 × 10–6.

At pλ > 300 kW/m,

$${{\tilde {p}}_{\varepsilon }}({{p}_{\lambda }}) = a + b\ln ({{p}_{\lambda }})\,\,\,\,[{{{\text{kW}}} \mathord{\left/ {\vphantom {{{\text{kW}}} {{{{\text{m}}}^{3}}],}}} \right. \kern-0em} {{{{\text{m}}}^{3}}],}}$$

where a = –28172998 and b = 6037033.1,

$${\text{and}}\,\,\,\,\tilde {g}({{p}_{\lambda }}) = \frac{{(a + c\ln {{p}_{\lambda }} + e\ln p_{\lambda }^{2})}}{{(1 + b\ln {{p}_{\lambda }} + d\ln p_{\lambda }^{2})}}\,\,\,\,[{{\text{S}} \mathord{\left/ {\vphantom {{\text{S}} {\text{m}}}} \right. \kern-0em} {\text{m}}}],$$

where a = 26.642965, b = –0.11180005, c = 99.005735, d = 0.0089423796, and e = 302.52812.

CALCULATION OF THE STABILIZED ARC COLUMN CHARACTERISTICS BY THE METHOD OF UNIVERSAL ARC CHARACTERISTICS

The arc universal characteristics (11)–(12) link the integral characteristics of the stabilized arc with the boundary parameter of the column pλ (2) (reflecting the heat transfer conditions for the arc compressed by the walls of the plasma torch discharge channel) by means of the algebraic equations for

– the linear electrical conductivity of the column

$$g = \tilde {g}({{p}_{\lambda }})r_{{\text{a}}}^{2}\,\,\,\,[{{\text{S}} \mathord{\left/ {\vphantom {{\text{S}} {\text{m}}}} \right. \kern-0em} {\text{m}}}];$$
(13)

– the linear density of the column intensity

$${{p}_{\varepsilon }} = {{\tilde {p}}_{\varepsilon }}(p\lambda )r_{{\text{a}}}^{2}\,\,\,\,[{{{\text{kW}}} \mathord{\left/ {\vphantom {{{\text{kW}}} {\text{m}}}} \right. \kern-0em} {\text{m}}}];$$
(14)

– the column radius

$$\begin{gathered} r_{{\text{a}}}^{2} = \sqrt {0.25{{{\left[ {\frac{{{{p}_{\lambda }}}}{{{{{\tilde {p}}}_{\varepsilon }}({{p}_{\lambda }})}}} \right]}}^{2}} + \frac{{{{I}^{2}}}}{{{{{\tilde {p}}}_{\varepsilon }}({{p}_{\lambda }}){{{10}}^{3}}\tilde {g}({{p}_{\lambda }})}}} \\ - \,\,\,0.5\frac{{{{p}_{\lambda }}}}{{{{{\tilde {p}}}_{\varepsilon }}({{p}_{\lambda }})}}\,\,\,[{{{\text{m}}}^{{\text{3}}}}], \\ \end{gathered} $$
(15)

where I is the arc current in amperes;

– and the electric field strength in the column

$$E = \frac{I}{{\tilde {g}({{p}_{\lambda }})r_{{\text{a}}}^{2}}}\,\,\,[{{\text{V}} \mathord{\left/ {\vphantom {{\text{V}} {\text{m}}}} \right. \kern-0em} {\text{m}}}].$$
(16)

To test the adequacy of the proposed method, we can take the known results of investigation on the electrical and the temperature characteristics of the stabilized arc of the spectrometric plasma torch [4]: here, the degree of arc compression in the discharge channel is about the values of the arc compression in the stabilization zone of the laminar plasma torch. As an example, we take the experimental results for the stabilized arc of the plasma generator with the discharge channel diameter of 5 mm operating in air at the arc current of 60 A.

The proposed method of universal characteristics (11)–(16) of the arc burning in air makes it possible to calculate the electrical, geometric, and boundary parameters of the compressed arc and to compare these data with the experimental results for the spectrometric plasma torch [4].

Below, we present the calculated values of the electrical and the temperature characteristics of the stabilized arc; in brackets are the experimental results [4] for these parameters:

– the electric field strength 2195 (2015) V/m;

– the temperature at the column axis 12 927 (12 700) K.

By the method of the universal arc characteristics, we calculate

– the degree of arc compression δr = 0.78;

– the linear density of the heat flux on the column surface due to the plasma thermal conductivity pλ = 127.5 kW/m;

– the linear density of the heat flux on the column surface due to the plasma radiation pε = 4.17 kW/m.

In [5], we determine the conditions of the laminar jet formation at the nozzle exit of the plasma torch with the interelectrode inserts when using the most widespread plasma-forming gases.

We note that the greater the degree of arc compression in the plasma torch discharge channel, the less is the fraction of the plasma radiation intensity in the arc column power. It is that very principle of arc compression that is applied in industrial plasma generators [6], thus providing acceptable efficiency values for plasma technology installations. For the arc under conditions of natural convection (in arc furnaces) and the arc stabilized by the gas jet (in plasma-arc furnaces in the absence of a mode of intense column compression), the plasma radiation intensity dominates in the arc power [6].

With allowance for (10) and for the calculated stabilized arc column radius (15), we can determine the temperature profile of the arc stabilized by the discharge channel walls. Figure 4 shows the comparison of the calculated temperature profile of the stabilized arc with the experimental results obtained for the plasma generator operating in air with the stabilized arc with the discharge channel diameter of 5 mm at the arc current of 60 A [4]. We note that the good agreement between the calculated and the experimental values ​​indicates the adequacy of the method of universal arc characteristics and its applicability in characteristic calculations of the stabilized arc compressed by the discharge channel walls, including the stabilization zone of the plasma jet of the laminar plasma torch. In our paper [7], we present the results of calculation of the electrical and the thermal characteristics of the stabilized arc of the jet plasma torch in argon and their comparison with the experimental results [4].

Fig. 4.
figure 4

Temperature profile of the stabilized arc column in air (de = 5 mm, I = 60 A).

Full size image

CONCLUSIONS

On the basis of the developed method of universal plasma arc characteristics, we propose a method of analytical calculation of the characteristics of the stabilized arc compressed by the discharge channel walls in the stabilization zone of the laminar plasma torch. The method accounts for the nonlinearity of the thermal characteristics of the plasma-forming gas and for the conditions of the heat exchange between the arc and the discharge channel wall of the plasma torch and makes it possible to calculate, with high confidence, the arc compression ratio and the heat flows on the column surface caused by the thermal conductivity and the plasma radiation.