Mixed Convection Flow across a Vertical Cone with Heat Source/Sink and Chemical Reaction Effects

Abstract

This contribution is concerned with mixed convection flow across a vertical cone in the presence of heat source/sink and chemical reaction effects; the two-dimensional, steady, laminar, viscous incompressible fluid flow case has been discussed with favorable applications in the science, engineering, and industries. The flow model is designed in the form of mathematical equations and, for the sake of numerical solution simplicity, non-dimensionalization has been performed and the gained non-similarity equations are solved numerically via an efficient numerical technique called the bivariate Chebyshev spectral collocation quasi-linearization method. A schematic illustration of the obtained results at various stream-wise locations of the velocity, temperature, and concentration profiles for variations of the governing parameters are exhibited in the results and discussions section; and we have noted that higher rate of heat generation made heat transfer to the surface from the flow, and it enhances temperature profile as well. Moreover, skin friction, heat, and mass transfer rate are also illustrated in tabular form. To authenticate the accuracy of the present computations, we organize a favorable comparison with prior published computation; the residual analysis study also depicted which determines the convergence of the framed numerical simulation.

1. INTRODUCTION

The boundary layer theory on mixed convection flow became most trendy portion nowadays and the heat source/sink is a key in this portion which has countless application in science, engineering, and industries; like, it’s presence may shift the temperature distribution in the fluid which alters the particle deposition rate in systems such as electronic chips, nuclear reactors, semiconductors, heat exchangers, nuclear waste disposal, and many more. This core of specialization has brought several researchers and many of them have worked on various shapes and flow models, some of them can be like: Yih [1] analyses heat source/sink effect over vertical permeable plate for MHD mixed convection stagnation flow. Heat transfer with viscous dissipation over a stretching sheet in a micropolar fluid was examined by Mohammadein and Gorla [2]. Ibrahim et al. [3] introduced unsteady MHD natural convection flow over a semi-infinite vertical permeable moving plate with radiation absorption and chemical reaction presence. An analysis of hydromagnetic flow over a stretching vertical surface with chemical reaction and hall current was proposed by Salem and El-Aziz [4]. Das et al. [5] presented a heat transfer analysis across a vertical porous plate of MHD flow in the presence of mass transfer effect. A mixed convection flow across a moving vertical plate with double diffusive and chemical reaction was presented by Patil et al. [6]. An analysis of heat transfer across vertical plate in a parallel free stream flow also introduced by Patil et al. [7]. Ibrahim and Shanker [8] considered boundary-layer flow over stretching sheet of an unsteady MHD flow. An analysis of heat and mass transfer of a visco-elastic fluid through porous medium was introduced by Mishra et al. [9]. Jena et al. [10] proposed MHD viscoelastic fluid flow over a vertical stretching sheet with chemical reaction effect. A natural convection flow over an infinite isothermal vertical plate in the presence of chemical reaction and thermal diffusion effects were examined by Islam and Ahmed [11].

Another segment in this manuscript is the chemical reaction impact which is also an essential terminology with vast applications in many transport processes; it appears in the water and air pollution, in nuclear reactor safety and combustion systems, fibrous insulation, solar collectors, atmospheric flows, chemical, and metallurgical engineering problems. If the reaction is directly proportional to the concentration, then called the first-order chemical reaction that we have considered here. A bit of research work has focused on it by numerous researchers on various geometries, few of them can be seen as; Nayak et al. [12] introduced an axisymmetric flow across a radially stretched sheet. A nonlinear boundary layer flow over a porous shrinking sheet in the presence of suction flow was proposed by Muhaimina et al. [13]. Nayak [14] analyzed MHD viscoelastic fluid across a stretching sheet saturated porous medium. An unsteady MHD flow with viscous dissipation effect over a semi-infinite vertical porous plate was proposed by Rao and Shivaiah [15]. Mahapatra et al. [16] studied natural convection flow in a bounded porous medium by a vertical surface. A natural convection MHD flow with slip flow region in a bounded porous medium over a vertical surface was examined by Senapati et al. [17]. Bhattacharyya and Layek [18] presented an MHD boundary layer flow with suction/blowing over a flat plate. A list of study can have seen here Subhas et al. [19, 20], Pal and Chatterjee [21], Nandeppanavar et al. [22], Noor et al. [23], Sharma [24], Srinivasacharya et al. [25], Mabood et al. [26], Hayat et al. [27] and Meena et al. [28–36] which ignored the chemical reaction impact, and it makes a situation to consider it throughout this manuscript.

It has been recognized throughout the existing literature that the study of mixed convection flow across a vertical cone with heat source/sink and chemical reaction effects together have not been examined by any researcher so far, which cannot be negated due to essential key application and the authors have targeted it throughout this contribution.

We compose this work as follows. In Section 2, we propose the geometry and mathematical formulation of the problem. In Section 3, we illustrate the numerical approach, while results and discussions are disclosed in Section 4, and we concluded in Section 5.

2. MATHEMATICAL FORMULATION

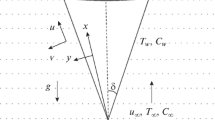
Consider a vertical cone with a half-angle $\omega$ saturated porous medium on a laminar steady two-dimensional mixed convection flow of a viscous incompressible fluid. The surface of the cone with its generator is aligned with $x$-axis and $y$-axis is normal to the surface. The flow moves in an upward direction, parallel to the axis of the cone. ${{T}_{\infty }}$ and ${{C}_{\infty }}$ are uniform temperature and concentration in the ambient region, and ${{T}_{w}}$ and ${{C}_{w}}$ are at the surface of the cone, respectively. Where ${{T}_{w}} < {{T}_{\infty }}$ corresponds to a cooled cone, ${{T}_{w}} > {{T}_{\infty }}$ correspond to a heated cone. ${{u}_{\infty }}$ is the uniform stream velocity in the ambient region. We consider heat source/sink and first-order chemical reaction impacts for better analysis of the heat and mass transfer. An illustration of the flow model and coordinates system is pictured in Fig. 1. We assumed that all the fluid properties are constant except the density variation in temperature and concentration (Boussinesq’s approximation).

Fig. 1.

Coordinate system and physical model.

The governing equations of the model are as follows, see [37, 38]:

$$\frac{{\partial \bar {u}}}{{\partial x}} + \frac{{\partial {\bar {v}}}}{{\partial y}} = 0,$$

(1)

$$\bar {u}\frac{{\partial \bar {u}}}{{\partial x}} + {\bar {v}}\frac{{\partial \bar {u}}}{{\partial y}} = U\frac{{dU}}{{dx}} + \nu \frac{{{{\partial }^{2}}\bar {u}}}{{\partial {{y}^{2}}}} + gK\cos \omega \left( {{{\beta }_{{\bar {T}}}}(\bar {T} - {{{\bar {T}}}_{\infty }}) - {{\beta }_{{\bar {C}}}}\left( {\bar {C} - {{{\bar {C}}}_{\infty }}} \right)} \right),$$

(2)

$$\bar {u}\frac{{\partial \bar {T}}}{{\partial x}} + {\bar {v}}\frac{{\partial \bar {T}}}{{\partial y}} = \frac{k}{{\rho {{C}_{p}}}}\frac{{{{\partial }^{2}}\bar {T}}}{{\partial {{y}^{2}}}} + \frac{{{{Q}_{0}}}}{{\rho {{C}_{p}}}}(\bar {T} - {{\bar {T}}_{\infty }}),$$

(3)

$$\bar {u}\frac{{\partial \bar {C}}}{{\partial x}} + {\bar {v}}\frac{{\partial \bar {C}}}{{\partial y}} = {{D}_{e}}\frac{{{{\partial }^{2}}\bar {C}}}{{\partial {{y}^{2}}}} - {{K}_{c}}\left( {\bar {C} - {{{\bar {C}}}_{\infty }}} \right).$$

(4)

Boundary conditions are:

$$\begin{gathered} \bar {u} = 0,\quad {\bar {v}} = 0,\quad \bar {T}(x,y) = {{{\bar {T}}}_{w}},\quad \bar {C}(x,y) = {{{\bar {C}}}_{w}}\quad {\text{at}}\quad y = 0, \\ \bar {u} \to U = {{u}_{\infty }}{{x}^{m}},\quad \bar {T}(x,y) \to {{{\bar {T}}}_{\infty }},\quad \bar {C}(x,y) \to {{{\bar {C}}}_{\infty }},\quad {\text{as}}\quad y \to \infty , \\ \end{gathered} $$

(5)

where, $\bar {u}$ and ${\bar {v}}$ are velocity components in $x$ and $y$ directions. $\omega$ is the half-angle of the cone, $\bar {T}$ is the fluid temperature, $\bar {C}$ is the concentration, $\nu$ is the kinematic viscosity, $g$ is the gravitational acceleration, $K$ is the permeability coefficient of the porous medium; ${{\beta }_{{\bar {T}}}}$ and ${{\beta }_{{\bar {C}}}}$ are volumetric coefficients of the thermal and concentration expansions, respectively. ${{D}_{e}}$ is the effective solute diffusivity; $k$ is the thermal conductivity of the fluid, ${{C}_{p}}$ is the specific heat at the constant temperature, ${{Q}_{0}}$ is the volumetric heat generation or absorption rate, and ${{K}_{c}}$ is the chemical reaction rate.

Introducing the following non-dimensional variables:

$$\begin{gathered} \xi (x) = {{\left( {\frac{2}{{m + 1}}\frac{{\nu x}}{U}} \right)}^{{1/2}}},\quad \eta (x,y) = y{{\left( {\frac{{m + 1}}{2}\frac{U}{{\nu x}}} \right)}^{{1/2}}}, \\ \psi (x,y) = {{\left( {\frac{2}{{m + 1}}\nu xU} \right)}^{{1/2}}}f\left( {\xi ,\eta } \right), \\ \bar {T}(x,y) = \left( {{{{\bar {T}}}_{w}} - {{{\bar {T}}}_{\infty }}} \right)\theta \left( {\xi ,\eta } \right) + {{{\bar {T}}}_{\infty }},\quad \bar {C}(x,y) = \left( {{{{\bar {C}}}_{w}} - {{{\bar {C}}}_{\infty }}} \right)\phi \left( {\xi ,\eta } \right) + {{{\bar {C}}}_{\infty }}. \\ \end{gathered} $$

(6)

By the definition of stream function, we introduce as:

$$\bar {u} = \frac{{\partial \psi }}{{\partial y}}\quad {\text{and}}\quad {\bar {v}} = - \frac{{\partial \psi }}{{\partial x}}.$$

(7)

Thus, we have:

$$\bar {u} = U\frac{{\partial f}}{{\partial \eta }},\quad {\bar {v}} = - \frac{1}{2}{{\left( {\frac{2}{{m + 1}}\frac{{\nu U}}{x}} \right)}^{{1/2}}}\left[ {\left( {m + 1} \right)f + \left( {m - 1} \right)\left( {\eta \frac{{\partial f}}{{\partial \eta }} - \xi \frac{{\partial f}}{{\partial \xi }}} \right)} \right].$$

(8)

Enforcing Eqs. (6)–(8) into Eqs. (2)–(4), we get the following forms, respectively,

$$\begin{gathered} \frac{{{{\partial }^{3}}f}}{{\partial {{\eta }^{3}}}} + \frac{{2m}}{{m + 1}}\left( {1 - {{{\left( {\frac{{\partial f}}{{\partial \eta }}} \right)}}^{2}}} \right) + f\frac{{{{\partial }^{2}}f}}{{\partial {{\eta }^{2}}}} + \frac{2}{{m + 1}}\frac{\lambda }{{{\text{Pr}}}}\left( {\theta + N\phi } \right) \\ = \xi \left( {\frac{{m - 1}}{{m + 1}}} \right)\left( {\frac{{{{\partial }^{2}}f}}{{\partial {{\eta }^{2}}}}\frac{{\partial f}}{{\partial \xi }} - \frac{{\partial f}}{{\partial \eta }}\frac{\partial }{{\partial \xi }}\left( {\frac{{\partial f}}{{\partial \eta }}} \right)} \right), \\ \end{gathered} $$

(9)

$$\frac{{{{\partial }^{2}}\theta }}{{\partial {{\eta }^{2}}}} + \Pr f\frac{{\partial \theta }}{{\partial \eta }} + {{\xi }^{2}}Q\theta = \Pr \left( {\frac{{m - 1}}{{m + 1}}} \right)\xi \left( {\frac{{\partial \theta }}{{\partial \eta }}\frac{{\partial f}}{{\partial \xi }} - \frac{{\partial f}}{{\partial \eta }}\frac{{\partial \theta }}{{\partial \xi }}} \right),$$

(10)

$$\frac{{{{\partial }^{2}}\phi }}{{\partial {{\eta }^{2}}}} + \operatorname{Sc} f\frac{{\partial \phi }}{{\partial \eta }} - \operatorname{Sc} {{\xi }^{2}}\Delta \phi = \operatorname{Sc} \left( {\frac{{m - 1}}{{m + 1}}} \right)\xi \left( {\frac{{\partial \phi }}{{\partial \eta }}\frac{{\partial f}}{{\partial \xi }} - \frac{{\partial f}}{{\partial \eta }}\frac{{\partial \phi }}{{\partial \xi }}} \right).$$

(11)

The boundary conditions Eq. (5) are reduced as:

$$\begin{gathered} \frac{{\partial f\left( {\xi ,\eta } \right)}}{{\partial \eta }} = 0,\quad f\left( {\xi ,\eta } \right) - \left( {\frac{{m - 1}}{{m + 1}}} \right)\xi \frac{{\partial f\left( {\xi ,\eta } \right)}}{{\partial \xi }} = 0,\quad \theta \left( {\xi ,\eta } \right) = 1,\quad \phi \left( {\xi ,\eta } \right) = 1\quad {\text{at}}\quad \eta = 0, \\ \frac{{\partial f\left( {\xi ,\eta } \right)}}{{\partial \eta }} \to 1,\quad \theta \left( {\xi ,\eta } \right) \to 0,\quad \phi \left( {\xi ,\eta } \right) \to 0\quad {\text{as}}\quad \eta \to \infty ; \\ \end{gathered} $$

(12)

here, $\lambda = \frac{{{\text{Gr}}}}{{{\text{Re}}_{x}^{2}}}$ is the buoyancy parameter, $N = \frac{{{{\beta }_{{\bar {C}}}}}}{{{{\beta }_{{\bar {T}}}}}}\left( {\frac{{{{{\bar {C}}}_{w}} - {{{\bar {C}}}_{\infty }}}}{{{{{\bar {T}}}_{w}} - {{{\bar {T}}}_{\infty }}}}} \right)$ is the buoyancy ratio, ${\text{R}}{{{\text{a}}}_{x}}$ = $\frac{{gK{{\beta }_{{\bar {T}}}}{{x}^{2}}\left( {{{{\bar {T}}}_{w}} - {{{\bar {T}}}_{\infty }}} \right)\cos \omega }}{{\nu \alpha }}$ is the modified local Rayleigh number, ${\text{Gr}} = \frac{{{\text{R}}{{{\text{a}}}_{x}}}}{{{\text{Pr}}}}$ is the local Grashof number, ${{\operatorname{Re} }_{x}} = \frac{{Ux}}{\nu }$ is the local Reynold number, $\Pr = \frac{\nu }{{{{\alpha }_{m}}}}$ is the Prandtl number, $Q = \frac{{{{Q}_{0}}}}{k}$ is the heat source parameter, ${\text{Sc}} = \frac{\nu }{{{{D}_{e}}}}$ is the Schmidt number, $\Delta = \frac{{{{K}_{c}}}}{\nu }$ is the chemical reaction parameter.

The principal bodily quantities of interest which can no longer be skipped are skin friction, heat and mass transfer rates in terms of local skin friction coefficient ${{C}_{f}}$, local Nusselt number ${\text{N}}{{{\text{u}}}_{x}}$, and local Sherwood number ${\text{S}}{{{\text{h}}}_{x}}$ can be written as:

$${{C}_{f}} = \frac{{2{{\tau }_{w}}}}{{\rho {{U}^{2}}}},~\quad {\text{N}}{{{\text{u}}}_{x}} = \frac{{{{q}_{w}}}}{{\left( {{{{\bar {T}}}_{w}} - {{{\bar {T}}}_{\infty }}} \right)}}\frac{x}{k},\quad {\text{and}}\quad {\text{S}}{{{\text{h}}}_{x}} = \frac{{{{q}_{m}}}}{{\left( {{{{\bar {C}}}_{w}} - {{{\bar {C}}}_{\infty }}} \right)}}\frac{x}{{{{D}_{f}}}};$$

here, ${{\tau }_{w}} = \mu {{\left( {\frac{{\partial \bar {u}}}{{\partial y}}} \right)}_{{y = 0}}}$, ${{q}_{w}} = - {{k}_{e}}{{\left( {\frac{{\partial \bar {T}}}{{\partial y}}} \right)}_{{y = 0}}}$, and ${{q}_{m}} = - {{D}_{e}}{{\left( {\frac{{\partial \bar {C}}}{{\partial y}}} \right)}_{{y = 0}}}$ are defined as wall skin friction, heat flux and mass flux, respectively.

Thus, we have

$${{C}_{f}}\operatorname{Re} _{x}^{{1/2}} = 2{{\left( {\frac{{m + 1}}{2}} \right)}^{{1/2}}}{\kern 1pt} f{\kern 1pt} ''{\kern 1pt} \left( {\xi ,0} \right),$$

(13)

$${\text{N}}{{{\text{u}}}_{x}}\operatorname{Re} _{x}^{{ - 1/2}} = - {{\left( {\frac{{m + 1}}{2}} \right)}^{{1/2}}}\theta {\kern 1pt} '{\kern 1pt} \left( {\xi ,0} \right),$$

(14)

$${\text{S}}{{{\text{h}}}_{x}}\operatorname{Re} _{x}^{{ - 1/2}} = - {{\left( {\frac{{m + 1}}{2}} \right)}^{{1/2}}}\phi {\kern 1pt} '{\kern 1pt} \left( {\xi ,0} \right).$$

(15)

3. NUMERICAL SOLUTION

The non-similar equations are solved numerically through the well explained numerical technique call the bivariate Chebyshev spectral collocation quasi-linearization method by Meena et al. [39, 40], Magagula et al. [41]. To test the efficiency of the numerical technique; the residual analysis study is computed, which converges up to ${{10}^{{ - 9}}}$.

4. RESULTS AND DISCUSSIONS

In this section the appropriate computations for the non-similarity solution of Eqs. (9)–(11) with the boundary condition Eq. (12) are presented via well explained numerical technique called as bivariate Chebyshev spectral collocation quasi-linearization method (BSQLM). The outcomes are computed in various ranges of the governing parameters: $0 \leqslant m \leqslant {\text{1/2}}$, $0.733 \leqslant \Pr \leqslant 6.7$, $1.0 \leqslant \lambda \leqslant 7.0$, $0.66 \leqslant {\text{Sc}} \leqslant 2.57$, $0 \leqslant Q \leqslant 2.0$, $- 2.0 \leqslant \Delta \leqslant 2.0$, $0 \leqslant \xi \leqslant 1.0$ and $- 2.0 \leqslant N \leqslant 2.0$. The edge of boundary layer region ${{\eta }_{\infty }}$ is carried in between $4.0$ to $5.0$ according to suitability of computations. To validate the accuracy of the adopted numerical technique, we examined the residual analysis study also which determined the convergence or error of the results and accomplished a perfect convergence after 7th iteration.

Figures 2–4 present the residual analysis over iterations of $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ for variation of $Q$ with $m = {\text{1/2}}$, $\Pr = 0.733$, $\lambda = 1.0$, $\Delta = 0.5$, ${\text{Sc}} = 0.66$, and $N = 1.0$, respectively. It measures the convergence of the adopted numerical technique. In Fig. 2, we observe that the method converges after nine iterations for variation of $Q$ to 10^–6, while in Fig. 3 the method converges after seven iterations for variation of $Q$ to 10^–9 and in Fig. 4 the method converges after six iterations for variation of $Q$ to 10^–9. This justifies the stability and convergence of the method, and, hence, the results are accurate to approximately eight d-igits.

Fig. 2.

Residual analysis of $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$.

Fig. 3.

Residual analysis of $\theta \left( {\xi ,\eta } \right)$.

Fig. 4.

Residual analysis of $\phi \left( {\xi ,\eta } \right)$.

Figure 5 presents a comparison of $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\theta \left( {\xi ,\eta } \right)$ profiles for Pr with prior published results Ravindran et al. [37], through this, we can recognize the agreement of present and past results that verifies working efficiency of the adopted technique code in the MATLAB.

Fig. 5.

Comparison of $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\theta \left( {\xi ,\eta } \right)$ profiles with Ravindran et al. [37].

Figures 6–8 proposes $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ for variation of Pr and $\lambda$ together with $m = {\text{1/2}}$, $Q = 1.0$, $\Delta = 0.5$, ${\text{Sc}} = 0.66$, and $N = 1.0$. In Fig. 6, $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile enhances with $\lambda$ and for low values of $\Pr = 0.733$ a sudden higher growth rate is observed close to cone surface, but it doesn’t occur for $\Pr = 6.7$ that is caused by the low viscosity of the fluid. In Figs. 7 and 8, $\theta \left( {\xi ,\eta } \right)$ and $\phi \left( {\xi ,\eta } \right)$ profiles decrease with an increment in $\lambda$, respectively, but $\phi \left( {\xi ,\eta } \right)$ profile is contrary with Pr, i.e., increases, while $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\theta \left( {\xi ,\eta } \right)$ profiles decrease. It can be noted from Figs. 6–8 that all the profiles growth or shrinking rates are greater in magnitude with the small $\Pr = 0.733$ because Pr is the ratio in between kinematic viscosity and thermal diffusivity and increment in this refers to increment in the fluid viscosity, thus the buoyancy $\lambda$ become more dominant on low viscosity (${\text{Pr}} = 0.733$) fluid comparing to higher (${\text{Pr}} = 6.7$).

Fig. 6.

$f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile for Pr and $\lambda$.

Fig. 7.

$\theta \left( {\xi ,\eta } \right)$ profile for Pr and $\lambda$.

Fig. 8.

$\phi \left( {\xi ,\eta } \right)$ profile for Pr and $\lambda$.

Figures 9–11 examines $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ boundary layer profiles, for variation of Pr and $Q$ together with $m = {\text{1/2}}$, $\lambda = 1.0$, $\Delta = 0.5$, ${\text{Sc}} = 0.66$, and $N = 1.0$. In Fig. 9, $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile decreases with $Q$ for heat absorption case $Q < 0$ but contrary for heat generation case $Q > 0$, i.e. enhances; while in Fig. 10, $\theta \left( {\xi ,\eta } \right)$ profile also decreases with $Q < 0$ and enhances with $Q > 0$ due to higher heat in the flow region, the flow particles interaction or velocity enhanced and that causes a reduction or acceleration in Fig. 9 also; in Fig. 11, $\phi \left( {\xi ,\eta } \right)$ profile boosts with $Q$ (in $Q < 0$ case) and decreases with $Q$ (in $Q > 0$ case). In Figs. 9–10 we can note a similar tendency on $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\theta \left( {\xi ,\eta } \right)$ profiles with Pr, i.e., decrease with Pr but $\phi \left( {\xi ,\eta } \right)$ profile in Fig. 11 has contrary trend, i.e., increases with Pr; we can notice that the shrinking or speeding up rates are higher in magnitude at low ${\text{Pr}}\;( = {\kern 1pt} 0.733)$ compared to the higher one ${\text{Pr}}\;( = {\kern 1pt} 6.7)$ and an increment in Pr reflects fluid viscosity increment; therefore, we can conclude that the heat generation/absorption impact is more prevailing in low viscosity fluid comparing to a higher one.

Fig. 9.

$f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile for Pr and $Q$.

Fig. 10.

$\theta \left( {\xi ,\eta } \right)$ profile for Pr and $Q$.

Fig. 11.

$\phi \left( {\xi ,\eta } \right)$ profile for Pr and $Q$.

Figures 12–14 reflects $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ profiles for Pr and $m$ variation together with $Q = 1.0$, $\lambda = 1.0$, $\Delta = 0.5$, ${\text{Sc}} = 0.66$, and $N = 1.0$; $m = \frac{\omega }{{\pi - \omega }}$; here, $\omega$ is the half-angle of the cone (for brief discussion, see Ravindran and Ganapathirao [42]); this implies the values of $m = \left[ {0,\;0.2,\;0.3,\;0.5} \right]$ typically represent half-angle of the cone $\left[ {0,\;30,\;45,\;60} \right]$ degrees, respectively; therefore, an increment in $m$ refers increment in the half-angle $\omega$ of the cone. In Fig. 12, $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile decreases with $m$ at $\Pr = 0.733$, but, on the contrary, at $\Pr = 6.7$ it increases Pr is the ratio in between kinematic viscosity and thermal diffusivity and an increment in Pr means an increment in the kinematic viscosity and reduction in thermal diffusivity; hence, velocity profile $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ decreases with the increment in the cone half-angle in the low viscosity fluid $\Pr = 0.733$, but, on the contrary, in the higher viscosity fluid ($\Pr = 6.7$) it enhances. In Fig. 13, $\theta \left( {\xi ,\eta } \right)$ profile enhances with $m$ in low viscosity fluid, but has a reverse behavior in higher viscosity fluid, i.e., decreases, and in Fig. 14, $\phi \left( {\xi ,\eta } \right)$ profile enhances with $m$ at $\Pr = 0.733$ and reduces at $\Pr = 6.7$. We can conclude from Figs. 12–14 that impact of $m$ is more dominating in low viscosity fluid compared to the higher and the enhancement and shrinking rates are higher in magnitude at $\Pr = 0.733$.

Fig. 12.

$f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile for Pr and $m$.

Fig. 13.

$\theta \left( {\xi ,\eta } \right)$ profile for Pr and $m$.

Fig. 14.

$\phi \left( {\xi ,\eta } \right)$ profile for Pr and $m$.

Figures 15–17 presents $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ profiles for variation of Sc and Δ together with $Q = 1.0$, $\lambda = 1.0$, $m = {\text{1/2}}$, ${\text{Pr}} = 0.733$, and $N = 1.0$. In Fig. 17, $\phi \left( {\xi ,\eta } \right)$ profile enhances with Δ (in consumption chemical reaction case $\Delta < 0$) that increases $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile also in Fig. 15, but $\theta \left( {\xi ,\eta } \right)$ profile is contrary, i.e., decreases with Δ (in consumption chemical reaction case $\Delta < 0$) in Fig. 16; but Δ (in generation chemical reaction case $\Delta > 0$) has a contrary impact on $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ profiles, i.e., $\phi \left( {\xi ,\eta } \right)$ profile decreases with Δ and, resultantly, $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile also decreases in Fig. 15, but $\theta \left( {\xi ,\eta } \right)$ profile has a little increment, see Fig. 16. In Figs. 15–17, $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\phi \left( {\xi ,\eta } \right)$ profiles reduces with Sc, but $\theta \left( {\xi ,\eta } \right)$ profile gained a little enhancement with Sc; Sc is the ratio in between kinematic viscosity and -solute diffusivity and an increment in this means an increment in kinematic viscosity and reduction in -solute diffusivity; Δ is the ratio between chemical reaction rate and kinematic viscosity, and an increment in this refers to an increment in chemical reaction rate and a reduction in kinematic viscosity; in Figs. 15–17, we can observe that impact of Δ reduced at ${\text{Sc}} = 2.57$ compared to ${\text{Sc}} = 0.66$ because of high kinematic viscosity; therefore, it can conclude that Δ is more realistic in low viscosity fluid.

Fig. 15.

$f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile for Sc and Δ.

Fig. 16.

$\theta \left( {\xi ,\eta } \right)$ profile for Sc and Δ.

Fig. 17.

$\phi \left( {\xi ,\eta } \right)$ profile for Sc and Δ.

Figures 18–20 proposes $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ profiles for Pr and $N$ variation together with $Q = 1.0$, $\lambda = 1.0$, $m = {\text{1/2}}$, ${\text{Sc}} = 0.66$, and $\Delta = 0.5$. In Fig. 18, $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile increases with $N$ (in the adding flow $N > 0$) and decreases in the opposing flow ($N < 0$), while in Figs. 19 and 20, $\theta \left( {\xi ,\eta } \right)$ and $\phi \left( {\xi ,\eta } \right)$ profiles decreases with $N$ in the adding flow $N > 0$ and contrary in the opposing flow $N < 0$, i.e., increases. In Figs. 18–20, we observe that $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$, and $\phi \left( {\xi ,\eta } \right)$ profiles thickness is higher at $\Pr = 0.733$ compared to $\Pr = 6.7$; hence, we can conclude that the buoyancy ratio has dominating activeness on flow quantities in low viscosity fluid.

Fig. 18.

$f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile for Pr and N.

Fig. 19.

$\theta \left( {\xi ,\eta } \right)$ profile for Pr and N.

Fig. 20.

$\phi \left( {\xi ,\eta } \right)$ profile for Pr and N.

Table 1 provides the governing parameters Pr, Sc, $m$, Δ, $\lambda$, $N$, and $Q$ impacts on the ${{C}_{f}}$, ${\text{N}}{{{\text{u}}}_{x}}$, and ${\text{S}}{{{\text{h}}}_{x}}$ with $Q = 1.0$, ${\text{Pr}} = 0.733$, $\lambda = 1.0$, $m = {\text{1/2}}$, $N = 1.0$, ${\text{Sc}} = 0.66$, and $\Delta = 1.0$. An increment in Pr improves ${\text{N}}{{{\text{u}}}_{x}}$ and reduces ${{C}_{f}}$ and ${\text{S}}{{{\text{h}}}_{x}}$. ${{C}_{f}}$, ${\text{N}}{{{\text{u}}}_{x}}$, and ${\text{S}}{{{\text{h}}}_{x}}$ flow quantities raise with an increment in $m$; that means while we are increasing the cone half-angle that pushes the cone radius also and the surface of the cone acts as a blocker in the flow which causes the increment in skin friction, but it has a positive impact on ${\text{N}}{{{\text{u}}}_{x}}$ and ${\text{S}}{{{\text{h}}}_{x}}$; i.e., ${\text{N}}{{{\text{u}}}_{x}}$ and ${\text{S}}{{{\text{h}}}_{x}}$ rates enhanced because of the surface contact time increment. An impact of Δ (for consumption chemical reaction $\Delta < 0$)) boosts ${{C}_{f}}$ and ${\text{N}}{{{\text{u}}}_{x}}$ due to the slows down in fluid-particle acceleration we can predict it from Fig. 9; therefore, it impacts ${\text{S}}{{{\text{h}}}_{x}}$ in a little decrement, but in generation chemical reaction case $\Delta > 0$ these have reverse trend, i.e., ${{C}_{f}}$ and ${\text{N}}{{{\text{u}}}_{x}}$ decrease, and ${\text{S}}{{{\text{h}}}_{x}}$ increases. ${{C}_{f}}$, ${\text{N}}{{{\text{u}}}_{x}}$, and ${\text{S}}{{{\text{h}}}_{x}}$ flow quantities enhance with $\lambda$ and $N > 0$ but decreases with $N < 0$. Impact of $Q$ ($Q < 0$ for heat absorption) enhances ${\text{N}}{{{\text{u}}}_{x}}$ but ${{C}_{f}}$ and ${\text{S}}{{{\text{h}}}_{x}}$ reduces; for $Q < 0$ heat absorption is acted as a sink inflow region; therefore, the heat transfer from the surface of the cone to the flow region enhances; for $Q > 0$ (heat generation) ${\text{N}}{{{\text{u}}}_{x}}$ decreases, and for higher values of $Q$ it took negative trend also which indicates when heat generation rate is higher than the heat is transferring from flow region to the surface, but ${{C}_{f}}$ and ${\text{S}}{{{\text{h}}}_{x}}$ enhances.

Table 1. Influence of Pr, Sc, $m,$ $\Delta$, λ, $N$, and $Q$ on ${{C}_{f}}$, ${\text{N}}{{{\text{u}}}_{x}}$, and ${\text{S}}{{{\text{h}}}_{x}}$ with respect to ${\text{Pr}} = 0.733$, $\lambda = 1.0$, $m = 0.5$, ${\text{Sc}} = 0.66$, $Q = 1.0$, $N = 1.0$, and $\Delta = 0.5$, respectively

5. CONCLUSIONS

Mixed convection flow of an incompressible viscous fluid across a vertical cone saturated porous medium with the heat source/sink and chemical reaction effects measured in this segment of contribution and reached to conclude follows:

• Impact of $Q$ boosts ${\text{N}}{{{\text{u}}}_{x}}$ and slows down ${{C}_{f}}$ and ${\text{S}}{{{\text{h}}}_{x}}$ for heat absorption ($Q < 0$); likewise, for heat generation ($Q > 0$) it boosts ${{C}_{f}}$ and ${\text{S}}{{{\text{h}}}_{x}}$ and slows down ${\text{N}}{{{\text{u}}}_{x}}$ and turned heat transfer as flow to surface. $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\theta \left( {\xi ,\eta } \right)$ profiles decrease with $Q$ but $\phi \left( {\xi ,\eta } \right)$ profile increases for $Q < 0$; likewise, $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\theta \left( {\xi ,\eta } \right)$ profiles increase with $Q$ but $\phi \left( {\xi ,\eta } \right)$ profile decreases for $Q > 0$.

• An impact of $\Delta < 0$ (for chemical reaction consumption) boosts ${{C}_{f}}$ and ${\text{N}}{{{\text{u}}}_{x}}$, and decreases ${\text{S}}{{{\text{h}}}_{x}}$ but the impact of $\Delta > 0$ (for chemical reaction generation) decrease ${{C}_{f}}$ and ${\text{N}}{{{\text{u}}}_{x}}$, and increases ${\text{S}}{{{\text{h}}}_{x}}$. $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ and $\phi \left( {\xi ,\eta } \right)$ profiles enhance with $\Delta < 0$ but $\theta \left( {\xi ,\eta } \right)$ profile decreases; similarly, $\Delta > 0$ turns $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$, $\theta \left( {\xi ,\eta } \right)$ and $\phi \left( {\xi ,\eta } \right)$ profiles in a contrary way.

• All the ${{C}_{f}}$, ${\text{N}}{{{\text{u}}}_{x}}$, and ${\text{S}}{{{\text{h}}}_{x}}$ quantities enhance with $\lambda$ and $N$ ($N > 0$ in adding flow case) but reduces in the opposing flow case ($N < 0$). $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile enhances with both the $\lambda$ and $N$, but $\theta \left( {\xi ,\eta } \right)$ and $\phi \left( {\xi ,\eta } \right)$ profiles decrease. Both the $\lambda$ and $N$ become more dominant in low viscosity fluid ($\Pr = 0.733$) comparing to higher one ($\Pr = 6.7$).

• ${{C}_{f}}$, ${\text{N}}{{{\text{u}}}_{x}}$, and ${\text{S}}{{{\text{h}}}_{x}}$ flow quantities raise with an increment in $m$. $f{\kern 1pt} '{\kern 1pt} \left( {\xi ,\eta } \right)$ profile decreases with $m$ but $\theta \left( {\xi ,\eta } \right)$ and $\phi \left( {\xi ,\eta } \right)$ profiles enhance in low viscosity fluid ($\Pr = 0.733$) but turned in reverse trend in higher viscosity fluid ($\Pr = 6.7$).