Comparison of Data Assimilation Methods in Hydrodynamics Ocean Circulation Models

Abstract

Two different data assimilation methods are compared: the author’s method of the generalized Kalman filter (GKF) proposed earlier and the standard ensemble objective interpolation (EnOI) method, which is a particular case of the ensemble Kalman filter (EnKF) scheme. The methods are compared with respect to different criteria, in particular, the criterion of the forecasting error minimum and a posteriori error minimum over a given time interval. The Archiving, Validating and Interpolating Satellite Oceanography Data (AVISO), i.e., the altimetry data, was used as the observation data; the Hybrid Circulation Ocean Model (HYCOM) model was used as a basic numerical model of ocean circulation. It has been shown that the GKF method has a number of advantages over the EnOI method in particular, it provides the better temporal forecast error. In addition, the results of numerical experiments with different data assimilation methods are analyzed and their results are compared with the control experiment, i.e., the HYCOM model without data assimilation. The computation results are also compared with independent observations. The conclusion is made that the studied assimilation methods can be applied to forecast the state of the ocean.

1 INTRODUCTION

Nowadays, the assimilation of observation data in hydrodynamic models is one of the important directions in the numerical modeling of the atmosphere and ocean dynamics. It aims to combine the numerical calculations of characteristics with the help of a mathematical model and the set of observation data, available to researchers from different platforms and instruments that carry out environmental monitoring. As a rule, the set of observation data is a subset of the phase states of the model and it differs quantitatively (sometimes significantly) from the calculated values. Notions such as the optimal waya and combine are used mainly as terms whose specific content depends on the problem statement; sometimes these terms are the subjects of research. Therefore, the theory and practical application of data assimilation methods are substantially based on the theory and methods of the optimal control, theory, and algorithm of the statistical estimation, calculus of variations, and other mathematical foundation.

The data assimilation problems have been studied in the scientific literature since the late 1960s. Apparently, the first contribution to solve these problems was made by Russian scientists under the leadership of Academician G.I. Marchuk [1]. In the mathematical modeling of the dynamics of the atmosphere and, later, the ocean dynamics, he and his disciples applied methods of the theory of adjoint equations to describe the processes of climatic variability, atmospheric anomalies, and others. It should also be noted that a significant contribution to the development of this direction was made by Academician A.S. Sarkisyan [2] and his followers, in particular, [3]. For forecasting the weather, in the Meteorological Office of the former Soviet Union, L.S. Gandin’s scheme based on the so-called objective analysis scheme [4] was applied. Simultaneously, data assimilation methods were developed in other institutes and research centers both in the former Soviet Union (Russia) and abroad (see, for example, [5, 6]). Due to the development of the observation base and the progress in computer engineering, the data assimilation methods and schemes were further developed in oceanology, forecasting the weather and climate, operational oceanography, and other domains at the end of the ХХ and beginning of the ХХI centuries.

Nowadays, there are several data assimilation algorithms which are used in problems of forecasting the weather, operational oceanology, and calculations of the state of the ocean in the regions of extraction and transportation of mineral resources, especially, hydrocarbons. The basic approaches are the so-called variation schemes and dynamic-stochastic schemes based on the Kalman filter theory; their modern versions are called 4D-VAR and the ensemble Kalman filter (EnKF), respectively. A detailed review of the methods used in this research domain can be found, for example, in [6]. In addition, lately, significant attention has been paid to the hybrid methods that combine these two basic approaches. In particular, the hybrid assimilation schemes based on the combination of the variation and dynamic-stochastic principles were considered in [7, 8]. The method we proposed in [9, 10] is also based on the variation principle in combination with the principle of the minimum of the variance of a specially constructed random process.

Generally speaking, to choose the best data assimilation method, it is necessary to determine precisely the criteria according to which the new or corrected model parameter filed is constructed. However, if we have determined a criteria unambiguously, for example, the metric, according to which the optimal corrected field of parameter values is sought, then the problem of constructing the assimilation method is correctly formulated in the sense that there is a solution to this problem and this solution is unique.

It is clear that for the same model and observation data different assimilation methods may be applied. This raises the question about a comparison of their quality. The quality criteria for the methods may be determined in a different way. For instance, the methods can be compared from the point of view of their realization and/or the calculation time. There can be criteria such as the required RAM resources or strictly imposed constraints on the time interval during which the corresponding correction is reasonable. Each such case has its own optimal assimilation method and it is meaningless to compare them. Therefore, it is necessary to determine the quality criterion or criteria according to which it is reasonable to formulate the problem of comparing the methods.

The quality criterion for the assimilation methods that does not depend on their type (variation, dynamic-stochastic, or any other) is estimating the forecast error; after each moment of correction, the corrected values of the parameters are the initial values for further calculation. It is also reasonable to compare the model forecast error obtained by the assimilation method with the error of the control calculation (with no assimilation of the observation data) with respect to the same data. It should be noted that this ideology of comparison depends neither on the model nor on the set of observation data. It is important only that they must be identical when using the compared assimilation methods.

Such comparisons of several assimilation methods, for example, for the ensemble Kalman filter and 4D-VAR were earlier made in [11]. For the Hybrid Circulation Ocean Model (HYCOM) [12] and the archive of the observation data from the ARGO drifters (www.argo.ucsd.edu), such comparisons of assimilation methods are presented in [13]. Analogous comparisons were performed in [14] for the method of objective interpolation [4] and the ensemble objective interpolation (EnOI) method with the use of the ocean dynamics model. For the HYCOM model and the Archiving, Validating and Interpolating Satellite Oceanography Data (AVISO) (www.aviso.oceanobs.com), the results of the comparison of the EnOI and the objective interpolation methods are presented in [15].

In the current study, we compare our author’s assimilation method [9, 10] and the EnOI method with the help of the AVISO archive and the HYCOM model using the forecast error criterion. Attention is paid to the analysis of the difference between the numeric fields constructed by different methods for the same input data and model configuration. The aim of this work is to show that the assimilation method we have developed earlier [10], which generalizes the known EnOI assimilation method, exceeds the latter with respect to both quality according to the above-mentioned criterion and the saving of computational resources. It is also shown that the basic ocean characteristics’ fields obtained as a result of the correction agree in general with the analogous fields obtained by using other models with the help of other assimilation methods described in the scientific literature; however, they have their specific features, and in particular, they correspond better to the synoptic variability, according to the observation data.

2 OCEAN MODEL AND OBSERVATION DATA

The HYCOM numerical model of ocean dynamics, namely, version 2.2.14 developed for studying the ocean’s thermohydrodynamic processes in a wide range of spatial and temporal scales is used in this work [12]. This model is well known and is not investigated; it is used only as a tool to analyze the data assimilation method. Therefore, let us give only a brief description of its configuration which was used in our study.

The model is based on a complete system of the equations of the three-dimensional ocean dynamics in which the ocean is divided from its surface to its bottom into layers with equal thicknesses whose values increase with depth. For each layer, the system of equations of hydrodynamics is solved in the “shallow water” approximations with the inclusion of equations for the temperature and salinity. Therefore, the coordinates of a point in this model are two coordinates in the Cartesian coordinate system on a plane (the Ox-axis direction is west–east; that of the Oy axis is south–north) and the number of the isopycnic (i.e., equivalent) density layer. There are 21 such layers in this configuration; the thickness of the equal-density layer at each point of the plane is a variable which has to be determined. The grid pitches in the horizontal direction are nonuniform and are approximately 0.25°, which correspond to about 30 km. The model phase space consists of 109 variables: 4 barotropic variables (that do not depend on the depth)—the ocean surface level, 2 components of velocity, and the pressure at the ocean surface—and 105 baroclinic variables (that depend on the depth), namely: the zonal and meridional components of the current horizontal velocity, temperature, and salinity at each of the 21 layers, respectively. In the data assimilation, all the calculation quantities change simultaneously. A more detailed description of the model, boundary conditions, and numerical experiments on its verification are presented in [15].

The satellite measurements of the ocean level taken from the AVISO archive, in which the data are obtained along the satellite tracks, are used as the observation data. On average, there are 30 000 observations for each day, while the array of calculation values of the ocean level is by one–two orders of magnitude larger, depending on the grid pitch. To compare the observation data with the modeling results, it is necessary to apply the operation of the projection of the vectors of the model parameters onto the space of the observation vectors.

3 GENERALIZED KALMAN FILTER (GKF) METHOD AND ENSEMBLE OPTIMAL INTERPOLATION METHOD

The generalized Kalman filter (GKF) method, which we developed earlier, is described in detail and theoretically grounded in [9, 10]. The basic equations of this method are as follows:

$${{X}_{{a,n + 1}}} = {{X}_{{b,n + 1}}} + {{K}_{{n + 1}}}({{Y}_{{n + 1}}} - H{{X}_{{b,n + 1}}}),\,\,\,\,K = \frac{{(\Lambda - C)(H\Lambda ){{'}}{{Q}^{{ - 1}}}}}{{(H\Lambda ){{'}}{{Q}^{{ - 1}}}H\Lambda }},$$

((1))

where ${{X}_{{a,n}}}\,\,{\text{and}}\,\,{{X}_{{b,n}}}$ are the vectors of the model state at the calculation time moment n, n = 0, 1, … after and before the data assimilation (the analysis and background) with dimension r; r is the number of grid points (its order of magnitude is 10⁶ for the ocean with a resolution of 0.25 degree) multiplied by the number of independent variables which have to be determined—the model parameters; ${{Y}_{n}}$ is the observation vector (with consideration of the instrumental measurement error) at the time moment n with dimension m; m is the number of observation points (which has an order of magnitude of 10⁴) multiplied by the number of independently observed quantities (for example, if one observes independently the temperature and salinity, then there will be two such quantities). It is assumed that ${{X}_{{a,0}}} = {{X}_{{b,0}}} = {{X}_{0}}$ is a known and given initial condition (a field); K is the Kalman gain matrix with dimension r × m; H is the matrix of the projection of the model parameter vectors onto the space of observation vectors that has dimension m × r; $\Lambda \,\,{\text{and}}\,\,C$ are the model and observed trends at the time step, which are defined by the formulas

$${{\Lambda }_{{n + 1}}} = \frac{{{{X}_{{b,{\kern 1pt} n + 1}}} - {{X}_{{a,{\kern 1pt} n}}}}}{{\Delta {\kern 1pt} {{t}_{n}}}},\,\,\,\,{{C}_{{n + 1}}} = \frac{{{{Y}_{{n + 1}}} - H{{X}_{{a,{\kern 1pt} {\kern 1pt} n}}}{\kern 1pt} }}{{\Delta {\kern 1pt} {{t}_{n}}}},$$

Q is the covariant matrix of the modeling errors with dimension $m \times m$; and ${{Q}_{{n + 1}}} = E({{Y}_{{n + 1}}} - H{{X}_{{a,n}}}){{({{Y}_{{n + 1}}} - H{{X}_{{a,n}}})}^{{\text{T}}}}$. The derivation of these formulas and their theoretical justification are presented in [9, 10].

In the calculations, the following algorithms are used to construct $C$ and $Q$.

Vector С is constructed as follows: at first, we set the ensemble ${{X}_{l}}$ of N_e model values with the total dimension r. It is assumed that the ensemble average $E{{X}_{0}} = N_{r}^{{ - 1}}\sum\nolimits_{l = 1}^{{{N}_{r}}} {{{X}_{l}}}$ is the estimate of the true value of the unknown partly observed field $E({{Y}_{1}} - H{{X}_{0}}) = 0$. Next, we construct the ensemble X₁ in such a way that $E({{Y}_{2}} - H{{X}_{1}}) = 0$. For this purpose, it is necessary to perform a one-step model calculation starting from field X₀ and replace the values $H{{X}_{1}}$ with the values of the observation parameters ${{Y}_{2}}$. Then, vector ${{C}_{{n + 1}}}$ can be calculated, according to the formula ${{C}_{{n + 1}}} = {{\left( {{{X}_{n}} - {{n}^{{ - 1}}}\sum\nolimits_{i = 1}^n {{{X}_{i}}} } \right)} \mathord{\left/ {\vphantom {{\left( {{{X}_{n}} - {{n}^{{ - 1}}}\sum\nolimits_{i = 1}^n {{{X}_{i}}} } \right)} {\Delta {\kern 1pt} {{t}_{n}}}}} \right. \kern-0em} {\Delta {\kern 1pt} {{t}_{n}}}}$. It was shown in [10] that under the condition $E({{Y}_{{n + 1}}} - H{{X}_{n}}) = 0$, vector C constructed in this way would actually describe the trend of the observation vector Y.

The components of the matrix Q are calculated by using the formula

$${{Q}_{{ij}}} = N_{e}^{{ - 1}}\sum\limits_{l = 1}^{{{N}_{e}}} {(Y_{i}^{l}} - H{{X}_{i}})(Y_{j}^{l} - H{{X}_{j}}),$$

where $Y_{i}^{l}\,\,{\text{and}}\,\,Y_{j}^{l}$ are the given values of the ensemble of observations of vector Y at the grid points $i\,\,{\text{and}}\,\,j$, respectively; and ${{X}_{i}}\,\,{\text{and}}\,\,{{X}_{j}}$ are the corresponding model values at these points. The ensemble ${{Y}^{l}},l = 1,...,{{N}_{e}}$, is chosen in such a way that $N_{e}^{{ - 1}}\sum\nolimits_{l = 1}^{{{N}_{e}}} {({{Y}^{l}}} - HX) = 0$ at any grid point.

Now, if we set vector С equal to zero at any time moment, chose the ensemble $X$ at each time interval on the assumption that $EX = Y$, where $Y$ is the observed or true field (the observation errors may be included additionally as an independent term), and take the ensemble average as the initial field, we obtain the standard EnKF method or, in its simplified variant, the EnOI method, if this ensemble is set beforehand instead of being calculated independently at each time step [16]. This fact is also shown in [10]. In the standard form, the EnKF method can be written as follows:

$$\begin{gathered} {{X}_{{a,n + 1}}} = {{X}_{{b,n + 1}}} + {{K}_{{n + 1}}}({{Y}_{{n + 1}}} - H{{X}_{{b,n + 1}}}), \\ K = \alpha {\kern 1pt} B{{H}^{{\text{T}}}}{{(HB{{H}^{{\text{T}}}} + R)}^{{ - 1}}},\,\,\,\,B = N_{e}^{{ - 1}}\sum\limits_{l = 1}^{{{N}_{e}}} {({{X}^{l}}} - \bar {X}){{({{X}^{l}} - \bar {X})}^{{\text{T}}}}, \\ \end{gathered} $$

((2))

where ${{X}^{l}},\,{\kern 1pt} l = 1,...,{{N}_{e}}$ are the elements of ensemble $X\,\,{\text{and}}\,\,\bar {X}$ is the ensemble average. The matrix of measurement error R and coefficient α are given from empirical considerations.

Thus, the GKF method generalizes the EnKF method and it is reasonable to compare their numerical realizations using the same archive of observation data.

4 NUMERICAL EXPERIMENTS AND ANALYSIS OF RESULTS

4.1 Program Realization of the Data Assimilation Algorithm

The assimilation of the observation data is realized in the form of a parallel program module DAM (Data Assimilation Module) written in FORTRAN-95 with the use of the MPI library. The calculation values of the parameters of the ocean model enter the input of the DAM, which uses another processor decomposition of the calculation region, which is important because the size of the three-dimensional arrays of the parameters for the ocean model with a resolution of 0.25° is a few gigabytes. We have succeeded in attaining a high degree of parallelism due to the independency of the data assimilation at each observation point, according to formulas (1) and (2). In the realization of the algorithm, we have taken into account the necessity to store a large volume of model parameters used in the calculations with data assimilation with a memory limit of 1.5–2 Gb per core. For this purpose, the MPI-nodes were gathered into groups consisting of 8 elements. In the parallel realization of the assimilation method, the correction of the calculated parameters on 24 processor cores takes about 40 minutes of calculation time instead of 4.5 hours when using one core, which would be comparable to the time necessary to calculate a daily model forecast; however, such an assimilation time is unacceptable.

The program module DAM was realized on the LOMONOSOV supercomputer at Moscow State University; its configuration and software are described in [17].

4.2 Realization of Numerical Experiments

To execute the numerical experiments on the comparison of the assimilation data methods in the HYCOM model of ocean dynamics, the Atlantic region with boundaries from 85° S to 55° N, including the Sargasso Sea and the Gulf of Mexico, was considered. The heat-and-mass transfer through the Strait of Gibraltar and the Drake Passage was not considered. The calculations with the use of the numerical model of ocean dynamics include the initial stage of modeling at which the model undergoes acceleration from the zero initial velocities of the currents by setting the wind velocity at the ocean surface (the so-called atmospheric forcing). The forcing of the HYCOM model was carried out on the temporal interval from 01.01.1968 to 05.01.2008 (40 years of the model time). The climatic temperature and salinity distributions were taken from the archive [18]. The atmosphere forcing from the NCEP/NCAR Reanalysis project [19] was performed for the corresponding period of time. In the process of model forcing, we stored the calculated values of the parameters for each day over the preceding 10 years; these values were later used to construct the ensemble elements. We used 50 values of the model field for a concrete date and the closest dates $\pm 5$ days as the elements of the ensemble $X = \left\{ {{{X}_{l}}} \right\},$$l = 1,...,{{N}_{e}},{{N}_{e}} = 50$. For example, for the ensemble of parameters for January 5, we used 5 values for each parameter (which corresponded to January 1, 3, 5, 7, and 9) for the preceding 10 years.

Then, we performed three numerical experiments on the time interval from 01.01.2010 to 01.10.2010 (10 days) with the atmospheric forcing, which was also set according to the data of the NCEP/NCAR Reanalysis project. Below, the analysis and comparison of the results of these experiments are presented.

Experiment А01 is the experiment with assimilation of the AVISO altimetry data for each day by the GKF method.

Experiment А02 is the experiment with assimilation of the AVISO altimetry data for each day by the EnOI method.

Experiment А03 is the control calculation experiment without data assimilation.

In all these experiments, a numerical solution for each model day is compared with the AVISO satellite altimetry data for the same real day. Before the data assimilation, we extract from the satellite and model data on the ocean level their average along the tracks; the obtained quantity is called the ocean level anomaly. We carry out this operation to ensure identical (zero) averages for the model and satellite data in order to provide their correct assimilation. After the data assimilation, the model’s average is added again to the ocean level anomaly.

For the vector С and covariant matrices Q in (1) and B in (2) calculated in the way described above, we take into account the covariance (relation) between the different model quantities: the ocean level anomaly, temperature, and salinity at different model horizons. Therefore, the assimilation of one of the quantities (in our case, the ocean level) will correct the entire vector of the model solution.

4.3 Analysis of the Results

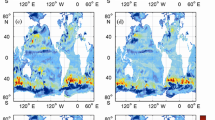
The model fields of the Atlantic level with the altimetry data assimilation by the GKF method (experiment А01), with data assimilation by the EnOI method (experiment А02), and without data assimilation (experiment А03) for the final time moment (the 10th model day) are shown in Fig. 1. It is seen from Fig. 1 that the fields in experiments А01 (Fig. 1a) and А03 (Fig. 1c) are relatively close to each other; however, the field constructed according to experiment А01 is more intensive; the dynamics in this field are more pronounced, especially its synoptic component, which is expressed in the number and size of the synoptical vortices. A considerable difference between these fields is seen in the regions of the confluence of the North-Atlantic current and Brazil-Malvinas, where the ocean’s dynamics are most pronounced. It should be noted that the calculation with the use of the EnOI method (Fig. 1b) is significantly different; the amplitude of the calculation field becomes considerably lower and does not exceed 0.3 m, as distinct from the control calculation field and the field calculated by the GKF method, in which the values of the amplitude are much greater: 0.7 and 1 m, respectively.

Fig. 1.

Model ocean level fields (m) on 10th day (January 10, 2010) obtained in three experiments: (a) А01 using GKF method, (b) А02 using EnOI method, (c) А03 after control calculation.

Figure 2 shows the surface temperature fields obtained in the same experiments on the tenth model day. It is seen in Fig. 2 that the variations in the temperature field are significantly less pronounced than those in the ocean level field and all three methods give close values. The most significant discrepancies are seen in the Gulf Stream area, where the spatial temperature gradient is more pronounced in the fields obtained in experiments A01 and A02 than in the field of experiment А03. These calculations show that the differences in the ocean level field do not cause a significant effect on the large-scale temperature field; such differences should be sought in the synoptic- and micro-scale.

To estimate quantitatively the data assimilation effect, let us use the error function, i.e., the root-mean-square deviation of the model solution calculated for all points where the measurements were made for a specific day from the observation data. Let us introduce the following quantities:

$$\sigma _{n}^{2} = {{N}^{{ - 1}}}\sum\limits_{i = 1}^N {({{Y}_{{n,i}}}} - H{{X}_{{n,i}}}{{)}^{2}},\,\,\,\,\sigma _{{a,n}}^{2} = {{N}^{{ - 1}}}\sum\limits_{i = 1}^N {({{Y}_{{n,i}}}} - H{{X}_{a}}_{{,n,i}}{{)}^{2}},\,\,\,\,\sigma _{{b,n}}^{2} = {{N}^{{ - 1}}}\sum\limits_{i = 1}^N {({{Y}_{{n,i}}}} - H{{X}_{b}}_{{,n,i}}{{)}^{2}},$$

where ${{Y}_{{n,i}}}$ is the observed level at the point with number i at moment n, $i = 1,...,N;n = 1,..,10$. In addition, ${{X}_{a}}_{{,n,i}}\,\,{\text{and}}\,\,{{X}_{b}}_{{,n,i}}$ are the analysis and forecast (background) at step n, respectively; $\sigma _{n}^{2}{\kern 1pt}$ is the variance of the control calculation error; $\sigma _{{a,n}}^{2}{\kern 1pt}$ is the variance of the analysis error (after data assimilation); and $\sigma _{{b,n}}^{2}{\kern 1pt}$ is the variance of the forecast error (one step forward after the data assimilation). All the errors are calculated at each time step.

Fig. 2.

Model ocean surface temperature fields (°C) on 10th day (January 10, 2010) obtained in three experiments: (a) А01 using GKF method, (b) А02 using EnOI method, (c) А03 after control calculation.

Figures 3 and 4 show the change in the error of the model ocean level depending on time.

Fig. 3.

Behavior of forecast error for ocean level (m²) in time in three experiments. Curve 1 is control calculation, curve 2 is calculation with data assimilation, using EnOI method, curve 3 is calculation with data assimilation, using GKF method.

Fig. 4.

Behavior of calculation error for ocean level (m²) in time for three experiments. Curve 1 is control calculation, curve 2 is calculation with data assimilation using EnOI method, curve 3 is calculation with data assimilation using GKF method.

It is seen from Fig. 3 that, since the calculations in all three experiments start with the identical initial conditions, the forecast error for the ocean level for the first day is identical for all three experiments; for the second day, the forecast error for the calculations using the EnOI and GKF methods are identical due to their algorithm construction; and further, the corresponding curves 2 and 3 diverge; 10 days later, the forecast error decreases approximately to a half for all three experiments. For the control calculation, the error drops from 0.12 m² to 0.06 m²; for the calculation using the EnOI method, from 0.06 m² to 0.04 m²; and for the calculation using the GKF method, from 0.06 m² to 0.02 m² and reaches the extreme value (attains the plateau). This means that it is impossible to reduce the forecast error without improving the numerical model itself. At the same time, it is clearly seen that the quality of the GKF method surpasses that of the EnOI method. This conclusion is also confirmed by analyzing the behavior of the error $\sigma _{{a,n}}^{2}{\kern 1pt}$ (see Fig. 4). In Fig. 4, the first curve coincides with that shown in Fig. 3, while the two others (for the EnOI and GKF methods) lie significantly lower than those in Fig. 3 and barely change, since they are calculated with the use of the same data as those used for the assimilation. These results demonstrate that the GKF method surpasses the EnOI method by a factor of 2 with respect to both the forecast error criterion and the analysis error criterion.

It is also possible to compare these data assimilation methods with respect to computational efforts. The analysis of formulas (1) and (2) shows that the difference between the calculations of the corresponding gain matrices K consist in calculating the matrices $(\Lambda - C){{(H\Lambda )}^{{\text{T}}}}$ and ${{(BH)}^{{\text{T}}}}$. However, for the first matrix, it is sufficient to have an ensemble of model calculations only for the first day of assimilation, where the calculations using both methods are identical and further the calculation of this matrix is reduced to the known values of the model fields at the previous time steps; while the calculation of the matrix ${{(BH)}^{{\text{T}}}}$ requires knowing or constructing the ensemble of model calculations at each time step. This requires much more time and short-term memory resources. The experiments have shown that the GKF method is about thrice as economical as the EnOI method with respect to the short-term memory costs and twice as economical with respect to computation time.

4.4 Estimation of the Acceleration and Effectiveness of the GKF Method

We calculated the acceleration and effectiveness of the parallel algorithms used in our work. Table 1 demonstrates the calculation time in minutes (${{t}_{{Np}}}$) depending on the number of processors (Np) for the numerical experiment А01 described above with data assimilation for the observations of the ocean level by using the GKF method. Figure 5 shows the graph of acceleration of the parallel algorithm ${{S}_{{Np}}} = {{{{t}_{1}}} \mathord{\left/ {\vphantom {{{{t}_{1}}} {{{t}_{{Np}}}}}} \right. \kern-0em} {{{t}_{{Np}}}}}$. Figure 6 shows the graph of the effectiveness of the computation ${\text{Ef}}{{{\text{f}}}_{{Np}}} = {{{{S}_{{Np}}}} \mathord{\left/ {\vphantom {{{{S}_{{Np}}}} {Np}}} \right. \kern-0em} {Np}}$. It is seen in these graphs that the acceleration increases with the growth of the number of processors, while the effectiveness decreases when the number of processors are greater than 24, which is related to the additional data exchanges and assembling of processors into groups with 8 processors in each group to store the model data.

Table 1.

Np	1	24	72	144	512	625
${{t}_{{Np}}}$, min	270	40	15	10	7	6

Fig. 5.

Acceleration of calculations depending on number of processors.

Fig. 6.

Effectiveness of calculations depending on number of processors.

5 CONCLUSIONS

Using the results of the numerical experiments, the GKF method created by the authors of this paper and the EnOI method are compared. These methods are applied in the model of the Atlantic dynamics HYCOM to assimilate the observation data of the ocean level.

It is shown that the GKF method has considerable advantages over the EnOI method with respect to both the forecast error criterion and the analysis error criterion. The forecast errors after the data assimilation are reduced in both methods compared with the control calculation, which proves their correctness; however, the GKF method reduces the forecast error from 0.06 m² to 0.02 m², while the EnOI reduces it from 0.06 m² to 0.04 m². It is also shown how the assimilation of the ocean level data influences the parameters which were not assimilated directly, namely, on the ocean surface temperature. Our calculations demonstrate that the obtained fields of the physical characteristics, in particular, the ocean’s surface temperature field, are physically reliable and agree with the calculations performed earlier [9, 10] and the observation data.