On Solvability of One Class of Nonlinear Integral Equations on Whole Line with Two Monotone Nonlinearities

Abstract

We investigate a class of nonlinear singular integral equations with two monotone nonlinearities on the whole line. These equations have both theoretical and practical interest. We prove the existence theorem of a solution and the uniqueness theorem in a certain class of continuous and odd on $\mathbb {R}\setminus\{0\}$ functions. The results of the work summarize some previously obtained research results in this direction. We find the limits of the solution of the equation at $\pm\infty$. For obtained solution we investigate some its properties. We also establish the integral asymptotic for the constructed solutions. The results are illustrated by examples of the equations under consideration.

1. Introduction

We consider the following nonlinear singular integral equation on the whole axis:

$$ Q(F(x))= \left( \mu(x)-1 \right) Q_0(F(x))+\int\limits_{-\infty}^{\infty} K(x-t)F(t)dt, \ \ x\in\mathbb{R}$$

(1.1)

with respect to a real-valued measurable function $F(x)$ on $\mathbb{R}$. Here the kernel $K$ is an even function on $\mathbb{R}$ and satisfies the following conditions:

$$K(x)>0,\ \ x\in \mathbb{R};\ \ K(x)\downarrow \ \ x \ \ \in [0, +\infty), $$

(1.2)

$$K\in C_M(\mathbb{R});\ \ \int\limits_{-\infty}^\infty K(x)\,dx =1,$$

(1.3)

$$\int\limits_{0}^\infty x^2 K(x)\,dx<+\infty,$$

(1.4)

where $C_M(\mathbb{R})$ is the space of functions continuous and essentially bounded on $\mathbb{R}$.

We assume that $\mu(x)$ is an even function on $\mathbb{R}$ and continuous on $\mathbb{R}\setminus \{$0\} with properties

$$\mu(0)=+\infty, \ \ \mu(x)\geq1, \ \ x\in \mathbb{R}, \ \ \lim\limits_{x\rightarrow +\infty}\mu(x)=1,$$

(1.5)

$$\mu |_{{\mathbb R}} -1 \in L_1 ({\mathbb R}) \cap L_2 ({\mathbb R}), \ \ {\mathbb R}:=(0,+\infty).$$

(1.6)

In view of (1.4) and (1.7) we denote

$$ M:=\sup \limits_{x\in \mathbb{R}} K(x)\, \int\limits_0^{\infty} \left( \mu(t)-1 \right) dt \,<+\infty.$$

(1.7)

Concerning with functions $Q(u)$ and $Q_0(u)$ we assume that there are odd continuous and monotone increasing functions on $\mathbb{R}$, strictly convex downward on the set $[0, +\infty)$, satisfying the following conditions:

• (a) $\eta$ is the first positive root of the equations $Q(u)=u$ and $Q_0(u)=u$,

• (b) $Q(0) = Q_0(0)=0, \ \ Q(u)\leq Q_0(u), \ u\in [0,\, \eta],$

  $P(u):=\dfrac{Q(u)}{Q_0(u)}$ is a strictly increasing function on ${\mathbb R},$

• (c) for inverse functions to the functions $Q$ and $Q_0$ the inequality holds

  $Q^{-1} \Big(\eta \left( 1+M \right) ^2 \mu^2 (x) \Big) \leq Q_0^{-1} \Big( \eta \left( 1+M \right) \mu(x)\Big), \ \ x \in {\mathbb R}.$

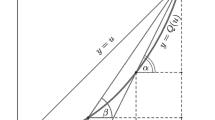
The approximate graphs of functions $Q(u)$ and $Q_0(u)$ and their inverse are plotted in Fig. 1.

Recently, of great interest for theoretical and practical research has been the question of the solvability of nonlinear integral equations on unbounded sets ([1-17] and references therein), in connection with their many important applications. Recent publications, including those abroad, emphasize the relevance and significance of studies of these equations.

However, as it is known, in most cases, studies of nonlinear equations are fraught with difficulties caused by the complexity of their structure. It should be noted that a significant number of publications in this direction [1-17] are devoted to the dynamics of the interaction of open-closed $p$-adic strings. In string field theory and in the theory of $p$-adic strings, it becomes necessary to study special real-valued (rolling) solutions of field equations with special boundary conditions given at $(+)$ and $(-)$ time infinities. Due to the fact that the field of string interaction is nonlocal, the theory of $p$-adic strings differs significantly from classical local field theory. Interest in the problem of constructing a classical solution is associated with possible applications in cosmology and in other areas of natural science ([6], [7] and references therein). It should also be noted that numerous physical problems are described by equations whose nonlinear component is determined by convex functions. So, for example, equations with power nonlinearity are found in the dynamic theory of $p$-adic open-closed strings, and with exponential nonlinearity in the kinetic theory of gases, in mathematical biology, and in the theory of the spatiotemporal spread of the epidemics ([10], [11] and references therein).

In the works [1-9] for studying the dynamics of tachyons of open-closed $p$-adic strings, particular cases of equation (1.1) with a kernel $K(x)$ representing a Gaussian distribution were considered

$$K(x)=\frac{1}{\sqrt{\pi}}e^{-x^2} .$$

In the recent paper [13], by one of the authors of present work, the results of [8] were generalized to the case of common even conservative kernels of $K.$

In reference [5] the equation (1.1) was investigated with a Gaussian kernel $K$ and with functions $Q, \ Q_0$ and $\mu$ of the forms

$$ Q(u)=u^m \ \ \text{and} \ \ Q_0(u)=u^n,$$

(1.8)

$$\mu(x)=\lambda^2 \, \frac{p-1}{2p} \left( \Phi^{p-1}(x)-1 \right) +1, \,\, x\in \mathbb{R}, \quad \lambda\in [0, 1),$$

where $\lambda$ is string interaction constant, $m, n, p$ are odd numbers and

$$\begin{aligned} \, & m=p^2, \ \ \qquad \qquad n=\frac{p(p-1)}2-1, \\ &\Phi(-0)=+\infty, \quad \Phi(-x)=-\Phi(x), \ x>0, \\ & \Phi(\pm\infty)=\mp1, \quad \Phi^{p-1}-1 \in L_1 (\mathbb{R}^+) \cap L_2 (\mathbb{R}^+). \end{aligned}$$

It should be noted that the study of this case is complicated by the presence of not only an even conservative kernel $K$, but also a singular function $\mu$. The equation (1.1) in the case of (2.9) for $m>2n$ and with a common kernel was studied in [14] and [15], in the first of which the existence of a solution and its limits at $\pm\infty$, and in second one the uniqueness of a solution in a certain class of functions have been proved. In paper [16] the corresponding system of equations (1.1) was studied. Moreover, in the indicated papers, the results were supported by particular examples of the kernel $K$ and the function $\mu$, which also have physical applications.

The main results of our paper are the theorems on the existence of a solution and uniqueness in a certain class of continuous and odd on $\mathbb {R}\setminus\{0\}$ functions (Theorem 2.1 and Theorem 4.1). Moreover, the limits of the solution are found and some properties of the solution are revealed, including an integral estimate (Theorem 3.1).

All the results of this paper below summarize the earlier results of [5], [9], [14], [15], [16]. With the expansion of the class of nonlinearities, it is thereby possible to expand range of applicability of the obtained results to the studied class of equations (1.1). In addition, setting $\mu(x) \equiv1, \ x\in \mathbb{R}$, we get exactly all the corresponding results of [17]. It should also be specially noted that the conditions $(b)$ and $(c)$ are not additional conditions restricting the class of equations (1.1). At the end of the work, we show that the conditions $(b)$ and $(c)$ in the above mentioned cases are also fulfilled.

2. On the solvability of equation (1.1)

First of all, we reduce equation (1.1) from the whole axis to the positive semi-axis ${\mathbb R}$. Using the facts that $Q(u),\ Q_0(u)$) are odd functions on $\mathbb{R}$, $\mu$ and $K$ are even functions on $\mathbb{R}\setminus \{0\}$ and ${\mathbb R}$, respectively, by direct verification we check that if $f(x)$ is a measurable solution of the following integral equation on the semi-axis

$$ Q(f(x))= \left( \mu(x)-1 \right) Q_0(f(x))+\int\limits_0^\infty (K(x-t)-K(x+t))f(t)dt, \ x\in\mathbb{R}^+,$$

(2.1)

then the odd extension of this function on $(-\infty, 0)$

$$ F{(x)= \begin{cases} \quad f(x), & \text{if $x>0$,} \\ -f(-x), & \text{if $x<0$} \end{cases}}$$

(2.2)

almost everywhere on $\mathbb{R}$ will be the solution of the equation (1.1).

Before proceeding with the solution of equation (1.2), we present some facts from [17]. Under conditions (1.3)–(1.5) and $(a)-(c)$, the following nonlinear integral equation with a sum-difference kernel:

$$ Q(\varphi(x))=\int\limits_0^\infty (K(x-t)-K(x+t))\varphi(t)dt,\quad x\geq0$$

(2.3)

has a bounded nonnegative nontrivial and continuous solution on $[0, +\infty)$, moreover

$$\varphi(0)=0,\quad \varphi(x)>0,\quad x>0,$$

(2.4)

$$\varphi(x)\uparrow\,\,\mbox{in}\,\, x\,\,\mbox{on}\,\, [0, +\infty),$$

(2.5)

$$\lim\limits_{x\rightarrow+\infty}\varphi(x)=\eta, \ \ \eta-\varphi\in L_1(\mathbb{R}^+).$$

(2.6)

The kernel $K$ satisfies the easily verified inequality

$$ K(x-t)\geq K(x+t)\ \ \text{on} \ \ \big\{\, (x,t): x\geq0,\ t\geq0 \, \big\}.$$

(2.7)

Now we consider the following successive approximations for equation (1.2)

$$\begin{gathered} \, Q(f^{(s+1)}(x))= \left( \mu(x)-1 \right) Q_0(f^{(s)}(x))+\int\limits_0^\infty (K(x-t)-K(x+t))f^{(s)}(t)\,dt, \\ s=0,1,2,\dots, \ \ x\in {\mathbb R} \nonumber. \end{gathered}$$

(2.8)

As a zero approximation, we choose the solution of equation (2.11)

$$\begin{gathered} \, f^{(0)}(x)=\varphi(x), \ x\in {\mathbb R}. \end{gathered}$$

(2.9)

Below inductively in $n$ we prove that

$$f^{(s)}(x)\quad \uparrow\quad \hbox{in}\quad s, \ \ x\in{\mathbb R},$$

(2.10)

$$f^{(s)}(x)\leq Q_0^{-1} \Big( \eta \left( 1+M \right) \mu (x) \Big) ,\quad s=0,1,2,\dots, \quad x\in {\mathbb R}.$$

(2.11)

Monotonicity of iterations. Putting $s=0$ in (2.16) taking into consideration (3.17), (1.6), (2.15), (2.12), (2.11) and $(b)$ convexity functions $Q$ and $Q_0$ on $[0, +\infty)$ we get

$$Q(f^{(1)}(x)) = \left( \mu(x)-1 \right) Q_0(\varphi(x))+\int\limits_0^\infty (K(x-t)-K(x+t))\varphi(t)\,dt \geq Q(\varphi(x))= Q(f^{(0)}(x)).$$

It means that $f^{(1)}(x)\geq f^{(0)}(x), \ \ x\in {\mathbb R}.$ Further, let (3.18) holds for some $s\in\mathbb{N}$. Then by the inductive assumption

$$\begin{gathered} \, Q(f^{(s+1)}(x))\geq \left( \mu(x)-1 \right) Q_0(f^{(s)}(x))+\int\limits_0^\infty (K(x-t)-K(x+t))f^{(s-1)}(t)\,dt =Q(f^{(s)}(x)), \end{gathered}$$

therefore, $f^{(s+1)}(x)\geq f^{(s)}(x) \ \text{for any} \ s=0,1,2,\dots, \ \ x\in {\mathbb R}.$

Boundedness of iterated functions. For $s=0$ based on (3.17), (2.11), (2.13), (2.14), (1.6) and properties $(a), \, (c)$ convexity functions $Q$ and $Q_0$ on set $[0, +\infty)$ from (2.16) we have

$$\begin{aligned} \, Q(f^{(1)}(x)) &= \left( \mu(x)-1 \right) Q_0(\varphi(x))+ Q(\varphi(x))\leq \left( \mu(x)-1 \right) Q_0(\eta)+ Q(\eta) \\ &= \left( \mu(x)-1 \right) \eta +\eta = \eta \mu(x) \leq \eta \left( 1+M \right) ^2 \mu^2 (x), \end{aligned}$$

from which it follows

$$f^{(1)}(x)) \leq Q^{-1} \Big( \eta \left( 1+M \right) ^{2} \mu^2(x)\Big) \leq Q_0^{-1} \Big( \eta \left( 1+M \right) \mu(x)\Big),\ \ x \in {\mathbb R}.$$

Let (3.19) takes place for some $s\in\mathbb{N}$. According to the properties of the functions $Q(u)$ and $Q_0(u)$ for their inverse $Q^{-1} (u)$ and $Q_0^{-1} (u)$ for $u\geq \eta$ the inequality $Q^{-1}(u)\leq Q_0^{-1}(u) \leq u$ holds (see Fig. 1), whence

$$ Q_0^{-1} \Big( \eta \left( 1+M \right) \mu (x) \Big)\leq \eta \left( 1+M \right) \mu (x), \ \ x\in{\mathbb R}.$$

(2.12)

Then by the inductive assumption we obtain

$$\begin{aligned} \, &Q(f^{(s+1)}(x)) \\ &\leq \left( \mu(x)-1 \right) \eta \left( 1+M \right) \mu(x) +\int\limits_0^\infty (K(x-t)-K(x+t)) Q_0^{-1} \Big( \eta \left( 1+M \right) \mu (t) \Big)\,dt \\ &\leq \eta \left( 1+M \right) \mu(x) \left( \mu(x)-1 \right) + \eta \left( 1+M \right) \Biggr( \int\limits_0^\infty K(x-t) (\mu (t)-1) \,dt + \int\limits_0^\infty K(x-t) \,dt \Biggr) \\ &\leq \eta \left( 1+M \right) \left( \mu^2(x)-\mu(x) \right) + \eta \left( 1+M \right) ^{2} \leq \eta \left( 1+M \right) ^{2} \mu^2(x). \end{aligned}$$

Figure 1.

Sketches of graphs of functions $Q, Q_0$ and their inverse functions.

Hence, taking into account $(c)$, we conclude that inequality (3.19) is valid for $s+1$

$$f^{(s+1)}(x)\leq Q^{-1} \Big( \eta \left( 1+M \right) ^{2} \mu^2(x)\Big) \leq Q_0^{-1} \Big( \eta \left( 1+M \right) \mu (x) \Big), \ \ x \in {\mathbb R},$$

therefore, and for any $s=0,1,2,\dots.$

It is easy to prove by induction on $s$ that all functions of the sequence $\left( {f^{(s)}(x)} \right)_{s\,\geq0}$ are measurable in $x$ on ${\mathbb R}$.

So, the sequence $\left( {f^{(s)}(x)} \right)_{s \,\geq0 }$ constructed by iterations is nondecreasing (in $s$) and is bounded above on ${\mathbb R}$. Therefore, the sequence converges pointwise as $s\to +\infty:\,\lim\limits_{s\to +\infty} f^{(s)}(x)=f(x), \ x\in{\mathbb R}.$ According to B. Levy’s theorem ([18]), the limit function $f(x)$ satisfies equation (1.2). Besides, the following two-sided estimate holds

$$ 0< \varphi(x) \leq f(x) \leq Q^{-1}_0 \Big( \eta \left( 1+M \right) \mu (x) \Big), \ \ x \in {\mathbb R}.$$

(2.13)

Continuity of the solution of equation (1.2) on $\mathbb{R}^+$. In view of the boundedness of the function $f(x)$ on ${\mathbb R},$ the summability of the kernel $K$ and the fact that convolution of summable and bounded functions is a continuous function ([19]) from (1.2), (3.21) we get that $Q_0(f(x))$ and $Q(f(x))- \left( \mu(x)-1 \right) Q_0(f(x))= Q_0(f(x) \left(P(f(x)) - \left( \mu(x)-1 \right) \right)$ are non-negative continuous functions on ${\mathbb R}$. Hence since by assumption $\mu (x)$ is continuous function on $\mathbb{R}\setminus\{0\}$ and $Q(u),\ Q_0(u), \ P(u)$ are monotone increasing and continuous functions on $\mathbb{R}^+$, we conclude that $f \in C({\mathbb R})$.

Remark 2.1.

It should be noted that from (1.1), taking into account property (2.15) of the kernel $K$, the following inequality immediately follows

$$Q(f(x))\geq \left( \mu(x)-1 \right) Q_0(f(x)), \ \ x\in{\mathbb R},$$

but $Q(f(x)) \not\equiv \left( \mu(x)-1 \right) Q_0(f(x))$ due to nonnegativity and non-triviality of the solution $f(x)$ of equation (2.11).

Thus, the following theorem holds.

Theorem 2.1.

$($the existence of a solution$)$. Let conditions (1.3), (1.4), (1.6), (1.7) and $(a)-(c)$ be satisfied. Then the equation (1.1) has a nonnegative nontrivial continuous and odd on $\mathbb{R}\setminus\{0\}$ solution $F(x)$ defined by formula (2.10). Furthermore,

$$0 < \varphi(x) \leq F(x) \leq Q_0^{-1} \Big( \eta \left( 1 + M \right) \mu(x) \Big) \ \textit{\ if} \ \ x>0,$$

(2.14)

$$- Q_0^{-1} \Big( \eta \left( 1 + M \right) \mu (x) \Big) \leq F(x) \leq -\varphi(-x) \ \textit{ if} \ \ x<0,$$

(2.15)

$$\hspace{4cm} F(\pm0) =\pm\infty.$$

(2.16)

Proof.

It remains to prove only assertions (1.1)–(2.16) and that $F(x)$ is a continuous function on $\mathbb{R}\setminus\{0\}$. Double estimations (1.1) and (2.15) follow immediately from (2.10) and (3.21). Statement (2.16) follows from (1.1) taking into consideration that $\mu$ and $K$ are even functions on $\mathbb{R}\setminus \{0\}$ and ${\mathbb R}$ respectively, the properties of the odd functions $Q(u)$ and $Q_0(u)$, remark 2.1 and (1.6).

It is obvious that due to the property (2.16), the solution $F(x)$ of equation (1.1), being odd extension to $(-\infty, \, 0)$ of the continuous function $f(x)$ on ${\mathbb R}$ will be continuous on $\mathbb{R}\setminus \{0\}$. $\square$

3. The Limit of Solution of the Equation and the Properties of this Solution

First, we prove that the function $f-\varphi \$ is summable function on ${\mathbb R}$. Then we find the limit for solution of equation (1.2) and reveal some properties of this solution. That will allow us to determine the corresponding properties for the sought solution of equation (1.1).

3.1. On the Connection Between the Solutions (1.2) and (2.11)

Let $0<r<+\infty .$ For $x \in(0,r)$ taking into account (3.20) from (3.21) we have

$$0 < \varphi(x) \leq f(x) \leq Q^{-1}_0 \Big( \eta \left( 1+M \right) \mu (x) \Big) \leq \eta \left( 1+M \right) \left( \mu(x) -1 \right) + \eta \left( 1+M \right) .$$

Then in view of condition (1.7) we conclude that $f \in L_1(0, r),\, \forall r\in{\mathbb R},$ and therefore, $f \in L^{loc}_1({\mathbb R}).$ Since $\varphi \in C\big([0,\, +\infty)\big),$ then $\varphi\in L_1(0, r)$ for any $r\in{\mathbb R}$.

Thus, $f -\varphi \in L^{loc}_1({\mathbb R}).$

Below we show that $f -\varphi \in L_1[r, +\infty)$. To do this, we first show by induction on $s$ that

$$ f^{(s)} -\varphi \in L_1 [r, +\infty), \ \ s=0,1,2, \dots.$$

(3.1)

In the case $s=0$ the inclusion (3.1) is obviously satisfied. Suppose that (3.1) takes place for some $s\in\mathbb{N}$. Then, taking into account the monotonicity of the function $Q$, as well as the boundedness (3.19) of the sequence $\left( {f^{(s)}(x)} \right)_{s\,\geq0 }$ with respect to $s$ from (2.16) we obtain the following chain of inequalities:

$$\begin{aligned} \, &0< Q \left( f^{(s+1)}(x) \right) - Q \left( \varphi(x) \right) \nonumber \\ &\leq \eta \left( 1+M \right) \mu (x) \, \left( \mu(x)-1 \right) +\int\limits_0^{\infty} \left( K(x-t) - K(x+t) \right) \left( f^{(s)} (t) -\varphi(t) \right) dt \nonumber \\ &\leq \eta \left( 1+M \right) \Big( \left( \mu(x)-1 \right) ^2 + \left( \mu(x)-1 \right) \Big) +\int\limits_0^{\infty} \left( K(x-t) - K(x+t) \right) \left( f^{(s)} (t) -\varphi(t) \right) dt . \end{aligned}$$

(3.2)

Due to the properties of the functions $K$ and $\mu$ and the induction assumption the left side of inequality (3.2) is a summable function on $[r, +\infty).$ Taking into account the convexity of the function $Q$ and properties (2.12) –(2.14) for $x\geq r>0$ and for every $s=0,1,2, \dots$ the following inequalities hold

• • on set $X_s=\big\{\,x\geq r: \ f^{(s+1)}(x) \leq \eta\, \big\}$

  $$0 \leq f^{(s+1)}(x)- \varphi (x) \leq \eta-\varphi(x),$$

  (3.3)
  $$0 < \frac{Q(\varphi(x))}{\varphi(x)} \ \left( f^{(s+1)}(x)-\varphi(x) \right) \leq Q(f^{(s+1)}(x))-Q(\varphi(x)),$$

  (3.4)

  (see Fig. 2)

• • on set $X_s^*=\big\{x \geq r: \ f^{(s+1)}(x) > \eta \big\}$

  $$ f^{(s+1)}(x)-\varphi(x) \leq \frac{ \eta-Q(\varphi(x))}{\eta -\varphi(x)} \left( f^{(s+1)}(x)-\varphi(x) \right) \leq Q(f^{(s+1)}(x))-Q(\varphi(x)),$$

  (3.5)

  because $Q(u)< u \ \text{when} \ 0< u < \eta$, and, as it is known, $0 < \varphi(x) < \eta, \ x >0$ (see Fig. 3).

Figure 2.

The behavior of the function $Q_0(u)$ in the case $u_1 < u_2 < \eta$.

$$\begin{gathered} \, \alpha > \beta \Rightarrow \tan\alpha > \tan\beta, \\ \alpha > \gamma \Rightarrow \tan \alpha > \tan \gamma,\\ \\ \tan\alpha=\frac{Q_0(u_2) -Q _0(u_1)}{u_2-u_1 }, \\ \tan\beta =\frac{Q_0 (u_1)}{u_1}, \\ \tan\gamma =\frac{Q_0 (u_2)}{u_2}.\\ \\ \end{gathered}$$

Figure 3.

The behavior of the function $Q(u)$ in the case $u_1 < \eta < u_2$.

$$\begin{gathered} \, 45^\circ < \beta < \alpha \\ \Rightarrow 1< \tan\beta < \tan\alpha, \\ \\ \tan\alpha=\frac{Q(u_2) -Q(u_1)}{u_2-u_1 }, \\ \tan\beta =\frac{\eta -Q (u_1)}{\eta-u_1}. \\ \\ \\ \end{gathered}$$

Due to (3.2)–(3.5), (2.14) and the fact that $Q \left( f^{(s+1)} \right) - Q \left( \varphi \right) \in L_1([r, +\infty))$ is obtained from (3.2) we confirm that the inclusion $f^{(s+1)}-\varphi \in L_1[r, +\infty)$ holds. So, we have proved inclusions (3.1).

Integrating both sides of inequality (3.2) over $x$ from $r$ to $+\infty$, in view of (3.2) we get

$$\begin{aligned} \, &\int\limits_{r}^{\infty} \left( Q \left( f^{(s+1)}(x) \right) - Q \left( \varphi(x) \right) \right) dx \leq \eta \left( 1+M \right) \Biggr( \int\limits_{r}^{\infty} \left( \mu(x)-1 \right) ^2 dx + \int\limits_{r}^{\infty} \left( \mu(x)-1 \right) dx \Biggr) \nonumber \\ &+\mathfrak {I}=\eta \left( 1+M \right) \Big( \| \mu-1 \| ^2_ {L_2(r, +\infty)}+ \| \mu-1 \|_{L_1(r, +\infty)} \Big)+\mathfrak {I}, \end{aligned}$$

(3.6)

where the designation is introduced

$$ \mathfrak {I}:= \int\limits_{r}^{\infty} \int\limits_0^{\infty} \left( K(x-t) - K(x+t) \right) \left( f^{(s+1)} (t) -\varphi(t) \right) dt \,dx, \ \ s=0,1,2\ldots.$$

(3.7)

Taking into account (3.18)– (3.20), (1.3)–(1.5) and using the Fubini theorem ([18]), from (3.7) we obtain the following inequality:

$$\mathfrak {I} \leq \eta \left( 1+M \right) \int\limits_{r}^{\infty} \int\limits_0^{r} K(x-t) \mu(t)\,dt \,dx + \int\limits_{r}^{\infty} \int\limits_{r}^{\infty} K(x-t) \left( f^{(s+1)} (t) -\varphi(t) \right) dt \,dx$$

$$\leq \eta \left( 1+M \right) \Big( \| \mu-1 \| _{L_1({\mathbb R})} + m_1 \Big) + \int\limits_{r}^{\infty} \left( f^{(s+1)} (t) -\varphi(t) \right) dt,$$

where we denoted by $m_1$ the first moment of the kernel: $m_1=\int\limits_0^{\infty} u K(u)\,du,$ its existence directly follows from (1.5).

Application of the obtained inequality in regard to (3.6) leads it to the form for any $s=0,1,2\ldots$

$$ \int\limits_{r}^{\infty} \left( Q \left( f^{(s+1)}(x) \right) - Q \left( \varphi(x) \right) \right) dx \leq C_{\eta,\,\mu,\, K} + \int\limits_{r}^{\infty} \left( f^{(s+1)} (t) -\varphi(t) \right) dt,$$

(3.8)

where we denoted by

$$C_{\eta, \,\mu, \, K}:=\eta \left( 1+M \right) \Big( \| \mu-1 \| ^2_{L_2(r, +\infty)} + \| \mu-1 \|_{L_1(r, +\infty)}+\| \mu-1 \| _{L_1({\mathbb R})} + m_1 \Big).$$

First, using inequality (3.3) we estimate the integral on the right-hand side of the last inequality (3.8)

$$\begin{aligned} \, &\int\limits_{r}^{\infty} \left( f^{(s+1)} (t) -\varphi(t) \right) dt= \int_{X_s} \left( f^{(s+1)} (t) -\varphi(t) \right) dt + \int_{X^*_s} \left( f^{(s+1)} (t) -\varphi(t) \right) dt \nonumber \\ &\leq \int_{X_s} \left( \eta -\varphi(t) \right) dt + \int_{X^*_s} \left( f^{(s+1)} (t) -\varphi(t) \right) dt. \end{aligned}$$

(3.9)

Then using inequality (3.9) from (3.8) we get

$$\begin{aligned} \, &\int_{X_s} \left( Q \left( f^{(s+1)}(x) \right) - Q \left( \varphi(x) \right) \right) dx +\int_{X^*_s} \left( Q \left( f^{(s+1)}(x) \right) - Q \left( \varphi(x) \right) \right) dx \\ &\leq C_{\eta,\,\mu,\, K} + \int_{X_s} \left( \eta -\varphi(t) \right) dt + \int_{X^*_s} \left( f^{(s+1)} (t) -\varphi(t) \right) dt. \end{aligned}$$

Taking into consideration (3.4), (3.5), the obvious inequality $\frac{ \eta-Q(u)}{\eta -u} >1> \frac{ Q(u)}{u}$ and the fact that functions $y=\frac{ Q(u)}{u}$ and $y=\frac{ \eta-Q(u)}{\eta -u}$ are nondecreasing on $[\varphi(r),\, \eta)$ it follows that

$$\begin{aligned} \, &\frac{Q(\varphi(r))}{\varphi(r)} \int_{X_s} \left( f^{(s+1)}(x)-\varphi(x) \right) dx + \frac{ \eta-Q(\varphi(r))}{\eta -\varphi(r)} \int_{X^*_s} \left( f^{(s+1)}(x)-\varphi(x) \right) dx \\ &\leq \int_{X^*_s} \left( Q \left( f^{(s+1)}(x) \right) - Q \left( \varphi(x) \right) \right) dx \leq C_{\eta,\,\mu,\, K} + \int_{X_s} \left( \eta -\varphi(t) \right) dt + \int_{X^*_s} \left( f^{(s+1)} (t) -\varphi(t) \right) dt, \end{aligned}$$

from which we have

$$\begin{aligned} \, &\frac{Q(\varphi(r))}{\varphi(r)} \int_{X_s} \left( f^{(s+1)}(x)-\varphi(x) \right) dx + \left( \frac{ \eta-Q(\varphi(r))}{\eta -\varphi(r)} -1 \right) \int_{X^*_s} \left( f^{(s+1)}(x)-\varphi(x) \right) dx \\ &\leq C_{\eta,\,\mu,\, K} + \int_{X_s} \left( \eta -\varphi(t) \right) dt, \end{aligned}$$

or

$$\begin{aligned} \, &\frac{Q(\varphi(r))}{\varphi(r)} \int_{X_s} \left( f^{(s+1)}(x)-\varphi(x) \right) dx + \frac{ \varphi(r)-Q(\varphi(r))}{\eta -\varphi(r)} \int_{X^*_s} \left( f^{(s+1)}(x)-\varphi(x) \right) dx \nonumber \\ &\leq C_{\eta,\,\mu,\, K} + \int_{X_s} \left( \eta -\varphi(t) \right) dt, \end{aligned}$$

(3.10)

Figure 4.

The behavior of the function $Q(u)$ when $0 < \varphi(r) < \eta$.

$$\begin{gathered} \, 0<\varphi (r) <\eta, \\ \alpha > \beta \Rightarrow \tan\alpha > \tan\beta, \\ \\ \tan\alpha=\frac{\varphi (r)- Q(\varphi (r)) }{\eta-\varphi (r)},\\ \tan\beta =\frac{Q (\varphi (r))}{\varphi (r)}. \\ \\ \\ \end{gathered}$$

Obvious that $0<\frac{Q(\varphi(r))}{\varphi(r)}< \frac{ \varphi(r)-Q(\varphi(r))}{\eta -\varphi(r)}, \ r>0$ (see Fig. 4). Let introduce a new notation in (3.10) $C_r^{\,*}:= \frac{\varphi(r)}{Q(\varphi(r))}.$ Taking into account (2.13) and (2.14) we come to the uniform estimate

$$ \int\limits_{r}^{\infty} \left( f^{(s+1)}(x) - \varphi(x) \right) dx \leq C_r^{\,*} \left( C_{\eta,\,\mu,\, K} + \int\limits_0^{\infty} \left( \eta -\varphi(t) \right) dt \right) , \ s=0,1,2\ldots.$$

(3.11)

By B. Levy’s theorem the inclusion $f-\varphi \in L_1[r, +\infty)$ holds. Further, the following integral estimate is valid

$$\begin{aligned} \, &\int\limits_{r}^{\infty} \left( f(x) - \varphi(x) \right) dx \leq \frac{\varphi(r)}{Q(\varphi(r))} \Big(\eta \left( 1+M \right) \Big( \| \mu-1 \| ^2_{L_2(r, +\infty)} + \| \mu-1 \|_{L_1(r, +\infty)}\Big) \nonumber \\ &+ \eta \left( 1+M \right) \Big( \| \mu-1 \| _{L_1({\mathbb R})} + m_1 \Big) + \| \eta -\varphi \|_{L_1({\mathbb R})} \Big), \ \ r>0 \end{aligned}$$

(3.12)

(recorded with the substitution of the values of the introduced notation $C_r^*$ and $C_{\eta,\,\mu,\, K}$).

On the other hand, as it is shown above, $f -\varphi \in L^{loc}_1({\mathbb R}),$ therefore,

$$ f - \varphi \in L_1({\mathbb R}).$$

(3.13)

Whence, by virtue of (2.14) and the triangle inequality, it follows that

$$ f-\eta \in L_1({\mathbb R}).$$

(3.14)

3.2. On the Limit of the Solution of Equation (1.2)

First of all, we prove that

$$ \lim\limits_{x\rightarrow+\infty} \left( f(x) -\varphi (x) \right) =0, \ \ i=1,2,\ldots,N.$$

(3.15)

Using (3.21), (3.20), (1.5) from (1.2) and (2.11) for $x \in{\mathbb R}$ we have

$$\begin{aligned} \, &0\leq Q \left( f (x) \right) -Q \left( \varphi (x) \right) \leq \eta \left( 1+M \right) \mu(x) \left( \mu(x)-1 \right) \nonumber \\ &+ \int\limits_0^{\infty} K (x-t)\, \frac{f(t) -\varphi (t)}{\mu(t)} dt + \int\limits_0^{\infty} K(x-t) \, \frac{\mu(t)-1}{\mu(t)} \left( f(t) -\varphi (t) \right) dt \nonumber \\ &\leq \eta \left( 1+M \right) \mu(x) \left( \mu(x)-1 \right) + \int\limits_0^{\infty} K (x-t)\, \frac{f(t) -\varphi (t)}{\mu(t)} dt +\int\limits_0^{\infty} K(x-t) \frac{\mu(t)-1}{\mu(t)} f(t) dt \nonumber \\ &\leq \eta \left( 1+M \right) \mu(x) \left( \mu(x)-1 \right) + \int\limits_0^{\infty} K (x-t)\, \frac{f(t) -\varphi (t)}{\mu(t)} dt \nonumber \\ &+ \eta \left( 1+M \right) \int\limits_0^{\infty} K(x-t) \left( \mu(t)-1 \right) dt. \end{aligned}$$

(3.16)

We show that the integrals on the right-hand side of (3.16) tend to zero at infinity. Indeed, since

$$0\leq \frac{f(t) -\varphi (t)}{\mu(t)}\leq \eta \left( 1+M \right) <+\infty \ \ \ \ \text{and} \ \ \ \ \frac{f(t) -\varphi (t)}{\mu(t)} \leq f(t) -\varphi (t)$$

then in view of $f -\varphi \in L_1(0, +\infty)$ ((3.13)) we can conclude that

$$ \frac{f -\varphi }{\mu} \in L_1(0, +\infty)\cap L_{\infty}(0, +\infty).$$

(3.17)

Hence, using the fact that the kernel $K\in L_1(\mathbb {R})\cap C_M(\mathbb{R}),$ in accordance with Lemma $5$ from [20] we get

$$ \lim\limits_{x\rightarrow +\infty} \int\limits_0^{\infty} K(x-t)\, \frac{f(t) -\varphi (t)}{\mu(t)} dt=0.$$

(3.18)

Based on the known limit relation of the convolution operation ([20], [21]) we will have

$$ \lim\limits_{x\rightarrow +\infty} \int\limits_0^{\infty} K(x-t)\, \left( \mu(t)-1 \right) dt= \lim\limits_{x\rightarrow \infty} \left( \mu(x)-1 \right) \int\limits_{-\infty}^{\infty} K(u)du= 0.$$

(3.19)

From (3.16) using (1.6), (3.18) and (3.19) we obtain $\lim\limits_{x\rightarrow+\infty} \left( Q(f(x)) -Q(\varphi(x)) \right) =0,$ whence follows the validity of the statement (3.15).

Taking into account that $\lim\limits_{x\rightarrow +\infty} \varphi(x)=\eta$ and obvious inequality

$$0\leq |f(x)-\eta|\leq |f(x)-\varphi(x)|+|\varphi(x)-\eta|,$$

we get

$$ \lim\limits_{x\rightarrow +\infty} f(x)=\eta.$$

(3.20)

So the following theorem holds.

Theorem 3.1.

Let conditions (1.3)– (1.7) and $(a)-(c)$ be satisfied. Then the solution $F(x)$ of equation (1.1) defined by (2.10) has a limit at $\pm \infty$

$$ \lim\limits_{x\rightarrow \pm \infty} F(x)= \pm \eta.$$

(3.21)

Moreover, the following inclusions hold

$$ \eta - F \in L_1(0,+\infty), \ \ \ \textit{and} \ \ \ \ \eta + F \in L_1(-\infty,0).$$

(3.22)

And also for any $r>0$ the integral estimates take place

$$\begin{aligned} \, \int_{\pm r}^{\pm \infty} \left( F(x) \mp \Phi(x) \right) dx &\leq \frac{\varphi(r)}{Q(\varphi(r))} \Biggr(\eta \left( 1+M \right) \Big( \| \mu-1 \| ^2_{L_2(r, +\infty)} + \| \mu-1 \|_{L_1(r, +\infty)}\Big) \\ &+ \eta \left( 1+M \right) \Big( \| \mu-1 \| _{L_1({\mathbb R})} + m_1 \Big) + \| \eta -\varphi \|_{L_1({\mathbb R})} \Biggr), \end{aligned}$$

where $\Phi$ is the odd extension of the solution $\varphi$ of equation (2.11) on $(-\infty, 0)$.

Proof.

In accordance with formula (2.10) all statements of the theorem are consequences of above proved (3.20), (3.14) and (3.12) facts, respectively. $\square$

4. Uniqueness of the solution of the equation in the certain class of functions

We proceed to study the uniqueness of the solution of equation (1.2). Below we use the result of [17], in which it is proved that the solution $\varphi$ of equation (2.11) with properties (2.12)–(2.14) is unique in the class of bounded on $\mathbb{R}^+$ functions

$$ \begin{array}{c} \mathfrak{M}:=\Big\{\varphi(x): \ 0< \varphi(x)\leq \eta,\ \ x \in {\mathbb R}; \ \ \eta-\varphi \in L_1 ( {\mathbb R}) \Big\}. \end{array}$$

(4.1)

Now consider the following class of continuous and bounded functions on $\mathbb{R}^+$:

$$\begin{aligned} \, \Lambda:=&\Big\{f\in C \left( {\mathbb R} \right) : \ \varphi(x)\leq f(x) \leq Q^{-1}_0 \Big( \eta \left( 1+M \right) \mu (x) \Big), \ x\in \mathbb{R}^+ , \ \ \varphi \in \mathfrak{M}; \nonumber \\ &\eta-f \in L_1 ( {\mathbb R} ) \Big\}. \end{aligned}$$

(4.2)

We prove that in class $\Lambda$ the solution of equation (1.2) is unique. Let equation (1.2) have two different solutions $f, \, \tilde{f} \in \Lambda.$ Then there is at least one point $x^*>0$ such that $f(x^*)\neq \tilde{f}(x^*).$ Due to continuity of functions $f$ and $\tilde{f}$ on $\mathbb{R}^+$ there is a number $\delta>0$ such that $f(x)\neq \tilde{f}(x),\,\, x\in(x^*-\delta,\, x^*+\delta).$

Consider the set

$$ \mathcal {D}:=\{x\in {\mathbb R}: \ \ f(x)\neq \tilde{f}(x)\}.$$

(4.3)

Therefore, in accordance with the definition of a neighborhood $(x^*-\delta, \, x^* +\delta) \subseteq \mathcal {D},$ from which it follows that

$$ mes \,\mathcal {D}\geq2\delta>0.$$

(4.4)

Given the fact that $f, \tilde{f}\in \Lambda$ and using inequality

$$0\leq|f(x)-\tilde{f}(x)|\leq |f(x)-\eta|+|\tilde{f}(x)-\eta|, \ \ x\in{\mathbb R}$$

we conclude that the following inclusion take place:

$$ f-\tilde{f} \in L_1(\mathbb{R}^+).$$

(4.5)

In view of (1.2), (2.15) and (3.21), we estimate the following difference:

$$\begin{aligned} \, \left| Q(f(x))-Q(\tilde{f}(x)) \right| &\leq \left( \mu(x)-1 \right) \left| Q_0(f(x))-Q_0(\tilde{f}(x)) \right| \nonumber \\ &+ \int\limits_0^{\infty} \left( K(x-t) - K(x+t) \right) \, \left| f(t)-\tilde{f}(t) \right| dt, \ \ x\in{\mathbb R}. \end{aligned}$$

(4.6)

Because of $K\in L_1(\mathbb {R}) \cap C_M(\mathbb{R})$ and $f-\tilde{f} \in L_1(\mathbb{R}^+)$ ((4.5)), the function

$$\mathcal{B}(x):=\int\limits_0^{\infty} \left( K(x-t) - K(x+t) \right) \, \left| f(t)-\tilde{f}(t) \right| dt, \ \ x\in{\mathbb R}$$

is a summable function on ${\mathbb R}$: $\mathcal{B} \in L_1(\mathbb{R}^+).$

Since $K \in C_M(\mathbb{R})$ and $f-\tilde{f} \in L_1(\mathbb{R}^+)$, then from representation of the function $\mathcal{B}$ it immediately follows that $\mathcal{B} \in L_{\infty} ( {\mathbb R}).$ Consequently, $\mathcal{B} \in L_{1} ( {\mathbb R}) \cap L_{\infty} ( {\mathbb R}).$

Let us now verify that $f \mathcal{B} \in L_{1} ( {\mathbb R}).$ Indeed, using inequalities (3.21) and (3.20) we get the following estimate:

$$0 \leq f(x) \mathcal{B}(x) \leq \eta \left( 1+M \right) \left( \mu (x)-1 \right) \mathcal{B}(x)+\eta \left( 1+M \right) \mathcal{B}(x) , \ \ x \in {\mathbb R}.$$

In view of $\mathcal{B} \in L_{\infty} ( {\mathbb R})$ it immediately follows that $f \mathcal{B} \in L_{1} ( {\mathbb R}).$

In addition, suppose that

$$ \mu-1 \in \bigcap_{p=1}^{3} L_p ({\mathbb R}).$$

(4.7)

Denoting by

$$I(x): = \left( \mu(x)-1 \right) f(x) \left| Q_0(f(x))-Q_0(\tilde{f}(x)) \right|,$$

we prove that $I\in L_{1} ( {\mathbb R}).$ Indeed, again taking into account inequalities (3.21) and (3.20) we obtain

$$\begin{aligned} \, 0 &\leq I(x)\leq \left( \mu(x)-1 \right) f(x) \left( Q_0(f(x))+Q_0 \left(\tilde{f}(x) \right) \right) \\ &\leq 2 \left( \mu(x)-1 \right) f(x) \left( Q_0 \left( Q^{-1}_0 \left( \eta \left( 1+M \right) \mu (x) \right) \right) \right) =2 \eta \left( 1+M \right) \mu (x) \left( \mu(x)-1 \right) f(x) \\ &\leq 2\eta^2 \left( 1+M \right) ^2 \mu (x) \left( \mu(x)-1 \right) ^2 = 2 \eta^2 \left( 1+M \right) ^2 \left( \left( \mu(x)-1 \right) ^3+ \left( \mu(x)-1 \right) ^2 \right) . \end{aligned}$$

Then in view of (4.7) it follows that $I\in L_{1} ( {\mathbb R}).$

Now, multiplying both sides of inequality (4.6) by the function $f(x)$ , we can integrate over $x$ in the range from $0$ to $+\infty.$ As a result, we obtain

$$\begin{gathered} \, \int\limits_0^{\infty} f(x) \left| Q(f(x))-Q(\tilde{f}(x)) \right| dx \leq \int\limits_0^{\infty} \left( \mu(x)-1 \right) f(x) \left| Q_0(f(x))-Q_0(\tilde{f}(x)) \right| dx \\ +\int\limits_0^{\infty} f(x) \int\limits_0^{\infty} \left( K(x-t) - K(x+t) \right) \, \left| f(t)-\tilde{f}(t) \right| dt dx. \end{gathered}$$

(4.8)

Since the kernel $K(x)$ is an even function and $f(x)$ is a solution of equation (1.2), then using Fubini theorem ([18]) from inequality (4.8) we get

$$\begin{aligned} \, \int\limits_0^{\infty} f(x) \left| Q(f(x))-Q(\tilde{f}(x)) \right| dx &\leq \int\limits_0^{\infty} \left( \mu(x)-1 \right) f(x) \left| Q_0(f(x))-Q_0(\tilde{f}(x)) \right| dx \\ &+\int\limits_0^{\infty} \left| f(t)-\tilde{f}(t) \right| \Bigl( Q(f(t))- \left( \mu(t)-1 \right) Q_0(f(t))\Bigr) dt, \end{aligned}$$

or

$$\begin{gathered} \, \int\limits_0^{\infty} \Biggl( f(x) \left| Q(f(x))-Q(\tilde{f}(x)) \right| - \left| f(x)-\tilde{f}(x) \right| Q(f(x) \Biggl) dx \\ - \int\limits_0^{\infty} \left( \mu(x)-1 \right) \Biggl( f(x) \left| Q_0(f(x))-Q_0(\tilde{f}(x)) \right| - \left| f(x)-\tilde{f}(x) \right| Q_0(f(x)) \Biggr) dx \leq 0. \end{gathered}$$

(4.9)

From the definition (4.3) of the set $\mathcal {D}$ it follows that for any $x\in {\mathbb R} \backslash\mathcal {D}$

$$f(x)= \tilde{f}(x) \ \ \text{and} \ \ \ Q( f(x))= Q( \tilde{f}(x)), \ Q_0 \left( f(x) \right) = Q_0 ( \tilde{f}(x))$$

(due to the continuity of the functions $Q$ and $Q_0$ on $\mathbb{R}$). Therefore, taking into account the monotonicity of the functions $Q$ and $Q_0$ on $\mathbb{R}$, inequality (4.9) can be written as

$$\begin{gathered} \, \int_{\mathcal {D}} \left| f(x)-\tilde{f}(x) \right| \Biggl( \frac{f(x) \left( Q(f(x))-Q(\tilde{f}(x)) \right) }{ f(x)-\tilde{f}(x)} - Q(f(x) ) \\ - \left( \mu(x)-1 \right) \Biggl[ \frac{f(x) \left( Q_0 (f(x))-Q_0(\tilde{f}(x)) \right) }{f(x)-\tilde{f}(x) }-Q_0(f(x)) \Biggr] \Biggr) dx \leq 0. \end{gathered}$$

(4.10)

Note that regardless of the values accepted by the functions $f$ and $\tilde{f}$ on $\mathcal {D}$ for the convexity $Q_0$ on $\mathbb{{\mathbb R}}$, as well as taking into account the fact $y=\frac{Q_0(u)}{u}$ is a nondecreasing function on ${\mathbb R}$ we can see that the following inequality holds

$$ \frac{ Q_0(f(x))-Q_0(\tilde{f}(x))}{ f(x)-\tilde{f}(x)} > \frac{ Q_0(f(x) )}{f(x)} , \ \ \forall x\in \mathcal {D}.$$

(4.11)

Figure 5.

The behavior of the function $Q_0(u)$ in the case $u_1 < \eta < u_2$.

Figure 6.

The behavior of the function $Q_0(u)$ in the case $\eta < u_1 < u_2$.

$$\begin{gathered} \, \alpha > \beta \Rightarrow \tan\alpha > tg \,\beta, \\ \alpha > \gamma \Rightarrow \tan\alpha > \tan\gamma,\\ \\ \tan\alpha=\frac{Q_0(u_2) -Q _0(u_1)}{u_2-u_1 }, \\ \tan\beta =\frac{Q_0 (u_1)}{u_1}, \\ \tan\gamma =\frac{Q_0 (u_2)}{u_2}.\\ \\ \\ \end{gathered}$$

In addition in view of condition $(b)$ connecting the functions $Q$ and $Q_0$ with each other the following inequality holds

$$ \frac{ Q(f(x))-Q(\tilde{f}(x))}{ f(x)-\tilde{f}(x)} > \frac{ Q(f(x) )}{f(x)}, \ \ \forall x\in \mathcal {D}.$$

(4.12)

Figures 2, 5 and 6 illustrate the validity of the statement (4.11) in all possible cases of the values of the functions $f,\tilde{f} \in \Lambda$ accepted on the set $\mathcal {D}$ with respect to the number $\eta$ (since $\varphi(x) < \eta, \ x \in{\mathbb R}$), i.e. in cases where both values of the functions do not exceed the number $\eta$, at least one of them is greater than $\eta$ and both values are not less than $\eta$ respectively.

Observe that in the reasoning below, when we use the inequality given in the remark 2.1, as the course of the proof shows, the choice of the functions $f$ and $\tilde{f}$ is not significant and does not affect on the result. Since, by our assumption, the functions $f$ and $\tilde{f}$ are solutions of equation (1.2), then for both of them the indicated inequality holds. Then, based on the foregoing, taking into account the inequalities (4.11) and (4.12) from (4.10) we obtain

$$\begin{gathered} \, \int_{\mathcal {D}} \ \left| f(x)-\tilde{f}(x) \right| \Biggr( \frac{f(x) \left( Q(f(x))-Q(\tilde{f}(x)) \right) }{ f(x)-\tilde{f}(x)} - Q(f(x) ) \\ - \frac{ Q(f(x) )}{Q_0(f(x))} \Biggl[ \frac{f(x) \left( Q_0 (f(x))-Q_0(\tilde{f}(x)) \right) }{f(x)-\tilde{f}(x) }-Q_0(f(x)) \Biggr] \Biggr) dx \leq 0. \end{gathered}$$

or in virtue of $(b)$

$$\begin{aligned} \, \int_{\mathcal {D}} \ f(x) \left| f(x)-\tilde{f}(x) \right| &\Biggr( \frac{ Q(f(x))-Q(\tilde{f}(x)) }{ f(x)-\tilde{f}(x)} \nonumber \\ &- P(f(x)) \frac{ Q_0 (f(x))-Q_0(\tilde{f}(x)) }{f(x)-\tilde{f}(x) } \Biggr) dx \leq 0. \end{aligned}$$

(4.13)

Next we show that the integrand in the bracket is positive at all points of the set $\mathcal {D}$. Really,

$$\begin{gathered} \, \frac{ Q(f(x))-Q(\tilde{f}(x)) }{ f(x)-\tilde{f}(x)} - \frac{ Q (f(x))-P(f(x)) Q_0(\tilde{f}(x)) }{f(x)-\tilde{f}(x) } \\ =\frac{ P(f(x)) Q_0(\tilde{f}(x)) -P (\tilde{f}(x)) Q_0(\tilde{f}(x)) }{f(x)-\tilde{f}(x) } = Q_0(\tilde{f}(x)) \frac{ P(f(x)) -P (\tilde{f}(x)) }{f(x)-\tilde{f}(x) } >0 , \ \ \forall x\in \mathcal {D} \end{gathered}$$

by the condition $(b)$ that the function $P$ is strictly monotonic on all ${\mathbb R}.$

Based on the statements obtained above for the solutions $f, \ \tilde{f} \in \Lambda$ and the positiveness of the measure (4.4) of the set $\mathcal {D}$ from (4.10) we come to a contradiction. Thus, $f(x)=\tilde{f}(x),\, x\in \mathbb{R}^+,$ as required.

So, using the formula (2.10) we arrive at the following result:

Theorem 4.1.

$($uniqueness of the solution$)$. Suppose that the conditions (1.3)–(1.6), (4.7), $(a)-(c)$ are fulfilled and the function $\varphi \in \mathfrak{M}$ is a solution of equation (2.11) with properties (2.12)–(2.14). Then the equation (1.1) cannot have more than one solution in the following class of odd functions

$$\begin{aligned} \, \Lambda ^*:= &\Big\{F\in C \left( \mathbb{R}\backslash \{0\} \right) : \ \varphi(x) \leq F(x) \leq Q^{-1}_0 \Bigl( \eta \left( 1+M \right) \mu (x) \Bigr),\ x\in \mathbb{R}^+,\ \varphi \in \mathfrak{M}, \\ &\eta - F \in L_1( {\mathbb R}) \Big\}. \end{aligned}$$

Remark 4.1.

If we consider (2.11) separately, as an independent equation, then the requirement of conditions for the evenness of the function $\mu$ and the oddness of the functions $Q(u),\ Q_0(u)$ disappear.

5. Examples

We show below that the conditions $(b)$ and $(c)$ are not additional conditions restricting the class of equations (1.1). They also hold for the case (2.9), which is of physical interest in the theory of a $p$-adic string.

So, we consider equation (1.1) with nonlinearities of the form (2.9), and for odd numbers $m, n \ \text {and } \ m>2n$. Let us verify the fulfillment of the conditions $(a)$–$(c)$ imposed on the functions $Q(u)$ and $Q_0(u)$. Indeed, the functions $Q(u)=u^m$ and $Q_0(u)=u^n$ defined by (2.9) formula are odd functions on $\mathbb{R}$ that are strictly convex downward on the set $[0, +\infty)$. The fulfillment of the conditions $(a)$ and $(b)$ obviously holds. Moreover, $\eta=1$ is the first positive root of the equations $u^m=u$ ш $u^n=u$ (since we are interested in real-valued solutions from a physical point of view). It remains to verify the corresponding condition

$$(c) \ \ Q^{-1} \Big(\left( 1+M \right)^2 \mu^2 (x) \Big) \leq Q_0^{-1} \Big( \left( 1+M \right) \mu(x)\Big), \ \ x \in{\mathbb R},$$

i.e.

$$\mu^{m-2n}(x)\geq \frac1{\left( 1+M \right)^{m-2n}}$$

or $\mu(x)\geq \frac1{ 1+M }, \ \ x \in{\mathbb R},$ since $m>2n$. The obtained inequality is true, since according to (1.8) $M\geq0,$ then $\frac1{ 1+M }\leq1$ and function $\mu(x)\geq1, \ x \in\mathbb{R}$ by assumption (1.6).

Remark 5.1.

Note that the general condition $(c)$ for the case under consideration is essentially the condition $m>2n$, and the oddness condition for the numbers $m, n$ is necessary only for constructing an odd physical solution.

As useful addition to the paper we give particular examples of functions $K$ and $\mu$, satisfying conditions (1.3)–(1.5) and (1.6), (1.7), respectively:

• • $\mu_\alpha(x)=1+\frac1{|x|^\alpha}e^{-x^2}, \ \alpha\in \left( 0,\frac12 \right) , \ x\in \mathbb{R}\setminus\{0\}.$

• • $\mu_{a,\,h}(x)=1+\frac{|h(x)|} {|x|^a(1+x^2)}, \ -\frac{5}3<a<\frac13, \ x\in \mathbb{R}\setminus\{0\},$ where $h(x)$ is a bounded function on $R$.

• • $K(x)=\frac{1}{\sqrt{4\pi \delta}}e^{- \frac {x^2}{4\delta}}, \quad \delta>0;$ $K(x)=\frac{1}{2}e^{-|x|};\ x\in \mathbb{R}.$

• • $K(x)={\int\limits_a^b} e^{-|x|s}G(s)\,ds, \ x\in \mathbb{R},\\ \text{where} \ \ a>0,\ \ b\geq+\infty,\ \ G(s)>0,\ \ s\in[a,\,b], \ \ {\int\limits_a^b}\frac{G(s)}s \, ds=\frac12, \ \ G\in L_1(a,\,b).$

Using the example of the kernel $K(x)=\frac{1}{\sqrt{\pi}}e^{-x^2}$ and the function $\mu$ of the form

$$\mu_\alpha (x)=1+\frac{e^{-x^2}}{|x|^\alpha}, \ \alpha\in \left( 0,\frac12 \right) , \ x \in \mathbb{R}$$

we calculate $M=\sup \limits_{x\in \mathbb{R}} K(x)\, \int\limits_0^{\infty} \left( \mu(t)-1 \right) dt$. Since $\sup \limits_{x\in \mathbb{R}} K(x)=\frac{1}{\sqrt{\pi}}$ and

$$\int_0^\infty (\mu_\alpha(t)-1)dt = \int_0^\infty \frac{e^{-t^2}}{t^\alpha} dt =\frac12 \Gamma\left(\frac12 - \frac{\alpha}{2}\right), \ \ \alpha \in \left( 0, \frac{1}{2} \right),$$

then in view of double inequality $\frac{\sqrt{\pi}}2 < \frac12 \Gamma\left(\frac12 - \frac{\alpha}{2}\right) < 2, \ \ \forall \alpha \in \left( 0, \frac{1}{2} \right)$ we obtain the following dual estimate:

$$\frac12 < M_{\alpha} < \frac 2{\sqrt{\pi}}, \ \ \forall \alpha \in \left( 0, \frac{1}{2} \right).$$

Graph of the function $\frac12 \Gamma\left(\frac12 - \frac{\alpha}{2}\right), \ \alpha \in \left[0, \frac{1}{2}\right)$ is plotted in Fig. 7.

Figure 7.

Graph of the function $\frac12 \Gamma\left(\frac12 - \frac{\alpha}{2}\right), \ \alpha \in \left[0, \frac{1}{2}\right)$.

Note that the theorem 4.1 (uniqueness) can be applied to a function $\mu,$ satisfying condition (4.7). Therefore, its application to the considered functions $\mu_\alpha$ is possible for $\alpha\in \left( 0,\frac13 \right)$.