A Family of Fifth-Order Iterative Methods for Finding Multiple Roots of Nonlinear Equations

Abstract

We present a family of fifth-order iterative methods for finding multiple roots of nonlinear equations. Numerical examples are considered to check the validity of the theoretical results. It is shown that the new methods are competitive with other methods for finding multiple roots. Basins of attraction for the new methods and some existing methods to observe the dynamics in the complex plane are drawn.

1. INTRODUCTION

In this study, we consider the problem of finding the multiple root $\alpha$ of multiplicity $m$, i.e., $f^{(j)}(\alpha)=0$, $j=0, 1,2,\ldots, m-1$, and $f^{m}(\alpha)\neq0$, of a nonlinear equation $f(x)=0$, where $f(x)$ is a smooth real or complex function of a single real or complex variable $x$. An important and basic method for finding multiple roots is the modified Newton method [1] defined by

$$x_{n+1} =x_{n}-m\frac{f(x_{n})}{f'(x_{n})}, \ \ \ n=0,1,2, \ldots , $$

(1)

which converges quadratically and requires the knowledge of the multiplicity $m$ of the root $\alpha$.

For improvement of the local order of convergence of scheme (1), some higher-order methods with known multiplicity $m$ have also been proposed and analyzed. Most of these are of third-order convergence and can be divided into two classes (see [2]). The first class, so called one-point methods, requires evaluation of $f$, $f'$, and $f''$ in each step; examples are the methods by Biazar and Ghanbari [3], Chun and Neta [4], Chun et al. [5], Hansen and Patrick [6], Neta [7], Osada [8], Sharma and Bahl [9], and Sharma and Sharma [10]. The second class is that of multipoint methods, which can be further divided into two subclasses. One subclass uses two evaluations of $f$ and one evaluation of $f'$, like the methods developed by Chun et al. [5], Sharma and Sharma [10], Dong [11], Homeier [12], Kumar et al. [13], Li et al. [14], Neta [15], Victory and Neta [16], and Zhou et al. [17]. The other subclass uses one evaluation of $f$ and two evaluations of $f'$, like the methods by Kumar et al. [13], Li et al. [14], and Dong [18].

In the multipoint class, some fourth-order methods are also presented. For example, Li et al. [19] have developed six fourth-order methods; four of them use one evaluation of $f$ and three evaluations of $f'$, whereas two methods use one evaluation of $f$ and two evaluations of $f'$. Li et al. [20], Neta [21], and Neta and Johnson [22] have presented fourth-order methods that require one evaluation of $f$ and three evaluations of $f'$.

In this paper, we propose a fifth-order multipoint family of iterative methods for finding the multiple roots of nonlinear equations. In Section 2, the scheme is developed and its convergence properties are investigated. Some particular cases of the family are presented in Section 3. For verification of the theoretical results, some numerical examples are considered in Section 4. A comparison of the new methods with existing methods is also shown in this section. Section 5 considers the basins of attraction for the new methods and some existing methods. Concluding remarks are given in Section 6.

2. DEVELOPMENT OF THE SCHEME

Our aim is to develop an iterative method that increases the convergence order of the basic Newton method. Therefore, we consider Newton’s double scheme for multiple roots:

$$\begin{array}{lll} z_k&=& x_k-m\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=& z_k-m \dfrac{f(z_k)}{f'(z_k)}. \end{array} $$

(2)

This is a modified Newton method, two steps of which are grouped together and treated as one step. Consequently, Newton’s double scheme has the fourth order of convergence.

It is clear that scheme (2) requires two evaluations of the function and two evaluations of the derivatives per iteration, and therefore the efficiency index (see [23]) of the scheme is equal to that of basic Newton’s method (1). This means that increase in the order of convergence does not lead to increase in the efficiency of the scheme. So, to improve the efficiency of the scheme by increasing its order, we modify scheme (2) as follows:

$$\begin{array}{lll} z_k&=& x_k-m\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=& z_k-m H(u)\dfrac{f(z_k)}{f'(z_k)}, \end{array} $$

(3)

where $u=\sqrt[m]{\frac{f(z_k)}{f(x_k)}}$ and $H: \mathbb{C}\rightarrow \mathbb{C}$ is an analytic function about a neighborhood of zero.

Through the following theorem we analyze the behavior of scheme (3).

Theorem 1.Let $f: \mathbb{C}\rightarrow \mathbb{C}$ be an analytic function in a region enclosing a multiple zero $\alpha$ with multiplicity $m$. Assume that the initial guess $x_0$ is sufficiently close to $\alpha$; then for $H(0)=1$, $H'(0)=0$, $H''(0)=2$, and $|H'''(0)|<\infty$, the order of convergence of the method defined by $(3)$ is five at least.

Proof. Let $e_k=x_k-\alpha$. Expanding $f(x_k)$ and $f'(x_k)$ at $\alpha$ into the Taylor series, we have

$$f(x_k)=\frac{f^{(m)}(\alpha)}{m!}e_k^m(1+C_1e_k+C_2e_k^2+C_3e_k^3+C_4e_k^4+C_5e_k^5+O(e_k^6)) $$

(4)

and

$$f'(x_k)=\frac{f^{(m)}(\alpha)}{(m-1)!}e_k^{m-1}(1+D_1e_k+D_2e_k^2+D_3e_k^3+D_4e_k^4+O(e_k^6)), $$

(5)

where $C_j=\frac{m!}{(m+j)!}\frac{f^{(m+j)}(\alpha)}{f^{(m)}(\alpha)}$, and $D_j=\frac{(m-1)!}{(m+j-1)!}\frac{f^{(m+j)}(\alpha)}{f^{(m)}(\alpha)}$, $j=1,2,3,\ldots\,$.

Using Eqs. (4) and (5), we can write

$$\begin{array}{lll} \dfrac{f(x_k)}{f'(x_k)}&=& \dfrac{1}{m}e_k-\dfrac{C_1}{m^2}e_k^2+\dfrac{(m+1) C_1^2-2 m C_2}{m^3}e_k^3\\[2ex] &&+\dfrac{m (3 m+4) C_1 C_2-3 m^2 C_3-(m+1)^2 C_1^3 }{m^4}e_k^4+O(e_k^5). \end{array} $$

(6)

Let $e_{z_k}=z_k-\alpha$. Substituting (6) into the first step of Eq. (3), we get

$$\begin{array}{lll} e_{z_k}&= &\dfrac{C_1 }{m}e_k^2+\dfrac{2 m C_2-(m+1) C_1^2 }{m^2}e_k^3\\[2ex] && +\dfrac{(m+1)^2 C_1^3-m (3 m+4) C_1 C_2+3 m^2 C_3 }{m^3}e_k^4+O(e_k^5). \end{array} $$

(7)

The Taylor series of $f(z_k)$ about $\alpha$ yields

$$f(z_k)=\frac{f^{(m)}(\alpha)}{m!}e_{z_k}^m(1+C_1e_{z_k}+C_2e_{z_k}^2+O(e_{z_k}^3)). $$

(8)

Moreover,

$$f'(z_k)=\frac{f^{(m)}(\alpha)}{(m-1)!}e_{z_k}^{m-1}(1+D_1e_{z_k}+D_2e_{z_k}^2+O(e_{z_k}^3)). $$

(9)

With the help of Eqs. (4) and (8) we get

$$\frac{f(z_k)}{f(x_k)}=\left(\frac{C_1}{m}\right)^m e_k^m\left(1+\frac{K_1}{C_1}e_k+\frac{K_2}{2mC_1^2}e_k^2-\frac{K_3}{6m^2C_1^3}e_k^3\right)+O(e_k^4), $$

(10)

where

$$\begin{array}{lll} K_1&=& 2mC_2-(m+2)C_1^2,\\ K_2&=& (m+1)^2 (m+3) C_1^4-2 m(2m+3)(m+1)C_1^2 C_2+4 (m-1) m^2C_2^2+6 m^2 C_1 C_3, \\ K_3&=& (m+1)^3 (m+2)(m+4) C_1^6-6 m (m^4+6 m^3+13 m^2+13 m+4) C_1^4 C_2\\ &&-8 m^3 (m-1)(m-2) C_2^3+6 m^2 (3 m^2+7 m+4) C_1^3 C_3\\ &&-36 (m-1) m^3 C_1 C_2 C_3+12 m^3 C_1^2 ((m+1)^2 C_2^2-2 C_4). \end{array}$$

Note that

$$(1+x)^{\frac{1}{m}}=1+\frac{1}{m}x-\frac{m-1}{2m^2}x^2+\frac{(m-1)(2m-1)}{6m^3}x^3+O(x^4),$$

and therefore, from (10) we have that

$$\begin{array}{lll} \sqrt[m]{\dfrac{f(z_k)}{f(x_k)}} &=& \dfrac{C_1}{m}e_k+\dfrac{K_1}{m^2}e_k^2+\dfrac{K_2-(m-1)K_1^2}{2m^3C_1}e_k^3\\[2ex] &&+\dfrac{(2m^2-3m+1)K_1^3-3(m-1)K_1K_2-K_3}{6m^4C_1^2}e_k^4+O(e_k^5). \end{array} $$

(11)

After using (11), we can write down the Taylor expansion of $H(u)$ around zero as follows:

$$\begin{array}{lll} H(u)&=& H(0)+\dfrac{C_1H'(0)}{m}e_k+\dfrac{2K_1H'(0)+C_1^2H''(0)}{2m^2}e_k^2\\[2ex] &&+\dfrac{3K_2H'(0)-3(m-1)K_1^2H'(0)+6C_1^2K_1H''(0)+C_1^4H'''(0)}{6m^3C_1}e_k^3+O(e_k^4). \end{array} $$

(12)

Substituting (8), (9), and (12) into the second step of (3), we get

$$e_{k+1}=L_0e_k^2+L_1e_k^3+L_2e_k^4+L_3e_k^5+O(e_k^6), $$

(13)

where

$$\begin{array}{lll} L_0&=& \dfrac{C_1 (1-H(0))}{m},\\[2ex] L_1&=& \dfrac{((m+1) C_1^2-2 m C_2)(H(0)-1)-C_1^2H'(0)}{m^2},\\[2ex] L_2&=& \dfrac{1}{2 m^3}\Big(6 m^2 C_3(1-H(0))+2 m C_1 C_2 ((3 m+4) (H(0)-1)-4 H'(0)) \\[2ex] &&\quad\quad\quad +C_1^3(2 (m+1)^2-2 m (m+2) H(0)+(4 m+6) H'(0)-H''(0))\Big),\\[2ex] L_3&=& \dfrac{1}{6 m^4}\Big(12 m^2 C_1 C_3 ((2 m+3)(H(0)-1)-3 H'(0))\\[2ex] && \quad\quad\quad +12 m^2(((m+2) C_2^2-2 m C_4) (H(0)-1)-2 C_2^2 H'(0))\\[2ex] && \quad\quad\quad +6 m C_1^2 C_2(2 (m+1) (2 m+3)-2 (m (2 m+5)+1)H(0)\\[2ex] && \quad\quad\quad\quad\quad\quad\quad\quad +(10 m+17) H'(0)-3 H''(0))\\[2ex] && \quad\quad\quad -C_1^4(3 (m+1) (2 (m+1)^2-2 (m (m+2)+1) H(0)+(6 m+11) H'(0))\\[2ex] && \quad\quad\quad\quad\quad -3(3 m+5) H''(0)+H'''(0))\Big). \end{array}$$

Thus, for us to obtain an iterative method of fifth order, the coefficients of $e_k^2$, $e_k^3$, and $e_k^4$ in error equation (13) should be zero. So, we have the following equations:

$$\left\{ \begin{array}{l} 1-H(0)=0,\\ H'(0)=0,\\ 2 (m+1)^2-2 m (m+2) H(0)+(4 m+6) H'(0)-H''(0)=0, \end{array} \right.$$

solving which gives

$$H(0)=1, \ \ \ H'(0)=0, \ \ \ H''(0)=2. $$

(14)

Substituting these values into (13), we get the final error equation as

$$e_{k+1}=-\frac{12 m C_1^2 C_2-C_1^4 (6 (m+3)-H'''(0))}{6 m^4}e_k^5+O(e_k^6).$$

This proves the fifth order of convergence. Hence, Theorem 1 is proved.

3. SOME PARTICULAR CASES

With conditions (14), many special cases of family (3) are possible. Below we present some simple special cases.

Case 1. Suppose $H(x)=A+Bx+Cx^2$. Then $H'(x)=B+2Cx$ and $H''(x)=2C$. Using (14), we get

$$A=1, \ \ \ B=0, \ \ \ C=1.$$

Thus we have the following new fifth-order method

$$\begin{array}{lll} z_k&=& x_k-m\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=&z_k-m \left(1+\left(\dfrac{f(z_k)}{f(x_k)}\right)^{\frac{2}{m}}\right)\dfrac{f(z_k)}{f'(z_k)}. \end{array}$$

We denote this method by $\mbox{NMM}_{5,1}$.

Case 2. Suppose

$$H(x)=\frac{A+Bx+Cx^2}{D+Ex+Fx^2}.$$

Then

$$H'(x)=\frac{(BD-AE)-2(AF-CD)x+(CE-BF)x^2}{(D+Ex+Fx^2)^2}$$

and

$$H''(x)=\frac{2(CD^2\!+\!AE^2\!-\!D(BE+AF)\!+\!3F(AE\!-\!BD)x\!+\!3F(AF\!-\!CD)x^2 \!+\!F(BF\!-\!CE)x^3)}{(D+Ex+Fx^2)^3}.$$

Using conditions (14), we obtain

$$A=D, \ \ \ B=E, \ \ \ F-C+D=0. $$

(15)

Subcase 1. Taking $A=1$, $B=1$, and $C=1$ and solving (15), we get $D=1$, $E=1$, and $F=0$. With these values, scheme (3) generates the following fifth-order method:

$$\begin{array}{lll} z_k&=& x_k-m\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=&z_k-m \left( \dfrac{1+\left(\frac{f(z_k)}{f(x_k)}\right)^{\frac{1}{m}} + \left(\frac{f(z_k)}{f(x_k)}\right)^{\frac{2}{m}}} {1+\left(\frac{f(z_k)}{f(x_k)}\right)^{\frac{1}{m}}} \right) \dfrac{f(z_k)}{f'(z_k)}. \end{array}$$

Let us denote this method by $\mbox{NMM}_{5,2}$.

Subcase 2. Taking $A=1$, $B=0$, and $C=-1$ and solving (15), we get $D=1$, $E=0$, and $F=-2$. After substitution of these values, the corresponding fifth-order method is given by

$$\begin{array}{lll} z_k&=&x_k-m\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=& z_k-m \left( \dfrac{(f(x_k))^{\frac{2}{m}} -(f(z_k))^{\frac{2}{m}}} {(f(x_k))^{\frac{2}{m}}-2(f(z_k))^{\frac{2}{m}}} \right) \dfrac{f(z_k)}{f'(z_k)}. \end{array}$$

We denote this method by $\mbox{NMM}_{5,3}$.

Remark 1. The computational efficiency of an iterative method is measured by the efficiency index $EI=p^{1/C}$ (see [23]), where $p$ is the order of convergence and $C$ is the computational cost measured as the number of new pieces of information required by the method per iterative step. A ‘piece of information’ typically is any evaluation of the function $f$ or one of its derivatives. The presented fifth-order methods require four evaluations of the function per iteration, so the efficiency index of the fifth-order methods is $EI=\sqrt[4]{5}\approx 1.495$ and excels the efficiency indices of the modified Newton method $(EI=\sqrt2\approx 1.414)$, existing third-order methods $(EI=\sqrt[3]{3}\approx 1.442)$, and fourth-order methods ($EI=\sqrt[4]{4}\approx 1.414$) presented in [19, 22].

4. NUMERICAL RESULTS

We employ the presented methods $\mbox{NMM}_{5,1}$, $\mbox{NMM}_{5,2}$, and $\mbox{NMM}_{5,3}$ to solve some nonlinear equations and compare their performance with some existing methods. For example, we consider the third-order methods by Dong [11], Neta [15], and Zhou, Chen, and Song [17] and the fourth-order methods by Li, Cheng, and Neta [19] and Li, Liao, and Cheng [20]. These methods are expressed as follows:

Dong Method $(\mbox{DM}_3)$:

$$\begin{array}{rll} y_k &=& x_k-\sqrt{m}\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=&y_k+\left(1-\dfrac{\sqrt{m}}{m}\right)^{-m} (\sqrt{m}-m)\dfrac{f(y_k)}{f'(x_k)}. \end{array}$$

Neta Method $(\mbox{NM}_3)$:

$$\begin{array}{rll} y_k&=& x_k-\dfrac{1}{2}\dfrac{m(m+3)}{m+1}\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=& x_k-\left(\dfrac{m^3+4m^2+9m+2}{(m+3)^2}+\dfrac{2^{m+1}(m+1)^m(m^2-1)}{(m+3)^2(m-1)^m}\dfrac{f(y_k)}{f(x_k)}\right)\dfrac{f(x_k)}{f'(x_k)}. \end{array}$$

Zhou–Chen–Song Method $(\mbox{ZCSM}_3)$:

$$\begin{array}{rll} y_k&=& x_k-\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=& x_k+m(m-2)\dfrac{f(x_k)}{f'(x_k)}-m(m-1)\left(\dfrac{m}{m-1}\right)^m\dfrac{f(y_k)}{f'(x_k)}. \end{array}$$

Li–Cheng–Neta Method $(\mbox{LCNM}_4)$:

$$\begin{array}{rll} y_k&=& x_k-\dfrac{2m}{m+2}\dfrac{f(x_k)}{f'(x_k)},\\[2ex] \eta_k&=& x_k-\dfrac{2m}{m+2}\dfrac{f(x_k)}{f'(x_k)}+2\Big(\dfrac{m}{m+2}\Big)^2\dfrac{f(x_k)}{f'(y_k)}, \\[2ex] x_{k+1}&=& x_k-\dfrac{f(x_k)}{a_1f'(x_k)+a_2f'(y_k)+a_3f'(\eta_k)}, \end{array}$$

where

$$a_1=-\displaystyle{\frac{1}{16}}\displaystyle{\frac{3m^4+16m^3+40m^2-176}{m(m+8)}},$$

$$a_2=\displaystyle{\frac{1}{8}}\displaystyle{\frac{m^4+3m^3+10m^2-4m+8}{\left(\frac{m}{m+2}\right)^mm(m+8)}},$$

and

$$a_3=\displaystyle{\frac{1}{16}}\displaystyle{\frac{m^5+6m^4+8m^3-16m^2-48m-32}{m^2(m+8)}}.$$

Li–Liao–Cheng Method $(\mbox{LLCM}_4)$:

$$\begin{array}{rll} y_k&=& x_k-\dfrac{2m}{m+2}\dfrac{f(x_k)}{f'(x_k)},\\[2ex] x_{k+1}&=& x_k-\dfrac{m((m-2)f'(y_k)-m(\frac{m}{m+2})^mf'(x_k))f(x_k)}{2f'(x_k)((\frac{m}{m+2})^mf'(x_k)-f'(y_k))}. \end{array}$$

Table 1. Test functions

Table 2. Comparison of methods for problem$f_1(x)$

Table 3. Comparison of methods for problem$f_2(x)$

Table 4. Comparison of methods for problem $f_3(x)$

Table 5. Comparison of methods for problem $f_{4}(x)$

Table 1 displays the test functions used for the comparison, the multiplicity $m$, and the root $\alpha$ correct up to 16 decimal places. All the computations are performed using multiple-precision arithmetic in Mathematica[24]. The computer specifications are as follows: Intel (R) Core (TM) i5-2430M CPU @ 2.40 GHz (32-bit) Microsoft Windows 7 Ultimate 2009. To verify the theoretical order of convergence, we calculate the computational order of convergence $p_c$ using the formula (see [25])

$$p_c=\frac{\mbox{log}|f(x_{k})/f(x_{k-1})|}{\mbox{log}|f(x_{k-1})/f(x_{k-2})|}, $$

(16)

taking into consideration the last three approximations in the iterative process.

For every method, we record the number of iterations $k$ needed for convergence to the solution for the stopping criterion

$$|x_{k-1}-x_{k}|+|f(x_{k})|<10^{-200}$$

to be satisfied. Tables 2–5 display the numerical results, which include the error $|x_{k+1}-x_k|$ of approximation for the first three iterations (where $A(-h)$ denotes $A \times 10^{-h}$), the required number of iterations $k$, the value of $|f(x_k)|$, and the computational order of convergence $p_c$, computed by formula (16). The numerical results show that the computational order of convergence is in accordance with the theoretical one. The higher order of convergence of the presented fifth-order methods makes them more accurate than the existing third- and fourth-order methods. We conclude the paper with the remark that many numerical applications require high precision in computations. The results of the numerical experiments show that the high-order efficient methods associated with a multiprecision arithmetic floating point are very useful because they yield a clear reduction in the iterations.

5. DYNAMICS OF METHODS

Study of the dynamical behavior of the rational function associated with an iterative method gives important information about the convergence and stability of the method (see for example [26, 27]). To start with, let us recall some basic dynamical concepts of rational function. Let $\phi:\mathbb{R}\rightarrow\mathbb{R}$ be a rational function; the orbit of a point $x_0\in\mathbb{R}$ is defined as the set

$$\{x_0, \phi(x_0),\ldots , \phi^{m}(x_0),\ldots \}$$

of successive images of $x_0$ by the rational function.

The dynamical behavior of the orbit of a point of $\mathbb{R}$ can be classified depending on its asymptotic behavior. In this way, a point $x_0\in\mathbb{R}$ is a fixed point of $\phi(\alpha)$ if $\phi(\alpha)=\alpha$ is true for it. Moreover, $x_0$ is called a periodic point of period $p > 1$ if it is such that $\phi^p (x_0) = x_0$ and $\phi^k (x_0) \neq x_0$ for each $k < p$. Moreover, a point $x_0$ is called pre-periodic if it is not periodic but there exists $k > 0$ such that $\phi^ k(x_0)$ is periodic. There exist different types of fixed points depending on the associated multiplier $|\phi'(x_0)|$. Depending on the associated multiplier, a fixed point $x_0$ is called

$\bullet$ attractor if $|\phi'(x_0)|<1$,

$\bullet$ superattractor if $|\phi'(x_0)|=0$,

$\bullet$ repulsor if $|\phi'(x_0)|>1$, and

$\bullet$ parabolic if $|\phi'(x_0)|=1$.

If $\alpha$ is an attracting fixed point of a rational function $\phi$, its basin of attraction $\mathcal{A}(\alpha)$ is defined as the set of pre-images of any order such that

$$\mathcal{A}(\alpha)=\{x_0\in\mathbb{R}:\phi^{m}(x^{(0)})\rightarrow \alpha, m\rightarrow\infty\}.$$

The set of points whose orbits tend to an attracting fixed point $\alpha$ is referred to as the Fatou set. Its complementary set, called the Julia set, is the closure of the set consisting of repelling fixed points, and establishes the borders between the basins of attraction. That means the basin of attraction of any fixed point belongs to the Fatou set and the boundaries of these basins of attraction belong to the Julia set.

From the dynamical considerations, as the initial point we take $z_0 \in D$, where $D$ is a rectangular region in $\mathbb{C}$ containing all the roots of $f(z) = 0$. The numerical methods starting at a point $z_0$ in a rectangle can converge to the zero of the function $f(z)$ or eventually diverge. We consider the stopping criterion for convergence as $10^{-3}$ up to a maximum of 25 iterations. If we have not obtained the desired tolerance in 25 iterations, we do not continue and we decide that the iterative method starting at $z_0$ does not converge to any root. The strategy is as follows. A color is assigned to each starting point $z_0$ in the basin of attraction of the zero. If the iteration starting from the initial point $z_0$ converges, then it represents basins of attraction with the particular color assigned to it, and if it fails to converge in 25 iterations, then its color is black.

To study dynamical behavior, we analyze the basins of attraction of the methods on the following two polynomials:

Example 1. In the first example, we consider the polynomial

$$p_1(z)=(z^2-1)^2,$$

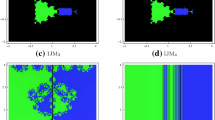
which has zeros $\{1,-1\}$ with multiplicity 2. In this case, we used a grid of $400 \times 400$ points in a rectangle $D\in\mathbb{C}$ of size $[-2.5,2.5]\times [-2.5,2.5]$. Figure 1 shows the pictures obtained. If we observe the behavior of the methods, we see that the presented new fifth-order method $\mbox{NMM}_{5,3}$ is more demanding as it possesses larger and brighter basins of attraction. Further, the methods $\mbox{LCNM}_4$ and $\mbox{LLCM}_4$ have higher number of divergent points as compared with the other methods.

Example 2. In the second example, let us take the polynomial

Fig. 1

Basins of attraction for polynomial $p_1(z)$.

Fig. 2

Basins of attraction for polynomial $p_2(z)$.

$$p_2(z)=(z^5-1)^3,$$

having zeros $\{1, 0.309017\pm 0.951057 i,-0.809017 \pm 0.587785 i\}$. Here, to see the dynamics, we consider a rectangle $D=[-1.5,1.5]\times [-1.5,1.5]\in\mathbb{C}$ with $400 \times 400$ grid points. Figure 2 shows basins of attraction for this problem. It can be seen that the method $\mbox{NMM}_{5,3}$ is the best and the method $\mbox{LCNM}_4$ contains the highest number of divergent points. Among the rest methods, $\mbox{LLCM}_4$ has stable basins of attraction.

6. CONCLUSIONS

In this paper, an attempt has been made to develop iterative methods for computing multiple roots. A two-point family of fifth-order methods has been derived in this way, which is based on a modified Newton method and requires two evaluations of $f$ and two evaluations of $f'$ per step. Some special cases of the family are presented. The efficiency index of the fifth- order methods is $E=\sqrt[4]{5}\approx 1.495$, which is better than that of the modified Newton method $(E=\sqrt{2}\approx1.414)$, third- order methods $(E=\sqrt[3]{3} \approx 1.442)$, and fourth-order methods, which require the same number of function evaluations as the presented fifth-order methods. The algorithms are employed to solve some nonlinear equations and are also compared with existing techniques. The numerical results show that the presented algorithms are competitive with methods available in literature. Moreover, the presented basins of attraction have also confirmed better performance of the methods as compared with other established methods in literature. We conclude the paper with the remark that many numerical applications require high precision in computations. The results of the numerical experiments show that the high-order efficient methods associated with a multiprecision arithmetic floating point are very useful because they yield a clear reduction in the iterations.

ACKNOWLEDGMENTS

We are very thankful to the reviewers whose suggestions enabled us to improve the article.