Abstract
The goal of this work is to study the existence and uniqueness of the solution to a nonlocal boundary value problem for a degenerate differential equation of mixed type. A parabolic-hyperbolic equation with a fractional Gerasimov–Caputo derivative is considered. The uniqueness of the solution is proved by the integral energy method using the some properties of hypergeometric functions and integro-differential operators of fractional order. The existence of the solution is proved by the method of integral equations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 PROBLEM STATEMENT
It is well known that the theory of fractional differential equations is one of the most frequently used directions in the theory of differential equations (see [1, 2]). In addition, fractional calculus is widely used in studying some problems of partial differential equations, as well as equations of mixed type with degenerations [3–7]. There are many papers (see, for example, [8–10]), in which the authors considered some classes of boundary value problems for nondegenerate and degenerate differential equations of mixed type with Gerasimov–Caputo and Riemann–Liouville fractional derivatives of the order \(0<\alpha\leqslant 1\). It should be also noted that some problems for partial differential equations with various integro-differential operators of fractional order were investigated in the works [11–25].
In this paper, we consider the questions of the existence and uniqueness of the solution to the problem for a mixed-type equation with two lines of degeneration, containing the Gerasimov–Caputo fractional derivative. So, we study a boundary value problem for the following parabolic-hyperbolic equation for \(0<\alpha<1\)
with operators
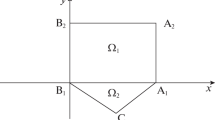
in the domain \(\Omega={\Omega_{1}}\cup{\Omega_{2}}\cup{I_{1}}\). The domain \({\Omega_{1}}\) is bounded by segments: \({A_{1}}A_{2}=\{(x,y):\ x=0,\,0<y<{h_{2}}\}\), \(A_{1}B_{1}=\{(x,y):\ y=0,\,0<x<{h_{1}}\}\), \(B_{1}B_{2}=\{(x,y):\ x={h_{1}},\,0<y<{h_{2}}\}\), \(A_{2}B_{2}=\{(x,y):\ y={h_{2}},\,0<x<{h_{1}}\}\) for \(y>0\), while \({\Omega_{2}}\) is characteristic triangle bounded by the segment \({A_{1}}{B_{1}}\) of the axes \(Ox\) and by two characteristics \({A_{1}}C:\ \frac{1}{q}{x^{q}}-\frac{1}{p}{(-y)^{p}}=0\), \({B_{1}}C:\ \,\frac{1}{q}{x^{q}}+\frac{1}{p}{(-y)^{p}}=1\) of the Eq. (1), emerging from points \({A_{1}}\left({0;0}\right)\), \(B_{1}\left({{h_{1}};0}\right)\) and intersecting at the point \(C\left({{{\left({\frac{q}{2}}\right)}^{{1\mathord{\left/{\vphantom{1q}}\right.\kern-1.2pt}q}}},\,-{{\left({\frac{p}{2}}\right)}^{{1\mathord{\left/{\vphantom{1p}}\right.\kern-1.2pt}p}}}}\right)\) for \(y<0\). Here \(2q=n+2\), \(2p=m+2\), \({h_{1}}={q^{{1\mathord{\left/{\vphantom{1q}}\right.\kern-1.2pt}q}}}\), \({h_{2}}>0\), \(m,\,n={\textrm{const}}>0,\>\ m>n\).
Let us introduce the following notations:
and
where \(\Gamma(z)\) is Gamma function, \(F(a,b,c;z)\) is Gaussian hypergeometric function, \({F_{0x}}\left[{...}\right]\) is known operator (see, [5]).
In the domain \(\Omega\) for the Eq. (1) we study the following
Problem. To find the function \(u(x,y)\) defining from the class:
1) \(\Delta=\left\{{u(x,y):\ u(x,y)\in C(\bar{\Omega})\cap{C^{2}}({\Omega^{-}}),\ {u_{xx}}\in C\left({{\Omega^{+}}}\right),\ {}_{C}D_{oy}^{\alpha}u\in C\left({{\Omega^{+}}}\right)}\right\}\);
2) \(u(x,y)\) satisfies the Eq. (1) in the domains \({\Omega_{1}}\) and \({\Omega_{2}}\);
3) \({y^{1-\alpha}}{u_{y}}\in C({\Omega_{1}})\), \({u_{y}}\in C({\Omega_{2}})\), moreover, these functions are continuous up to the boundary \({A_{1}}{B_{1}}\). In addition, on \({A_{1}}{B_{1}}\) is fulfilled the following bonding condition
where the function \({\nu^{\pm}}(x)\) may have a singularity of order less than one as \(x\to 0\) and is bounded as \(x\to{h_{1}}\);
4) \(u(x,y)\) satisfies the boundary conditions
where \({\gamma_{1}},\,{\gamma_{2}},\,{\delta_{1}},\,{\delta_{2}}={\textrm{const}}\) and \({\lambda_{i}}(x)\>(i=\overline{1,3})\), \({\varphi_{1}}(y),\,{\varphi_{2}}(y)\), \(\tilde{a}(x)=a({x^{1/2q}})\), \(\tilde{b}(x)=b({x^{1/2q}})\) are given functions, \({F_{0x}}\left[{...}\right]\) is generalized fractional integral operator [5] and
is the point of intersection of the characteristics of the Eq. (1) emerging from the point \((x,0)\in{I_{1}}\) with characteristic \(AC\).
2 BASIC FUNCTIONAL RELATIONSHIP
In proving the uniqueness and existence of the solution to the problem, an important role is played some functional relations between \(\tau\,(x)\) and \(\nu\,(x)\), which have brought on \({I_{1}}\) from \({\Omega_{i}}\,(i=1,2)\). It is known that in domain \(\Omega_{2}^{-}\) the solution to the Cauchy problem for the Eq. (1) with initial value conditions \(u(x,-0)={\tau^{-}}(x)\), \(0\leqslant x\leqslant{h_{1}}\), \({u_{y}}(x,-0)={\nu^{-}}(x)\), \(0<x<{h_{1}}\) can by represented as [5]
where \(\rho=\frac{{q{{(-y)}^{\frac{1}{p}}}z(1-z)}}{{{p^{2}}{x^{q}}\left[{\frac{1}{p}{{(-y)}^{p}}\left({2z-1}\right)+\frac{1}{q}{x^{q}}}\right]}}\).
Based on the solution to the Cauchy problem (10), (9), taking into account the property of the Gamma function, we have
where \({\gamma_{1}}={\frac{{\Gamma(2{\beta_{1}})}}{{\Gamma({\beta_{1}})}}}{2^{{\alpha_{1}}-{\beta_{1}}}}\), \({\gamma_{2}}=\frac{{{2^{{\alpha_{1}}+3{\beta_{1}}-2}}\Gamma(2-2{\beta_{1}})}}{{\Gamma(1-{\beta_{1}})}}{\left({\frac{p}{q}}\right)^{1-2{\beta_{1}}}}\). Substituting (11) into (8), we obtain a functional relationship between \(\tau^{-}(x)\) and \(\nu^{-}(x)\) on the segment \({I_{1}}\), which have brought from the domain \(\Omega_{2}^{-}\):
where \({\gamma_{1}}={\frac{{\Gamma(2{\beta_{1}})}}{{\Gamma({\beta_{1}})}}}{2^{{\alpha_{1}}-{\beta_{1}}}}\), \({\gamma_{2}}=\frac{{{2^{{\alpha_{1}}+3{\beta_{1}}-2}}\Gamma(1-2{\beta_{1}})}}{{\Gamma(1-{\beta_{1}})}}{\left({\frac{p}{q}}\right)^{1-2{\beta_{1}}}}\), \(\overline{a}(x)\equiv{\gamma_{2}}+{\left({{x^{2q}}}\right)^{\frac{{1-{\alpha_{1}}+{\beta_{1}}}}{2}}}a(x)\).
On the other hand, by the aid of given notation \(u(x,-0)={\tau^{-}}(x),\,0\leqslant x\leqslant{h_{1}}\), \({u_{y}}(x,-0)={\nu^{-}}(x),\,0<x<{h_{1}}\) and \(\mathop{\lim}\limits_{y\to+0}{y^{1-\alpha}}{u_{y}}(x,y)=\nu^{+}(x)\), \(0<x<{h_{1}}\) from the bond condition (5) we obtain
Taking (2), (13) and
into account, from the Eq. (1) as \(y\to+0\) we derive
3 UNIQUENESS OF SOLUTION TO THE PROBLEM
Theorem 1. If the following conditions are fulfilled: (3), \(\lambda_{i}(x)>0\,(i=1,2)\) and
then the solution of the problem is unique.
Proof. As usual, consider a homogeneous problem, i.e. suppose \({{\varphi_{1}}(y)\equiv{\varphi_{2}}(y)\equiv 0}\). We will prove that \(u(x,y)\equiv 0\). For this purpose, we will multiply the Eq. (14) by \(\tau(x)\) and integrate from 0 to \({h_{1}}\):
Let be \({\gamma_{1}}={\delta_{1}}=0\). Then from the conditions (6) and (7) we have \(\tau(0)=\tau({h_{1}})=0\). Taking into account the last conditions and integrating by parts the right-hand side of the Eq. (15), by applying (13) we obtain
Now we will prove that \(\int\limits_{0}^{{h_{1}}}{\lambda_{1}(x)\tau(x){\nu^{-}}(x)dx\geqslant 0}\). Using the formula (4), we make some simplifications in (12):
Introducing the replacement \(t=x\,z\), after some simplifications we have
Further, performing the reverse change \(s=x\,z\), we can obtain
To complete the proof of the theorem, we need to apply the following lemma.
Lemma. If the function \(\tau(x)\) has a positive maximum (negative minimum) at the point \(x={x_{0}}\in(0,{h_{1}})\), then \({\nu^{-}}({x_{0}})>0\) (\({\nu^{-}}({x_{0}})<0\)).
Proof. Let the function \(\tau(x)\) has a positive maximum and \(b(x)\equiv 0\). Then from the last relation (18) we have
It is obviously that
Then, by virtue of (3), from the last relation we obtain \({\nu^{-}}({x_{0}})>0\). In a similar way, one can prove that at the given point it has a negative minimum \({\nu^{-}}\left({{x_{0}}}\right)<0\). Lemma is proved. \(\Box\)
Based on the lemma just proved above, we conclude that
in the case \({\lambda_{i}}(x)\geqslant 0\) \((i=1,2)\). So, from the formula (16) follows that \({\nu^{-}}(x)\equiv\tau(x)\equiv 0\). Consequently, by virtue of the solution of the first boundary value problem, for the Eq. (1) ([9, 26]), (6) and (7) we derive \(u(x,y)\equiv 0\) in \(\overline{\Omega}^{+}\). From the solution of the Cauchy problem (10) we obtained \(u(x,y)\equiv 0\) in the closed domain \(\overline{\Omega}^{-}\). Theorem 1 is proved. \(\Box\)
4 EXISTENCE OF SOLUTION OF THE PROBLEM
Theorem 2. If the conditions of the Theorem 1 are satisfied and
then the solution to the problem exists.
Proof. By virtue of (13), from the Eq. (14) we obtained
where
The solution of the problem (21) with condition
we write as
where \(G(x,t)\) is Green function of the problem (21)–(23).
The presentation (24) is functional relationship between \({\tau^{+}}(x)\) and \({\nu^{+}}(x)\), brought from the area \({\Omega_{1}}\) to \({I_{1}}\). By replacing \(x={({q^{2}}x^{\prime})^{1/2q}},\quad t={({q^{2}}t^{\prime})^{1/2q}}\) in (12) and (24), we obtain
where
By excluding \(\tilde{\tau}^{+}(x)\) from the relationship (25) and (26), we derived
The expression (27) we will write in the form of Fredholm integral equation of the second kind
where
By replacing \(t=x\mu\) in (29), we have
After differentation the expressions (31) and (32) on \(x\), by virtue of (3), (19), we conclude that the kernel of the integral Eq. (28) and the right-hand side admit the estimates
Since the integral Eq. (28) is a Fredholm integral equation of the second kind with a weak singularity, by virtue of (33) and (3), we deduce that the solvability of the Eq. (28) follows from the uniqueness of the solution to the problem. So, the solution of the Eq. (28) can be represented as
and belongs to the class \(\nu^{-}(x)\in{C^{2}}(0,{h_{1}})\). Moreover, the function \(\nu^{-}(x)\) may have a singularity of order less than \(\frac{{1-2{\beta_{1}}}}{2}\) as \(x\to{h_{1}}\). But, this function as \(x\to 0\) is bounded, where \(\Re(x,z)\) is resolvent of the kernel \(S(x,z)\).
Now \(\nu^{-}(x)\) is known. So, from (13) we can find \(\nu^{+}(x)\) for \(\lambda_{1}(x)\neq 0\). Further, from the relation (24) we can determine \(\tau^{+}(x)=\tau^{-}(x)=\tau(x)\) in the class \(\tau\in C({\overline{I}_{1}})\cap{C^{2}}({I_{1}})\). We restore the solution of the problem in the domain \({\Omega^{+}}\) as the solution of the first boundary value problem (for \(\gamma_{1}=\delta_{1}=0\)) [9, 27]:
where
\(G(x,y,\xi,\eta)=\frac{{{{(y-\eta)}^{\frac{\alpha}{2}-1}}}}{2}\sum\limits_{n=-\infty}^{\infty}{\left[{e_{1,{\alpha\mathord{\left/{\vphantom{\alpha 2}}\right.\kern-1.2pt}2}}^{1,{\alpha\mathord{\left/{\vphantom{\alpha 2}}\right.\kern-1.2pt}2}}\left({-\frac{{\left|{x-\xi+2n}\right|}}{{{{(y-\eta)}^{{\alpha\mathord{\left/{\vphantom{\alpha 2}}\right.\kern-1.2pt}2}}}}}}\right)-e_{1,{\alpha\mathord{\left/{\vphantom{\alpha 2}}\right.\kern-1.2pt}2}}^{1,{\alpha\mathord{\left/{\vphantom{\alpha 2}}\right.\kern-1.2pt}2}}\left({-\frac{{\left|{x+\xi+2n}\right|}}{{{{(y-\eta)}^{{\alpha\mathord{\left/{\vphantom{\alpha 2}}\right.\kern-1.2pt}2}}}}}}\right)}\right]}\) is Green’s function of the first boundary value problem for the Eq. (1) in the domain \({\Omega^{+}}\) [27], \(e_{1,\delta}^{1,\delta}(z)=\sum\limits_{n=0}^{\infty}{\frac{{{z^{n}}}}{{n!\Gamma(\delta-\delta n)}}}\) is Wright type function [26].
The solution of the second and mixed boundary value problem for the Eq. (1) in the domain \({\Omega^{+}}\), can also be restored following the work of Pskhu [27]. Theorem 2 is proved. \(\Box\)
REFERENCES
A. A. Kilbas, H. M. Srivastava, and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Vol. 204 of North-Holland Mathematics Studies (Elsevier Science, Amsterdam, 2006).
I. Podlubny, Fractional Differential Equations (Academic, New York, 1999).
O. Kh. Abdullaev, ‘‘On the problem for a mixed-type degenerate equation with Caputo and Erdelyi–Kober operators of fractional order,’’ Ukr. Math. J. 71, 825–842 (2019).
B. I. Islomov, O. Kh. Abdullayev, and N. K. Ochilova, ‘‘On a problem for the loaded degenerating mixed type equation involving integral-differential operators,’’ Nanosyst.: Phys., Chem., Math. 8, 323–333 (2017).
B. I. Islomov, N. K. Ochilova, and K. S. Sadarangani, ‘‘On a Frankl type boundary value problem for a mixed type degenerating equation,’’ Ukr. Math. J. 71, 1347–1359 (2019).
O. I. Marichev, A. A. Kilbas, and A. A. Repin, Boundary Value Problems for Partial Differential Equations with Discounting Coefficients (Samar. Gos. Ekon. Univ., Samara, 2008) [in Russian].
O. A. Repin, Boundary Value Problems with Shift for Equations of Huperbolic and Mixed Type (Saratov Univ., Saratov, 1992) [in Russian].
O. Kh. Abdullaev, ‘‘On a problem for the degenerating parabolic-hyperbolic equation involving Caputo derivative of fractional order and non-linear terms,’’ Uzbek Math. J. 65 (1), 5–16 (2021).
A. A. Kilbas and O. A. Repin, ‘‘An analog of the Tricomi problem for a mixed type equation with a partial fractional derivative,’’ Fract. Calc. Appl. Anal. 13, 69–84 (2010).
K. B. Sadarangani and O. Kh. Abdullaev, ‘‘About a problem for loaded parabolic-hyperbolic type equation with fractional derivatives,’’ Int. J. Differ. Equat. 2016, 9815796 (2016).
O. Kh. Abdullaev, ‘‘On the problem for a mixed-type degenerate equation with Caputo and Erdelyi–Kober operators of fractional order,’’ Ukr. Math. J. 71, 825–842 (2019).
Sh. A. Alimov and R. R. Ashurov, ‘‘Inverse problem of determining an order of the Caputo time-fractional derivative for a subdiffusion equation,’’ J. Inverse Ill-Posed Probl. 28, 651–658 (2020).
R. R. Ashurov, A. Cabada, and B. Turmetov, ‘‘Operator method for construction of solutions of linear fractional differential equations with constant coefficients,’’ Fract. Calc. Appl. Anal. 1, 229–252 (2016).
R. R. Ashurov and Yu. Fayziev, ‘‘Determination of fractional order and source term in a fractional subdiffusion equation,’’ arXiv: submit/3264960 [math.AP] (2020).
R. R. Ashurov and S. Umarov, ‘‘Determination of the order of fractional derivative for subdiffusion equations,’’ Fract. Calc. Appl. Anal. 23, 1647–1662 (2020).
L. M. Eneeva, ‘‘Mixed boundary value problem for an ordinary differential equation with fractional derivatives with different origins,’’ Vestn. KRAUNTS, Fiz.-Mat. Nauki 36 (3), 65–71 (2021).
M. S. Salakhitdinov and E. T. Karimov, ‘‘Uniqueness of inverse source non-local problem for fractional order mixed type equation,’’ Euras. Math. J. 7, 74–83 (2016).
T. K. Yuldashev and O. Kh. Abdullaev, ‘‘Unique solvability of a boundary value problem for a loaded fractional parabolic-hyperbolic equation with nonlinear terms,’’ Lobachevskii J. Math. 42, 1113–1123 (2021).
T. K. Yuldashev, B. I. Islomov, and U. Sh. Ubaydullaev, ‘‘On boundary value problems for a mixed type fractional differential equation with Caputo operator,’’ Bull. Karaganda Univ., Math. Ser. 101, 127–137 (2021).
T. K. Yuldashev and B. J. Kadirkulov, ‘‘Nonlocal problem for a mixed type fourth-order differential equation with Hilfer fractional operator,’’ Ural Math. J. 6, 153–167 (2020).
T. K. Yuldashev and B. J. Kadirkulov, ‘‘Inverse boundary value problem for a fractional differential equations of mixed type with integral redefinition conditions,’’ Lobachevskii J. Math. 42, 649–662 (2021).
T. K. Yuldashev and B. J. Kadirkulov, ‘‘Inverse problem for a partial differential equation with Gerasimov–Caputo type operator and degeneration,’’ Fract. Fractions 5 (2), 58-1–13 (2021).
T. K. Yuldashev and E. T. Karimov, ‘‘Inverse problem for a mixed type integro-differential equation with fractional order Caputo operators and spectral parameters,’’ Axioms 9 (4), 121-1–24 (2020).
T. K. Yuldashev and E. T. Karimov, ‘‘Mixed type integro-differential equation with fractional order Caputo operators and spectral parameters,’’ Izv. IMI Udmurt. Univ. 57, 190–205 (2021).
T. K. Yuldashev and F. D. Rakhmonov, ‘‘Nonlocal problem for a nonlinear fractional mixed type integro-differential equation with spectral parameters,’’ AIP Conf. Proc. 2365, 060003-1–20 (2021).
A. V. Pskhu, Partial Differential Equation of Fractional Order (Nauka, Moscow, 2005) [in Russian].
A. V. Pskhu, ‘‘Solution of boundary value problems fractional diffusion equation by the Green function method,’’ Differ. Equat. 39, 1509–1513 (2003).
Funding
The research of second author Yuldashev T. K. is funded by the Ministry of Innovative development of the Republic of Uzbekistan (grant F-FA-2021-424).
Author information
Authors and Affiliations
Corresponding authors
Additional information
(Submitted by A. M. Elizarov)
Rights and permissions
About this article
Cite this article
Ochilova, N.K., Yuldashev, T.K. On a Nonlocal Boundary Value Problem for a Degenerate Parabolic-Hyperbolic Equation with Fractional Derivative. Lobachevskii J Math 43, 229–236 (2022). https://doi.org/10.1134/S1995080222040175
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1995080222040175