Tension-Compression and Shear of Plane Test Specimens from Laminated Composites with $\boldsymbol{[90^{\circ}]}_{\boldsymbol{s}}$ Structure: Numerical Method of Linearized Problem and Multiscale Buckling Modes

Abstract

As a development of the previously obtained results, a refined statement of linearized problems on the plane shear buckling modes of specimens made of fiber reinforced plastic with $[90^{\circ}]_{s}$ lay-up under tension-compression with shear is given. Micro- and mesoscale buckling modes of their structural elements in the form of fibers and bundles of fibers in a prebuckling state under shear and tension (compression) stresses in the direction across the fibers were considered. To formulate the problems, there are used the equations that were constructed earlier by reducing a consistent version of the geometrically nonlinear equations of the theory of elasticity to the one-dimensional equations of the theory of laminated straight beams with a layered structure through the thickness. It is based on the use of S.P. Timoshenko shear model taking into account tensile-compression transverse strain for each lamina. It is shown that a macroscale buckling in a purely shear mode is possible only under compression, and continuous rearrangement of the composite structure due to the implementation and continuous change of micro- and mesoscale internal buckling modes with a continuous change in wave formation parameters is also possible under other types of loading (compression, tension-compression with shear, pure shear). This, in particular, can explain the previously revealed decrease in the averaged shear modulus of the fiber reinforced plastic with an increase in shear strains.

1 INTRODUCTION

In the theory of the strength of fiber reinforced plastics (FRP), one of the objectives is to study the buckling of the composite phases, since when they are compressed along the fibers, failure is most possible due to the implementation of shear buckling mode of the reinforcing fibers of the composite. A large number of scientific works [1–8] et al. are currently dedicated to theoretical and experimental studies of this phenomenon. In general in these works are issues in developing models that describes the formation of the shear band, as well as assessing the level of normal compressive stresses. In accordance with the proposed model, they turned out to be equal to the average value of the transverse shear modulus of the FRP. For example, the work [2] is of a survey nature and also develops a model of shear band formation by taking into account the plasticity and hardening of the composite binder. A review of fracture models associated with the shear buckling mode is contained in [4]. It examines the features of the developed models and notes the development opportunities for each of them.

With the spread of research optical technology, it became possible to study the structure of the composites and the type of phase failure. The surface of fiber fracture in the place of failure of the specimen after compression tests has been investigated in works like [3]. Also in this work, the values of the ultimate compressive stress for various models are given in comparison with the experimental results.

An example of a new approach for describing the shear buckling mechanics modes of the phases of a FRP was proposed in [6]. In the described approach, as well as in [2], the plastic properties of the epoxy binder has been taken into account. There is showed that the magnitude of the critical compressive stress does not necessarily depend on the onset of yield of the binder, but may also depend on a combination of yield stress of the binder as well as on fiber deflection from the axial direction. In this work, the postbuckling branch of the compression deformation diagram after the shear buckling mode of the composite is constructed.

The range of problems and their solutions, which are simple enough to understand, related to compression tests of the specimens made of such FRP and the analysis of types of failure in compression, are presented in an accessible form in the monograph [9]. It is known that during of testing specimens, the behavior of a FRP in compression along the fibers is fundamentally different from the behavior in tension: under tension, both the specimen and the structure of the material are self-oriented along the load, while during compression the material (specimen) tends to ‘leave’ the line of the load [9].

At the end of the review, which does not claim to be exhaustive, it should be noted that, despite the huge number of works on the subject of failure of FRP under compression, many questions remain unexplored. It is known that during compression tests, the specimens in the region of clamps is in a complexly stressed state. Therefore, one of the key questions, according to the authors, is the formulation of such a theory or such a strength criterion that would not require complex experiments to implement a complex stressed state, since such an experiment requires very complex experimental equipment and structurally difficult to manufacture the specimens. The results of such experiments require a long and resource-intensive interpretation. The creation of such a strength criterion or a failure model based on simple experimental input characteristics of the material is a priority in the mechanics of FRP.

One of the failure criteria of flat plates without using the energy theory of strength in the framework of the Cosserat medium using the six-parameter theory of shells [10] was proposed in [11]. The fracture model is realized in the form of torsional instability of a semi-infinite medium, which is presented in the form of alternating axial and torsional elastic elements.

2 STATEMENT OF THE LINEARIZED PROBLEM TO IDENTIFICATION THE POSSIBLE BUCKLING MODES

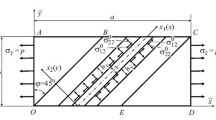
At arbitrary displacements and small strains, the equilibrium of a flat FRP specimen of rectangular shape with $[90^{0}]_{s}$ lay-up, consisting of $M=N-1$ laminas (Fig. 1), is described by a system of geometrically nonlinear differential equations [12]

$$f_{1}^{\left(k\right)}=S{{{}_{11}^{\left(k\right)}}_{,1}}-N_{13}^{\left(k\right)}=0,\quad f_{2}^{\left(k\right)}=S{{{}_{13}^{\left(k\right)}}_{,1}}-N_{33}^{\left(k\right)}=0,\quad k=\overline{1,N},$$

(1)

where

$$S_{1\alpha}^{\left(k\right)}=\frac{S_{1\alpha}^{\left[k-1\right]}+S_{1\alpha}^{\left[k\right]}}{2}+\frac{H_{1\alpha}^{\left[k-1\right]}}{h_{\left[k-1\right]}}-\frac{H_{1\alpha}^{\left[k\right]}}{h_{\left[k\right]}},\quad N_{\alpha 3}^{\left(k\right)}=\frac{N_{\alpha 3}^{\left[k-1\right]}}{{{h}_{\left[k-1\right]}}}-\frac{N_{\alpha 3}^{\left[k\right]}}{{{h}_{\left[k\right]}}},\quad k=\overline{2,N-1},\quad\alpha=1,3.$$

(2)

Equations (1) and relations (2) are based on the use of a S.P. Timoshenko kinematic model for each $\left[k\right]$th lamina and introducing into consideration $N$ unknown vectors of displacements ${{\mathbf{v}}^{\left(k\right)}}=u^{\left(k\right)}{{\mathbf{e}}_{1}}+{{w}^{\left(k\right)}}\mathbf{m}$; $k=\overline{1,N}$ of points of boundary planes, and internal planes ${{z}_{\left[1\right]}}={-{{h}_{\left[1\right]}}}/{2}$, ${{z}_{\left[N-1\right]}}={{{h}_{\left[N-1\right]}}}/{2}$ of conjugation of laminas.

Fig. 1

Calculation diagram of multilayer structure.

In order to identify all possible macro-, meso- and microscale buckling modes [13, 14], we will linearize the equilibrium equations (1) in the vicinity of the prebuckling state, which will be determined by the following initial forces formed in laminas of the FRP, found [15] in the approximation, $Q_{z}^{\text{o}\left[k\right]}={{h}_{\left[k\right]}}\sigma_{13}^{\text{o}\left[k\right]}=\textrm{const}$, $T_{z}^{\text{o}\left[k\right]}={{h}_{\left[k\right]}}\sigma_{33}^{\text{o}\left[k\right]}=$ const. In order to simplify the problem, in what follows, we will assume that in the prebuckling state the structural elements of the composite are stressed, but not deformed. This assumption allows us to discard all ‘‘strain’’ parametric terms in the linearized equations, which have the same form as (1), assuming that the following relations are valid ($\lambda$ – the external load parameter to be determined)

$$S_{11}^{\left[k\right]}=Q_{x}^{\left[k\right]}+\lambda Q_{z}^{\text{o}\left[k\right]}\gamma_{x}^{\left[k\right]},\ \ S_{13}^{\left[k\right]}=Q_{z}^{\left[k\right]}+\lambda Q_{z}^{\text{o}\left[k\right]}\gamma^{\left[k\right]},$$

$$N_{13}^{\left[k\right]}=Q_{z}^{\left[k\right]}+\lambda Q_{z}^{\text{o}\left[k\right]}u_{,x}^{\left[k\right]}+\lambda T_{z}^{\text{o}\left[k\right]}\gamma_{x}^{\left[k\right]},\ \ N_{33}^{\left[k\right]}=T_{z}^{\left[k\right]}+\lambda Q_{z}^{\text{o}\left[k\right]}w_{,x}^{\left[k\right]},$$

$$H_{11}^{\left[k\right]}=M_{y}^{\left[k\right]},\ H_{13}^{\left[k\right]}=S_{xz}^{\left[k\right]}.$$

(3)

In a perturbed state, the boundary conditions in the end sections ${{x}_{1}}=0$, ${{x}_{1}}=L$ for the inner layers ($k=\overline{2,N-1}$) are formulated in the form

$$S_{11}^{\left(k\right)}=0,S_{13}^{\left(k\right)}=0,$$

(4)

and the boundary surfaces of the peripheral layers ($k=1$ and $k=N$) will be assumed to be fixed [16], taking in what follows the equalities

$$u^{(1)}=U_{1}=0,\quad{{w}^{(1)}}={{W}_{1}}=0,\quad{{u}^{(N)}}={{U}_{N}}=0,\quad{{w}^{(N)}}={{W}_{N}}=0.$$

(5)

Using the elasticity relations (14) in [15] and dependences (2), (3), the equilibrium equations (1), expressed in terms of the displacement components ${{u}^{\left(k\right)}},{{w}^{\left(k\right)}}$, in accordance with the finite sum method used below in [17] there will be reduced, as in [15], to integral equations of Volterra type. In this case, the study of the stability problem will be reduced to a generalized eigenvalue problem [18]

$$\left(\mathcal{A}+\lambda\mathcal{P}\left(Q_{z}^{\text{o}\left[k\right]},T_{z}^{\text{o}\left[k\right]}\right)\right)\mathbf{x}=0.$$

(6)

The operator $\mathcal{A}:W\to W$ in (6) was introduced and investigated in [15], and

$$\mathcal{P}=\left(\begin{matrix}P&Q\\ {{R}_{1}}&{{R}_{2}}\end{matrix}\right):W\to W,W:{{H}^{\text{x2N}}}\text{x}{{\mathbb{R}}^{\times\text{2N}}}\to{{H}^{\times\text{2N}}}\text{x}{{\mathbb{R}}^{\times\text{2N}}},\quad H={{L}_{2}}(0,L),$$

$$P=\left(\begin{matrix}{{P}_{11}}&0\\ 0&{{P}_{22}}\end{matrix}\right),\quad P:{{H}^{\times 2(N-2)}}\to{{H}^{\times 2(N-2)}},$$

$${{P}_{ii}}=\left(\begin{matrix}B_{ii}^{(2)}&C_{ii}^{(2)}&0&0&0\\ A_{ii}^{(3)}&B_{ii}^{(3)}&C_{ii}^{(3)}&0&0\\ 0&\ddots&\ddots&\ddots&0\\ 0&0&A_{ii}^{(N-2)}&B_{ii}^{(N-2)}&C_{ii}^{(N-2)}\\ 0&0&0&A_{ii}^{(N-1)}&B_{ii}^{(N-1)}\end{matrix}\right),$$

(7)

$$A_{11}^{(k)}={{\alpha}^{[k-1]}}\left(\mathcal{J}-{{\mathcal{J}}^{*}}\right)+{{\beta}^{[k-1]}}{{\mathcal{J}}^{*}}\mathcal{J},$$

$$B_{11}^{(k)}=-\left({{\alpha}^{[k-1]}}-{{\alpha}^{[k]}}\right)\left(\mathcal{J}+{{\mathcal{J}}^{*}}\right)-\left({{\beta}^{[k-1]}}+{{\beta}^{[k]}}\right){{\mathcal{J}}^{*}}\mathcal{J},$$

$$C_{11}^{(k)}={{\alpha}^{[k]}}\left({{\mathcal{J}}^{*}}-\mathcal{J}\right)+{{\beta}^{[k]}}{{\mathcal{J}}^{*}}\mathcal{J},$$

$$A_{22}^{(k)}={{\alpha}^{[k-1]}}\left(\mathcal{J}-{{\mathcal{J}}^{*}}\right),$$

$$B_{22}^{(k)}=-\left({{\alpha}^{[k-1]}}-{{\alpha}^{[k]}}\right)\left(\mathcal{J}+{{\mathcal{J}}^{*}}\right),$$

$$C_{22}^{(k)}={{\alpha}^{[k]}}\left({{\mathcal{J}}^{*}}-\mathcal{J}\right),\quad k=\overline{2,N-1},$$

where the notation

$${{\alpha}^{[k]}}=\frac{{Q_{z}^{0[k]}}}{2{{h}_{[k]}}},\quad{{\beta}^{[k]}}=\frac{{\mathop{T_{z}^{0[k]}}}}{h_{[k]}^{2}},\quad Q=\left(\begin{matrix}{{\mathcal{J}}^{*}}e\otimes{{Q}_{11}}+e\otimes{{Q}_{22}}&0\\ 0&e\otimes{{Q}_{22}}\end{matrix}\right),$$

$$Q:{{\mathbb{R}}^{\times 2(N-2)}}\to{{H}^{\times 2(N-2)}},$$

$${{Q}_{11}}=\left(\begin{matrix}-\left({{\beta}^{[1]}}+{{\beta}^{[2]}}\right)&{{\beta}^{[2]}}&0&0&0\\ {{\beta}^{[2]}}&-\left({{\beta}^{[2]}}+{{\beta}^{[3]}}\right){{\mathcal{J}}^{*}}&{{\beta}^{[2]}}&0&0\\ 0&\ddots&\ddots&\ddots&0\\ 0&0&{{\beta}^{[N-2]}}&-\left({{\beta}^{[N-2]}}+{{\beta}^{[N-1]}}\right)&{{\beta}^{[N-1]}}\\ 0&0&0&{{\beta}^{[N-1]}}&-\left({{\beta}^{[N-1]}}+{{\beta}^{[N]}}\right)\end{matrix}\right),$$

$${{Q}_{22}}=\left(\begin{matrix}-\left({{\alpha}^{[1]}}-{{\alpha}^{[2]}}\right)&-{{\alpha}^{[2]}}&0&0&0\\ {{\alpha}^{[2]}}&-\left({{\alpha}^{[2]}}-{{\alpha}^{[3]}}\right)&-{{\alpha}^{[3]}}&0&0\\ 0&\ddots&\ddots&\ddots&0\\ 0&0&{{\alpha}^{[N-2]}}&-\left({{\alpha}^{[N-2]}}-{{\alpha}^{[N-1]}}\right)&-{{\alpha}^{[N-1]}}\\ 0&0&0&{{\alpha}^{[N-1]}}&-\left({{\alpha}^{[N-1]}}-{{\alpha}^{[N]}}\right)\end{matrix}\right),$$

$$R=\left(\begin{matrix}{{R}_{1}}&{{R}_{2}}\end{matrix}\right)=\left(\begin{matrix}{{\mathcal{J}}_{3}}\mathcal{J}\otimes{{R}_{11}}+{{\mathcal{J}}_{3}}\otimes{{R}_{22}}&0&{{\mathcal{J}}_{3}}\otimes{{R}_{13}}&0\\ 0&\,{{\mathcal{J}}_{3}}\otimes{{R}_{22}}&0&0\end{matrix}\right),$$

$$R:\,{{H}^{\times 2(N-2)}}\times{{\mathbb{R}}^{\times 2(N-2)}}\to{{\mathbb{R}}^{\times 2(N-2)}},\quad{{R}_{11}}=R_{11}^{T}={{Q}_{11}},\quad{{R}_{22}}=Q_{22}^{T}.$$

To approximate the linearized problem (6), it is replaced the integral operators of the Volterra type included in it with their finite-dimensional analogs in the form of integrating matrices [17], which were constructed in [15]. In accordance with the self-adjointness of the operator $\mathcal{A}$ investigated in [15] and the operator $\mathcal{P}:W\to W$ (applications, Theorem 1), as well as the used numerical finite sum method, the considered buckling problem will be reduced to a symmetric generalized eigenvalue problem (6) with respect to a pair $\left(\lambda,\mathbf{x}\right)$, in which all eigenvalues $\lambda$ are real.

3 RESULTS OF NUMERICAL CALCULATIONS

For specimens made by cold curing from ELUR-P unidirectional carbon tape and XT-118 binder (epoxy resin), the following effective (averaged) physical and mechanical characteristics [19] were found: tension and compression moduli of elasticity $E_{1}^{+}\approx E_{1}^{-}\approx 100$ GPa, ultimate tension $\sigma_{1}^{\textrm{max}}\approx 477$ MPa and compression $\sigma_{1}^{\textrm{max}}\approx 529$ MPa stress, Poisson’s ratio ${{\nu}_{13}}=0.34$; transversal moduli of elasticity $E_{3}^{+}\approx 5.7$ GPa and transversal ultimate stress $\sigma_{3}^{\textrm{max}}\approx 16.6$ MPa, ultimate stress $\sigma_{{{45}^{\circ}}}^{\textrm{max}}\approx 90.5$ MPa for $\pm{{45}^{\circ}}$ cross-ply lay-up, moduli of elasticity and ultimate stress for epoxy $E=2.7$ GPa, $\sigma^{\textrm{max}}\approx 27.6$ MPa. Note that, in view of the above characteristics of the FRP, it is interesting to study only those macroscale buckling modes of the specimen as a whole which are realized at critical stresses ${{p}^{cr}}$ limited by inequalities $0\leq{{p}^{cr}}\leq\sim 90$ MPa. Also it is interesting micro- and mesoscale buckling modes of a lamina consisting either of individual fibers or bundles of fibers and having a thickness equal to the diameter or an individual fiber, or a bundle of fibers, respectively in the specified stress range.

On the basis of the developed numerical method, computational experiments were carried out for different calculation cases to identify all possible buckling modes of the specimen as a whole, as well as its structural elements.

The first calculation case corresponds to the study of the possibility of realizing macroscale buckling mode of the specimen as a whole under tension or compression by stress $p=\sigma_{33}^{\text{o}}$. To identify such buckling mode, the characteristics of the FRP were set to be the same for each $[k]$-th layer and equal to the averaged values indicated above, the lamina thickness was taken equal to the thickness of the lamina ${{h}_{[k]}}=0.2$ mm of the FRP with the total size of the specimen $H=\sum\limits_{k=1}^{N-1}{{{h}_{[k]}}}$.

The second calculation case was considered with the aim of investigating the possibility of realizing mesoscale buckling mode of a separate rigid lamina of a FRP isolated from a specimen, consisting of bundles of fibers and surrounded on both sides by soft layers of epoxy with a weakened physical and mechanical characteristics. For calculations, the thicknesses of the hard and soft layers were taken to be the same and equal to the average thickness of the initial semi-finished FRP in the form of prepreg (${{h}_{[k]}}=0.2$ mm).

The third computational case was considered with the aim of investigating the possibility of realizing microscale buckling mode of a separate layer isolated from the composite. This layer consists only of rigid fibers. It is assumed that such a rigid layer is surrounded on both sides by soft epoxy layers with weakened physical and mechanical characteristics. In the calculations, the thicknesses of the hard and soft layers were taken to be the same and equal to the average diameter of an individual fiber (${{h}_{[k]}}=5$ $\mu$m).

Macroscale buckling mode under compression with shear. To identify possible buckling modes of the whole specimen, for all layers of FRP, the averaged elastic characteristics ${{E}_{1}}=100$ GPa, ${{E}_{3}}=5.7$ GPa, ${{G}_{13}}=459$ MPa given above and in [19] were taken at fixed geometric dimensions $L=25$ mm, ${{h}_{[k]}}=0.2$ mm. When carrying out computational calculations, the number of layers $M=N-1$ in the specimen was varied, when values $N=4,6,8,10,20,30$ were taken at different numbers of grid nodes $n$. Cases were considered under $\sigma_{33}^{0[{k}]}=\sigma_{13}^{0[{k}]}$ (tension-compression with shear), $\sigma_{33}^{0[{k}]}\neq 0$ , $\sigma_{13}^{0[{k}]}=0$ (tension or compression without shear), $\sigma_{33}^{0[{k}]}=0$, $\sigma_{13}^{0[{k}]}\neq 0$ (pure shear).

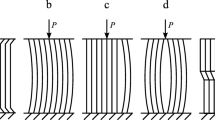
As an illustration, for the case of compression of the specimen, Fig. 2 shows its shape in a perturbed equilibrium state, obtained at $N=30$, $n=50$ and corresponding to the minimum buckling stress value $\sigma_{33}^{*}\approx-459$ MPa. It is possible to observe that, in the workingcase, an almost purely shear macroscale buckling mode of the whole specimen is realized. It turned out that the found critical stress (minimum positive eigenvalue of problem (6)) $\sigma_{33}^{*}=-{{\lambda}_{1}}\approx-459$ MPa is equal to the accepted value of the FRP shear modulus ${{G}_{13}}$. However, it does not have any practical significance, since the failure of FRP during testing occurs at lower ultimate values of the compressive stress. The computational calculations carried out have shown that for all $N=4,6,8,10,20,30$ the minimum value of the critical stress does not change, while the realized buckling mode remains unchanged that in the scales $L$ and $h$. It was also found that the rejection of the parametric terms $Q_{z}^{0[k]}$ containing in the linearized equations (6) practically does not affect the value of the critical stress and the realized buckling mode. Consequently, the revealed purely macroscale shear buckling mode of the specimens under consideration is not realized under the conditions of pure shear, it is not realized also under the conditions of tension.

Fig. 2

Macroscale buckling mode (perturbed state).

Shear mesoscale buckling mode under compression. A FRP was considered, the characteristics of the laminas of which were set is equal to the averaged values indicated above, with the exception of the central layer with the same characteristics, which is surrounded by two soft layers of epoxy with weakened values of elastic characteristics $G_{13}^{0}=25$ MPa, $E_{3}^{0}=50$ MPa (transversely soft layer). The thicknesses of each layer were set to be equal to the thickness of the lamina ${{h}_{[k]}}=0.2$ mm, length $L=25$ mm.

Figure 3 shows the shape of the specimen in its perturbed equilibrium state, obtained at $N=30$, $n=50$. It can be seen that, with the adopted design scheme, a shear buckling mode of soft layers with mesoscale dimensions in the $z$ direction and macroscale dimensions in the $x$-direction is revealed. The critical value of the compression stress of the specimen, which is formed during the buckling, in the considered case turned out to be equal to $\sigma_{33}^{*}\approx-G_{13}^{0}=-25$ MPa. It should be especially noted that the determined minimum critical stress value and the corresponding buckling mode, as in the first calculation case, do not depend on the number of hard layers located above and below the soft layers. In the perturbed state, the displacements of all rigid layers, except for the middle one, are practically equal to zero (Fig. 3). In this regard, to study other meso- and microscale buckling modes in the future, when forming the computational scheme, it is permissible to consider only a representative cell consisting of three layers. Identification such buckling modes is possible only with a significant thickening of the computational grid. From layers, the middle hard layer (a lamina of fibers or bundles of fibers) is located between two soft layers of a binder with weakened physical and mechanical characteristics, in which, in a perturbed state, the displacements of the points of conjugation with other rigid layers located above or below are equal to zero.

Fig. 3

Mesoscale shear buckling mode of layer with weakend mechanical characteristics (perturbed state).

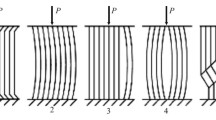
Mesoscale flexural-shear buckling modes under compression with shear. To identify the investigated buckling modes in accordance with the above conclusion, a design scheme is used, consisting of a rigid central layer with physical and mechanical characteristics of ${{E}_{1}}=100$ GPa, ${{\nu}_{13}}=0.34$ and weakened values of other characteristics ${{E}_{3}}=50$ MPa, ${{G}_{13}}=25$ MPa. The transversely soft epoxy layers located above and below the central layer have characteristics $G_{13}^{0}=25$ MPa, $E_{3}^{0}=50$ MPa. The geometric dimensions of all three layers are taken equal to $L=25$ mm, ${{h}_{[k]}}=0.2$ mm. The numerical solution of the formulated eigenvalue problem (6) was carried out with the number of grid nodes $n=500$. The solution results showed that the first realized buckling mode (corresponding to the minimum eigenvalue ${{\lambda}_{1}}$), like the one described above, is practically purely shear. The distribution of displacements and shear strain in the pertrubed state qualitatively coincides with the result shown in Fig. 3, and the minimum critical stress value $\sigma_{33}^{o}$ also turned out to be equal to the transverse shear modulus of the fiber bundle ($\sigma_{33}^{*}\approx{{G}_{13}}=25$ MPa). As a result of the analysis of the obtained eigenvalue spectrum (${{\lambda}_{1}}<{{\lambda}_{2}}<...<{{\lambda}_{m}},\,m=2N(n+1)$) it was revealed that in the process of specimen’s loading, shear buckling mode are transformed: at the beginning, into flexural-shear buckling mode with wave formation in the vicinity of the edge of the specimen (Fig. 4), and then flexural-shear buckling mode are transformed in purely flexural with frequent wave formation along the entire width of the specimen (Fig. 5). In Fig. 4 shows the flexural-shear buckling mode of a laminated structure for ${{\lambda}_{5}}=\sigma_{33}^{*}=\sigma_{13}^{*}=56$ MPa, which is transitional from shear to flexural. In Fig. 5 for ${{\lambda}_{10}}=\sigma_{33}^{*}=\sigma_{13}^{*}=81$ MPa shows a purely flexural buckling mode of a laminated structure. It should be noted that the length of the resulting buckling half-waves turned out to be equal to $l^{*}\approx 0.25$ mm (Figs. 4 and 5), and $l^{*}\sim{{h}_{[k]}}=0.2$ mm.

Fig. 4

Flexural-shear buckling mode ($\sigma_{33}^{*}=\sigma_{13}^{*}=56\text{ MPa})$.

Fig. 5

Flexural buckling mode ($\sigma_{33}^{*}=\sigma_{13}^{*}=81\text{ MPa})$.

Mesoscale flexural-shear buckling modes under tension with shear. The results of numerical studies of the stability problem at the mesoscale under tension with shear are shown in Figs. 6, 7. It follows from them that a flexural-shear buckling mode with a wave formation is obtained mainly in the region of free edges with a half-wave length of ${{l}^{*}}\sim 0.3$ mm. It was found that dropping the ‘‘force’’ parametric term $T_{z}^{0[k]}$ practically does not affect the value of critical stresses and buckling mode, therefore, their implementation is possible when the specimen is loaded with shear forces. The minimum critical stress value $\sigma_{13}^{0}$ corresponds to the first eigenvalue ${{\lambda}_{1}}$, of the problem, it turned out to be equal to $\sigma_{13}^{*}=84.7$ MPa.

Fig. 6

Mesoscale flexural-shear buckling mode ($T_{z}^{0[k]}>0$, $\sigma_{13}^{0}\neq 0$).

Fig. 7

Mesoscale flexural-shear buckling mode ($T_{z}^{0[k]}>0$, $\sigma_{13}^{0}\neq 0$).

Fig. 8

Flexural microscale buckling mode of the fiber.

Microscale flexural buckling mode of fiber under compression with shear. To identify the buckling mode at the microscale of the fiber with the adopted elastic and geometric characteristics ${{E}_{1}}=200$ GPa, ${{E}_{3}}=200$ GPa, ${{G}_{13}}=77$ GPa, $G_{13}^{0}=25$ MPa, $E_{3}^{0}=50$ MPa, ${{\nu}_{13}}=0.34$, $L=25$ mm, ${{h}_{[k]}}=5\mu$m integration region was ${{x}_{1}}=[0,\ L]$ decomposed by dividing it into three subdomains $x^{(1)}=[0,{{l}_{1}})$, $x^{(2)}=[{{l}_{1}},L-{{l}_{1}}]$, $x^{(3)}=(L-{{l}_{1}},L]$. For each subdomain, the corresponding grids are introduced according to the Gauss quadrature formula [17], where $\left\{x_{i}^{(j)}\right\}$ according the nodes of collocations of the Gauss quadrature formula, which are the roots of the Legendre polynomial of degree $N$, on the segment ${{x}^{j}}$. As in [15], by expanding interpolating functions (Lagrange basis functions) in Legendre polynomials, integrating matrices ($\text{L}_{h}^{(j)}$, $\text{R}_{h}^{(j)}$) are constructed. The number of layers of the selected representative cell was set equal $N-1=3$, the total number of collocation nodes - $n=600$, and local refinement of the grid with dimensions ${{n}_{1}}={{n}_{3}}=100$ at the free edges in areas with dimensions ${{l}_{1}}=0.0025L$ was performed. The given buckling mode corresponds to the minimum critical value of stress $\sigma_{33}^{*}=\sigma_{13}^{*}\approx 25$ MPa, and when the initial forces $Q_{z}^{0[k]}$ are discarded in relations (3), the minimum value of critical stresses practically does not change, and the corresponding buckling mode changes insignificantly. It should be noted that under the considered types of loading, a flexural buckling mode of a rigid layer, consisting of fibers, is realized with wave formation along the entire length of the fiber, and the buckling half-wave length ${{l}^{*}}\sim 8$ $\mu$m is of the same order as the fiber diameter ${{h}_{[k]}}=5$ $\mu$m.

LEMMA

Lemma 1. The operator $P:{{H}^{\text{x2N}}}\to{{H}^{\text{x2N}}}$ is self-adjoint.

To prove self-adjointness $P$ we prove the self-adjointness property of the blocks ${{P}_{ii}}$, $i=1,2$ from which the operator is constructed:

1. ${{P}_{11}}=P_{11}^{*}$, the proof of the equality is based on Lemma 1 in [15].

$(B_{11}^{(k)}u,v)=((-({{\alpha}^{[k-1]}}-{{\alpha}^{[k]}})(\mathcal{J}+{{\mathcal{J}}^{*}})-({{\beta}^{[k-1]}}+{{\beta}^{[k]}}){{\mathcal{J}}^{*}}\mathcal{J})u,v)=(u,(-({{\alpha}^{[k-1]}}-{{\alpha}^{[k]}})\times(\mathcal{J}+{{\mathcal{J}}^{*}})-({{\beta}^{[k-1]}}+{{\beta}^{[k]}}){{\mathcal{J}}^{*}}\mathcal{J})v)=(u,B_{11}^{(k)}v)$, $B_{11}^{(k)*}=B_{11}^{(k)}$,

$(A_{11}^{(k)}u,v)=(({{\alpha}^{[k-1]}}(\mathcal{J}-{{\mathcal{J}}^{*}})+{{\beta}^{[k-1]}}{{\mathcal{J}}^{*}}\mathcal{J})u,v)=(u,({{\alpha}^{[k-1]}}({{\mathcal{J}}^{*}}-\mathcal{J})+{{\beta}^{[k]}}{{\mathcal{J}}^{*}}\mathcal{J})v)=(u,C_{11}^{(k-1)}v)$, i.e. $A_{11}^{(k)*}=C_{11}^{(k-1)}$.

Lemma 2. Operator ${{R}_{1}}:{{H}^{\text{x2(N-1)}}}\to{{\mathbb{R}}^{\text{x2(N-1)}}}$ is self-adjoining to operator $Q:{{\mathbb{R}}^{\times 2(N-2)}}\to{{H}^{\times 2(N-2)}}$.

By virtue of statement 1 in [15], an easily verifiable identity ${{({{\mathcal{J}}_{3}}a,b)}_{\mathbb{R}}}={{(a,eb)}_{H}}$, where $a\in H$, $b\in\mathbb{R}$, and also by virtue $R_{11}^{T}={{Q}_{11}}$, $R_{22}^{T}={{Q}_{22}}$, it is easy to show that the blocks of the operator matrix${{R}_{1}}$ are conjugate to the blocks of the matrix $Q$, and hence $R_{1}^{*}=Q$:

${{(({{\mathcal{J}}_{3}}\mathcal{J}\otimes{{R}_{11}}+{{\mathcal{J}}_{3}}\otimes{{R}_{22}})(u),v)}_{{{\mathbb{R}}^{N-2}}}}={{(u,({{\mathcal{J}}^{*}}e\otimes R_{11}^{T}+e\otimes R_{22}^{T})(v))}_{{{H}^{N-2}}}}=(u,({{\mathcal{J}}^{*}}e\otimes{{Q}_{11}}+e\otimes{{Q}_{22}})(v)),$ where $u\in{{H}^{\text{N-2}}},v\in{{\mathbb{R}}^{\text{N-2}}}$.

Theorem 1. $\mathcal{P}:W\to W$ , defined by (4), is symmetric.

The proof is based on Lemmas 1, 2.