Effect of the Polarization of Isolated Three-Spin Groups on the Free Induction Decay and Solid Echo of Nuclear Magnetic Resonance

Abstract

The kinetic equation for the NMR spectra of solids containing isolated three-spin groups with arbitrary dipole–dipole interaction constants was derived. Analytical expressions for signals of free induction decay and solid echo for a system of three dipole-coupled spins were obtained from the equation for the density matrix.

1 INTRODUCTION

The NMR spectrum of an isolated group of spins can be complex and comprise a large number of discrete resonance lines [1, 2]. The observed spectra are usually simpler because of their broadening under the effects of the surrounding spins and the partial averaging, and they contain information on the structure and orientation of the group. Three-spin groups are typically considered using a model of equivalent nuclei located at the vertices of an equilateral triangle. However, it was considered of interest to study a three-spin group with different dipole–dipole interaction (DDI) constants. Initially [1], the frequencies and probabilities of transitions between energy levels were calculated, and formulas for calculating the line shape were derived. These results were further compared to the characteristics of the observed signal in trichloroethane [3], with rapidly rotating groups being taken into account. The broadening of a line was determined using the Gaussian distribution of longitudinal local fields. This distribution of local magnetic fields was characteristic of polycrystals or amorphous solids. However, there has hitherto been no theoretical description of the line shape for substances with an isolated three-spin group in the crystalline state.

The experimental and theoretical investigation of spin echoes in solids (solid echo, SE) after exposure to a two-pulse sequence was initiated by Powles and Mansfield [4] and Allen et al. [5], who found that SE amplitude depends on the magnetization rotation angle β and is maximum at β = 90° [5, 6]. The SE signal enables us to accurately determine the second moment M₂ of the NMR line at time 2t [7]. A more complex pulse response was observed in solids with isolated three-spin groups [5, 7]. In this case, the echo is due to the DDI within the group, and the dependence of the amplitude of the echo on the duration of the second pulse is similar to the dependence of the amplitude of a quadrupolar nucleus with the spin 3/2 on the same parameter.

Spin echo can also be used for information processing systems in magnetically ordered substances [8]. The first (information) pulse is weak, and the spectrum width is smaller than the NMR line width, while the second (control) pulse allows the appearance of an echo signal with a varying interpulse interval to be controlled. In the considered works [1, 7], no analytical expressions for free induction decay (FID) and SE were presented, because of which it is difficult to make calculations and obtain information on the structure and orientation of three-spin groups from NMR signals. In this work, a new method was proposed to calculate FID, line shape, and SE in a system of three dipole-coupled spins 1/2 with arbitrary DDI constants. In this method, for the first time, symmetries are used that are determined by the spin exchange and by the flip of all the spins about the axis of the initial polarization or the direction of the pulses during the formation of the solid echo [9–12]. Using these symmetries enables the calculations in two three-dimensional spaces and two one-dimensional spaces.

The effects of the other spins of the system was taken into account based on the unified theory of NMR spin dynamics [13] to calculate FID, based on spin–spin relaxation for calculating SE.

2 THEORETICAL RESULTS AND DISCUSSION

2.1 Theory of Free Induction Decay in a Three-Spin Group

The Hamiltonian of the secular part of the dipole–dipole interaction for a three-spin group comprising nuclei with the spin 1/2, coupled by various DDI constants ${{b}_{{ij}}}$ (i, j = 1, 2, 3), has the form

$$\begin{gathered} \hat {H}_{d}^{z} = {{b}_{{12}}}\left( {2\hat {S}_{1}^{z}\hat {S}_{2}^{z} - \hat {S}_{1}^{x}\hat {S}_{2}^{x} - \hat {S}_{1}^{y}\hat {S}_{2}^{y}} \right) \\ + \,\,{{b}_{{31}}}\left( {2\hat {S}_{3}^{z}\hat {S}_{1}^{z} - \hat {S}_{3}^{x}\hat {S}_{1}^{x} - \hat {S}_{3}^{y}\hat {S}_{1}^{y}} \right) \\ + \,\,{{b}_{{23}}}\left( {2\hat {S}_{2}^{z}\hat {S}_{3}^{z} - \hat {S}_{2}^{x}\hat {S}_{3}^{x} - \hat {S}_{2}^{y}\hat {S}_{3}^{y}} \right), \\ \end{gathered} $$

(1)

where

$${{b}_{{ij}}} = \frac{{{{\gamma }^{2}}{{\hbar }^{2}}\left( {3{{{\cos }}^{2}}{{\theta }_{{ij}}} - 1} \right)}}{{2r_{{ij}}^{3}}},\,\,\,\,i,j = 1,2,3,$$

(2)

${{\theta }_{{{\kern 1pt} i{\kern 1pt} j}}}$ is the angle between the vector ${{{\mathbf{r}}}_{{ij}}}$ connecting spins i and j and the direction of the magnetic field; ${{r}_{{{\kern 1pt} i{\kern 1pt} j}}}$ is the vector length; and $\hat {S}{\kern 1pt} _{i}^{k}$ are the operators of the projections of the moments of the ith nuclear spin onto the axes x, y, and z.

The following notation is also used:

$$\begin{gathered} {{\sigma }_{1}} = {{b}_{{12}}} + {{b}_{{23}}} + {{b}_{{31}}},\,\,\,\,{{\sigma }_{2}} = {{b}_{{12}}}{{b}_{{23}}} + {{b}_{{12}}}{{b}_{{31}}} + {{b}_{{23}}}{{b}_{{31}}}, \\ \chi = {{\left( {9{{\sigma }_{1}} - 24{{\sigma }_{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,\cos \beta = \frac{{{{\sigma }_{1}}}}{\chi }. \\ \end{gathered} $$

(3)

The eigenvalues of the interaction Hamiltonian are

$$\begin{gathered} {{\lambda }_{1}} = \frac{{{{\sigma }_{1}}}}{2},\,\,\,\,{{\lambda }_{2}} = \frac{{ - {{\sigma }_{1}} - \chi }}{4}, \\ {{\lambda }_{3}} = \frac{{ - {{\sigma }_{1}} + \chi }}{4},\,\,\,\,{{\lambda }_{4}} = 0. \\ \end{gathered} $$

(4)

The initial polarization is ${{\hat {S}}^{x}} = \hat {S}_{1}^{x} + \hat {S}_{2}^{x} + \hat {S}_{3}^{x}.$

The FID is calculated using the symmetries generated by the operation of the flip of all the spins about the x axis and the operation of spin exchange, which commute with each other. Taking these symmetries into account, the problem reduces to the replacement of the calculation in the eight-dimensional state space R by calculations in two three-dimensional subspaces and two one-dimensional subspaces:

$$\begin{gathered} R = {{R}_{{es}}} \oplus {{R}_{{os}}} \oplus {{R}_{{ea}}} \oplus {{R}_{{oa}}} \\ = {{{\hat {P}}}_{e}}{{{\hat {P}}}_{s}}R \oplus {{{\hat {P}}}_{o}}{{{\hat {P}}}_{s}}R \oplus {{{\hat {P}}}_{e}}{{{\hat {P}}}_{a}}R \oplus {{{\hat {P}}}_{o}}{{{\hat {P}}}_{s}}R, \\ {{{\hat {S}}}^{x}} = {{{\hat {P}}}_{e}}{{{\hat {P}}}_{s}}{{{\hat {S}}}^{x}} + {{{\hat {P}}}_{o}}{{{\hat {P}}}_{s}}{{{\hat {S}}}^{x}} + {{{\hat {P}}}_{e}}{{{\hat {P}}}_{a}}{{{\hat {S}}}^{x}} + {{{\hat {P}}}_{o}}{{{\hat {P}}}_{a}}{{{\hat {S}}}^{x}}, \\ \hat {H}_{d}^{z} = {{{\hat {P}}}_{e}}{{{\hat {P}}}_{s}}\hat {H}_{d}^{z} + {{{\hat {P}}}_{o}}{{{\hat {P}}}_{s}}\hat {H}_{d}^{z} + {{{\hat {P}}}_{e}}{{{\hat {P}}}_{a}}\hat {H}_{d}^{z} + {{{\hat {P}}}_{o}}{{{\hat {P}}}_{a}}\hat {H}_{d}^{z}. \\ \end{gathered} $$

(5)

The projectors determined by the flip of all the spins are

$${{\hat {P}}_{{e,o}}} = \frac{1}{2}\left( {1 \pm \hat {I}} \right),$$

where

$$\hat {I} = \exp \left[ {i\pi \left( {{{{\hat {S}}}^{x}} - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)} \right] = 8\hat {s}_{1}^{x}\hat {s}_{2}^{x}\hat {s}_{3}^{x}.$$

(6)

The projectors determined by the spin exchange are [11]

$${{\hat {P}}_{{s,a}}} = \frac{1}{2}\left( {1 \pm {{{\hat {E}}}_{x}}} \right),$$

where

$$\hat {E}x = \frac{{\left( {{{b}_{{12}}} - {{b}_{{23}}}} \right)\left( {{{b}_{{12}}} - {{b}_{{31}}}} \right)\hat {E}_{x}^{{12}} + \left( {{{b}_{{23}}} - {{b}_{{31}}}} \right)\left( {{{b}_{{23}}} - {{b}_{{12}}}} \right)\hat {E}_{x}^{{23}} + \left( {{{b}_{{31}}} - {{b}_{{12}}}} \right)\left( {{{b}_{{31}}} - {{b}_{{23}}}} \right)\hat {E}_{x}^{{31}}}}{{\sigma _{1}^{2} - 3{{\sigma }_{2}}}};$$

(7)

here, $\hat {E}_{x}^{{kl}} = \frac{1}{2} + 2{{{\mathbf{S}}}^{k}}{{{\mathbf{S}}}^{l}}.$

The matrices of the operators $\hat {H}{\kern 1pt} _{d}^{z}$ and ${{\hat {S}}^{{{\kern 1pt} x}}}$ in subspaces (3) in the eigenbasis of the interaction Hamiltonian have the following form:

in the subspace ${{R}_{{es}}}$,

$$\begin{gathered} \left( {\begin{array}{*{20}{c}} {{{\lambda }_{1}}}&0&0 \\ 0&{{{\lambda }_{2}}}&0 \\ 0&0&{{{\lambda }_{3}}} \end{array}} \right); \\ \frac{1}{2}\left( {\begin{array}{*{20}{c}} 0&{\sqrt 3 \cos \frac{\beta }{2}}&{ - \sqrt 3 \sin \frac{\beta }{2}} \\ {\sqrt 3 \cos \frac{\beta }{2}}&{3{{{\cos }}^{2}}\frac{\beta }{2} - 1}&{ - \frac{3}{2}\sin \beta } \\ { - \sqrt 3 \sin \frac{\beta }{2}}&{ - \frac{3}{2}\sin \beta }&{3{{{\sin }}^{2}}\frac{\beta }{2} - 1} \end{array}} \right) \\ \end{gathered} $$

(8)

in the subspace ${{R}_{{os}}}$,

$$\begin{gathered} \left( {\begin{array}{*{20}{c}} {{{\lambda }_{3}}}&0&0 \\ 0&{{{\lambda }_{2}}}&0 \\ 0&0&{{{\lambda }_{1}}} \end{array}} \right), \\ \frac{1}{2}\left( {\begin{array}{*{20}{c}} {1 - 3{{{\sin }}^{2}}\frac{\beta }{2}}&{\frac{3}{2}\sin \beta }&{ - \sqrt 3 \sin \frac{\beta }{2}} \\ {\frac{3}{2}\sin \beta }&{1 - 3{{{\cos }}^{2}}\frac{\beta }{2}}&{\sqrt 3 \cos \frac{\beta }{2}} \\ { - \sqrt 3 \sin \frac{\beta }{2}}&{\sqrt 3 \cos \frac{\beta }{2}}&0 \end{array}} \right), \\ \end{gathered} $$

in the subspace ${{R}_{{ea}}}$, $\left( 0 \right),$$\left( { - \frac{1}{2}} \right);$

in the subspace ${{R}_{{oa}}}$, $\left( 0 \right),$$\left( {\frac{1}{2}} \right).$

Calculation of the FID in each of the subspaces gives [12]

$$\begin{gathered} {{G}_{3}}(t) = \frac{{{\text{Tr}}\left( {\exp \left( { - i\hat {H}_{d}^{z}t} \right){{{\hat {S}}}^{x}}\exp \left( {i\hat {H}_{d}^{z}t} \right){{{\hat {S}}}^{x}}} \right)}}{{{\text{Tr}}{{{\left( {{{{\hat {S}}}^{x}}} \right)}}^{2}}}} \\ = \frac{1}{8}\left( {1 + 3{{{\cos }}^{2}}\beta } \right) + \frac{3}{8}{{\sin }^{2}}\beta \cos {{\omega }_{{23}}}t \\ + \,\,\frac{1}{2}{{\sin }^{2}}\frac{\beta }{2}\cos {{\omega }_{{13}}}t + \frac{1}{2}{{\cos }^{2}}\frac{\beta }{2}\cos {{\omega }_{{12}}}t, \\ \end{gathered} $$

(9)

where ${{\omega }_{{12}}} = \frac{{3{{\sigma }_{1}} + \chi }}{4},$${{\omega }_{{13}}} = \frac{{3{{\sigma }_{1}} - \chi }}{4},$ and ${{\omega }_{{23}}} = - \frac{\chi }{2}$ are the frequencies in the FID and SE frequencies.

For a more detailed determination of the structure of the substance and the position of the three-spin group in the molecule, it is necessary to calculate the FID of the entire sample. The effect of all the other spins of the system on the NMR line shape was taken into account using the general kinetic equation for partial densities of magnetic dipoles [13].

2.2 General Kinetic Equation for the Partial Densities of Magnetic Dipoles

In recent years, for the first time in NMR theory, kinetic equations for the densities of magnetic dipoles and spin temperatures have been successfully derived that are applicable for the analysis of NMR spectra at arbitrary amplitude ω₁ of the resonance field [13]. The most convenient variables for deriving the kinetic equations are the partial densities σ^β(h, t), where β = x, y, z, of the dipoles that are at time t in the same layer as the longitudinal local dipole field h is (also called the polarization of layers). This theory enabled the derivation of the general kinetic equations for the densities of magnetic dipoles and the spin temperatures of the Zeeman and dipole–dipole reservoirs and the study of the kinetics of the polarization of magnetic dipoles on exposure to an arbitrary saturation field with amplitude ω₁ in condensed matter. The interaction Hamiltonian in a rotating reference frame has the form

$$\hat {H} = \omega {{\hat {S}}^{z}} + {{\omega }_{{{\kern 1pt} 1}}}{{\hat {S}}^{x}} + \hat {H}_{d}^{z},$$

(10)

where ω is the detuning of the resonance magnetic field; ${{\hat {S}}^{{x,z}}}$ are the nuclear spin operators; ω₁ is the resonance field amplitude; and $\hat {H}_{d}^{z}$ is the secular part of the DDI Hamiltonian [1, 5],

$$\hat {H}_{d}^{z} = \sum\limits_{i > k} {{{b}_{{ik}}}} (3\hat {S}_{i}^{z}\hat {S}_{k}^{z} - {{{\mathbf{S}}}_{i}}{{{\mathbf{S}}}_{k}}) = 3{{\hat {H}}_{{zz}}} + {{\hat {H}}_{{is}}};$$

(11)

b_ik are the DDI coefficients; and ${{\hat {H}}_{{is}}}$ is the part of the isotropic interaction, which describes the exchange of polarizations between layers and characterizes the contribution (proportional to $h{{\sigma }^{{x,y}}}$) to the rates of change of the layer polarizations to the local dipole fields [13].

In the derivation of the equations, account was taken of both regular processes determined by interaction Hamiltonian (11), such as the precession of dipoles in external fields and local dipole fields created by neighboring dipoles, or polarization transfer, and the random process of spectral diffusion, which characterizes the random change in the longitudinal local field under the effect of spin exchange and thermal motion of atoms. In the equations, the following notation was used:

$$\begin{gathered} \sigma _{0}^{\beta }\left( t \right) = \int\limits_{ - \infty }^\infty {{{\sigma }^{\beta }}(h,t)g(h)dh} , \\ \sigma _{1}^{\beta }\left( t \right) = \int\limits_{ - \infty }^\infty {{{\sigma }^{\beta }}(h,t)hg(h)dh} , \\ \end{gathered} $$

(12)

where $\sigma _{0}^{\beta }\left( t \right)$ and $\sigma _{1}^{\beta }\left( t \right)$ are the layer polarizations in the Zeeman and dipole–dipole reservoirs, respectively, and g(h) is an even distribution function of longitudinal local fields in the spin system, $g\left( h \right) = g\left( { - h} \right).$ In these terms, the system of the kinetic equations has the form

$$\begin{gathered} \frac{{d{{\sigma }^{x}}}}{{dt}} = - \left( {\omega + \frac{{3h}}{2}} \right){{\sigma }^{y}} - \left( {\frac{3}{2} - \alpha } \right)\left( {h\sigma _{0}^{y} + \sigma _{1}^{y} - h{{\sigma }^{y}}} \right) \\ + \,\,\frac{{\sigma _{0}^{x} - {{\sigma }^{x}}}}{{{{\tau }_{ \bot }}}} - \frac{{{{\sigma }^{x}}}}{{{{T}_{ \bot }}}},\,\,\,\,\frac{{d{{\sigma }^{y}}}}{{dt}} = \left( {\omega + \frac{{3h}}{2}} \right){{\sigma }^{x}} \\ + \,\,\left( {\frac{3}{2} - \alpha } \right)\left( {h\sigma _{0}^{x} + \sigma _{1}^{x} - h{{\sigma }^{x}}} \right) - {{\omega }_{1}}{{\sigma }^{z}} \\ + \,\,\frac{{\sigma _{0}^{y} - {{\sigma }^{y}}}}{{{{\tau }_{ \bot }}}} - \frac{{{{\sigma }^{y}}}}{{{{T}_{ \bot }}}},\,\,\,\,\frac{{d{{\sigma }^{z}}}}{{dt}} = {{\omega }_{1}}{{\sigma }^{y}} \\ + \,\,\frac{1}{{{{\tau }_{{||}}}}}\left( {\sigma _{0}^{z} + \frac{{h\sigma _{1}^{z}}}{{\left\langle {{{h}^{2}}} \right\rangle }} - {{\sigma }^{z}}} \right) + \frac{{\sigma _{{eq}}^{z} - {{\sigma }^{z}}}}{{{{T}_{{||Z}}}}} - \frac{{h\sigma _{1}^{z}}}{{\left\langle {{{h}^{2}}} \right\rangle {{T}_{{||d}}}}}, \\ \end{gathered} $$

(13)

where ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{ \bot }}}}} \right. \kern-0em} {{{\tau }_{ \bot }}}}$ is the rate of change in the longitudinal polarization of a layer in the course of the spectral diffusion; ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{{\text{II}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{II}}}}}}}$ is the rate of equilibration in the spin system; ${1 \mathord{\left/ {\vphantom {1 {{{T}_{ \bot }}}}} \right. \kern-0em} {{{T}_{ \bot }}}}$ is the transverse relaxation rate related to the thermal motion leading to the absorption of quanta ħω₀ at Larmor frequency ω₀; T_||Z and T_||d are the times of longitudinal spin–lattice relaxation of the Zeeman and dipole–dipole reservoirs, respectively; and $\sigma _{{eq}}^{z}$ is the equilibrium longitudinal polarization of the sample. The parameter $\frac{3}{2}$ – α characterizes the unaveraged part of the isotropic DDI, ${{\hat {H}}_{{is}}},$ which depends on the structure of the substance and its orientation with respect to the constant magnetic field [13].

Note that kinetic equations (13) describe the organization of the Zeeman and dipole–dipole reservoirs, which manifests itself in establishing the average orientation order, the same for all the dipoles:

$${{\sigma }^{{\beta }}} = \sigma _{0}^{{\beta }} + \frac{h}{{\left\langle {{{h}^{2}}} \right\rangle }}\sigma _{1}^{{\beta }},\,\,\,\,\beta = x,y,z.$$

(14)

Here, $\sigma _{0}^{\beta }$ was defined previously [14], ${{h\sigma _{0}^{\beta }} \mathord{\left/ {\vphantom {{h\sigma _{0}^{\beta }} {\left\langle {{{h}^{2}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{h}^{2}}} \right\rangle }}$ is the contribution to the layer polarization of the dipole–dipole reservoir, and $\left\langle {{{h}^{2}}} \right\rangle$ is the second moment of g(h).

It has been shown [13] that, under certain conditions, kinetic equations (13) transform into the Bloch [14], Redfield [15], and Provotorov [16] equations in the known applications of these equations.

The steady-state solution of the system of Eqs. (13) for the line shape F(ω) has the form [13, 17]

$$F(\omega ) = \frac{{\sigma _{0}^{y}(\omega )}}{{\sigma _{{eq}}^{z}}} = \frac{{B\left( \omega \right)}}{{C\left( \omega \right)}}.$$

(15)

Here, $\sigma _{{eq}}^{z}$ is the equilibrium longitudinal polarization. All the calculations were performed for the case where g(h) is a Gaussian distribution function of longitudinal local fields:

$$g\left( h \right) = \frac{1}{{{{{\left( {2\pi \left\langle {{{h}^{2}}} \right\rangle } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}\exp \left( { - \frac{{{{h}^{2}}}}{{2\left\langle {{{h}^{2}}} \right\rangle }}} \right),$$

(16)

where

$$\left\langle {{{h}^{2}}} \right\rangle = \int\limits_{ - \infty }^\infty {{{h}^{2}}g\left( h \right)dh} ,\,\,\,\,\left\langle {{{h}^{2}}} \right\rangle = \frac{4}{9}{{M}_{{2cr}}}.$$

The unified theory of NMR spin dynamics [13] enables one to describe virtually all the signals of line shape and FID that are observed in solids. The FID in CaF₂ was calculated from formula (15) with local field distribution function (16) for three orientations of the single crystal.

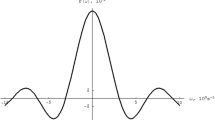
Analysis of the spectra using the above theory showed that the oscillating part of the FID depends on the observed part of the isotropic exchange dipole–dipole interaction, which is characterized by the parameter $\frac{3}{2} - \alpha$ and describes the spatially uniform collective coherent oscillations of dipoles, for which the polarizations of individual dipoles simultaneously become zero. Figure 1 presents the line shapes calculated at the following parameters: M₂ = 8.08 × 10⁸ s^–2, Т_||d = 20 s, T_||z = 480 s, T_⊥ = 2 s, ω₁ = 10^–6 s^–1, and α = 1.25 at various α.

Fig. 1.

Line shapes in the model substance CaF₂ at α = (1) 1, (2) 1.22, and (3) 1.5.

Figure 1 shows that the line shape F(ω) also varies with increasing α: two extrema or a flat peak, related to the decrease in the exchange DDI, vanishes, and at α = 3/2, the line shape becomes Gaussian.

Currently, the unified theory of spectra [13] is used to study the supramolecular structure of heterogeneous polymer systems (fluoropolymers, chitosan, cellulose) over a wide temperature range [17–19].

2.3 Theory of Solid Echo in a Three-Spin Group

In this work, the SE signal of an isolated group of three spins 1/2 with arbitrary DDI was analytically calculated. The calculation is based on the above symmetries generated by the flip of all the spins about the x axis and the spin exchange.

The SE signal is observed after the spin system is affected by the pulse sequence

$${{\left( {\frac{\pi }{2}} \right)}_{y}} - \tau - {{\left( {\frac{\pi }{2}} \right)}_{x}} - t.$$

The calculated formula for the signal has the form

$$A\left( {\tau ,t} \right) = \frac{{{\text{Tr}}{{{\hat {S}}}^{x}}\left( {\tau ,t} \right){{{\hat {S}}}^{x}}}}{{{\text{Tr}}{{{\left( {{{{\hat {S}}}^{x}}} \right)}}^{2}}}} = \frac{{{\text{Tr}}{{{\hat {S}}}^{x}}\left( {\tau ,t} \right){{{\hat {S}}}^{x}}}}{6},$$

(17)

where

$$\begin{gathered} {{{\hat {S}}}^{x}}\left( {\tau ,t} \right) = \exp \left( { - i\hat {H}_{d}^{z}t} \right)\exp \left( { - i\frac{\pi }{2}{{{\hat {S}}}^{x}}} \right) \\ \times \,\,\exp \left( { - i\hat {H}_{d}^{z}\tau } \right){{{\hat {S}}}^{x}}\exp \left( {i\hat {H}_{d}^{z}\tau } \right)\exp \left( {i\frac{\pi }{2}{{{\hat {S}}}^{x}}} \right)\exp \left( {i\hat {H}_{d}^{z}t} \right). \\ \end{gathered} $$

In the subspaces R_ea and ${{R}_{{{\text{oa}}}}}{\text{,}}\,\,{\text{Tr}}{{\hat {S}}^{x}}(t){{\hat {S}}^{x}} = 1{\text{/}}4;$ consequently, in them, time-constant identical signals form:

$${{A}_{{ea}}}\left( {t,\tau } \right) = {{A}_{{oa}}}\left( {t,\tau } \right) = \frac{1}{4} \cdot \frac{1}{6} = \frac{1}{{24}}.$$

Then the contribution of these subspaces to the signal is A_a(t, τ) = 1/12.

For convenience of calculations, the momentum operators in the subspaces ${{R}_{{es}}}$ and ${{R}_{{os}}}$ were replaced respectively by

$$\begin{gathered} {{{\hat {P}}}_{e}}{{{\hat {P}}}_{s}}\exp \left\{ {i\frac{\pi }{2}\left( {{{{\hat {S}}}^{x}} - \frac{3}{2}} \right)} \right\}\,\,\,\,{\text{and}} \\ {{{\hat {P}}}_{o}}{{{\hat {P}}}_{s}}\exp \left\{ {i\frac{\pi }{2}\left( {{{{\hat {S}}}^{x}} - \frac{1}{2}} \right)} \right\}. \\ \end{gathered} $$

The eigenvalues of operator ${{\hat {S}}^{x}}$ in the subspace ${{R}_{{es}}}$ are $\left( {\frac{3}{2}, - \frac{1}{2}, - \frac{1}{2}} \right),$ and those of the momentum operator ${{\hat {P}}_{e}}{{\hat {P}}_{s}}\exp \left\{ {i\frac{\pi }{2}\left( {{{{\hat {S}}}^{x}} - \frac{3}{2}} \right)} \right\}$ are $\left( {1, - 1, - 1} \right).$ Consequently,

$${{\hat {P}}_{e}}{{\hat {P}}_{s}}\exp \left[ {i\frac{\pi }{2}\left( {{{{\hat {S}}}^{x}} - \frac{3}{2}} \right)} \right] = {{\hat {P}}_{e}}{{\hat {P}}_{s}}\left( {{{{\hat {S}}}^{x}} - \frac{1}{2}} \right).$$

Similarly, in the subspace ${{R}_{{os}}}$, we obtain

$${{\hat {P}}_{o}}{{\hat {P}}_{s}}\exp \left[ {i\frac{\pi }{2}\left( {{{{\hat {S}}}^{x}} - \frac{1}{2}} \right)} \right] = {{\hat {P}}_{o}}{{\hat {P}}_{s}}\left( {{{{\hat {S}}}^{x}} + \frac{1}{2}} \right).$$

Then the matrices of the momentum operators in the subspaces R_es and R_os have the respective forms

$$\begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2}\left( {\begin{array}{*{20}{c}} { - 1}&{\sqrt 3 \cos \frac{\beta }{2}}&{ - \sqrt 3 \sin \frac{\beta }{2}} \\ {\sqrt 3 \cos \frac{\beta }{2}}&{3{{{\cos }}^{2}}\frac{\beta }{2} - 2}&{ - \frac{3}{2}\sin \beta } \\ { - \sqrt 3 \sin \frac{\beta }{2}}&{ - \frac{3}{2}\sin \beta }&{3{{{\sin }}^{2}}\frac{\beta }{2} - 2} \end{array}} \right) \hfill \\ {\text{and}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2}\left( {\begin{array}{*{20}{c}} {2 - 3{{{\sin }}^{2}}\frac{\beta }{2}}&{\frac{3}{2}\sin \beta }&{ - \sqrt 3 \sin \frac{\beta }{2}} \\ {\frac{3}{2}\sin \beta }&{2 - 3{{{\cos }}^{2}}\frac{\beta }{2}}&{\sqrt 3 \cos \frac{\beta }{2}} \\ { - \sqrt 3 \sin \frac{\beta }{2}}&{\sqrt 3 \cos \frac{\beta }{2}}&1 \end{array}} \right). \hfill \\ \end{gathered} $$

(18)

The calculations for the spin systems with arbitrary DDI constants gave the following formula for the formation of the solid echo signal A₂ (τ, t):

$$\begin{gathered} {\text{ }}{{A}_{{\text{2}}}}(\tau ,t) = \frac{1}{{64}}\left( {27{{{\cos }}^{4}}\beta - 18{{{\cos }}^{2}}\beta + 7} \right) \\ + \,\,\frac{3}{{32}}\left( {{{{\cos }}^{2}}\beta + 2\cos \beta + 1} \right)\cos {{\omega }_{{12}}}\left( {t - \tau } \right) \\ + \frac{3}{{32}}\left( {{{{\cos }}^{2}}\beta - 2\cos \beta + 1} \right)\cos {{\omega }_{{13}}}\left( {t - \tau } \right) \\ + \,\,\frac{{27}}{{128}}\left( {{{{\cos }}^{4}}\beta - 2{{{\cos }}^{2}}\beta + 1} \right)\cos {{\omega }_{{23}}}\left( {t - \tau } \right) \\ + \,\,\frac{1}{{32}}\left( { - 3{{{\cos }}^{2}}\beta - 2\cos \beta + 1} \right)\cos {{\omega }_{{12}}}\left( {t + \tau } \right) \\ + \,\,\frac{1}{{32}}\left( { - 3{{{\cos }}^{2}}\beta + 2\cos \beta + 1} \right)\cos {{\omega }_{{13}}}\left( {t + \tau } \right) \\ + \,\,\frac{3}{{128}}\left( {9{{{\cos }}^{4}}\beta - 10{{{\cos }}^{2}}\beta + 1} \right)\cos {{\omega }_{{23}}}\left( {t + \tau } \right) \\ + \,\,\frac{1}{{32}}\left( {9{{{\cos }}^{3}}\beta + 3{{{\cos }}^{2}}\beta - 5\cos \beta + 1} \right) \\ \end{gathered} $$

$$\begin{gathered} \times \,\,\left( {\cos {{\omega }_{{12}}}t + \cos {{\omega }_{{12}}}\tau } \right) + \frac{1}{{32}} \\ \times \,\,\left( { - 9{{{\cos }}^{3}}\beta + 3{{{\cos }}^{2}}\beta + 5\cos \beta + 1} \right) \\ \times \,\,\left( {\cos {{\omega }_{{13}}}t + \cos {{\omega }_{{13}}}\tau } \right) + \frac{3}{{64}} \\ \times \,\,\left( { - 9{{{\cos }}^{4}}\beta + 10{{{\cos }}^{2}}\beta - 1} \right)\left( {\cos {{\omega }_{{23}}}t + \cos {{\omega }_{{23}}}\tau } \right) \\ + \,\,\frac{3}{{32}}\left( { - {{{\cos }}^{2}}\beta + 1} \right)\left[ {\cos \left( {{{\omega }_{{12}}}t - {{\omega }_{{13}}}\tau } \right)} \right. \\ \left. { + \,\,\cos \left( {{{\omega }_{{13}}}t - {{\omega }_{{12}}}\tau } \right)} \right] + \frac{3}{{64}} \\ \times \,\,\left( { - 3{{{\cos }}^{3}}\beta + {{{\cos }}^{2}}\beta + 3\cos \beta - 1} \right) \\ \times \,\,\left[ {\cos \left( {{{\omega }_{{12}}}t - {{\omega }_{{23}}}\tau } \right) + \cos \left( {{{\omega }_{{23}}}t - {{\omega }_{{12}}}\tau } \right)} \right] \\ \end{gathered} $$

(19)

$$\begin{gathered} + \,\,\frac{9}{{64}}\left( {{{{\cos }}^{3}}\beta - {{{\cos }}^{2}}\beta - \cos \beta + 1} \right) \\ \times \,\,\left[ {\cos \left( {{{\omega }_{{13}}}t - {{\omega }_{{23}}}\tau } \right) + \cos \left( {{{\omega }_{{23}}}t - {{\omega }_{{13}}}\tau } \right)} \right] \\ + \,\,\frac{3}{{32}}\left( {{{{\cos }}^{2}}\beta - 1} \right)\left[ {\cos \left( {{{\omega }_{{12}}}t + {{\omega }_{{13}}}\tau } \right)} \right. \\ \left. { + \,\,\cos \left( {{{\omega }_{{13}}}t + {{\omega }_{{12}}}\tau } \right)} \right] + \frac{9}{{64}} \\ \times \,\,\left( { - {{{\cos }}^{3}}\beta - {{{\cos }}^{2}}\beta + \cos \beta + 1} \right) \\ \times \,\,\left[ {\cos \left( {{{\omega }_{{12}}}t + {{\omega }_{{23}}}\tau } \right) + \cos \left( {{{\omega }_{{23}}}t + {{\omega }_{{12}}}\tau } \right)} \right] \\ + \,\,\frac{3}{{64}}\left( {3{{{\cos }}^{3}}\beta + {{{\cos }}^{2}}\beta - 3\cos \beta - 1} \right) \\ \times \,\,\left[ {\cos \left( {{{\omega }_{{13}}}t + {{\omega }_{{23}}}\tau } \right) + \cos \left( {{{\omega }_{{23}}}t + {{\omega }_{{13}}}\tau } \right)} \right]. \\ \end{gathered} $$

It is seen from formula (19) that, at t = τ, there is a solid echo signal.

3 RESULTS AND DISCUSSION

3.1 NMR Line Shape in Substances with Isolated Three-Spin Group

The above theories enable the description of the FID and line shape in solids containing isolated three-spin groups. The expression for the FID of the entire spin system has the form

$$G(t) = {{G}_{3}}(t){{G}_{r}}(t),$$

(20)

where ${{G}_{r}}(t)$ is the FID signal, which is related to the relaxation and diffusion processes in the spin system and is calculated from the general kinetic equation [5]. The line shape is calculated by the Fourier transform:

$$F\left( \omega \right) = \sqrt {\frac{2}{\pi }} \int\limits_0^\infty {G\left( t \right)\cos \left( {\omega t} \right)dt} .$$

(21)

The FID and the line shape were modeled using formula (20) under the strong and weak effect of the environment on the three-spin groups. The strong effect of the neighboring spins was calculated at the second moment of the line shape ${{M}_{{2r}}} = 8 \times {{10}^{8}}\,\,{{{\text{s}}}^{{ - 2}}},$ and their weak effect, at ${{M}_{{2r}}} = 8 \times {{10}^{7}}\,\,{{{\text{s}}}^{{ - 2}}}.$

Figure 2 presents the line shapes with equivalent spins and equal DDI constants ${{b}_{{ij}}} = 4.83 \times {{10}^{4}}\,\,{{{\text{s}}}^{{ - 2}}}$ (curve 1). In this case, to calculate G₃(t) from formula (9), s₁ and s₂ were taken to be $1.45 \times {{10}^{5}}\,\,{\text{s}}$ and $7 \times {{10}^{9}}\,\,{{{\text{s}}}^{2}}$ , respectively. At such values of s₁ and s₂, as follows from formula (3), $\cos {\kern 1pt} \beta \approx 1.$Figure 2 also illustrates the results of calculations under the Gaussian broadening (curve 2), as was done previously [1]. In this case, ${{G}_{r}}(t) = \exp \left( {{{ - {{M}_{{2r}}}{{t}^{2}}} \mathord{\left/ {\vphantom {{ - {{M}_{{2r}}}{{t}^{2}}} 2}} \right. \kern-0em} 2}} \right).$ It is seen from Fig. 2 that the signal F(ω) consists of three lines: in the crystal lattice, the lines are broad with flat peaks; and under the Gaussian broadening, the lines narrow.

Fig. 2.

Line shapes under the strong effect of the environment: (1) as calculated from kinetic equations (13) and (2) under the Gaussian broadening [1].

The modeling of the FID and the line shape at various s₁ and s₂ demonstrated that, in some cases, the central peak can vanish because of the broadening of the neighboring lines. Figure 3 presents the line shape calculated at ${{\sigma }_{1}} = 1.58 \times {{10}^{5}}\,\,{\text{s}},$${{\sigma }_{2}} = 7 \times {{10}^{9}}\,\,{{{\text{s}}}^{2}},$ and $\cos \beta = 2{\text{/}}3.$

Fig. 3.

Line shape in the model substance CaF₂ under the weak effect of the environment and various s₁ and s₂.

Figure 4 presents the line shape calculated at ${{\sigma }_{1}} = 0.$ In this instance, as follows from (3), at least one of the DDI constants is negative: ${{\sigma }_{2}} = - 7 \times {{10}^{9}}\,\,{{{\text{s}}}^{2}},$ and $\cos \beta = 0.$

Fig. 4.

Line shape under the weak effect of the environment and at σ₁ = 0.

The calculations under the weak effect of the environment on the three-spin group showed that the line shape comprises three to seven pronounced peaks, and the central extremum always exists.

The obtained results showed that the observed signals are more conveniently analyzed by line shape. Noteworthily, the existence of the central peak is a necessary sign of the presence of three-spin groups in a substance, and under the weak broadening (Figs. 3, 4), the central peak always exists. However, under the strong broadening, the central peak can vanish, and then at least one of the DDI constants is negative.

3.2 NMR Solid Echo Signals in Substances with an Isolated Three-Spin Group

The signal after the second pulse is the SE signal described by formula (19). The effect A_r(t) of the other spins of the system on the solid echo and the NMR line shape was taken into account by the spin–spin relaxation time Т₂:

$$A\left( t \right) = {{A}_{2}}\left( t \right){{A}_{r}}\left( t \right)$$

(22)

where ${{A}_{r}}(t) = {{e}^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} {{{T}_{2}}}}} \right. \kern-0em} {{{T}_{2}}}}}}}.$ The line shape is found by Fourier cosine transform (21).

Numerical calculations for the SE and the Fourier transforms were made using formulas (19), (21), and (22) at various DDI constants: (1) one DDI constant is negative, τ = 10^–5 s, σ₁ = 0, σ₂ = –7 × 10⁹ s^–2, cos β = 0, T₂ = 10^–5 s (Figs. 5, 6); (2) one DDI constant is zero, τ = 10^–5 s, σ₁ = 1.45 × 10⁵ s, σ₂ = 0, cos β = 1/3, T₂ = 10^–5 s (Fig. 7).

Fig. 5.

Solid echo after the second π/2 pulse at σ₁ = 0.

Fig. 6.

Fourier transform of the solid echo at σ₁ = 0.

Fig. 7.

Fourier transform of the solid echo at σ₂ = 0.

The calculations under the weak effect of the environment on the three-spin group showed that the echo signal shifts to the left from $2{\tau },$ which suggests a significant effect of the environment. The line shape contains two peaks, extending to negative values, and the central extremum. Note that the existence of the central extremum is a necessary sign of the presence of three-spin groups in a substance, and under the weak effect of the environment, the central peak always exists [4].

4 CONCLUSIONS

The modeling of the signals of FID, line shape, and solid echo in solids demonstrated the effect of isolated three-spin groups on the observed signals at various values of the DDI constants. This makes it possible to estimate the dipole–dipole interaction constants ${{b}_{{ij}}}\,\,(i,j = 1,2,3),$ compare calculated and experimental data, and obtain information on the position (orientation) of three-spin groups in the substance under investigation. The SE calculation method proposed in this work is applicable to calculating the primary and stimulated echoes and investigating the effect of three-spin groups on the molecular mobility and diffusion in polymer networks [20–22].