RETRACTED ARTICLE: Study of Mass Spectra and Decay Properties of D Meson in a Relativistic Independent Quark Model

Abstract

We compute the S-wave$~D(c\bar {s})$ meson spectra using the independent quark model of scalar plus vector with square root potential model. The calculated states in S-wave, 1³S₁(2009.14), 1¹S₀(1865.96), 2³S₁(2607.19), 2¹S₀(2536.73), 3³S₁(3215.43), 3¹S₀(3189.12), 4³S₁(3552), 4¹S₀(3492) are closely matching with experimental data of the BABAR collaboration. According to this relativistic Dirac formalism, radiative decay and pseudoscalar decay constant (${{f}_{{\text{p}}}} = 204.26{\text{ MeV }}$) of D meson is nearly identical to the theoretical, lattice, and experimental results. We get results for leptonic decay width and branch ratio of D meson more consistent with experimental and theoretical data calculated. The computed Cabibbo-favored mesonic decay width and a branching fraction BF $({{D}^{0}} \to {{K}^{ - }}{{\pi }^{ + }})$, and BF ${{({{D}^{0}} \to {{K}^{ + }}{{\pi }^{ - }})}^{{''}}}i$ is also in excellent agreement with experimental data obtained by CLEO collaboration in the respective experiments. We compute the necessary mesonic form factors using our developed independent confined quark model over the entire kinematical range of momentum transfer. Further, we calculate branching fractions for semileptonic decays (${{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}~{\kern 1pt} ,$ ${{D}^{0}} \to {{K}^{ - }}{{\mu }^{ + }}{{\nu }_{{\mu ~}}},$ ${{D}^{0}}{{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}},~\,\,{\text{and}}\,\,~{{D}^{0}} \to {{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})$ and their ratios, which demonstrate excellent agreement with the available experimental data (BESIII), are provided. BABAR and BELLE collaboration results are matching closely to our computed hybrid parameters$~~{{x}_{q}}{{\;}}$ (4.95 × 10^–3), ${{y}_{q}}$ (6.47 ×10^–3) and ${{R}_{{\text{M}}}}{{\;}}$ (3.317 × 10^–5) of $~{{D}^{0}} - {{\bar {D}}^{0}}~$ Meson oscillations.

1 INTRODUCTION

LHCb experiments [1] have found significant D_J resonances in the 2.0 to 4.0 GeV/c² range, where many are usually excited D meson, although somewhat few are unnatural [1]. To make unconventional representations of $~q\bar {Q}~$ excitations [2] are essential and sufficient to the exotic feasible usual definition [3, 4]. Yet more research is also needed to clarify the latest experimental results relating to such open-charm states satisfactorily. In addition to exotic problems, several states are often admixtures of the adjacent natural states. Findings like D(2550) [5], D(2610) [5], D(2640) [6], D(2760) [5], and other recent resonances have also provided rise to substantial concern in the spectroscopy of many D_J, D_S mesons. Although being a two-flavored hadron ($c,\bar {u},\bar {d}$), this analysis of the D meson is fundamental. Their decay appears to reduce in strong interactions. Therefore, such resonance states allow one to investigate electromagnetic and weak interactions inside a research lab. D meson’s ground states and excited states have been measured experimentally [2] and theoretically [7–11]. Although LQCD and QSR are very accurate, there are hardly any forecasts for the exciting open flavor mesons in the heavy sector.

Nevertheless, the latest results obtained in excited D states are partly incomplete and require further study of its decay properties. To properly extract the quark hybrid parameters and analyze non-leptonic decays and CP-violating effects, it is crucial to understand heavy mesons’ weak transition form factors. The QCD Sum rule (QSR) [12–16] is a non-perturbational method of assessing hadron characteristics using a quark currents correlator over a physical vacuum (OPE).

LQCD [17–19] often represents a non-perturbative method to minimize the mathematically intractable path integrals of the continuum theory rather complex computational calculation using a discrete set of lattice points. QSR (QCD sum rules) is suitable for form factor explanation of low q² region; the lattice QCD provides robust predictions of high q². However, QCD and LQCD fail to explain the form factors and various decay channel relations fully. Different potential models with specific confinement are employed to get a complete picture of form factors and various decay channel relations.

Any effort to explain these newly discovered states is, therefore, necessary if we are to understand the light-quark/anti-quark dynamics in $~{{q\bar {Q}} \mathord{\left/ {\vphantom {{q\bar {Q}} {\bar {q}Q}}} \right. \kern-0em} {\bar {q}Q}}$ bound states. Thus, valuable knowledge regarding quark/anti-quark interactions and QCD behaves inside the double-open flavored mesonic structure is intended for the efficient theoretical model. In contrast, there are numerous theoretical models [7–9] for studying the properties of the hadrons according to their quark structures. Forecasts for ground states and excited states are differed by 60 to 90 MeV. Furthermore, the mesonic state hyperfine and fine structure splitting and their complex relationship with constituent quark masses and the functional strong coupling constant remain unsolved. However, the validity of the non-relativistic model for the classification of a heavy meson is well known and proven, and there are discrepancies in the description of mesons confining light $q\bar {Q}~$ system.

To explain these states successfully, mass spectra accurately predicted and forecasted their decay properties. Like radiative and higher-order QCD corrections, some models have added extra contributions to help indicate the decay widths of mesons [20–23]. In this article, we study the mass spectra, radiative decays, leptonic decay, mesonic decays, semileptonic decays, and $D - \bar {D},~~$ oscillation parameters of D‑meson, within this framework of confinement square root potential model. Earlier, we investigated mass spectra, decay properties of baryons and meson in this framework with square-root confinement potential [24].

In addition to the mass spectra, in the form of several QCD-motivated approximations, pseudoscalar decay constants of the light mesons have also been calculated. Multiple values are using to predict these techniques [25, 26]. Additionally, it is critical to make a precise estimation of the decay constant. However, this is an essential consideration in many weak processes that includes quark mixing, CP violation, etc. Via the exchange of virtual ${{W}^{ \pm }}~$ Bosons, the leptonic decay of charge meson, is yet another effective annihilation channel. The appearance of highly energetic lepton in final states gives this annihilation process a distinct laboratory signature, despite its rarity. The leptonic decay of mesons necessitates a proper representation of the decaying vector meson’s initial state based on constituent quarks and anti-quarks, as well as their corresponding momenta and spins. However, the magnitude of the constituent quark and anti-quark momentum distributions inside the meson is determined only before the constituent quark, and anti-quark annihilate to form a lepton pair. Within the meson, the bound constituent quark and anti-quark are in specific energy states with no definite momenta. Mainly, as a result, computing the leptonic branching fraction and comparing our results to experimental values and a projection based on other models is a good idea.

2 POTENTIAL COMPATIBILITY MODELS

We consider that the non-perturbative multi-gluon mechanism confines quarks inside mesons. This mechanism is hard to ascertain the theoretical first principle of QCD. It obvious, the quark structure of hadron is encouraged in many experiments. That would be the basis of phenomenological approaches, which are developing to explain the characteristics and quark dynamics of hadrons at the mesonic scale. We take “the first approximation for the confining part of the interaction which provides the zeroth-order quark dynamics within the meson via the quark Lagrangian density” as

$$\mathcal{L}_{q}^{{0{{\;}}}}(x) = {{\bar {\psi }}_{q}}\left( x \right)\left[ {\frac{i}{2}{{\gamma }^{{{\mu }}}}\overrightarrow {\partial {{\mu }}} - {{U}_{q}}\left( r \right) - {{m}_{q}}} \right]{{\psi }_{q}}\left( x \right).$$

(2.1)

In the current analysis, we consider that the constituent quark and anti-quark within a meson is independently confined potential of the form [24, 27, 28]

$$\begin{gathered} {{U}_{q}}\left( r \right) = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}(1 + {{\gamma }_{0}})U\left( r \right) \\ {\text{and}}\,\,U\left( r \right) = ({{a}^{{3/2}}}{{r}^{{1/2}}} + {{U}_{0}})\,\,a > 0. \\ \end{gathered} $$

(2.2)

The potential parameters in this equation are $a,{{U}_{0}}~$ which indicate the dynamics of the quark inside the meson.

The radial part of the quark wave function ${{\psi }_{q}}\left( {\vec {r}} \right)$ solves the Dirac equation in the stationary case written by

$$\left[ {{{\gamma }^{0}}{{E}_{q}} - \vec {\gamma }\vec {P} - {{m}_{q}} - {{U}_{q}}\left( r \right)} \right]{{\psi }_{q}}\left( {\vec {r}} \right) = 0,$$

(2.3)

where it would be possible to write the normalized quark wave function in two-component form as

$${{\psi }_{{nlj}}}\left( r \right) = \left( {\begin{array}{*{20}{c}} {\psi _{{nlj}}^{{\left( + \right)}}} \\ {\psi _{{nlj}}^{{\left( - \right)}}} \end{array}} \right),$$

(2.4)

where $\psi _{{nlj}}^{{\left( + \right)}}\left( r \right) = {{N}_{{nlj}}}\left( {\begin{array}{*{20}{c}} {{{ig(r)} \mathord{\left/ {\vphantom {{ig(r)} r}} \right. \kern-0em} r}} \\ {{{\left( {\sigma \hat {r}} \right)f(r)} \mathord{\left/ {\vphantom {{\left( {\sigma \hat {r}} \right)f(r)} r}} \right. \kern-0em} r}} \end{array}} \right){{y}_{{ljm}}}(\hat {r})$ and $\psi _{{nlj}}^{{\left( - \right)}}\left( r \right) =$ ${{N}_{{nlj}}}\left( {\begin{array}{*{20}{c}} {{{i\left( {\sigma \hat {r}} \right)f(r)} \mathord{\left/ {\vphantom {{i\left( {\sigma \hat {r}} \right)f(r)} r}} \right. \kern-0em} r}} \\ {{{g(r)} \mathord{\left/ {\vphantom {{g(r)} r}} \right. \kern-0em} r}} \end{array}} \right){{( - 1)}^{{j + {{m}_{j}} - l}}}{{y}_{{ljm}}}(\hat {r})$ and ${{N}_{q}}$ is a normalization constant that obtained as quickly as

$$N_{q}^{2} = \frac{{5\left( {{{E}_{q}} + {{m}_{q}}} \right)}}{{\left( {6{{E}_{q}} + 4{{m}_{q}} - 2{{U}_{0}}} \right)}}.$$

(2.5)

The normalized spin angular component represented as

$${{y}_{{ljm}}}(\hat {r}) = \sum\limits_{{{m}_{l}},{{m}_{s}}} {\left\langle {\left. {l,{{m}_{l}},\frac{1}{2},{{m}_{s}}} \right|j,{{m}_{j}}} \right\rangle } Y_{l}^{{{{m}_{l}}}}\chi _{{\frac{1}{2}}}^{{{{m}_{s}}}}.$$

(2.6)

The eigenfunctions of the spin operator, $~{{\chi }_{{\frac{1}{2}{{m}_{s}}}}}$ is defined as

$${{\chi }_{{\frac{1}{2}\frac{1}{2}}}} = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)~{\kern 1pt} ,~\,\,\,\,~{{\chi }_{{\frac{1}{2} - \frac{1}{2}}}} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right).$$

(2.7)

Here Dirac spinor is $~{{\psi }_{{nlj}}}\left( {\vec {r}} \right)~$ whose upper component and lower component are $g(r)$ and $f(r)$ respectively

$$\begin{gathered} \frac{{{{d}^{2}}{{g}_{{nlj}}}(r)}}{{d{{r}^{2}}}} \\ + \,\,\left[ {\left( {{{E}_{D}} + {{m}_{q}}} \right)\left[ {{{E}_{D}} - {{m}_{q}} - U(r)} \right] - \frac{{k\left( {k + 1} \right)}}{{{{r}^{2}}}}} \right] \\ \times \,\,g(r) = 0, \\ \end{gathered} $$

(2.8)

$$\begin{gathered} {\text{and}}\,\,\,\,\frac{{{{d}^{2}}{{f}_{{nlj}}}\left( r \right)}}{{d{{r}^{2}}}} + \left[ {\left( {{{E}_{D}} + {{m}_{q}}} \right)} \right. \times \\ \times \,\,\left. {\left[ {{{E}_{D}} - {{m}_{q}} - U\left( r \right)} \right] - \frac{{k\left( {k - 1} \right)}}{{{{r}^{2}}}}} \right]f\left( r \right) = 0. \\ \end{gathered} $$

(2.9)

It is now possible to convert Eqs. (2.8) and (2.9) into a convenient dimensionless form [28] taking ${{\rho }}$ = (r/r_0q) as

$${{r}_{{0q}}} = {{\left[ {2{{\lambda }_{q}}{{a}^{{\frac{3}{2}}}}} \right]}^{{\frac{{ - 2}}{5}}}},$$

(2.9)

$$\frac{{{{d}^{2}}g\left( \rho \right)}}{{d{{{{\rho }}}^{2}}}} + ({{\epsilon }_{q}} - {{\rho }^{{\frac{1}{2}}}}){{g}_{q}}\left( \rho \right) = 0,$$

(2.10)

$$\frac{{{{d}^{2}}f\left( \rho \right)}}{{d{{{{\rho }}}^{2}}}} + ({{\epsilon }_{q}} - {{\rho }^{{\frac{1}{2}}}}){{f}_{q}}\left( \rho \right) = 0,$$

(2.11)

and ${{\epsilon }_{q}}$ is

$${{\epsilon }_{q}} = {{\left( {\frac{{{{\lambda }_{q}}}}{{16{{a}^{6}}}}} \right)}^{{\frac{1}{5}}}}\left( {{{E}_{q}} - {{m}_{q}} - 2{{U}_{0}}} \right).$$

(2.12)

Following the discussion given in our previous work [27, 28], the basic eigenvalue Eqs. (2.10) and (2.11) can be easily solved by yielding $~{{\epsilon }_{q}} = ~\,\,1.8418$. From the eigenvalue Eq. (2.12), we find the ground state energy ${{E}_{q}},$ in zeroth order.

Here k is a quantum number taken as

$$k = \left\{ \begin{gathered} - \left( {\ell + 1} \right) = - \left( {j + \frac{1}{2}} \right)\,\,{\text{for}}\,\,j = \ell + \frac{1}{2} \hfill \\ \ell \,\, = \,\,~ + \left( {j + \frac{1}{2}} \right)\,\,{\text{for}}\,\,j = \ell - \frac{1}{2} \hfill \\ \end{gathered} \right..$$

(2.13)

Equations (2.10) and (2.11) is solved numerically [28] in each of the k options.

Normalized condition for $g~\left( {{\rho }} \right)$ and $f~\left( {{\rho }} \right)$ defined as

$$\mathop \smallint \limits_0^\infty \left( {f_{q}^{2}\left( \rho \right) + g_{q}^{2}\left( \rho \right)} \right)d\rho = 1.$$

(2.14)

Equation (2.5) now be used to create the $D\left( {c\overline {q~} } \right)$ meson wave function and to write down the resultant quark-antiquark mass

$${{M}_{{Q\bar {q}}}}\left( {{{n}_{1}}{{l}_{1}}{{j}_{1}},{{n}_{2}}{{l}_{2}}{{j}_{2}}} \right) = E_{D}^{Q} + E_{D}^{{\bar {q}}},$$

(2.15)

where Eqs. (2.13) and (2.14) were used to find $E_{D}^{{Q/\bar {q}}}$. This $E_{D}^{{Q/\bar {q}}}$, include the centrifugal repulsion of the center of mass. The option (${{j}_{1}},{{j}_{2}})$ are $\left( {\left( {{{l}_{1}} + \frac{1}{2}} \right),\left( {{{l}_{2}} + \frac{1}{2}} \right)} \right)$ and $\left( {\left( {{{l}_{{1,2}}} + \frac{1}{2}} \right),\left( {{{l}_{{1,2}}} - \frac{1}{2}} \right)} \right)$, respectively for spin-triplet (vector) and spin-singlet (pseudoscalar).

Apart from the j–j coupling of the quark-antiquark, previous work [24, 27, 28] is extended in this sense to include the spin–orbit and one-gluon exchange (OGE) interaction [29, 30].$~{{M}_{{2S + {{1}_{{{{L}_{J}}}}}}}}$ is the mass of the each ^{2S + 1}L_J states of the meson shall be written finally

$$\begin{gathered} {{M}_{{2S + {{1}_{{{{L}_{J}}}}}}}} = {{M}_{{Q\bar {q}}}}\left( {{{n}_{1}}{{l}_{1}}{{j}_{1}},{{n}_{2}}{{l}_{2}}{{j}_{3}}} \right) \\ + \,\,\left\langle {U_{{Q\bar {q}}}^{{{{j}_{1}}{{j}_{2}}}}} \right\rangle + \left\langle {U_{{Q\bar {q}}}^{{LS}}} \right\rangle + \left\langle {U_{{Q\bar {q}}}^{T}} \right\rangle . \\ \end{gathered} $$

(2.16)

We establish ${{\sigma }}$ is the j–j coupling constant and described the spin–spin component as,

$$\left\langle {U_{{Q\bar {q}}}^{{{{j}_{1}}{{j}_{2}}}}(r)} \right\rangle = ~\frac{{\sigma \left\langle {{{j}_{1}}{{j}_{2}}JM\left| {{{{\hat {j}}}_{1}} \cdot {{{\hat {j}}}_{2}}} \right|{{j}_{1}}{{j}_{2}}JM} \right\rangle }}{{\left( {{{E}_{Q}} + {{m}_{Q}}} \right) + \left( {{{E}_{{\bar {q}}}} + {{m}_{{\bar {q}}}}} \right)}}.$$

(2.17)

The expectation value $~\left\langle {{{j}_{1}}{{j}_{2}}JM\left| {{{{\hat {j}}}_{1}}{{{\hat {j}}}_{2}}} \right|{{j}_{1}}{{j}_{2}}JM} \right\rangle ,~$ the j‒j coupling constant and the square of CG coefficients are present. We define $~{{S}_{{Q\bar {q}}}} = \left[ {3\left( {{{\sigma }_{Q}} \cdot \hat {r}} \right)\left( {{{\sigma }_{{\bar {q}}}} \cdot \hat {r}} \right) - {{\sigma }_{Q}} \cdot {{\sigma }_{{\bar {q}}}}} \right]~$ and the unit vector in the direction of $\vec {r}$ is $\hat {r} = {{\hat {r}}_{Q}} - {{\hat {r}}_{{\bar {q}}}}$.

The tensor part of one gluon exchange interaction (OGE) [29, 30]

$$\begin{gathered} U_{{Q\bar {q}}}^{T}(r) = - \frac{{{{\alpha }_{s}}}}{4}\frac{{N_{Q}^{2}N_{{\bar {q}}}^{2}}}{{\left( {{{E}_{Q}} + {{m}_{Q}}} \right)\left( {{{E}_{{\bar {q}}}} + {{m}_{{\bar {q}}}}} \right)}} \\ \otimes \,\,{{\lambda }_{q}}{{\lambda }_{{\bar {q}}}}\left( {\left( {\frac{{D_{1}^{{''}}\left( r \right)}}{3} - \frac{{D_{1}^{'}\left( r \right)}}{{3~r}}} \right){{S}_{{Q\bar {q}}}}} \right). \\ \end{gathered} $$

(2.18)

And again define the spin-orbit parts of one gluon exchange interaction (OGE) written as [29, 30]

$$\begin{gathered} U_{{Q\bar {q}}}^{{LS}}\left( r \right) = \frac{{{{\alpha }_{s}}}}{4}\frac{{N_{Q}^{2}N_{{\bar {q}}}^{2}}}{{\left( {{{E}_{Q}} + {{m}_{Q}}} \right)\left( {{{E}_{{\bar {q}}}} + {{m}_{{\bar {q}}}}} \right)}}\frac{{{{\lambda }_{Q}} \cdot {{\lambda }_{{\bar {q}}}}}}{{2~r}} \\ \otimes \,\,\left[ {\left[ {\vec {r} \times \left( {{{{\hat {p}}}_{Q}} - {{{\hat {p}}}_{{\bar {q}}}}} \right)\left( {{{\sigma }_{Q}} + {{\sigma }_{q}}} \right)} \right]\left( {D_{0}^{'}\left( r \right) + 2D_{1}^{'}\left( r \right)} \right)} \right] \\ + \,\,\left[ {\left[ {\vec {r} \times \left( {{{{\hat {p}}}_{Q}} + {{{\hat {p}}}_{q}}} \right)\left( {{{\sigma }_{i}} - {{\sigma }_{j}}} \right)} \right](D_{0}^{{\text{'}}}\left( r \right) - D_{1}^{{\text{'}}}\left( r \right))} \right], \\ \end{gathered} $$

(2.19)

where ${{\alpha }_{s}}$ the strong coupling constant and shall be determined as

$${{\alpha }_{s}} = \frac{{4\pi }}{{\left( {11 - \frac{2}{3}{{n}_{f}}} \right)\log \left( {\frac{{E_{Q}^{2}}}{{\Lambda _{{QCD}}^{2}}}} \right)}}.$$

(2.20)

Through Eq. (2.19) the spin–orbit term is separated into a symmetrical term $\left( {{{\sigma }_{Q}} + {{\sigma }_{q}}} \right)~$ and anti-symmetric term $\left( {{{\sigma }_{Q}} - {{\sigma }_{q}}} \right).~$ With$~{{n}_{f}} = 2 \pm 1$ lattice QCD and Λ_QCD = 0.210 GeV. The confined gluon propagators described as [32, 33]

$$\begin{gathered} {{D}_{0}}\left( r \right) = \left( {\frac{{{{\alpha }_{1}}}}{r} + {{\alpha }_{2}}} \right){\text{exp}}\left( {\frac{{ - {{r}^{2}}c_{0}^{2}}}{2}} \right)~ \\ {\text{and}}~~{{D}_{1}}\left( r \right) = \frac{\gamma }{r}{\text{exp}}\left( {\frac{{ - {{r}^{2}}c_{1}^{2}}}{2}} \right). \\ \end{gathered} $$

(2.21)

Here, $~{{C}_{0}} = 0.1013$ GeV, ${{C}_{1}} = ~$ 0.1533 GeV, $~{{\alpha }_{1}} =$ 0.038, ${{\alpha }_{2}} = ~$ 0.06, $\gamma = 0.0129$. Table 1 lists some of the correct model parameters used in this study. The current 1.29 GeV quark mass-take from PDG (Particle Data Group) [2]. For ground-state, the values of ${{U}^{T}}~$ and ${{U}^{{LS}}}$ found to be zero. Table 2 lists the calculated S-wave masses of D-meson.

Table 1.   The relevant model parameters of the charmed meson (D) systems

Table 2.   S-state ($c\bar {s}$) D meson spectrum (in MeV)

3 RADIATIVE DECAYS OF D-MESON

Using spectroscopic data, we calculate the permissible decay width of radiative decay $~A \to B + \gamma ~$ to have occurred in the D meson between several vectors and pseudoscalar states. Vector meson decay to pseudoscalar $~V \to P\gamma ~$ occurs due to spin-flip, and thus a standard radiative transition. Experimentally, an essential transition in discovering a new state trigger by this transition. The S-matrix elements in the rest frame of the initial meson are expressed in the form, suggesting that these transitions are a single vertex process represented by photon emission from independently confined quark and anti-quark within the meson.

$$\begin{gathered} {{S}_{{BA}}} \\ = \,\left\langle {B\gamma \left| { - ie\int {{{d}^{4}}xT} \left[ {\mathop \sum \limits_q {{e}_{q}}{{{\bar {\psi }}}_{q}}(x){{\gamma }^{\mu }}{{\psi }_{q}}(x){{A}_{\mu }}(x)} \right]} \right|{\kern 1pt} A} \right\rangle . \\ \end{gathered} $$

(3.1)

The photon field ${{A}_{\mu }}\left( x \right)$ is chosen the Coulomb gauge is here, with $\epsilon \left( {k,{{\lambda }}} \right)$ is the polarization vector of the emitted photon with energy-momentum $\left( {{{k}_{0}} = \left| K \right|k} \right)$ of the rest frame A. The quark field operator come up with different expansions in terms of the entire set of positive and negative energy solutions presented by Eq. (2.5), as

$$\begin{gathered} {{\psi }_{q}}\left( x \right) = \sum\limits_\xi {\left[ {{{a}_{{q\xi }}}\psi _{{q\xi }}^{{\left( + \right)}}\left( r \right)} \right.} \\ \times \,\,\left. {\exp \left( { - i{{E}_{{q{{\xi }^{\dag }}}}}} \right) + a_{{q\xi }}^{\dag }\psi _{{q\xi }}^{{\left( - \right)}}\left( r \right)\exp \left( {i{{E}_{{q{{\xi }^{\dag }}}}}} \right)} \right], \\ \end{gathered} $$

(3.2)

q and $~\xi ~$ denote the quark flavor and a set of Dirac quantum numbers, respectively. The quark annihilation and the anti-quark creation operators corresponding to the eigenmodes ξ are $~{{a}_{{q\xi }}}$, $~a_{{q\xi }}^{\dag }{{\;}}$. S-matrix elements can be represented by following [35–37]

$${{S}_{BA}}=~i\sqrt{\left( \frac{\alpha }{k} \right)}{\kern 1pt} \delta \left( {{E}_{B}}+k-{{E}_{A}} \right)\sum\limits_{q,m,m{\kern 1pt} {\kern 1pt} '}{\left\langle B\left| J_{m{\kern 1pt} 'm}^{q}\left( k,\lambda \right)a_{qm{\kern 1pt} '}^{\dagger }{{a}_{qm}}-{\mathop{\overset{\prime }{J}_{m{\kern 1pt} 'm}^{{'\mathop{q}}\,}}}\,\left( k,\lambda \right){\mathop{\overset{\backprime }{a}_{qm{\kern 1pt} '}^{\dagger }}}\,{{\overset{\prime }{\mathop{a}}\,}_{qm}} \right|A \right\rangle }.$$

(3.3)

Here, the possible spin quantum numbers of confined quarks relating to mesons ¹S₀ states are $m$, $~m{\kern 1pt} '$ and E_A = M_A, E_B = $\sqrt {{{k}^{2}} + M_{B}^{2}}$

Now

$$\begin{gathered} J_{{m{\kern 1pt} 'm}}^{q}\left( {k,\lambda } \right) = {{e}_{q}}\int {{{d}^{3}}r} \exp ( - i\vec {k}\vec {r}) \\ \times \,\,\left[ {\vec {\psi }_{{qm{\kern 1pt} '}}^{{\left( + \right)}}\left( r \right)\vec {\gamma }\vec {\epsilon }\left( {k\lambda } \right)\psi _{{qm}}^{{\left( + \right)}}\left( r \right)} \right], \\ \end{gathered} $$

(3.4)

$$\begin{gathered} \tilde {J}_{{mm\,'}}^{{\tilde {q}}}\left( {k,\lambda } \right) = {{e}_{q}}\int {{{d}^{3}}r} {\kern 1pt} {\text{exp(}} - i\vec {k}\vec {r}{\text{)}} \\ \times \,\,\left[ {\vec {\psi }_{{qm}}^{{\left( - \right)}}\left( r \right)\vec {\gamma }\vec {\epsilon }\left( {k\lambda } \right)\psi _{{qm{\kern 1pt} '}}^{{\left( - \right)}}\left( r \right)} \right]. \\ \end{gathered} $$

(3.5)

Equations (3.4) and (3.5) simplified as

$$\begin{gathered} J_{{m{\kern 1pt} 'm}}^{q}\left( {k,\lambda } \right) = - i{{\mu }_{q}}\left( k \right)\left[ {\chi _{m}^{\dag }{\kern 1pt} (\vec {\sigma }\vec {K}){\kern 1pt} {{{{\chi }}}_{m}}} \right] \\ {\text{and}}\,\,\tilde {J}_{{mm{\kern 1pt} '}}^{{\tilde {q}}}\left( {k,\lambda } \right) = i{{\mu }_{q}}\left( k \right)\left[ {\tilde {\chi }_{m}^{\dag }{\kern 1pt} (\vec {\sigma }\vec {K}){{{\tilde {\chi }}}_{m}}} \right], \\ \end{gathered} $$

(3.6)

where $\vec {K} = \vec {k} \times \vec {\epsilon }\left( {k,\lambda } \right)$. Now reduce Eq. (3.3) as

$${{S}_{{BA}}} = ~i\sqrt {\left( {\frac{\alpha }{k}} \right)} ~~\delta \left( {{{E}_{B}} + k - {{E}_{A}}} \right)\sum\limits_{q,m,m{\kern 1pt} '} {\left\langle {B\left| {{{\mu }_{q}}\left( k \right)\left[ {\chi _{{m{\kern 1pt} '}}^{\dag }\vec {\sigma }\vec {K}{{\chi }_{m}}a_{{qm{\kern 1pt} '}}^{\dag }{{a}_{{qm}}} + \tilde {\chi }_{{m{\kern 1pt} '}}^{\dag }\vec {\sigma }\vec {K}{{{\tilde {\chi }}}_{m}}\tilde {a}_{{qm{\kern 1pt} '}}^{\dag }{{{\tilde {a}}}_{{qm}}}} \right]} \right|A~} \right\rangle } ,~$$

(3.7)

where ${{\mu }_{q}}\left( k \right)$ is expressed as

$${{\mu }_{q}}\left( k \right) = \frac{{2{{e}_{q}}}}{k}\int\limits_0^\infty {{{j}_{1}}\left( {kr} \right){{f}_{q}}\left( r \right){{g}_{q}}\left( r \right)dr} .$$

(3.8)

For example, when a vector meson has a radiative decay to its pseudoscalar state $(D^* \to D\gamma )$ for which the spherical Bessel function is ${{j}_{1}}\left( {kr} \right){{\;}}$ and the radiative transition photon energy is defined as

$$k = \frac{{M_{{D^*}}^{2} - M_{D}^{2}}}{{2{{M}_{{D^*}}}}}.$$

(3.9)

The important $~{{M}_{1}}$ transition is denoted by

$$\begin{gathered} {{\mu }_{{{{D}^{ + }}{{D}^{{*~ + }}}}}}\left( k \right) = \frac{1}{3}\left[ {2{{\mu }_{c}}\left( k \right) - {{\mu }_{d}}\left( k \right)} \right] \\ {\text{and}}\,\,{{\mu }_{{{{D}^{0}}{{D}^{{*~0}}}}}}\left( k \right) = \frac{2}{3}\left[ {2{{\mu }_{c}}\left( k \right) + {{\mu }_{u}}\left( k \right)} \right]. \\ \end{gathered} $$

(3.10)

Eventually, it is possible to obtain the radiative decay width of $~D^* \to D\gamma$

$$\begin{gathered} {{\Gamma}_{{D{{~}^{{* + }}} \to {{D}^{ + }}\gamma }}} = \frac{{4\alpha }}{3}{{k}^{3}}{{\left| {{{\mu }_{{{{D}^{ + }}{{D}^{{*~ + }}}}}}\left( k \right)} \right|}^{2}} \\ {\text{and}}\,\,{{\Gamma}_{{{{D}^{{*~0}}} \to {{D}^{0}}\gamma }}} = \frac{{4\alpha }}{3}{{k}^{3}}{{\left| {{{\mu }_{{{{D}^{0}}{{D}^{{*~0}}}}}}\left( k \right)} \right|}^{2}}. \\ \end{gathered} $$

(3.11)

Low lying S-wave states of the determined radiative decay width listed in Table 5 and table show the decay width compared with other model estimates.

Table 3.   Center of mass of neutral charmed meson in MeV

Table 4.    Mass splitting in charmed meson (D) in MeV

Table 5.   Radiative decay of ${{D}^{{*0}}}$ and ${{D}^{{* + }}}$ meson

4 ELECTROMAGNETIC DECAY CONSTANT OF D MESON

In the studies of both leptonic and non-leptonic weak decay processes, the electromagnetic decay constant of a meson is a significant parameter. For example, to obtain the decay constant $\left( {{{f}_{p}}} \right)~$ of a D meson pseudoscalar state, parameterize the weak current matrix elements observed between the corresponding meson and vacuum [38], as below.

$$\left\langle {0\left| {\bar {q}{{\gamma }^{\mu }}{{\gamma }_{5}}c} \right|{{P}_{\mu }}} \right\rangle = i{{f}_{p}}{{P}^{\mu }}.$$

(4.1)

The quark–antiquark eigenmodes are expressed in the form of the respective momentum distribution amplitudes ¹S₀ states of the mesons, and one can describe the eigenmodes $~\psi _{A}^{{\left( + \right)}}$ as being defined in the state of specific momentum p and spin projection $s_{p}^{'}$, taking usual Dirac spinor $~{{V}_{q}}(p,s_{p}^{'})$ could be written as

$$\psi _{A}^{{\left( + \right)}} = \sum\limits_{s_{p}^{'}} {\int {{{d}^{3}}p} } {\kern 1pt} {{G}_{q}}(p,s_{p}^{'})\sqrt {\frac{m}{{{{E}_{p}}}}} {{V}_{q}}(p,s_{p}^{'}){\kern 1pt} {\text{exp}}\left( {i\vec {p} \cdot \vec {r}} \right).$$

(4.2)

The electromagnetic decay constant in the relativistic quark models can indeed be represented in momentum space by the meson wave function ${{G}_{q}}\left( p \right){{\;}}$ [36, 39] and the mass of pseudoscalar meson (M_p)

$${{\;}}{{f}_{p}} = {{\left( {\frac{{3{{{\left| {{{I}_{p}}} \right|}}^{2}}}}{{2{{\pi }^{2}}{{M}_{p}}{{J}_{p}}}}} \right)}^{{\frac{1}{2}}}},$$

(4.3)

where $~{{I}_{p}}\,\,{\text{and}}\,\,{{J}_{p}}{{\;}}$ are expressed as

$$\begin{gathered} {{I}_{p}} = \int\limits_0^\infty {dp{{p}^{2}}} A\left( p \right){{\left[ {{{G}_{{q1}}}\left( p \right)G_{{q2}}^{*}\left( { - p} \right)} \right]}^{{\frac{1}{2}}}} \\ {\text{and}}\,\,{{J}_{p}} = \int\limits_0^\infty {dp{{p}^{2}}} \left[ {{{G}_{{q1}}}\left( p \right)G_{{q2}}^{*}\left( { - p} \right)} \right], \\ \end{gathered} $$

(4.4)

where

$$\begin{gathered} A\left( p \right) = \frac{{\left( {{{E}_{{p1}}} + {{m}_{{q1}}}} \right)\left( {{{E}_{{p2}}} + {{m}_{{q2}}}} \right) - {{p}^{2}}}}{{{{{\left[ {{{E}_{{p1}}}{{E}_{{p2}}}\left( {{{E}_{{p1}}} + {{m}_{{q1}}}} \right)\left( {{{E}_{{p2}}} + {{m}_{{q2}}}} \right)} \right]}}^{{\frac{1}{2}}}}}} \\ {\text{and}}\,\,{{E}_{{pi}}} = \sqrt {k_{i}^{2} + m_{{qi}}^{2}} . \\ \end{gathered} $$

(4.5)

Table 6 lists the calculated electromagnetic decay constant of the D meson from 1S to 4S states. The current results of the 1S state compared to experimental and other model predictions. There is no model prediction for comparing the decay constant of 2S to the 4S States.

Table 6.   Pseudoscalar decay constant (${{f}_{p}})$ of charmed meson (D) system (in MeV)

5 LEPTONIC DECAY OF D-MESON

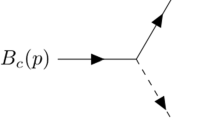
When the quarks and anti-quarks annihilate through a virtual ${{W}^{ \pm }}$ Boson inside a meson, as illustrated in Fig. 1, a charged meson decays into a pair of charged lepton. Despite being among the rarest decay processes [44, 45], open flavor meson decays that employ leptonic decays appear with clear experimental evidence because the meson becomes energetic in the final state leptons. Also, the decay processes are relatively clean [46] because there are no hadrons in the final state. As demonstrated by the equivalence to ${{\pi }^{ + }} \to {{l}^{ + }}\nu$, the leptonic decay width of D meson calculated using the expression [2]

$$\Gamma \left( {D \to {{l}^{ + }}{{\nu }_{l}}} \right) = \frac{{G_{F}^{2}}}{{8\pi }}f_{D}^{2}{{\left| {{{U}_{{cd}}}} \right|}^{2}}m_{l}^{2}{{\left( {1 - \frac{{m_{l}^{2}}}{{M_{D}^{2}}}} \right)}^{2}}{{M}_{D}}.$$

(5.1)

Fig. 1.

Feynman diagram for leptonic decay.

As stated above, the transition of the type is helicity suppressed, which means that the amplitude of the transition is proportional to the mass $\left( {~{{m}_{\ell }}} \right)$) of the lepton $\ell$. Using Eq. (5.1), the estimated results of pseudoscalar decay constant $~{{f}_{D}}$, besides the masses of D meson (M_D) and the particle data group value for ${{U}_{{CD}}} =$ 0.2286, are being used to determine leptonic decay widths of D meson (1¹S₀).

For each of the values of $~{{m}_{{\left( {l = \tau ,\mu ,e} \right)}}}$, the individual lepton channel’s leptonic widths will now calculate. Following that, the branching fraction of these leptonic widths determine as

$${\text{Branching fraction}} = \,\,~\Gamma (D \to {{l}^{ + }}{{\nu }_{l}}) \times \tau ,$$

(5.2)

where the experimental lifetime of D meson state is τ. The measured leptonic widths and the available experimental values are tabulated in Table 7 along with other model predictions. Our findings are basing on experimental values recorded.

Table 7.   The leptonic decay width and leptonic branching fraction (BF) of charmed meson (D)

6 D MESON’S MESONIC DECAY

Flavor changing decays research and development; it is possible to use changing decays of heavy flavor quarks to determine the standard model parameters and phenomenological test models that include strong effects. Due to the impact of the strong interaction and its interaction with weak interaction, the interpretations of the mesonic decay of D meson within mesonic states are complex and challenging. It is possible to understand the mesonic decays of heavy mesons in the present model, and we supposed that Cabibbo-favored mesonic decays continue via the primary process; ($c \to q + u + \bar {d};q \in s,d$) and that decay width is offered by [38]

$$\begin{gathered} \Gamma ({{D}^{0}} \to {{K}^{ - }}{{\pi }^{ + }}) = {{C}_{f}}\frac{{G_{F}^{2}{{{\left| {{{U}_{{cs}}}} \right|}}^{2}}{{{\left| {{{U}_{{ud}}}} \right|}}^{2}}f_{\pi }^{2}}}{{32\pi M_{{{{D}_{s}}}}^{3}}} \\ \times \,\,\left[ {\lambda {{{\left( {M_{D}^{2},M_{{{{K}^{ - }}}}^{2},M_{\pi }^{2}} \right)}}^{{\frac{3}{2}}}}} \right]\left| {f_{ + }^{2}({{q}^{2}})} \right|, \\ \end{gathered} $$

(6.1)

for$~q = s$ and

$$\begin{gathered} \Gamma ({{D}^{0}} \to {{K}^{ + }}{{\pi }^{ - }}) = {{C}_{f}}\frac{{G_{F}^{2}{{{\left| {{{U}_{{cd}}}} \right|}}^{2}}{{{\left| {{{U}_{{us}}}} \right|}}^{2}}f_{\pi }^{2}}}{{32\pi M_{{{{D}_{s}}}}^{3}}} \\ \times \,\,\left[ {\lambda {{{\left( {M_{D}^{2},M_{{{{K}^{ + }}}}^{2},M_{\pi }^{2}} \right)}}^{{\frac{3}{2}}}}} \right]\left| {f_{ + }^{2}({{q}^{2}})} \right|, \\ \end{gathered} $$

(6.2)

for q = d. The color factor is here$~{{C}_{f}}$ and CKM matrices are $\left( {\left| {{{U}_{{cs}}}} \right|.\left| {{{U}_{{cd}}}} \right|.\left| {{{U}_{{us}}}} \right|} \right)$. The ${{f}_{\pi }}{{\;}}$ meson decay constant, and the value of it is considered 0.136 GeV. The factor $\lambda \left( {M_{D}^{2},M_{{{{K}^{ + }}}}^{2},M_{\pi }^{2}} \right){{\;}}$ and the form factor ${{f}_{ + }}({{q}^{2}})$ can be written as

$$\lambda \left( {x,y,z} \right) = {{x}^{2}} + {{y}^{2}} + {{z}^{2}} - xy - yz - zx.$$

(6.3)

As per [38] the coefficient C_A and C_B are expressed as

$${{C}_{A}} = \frac{1}{2}\left( {{{C}_{ + }} + {{C}_{ - }}} \right)\,\,\,\,{\text{and}}\,\,\,{{C}_{B}} = \frac{1}{2}\left( {{{C}_{ + }} - {{C}_{ - }}} \right),$$

(6.4)

where

$$\begin{gathered} {{C}_{ + }} = 1 - \frac{{{{\alpha }_{s}}}}{\pi }\log \left( {\frac{{{{M}_{W}}}}{{{{m}_{c}}}}} \right) \\ {\text{and}}\,\,\,\,{{C}_{ - }} = 1 + 2\frac{{{{\alpha }_{s}}}}{\pi }\log \left( {\frac{{{{M}_{W}}}}{{{{m}_{c}}}}} \right), \\ \end{gathered} $$

(6.5)

where ${{W}^{ \pm }}~$ Boson mass is $~{{M}_{W}}$. Without the interference effect due to QCD, the renormalization color factor is defined as $\left( {C_{A}^{2} + C_{B}^{2}} \right).$ Therefore, the form factors for f (q2) are related to the final D-State of Isgur Wise function [38].

$${{f}_{ \pm }}({{q}^{2}}) = {{\zeta }}\left( w \right)\frac{{{{M}_{D}} \pm {{M}_{\emptyset }}}}{{2\sqrt {{{M}_{D}}{{M}_{\emptyset }}} }}.$$

(6.6)

The IsgurWise function, i.e., ζ (w) be assessed based on the relationship established by

$$\zeta ~\left( w \right) = \frac{2}{{w - 1}}\left\langle {{{j}_{0}}\left( {2{{E}_{q}}\sqrt {\frac{{w - 1}}{{w + 1}}} ~r} \right)} \right\rangle ,$$

(6.7)

where the binding energy of the meson that decays is ${{E}_{q}}~$ and w is given through,

$$w = \frac{{M_{D}^{2} + M_{{({{K}^{ + }},{{K}^{ - }})}}^{2} - {{q}^{2}}}}{{2{{M}_{D}}{{M}_{{({{K}^{ + }},{{K}^{ - }})}}}}}.$$

(6.8)

Because of the form factor ${{f}_{ - }}({{q}^{2}})$, according to a fair assessment, it will not contribute to the decay rate, which we have excluded in this calculation. Due to heavy flavor symmetry, the weak form factor $~{{f}_{ \pm }}({{q}^{2}})$ can be normalized in a model-independent manner at any point $q = \,\,~0~$ or $q = \,\,~{{q}_{{{\text{max}}}}}$, and we have used a value of $~q = ~\,\,{{q}_{{{\text{max}}}}}$ in Eqs. (6.1) and (6.2) for mesonic decay. The branching fraction calculated from the specific Semi leptonic and mesonic decay widths as

$${\text{Branching fraction}} = \Gamma \times \tau .$$

(6.9)

The lifetime of D$\left( \tau \right)$ (${{\tau }_{{{{D}^{ + }}}}}$ = 1.040 ps^–1 and $~{{\tau }_{{{{D}^{0}}}}}$ = 0.410 ps^–1) is considered now as the Particle Data Group’s (PDG-2018) world average value [2]. Decay widths and their branching fractions and the established experimental and other theoretical predictions are stated in Table 8.

Table 8.   The mesonic decay width and branching fraction (BF) of charmed meson (D)

7 BRANCHING FRACTION (BF) FOR SEMI LEPTONIC DECAYS OF D⁰ MESON

We extend our investigation to the calculation of the branching fraction for the semileptonic decay (${{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}~,$ ${{D}^{0}} \to {{K}^{ - }}{{\mu }^{ + }}{{\nu }_{{\mu ~}}},$ ${{D}^{0}}{{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}},~$ and ${{D}^{0}} \to {{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }}~)$ and their ratios R = BF $\left( {{{D}^{0}} \to } \right.$ ${{\left. {{{K}^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }}} \right)} \mathord{\left/ {\vphantom {{\left. {{{K}^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }}} \right)} {{\text{BF(}}{{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}{\text{)}}}}} \right. \kern-0em} {{\text{BF(}}{{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}{\text{)}}}}$, BF $\left( {{{D}^{0}} \to } \right.{{\left. {{{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }}} \right)} \mathord{\left/ {\vphantom {{\left. {{{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }}} \right)} {}}} \right. \kern-0em} {}}$ ${\text{BF}}({{D}^{0}} \to {{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}})$ of the ${{D}^{0}}~$ meson. As the weak and strong effects exhibit differences in semileptonic decay for D meson according to the Standard Model, we use the differential decay rate [83],

$$\frac{{d{{\Gamma }}}}{{d{{q}^{2}}}} = \frac{{{{B}_{{D \to M{{\ell }^{ + }}{{\nu }_{\ell }}}}}}}{{{{\tau }_{{{{D}_{s}}}}}}} = X\frac{{G_{F}^{2}}}{{24{{\pi }^{3}}}}{{\left| {{{V}_{{CS\left( d \right)}}}} \right|}^{2}}\left| {P_{M}^{3}} \right|{{\left| {f_{ + }^{M}({{q}^{2}})} \right|}^{2}},$$

(7.1)

where X is a multiplicative factor due to isospin, which equals to ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$for the decay ${{D}^{ + }} \to {{\pi }^{0}}{{e}^{ + }}{{\nu }_{e}}$ and 1 for the other decays, the Fermi coupling constant, the meson momentum in the D meson rest frame are ${{G}_{F}}$, ${{P}_{M}}~$ respectively and $~f_{ + }^{M}({{q}^{2}})$ is the form factor of mesonic weak current depending on the square of the transferred four-momentum $q = {{P}_{D}} - {{P}_{M}}$. Based on the analysis of the dynamics of Semi leptonic decays, one can obtain the product of $f_{ + }^{M}\left( 0 \right)$ and $\left| {{{V}_{{cd\left( s \right)}}}} \right|$. The form factor $f_{ + }^{M}\left( 0 \right)\left| {{{V}_{{cd\left( s \right)}}}} \right|$ we extract from a fit to the measured partial decay rates in separated ${{q}^{2}}~$ intervals. Our previous work [87] makes it convenient to use a momentum vector for the daughter meson in the rest frame of the parent meson as a starting point. And with the use of the form factors Eq. (6.8), it is simple to calculate the semileptonic decay rates and thus the branching fraction and their ratios R = BF ${{({{D}^{0}} \to {{K}^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} \mathord{\left/ {\vphantom {{({{D}^{0}} \to {{K}^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} {{\text{BF(}}{{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}{\text{)}}~}}} \right. \kern-0em} {{\text{BF(}}{{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}{\text{)}}~}}$, BF $({{D}^{0}} \to$ ${{{{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} \mathord{\left/ {\vphantom {{{{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} {{\text{BF}}({{D}^{0}} \to {{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}})}}} \right. \kern-0em} {{\text{BF}}({{D}^{0}} \to {{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}})}}$ once the form factors have been determined. Our results for the branching fractions and their ratios are consistent with experimental data, and other theoretical calculations are displayed in Table 9.

Table 9.   Branching fractions (BF) for semi-leptonic decays of ${{D}^{0}}$ meson

8 $D - \bar {D}~$ OSCILLATION (HYBRID PARAMETERS)

Several experimental groups have demonstrated scientific proof of ${{D}^{0}} - {{\bar {D}}^{0}}$ oscillations using a distinct ${{D}^{0}}$ decay process [58–62]. Using our spectroscopic parameters for the current study, we bring up the mass oscillation of ${{D}^{0}} - {{\bar {D}}^{0}}$ meson and unified oscillation rate. The weak interaction can mediate the transition process ${{D}^{0}} - {{\bar {D}}^{0}}~$ and ${{\bar {D}}^{0}} - {{D}^{0}}$. If the ${{D}^{0}}$ meson combines with ${{\bar {D}}^{0}}$ meson, then the mass eigenstate be oscillating back and forth between each other. We use the formulae proposed in [2] in the following and say CPT conservation when performing our calculation. The oscillation rates for neutral charmed meson and their anti-particle will vary if CP symmetry is broken, further improving the phenomenology. The discovery of CP violation in neutral charmed meson oscillation could help develop a growing knowledge of previously unknown dynamics beyond the standard model [63‒65].

A neutral charmed meson doublet has an effective two-dimensional Schrodinger equation with a Hamiltonian of [38, 66] describing its time evaluation.

$$i\frac{d}{{dt}}\left( {\frac{{{{D}^{0}}\left( t \right)}}{{{{{\bar {D}}}^{0}}\left( t \right)}}} \right) = \left( {M - \frac{i}{2}\Gamma } \right)\left( {\frac{{{{D}^{0}}\left( t \right)}}{{{{{\bar {D}}}^{0}}\left( t \right)}}} \right),$$

(8.1)

here Hermitian matrices M and Г, we define as

$$\left( {M - \frac{i}{2}\Gamma } \right) = \left[ {\left( {\begin{array}{*{20}{c}} {M_{{11}}^{q}}&{M_{{12}}^{{q*}}} \\ {M_{{12}}^{q}}&{M_{{11}}^{q}} \end{array}} \right) - \frac{i}{2}\left( {\begin{array}{*{20}{c}} {\Gamma _{{11}}^{q}}&{\Gamma _{{12}}^{{q*}}} \\ {\Gamma _{{12}}^{q}}&{\Gamma _{{12}}^{q}} \end{array}} \right)} \right].$$

(8.2)

Invariance of CPT establishes

$${{M}_{{11}}} = {{M}_{{22}}} \equiv M,\,\,\,\,~{{\Gamma }_{{11}}} = {{\Gamma }_{{22}}} \equiv \Gamma .$$

(8.3)

These matrices “off-diagonal elements represent the dispersive and absorptive components of ${{D}^{0}} - {{\bar {D}}^{0}}~$ mixing” [67]. The effective Hamiltonian matrix $\left( {M - \frac{i}{2}\Gamma } \right)$ has two eigenstates denoted by D₁ and D₂

$$\begin{gathered} \left| {{{D}_{1}}} \right\rangle = \frac{1}{{\sqrt {{{{\left| p \right|}}^{2}} + {{{\left| q \right|}}^{2}}} }}\left( {p\left| {{{D}^{0}}} \right\rangle + q\left| {{{{\bar {D}}}^{0}}} \right\rangle } \right) \\ {\text{and}}\,\,\left| {{{D}_{2}}} \right\rangle = \frac{1}{{\sqrt {{{{\left| p \right|}}^{2}} + {{{\left| q \right|}}^{2}}} }}\left( {p\left| {{{D}^{0}}} \right\rangle - q\left| {{{{\bar {D}}}^{0}}} \right\rangle } \right). \\ \end{gathered} $$

(8.4)

Their eigenvalues are as follows

$${{\lambda }_{{{{D}_{1}}}}} = {{m}_{1}} - \frac{i}{2}{{\Gamma }_{1}} = \left( {M - \frac{i}{2}\Gamma } \right) + \frac{q}{p}\left( {{{M}_{{12}}} - \frac{i}{2}{{\Gamma }_{{12}}}} \right),$$

(8.5)

$${{\lambda }_{{{{D}_{2}}}}} = {{m}_{2}} - \frac{i}{2}{{\Gamma }_{2}} = \left( {M - \frac{i}{2}\Gamma } \right) - \frac{q}{p}\left( {{{M}_{{12}}} - \frac{i}{2}{{\Gamma }_{{12}}}} \right)$$

(8.6)

here the mass and width of$~{{D}_{1}}\left( {{{D}_{2}}} \right)$ are, respectively, m₁(m₂₎ and ${{\Gamma }_{1}}\left( {{{\Gamma }_{2}}} \right)$

$$\frac{q}{p} = {{\left( {\frac{{M_{{12}}^{*} - \frac{i}{2}\Gamma _{{12}}^{*}}}{{{{M}_{{12}}} - \frac{i}{2}{{\Gamma }_{{12}}}}}} \right)}^{{\frac{1}{2}}}}$$

(8.7)

variations in mass and width obtain from Eqs. (8.5) and (8.6),

$$\begin{gathered} \Delta m \equiv {{m}_{2}} - {{m}_{1}} = - 2Re\left[ {\frac{q}{p}\left( {{{M}_{{12}}} - \frac{i}{2}{{\Gamma }_{{12}}}} \right)} \right] \\ {\text{and}}\,\,~\Delta \Gamma \equiv {{\Gamma }_{2}} - {{\Gamma }_{1}} = - 2Im\left[ {\frac{q}{p}\left( {{{M}_{{12}}} - \frac{i}{2}{{\Gamma }_{{12}}}} \right)} \right]. \\ \end{gathered} $$

(8.8)

We define ${{G}_{F}},{{m}_{W}},~{{m}_{c}},{{m}_{{{{D}^{0}}}}},{{f}_{{{{D}^{0}}}}}{{\;}}$ and ${{B}_{{{{D}^{0}}}}}{{\;}}$ are the Fermi constant, W boson mass, the mass of c quark, the ${{D}^{0}}{{\;}}$ mass, weak decay constant, and bag parameter, respectively. To calculate the off-diagonal elements of mass and decay matrices, the equation of the dispersive and absorptive parts of the box diagrams represents the current expressions; e.g. ${S \mathord{\left/ {\vphantom {S {\bar {S}}}} \right. \kern-0em} {\bar {S}}}$ as the intermediate quark state [68],

$$\begin{gathered} {{M}_{{12}}} = - \frac{{G_{F}^{2}m_{W}^{2}{{\eta }_{{{{D}^{0}}}}}{{m}_{{{{D}^{0}}}}}{{B}_{{{{D}^{0}}}}}f_{{{{D}^{0}}}}^{2}}}{{12{{\pi }^{2}}}}{{S}_{0}}\left( {\frac{{m_{s}^{2}}}{{m_{W}^{2}}}} \right){{(U_{{us}}^{*}{{U}_{{cs}}})}^{2}} \\ {\text{and}}\,\,{{\Gamma }_{{12}}} = \frac{{G_{F}^{2}m_{c}^{2}\eta _{{{{D}^{0}}}}^{'}{{m}_{{{{D}^{0}}}}}{{B}_{{{{D}^{0}}}}}f_{{{{D}^{0}}}}^{2}}}{{8\pi }}{{S}_{0}}{{(U_{{us}}^{*}{{U}_{{cs}}})}^{2}}. \\ \end{gathered} $$

(8.9)

It is known that the function ${{S}_{0}}\left( {{{x}_{q}}} \right)$ has a very well approximate value of 0.784$x_{q}^{{0.76}}$ [69].$~{{U}_{{ij}}}$ [70] the CKM matrix. The parameters corresponding to gluonic correction are$~{{\eta }_{{{{D}^{0}}~}}}~$ and $\eta _{{{{D}^{0}}}}^{'}$. Box diagrams involving $s$($\bar {s}$), $~d$($\bar {d}$), $~b\left( {\bar {b}} \right)$ intermediate quarks in Fig. (2) are the only non-negligible contributions to ${{M}_{{12}}}$.

Fig. 2.

${{D}^{0}} - {{\bar {D}}^{0}}$ mixing.

The $~{{M}_{{12}}}$ and ${{\;}}{{{{\Gamma }}}_{{12}}}$ fulfill this requirement.

$${{\emptyset }_{M}} - {{\emptyset }_{\Gamma }} = \pi + O\left( {\frac{{m_{c}^{2}}}{{m_{b}^{2}}}} \right),$$

(8.10)

which suggest that the heavy state can have lower decay width than the light state since it is in the$~{{K}^{0}} - {{\bar {K}}^{0}}$ system: ${{\Gamma }_{1}} < {{\Gamma }_{2}}$. Therefore, in the standard model $\Delta \Gamma = {{\Gamma }_{2}} - {{\Gamma }_{1}}$.

In comparison, the quantity

$$\left| {\frac{{{{\Gamma }_{{12}}}}}{{{{M}_{{12}}}}}} \right| \simeq \frac{{3\pi }}{2}\frac{{m_{c}^{2}}}{{m_{W}^{2}}}\frac{1}{{{{S}_{0}}\left( {\frac{{m_{q}^{2}}}{{m_{W}^{2}}}} \right)}}~\sim \,\,~\mathcal{O}\left( {\frac{{m_{q}^{2}}}{{m_{t}^{2}}}} \right)$$

(8.11)

is small with power expansion of gives

$$\begin{gathered} {{\left| {\frac{q}{p}} \right|}^{2}}\,\,{\text{and}}\,\,{{\;}}{{\left| {\frac{q}{p}} \right|}^{2}} \\ = 1 + \left| {\frac{{{{\Gamma }_{{12}}}}}{{{{M}_{{12}}}}}} \right|{\text{sin}}\left( {{{\emptyset }_{M}} - {{\emptyset }_{\Gamma }}} \right) + \mathcal{O}\left( {{{{\left| {\frac{{{{\Gamma }_{{12}}}}}{{{{M}_{{12}}}}}} \right|}}^{2}}} \right). \\ \end{gathered} $$

(8.12)

Consequently, the CP-violating parameter given by Eqs. (8.10) and (8.11)

$$1 - {{\left| {\frac{q}{p}} \right|}^{2}} \simeq Im\left( {\frac{{{{\Gamma }_{{12}}}}}{{{{M}_{{12}}}}}} \right).$$

(8.13)

It is supposed to be very small: for the ${{D}^{0}} - {{\bar {D}}^{0}}~$ the system, it is $\sim ~\mathcal{O}({{10}^{{ - 3}}})$. In approximation, when the CP violation in the mixing ignores, the ${{\Delta \Gamma } \mathord{\left/ {\vphantom {{\Delta \Gamma } {\Delta m}}} \right. \kern-0em} {\Delta m}}$ the ratio is equal to the small value $\left| {\frac{{{{\Gamma }_{{12}}}}}{{{{M}_{{12}}}}}} \right|{{\;}}$ of Eq. (8.11); therefore, it is independent of the CKM matrix elements, that is, same as the system ${{D}^{0}} - {{\bar {D}}^{0}}$.

In theory, the lifetime of meson $\left( {{{\tau }_{{{{D}^{0}}}}}} \right){{\;}}$ is related to ${{\Gamma }_{{11}}}\left( {{{\tau }_{{{{D}^{0}}}}} = \frac{1}{{{{\Gamma }_{{11}}}}}} \right)~$, while ∆m and ∆Г observable are related to ${{M}_{{12}}}{{\;}}$ and ${{\Gamma }_{{12}}}$ as [2]

$$\Delta m = 2\left| {{{M}_{{12}}}} \right|\,\,\,{\text{and}}\,\,\,\Delta \Gamma = 2\left| {{{\Gamma }_{{12}}}} \right|.$$

(8.14)

Various models, such as Wilson’s coefficient and the evolution of Wilson’s coefficient from a new physics scale, provide a basis for gluonic correction [65]. We took the gluonic correction value in [71, 72] (${{\eta }_{{{{D}^{0}}}}}$ = 0.86; $\eta _{{{{D}^{0}}}}^{'}$ = 0.21). ${{B}_{{{{D}^{0}}}}}\left( {{\text{Bag parameter }}} \right)$ = 1.34, is used based on the lattice result [73]; in addition to this, the pseudoscalar mass (${{M}_{{{{D}^{0}}}}}$) and the pseudoscalar decay constant (${{f}_{D}}$) of the meson (D) found we use a relativistic independent square root potential model in our present study. Particle data group [2] shall take values from ${{m}_{s}}$ (0.1 GeV), M_W (80.403 GeV) and CKM matrix elements U_CS(1.006) and U_CS(0.2252). With the new experimental findings, the resulting mass oscillation parameter Δm Table 10 recorded. The integrated rate of oscillation $\left( {{{\chi }_{p}}} \right)$ is the probability to view $\bar {D}$ meson in a jet caused by $\bar {c}$ quark. The main difference is $\Delta {{m}_{D}}{{\;}}$, the measure of frequency change from neutral charmed meson into their anti-particles or vice versa. This adjustment is expressing in time-dependent oscillation, or time-integrated rates are associated with di-lepton events with a similar sign “We derive the Time evolution of neutral states from the pure $\left| {D_{{{\text{phy}}}}^{0}} \right\rangle ~\,\,{\text{or}}\,\,~\left| {\bar {D}_{{{\text{phy}}}}^{0}} \right\rangle$” states at t = 0 as

$$\begin{gathered} \left| {D_{{phy}}^{0}(t)} \right\rangle = {{g}_{ + }}(t)\left| {{{D}^{0}}} \right\rangle + \frac{q}{p}{{g}_{ - }}(t)\left| {{{{\bar {D}}}^{0}}} \right\rangle \\ {\text{and}}\,\,\left| {\bar {D}_{{phy}}^{0}\left( t \right)} \right\rangle = {{g}_{ + }}(t)\left| {{{{\bar {D}}}^{0}}} \right\rangle + \frac{q}{p}{{g}_{ - }}(t)\left| {{{D}^{0}}} \right\rangle \\ \end{gathered} $$

(8.15)

this means that the flavor states said to remain the same (${{g}_{ + }}$), or oscillate with each other (${{g}_{ - }}$), and the probability time-independent proportion to

$$\begin{gathered} {{g}_{ + }}(t) = {{e}^{{\frac{{ - \Gamma t}}{2}}}}{{e}^{{ - i~t~{{m}_{{{{D}^{0}}}}}}}}\cos \left( {\frac{{t\Delta m}}{2}} \right) \\ {\text{and}}\,\,{{g}_{ - }}(t) = {{e}^{{\frac{{ - \Gamma t}}{2}}}}{{e}^{{ - i~t~{{m}_{{{{D}^{0}}}}}}}}\sin \left( {\frac{{t\Delta m}}{2}} \right). \\ \end{gathered} $$

(8.16)

Table 10.   Hybrid parameters ${{x}_{{q~}}},{{y}_{q}}~,~~{{\chi }_{q}}$ and$~~{{R}_{M}}$ of charmed meson (D)

Starting from t = 0 of pure ${{D}^{0}}$, the probability of getting ${{\bar {D}}^{0}}$ (${{D}^{0}})~$while $t \ne 0~$ is given by ${{\left| {{{g}_{ + }}\left( t \right)} \right|}^{2}}{{\left| {{{g}_{ - }}\left( t \right)} \right|}^{2}}$. Taking $\left| {\frac{q}{p}} \right| = 1$, we find

$${{\left| {{{g}_{ \pm }}\left( t \right)} \right|}^{2}} = \frac{1}{2}{{e}^{{\frac{{ - {{\Gamma }_{{{{D}^{t}}}}}}}{2}}}}\left[ {1 \pm \cos \left( {t\Delta m} \right)} \right].$$

(8.17)

Conversely, the initial purity of the first ${{\bar {D}}^{0}}$ at t = 0, the probability of receiving ${{\bar {D}}^{0}}({{D}^{0}})$ while $t \ne 0~$ is also determined by ${{\left| {{{g}_{ + }}\left( t \right)} \right|}^{2}}{{\left| {{{g}_{ - }}\left( t \right)} \right|}^{2}}$. ${{D}^{{0~}}}$ or $~{{\bar {D}}^{0}}$ oscillation as indicated in Eq. (8.17) provided Δm directly. From t = 0 to t = ∞, Integral ${{\left| {{{g}_{ \pm }}\left( t \right)} \right|}^{2}}$, we find

$$\int\limits_0^\infty {{{{\left| {{{g}_{ \pm }}\left( t \right)} \right|}}^{2}}} dt = \frac{1}{2}\left[ {\frac{1}{\Gamma } \pm \frac{\Gamma }{{{{\Gamma }^{2}} + {{{\left( {\Delta m} \right)}}^{2}}}}} \right],$$

(8.18)

where $\Gamma = {{\Gamma }_{D}} = \frac{{\left( {{{\Gamma }_{1}} + {{\Gamma }_{2}}} \right)}}{2}$. And the average is

$$~{{r}_{0}} = \frac{{{{D}^{0}} \leftrightarrow {{{\bar {D}}}^{0}}}}{{{{D}^{0}} \leftrightarrow {{D}^{0}}}} = \frac{{\int\limits_0^\infty {{{{\left| {{{g}_{ - }}\left( t \right)} \right|}}^{2}}dt} }}{{\int\limits_0^\infty {{{{\left| {{{g}_{ + }}\left( t \right)} \right|}}^{2}}dt} }} = \frac{{{{x}^{2}}}}{{2 + {{x}^{2}}}},$$

(8.19)

where

$$\begin{gathered} ~{{x}_{q}} = x = \frac{{\Delta m}}{\Gamma } = \Delta m~{{\tau }_{D}},~\,\,\,\,{{y}_{q}} = y = \frac{{\Delta \Gamma }}{{2\Gamma }} = \frac{{\Delta \Gamma {{\tau }_{D}}}}{2}, \\ {{\chi }_{q}} = \frac{{x_{q}^{2} + y_{q}^{2}}}{{2\left( {x_{q}^{2} + 1} \right)}} \\ \end{gathered} $$

(8.20)

indicates a change from $~{{D}^{0}}$ to ${{\bar {D}}^{0}}~$ and vice versa. For semileptonic decay [2], we compare the time Integrated mixing rate with the correct sign decay rate.

$$\begin{gathered} ~{{R}_{M}} = \int\limits_0^\infty {r\left( t \right)dt} = \int\limits_0^\infty {{{{\left| {{{g}_{ - }}\left( t \right)} \right|}}^{2}}} {{\left| {\frac{q}{p}} \right|}^{2}}dt \\ {\text{and}}\,\,{{R}_{M}} = \int\limits_0^\infty {\frac{{{{e}^{{ - t}}}}}{4}} ({{x}^{2}} + {{y}^{2}}){{t}^{2}}{{\left| {\frac{q}{p}} \right|}^{2}} \simeq \frac{1}{2}\left( {{{x}^{2}} + {{y}^{2}}} \right). \\ \end{gathered} $$

(8.21)

In a Standard Model, the CP violation in the mixing of D⁰ meson is minor and $~\left| {\frac{q}{p}} \right| \simeq 1$. According to the current measurement of the hybrid parameters $~{{x}_{q}},{{y}_{q}}$ and $~{{\chi }_{q}}$, we use our calculated $\Delta m$ values and the mean lifetime of PDG [2] of a D meson.

9 RESULTS AND DISCUSSION

This paper investigated the S-wave spectrum and decay properties of the D meson using a relativistic independent quark model. Our calculated D meson S‑wave spectrum states agree well with the published PDG data of established states. The computed masses of S-wave spectrum states of D meson 2³S₁ (2607.88 MeV) and 2¹S₀ (2534.40 MeV) are very quite close to the corresponding experimental data of the BABAR collaboration 2608.7 ± 2.4 ± 2.5 MeV [34] and 2539.4 ± 4.5 ± 6.8 MeV [34]. Furthermore, according to values published, some S-wave spectrum excited states of D meson desired results are also perfect [11, 31–33]. Additionally, we have presented the lattice QCD and QCD sum rule simulation data with our computed results in Table 2.

We use this expression because the spin degeneracy is broken mainly in the relativistic independent quark model.

$${{M}_{{CW}}} = \frac{{\sum\limits_J {\left( {2J + 1} \right)} {{M}_{J}}}}{{\sum\limits_J {\left( {2J + 1} \right)} }}$$

to compare the spin average mass. As shown in Table 3, the center of masses is computed from the established values of the S-wave D meson states and then compared to the other model estimates [11, 32] to determine the most accurate spin average. Table 3 also incorporates the various spin-dependent contribution to the measured states that can find in the experiment.

Detail experimental data from the masses of D meson state put the preference of hyperfine and the fine structure interactions used during the research of D meson spectroscopic to the ultimate challenge. For reference, a recent analysis of D meson mass splitting in lattice QCD [LQCD] [40] by the PACS-CS collaboration [40], using 2 ± 1 flavor configurations generated via the Clover–Wilson fermion action, was being mentioned. As shown in Table 4, the current findings are consistent with the experimental data reported [40]. In this Table 4, the recent findings, on average, coincided with experimental results within 10% deviations, whereas the lattice QCD [LQCD] [40] forecast varies by 28%.

To investigate the internal charge structure of hadrons, radiative decays are expecting to help ascertain the mesonic structure of D meson, which the radiative decay will determine. The current radiative decay widths of D meson states, listed in Table 5, are consistent with the model estimation of [42], whereas the upper limit given by PDG [2] is vast. Unfortunately, we cannot locate whatever estimates for the radiative decay widths of excited states that could be used for comparative analysis. As a result, we are only hoping for good experimental confirmation of our prognostication.

Table 6 incorporates the computed pseudoscalar decay constant (${{f}_{P}}$) several other models predicted and experimental data for this D meson. We found that the value of ${{f}_{D}}$(1S) = 204.26 MeV in our current research is very close to the value predicted by other theoretical results for the ground state (1S). The predicted $~{{f}_{D}}$, for the excited S-wave state is observed to increase with energy. However, there are no experimental or theoretical values used as a point of reference.

The leptonic decay widths of the D meson, also investigated in this paper, are another significant particle feature. Over much other theoretical computation, the current branch fraction for ${{D}^{ + }} \to {{\tau }^{ + }}{{\nu }_{\tau }}$ (1.250 $\times {{10}^{{ - 3}}}$) and $~{{D}^{ + }} \to {{\mu }^{ + }}{{\nu }_{\mu }}$ (3.935 $\times {{10}^{{ - 4}}}$) are consistent with experimental findings (<1.2 $\times {{10}^{{ - 2}}}$) and (3.82 $\times {{10}^{{ - 4}}}$) including both in Table 7. Because of the excellent degree of experimental uncertainties in the electron channel, it is difficult to reach any kind of rational conclusion.

Cabibbo favored mesonic branch fraction ${\text{BF}}({{D}^{0}} \to {{K}^{ - }}{{\pi }^{ + }})~$ and $~{\text{BF}}({{D}^{0}} \to {{K}^{ + }}{{\pi }^{ - }})$ computed as 3.91 $\pm$ 0.08% and (1.48 $\pm$ 0.07) $\times {{10}^{{ - 4}}}$, including both, seem to be consistent with the experimental values 3.835% and 1.355 $\times {{10}^{{ - 4}}}{{\;}}$ [57] displayed in Table 8.

The computed branching fractions for semileptonic decays (${{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}~,$ ${{D}^{0}} \to {{K}^{ - }}{{\mu }^{ + }}{{\nu }_{{\mu ~}}},$ ${{D}^{0}} \to {{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}},~$and ${{D}^{0}} \to {{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }}~$) and their ratios R = BF(${{{{D}^{0}} \to {{K}^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} \mathord{\left/ {\vphantom {{{{D}^{0}} \to {{K}^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} {{\text{BF(}}{{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}{\text{)}}}}} \right. \kern-0em} {{\text{BF(}}{{D}^{0}} \to {{K}^{ - }}{{e}^{ + }}{{\nu }_{e}}{\text{)}}}}$, BF $({{D}^{0}} \to$ (${{{{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} \mathord{\left/ {\vphantom {{{{\pi }^{ - }}{{\mu }^{ + }}{{\nu }_{\mu }})} {{\text{BF}}({{D}^{0}} \to {{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}})~}}} \right. \kern-0em} {{\text{BF}}({{D}^{0}} \to {{\pi }^{ - }}{{e}^{ + }}{{\nu }_{e}})~}}$ of the ${{D}^{0}}~$ meson. is reasonable agreement with both theoretical models [78, 79], and experimental data of BESIII [80–82] display in Table 9. Although, our findings have differed slightly from those of BABAR, CLEO, and BESIII. When making all of our predictions, we come up with branching fractions within 10% of experimental data. Additionally, our estimates for branching fraction ratios fully agree with experimental findings, necessary for a future experiment.

We can find the CP violation parameter in mixing $\left| {\frac{q}{p}} \right|$(0.9996), therefore, in this model and the ${{D}^{0}}{{\;}}$ and ${{\bar {D}}^{0}}$ decays do not indicate CP violation, and this offers a much more strict limitation on the hybrid parameters to be determined. As can be seen in Table 10 the hybrid parameters ${{x}_{q}},{{y}_{q}}$, and mixing rate (R_M) in very excellent accordance with BABAR, BELLE, and other collaboration. Nevertheless, because of the more significant uncertainty in the experimental data, we are unable to bring continuous conclusions about $~{{x}_{q}},{{y}_{{q~}}}$, and the mixing rate (R_M). Because of this, the hybrid parameter of ${{D}^{0}} - {{\bar {D}}^{0}}~$ meson oscillation successfully determined in the present study. As a result, the current research attempts to demonstrate spectroscopic (strong interaction) parameters in the weak decay process.

Eventually, we hope to see future experimental evidence and lattice QCD [LQCD] findings for several of our observations about the open charm meson’s excited states and decay properties.