Hypothetical Triangulation of Aerial and Ground Objects by a Group of Aircraft

Abstract

The problem of increasing the accuracy of “covert” route tracking of radio and heat-emitting objects onboard an aircraft (AC) is solved by the suboptimal estimation of their phase coordinates by a multidimensional nonlinear hypothetical filter. The triangulation ranges calculated by the criterion of the minimum discrepancy between the measured bearings of tracked objects received from another AC of the group and the calculated bearings of these objects are fed to the filter’s input.

INTRODUCTION

On board an aircraft (AC), in the presence of radio reconnaissance equipment (RRE), the thermal radiation detection posts of an optical-location station (OLS) and an airborne radar station (ARS) bearing active interference sources, the following measured information on radio and heat-emitting air and ground facilities is covertly available:

the RRE identifier of the object’s radio-electronic system, time of measurement of the signal parameters, measurement of the bearing in the XOZ plane of the related coordinate system (RCS), roll, pitch, and the AC’s direction at the time of the measurement;

the OLS identifier of the object’s thermal radiation, measurement time, measurement of bearings in the RCS, roll, pitch, and direction of the AC at the time of measurement;

and the ARS identifier of the active jammer (AJ), measurement time, and the measured azimuth and elevation angle of the AJ.

Information on the coordinates of emitting airborne objects (AOs) and ground objects (GOs) is incomplete (incomplete instrumentation (II)). The range is not measured, and in the case of RRE, the second bearing in the RCS is also not measured. Comprehensive hypothetical tracking [1, 2] of the radiating AOs and GOs onboard each AC group forms the routes of these objects in two AC coordinate systems: the normal moving coordinate system (NMCS) related to the center of mass of the AC and stabilized in the roll, and the ground coordinate system (GCS) with the origin at a conditional point selected on the AC with geographic coordinates (λ_ut, φ_ut) [2].

All the main tracking processes—capture by the first measurement, association and filtering of all measurements, and the ambiguous extrapolation of phase coordinate estimates—are performed using hypothetical routes. Hypothetical routes provide route support for the AO and GO when there is II.

The following information is given on the radiating AO (Fig. 1):

Fig. 1.

(a) II3, (b) II2 (PR_FK = 0), (c) II2 (PR_FK = 1), (d) CI (PR_FK = 0), (e) CI or II1 (PR_FK = 1).

a numbered shortened bearing and the most likely location of the AO on it when the standard error ϭ_R of the current range R is more than 5%R (ϭ_R > 5%R) and the hemisphere has not yet been determined (II3) (Fig. 1a);

a shortened bearing and the most probable location of the AO on it, indicating the hemisphere when ϭ_R > 5%R and the hemisphere is defined, but the accuracy of the estimate of the velocity vector ϭ_ψ > 5° (II2 with a sign of the formation of the course PR_FK = 0) (Fig. 1b);

a shortened bearing and the most probable location of the tracked object on it with the velocity vector when ϭ_R > 5%R and ϭ_ψ ≤ 5° (II2 with a sign of the formation of the course PR_FK = 1) (Fig. 1c);

the location of the AO with the velocity vector when ϭ_R ≤ 5%R and ϭ_ψ ≤ 5° (II1) or complete instrumentation (CI) (CI with PR_FK = 1) (Fig. 1e); and

the location of the AO, when at the first range measurement PR_FK = 0 (Fig. 1d).

The feature of the instrumentation PR_PO characterizes the type of II: PR_PO = 1 in II1, PR_PO = 2 in II2, and PR_PO = 3 in II3. With CI PR_PO = 0.

The location of the tracked object is indicated by a small circle indicating all current sources of information on this object: ARS, OLS, RRE, and communications complex (CC) (Fig. 2).

Fig. 2.

To indicate the altitude and vertical speed of the tracked AO, it is advisable to enter the onboard logbook button on the remote control, which when pressed, in addition to the number of the tracked object, results in the height being given in hundreds of meters (absolute or relative) and the direction of the vertical speed, which is indicated by an arrow (up or down) (Fig. 3).

Fig. 3.

(a) absolute height 10.1 km, horizontal flight, (b) relative height 2.5 km, descent.

The following information on the radiating GO is output on the indicator (Figs. 1a, 1d):

a numbered shortened bearing and the most probable location of the tracked object on it, when the accuracy of the distance estimate is σ_R > 5%R (II2); and

the location of the tracked object when σ_R ≤ 5%R (II1) or CI.

The accuracy of the route tracking of the radiating AO and GO onboard a single AC depends on the ranges [R_min, R_max] and [V_min, V_max] of the possible values of the initial range and speed, as well as the trajectory of the movement, of the AC itself. In the case of a single AC, in order to improve the accuracy of tracking II2 (II3) objects (transferring them into II1 objects), an informational maneuver and the introduction of a hypothetical II1 route (routes with an initial trial range of R and standard error σ_R ≤ 5%R) are undertaken. The possibility of identifying the hypothetical route II1 depends on the proximity of the trial range to the true range, and the selection time depends on the trajectory of the AC (informational maneuver). The time to achieve accuracy II1 for a single AC is estimated in tens of seconds.

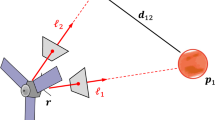
In the AC group, it is possible to significantly reduce the time of the guaranteed achievement of II1 by performing hypothetical triangulation. For the hypothetical triangulation through the channels of the CC between the AC of the group, the following information is exchanged:

the geographical coordinates of the conditional points λ_ut and φ_ut of the AC group;

the AC coordinates and speeds in the GCS;

routes tracked by the AO and GO in the GCS (route support); and

the measured information on the radiating AO and GO and the geographic coordinates of the AC at the time of measurement (measurements).

1. PROBLEM STATEMENT

In the NMCS, the emitting AO is determined by seven phase coordinates: azimuth β, range R, radial speed ${{{v}}_{r}}$, tangential speed ${{{v}}_{t}}$, angular rate of rotation along course ω_ψ, elevation angle ε, and vertical velocity ${{{v}}_{h}}$; and the radiating NO, by three coordinates: β, R, and ε. We denote the phase coordinates of the pth AO as follows: Θ$_{1}^{{(p)}}$ = β^(p), Θ$_{2}^{{(p)}}$ = 1/(R^(p)cosε^(p)), Θ$_{3}^{{(p)}}$= ${v}_{r}^{{(p)}}$, Θ$_{4}^{{(p)}}$= ${v}_{t}^{{(p)}}$, Θ$_{5}^{{(p)}}$= |ω$_{\psi }^{{(p)}}$|, Θ$_{6}^{{(p)}}$= ε^(p), and Θ$_{7}^{{(p)}}$ = |${v}_{h}^{{(p)}}$|; and we denote the coordinates of the qth GO as follows: Θ$_{1}^{{(q)}}$ = β^(q), Θ$_{2}^{{(q)}}$ = 1/(R^(q)cosε^(q)), and Θ$_{6}^{{(p)}}$ = ε^(q).

The equations for pth AO have the form [2]

$$\begin{gathered} \dot {\Theta }_{1}^{{(p)}} = \Theta _{2}^{{(p)}}({{V}_{x}}\sin \Theta _{1}^{{(p)}} + {{V}_{z}}\cos \Theta _{1}^{{(p)}} - \Theta _{4}^{{(p)}}), \\ \dot {\Theta }_{2}^{{(p)}} = \Theta _{2}^{{(p)2}}({{V}_{x}}\cos \Theta _{1}^{{(p)}} - {{V}_{z}}\sin \Theta _{1}^{{(p)}} - \Theta _{3}^{{(p)}}), \\ \end{gathered} $$

$$\begin{gathered} \dot {\Theta }_{3}^{{(p)}} = - \Theta _{4}^{{(p)}}[{{j}_{\psi }}\Theta _{5}^{{(p)}} + \Theta _{2}^{{(p)}}({{V}_{x}}\sin \Theta _{1}^{{(p)}} + {{V}_{z}}\cos \Theta _{1}^{{(p)}} - \Theta _{4}^{{(p)}})], \\ \dot {\Theta }_{4}^{{(p)}} = \Theta _{3}^{{(p)}}[{{j}_{\psi }}\Theta _{5}^{{(p)}} + \Theta _{2}^{{(p)}}({{V}_{x}}\sin \Theta _{1}^{{(p)}} + {{V}_{z}}\cos \Theta _{1}^{{(p)}} - \Theta _{4}^{{(p)}})], \\ \dot {\Theta }_{5}^{{(p)}} = 0; \\ \end{gathered} $$

(1.1)

$$\begin{gathered} \dot {\Theta }_{6}^{{(p)}} = \Theta _{2}^{{(p)}}[( - {{V}_{y}} + {{j}_{h}}\Theta _{7}^{{(p)}})\cos \Theta _{6}^{{(p)}} + ({{V}_{x}}\cos \Theta _{1}^{{(p)}} - {{V}_{z}}\sin \Theta _{1}^{{(p)}} - \Theta _{3}^{{(p)}})\sin \Theta _{6}^{{(p)}}]\Theta _{6}^{{(p)}} \\ + \;({{V}_{x}}\cos \Theta _{1}^{{(p)}} - {{V}_{z}}\sin \Theta _{1}^{{(p)}}){\text{/}}(N(\varphi ) + H), \\ \dot {\Theta }_{7}^{{(p)}} = 0, \\ \end{gathered} $$

where V_x, V_y, and V_z are the vector projections of the AC’s speed in the NMCS, H and φ are the altitude and geographical latitude of the AC’s location, and N(φ) is the length of the normal to a point on the surface of the Earth’s ellipsoid at latitude φ from the OX axis.

The maneuver of the pth AO in terms of its course and altitude is represented by the products of  j_ψΘ$_{5}^{{(p)}}$ and  j_hΘ$_{7}^{{(p)}}$, where

$${{j}_{\psi }} = \left\{ \begin{gathered} -1,{\text{ maneuver to the left on the course}}, \hfill \\ 0,{\text{ no heading maneuver}}, \hfill \\ 1,{\text{ maneuver to the right on the course}}{\text{,}} \hfill \\ \end{gathered} \right.\quad {{j}_{h}} = - \left\{ \begin{gathered} -1,{\text{ decrease}}, \hfill \\ 0,{\text{ no altitude maneuver}}{\text{,}} \hfill \\ 1,{\text{ climb}}{\text{.}} \hfill \\ \end{gathered} \right.$$

Equations for the qth GO have the form

$$\begin{gathered} \dot {\Theta }_{1}^{{(q)}} = \Theta _{2}^{{(q)}}({{V}_{x}}\sin \Theta _{1}^{{(q)}} + {{V}_{z}}\cos \Theta _{1}^{{(q)}}), \\ \dot {\Theta }_{2}^{{(q)}} = \Theta _{2}^{{(q)2}}({{V}_{x}}\cos \Theta _{1}^{{(q)}} - {{V}_{z}}\sin \Theta _{1}^{{(q)}}), \\ \dot {\Theta }_{6}^{{(q)}} = \Theta _{2}^{{(q)}}[ - {{V}_{y}}\cos \Theta _{6}^{{(q)}} + ({{V}_{x}}\cos \Theta _{1}^{{(q)}} - {{V}_{z}}\sin \Theta _{1}^{{(q)}})\sin \Theta _{6}^{{(q)}}]\cos \Theta _{6}^{{(q)}} \\ + \;({{V}_{x}}\cos \Theta _{1}^{{(q)}} - {{V}_{z}}\sin \Theta _{1}^{{(q)}}){\text{/}}(N(\varphi ) + H). \\ \end{gathered} $$

(1.2)

Onboard the nth AC of the group, p_n AO and q_n GO were detected by the RRE, OLS, and ARS equipment; moreover, each of these objects can be detected by different sources of information:

one, by the RRE, OLS or ARS;

two, by the RRE and ARS, RRE and OLS, and ARS and OLS; and

three, by the RRE, ARS, and OLS.

When describing the RRE measurement channel, the formula for calculating the measured azimuth $x_{{1,R}}^{{(p,q)}}$ from the bearing $\varphi _{y}^{{(p,q)}}$ in the RCS and the elevation angle ε^j of the jth hypothetical route, roll γ, pitch υ, and course ψ of the AC is used:

$$x_{{1,R}}^{{(p,q)}} = {\text{arcsin}}({\text{cos}}\varphi _{z}^{j}{\text{cos}}\varphi _{y}^{{(p,q)}}{\text{sin}}\upsilon + {\text{sin}}\varphi _{z}^{j}{\text{cos}}\gamma {\text{cos}}\upsilon + {\text{cos}}\varphi _{z}^{j}{\text{sin}}\varphi _{y}^{{(p,q)}}{\text{sin}}\gamma {\text{cos}}\upsilon ),~$$

where φ$_{z}^{j}$ = 2arctan[(B – $\sqrt {{{A}^{2}} + {{B}^{2}} - \sin {}^{2}{{\varepsilon }^{j}}}$)/(A + sin${{\varepsilon }^{j}}$)], A = cosφ$_{y}^{{(p,q)}}$sinυ + sinφ$_{y}^{{(p,q)}}$sinγcosυ, and B = cosγcosυ.

The RRE measurement channel:

RRE identifier N_R,

attribute of the object (AO or GO),

measurement time t_z and measured azimuth:

$$x_{{1,R}}^{{(p,q)}}({{t}_{z}}) = \Theta _{1}^{{(p,q)}}({{t}_{z}}) + \xi _{{\beta ,R}}^{{(n)}}({{t}_{z}}),~~$$

(1.3)

where the measurement calculation error $\xi _{{\beta ,R}}^{{(n)}}\left( {{{t}_{z}}} \right)$ is an independent Gaussian sequence with zero mean and variance $\sigma _{{\beta ,R}}^{2}$(t_z).

When describing the OLS measurement channel, the formulas for calculating the measured azimuths $x_{{1,O}}^{{(p,q)}}$ and elevation angle $x_{{6,O}}^{{(p,q)}}$ from the bearings $\varphi _{y}^{{(p,q)}}$ and φ$_{z}^{{(p,q)}}$, roll γ, pitch υ, and course ψ of the AC are used:

$$\begin{gathered} ~x_{{6,O}}^{{(p,q)}} = {\text{arcsin}}({\text{cos}}\varphi _{z}^{{(p,q)}}{\text{cos}}\varphi _{y}^{{(p,q)}}{\text{sin}}\upsilon + {\text{sin}}\varphi _{z}^{{(p,q)}}{\text{cos}}\gamma {\text{cos}}\upsilon + {\text{cos}}\varphi _{z}^{{(p,q)}}{\text{sin}}\varphi _{y}^{{(p,q)}}{\text{sin}}\gamma {\text{cos}}\upsilon ),~ \\ x_{{1,O}}^{{(p,q)}} = {\text{arcsin}}\{ -{\text{ }}[{\text{cos}}\varphi _{z}^{{(p,q)}}{\text{sin}}\varphi _{y}^{{(p,q)}}{\text{cos}}\upsilon {\text{sin}}\psi + {\text{sin}}\varphi _{z}^{{(p,q)}}({\text{sin}}\gamma {\text{cos}}\psi -{\text{cos}}\gamma {\text{sin}}\upsilon {\text{sin}}\psi ){\text{ }}~ \\ -\,{\text{cos}}\varphi _{z}^{{(p,q)}}{\text{sin}}\varphi _{y}^{{(p,q)}}({\text{cos}}\gamma {\text{cos}}\psi + {\text{sin}}\gamma {\text{sin}}\upsilon {\text{sin}}\psi )]{\text{ /cos}}x_{{6,O}}^{{(p,q)}}\} . \\ \end{gathered} $$

OLS measurement channel:

OLS identifier N_O,

feature of the object,

measurement time t_z, measured azimuths, and elevation angle:

$$x_{{1,O}}^{{(p,q)}}({{t}_{z}}) = \Theta _{1}^{{(p,q)}}({{t}_{z}}) + \xi _{{\beta ,O}}^{{(p,q)}}({{t}_{z}}),\quad x_{{6,O}}^{{(p,q)}}({{t}_{z}}) = \Theta _{6}^{{(p,q)}}({{t}_{z}}) + \xi _{{\varepsilon ,O}}^{{(n)}}({{t}_{z}}),~$$

(1.4)

where the vector of the measurement calculation errors {ξ$_{{\beta ,O}}^{{(n)}}$(t_z), ξ$_{{\varepsilon ,O}}^{{(n)}}$(t_z)} is an independent Gaussian sequence with zero mathematical expectation and correlation matrix R_O(t_z).

The ARS measurement channel by the AJ:

ARS identifier N_L,

feature of object,

measurement time t_z, measured azimuths, and elevation angle:

$$x_{{1,L}}^{{(p,q)}}({{t}_{z}}) = \Theta _{1}^{{(p,q)}}({{t}_{z}}) + \xi _{{\beta ,L}}^{{(p,q)}}({{t}_{z}}),\quad x_{{6,L}}^{{(p,q)}}({{t}_{z}}) = \Theta _{6}^{{(p,q)}}({{t}_{z}}) + \xi _{{\varepsilon ,L}}^{{(p,q)}}({{t}_{z}}),~$$

(1.5)

where the vector of measurement errors {ξ$_{{\beta ,L}}^{{(n)}}$(t_z), ξ$_{{\varepsilon ,L}}^{{(n)}}$(t_z)} is an independent Gaussian sequence with zero mathematical expectation and correlation matrix ${{R}_{L}}$(t_z).

The solution of the problem of complex hypothetical tracking of the AO p_n and GO q_n with such gauges onboard the nth AC is given in [2]. It is performed by capture, selection, association, filtering, hypothesis management, extrapolation, and output route generation algorithms.

In the capture algorithm based on the RRE measurement, 24 hypothetical velocity routes for the AO (Fig. 4a) and 9 hypothetical routes in terms of the range for the GO (Fig. 4b) are generated.

Fig. 4.

(a) AO RRE or ARS (forward hemisphere (FHS)), (b) GO RRE object.

In the capture algorithm based on the OLS measurement, 10 hypothetical velocity routes are formed for the AO (Fig. 5a) and 5 hypothetical distance routes are formed for the GO (Fig. 5b).

Fig. 5.

(a) AO OLS (FHS, rear hemisphere (RHS)), (b) GO OLS or ARS.

In the capture algorithm based on the ARS measurement, 24 hypothetical velocity routes for the AO (Fig. 4a) and 5 hypothetical routes in terms of the range for the GO (Fig. 5b) are generated.

The azimuth-elevation angle filter F_βε [2] is used as a filtering algorithm for OLS and ARS measurements, and the azimuthal filter F_β is a special case for RRE measurements.

In the problem of hypothetical triangulation under consideration, the presence of a single time system in the AC group is assumed and the following actions must be performed.

1. Determine the composition of the route support transmitted by the AC over the CC that is required to solve the problem of hypothetical triangulation.

2. Determine the composition of the measured information transmitted by the AC over the CC that is required to solve the problem of hypothetical triangulation.

3. Recalculate the route support received from the AC of the group into its own NMCS.

4. Perform an unambiguous identification by the identifiers and coordinates of all recalculated route support received from the AC of the group of II objects with the internal routes of their tracked objects.

5. For each of its identified pth (qth) object, determine three hypothetical routes j₁, j₂, and j₃ according to the criterion of the minimum reduced discrepancy: the discrepancy divided by the number of measured coordinates:

five, azimuth, return range, radial and tangential velocities, and elevation angle for AO with PR_FK = 1;

three, azimuth, return range, elevation angle for the GO and AO with PR_FK = 0:

$${{j}_{1}} = \mathop {\min }\limits_j \overline {\chi _{j}^{2}} ,\quad {{j}_{2}} = \mathop {\min }\limits_{j \ne {{j}_{1}}} \overline {\chi _{j}^{2}} ,\quad {{j}_{3}} = \mathop {\min }\limits_{j \ne {{j}_{1}},{{j}_{2}}} \overline {\chi _{j}^{2}} ,$$

$$\overline {\chi _{j}^{2}} = \frac{1}{5}\sum\limits_{k = \overline {1,4} ,6} {[{{{(x_{k}^{{(p)}}({{t}_{z}}) - m_{k}^{j}({{t}_{z}}))}}^{2}}{\text{/}}(\sigma _{k}^{{(n)2}} + d_{{kk}}^{j})} ]\quad {\text{for}}\,\,{\text{GO}}\,\,{\text{with}}\quad PR\_FK = 1,~$$

(1.6)

$$\overline {\chi _{j}^{2}} = \frac{1}{3}\sum\limits_{k = 1,2,6} {[{{{(x_{k}^{{(p,q)}}({{t}_{z}}) - m_{k}^{j}({{t}_{z}}))}}^{2}}{\text{/}}(\sigma _{k}^{{(n)2}} + d_{{kk}}^{j})} ]\quad {\text{for}}\,\,{\text{AO}}\,\,{\text{with}}\quad PR\_FK = 0;$$

and write down the measurements.

6. Calculate the triangulation range R ^j and its variance $d_{{DD}}^{j}$ for each jth hypothetical route with measurement according to the criterion $\mathop {\min }\limits_{{{D}^{j}}}$${{\Delta }^{j}}$ (or $\mathop {\max }\limits_{{{D}^{j}}}$cos²${{\Delta }^{j}}$), where ${{\Delta }^{j}}$ is the angle between the vector of measured bearings {y₀, y₂, y₄} and bearing vector {${{R}^{j}}{{a}^{j}}$ + m_x0, ${{R}^{j}}{{b}^{j}}$ + m_y0, ${{R}^{j}}{{c}^{j}}$ + m_z0} of the jth hypothetical route on the transmitting AC at the time of measurement, calculated from the azimuth ${{\beta }^{j}}$, elevation angle ${{\varepsilon }^{j}}$, and range R ^j of this hypothetical route on the receiving AC:

$${{\cos }^{2}}{{\Delta }^{j}}({{R}^{j}}) = \frac{{{{{({{R}^{j}}{{A}^{j}} + B)}}^{2}}}}{{{{{({{R}^{j}})}}^{2}}{{E}^{j}} + 2{{R}^{j}}{{F}^{j}} + H}},$$

(1.7)

where ${{A}^{j}}$ = ${{a}^{j}}$y₀ + ${{b}^{j}}$y₂ + ${{c}^{j}}$y₄, B = $m_{{x0}}^{s}$y₀ + $m_{{y0}}^{s}$y₂ + $m_{{z0}}^{s}$y₄, ${{E}^{j}}$ = (${{a}^{j}}$)² + (${{b}^{j}}$)² + (${{c}^{j}}$)²,

$${{F}^{j}} = {{a}^{j}}m_{{x0}}^{s} + {{b}^{j}}m_{{y0}}^{s} + {{c}^{j}}m_{{z0}}^{s},\quad H = {{(m_{{x0}}^{s})}^{2}} + {{(m_{{y0}}^{s})}^{2}} + {{(m_{{z0}}^{s})}^{2}},$$

(1.8)

$${{y}_{0}} = \cos x_{1}^{s}\cos x_{6}^{s},\quad {{y}_{2}} = \sin x_{6}^{s},\quad {{y}_{4}} = - \cos x_{1}^{s}\sin x_{6}^{s},$$

$${{a}^{j}} = m_{{xx}}^{s}\cos m_{6}^{j}\cos m_{1}^{j} + m_{{xy}}^{s}\sin m_{6}^{j} - m_{{zx}}^{s}\cos m_{6}^{j}\sin m_{1}^{j},$$

$${{b}^{j}} = m_{{yx}}^{s}\cos m_{6}^{j}\cos m_{1}^{j} + m_{{yy}}^{s}\sin m_{6}^{j} - m_{{yz}}^{s}\cos m_{6}^{j}\sin m_{1}^{j},$$

$${{c}^{j}} = m_{{zx}}^{s}\cos m_{6}^{j}\cos m_{1}^{j} + m_{{zy}}^{s}\sin m_{6}^{j} - m_{{zz}}^{s}\cos m_{6}^{j}\sin m_{1}^{j},$$

$m_{{xx}}^{s}$, …, $m_{{zz}}^{s}$, $m_{{x0}}^{s}$, $m_{{y0}}^{s}$, and $m_{{y0}}^{s}$ are the coefficients of transition from the NMCS of its own AC to the NMCS of the transmitting AC at the time of the measurement.

7. For a suboptimal estimate of the phase coordinates of the tracked object derive a multidimensional nonlinear hypothesis filter, whose input is the calculated triangulation range.

2. THE SOLUTION OF THE PROBLEM

We consider the implementation of these requirements.

2.1. The Composition of the Route Support Transmitted by the AC over the CC

Nf is the number of the form of the route of the object; O is an attribute of the object; ListI is the list of sources of information; PR_PO is a feature of instrumentation; t_z is the time of the last measurement; x(t_z), y(t_z), and z(t_z) are the nonextrapolated Cartesian coordinates of the object in the GCS; ${{{v}}_{x}}$(t_z), ${{{v}}_{y}}$(t_z), and ${{{v}}_{z}}$(t_z) are the nonextrapolated object velocity projections in the GCS; β(t_z) is the nonextrapolated azimuth of the object; s_R(t_z), s_L(t_z), s_h(t_z), ${{s}_{{v}}}$(t_z), s_ψ(t_z), and ${{k}_{{{v}\psi }}}$(t_z) are the standard errors for R, L (normal to sighting beam), h (height), ${v}$, ψ, the correlation coefficient ${v}$, and ψ calculated from the probabilities π_j(t_z); estimated m$_{k}^{j}$(t_z); the correlation moments d$_{{kl}}^{j}$(t_z) of the hypothetical routes of the tracked object; and PR_UM and PR_FK are the features of the elevation angle measurement and course formation.

2.2. The Composition of the Measured Information Transmitted by the AC via the C

Nf is the number of the form of the route of the object, β^s(t_z) is the measured azimuth of the object, ε^s(t_z) is the measured elevation angle of the object, $s_{\beta }^{s}$(t_z) and $s_{\varepsilon }^{s}$(t_z) are the standard errors for β^S and ε^S, PR_UM is a feature of the elevation angle measurement, and λ^s(t_z), φ^s(t_z), and H^s(t_z) are the geographic coordinates of the AC at the time of measurement t_z.

2.3. Formation of the Measurement Mark According to the Route Support Received from the AC of the Grou

In order to identify the route support with the internal routes of their tracked objects, measurement marks are formed, in three stages:

write object identifiers N_R, N_O, N_L and signs PR_PO, PR_UM, PR_FK to the measurement mark,

recalculate the route supports in the NMCS of its AC, and

determine the spherical coordinates of the transferred object.

Recalculation is carried out according to the formulas

$$\begin{gathered} {{x}_{0}} = {{m}_{{xx}}}x({{t}_{z}}) + {{m}_{{xy}}}y({{t}_{z}}) + {{m}_{{xz}}}z({{t}_{z}}) + {{m}_{{x0}}}, \hfill \\ {{y}_{0}} = {{m}_{{yx}}}x({{t}_{z}}) + {{m}_{{yy}}}y({{t}_{z}}) + {{m}_{{yz}}}z({{t}_{z}}) + {{m}_{{y0}}}, \hfill \\ {{z}_{0}} = {{m}_{{zx}}}x({{t}_{z}}) + {{m}_{{yy}}}y({{t}_{z}}) + {{m}_{{zz}}}z({{t}_{z}}) + {{m}_{{z0}}}. \hfill \\ \end{gathered} $$

(2.1)

For the AO at PR_FK = 1, the projections of the velocity vector are also calculated:

$$\begin{gathered} {{{v}}_{{x0}}} = {{m}_{{xx}}}{{{v}}_{x}}({{t}_{z}}) + {{m}_{{xy}}}{{{v}}_{y}}({{t}_{z}}) + {{m}_{{xz}}}{{{v}}_{z}}({{t}_{z}}), \hfill \\ {{{v}}_{{z0}}} = {{m}_{{zx}}}{{{v}}_{x}}({{t}_{z}}) + {{m}_{{zy}}}{{{v}}_{y}}({{t}_{z}}) + {{m}_{{zz}}}{{{v}}_{z}}({{t}_{z}}), \hfill \\ {{{v}}_{{y0}}} = {{m}_{{yx}}}{{{v}}_{x}}({{t}_{z}}) + {{m}_{{yy}}}{{{v}}_{y}}({{t}_{z}}) + {{m}_{{yz}}}{{{v}}_{z}}({{t}_{z}}), \hfill \\ \end{gathered} $$

(2.2)

where the following transition coefficients are given:

$$\begin{gathered} \Delta \lambda = {{\lambda }_{{ut}}}-\lambda ({{t}_{z}}); \\ ~{{m}_{{zz}}} = {\text{cos}}\left( {\Delta \lambda } \right); \\ ~{{m}_{{xx}}} = {{m}_{{zz}}}{\text{sin}}{{\varphi }_{{ut}}}{\text{sin}}\varphi ({{t}_{z}}) + {\text{cos}}{{\varphi }_{{ut}}}{\text{cos}}\varphi ({{t}_{z}}), \\ ~{{m}_{{xy}}} = {\text{sin}}{{\varphi }_{{ut}}}{\text{cos}}\varphi ({{t}_{z}}) - {{m}_{{zz}}}{\text{cos}}{{\varphi }_{{ut}}}{\text{sin}}\varphi ({{t}_{z}}), \\ {{m}_{{xz}}} = \sin \varphi ({{t}_{z}})\sin \Delta \lambda , \\ \end{gathered} $$

$$\begin{gathered} {{m}_{{yx}}} = {\text{cos}}{{\varphi }_{{ut}}}{\text{sin}}\varphi ({{t}_{z}})-{{m}_{{zz}}}{\text{sin}}{{\varphi }_{{ut}}}{\text{cos}}\varphi ({{t}_{z}}),~ \hfill \\ {{m}_{{yy}}} = {\text{sin}}{{\varphi }_{{ut}}}{\text{sin}}\varphi ({{t}_{z}}) + {{m}_{{zz}}}{\text{cos}}{{\varphi }_{{ut}}}{\text{cos}}\varphi ({{t}_{z}}),~~~ \hfill \\ \end{gathered} $$

(2.3)

$$\begin{gathered} {{m}_{{yz}}} = -{{\cos}}\varphi ({{t}_{z}}){{\sin}}\Delta \lambda , \\ ~{{m}_{{zx}}} = -{{\sin}}{{\varphi }_{{ut}}}{{\sin\Delta }}\lambda , \\ {{m}_{{zy}}}~ = {{\cos}}{{\varphi }_{{ut}}}{{\sin}}\Delta \lambda , \\ \end{gathered} $$

$$\begin{gathered} ~N(\varphi ) = 6378.243{\text{/}}\sqrt {1 - e{\text{si}}{{{\text{n}}}^{2}}\varphi } ,\quad e = {\text{ }}0.00669421623, \\ ~{{m}_{{x0}}} = N({{\varphi }_{{ut}}}){{m}_{{xy}}} + e[N(\varphi ({{t}_{z}})){\text{sin}}\varphi ({{t}_{z}})-N({{\varphi }_{{ut}}}){\text{sin}}{{\varphi }_{{ut}}}]{\text{ cos}}\varphi ({{t}_{z}}), \\ ~{{m}_{{y0}}} = N({{\varphi }_{{ut}}})~{{m}_{{yy}}}-(N(\varphi ({{t}_{z}})) + H({{t}_{z}})) + e[N(\varphi ({{t}_{z}})){\text{sin}}\varphi ({{t}_{z}})-N({{\varphi }_{{ut}}}){\text{sin}}{{\varphi }_{{ut}}}]{\text{sin}}\varphi ({{t}_{z}}), \\ \end{gathered} $$

$${{m}_{{z0}}} = N({{\varphi }_{{ut}}}){{m}_{{zy}}}.$$

Here, λ(t_z), φ(t_z), and H(t_z) are the geographic coordinates of its AC at the time of measurement t_z:

$$\begin{gathered} ~\lambda ({{t}_{z}}) = \lambda (t) + {{V}_{z}}({{t}_{z}}-t){\text{/}}[(N(\varphi ) + H){\text{cos}}\varphi -{{V}_{x}}{\text{sin}}\varphi ({{t}_{z}}-t)], \\ \varphi ({{t}_{z}}) = \varphi (t) + {{V}_{x}}{\text{cos}}\varphi ({{t}_{z}}-t){\text{/}}[(N(\varphi ) + H){\text{cos}}\varphi -{{V}_{x}}{\text{sin}}\varphi ({{t}_{z}}-t)], \\ H({{t}_{z}}) = H(t) + {{V}_{y}}({{t}_{z}}-t), \\ \end{gathered} $$

(2.4)

where t is the current time.

The spherical coordinates are determined by the formulas

$$d({{t}_{z}}) = \sqrt {{{x}_{0}}{{x}_{0}} + {{z}_{0}}{{z}_{0}}} ,\quad {{x}_{1}}({{t}_{z}}) = {\text{arcsin}}(-{{z}_{0}}{\text{/}}d({{t}_{z}})),\quad D({{t}_{z}}) = \sqrt {{{d}^{2}}({{t}_{z}}) + {{y}_{0}}{{y}_{0}}} .$$

(2.5)

At PR_UM = 1 we have x₆(t_z) = arcsin(y₀/R(t_z)).

Next, the correlation moments s₁₁, s_1R, s_RR, and s₆₆ of the spherical coordinates x₁, R, and x₆ of the object are calculated:

$$\begin{gathered} \Delta \beta = {{x}_{1}}({{t}_{z}})-\beta ({{t}_{z}}); \\ {{s}_{{DD}}} = {{({{s}_{D}}({{t}_{z}}){\text{cos}}\Delta \beta )}^{2}} + {{{\text{(}}{{s}_{L}}({{t}_{z}}){\text{sin}}\Delta \beta )}^{2}} + \sigma _{{XZ}}^{2}, \\ {{s}_{{11}}} = [{{({{s}_{D}}({{t}_{z}}){\text{cos}}\Delta \beta )}^{2}} + {{{\text{(}}{{s}_{L}}({{t}_{z}}){\text{sin}}\Delta \beta )}^{2}} + \sigma _{{XZ}}^{2}]{\text{/}}{{d}^{2}}({{t}_{z}}), \\ {{s}_{{1D}}} = (s_{L}^{2}({{t}_{z}}) - s_{D}^{2}({{t}_{z}}))\sin \Delta \beta \cos \Delta \beta {\text{/}}d({{t}_{z}}), \\ {{s}_{{66}}} = (\sigma _{H}^{2} + s_{h}^{2}({{t}_{z}})){{\cos }^{2}}{{x}_{6}}({{t}_{z}}) + [{{({{s}_{D}}({{t}_{z}})\sin {{x}_{6}}({{t}_{z}}){\text{/}}R({{t}_{z}})]}^{2}}, \\ \end{gathered} $$

(2.6)

where $\sigma _{{XZ}}^{2}$ and $\sigma _{H}^{2}$ are the variances of the Cartesian coordinates and flight altitude of the transmitting AC, calculated from the data sheet of its navigation system.

At PR_FK = 1, the object’s velocity projections and their correlation moments are determined:

$$\begin{gathered} {{x}_{3}}({{t}_{z}}) = {{{v}}_{{x0}}}\cos {{x}_{1}}({{t}_{z}}) - {{{v}}_{{z0}}}\sin {{x}_{1}}({{t}_{z}}), \\ {{x}_{4}}({{t}_{z}}) = {{{v}}_{{x0}}}\sin {{x}_{1}}({{t}_{z}}) + {{{v}}_{{z0}}}\cos {{x}_{1}}({{t}_{z}}), \\ {{s}_{{{\bar {v}}}}}({{t}_{z}}) = \sqrt {(s_{{v}}^{2}({{t}_{z}}){\text{/}}({v}_{x}^{2}({{t}_{z}}) + {v}_{z}^{2}({{t}_{z}}))} , \\ {{s}_{{43}}} = {{x}_{3}}({{t}_{z}}){{x}_{4}}({{t}_{z}})[s_{{{\bar {v}}}}^{2}({{t}_{z}}) - (s_{\psi }^{2}({{t}_{z}}) + {{s}_{{11}}})] + (x_{3}^{2}({{t}_{z}}) - x_{4}^{2}({{t}_{z}})){{k}_{{{v}\psi }}}({{t}_{z}}){{s}_{{{\bar {v}}}}}({{t}_{z}}){{s}_{\psi }}({{t}_{z}}), \\ {{s}_{{33}}} = x_{3}^{2}({{t}_{z}})s_{{{\bar {v}}}}^{2}({{t}_{z}}) + x_{4}^{2}({{t}_{z}})(s_{\psi }^{2}({{t}_{z}}) + {{s}_{{11}}}) - 2{{x}_{3}}({{t}_{z}})x_{4}^{{}}({{t}_{z}}){{k}_{{{v}\psi }}}({{t}_{z}}){{s}_{{{\bar {v}}}}}({{t}_{z}}){{s}_{\psi }}({{t}_{z}}), \\ {{s}_{{44}}} = x_{4}^{2}({{t}_{z}})s_{{{\bar {v}}}}^{2}({{t}_{z}}) + x_{3}^{2}({{t}_{z}})(s_{\psi }^{2}({{t}_{z}}) + {{s}_{{11}}}) + 2{{x}_{3}}({{t}_{z}})x_{4}^{{}}({{t}_{z}}){{k}_{{{v}\psi }}}({{t}_{z}}){{s}_{{{\bar {v}}}}}({{t}_{z}}){{s}_{\psi }}({{t}_{z}}). \\ \end{gathered} $$

(2.7)

2.4. Association of the Generated Measurement Marks with the Internal Routes of Their Tracked Objects

We need to establish a one-to-one correspondence: each measurement mark of one AC of the group corresponds to one internal route, and each internal route contains no more than one measurement mark of this AC. For each internal route with marks of this AC, these marks are ranked according to the average reduced discrepancy $s_{\chi }^{2}$ calculated from the hypothetical routes. The internal route of the AO contains nonmaneuvering and maneuvering hypothetical routes, and the internal route of the GO contains only nonmaneuvering hypothetical routes of the object’s movement in the NMCS.

$s_{\chi }^{2}$ is first calculated on nonmaneuvering hypothetical routes j = 0 with probabilities π_j

$$s_{\chi }^{2} = \frac{{\sum\limits_{j = 0} {\overline {\chi _{j}^{2}} {{\pi }_{j}}} }}{{\sum\limits_{j = 0} {{{\pi }_{j}}} }}.$$

In the presence of maneuvering hypothetical routes, it is possible to correct it. For each maneuvering hypothetical route (j $\ne$ 0) in the cycle, the intensity of the shooting maneuver determines the minimum reduced discrepancy $\overline {\chi _{j}^{2}}$. At $\overline {\chi _{j}^{2}}$ < $s_{\chi }^{2}$ the following adjustment is made: $s_{\chi }^{2}$ = $\overline {\chi _{j}^{2}}$. If, in order to mark the AC of the group in the nearest (discrepancy $s_{\chi }^{2}$) inner route, this mark is also the closest of the marks of this AC (one-to-one association), then it alone remains in this inside route and is crossed out from the rest of the inside routes. Otherwise, from the possible association options, the one with the minimum sum of the average reduced residuals is selected.

For route supports with the sign PR_PO > 1, identified with internal routes without range measurement, the hypothetical triangulation mode is assigned and the composition of the measurement is corrected: only the range remains. The coefficients of transition are calculated from the NMCS of their own AC at the time of measurement with the center λ(t_z), ϕ(t_z), and H(t_z) to the NMCS of the AC of the group with center λ^s(t_z), φ^s(t_z), and H^s(t_z):

$$\begin{gathered} \Delta \lambda = \lambda ({{t}_{z}})-{{\lambda }^{s}}({{t}_{z}}){\text{ }}, \\ m_{{zz}}^{s} = {\text{cos}}\left( {\Delta \lambda } \right), \\ m_{{xx}}^{s} = m_{{zz}}^{s}{\text{sin}}\varphi ({{t}_{z}}){\text{sin}}{{{{\varphi }}}^{s}}({{t}_{z}}) + {\text{cos}}\varphi ({{t}_{z}}){\text{cos}}{{\varphi }^{s}}({{t}_{z}}), \\ m_{{xy}}^{s} = {\text{sin}}\varphi ({{t}_{z}}){\text{cos}}{{\varphi }^{s}}({{t}_{z}})-m_{{zz}}^{s}{\text{cos}}\varphi ({{t}_{z}}{\text{)sin}}{{\varphi }^{s}}({{t}_{z}}), \\ \end{gathered} $$

$$\begin{gathered} m_{{xz}}^{s} = {\text{sin}}{{\varphi }^{s}}({{t}_{z}}){\text{sin}}\Delta \lambda , \\ m_{{yx}}^{s} = {\text{cos}}\varphi ({{t}_{z}}){\text{sin}}{{\varphi }^{s}}({{t}_{z}})-m_{{zz}}^{s}{\text{sin}}\varphi ({{t}_{z}}){\text{cos}}{{\varphi }^{s}}({{t}_{z}}),~ \\ m_{{yy}}^{s} = {\text{sin}}\varphi ({{t}_{z}}){\text{sin}}{{\varphi }^{s}}({{t}_{z}}){{ + }_{~}}m_{{zz}}^{s}{\text{cos}}\varphi ({{t}_{z}}){\text{cos}}{{\varphi }^{s}}({{t}_{z}}),~ \\ \end{gathered} $$

(2.8)

$$\begin{gathered} m_{{yz}}^{s} = -{\text{cos}}{{\varphi }^{s}}({{t}_{z}}){\text{sin}}\Delta \lambda , \\ m_{{zx}}^{s} = -{\text{sin}}\varphi ({{t}_{z}}){\text{sin}}\Delta \lambda , \\ m_{{zy}}^{s} = {\text{cos}}\varphi ({{t}_{z}}){\text{sin}}\Delta \lambda , \\ \end{gathered} $$

$$N\left( \varphi \right) = 6378.243{\text{/}}\sqrt {1 - e{{{\sin }}^{2}}\varphi } ,\quad e = 0.00669421623,$$

$$m_{{x0}}^{s} = (N(\varphi ({{t}_{z}})) + H({{t}_{z}}))m_{{xy}}^{s} + e[N({{\varphi }^{s}}({{t}_{z}})){\text{sin}}{{\varphi }^{s}}({{t}_{z}})-N(\varphi ({{t}_{z}})){\text{sin}}\varphi ({{t}_{z}})]{\text{cos}}{{\varphi }^{s}}({{t}_{z}}),$$

$$m_{{y0}}^{s} = (N(\varphi ({{t}_{z}})) + H({{t}_{z}}))m_{{yy}}^{s}-(N({{\varphi }^{s}}({{t}_{z}})) + {{H}^{s}}({{t}_{z}})) + e[N({{\varphi }^{s}}({{t}_{z}})){\text{sin}}{{\varphi }^{s}}({{t}_{z}})-N(\varphi ({{t}_{z}})){\text{sin}}\varphi ({{t}_{z}})]{\text{sin}}{{\varphi }^{s}}({{t}_{z}}),$$

$$m_{{z0}}^{s} = (N(\varphi ({{t}_{z}})) + H({{t}_{z}}))m_{{zy}}^{s}.$$

2.5. Determination of Three Hypothetical Routes Closest to the Discrepancy and Recording the Addresses of Measurement Marks in Them

During the calculation of the average reduced discrepancy $s_{\chi }^{2}$ for the inner route, the reduced discrepancy $\overline {\chi _{j}^{2}}$ is calculated on each of its jth hypothetical routes, and the hypothetical routes are ranked accordingly, which is recorded in the measurement mark. As a result of the association, one measurement mark remains in the inner route. We select the first three hypothetical routes in this measurement mark and exclude this measurement mark in the remaining hypothetical routes.

2.6. Calculation of the Triangulation Range and Its Variance

The triangulation range R^j is calculated for each of the three selected hypothetical routes of the object as the minimum point of the function (1.7):

$$f({{R}^{j}}) = \frac{{{{{({{R}^{j}}{{A}^{j}} + B)}}^{2}}}}{{{{{({{R}^{j}})}}^{2}}{{E}^{j}} + 2{{R}^{j}}{{F}^{j}} + H}},\quad j = {{j}_{1}},{{j}_{2}},{{j}_{3}}.$$

For the three selected hypothetical routes of the object’s OLS and ARS

$${{R}^{j}}({{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{j}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})) = \frac{{B{{F}^{j}} - {{A}^{j}}H}}{{{{A}^{j}}{{F}^{j}} - B{{E}^{j}}}},\quad j = {{j}_{1}},{{j}_{2}},{{j}_{3}},$$

where A ^j, B, E ^j, F  ^j, and H are calculated by formulas (1.8).

For the three selected hypothetical routes of the object’s RRE

$${{R}^{j}}({{\beta }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}})) = \frac{{B{{F}^{j}} - {{A}^{j}}H}}{{{{A}^{j}}{{F}^{j}} - B{{E}^{j}}}},\quad j = {{j}_{1}},{{j}_{2}},{{j}_{3}},$$

where E ^j, F  ^j, and H are calculated by formulas (1.8), ${{A}^{j}}$ = ${{a}^{j}}$y₀ + ${{c}^{j}}$y₄, B = m_x0y₀ + m_z0y₄,

y₀ = cos$x_{1}^{s}$, y₄ = –sin$x_{1}^{s}$, ${{a}^{j}}$ = $m_{{xx}}^{s}$cosm$_{1}^{j}$ – $m_{{xz}}^{s}$sinm$_{1}^{j}$, ${{c}^{j}}$ = $m_{{zx}}^{s}$cosm$_{1}^{j}$ – $m_{{zz}}^{s}$sinm$_{1}^{j}$.

Because the angles ${{\beta }^{s}}$(t_z), ${{\varepsilon }^{s}}$(t_z), m$_{1}^{j}$(t_z), and m$_{6}^{j}$(t_z) are determined with the standard mistakes $s_{\beta }^{s}$(t_z), $s_{\varepsilon }^{s}$(t_z), s$_{1}^{j}$(t_z) = $\sqrt {d_{{11}}^{j}({{t}_{z}})}$, and s$_{6}^{j}$(t_z) = $\sqrt {d_{{66}}^{j}({{t}_{z}})}$, where $d_{{11}}^{j}({{t}_{z}})$ and $d_{{66}}^{j}({{t}_{z}})$ are the azimuth and elevation angle’s variances in the jth hypothesized route, and the transition coefficients are nonlinear functions, in order to calculate the unbiased triangulation range and its variance by statistical modeling, we replace the continuous distribution of the calculation errors ${{\beta }^{s}}$(t_z), ${{\varepsilon }^{s}}$(t_z), m$_{1}^{j}$(t_z), and m$_{6}^{j}$(t_z) for the objects OLS and ARS by a discrete distribution with equal probabilities at nine points:

$${{\{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} }_{0}} = \{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} ,$$

$${{\{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} }_{{1,2}}} = \{ {{\beta }^{s}}({{t}_{z}}) \pm 1.393s_{\beta }^{s}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} ,$$

$${{\{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} }_{{3,4}}} = \{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}) \pm 1.393s_{\varepsilon }^{s}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} ,$$

$${{\{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} }_{{5,6}}} = \{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}) \pm 1.393s_{1}^{s}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} ,$$

$${{\{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}})\} }_{{7,8}}} = \{ {{\beta }^{s}}({{t}_{z}}),{{\varepsilon }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}),m_{6}^{j}({{t}_{z}}) \pm 1.393s_{6}^{s}({{t}_{z}})\} ;$$

and the continuous distribution of the calculation errors β^s(t_z) and m$_{1}^{j}$(t_z) for the objects’ RRE by a discrete distribution with equal probabilities at five points:

$${{\{ {{\beta }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}})\} }_{0}} = \{ {{\beta }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}})\} ,$$

$${{\{ {{\beta }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}})\} }_{{1,2}}} = \{ {{\beta }^{s}}({{t}_{z}}) \pm 1.393s_{\beta }^{s}({{t}_{z}}),m_{1}^{j}({{t}_{z}})\} ,$$

$${{\{ {{\beta }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}})\} }_{{3,4}}} = \{ {{\beta }^{s}}({{t}_{z}}),m_{1}^{j}({{t}_{z}}) \pm 1.393s_{1}^{s}({{t}_{z}})\} .$$

For three hypothetical routes of the object’s OLS and ARS, the triangulation range

$${{R}^{j}}({{t}_{z}}) = \frac{1}{9}\sum\limits_{k = \overline {0,8} }^{} {{{R}^{j}}(k),\quad j = {{j}_{1}},{{j}_{2}},{{j}_{3}}.} $$

Its variance

$$d_{{RR}}^{j} = \frac{1}{8}\sum\limits_{k = \overline {0,8} }^{} {{{{({{R}^{j}}(k) - {{R}^{j}}({{t}_{z}}))}}^{2}},\quad j = {{j}_{1}},{{j}_{2}},{{j}_{3}}.} $$

For three hypothetical routes of the object’s RRE triangulation horizontal range

$${{d}^{j}}({{t}_{z}}) = \frac{1}{5}\sum\limits_{k = \overline {0,4} }^{} {{{R}^{j}}(k),\quad j = {{j}_{1}},{{j}_{2}},{{j}_{3}}.} $$

Its variance

$$d_{{DD}}^{j} = \frac{1}{4}\sum\limits_{k = \overline {0,4} }^{} {{{{({{R}^{j}}(k) - {{d}^{j}}({{t}_{z}}))}}^{2}},\quad j = {{j}_{1}},{{j}_{2}},{{j}_{3}}.} $$

2.7. A Multidimensional Nonlinear Hypothesis Filter of the Triangulation Range

The triangulation range filter is derived from the range filter RF [2] and has the form

$$\begin{gathered} \Delta _{2}^{j} = 1{\text{/}}{{d}^{j}}({{t}_{z}}) - m_{2}^{j}({{t}_{z}} - 0), \\ \lambda _{{22}}^{j} = d_{{22}}^{j} + s_{{22}}^{j},\quad s_{{22}}^{j} = d_{{DD}}^{j}{\text{/}}{{({{d}^{j}}({{t}_{z}}))}^{4}},\quad A_{{2k}}^{j} = d_{{2k}}^{j}{\text{/}}\lambda _{{22}}^{j}, \\ m_{k}^{j}({{t}_{z}}) = m_{k}^{j}({{t}_{z}} - 0) + \Delta _{2}^{j}A_{{2k}}^{j}, \\ \end{gathered} $$

(2.9)

$$d_{{kl}}^{j}({{t}_{z}}) = d_{{kl}}^{j}({{t}_{z}} - 0) - d_{{2k}}^{j}A_{{2l}}^{j},\quad l \leqslant k = 1{-} 7\quad {\text{for}}\,\,{\text{AO}},\quad l \leqslant ~\;k = 1,2,6\quad {\text{for}}\,\,{\text{GO}}{\text{.}}$$

The a posteriori probabilities of the hypothetical routes are recalculated using the formulas

$${{\pi }_{j}}({{t}_{z}}) = \left\{ \begin{gathered} {{\pi }_{j}}({{t}_{z}} - 0)(1 - {{P}_{o}}){{H}_{1}},\quad j \ne {{j}_{1}},{{j}_{2}},{{j}_{3}}, \hfill \\ {{\pi }_{j}}({{t}_{z}} - 0)\sqrt {s_{{22}}^{j}{\text{/}}\lambda _{{22}}^{j}} \exp ({{(\Delta _{2}^{j})}^{2}}{\text{/}}\lambda _{{22}}^{j}){{H}_{2}},\quad j \ne {{j}_{1}},{{j}_{2}},{{j}_{3}}, \hfill \\ \end{gathered} \right.$$

(2.10)

$${{H}_{1}} = \frac{1}{{\sum\limits_{j \ne {{j}_{1}},{{j}_{2}},{{j}_{3}}} {[{{\pi }_{j}}\left( {{{t}_{z}} - 0} \right)\left( {1 - {{P}_{o}}} \right)]} + \sum\limits_{j = {{j}_{1}},{{j}_{2}},{{j}_{3}}} {{{\pi }_{j}}({{t}_{z}} - 0)} }},$$

$${{H}_{2}} = \frac{{1 - \sum\limits_{j \ne {{j}_{1}},{{j}_{2}},{{j}_{3}}} {\left[ {{{\pi }_{j}}({{t}_{z}} - 0)(1 - {{P}_{o}}){{H}_{1}}} \right]} }}{{\sum\limits_{j = {{j}_{1}},{{j}_{2}},{{j}_{3}}} {[{{\pi }_{j}}\left( {{{t}_{z}} - 0} \right)\sqrt {s_{{22}}^{j}{\text{/}}\lambda _{{22}}^{j}} \exp ({{{(\Delta _{2}^{j})}}^{2}}{\text{/}}\lambda _{{22}}^{j})]} }},$$

where H₁ and H₂ are normalizing factors. Here π_j(t_z – 0), m$_{k}^{j}$(t_z – 0), and d$_{{kl}}^{j}$(t_z – 0) are the values of the parameters π_j, m$_{k}^{j}$, and d$_{{kl}}^{j}$ at the point t_z on the left before filtering, i.e., extrapolated to time t_z.

3. EXAMPLE

The hypothetical triangulation of the AO and GO’s RRE by a pair of AC. The RRE measures the φ_y bearing in the XOZ plane of the RCS. The exchange of information in the CC is carried out after the routes have been linked and verified (Fig. 6). Therefore, in the first exchange, information is received only according to the GO. Between receipts of information on the CC onboard each AC, the measurements of its RRE are processed.

Fig. 6.

Figures 6–11 show a view of the tactical indicator of the slave AC at the characteristic time points: the exit route is first issued according to the RRE information (Fig. 7), identification of a hypothetical route, determination of the AO’s velocity vector, and achievement of II1. The red lines show the measured bearings on each AC, and the shortened green bearing shows the current range in the range with II2.

Fig. 7.

Fig. 8.

Fig. 9.

Fig. 10.

Fig. 11.

The hypothetical GO route is identified after the second exchange by the CC (Fig. 8). The standard error of the range estimate exceeds those required for II1 by 5%R (Fig. 9). For the GO, an additional hypothetical route is introduced with the parameters of II1 and on the following third exchange, σ_R < 5%R (Fig. 10).

The information on the AO arrives starting from the second exchange via the CC. At the first receipt of information on the AO, the feature PR_FK = 1 is formed, i.e., the standard velocity vector estimation error on the course does not exceed 5°.

The AO’s hypothetical route is selected after the third exchange by the CC (information on the AO is received for the second time via the CC). The standard error estimates of the range while σ_R = 6.21%R (Fig. 9). As σ_ψ < 5°, in order to achieve II1, it is necessary to reduce the error in the range. An additional hypothetical route II1 is also introduced at the next fourth exchange (the third receipt of information on the AO by the CC) and σ_R <5%R is achieved (Fig. 11). Thus, in order to achieve II1 for the GO and for the AO, three cycles of triangulation are sufficient.

CONCLUSIONS

The problem of increasing the accuracy of covert route tracking of radio and heat-emitting AOs and GOs onboard an AC has been solved through hypothetical triangulation:

a reset of unidentified hypothetical routes (the span of the range values decreases; and for the AO, the velocity also decreases);

filtering in identified hypothetical routes by the multidimensional nonlinear hypothetical filter F_R of the triangulation ranges calculated by the criterion of the minimum discrepancy of the measured bearings and their calculated values for these hypothetical routes;

and the introduction of an additional hypothetical route with a trial range and accuracy of II1 to accelerate the achievement of II1.

Hypothetical triangulation makes it possible to achieve the accuracy of II1 (σ_R ≤ 5%R for the GO and σ_R ≤ 5%R and σ_ψ ≤ 5° for the AO) after three exchanges of information on the CC.