INTRODUCTION

Various information services available on the market of space services are continuously growing and developing. In other words, to ensure a leading position in this segment, not does the area of the services provided, including communications, navigation, and monitoring, need to be constantly extended but the quality of the services also needs to be constantly improved and maintained at a level exceeding the global standards. Technologies that increase the precision and the independence of space constellations of information satellite systems from the ground operating segment are a core factor that helps achieve the best quality of services for consumers. Although many international modern satellite systems capable of implementing the specified technology, there remains a significant gap related to the influence of uncertainties of the knowledge of geodynamic Earth parameters on long prediction intervals. They prevent us from providing the best (with the other conditions being equal) quality of the ephemeride-time delivery for spacecraft (SC). The uncertainty of the values of these parameters leads to considerable resources being spent on complicated computations based on the external data, which are then maintained. It is obvious that being able to refine the chain of the Earth’s geodynamic parameters onboard an SC by measuring long time periods that available onboard would offer an undisputable competitive advantage.

We mean refining the current values of the shift of the Earth’s instant pole and of the irregularity of its rotation, which is the difference between the Earth’s Universal time (UT1) and the Coordinated Universal Time (UTC) used in different applications of the coordinated scale. By refining all the listed parameters, we can eliminate the substantial uncertainty in computing a SC’s motion and therefore increase the quality of the data obtained by the consumer from various target devices of the SC’s satellite information systems.

Thus, in this study, we consider setting the following problem: on a long-time interval, refine the Earth Orientation Parameters (EOP), based on the possibility of measuring onboard the distance between the SC and the ground station, as well as collecting the measurement data in order to refine the precision of recalculating the ephemerides in the Earth’s coordinate system.

The problem of refining the ephemerides onboard is actual for navigational systems such as Glonass (see [1, 2]), GPS, and Beidou (see [3]).

A more general form of the problem of refining the ephemerides onboard a SC is to be solved jointly with refining the EOP. For example, intersatellite measurements and measurements of the distance between SC and ground stations. However, in this work, refining the EOP according to the measurements of the distance between SC and ground stations (intersatellite measurement does not help refine the EOP) is treated as an independent problem; the aim of such an approach is to study the properties of the information technology and obtain a preliminary estimate of the feasibility of refining the EOP onboard an SC.

1. EVOLUTION OF THE EARTH ORIENTATION PARAMETERS: EXISTING APPROACHES

We consider the evolving EOP and the problem of predicting them; currently, this problem imposes a number of restrictions for operating multipurpose space constellations. As is well known, the pole shift and the irregularity of the Earth’s rotation are caused mainly by internal processes in the Earth’s body and the gravitational influence of celestial bodies. At the moment, a number of models (based on the long-term observation of the dynamics of these processes) have been developed (see [4–6]); they partially describe the evolution of the EOP, based on deterministic expressions that are sums of a linear trend and trigonometric functions. However, the description and prediction of the EOP using the existing models, based on processing the real data collected by radiointerferometers with very long baselines and the laser ranging stations of the real data, remains imprecise. Analysis of the works [7–9] devoted to predicting and describing the evolution of the EOP and our own estimates show that the most precise predictions of the pole shift for periods longer than a month at the level of the two squared deviations from the mean are dozens of milliarcseconds or angular milliseconds (mas); and for the irregularity of the Earth rotation, they are dozens of milliseconds (ms) of the difference between UT1 and UTC at the same precision level.

It is obvious that such computing precision for the EOP cannot be sufficient for the computation of SC ephemerides because in passing from the inertial coordinate system to the Earth’s coordinate system through the conventional relations (see [6]), the errors increase to dozens of meters. Thus, if our goal is to increase the independence of satellite constellations operating from the ground segment, then the onboard model of the prediction of the EOP cannot be used for intermediate ephemerides computations onboard a SC without harming their precision and therefore their consumptive qualities.

2. REFINING THE EARTH ORIENTATION PARAMETERS BY SPACECRAFT: CONCEPT, METHODS, AND ALGORITHMS

Analyzing the situation described above with the prediction of the EOP, we see that it is necessary to create a concept of the onboard estimates of such parameters while the SC is in operation. The physical nature of the evolution of the EOP make it impossible to do this without using some technical tools located on the Earth’s surface. Thus, to monitor even indirect variations of the EOP, we have to place equipment (stations) on the Earth in order to detect the relation between the EOP and the SC’s coordinates. Once such a relation is detected, we can estimate the EOP or correct their forecast values by a special type of processing of the measurement between the SC and the ground stations. To discuss an acceptable implementation variant for such a technology, consider the following matrix of the transition between the Terrestrial Intermediate Coordinate System (TIRS), whose orientation with respect to the inertial Geocentric Celestial Reference System (GCRS) on the epoch J2000 (see [6]) is determined by the relations accounting for the precession and nutation of the Earth’s axis and by the stellar evolution, and the International Terrestrial Reference System (ITRF), whose orientation is determined by the current pole location and the irregularity of the Earth’s rotation:

$$\begin{gathered} {\mathbf{A}}_{{ITRF}}^{{TIRS}} = ({\mathbf{A}}_{X}^{{\text{T}}}({{y}_{p}})) \times ({\mathbf{A}}_{Y}^{{\text{T}}}({{x}_{p}})) \times ({\mathbf{A}}_{Z}^{{\text{T}}}\left( {\Delta {\text{UT}}} \right)) \\ = \;\left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos {{y}_{p}}}&{ - \sin {{y}_{p}}} \\ 0&{\sin {{y}_{p}}}&{\cos {{y}_{p}}} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {\cos {{x}_{p}}}&0&{\sin {{x}_{p}}} \\ 0&1&0 \\ { - \sin {{x}_{p}}}&0&{\cos {{x}_{p}}} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {\cos \Delta {\text{UT}}}&{ - \sin \Delta {\text{UT}}}&0 \\ {\sin \Delta {\text{UT}}}&{\cos \Delta {\text{UT}}}&0 \\ 0&0&1 \end{array}} \right) \\ = \;\left( {\begin{array}{*{20}{c}} {\cos {{x}_{p}}\cos \Delta {\text{UT}}}&{\cos \left( {xp} \right)\sin \Delta {\text{UT}}}&{\sin {{x}_{p}}} \\ {\sin {{y}_{p}}\sin {{x}_{p}}\cos \Delta {\text{UT}} - \cos {{y}_{p}}\sin \Delta {\text{UT}}}&{\sin {{y}_{p}}\sin {{x}_{p}}\sin \Delta {\text{UT}} + \cos {{y}_{p}}\cos \Delta {\text{UT}}}&{ - \sin {{y}_{p}}\cos {{x}_{p}}} \\ { - \cos {{y}_{p}}\sin {{x}_{p}}\cos \Delta {\text{UT}} - \sin {{y}_{p}}\sin \Delta {\text{UT}}}&{ - \cos {{y}_{p}}\sin {{x}_{p}}\sin \Delta {\text{UT}} + \sin {{y}_{p}}\cos \Delta {\text{UT}}}&{\cos {{y}_{p}}\cos {{x}_{p}}} \end{array}} \right), \\ \end{gathered} $$

where xp, yp is the pole shift, ΔUT = UT1 – UTC is the irregularity of the Earth’s rotation expressed in the angular measure of the half-turn of the ITRF with respect to TIRS (1 ms ΔUT corresponds to 15 mas).

According to the evolution of the elements of this matrix, changes in the EOP lead to changes of the SC’s state-vector representation in the ITRF provided that the coordinates of the station fixed on the Earth are fixed; this leads to a change of the mutual location of the stations and the SC. Hence, by processing the signals of such stations, which can be received onboard the SC and interpreted as measurements of the distance between the SC and the station, we can estimate the component variations for the specified matrix.

Let us formalize the expression of the distance between the station and the SC:

$$\rho = f({\mathbf{X}}_{{{\text{station}}}}^{{i\;{\text{ITRF}}}}\left( {{{t}_{l}}} \right),{\mathbf{X}}_{{{\text{SC}}}}^{{j\;{\text{GCRS}}}}\left( {{{t}_{k}}} \right)),$$
(2.1)

where \({\mathbf{X}}_{{{\text{SC}}}}^{{j\;{\text{GCRS}}}}\left( {{{t}_{k}}} \right)\) are the coordinates of the jth SC in the inertial coordinate system GCRS at time tk of receiving the signal from the ground station, while \({\mathbf{X}}_{{{\text{station}}}}^{{i\;{\text{ITRF}}}}({{t}_{l}})\) are the coordinates of the ith ground station in the ITRF at time tl of the signal is sent.

It is obvious that, to use expression (2.1) in processing algorithms for measurements, we have to represent location vectors for the ground station and the SC in the same coordinate system. To represent vector (2.1) in the ITRF, we represent the expression for computing the geometric distance between the SC and the station as follows:

$$\rho = f({\mathbf{X}}_{{{\text{station}}}}^{i}\left( {{{t}_{l}}} \right),{{{\mathbf{A}}}^{{\text{T}}}}\left( {{{x}_{p}}\left( {{{t}_{s}}} \right),{{y}_{p}}\left( {{{t}_{s}}} \right),\Delta {\text{UT}}\left( {{{t}_{s}}} \right)} \right){\mathbf{X}}_{{{\text{SC}}}}^{{'j}}\left( {{{t}_{k}}} \right)).$$
(2.2)

In relation (2.2), time ts can be assumed to be equal to tk or tl. The correct choice is to take ts as the time when the signal is received and the change is generated. Taking into account that the station signal is received onboard an SC, we have to use \({\mathbf{X}}_{{{\text{station}}}}^{i}\left( {{{t}_{l}}} \right)\) in the ITRF for the vector of coordinates of the station, transform the vector of coordinates of the SC into the Earth’s coordinate system, and use expression (2.2) with ts corresponding to the time of receiving the signal onboard.

Transform (2.2) into components including components of the vector of the EOP. Specify the content of the components of the vectors \({\mathbf{X}}_{{{\text{station}}}}^{i}\left( {{{t}_{l}}} \right)\) = \((x_{s}^{i}({{t}_{l}})\,\,y_{s}^{i}({{t}_{l}})\,\,z_{s}^{i}({{t}_{l}}))\) and \({\mathbf{X}}_{{{\text{SC}}}}^{{'j}}\left( {{{t}_{k}}} \right) = (x_{G}^{j}({{t}_{k}})\,\,y_{G}^{j}({{t}_{k}})\,\,z_{G}^{i}({{t}_{k}}))\) and simplify them in the transformations: \({\mathbf{X}}_{{{\text{station}}}}^{i}\left( {{{t}_{l}}} \right) = \left( {\begin{array}{*{20}{c}} {{{X}_{s}}}&{{{Y}_{s}}}&{{{Z}_{s}}} \end{array}} \right)\) and \({\mathbf{X}}_{{{\text{SC}}}}^{{'j}}\left( {{{t}_{l}}} \right) = \left( {\begin{array}{*{20}{c}} {{{X}_{g}}}&{{{Y}_{g}}}&{{{Z}_{g}}} \end{array}} \right)\). Then the expression for the distance between the SC and the station takes the form

$$\begin{gathered} \rho = \sqrt {\rho _{1}^{2} + \rho _{2}^{2} + \rho _{3}^{2}} , \\ {{\rho }_{1}} = {{Y}_{s}} - {{X}_{g}}\left( {\cos {{y}_{p}}({{t}_{s}})\sin \Delta {\text{UT}}({{t}_{s}}) + \cos \Delta {\text{UT}}({{t}_{s}})\sin {{x}_{p}}({{t}_{s}})\sin {{y}_{p}}({{t}_{s}})} \right) \\ - \;{{Y}_{g}}({\text{cos}}\Delta {\text{UT}}({{t}_{s}}){\text{cos}}{{y}_{p}}({{t}_{s}}) - {\text{sin}}\Delta {\text{UT}}({{t}_{s}}){\text{sin}}{{x}_{p}}({{t}_{s}}){\text{sin}}{{y}_{p}}({{t}_{s}})) + {{Z}_{g}}{\text{cos}}{{x}_{p}}({{t}_{s}}){\text{sin}}{{y}_{p}}({{t}_{s}}), \\ {{\rho }_{2}} = {{X}_{g}}\left( {\sin \Delta {\text{UT}}({{t}_{s}})\sin {{y}_{p}}({{t}_{s}}) - \cos \Delta {\text{UT}}({{t}_{s}})\cos {{y}_{p}}({{t}_{s}})\sin {{x}_{p}}({{t}_{s}})} \right) \\ - \;{{Z}_{s}} + {{Y}_{g}}({\text{cos}}\Delta {\text{UT}}({{t}_{s}}){\text{sin}}{{y}_{p}}({{t}_{s}}) + {\text{cos}}{{y}_{p}}({{t}_{s}}){\text{sin}}\Delta {\text{UT}}({{t}_{s}}){\text{sin}}{{x}_{p}}({{t}_{s}})) + {{Z}_{g}}{\text{cos}}{{x}_{p}}({{t}_{s}}){\text{cos}}{{y}_{p}}({{t}_{s}}), \\ {{\rho }_{3}} = {{X}_{s}} - {{Z}_{g}}\sin {{x}_{p}}({{t}_{s}}) - {{X}_{g}}\cos \Delta {\text{UT}}({{t}_{s}})\cos {{x}_{p}}({{t}_{s}}) + {{Y}_{g}}\cos {{x}_{p}}({{t}_{s}})\sin \Delta {\text{UT}}({{t}_{s}}). \\ \end{gathered} $$
(2.3)

Taking into account that the rotation angles of the ITRF caused by the pole shifts and the irregularity of the Earth’s rotation are small, we change each cosine by 1 and each sine by its angle (in the relation given above). Sine products can be disregarded because their orders of smallness are equal to two or three. Thus, the final expression is transformed as follows:

$$\rho = \sqrt {\begin{gathered} {{({{Y}_{s}} - {{X}_{g}}\Delta {\text{UT}} - {{Y}_{g}} + {{Z}_{g}}{{y}_{p}})}^{2}} + {{( - {{X}_{g}}{{x}_{p}} - {{Z}_{s}} + {{Y}_{g}}{{y}_{p}} + {{Z}_{g}})}^{2}} \hfill \\ + \,{{({{X}_{s}} - {{Z}_{g}}{{x}_{p}} - {{X}_{g}} + {{Y}_{g}}\Delta {\text{UT}})}^{2}} \hfill \\ \end{gathered}} .$$
(2.4)

Analyzing expression (2.4), we can form shift components of the SC’s location in the new coordinate system caused by the variation of the EOP compared with the location of its center of mass in the previous coordinate system and, therefore, formalize the contribution of the variation of the EOP into the SC’s ephemerides error in the Earth’s coordinate system:

$$\Delta \rho = \left( {\begin{array}{*{20}{c}} {{{Y}_{g}}\Delta {\text{UT}} - {{Z}_{g}}{{x}_{p}}} \\ { - {{X}_{g}}\Delta {\text{UT}} + {{Z}_{g}}{{y}_{p}}} \\ { - {{X}_{g}}{{x}_{p}} + {{Y}_{g}}{{y}_{p}}} \end{array}} \right),$$

where Δρ is the vector of the residuals of the SC’s ephemerides caused by the errors in forecasting the EOP. Now we return to expressions (2.3) and (2.4) for distances. The following analytic expressions of partial derivatives computed, based on them, are of interest by themselves (in our opinion) for developers of refining algorithms for the EOP:

\(\frac{{\partial \rho }}{{\partial {{x}_{p}}}} = - \frac{1}{k}\)(2(Zgcosypsinxp + XgcosΔUTcosxpcosyp – YgcosxpcosypsinΔUT)(Xg(sinΔUTsinyp – cosΔUTcosypsinxp) – Zs + Yg(cosΔUTsinyp + cosypsinΔUTsinxp) + Zgcosxpcosyp) + 2(Zgcosxp – XgcosΔUTsinxp + YgsinΔUTsinxp)(Xs – Zgsinxp – XgcosΔUTcosxp + Ygcos xpsinΔUT) + 2(Zgsinxpsinyp + XgcosΔUTcosxpsinyp – YgcosxpsinΔUTsinyp) ×  (Ys – Xg(cosypsinΔUT + cosΔUTsinxpsinyp) – Yg(cosΔUTcosyp – sinΔUTsinxpsinyp) + Zgcosxpsinyp)),

\(\frac{{\partial \rho }}{{\partial {{y}_{p}}}} = - \frac{1}{k}\) (2(Xg(cosypsinΔUT + cosΔUTsinxpsinyp) + Yg(cosΔUTcosyp – sinΔUTsinxpsinyp) – Zgcosxpsinyp)(Xg(sinΔUTsinyp – cosΔUTcosypsinxp) – Zs + Yg(cosΔUTsinyp

+ cosypsinΔUTsinxp) + Zgcosxpcosyp) + 2(Xg(sinΔUTsinyp – cosΔUTcosypsinxp)

+ Yg(cosΔUTsinyp + cosypsinΔUTsinxp) + Zgcosxpcosyp)(Ys – Xg(cosypsinΔUT

+ cosΔUTsinxpsinyp) – Yg(cosΔUTcosyp – sinΔUTsinxpsinyp) + Zgcosxpsinyp)),

\(\frac{{\partial \Delta {\text{UT}}}}{{\partial {{x}_{p}}}} = - \frac{1}{k}\) (2(Xg(cosΔUTsinyp + cosypsinΔUTsinxp) – Yg(sinΔUTsinyp – cosΔUTcosypsinxp)),

(Xg(sinΔUTsinyp – cosΔUTcosypsinxp) – Zs + Yg(cosΔUTsinyp + cosypsinΔUTsinxp)

+ Zgcosxpcosyp) – 2(Xg(cosΔUTcosyp – sinΔUTsinxpsinyp) – Yg(cosypsinΔUT + cosΔUTsinxpsinyp)),

(Ys – Xg(cosypsinΔUT + cosΔUTsinxpsinyp) – Yg(cosΔUTcosyp – sinΔUTsinxpsinyp) + Zgcosxpsinyp) + 2(YgcosΔUTcos xp + XgcosxpsinΔUT)(Xs – Zgsinxp – XgcosΔUTcosxp + YgcosxpsinΔUT)),

k = 2((Ys – Xg(cosypsinΔUT + cosΔUTsinxpsinyp) – Yg(cosΔUTcosyp – sinΔUTsinxpsinyp)

+ Zgcosxpsinyp)(Ys – Xg(cosypsinΔUT + cosΔUTsinxpsinyp) – Yg(cosΔUTcosyp – sinΔUTsinxpsin yp) + Zgcosxpsinyp) + (Xg(sinΔUTsin yp – cosΔUTcosypsinxp) – Zs + Yg(cosΔUTsinyp + cosypsinΔUTsinxp) + Zgcosxpcosyp)(Xg(sinΔUTsinyp – cosΔUTcosypsinxp) – Zs + Yg(cosΔUTsinyp + cosypsinΔUTsinxp) + Zgcosxpcosyp)

$$\begin{gathered} + {\text{ }}({{X}_{s}}-{{Z}_{g}}{\text{sin}}{{x}_{p}}-{{X}_{g}}{\text{cos}}\Delta {\text{UTcos}}{{x}_{p}} + {{Y}_{g}}{\text{cos}}{{x}_{p}}{\text{sin}}\Delta {\text{UT}})({{X}_{s}}-{{Z}_{g}}{\text{sin}}{{x}_{p}} \\ \,-{{X}_{g}}{\text{cos}}\Delta {\text{UTcos}}{{x}_{p}} + {{Y}_{g}}{\text{cos}}{{x}_{p}}{\text{sin}}\Delta {\text{UT}}){{)}^{{0.5}}}. \\ \end{gathered} $$
(2.5)

These expressions were eventually verified by being used in the simulation modeling for refining the EOP. In particular, if there are no errors, then, applying these expressions, we obtain the convergence of the obtained estimates to the genuine values of the EOP.

Finally, to simplify expressions (2.5), we can linearize the following trigonometric functions:

\(\frac{{\partial \rho }}{{\partial {{x}_{p}}}}\)= –((Zgxp + Xg – YgΔUT)(–Xgxp – Zs + Yg yp + Zg) + (Zg – Xgxp)(Xs – Zgxp – Xg + YgΔUT)+ Xgyp(Ys – XgΔUT – Yg + Zgyp))((Ys – XgΔUT – Yg + Zgyp)2 + (–Xgxp – Zs + Ygyp + Zg)2+ (Xs – Zgxp – Xg + YgΔUT)2)–0.5,

\(\frac{{\partial \rho }}{{\partial {{y}_{p}}}}\)= ((XgΔUT + Yg – Zgyp)(–Xgxp – Zs + Ygyp + Zg) + (–Xgxp + Ygyp + Zg)(Ys – XgΔUT – Yg + Zgyp)), ((Ys – XgΔUT – Yg + Zgyp)2 + (–Xgxp – Zs + Ygyp + Zg)2 + (Xs – Zgxp – Xg + YgΔUT)2)–0.5,

\(\frac{{\partial {\Delta UT}}}{{\partial {{x}_{p}}}}\)= ((Xgyp + Ygxp)(–Xgxp – Zs + Ygyp + Zg)(Xg – YgΔUT)(Ys – XgΔUT – Yg + Zgyp)+ (Yg + XgΔUT)(Xs – Zgxp – Xg + YgΔUT))((Ys – Xg ΔUT – Yg + Zgyp)2 + (–Xgxp – Zs + Ygyp + Zg)2

$$ + \,{{({{X}_{s}}-{{Z}_{g}}{{x}_{p}}-{{X}_{g}} + {{Y}_{g}}\Delta {\text{UT}})}^{2}}{{)}^{-0.5}}.$$
(2.6)

3. REFINING THE EARTH ORIENTATION PARAMETERS BASED ON THE SPACECRAFT–GROUND STATION DISTANCE MEASUREMENT: CHOICE OF METHOD AND DESIGN OF ALGORITHM

To process a batch of distance measurements, it is reasonable to use the least squares method (LSM) because, unlike various modifications of the Kalman filter (see [1]) it does not need to be tuned. Our processing algorithm for measurements is based on the canonical equation

$$\Delta \bar {X}\text{*} = {{({{{\mathbf{H}}}^{{\text{T}}}}{\mathbf{D}}_{\eta }^{{ - 1}}{\mathbf{H}})}^{{ - 1}}}{{{\mathbf{H}}}^{{\text{T}}}}{\mathbf{D}}_{\eta }^{{ - 1}}\Delta {{y}^{N}},$$

where \(\Delta \bar {X}{\text{*}}\) is a correction to estimates of the state vector of the EOP formed based on processing a sample yN of N measurements, Dη is the covariance matrix of measurement errors, and H is the block matrix of partial derivatives such that the variant of its appearance depends on the operation mode, and in the general case, its content is as follows:

$${\mathbf{H}} = \left( {\begin{array}{*{20}{c}} {\left\{ {{\text{EOP}}} \right\}}&{\left\{ {{\text{Measurements}}} \right\}}&{\left\{ {{\text{Ephemerides}}} \right\}} \end{array}} \right),$$
(3.1)

where {EOP} is a compulsory block of the matrix of partial derivatives, including derivatives of distance measurements with respect to components of vector (3.1) of the estimated EOP:

$$\{ {\text{EOP}}\} = {{\left( {\begin{array}{*{20}{c}} {\frac{{\partial {{\rho }_{i}}}}{{\partial {{x}_{p}}}}}&{\frac{{\partial {{\rho }_{i}}}}{{\partial {{y}_{p}}}}}&{\frac{{\partial {{\rho }_{i}}}}{{\partial \Delta {\text{UT}}}}} \end{array}} \right)}^{{\text{T}}}}.$$
(3.2)

The blocks “Measurements” and “Ephemerides” are additional blocks of the matrix of partial derivatives. In such a case, this matrix (as well as the estimated state vector) includes other components apart from the original three components of the EOP. If the LSM is applied to estimate the parameters of the linear model of the evolution of components of the EOP, then the block of the EOP differs from (3.1): in this case, we have

$$\{ {\text{EOP}}\} = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{{\partial {{\rho }_{i}}}}{{\partial {{x}_{p}}}}}&{\frac{{\partial {{\rho }_{i}}}}{{\partial {{y}_{p}}}}} \end{array}}&{\frac{{\partial {{\rho }_{i}}}}{{\partial \Delta {\text{UT}}}}}&{\frac{{\partial {{\rho }_{i}}}}{{\partial x_{p}^{'}}}} \end{array}}&{\frac{{\partial {{\rho }_{i}}}}{{\partial y_{p}^{'}}}}&{\frac{{\partial {{\rho }_{i}}}}{{\partial \Delta {\text{UT}'}}}} \end{array}} \right),$$

where \(\partial y_{p}^{'}\), \(\partial x_{p}^{'}\), and \(\partial \Delta {\text{UT}'}\) are the velocities of the daily variations of the EOP, xp, yp, and ΔUT, measured in mas/day, respectively.

If the block {Measurements} is used for the LSM estimates, then it includes partial derivatives of the distance measurements with respect to the components of the measurement biases (e.g., measurement errors for distances caused by the time-scale offset for the ground stations) and has the form

$$\begin{gathered} {{\left\{ {{\text{Measurements}}} \right\}}_{i}} = \underbrace {{{{\left( {\begin{array}{*{20}{c}} 0&0&0&{...}&{1(i)}&0&{...}&0&0 \end{array}} \right)}}^{{\text{T}}}}}_{N\quad {\text{SC}}}, \\ {{\left\{ {{\text{Measurements}}} \right\}}_{j}} = \underbrace {{{{\left( {\begin{array}{*{20}{c}} 0&0&0&{...}&0&{1(j)}&{...}&0&0 \end{array}} \right)}}^{{\text{T}}}}}_{N\quad {\text{SC}}}, \\ \end{gathered} $$

where i and j are the numbers of the SCs from the series of N SCs such that their measurements get into the processing.

If the block {Ephemerides} is used for the LSM estimates, then it includes partial derivatives of the distance measurements with respect to the components of the biases of the SC’s ephemerides (e.g., the errors with respect to the radius vector and binormal and the error along the orbit) and has the form

$${{\left\{ {{\text{Ephemerides}}} \right\}}_{i}} = \underbrace {{{{\left( {\begin{array}{*{20}{c}} 0&0&0& \ldots &0&{\underbrace {\begin{array}{*{20}{c}} {\frac{{\partial \rho }}{{\partial r}}}&{\frac{{\partial \rho }}{{\partial n}}}&{\frac{{\partial \rho }}{{\partial l}}} \end{array}}_i}& \ldots &0&0 \end{array}} \right)}}^{{\text{T}}}}}_{3 \times N\quad {\text{SC}}},$$

where \(\frac{{\partial \rho }}{{\partial r}}\) (is close to 1), \(\frac{{\partial \rho }}{{\partial n}}\), and \(\frac{{\partial \rho }}{{\partial l}}\) are the derivatives of the geometric distance expressed via the components of the ephemerides errors of the ith SC in the direction of the radius vector, normal direction, and the direction along the orbit, respectively.

Once M different measurements are collected, the matrix H presented by (3.1) becomes the N × M-matrix such that its columns contain the computed partial derivatives with respect to each dimension (note that, in the special case, it is an N × 1 column, where N is the number of estimated components of the state vector of the solved problem). If a six-component state vector is used, then the corresponding values of the matrix H in expression (3.1) differ from expressions (2.5) and (2.6). It would be too cumbersome to present all six here.

4. ANALYSIS OF THE POSSIBILITY TO OPTIMIZE MEASUREMENT CONDITIONS TO REFINE THE EARTH ORIENTATION PARAMETERS AUTONOMOUSLY, BASED ON THE FORECAST OF THE PARTIAL DERIVATIVES OF THE DISTANCES BETWEEN THE SC AND STATIONS BY THE COMPONENTS OF THE EOP

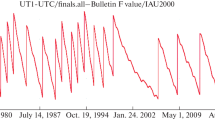
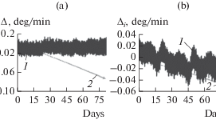
Hereinafter, the relations presented above are treated as elements of the refining algorithm for the EOP based on the LSM. Before we use them onboard, we have to design a special software including additional compensating procedures for measurement errors, errors of the SC’s ephemerides, and other error sources for the obtained estimation of the EOP. In other words, creating a comprehensive refining technology for the EOP onboard an SC based on measurements to ground stations is a complex problem; its solution has to be broken down into stages and its workability and efficiency have to be verified (by simulation modeling) at each stage. In order to implement the potential possibility to refine the EOP based on the concept developed in this paper, we need to estimate the influence of the evolution of the EOP on the measurement results for the distance between the SC and the station. To estimate the character of such an influence, we can use analytical expressions for the partial derivatives computed for the SC of constellations of satellite systems on mid-altitude orbits and stations distributed on Earth. In this case, for the evolution data of the EOP, it is reasonable to use real bulletins (see [7]). In Fig. 1, we present dependences describing the evolution of values of partial derivatives of distances between a mid-altitude SC and a surface station located near Vladivostok according to the components of the EOP over a period of several days. Note that the dependences have periodically repeating maximums and minimums caused by the variable influence of the EOP on the obtained measurements between the SC and ground stations.

Fig. 1.
figure 1

Partial derivatives of distances with respect to components of the EOP, cm/mas: — xp, ⋅⋅⋅⋅⋅⋅⋅⋅ yp, –⋅–⋅– ΔUT.

Full size image

The character and amplitude of the dependences in Fig. 1 show the following points. First, the periods when the EOP significantly affect the measurement residuals occur quite rarely and their duration is bounded. Secondly, for each of the EOP, a change in its “weight” by just 1-mas leads to the growth of the residuals between the real and forecast measurements of the distances between the SC and station of up to 2.5 cm (its theoretical maximum is 3.1 cm). The average residual size per day, depending on the station’s location and the selected SC, varies from 0.2 to 0.5 cm per mas of the EOP, provided that the worst conditions and hidden areas are excluded. Also, it can be seen that all components of the EOP affect the residual size of the measurements simultaneously; however, sometimes the influence of a particular parameter of EOP  is significantly greater than that of the others. Due to the diversity of the perturbing agents mentioned in the previous section, such as errors in the measurements and ephemerides of an SC, the actual frequency of the measurement sessions with the use of only one SC may not be sufficient to refine the EOP. Let us estimate the influence of the evolution of the EOP on the measurements for the SC–station distance by using several SCs. To do this, we construct the dependences of the partial derivatives of the distance between several SCs and ground stations for each parameter of the EOP separately. The dependences are presented in Figs. 2–4.

Fig. 2.
figure 2

Partial derivatives of distances with respect to xp for various SCs on near mid-altitude orbits and one ground station. The conditional index numbers of the SCs are as follows: — 1, ⋅⋅⋅⋅⋅⋅⋅⋅ 2, - - - 3, – – – 4, –⋅–⋅– 5.

Full size image
Fig. 3.
figure 3

Partial derivatives of distances with respect to yp for various SCs on near mid-altitude orbits and one ground station. The conditional index numbers of the SCs are as follows: — 1, ⋅⋅⋅⋅⋅⋅⋅⋅ 2, - - - 3, – – – 4, –⋅–⋅– 5.

Full size image
Fig. 4.
figure 4

Partial derivatives of distances with respect to ΔUT for various SCs on near mid-altitude orbits and one ground station. The conditional index numbers of the SCs are as follows: — 1, ⋅⋅⋅⋅⋅⋅⋅⋅ 2, - - - 3, – – – 4, –⋅–⋅– 5.

Full size image

Analyzing the dependences presented in Figs. 2–4, we see that if the SC is used in the orbits nearby, then the curves describing the partial derivatives of the distances between the SC and ground station repeat each other. Thus, it is possible to plan experiments in order to ensure that the process of obtaining the maximum volume of informal measurements is continuous, provided that the number of SCs able to receive signals from ground stations is fixed. In the future, constructing a comprehensive refining procedure for the EOP onboard an SC, this has to be taken into account as a crucial factor in planning sessions. This is also important in terms of the potentially achievable precision of the obtained estimates of the EOP. The results presented in Figs. 2–4 can be treated as original data for the problem of optimizing the experiment on refining the EOP. We develop an approach that allows solving this problem formally using the necessary optimality conditions (see [10]). However, this problem itself is sufficiently hard and therefore can be considered in a separate paper.

5. REFINING PROCESS FOR EOP: SIMULATION RESULTS

We carry out simulation modeling in order to obtain the results of refining the EOP onboard an SC by the algorithms given above. The conditions and specific properties of the used models are as follows:

—SC’s motion trajectories are simulated by interpolating the final data of the system of the Precise Detection of the Ephemeris–Time Corrections by a special software (see [11]);

—we use IERS models (see [6]) and their C04 bulletins to simulate the Earth’s rotation taking into account the precession, nutation, rotation and pole shifts;

—measurements are processed in sessions consisting of collections of measurements of the distances between the SC and station accumulated over a period of several hours; as a result of processing the measurements, we obtained an estimate of the EOP used to predict them and to form a new session of accumulated measurements.

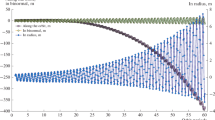
Below, we have presented the main results of simulating the refining process for the EOP based on the algorithm described above. In particular, two curves are shown in Fig. 5: the genuine evolution of the component xp of the EOP (x_true), i.e., the evolution based on the database from the IERS bulletins, is a smooth curve, while the second curve is an estimate of the component xp obtained by the LSM processing of the distances between the SC and stations (x_est).

Fig. 5.
figure 5

The dynamics of the genuine evolution of the EOP and of the estimate obtained by LSM, where MJD is the Modified Julian Day.

Full size image

The error level of the estimates of the EOP achieved in this experiment by using the algorithm described above is illustrated in Fig. 6, which presents the errors of refining the EOP dxp, dyp, and dΔUT, respectively.

Fig. 6.
figure 6

Errors of estimates of the EOP, obtained for the iterative processing of 500-measurement sessions, mas: — dxp, ⋅⋅⋅⋅⋅⋅⋅⋅ dyp, –⋅–⋅– dΔUT.

Full size image

In this experiment, the amplitudes of the estimation errors on the level of 2 mean-square deviations do not exceed 10 mas; i.e., they are less accurate than the estimations ensured by using the data from [7]. The simulation was carried out under the influence of random and systematic measurement errors; also, the increasing errors of the SC’s ephemerides are taken into account. According to the experiments, the errors of estimates of the EOP depend on the following agents:

—the dynamics of the actual evolution of the EOP;

—the number and orbital location of the SCs participating in the refining process for the EOP;

—the number and ITRF-coordinates of the ground stations participating in the refining process for the EOP;

—the level and dynamics of the evolution of errors of the ephemerides of the SCs participating in the refining process for the EOP;

—the random and systematic measurement errors for distances between the SC and ground stations;

—the length of the surveillance, the repetition frequency of significant measurements, the planning criterion of the experiment, the way measurements are rejected, and the condition of the iterated initialization of the obtained estimates based on the forecast values of the EOP. As we noted above, the results of such investigations could be studied in an independent paper.

In the future, we plan additional simulation–modeling investigations of the functioning of a prototype of the onboard refining algorithm for the EOP, taking into account the influence of a broad range of uncontrollable agents.

CONCLUSIONS

The concept for refining an SC’s onboard model to predict the EOP using the measurements between the SC and ground stations is developed. Implementing of the developed concept is proposed as an information technology of the SC’s onboard refining of the EOP aimed at refining the precision of the onboard formation of the SC’s ephemerides and to improve the quality of the corresponding services provided to consumers. The refining algorithm for the evolution of the EOP based on the measurements of the distances between the SC and ground stations is proposed too. The main relations necessary to implement the estimation algorithm for the EOP, including the analytic relations for the partial derivatives of the SC-station distance measurements with respect to the components of the vector of the EOP; this allows applying them to refine the EOP onboard an SC. The results of the simulation modeling of the onboard refining process for the EOP are presented: they show that the errors of estimates of the EOP are on the level of several mas. The rules to compute and plan measurement sessions (including measurements by several SCs) are proposed. In our opinion, the obtained results provide the necessary conditions for the further numerical experiments to simulate onboard refining processes for the EOP, taking into account the influence of a wide range of uncontrollable factors and to detail onboard algorithms to refine the EOP.