Model of Representation and Acquisition of New Knowledge by an Autonomous Intelligent Robot Based on the Logic of Conditionally Dependent Predicates

Abstract

The model for the representation of declarative and procedural knowledge of an autonomous intelligent robot is developed without reference to a specific subject area. The logic of conditionally dependent predicates underlies the construction of this model. Procedures that allow an autonomous intelligent robot to automatically generate new knowledge needed for a readout in the process of planning goal-seeking behavior in undetermined conditions of a problem-solving environment are proposed. The method of proving the satisfiability of the formulas under the logic of conditionally dependent predicates with linear complexity is based on the attribution of object variables in them as objects of the problem-solving environment and serves to process knowledge that is used by an autonomous intelligent robot to automatically build plans for goal-seeking behavior under undetermined operating conditions.

INTRODUCTION

One of the relevant problems of artificial intelligence is the development of effective models for representation and processing the knowledge of an autonomous intelligent robot (AIR) for planning goal-seeking behavior in various problematic a priori undetermined conditions of a problem-solving environment (PSE). An effective solution to this problem makes it possible to create AIRs that can function purposefully in PSEs that are difficult to reach and aggressive for humans, for example, underwater and space robots, speleologists’ robots, robots for various operations on terrain that is dangerous for humans, etc.

Considering that a detailed description of the regularities of a real PSE that is difficult to reach is almost impossible, the model of knowledge representation that is stored in the AIR’s memory should be formed without reference to a specific subject area. In other words, the knowledge representation model of an AIR should be presented in such a way that it provides an opportunity for effectively planning goal-seeking behavior with incomplete initial information about the PSE laws after it is specified in the current operating conditions.

It should be noted that it is advisable to endow the robot’s brain, by analogy with a human [1], with the capabilities of visually effective, visually figurative, and conceptual thinking [2], in order to create AIRs that can function purposefully in a priori real undetermined PSEs. Consequently, this makes it possible to solve the following classes of behavior problems.

1. The robot a priori does not have knowledge of the laws governing the transformation of situations in a PSE related to the achievement of a goal, and it must identify effective actions by self-study, using trial and error, and forming a conditionally unconditional program of goal-seeking behavior based on this [3].

2. An AIR takes the situation in which the goal of the behavior is directly achieved, through its purposeful transformations, and a regularity model of the change in situations of a PSE is given to the AIR. In this case, the robot needs to automatically plan and effectively implement its goal-seeking behavior based on the model of knowledge stored in its memory and the model of the current PSE situation generated by it.

3. The robot, while it is in a PSE, does not directly take the situation in which the goal of the behavior given to it is achieved. In such conditions, having processed the knowledge stored in its memory based on reasonable grounds, the AIR must form a plan of the polyphase goal-seeking behavior, providing for a total change of the current PSE situations in a given sequence after reaching a specific sub-goal in each of them related to achieving a common goal [4].

It should also be noted that, at the initial stage of development, the models of representation and processing knowledge based on the use of a first-order predicate logic are most widely used in artificial intelligence systems for various purposes, including in AIRs’ systems of solutions. For example, an adaptive inference strategy in undetermined PSEs was proposed in [5]; the possibilities of applying the first-order predicate logic to representing and processing knowledge on the example of domestic and foreign solvers of various problems are considered in [6]; the general theory and problems associated with the automatic proof of theorems are presented in [7]; in-depth analysis and the opportunities and problems associated with the application of first-order predicate logic are shown in [8], and the main fundamental achievements of foreign researchers in the application of first-order predicate logic in artificial intelligence systems are given in [9–11]. The effective procedures for deductive inference in non-monotonic environments are developed as part of a logical approach in [12].

However, the effective application of models of representation and processing of knowledge based on first-order logic and for planning the goal-seeking behavior of AIRs in a priori undetermined PSE conditions is limited by the following main problems.

1. The need to specify a detailed model for the representation of knowledge about PSE laws to derive solutions [13, 14].

2. The lack of use of second-order predicates and predicates of higher orders in knowledge representation models, which significantly reduces the functionality of intelligent problem solvers for autonomous robots based on them [7, 15].

3. The complexity of finding solutions to complex problems in processing the knowledge, which is reduced to proving theorems by a search method [8, 15]. If this search is partially streamlined based on various inference strategies, the procedures for planning the behavior of an AIR, based on the application of the automatic proof of theorems in first-order predicate logic, still remain in the general case with exponential complexity. This disadvantage is due to the fact that the semantic component in the formal description of objects, events, and PSE laws is not used in the logic of first-order predicates either in the knowledge representation models or in the procedures for processing them when deriving solutions. However, a significant contribution to the solution of this problem of deductive inference was made in [16], which offers a deduction algorithm based on the transformation of semantic networks, which makes it possible to organize several types of parallel inference and significantly reduce the complexity of the theorem’s proof. However, taking into account the relatively low computational resources of the onboard computer of an autonomous robot and the fact that this approach does not completely solve the problem of deriving solutions related to the use of first-order predicate logic, its use is limited to planning the behavior of AIRs under a priori undetermined PSE conditions.

The circumstances mentioned above led to the transition to a new paradigm for the development of a logical approach to the creation of artificial intelligence associated with the use of special knowledge representation models using fuzzy logics for their synthesis and processing [2, 17, 18]. However, the problem of creating effective procedures for planning the goal-seeking behavior of AIRs under a priori undetermined PSEs with the linear complexity of finding decisions remains open today, despite the diversity of the research undertaken in this direction [18, 19].

Considering the issues related to the generation of new knowledge for the decisions of AIRs in the process of the goal-seeking behavior in undetermined PSE conditions, the following points should be noted:

1. A robot can use only the information incorporated in the model of the presentation set to it, and information emerging from the PSE to obtain new knowledge when planning goal-seeking behavior.

2. The problem of the acquisition of new knowledge is the closest in its content to the problem of its automatic generation. Three principles are widely used to solve this problem at the present time: simulating common sense models [20], using scripts [21], and using pseudophysical logic [22].

Unfortunately, the use of different models in a single problem solver for behavior planning and knowledge acquisition underlies the implementation of these principles. As a rule, this knowledge consists of production models and special models for describing PSE situations. However, it is advisable to use the same representation model both for the automatic generation of new knowledge and for the prompt derivation of decisions in the process of planning the goal-seeking behavior of AIRs in a priori undetermined PSEs. This requirement is due to the need for planning the behavior of AIRs in undetermined PSEs in real time, and the use of different models for the representation and acquisition of knowledge does not allow solving complex problems in an operational way.

In addition, these principles of knowledge acquisition are focused on the creation of highly specialized intelligent systems operating in a specific subject area. In this respecty, they cannot provide an effective solution to the main problems associated with the automatic generation of new knowledge in the process of planning the behavior of AIRs in undetermined PSE conditions.

The use of Mivar technologies can be attributed to one of the attempts to combine the procedures for deriving decisions and acquiring knowledge in the context of a single model of knowledge representation for an AIR [23]. However, the model of knowledge representation and conclusion procedures proposed in this case do not provide for the solution of the following important problems that significantly affect the effectiveness of planning the goal-seeking behavior of an AIR in a priori undetermined operating conditions.

1. Identification of differences between the current and target situations of PSEs and the automatic construction of a plan of the goal-seeking behavior based on this [13, 24, 25].

2. Automatic determination of the procedure for eliminating the differences observed by the AIR between the actual and target situations of the PSE when planning its behavior in real time [26]. As a result, the main advantage of using production models of knowledge representation in problem solvers is lost. This advantage is associated with the construction of plans for the goal-seeking behavior of an AIR in the a priori undetermined PSE conditions with a linear complexity of inference. This is due to the fact that the search for a solution to a complex task of goal seeking behavior, as a rule, comes down to a complete and exhaustive search with an arbitrary choice of the difference, after the elimination of which the AIR begins to construct a plan for transforming the current situation into the target situation of the PSE. In addition, cycles of chains of unproductive actions can occur in planning goal-seeking behavior that is being formed in this case; they need to be removed before implementation of this plan.

3. Isolation of an area in the PSE which is related directly to the achievement of the current goal or sub-goals of the behavior [27].

4. The decision making by analogy, which does not allow obtaining new information about objects and events observed in the PSE, based on the knowledge available in the model, when there is such a need in the process of automatically constructing a plan of goal-seeking behavior in a priori underdetermined operating conditions [24, 28].

The model of representation and automatic generation of new knowledge, which allows the AIR to plan goal-seeking behavior under undetermined PSE conditions when combining visually figurative thinking with individual elements of conceptual thinking, is proposed in this work. The construction of the developed model is based on the logic of conditionally dependent predicates [29] (the formalization language is given in the Appendix), which allows representing declarative and procedural knowledge of the AIR, regardless of the specific subject area, and circumvent the above-mentioned disadvantages of the well-known logical models. In this case, the automatic construction of a plan for the goal-seeking behavior of an AIR in an a priori undetermined PSE is reduced to performing the following basic steps:

1. Attribution of object variables in conditionally dependent predicates of the knowledge representation model by objects in the PSE in order to adapt the general information of the robot to the current operating conditions.

2. The direct planning of goal seeking behavior based on production inference rules that are formed after the attribution of objects in a PSE to object variables in typical knowledge representation structures.

The generation of new knowledge in this model also relies on the attribution of conditionally dependent predicates, which are used to construct typical constructions for the representation of declarative and procedural knowledge, and is reduced to proving the validity of formulas with linear complexity in the resulting PSE pattern in this way. For example, the procedures for adding and obtaining new knowledge of AIRs based on the logic of conditionally dependent predicates by drawing complex inferences are proposed in [30].

1. EXPERIMENTAL

Model of Representation and Generation of New Knowledge of an AIR

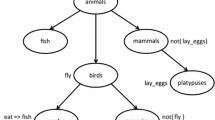
In the logic of conditionally dependent predicates, the region of acceptability of each object variable ${{y}_{i}}({{X}_{i}}) \in Y,\,\,\,Y = \{ {{y}_{i}}({{X}_{i}})\}$, $i = \overline {1,m}$, in conditionally dependent formulas (hereinafter, variables and formulas) is determined by the set of characteristics X_i. In turn, each object or event of the PSE $O = \{ {{o}_{j}}({{X}_{j}})\}$, $j = \overline {1,{{m}_{1}}}$, is also determined by the set X_j of the characteristics describing them. The attribution of the object variable ${{y}_{i}}({{X}_{i}})$ in an arbitrary formula of logic of conditionally dependent predicates is allowed by various objects of the PSE ${{o}_{j}}({{X}_{j}})$ if and only if they have a set of characteristics X_i; i.e., condition ${{X}_{i}} \subseteq {{X}_{j}}$ is satisfied for them [29]. In this case, the resulting statement is true. For example, the formula Fly (birds (the main characteristics of birds, developed wings, no damage)) becomes a true statement only when the constant substituted in it, for example “Sparrow,” develops wings and has no damage.

Thus, in the logic of conditionally dependent predicates, as a result of the attribution of an arbitrary n-place formula $M[{{y}_{1}}({{X}_{1}}),\; \ldots ,\;{{y}_{k}}({{X}_{k}}),\; \ldots ,\;{{y}_{n}}({{X}_{n}})]$, the resulting statement is true if and only if the conditions${{X}_{k}} \subseteq {{X}_{{ok}}}$ are satisfied for objects of the PSE ${{o}_{k}}({{X}_{{ok}}})$, $k = \overline {1,n}$, used to attribute the object variables ${{y}_{k}}({{X}_{k}})$ in it. Here,${{X}_{{ok}}}$ and X_k are the sets of characteristics describing the object of the problem-solving environment ${{o}_{k}}({{X}_{{ok}}})$ and the object variable ${{y}_{k}}({{X}_{k}})$. The conditionally dependent predicates themselves are not directly interpreted, and their feasibility in a given PSE model is checked by the truth value of the statements obtained as a result of the attribution of object variables in them by objects from this model in the process of planning the behavior of AIRs.

Let us consider various formulas of the logic of conditionally dependent predicates, which allow us to represent the knowledge of AIRs without regard to a specific subject area.

Let two formulas be given, ${{P}_{1}}(y({{X}_{1}}))$ is To be (living object$y({{X}_{1}})$) and ${{P}_{2}}({{f}_{i}}(y({{X}_{{fi}}})))$ is To be able to fly$(y({{X}_{{fi}}}))$. Here f_i is a functional symbol, meaning that all objects of the PSE having characteristics X_fi can fly. By connecting these formulas with a conjunction, we get the formula $D = {{P}_{1}}(y({{X}_{1}}))\& {{P}_{2}}({{f}_{i}}(y({{X}_{{fi}}})))$, which means To be a living object and to be able to fly. This formula is true if ${{X}_{{fi}}} \subseteq {{X}_{1}}$, otherwise it is inconsistent.

Definition 1. A formula ${{P}_{1}}({{y}_{1}}({{X}_{1}}))\& {{P}_{2}}({{f}_{i}}(y({{X}_{{fi}}})))$ is called a conditionally-dependent logical addition (hereinafter, addition) of the first type of formula ${{P}_{1}}({{y}_{1}}({{X}_{1}}))$ and is denoted by ${{P}_{1}}({{y}_{1}}({{X}_{1}}),{{f}_{i}}({{X}_{{fi}}}))$ if the condition ${{X}_{{fi}}} \subseteq {{X}_{1}}$ is satisfied.

Thus, an AIR can replenish its knowledge of various objects and events of PSE-based on additions of the first type, for example, to determine whether an object can fly. The answer to this request will be affirmative if the condition ${{X}_{1}} \subseteq {{X}_{j}}$ is fulfilled for the addition ${{P}_{1}}({{y}_{1}}({{X}_{1}}),{{f}_{i}}({{X}_{{fi}}}))$ and the object ${{o}_{j}}({{X}_{j}})$. As a result of such an attribution, the true statement ${{P}_{1}}({{o}_{j}}({{X}_{j}}),{{f}_{i}}({{X}_{{fi}}}))$ is obtained, The object${{o}_{j}}({{X}_{j}})$ is a living object and it can fly.

Let two additions ${{Q}_{1}} = {{P}_{1}}(y({{X}_{1}}),{{f}_{1}}({{X}_{{f1}}}))$ and ${{Q}_{2}} = {{P}_{2}}(y({{X}_{2}}),{{f}_{2}}({{X}_{{f2}}}))$ of the first type be given.

Definition 2. If the condition $({{X}_{1}} \subset {{X}_{2}}) \otimes ({{X}_{{f2}}} = {{X}_{{f1}}})$ is fulfilled for two additions Q₁ and Q₂, and the meaningful words bijectively corresponding to the predicate symbols Р₁ and Р₂ are the same, then the first one is a generalization of the second, where the sign $\otimes$ means that both parts of the condition are to be fulfilled simultaneously.

For example, the logical addition To be (living object$y({{X}_{1}})$ and able to fly) in the subject area living objects is a generalization of the logical addition To be (bird$y({{X}_{2}})$ and able to fly).

Suppose that the addition Q₁ is a generalization of the addition Q₂, then we can prove the following statements for a given pair of logical additions.

Statement 1. If the addition Q₁ is a generalization of the addition Q₂, then the set of PSE objects ${{O}_{1}} \subset O$, defining the region of acceptability of the variable $y({{X}_{1}})$, conditionally dependently expands the set of PSE objects ${{O}_{2}} \subset O$ which satisfy the requirements for the attribution of variable $y({{X}_{2}})$, i.e., ${{O}_{2}} \subset {{O}_{1}}$. In this case, the variable $y({{X}_{1}})$ is a conditionally dependent generalization of the variable $y({{X}_{2}})$, where the region of acceptability, for example, the object variable $y({{X}_{2}})$ is determined by the PSE objects ${{o}_{j}}({{X}_{j}}) \in O$ for which the condition ${{X}_{2}} \subseteq {{X}_{j}}$ is satisfied.

Proof. The validity of this statement follows from the fact that, according to Definition 2, the condition $\left| {{{X}_{1}}} \right| < \left| {{{X}_{2}}} \right|$ is satisfied for the cardinalities of the sets of characteristics X₁ and X₂ respectively, describing the variables in formulas Q₁ and Q₂. Consequently, the number of PSE objects satisfying the requirements for the variable $y({{X}_{1}})$, which is determined by a smaller number of characteristics, will be greater than the number of objects that satisfy the requirements for the variable $y({{X}_{2}})$, and ${{O}_{2}} \subset {{O}_{1}}$ follows from condition $({{X}_{1}} \subset {{X}_{2}}) \otimes ({{X}_{{f2}}} = {{X}_{{f1}}})$. Therefore, Statement 1 is true.

Statement 2. Let the addition Q₁ be a generalization of the addition Q₂. Then, if the statement $Q_{1}^{*} = {{P}_{1}}(a({{X}_{a}}),{{f}_{1}}({{X}_{{f1}}}))$ is false when the variables included in these logical additions are attributed by the same constant $a({{X}_{a}})$, then the statement $Q_{2}^{*} = {{P}_{2}}(a({{X}_{a}}),{{f}_{2}}({{X}_{{f2}}}))$ will also be false, and when the statement $Q_{2}^{*}$ is true, then the statement $Q_{1}^{*}$ will be true.

Proof. 1. Suppose that a false statement $Q_{1}^{*}$ is obtained by the attribution of a variable in a generalization of Q₁ by the constant $a({{X}_{a}})$. Therefore, the condition ${{X}_{1}} \subseteq {{X}_{a}}$ is not feasible for this addition and the constant $a({{X}_{a}})$. Then, from the condition that the addition Q₁ is a generalization of the addition Q₂, it follows that ${{X}_{1}} \subset {{X}_{2}}$. Therefore, the condition ${{X}_{2}} \subseteq {{X}_{a}}$ is also not feasible for the addition of Q₂ and the constant $a({{X}_{a}})$.

2. Suppose that the true statement $Q_{2}^{*}$ is obtained by denoting a variable in the addition Q₂ by the constant $a({{X}_{a}})$. Thus, condition ${{X}_{{f2}}} \subseteq {{X}_{2}} \subseteq {{X}_{a}}$ is true for the logical addition Q₂ and the constant $a({{X}_{a}})$.

Since the addition of Q₁ is a generalization of the addition of Q₂, the condition $({{X}_{{f1}}} = {{X}_{{f2}}}) \otimes ({{X}_{1}} \subset {{X}_{2}})$ is satisfied. Hence condition ${{X}_{{f1}}} \subseteq {{X}_{1}} \subseteq {{X}_{a}}$ is true for the addition of Q₁ and the constant $a({{X}_{a}})$. Consequently, the true statement $Q_{1}^{*}$ is obtained as a result of the variable attribution in the addition Q₁ by the constant $a({{X}_{a}})$.

3. The validity of Statement 2 follows obviously from steps 1 and 2.

Thus, the permissible attribution of a variable in the addition Q₂ by various PSE objects generates statements, which are particular examples for the addition Q₁.

In the general case, the replacement of variables with other variables with a narrower level of generality than the replaced variable is allowed in conditionally dependent formulas.

Example 1. Let the variable $y({{X}_{5}})$ mean Different birds. Then, as a result of replacing the variable $y({{X}_{1}})$ in the logical addition Q₁To be (living object$y({{X}_{1}})$), able to fly to the variable $y({{X}_{5}})$, we obtain a logical addition ${{Q}_{3}} = {{P}_{1}}(y({{X}_{5}}),{{f}_{1}}({{X}_{{f1}}}))$To be (bird$y({{X}_{5}})$), able to fly. Such an addition is feasible if the variables $y({{X}_{1}})$ and $y({{X}_{5}})$ satisfy the condition ${{X}_{1}} \subset {{X}_{5}}$. Therefore, the addition of Q₃ is obtained by replacing the variable $y({{X}_{1}})$ in the addition Q₁ with the variable $y({{X}_{5}})$; in this case, the initial logical addition will be a generalization.

Thus, in the general case, the substitution of variables $y({{X}_{j}})$, $j = \overline {1,n}$, instead of the variable $y({{X}_{i}})$ into an arbitrary addition ${{P}_{i}}(y({{X}_{i}}),{{f}_{1}}({{X}_{{f1}}}))$ is allowed if the variable $y({{X}_{i}})$ is their generalization.

Consequently, replacing the variable $y({{X}_{5}})$ in the addition Q₃ with the variable Sparrows$y({{X}_{6}})$, we get a logical addition ${{Q}_{4}} = {{P}_{1}}(y({{X}_{6}}),{{f}_{1}}({{X}_{{f1}}}))$To be (a sparrow$y({{X}_{6}})$able to fly). The addition thus formed has a lower level of generality than the original addition.

It should be noted that the formulas obtained in this way are satisfiable in the region of acceptability of the variables contained in them only if the initial formula is satisfiable in this region according to the condition that the variables in the formulas are replaced by other variables. For the statement $Q_{4}^{*} = {{P}_{1}}(a({{X}_{a}})$, f₁(X_f1)), which is the result of the attribution of a variable in the addition Q₄ by the constant $a({{X}_{a}})$Specific sparrow, all logical additions Q₁, Q₃, and Q₄ are its generalizations.

In this case, the additions Q₁, Q₃, and Q₄ and the statement $Q_{4}^{*}$ can be ordered in the form of a tuple $M = \langle {{Q}_{1}};{{Q}_{3}};{{Q}_{4}};Q_{4}^{*}\rangle$ according to the level of generality of the variables and constants included in them, with the condition ${{X}_{1}} \subset {{X}_{4}} \subset {{X}_{6}} \subseteq {{X}_{a}}$.

Example 2. The tuple M formed based on the formulas obtained above will have the following content 〈(Living objects y(X₁), able to fly (Х_f1)); (Birds y(X₄), able to fly (Х_f1)); (Sparrows y(X₆), able to fly (Х_f1)); (Sparrow а(Х_а) able to fly (Х_f1))〉, where Х_f1 = {the main characteristics of living objects, to have developed wings, no damage}.

Let an arbitrary object of the PSE ${{o}_{j}}({{X}_{j}})$ satisfy the requirements of the variable ${{y}_{i}}({{X}_{i}})$ at least in one of the additions included in the structure of the tuple M. Then, moving along the elements of the tuple M from the right to the left of the statement obtained as a result of the valid attribution of the object ${{o}_{j}}({{X}_{j}})$, an AIR can summarize its knowledge about this object if it is required in the decision-making process.

Definition 3. Let an arbitrary tuple M be given; it consists of a set of additions Q of the first type. Let us call the first addition Q₁ in the tuple M the formula generating it and note that in this formula the set of characteristics X₁ defining its variable ${{y}_{1}}({{X}_{1}})$ has the minimal power $\left| {{{X}_{1}}} \right|$. For example, the predicate To be (living object y(X₁)), able to fly (Х_f1)) is the generating formula for the tuple M given above.

It should be noted that using generic relations [31] based on the element Q₁ of the tuple M, we can generate a tree G, each branch of which R_j, $j = \overline {1,m}$, is built and then branched based on the formulas with variables ${{y}_{i}}({{X}_{i}})$, $i = \overline {1,n}$, for which the variable in the generating formula is their generalization. In this case, the formula ${{P}_{k}}({{y}_{{}}}({{X}_{k}}),{{f}_{1}}({{X}_{{f1}}}))$, which marks an arbitrary vertex ${{{v}}_{k}} \in {{R}_{j}}$ is a generalization of all the subordinate formulas ${{P}_{j}}({{y}_{j}}({{X}_{j}}),{{f}_{1}}({{X}_{{f1}}}))$ in the branch R_j of the tree G, since the condition ${{X}_{k}} \subset {{X}_{j}}$ is satisfied for them.

For example, let the formula Q₁, which generates a tuple M, be defined by the variable Living objects, then based on it, we can generate a branched tree G with branches ${{R}_{j}} \in G$ based on the formulas generating the branches, containing the variables Birds, Fishes, etc.

Thus, an AIR can efficiently generalize or clarify the necessary knowledge in the decision-making process about objects of an arbitrary problem environment with the help of declarative knowledge that defines the properties and skills of various classes of objects, formed as a set of corresponding G_h$h = \overline {1,d}$ trees.

Let us define the rules of substitution which provide the possibility of expanding the declarative knowledge existing in AIR about the objects of a PSE by forming different branches R_j of the tree ${{G}_{h}}$ based on the formulas contained in them.

Substitution rule 1. Let there be an addition ${{Q}_{1}} = {{P}_{1}}(y({{X}_{1}}),{{f}_{1}}({{X}_{{f1}}}))$ and a set of conditionally dependent functional symbols $F = \{ {{f}_{i}}({{X}_{{fi}}})\}$, $i = \overline {2,n}$, defining the corresponding properties and skills of various objects ${{o}_{j}}({{X}_{j}})$ of the PSE for which the condition ${{X}_{{f1}}} \subset {{X}_{{f2}}} \subset {{X}_{{f3}}},\; \ldots ,\; \subset {{X}_{{fn}}} \subset {{X}_{1}} \subseteq {{X}_{j}}$ is fulfilled. Then a complex logical addition can be formed based on the formula Q₁ by the recursive substitution of functional symbols ${{f}_{2}}({{X}_{{f2}}}),{{f}_{3}}({{X}_{{f3}}}),\; \ldots ,\;{{f}_{n}}({{X}_{{f{\text{n}}}}})$. The order of such a substitution is determined by the order laid down in the condition ${{X}_{{f1}}} \subset {{X}_{{f2}}} \subset {{X}_{{f3}}},\; \ldots ,\; \subset {{X}_{{fn}}}$. The result is a complex logical addition ${{P}_{1}}[y({{X}_{1}}),{{f}_{1}}({{f}_{2}}({{f}_{3}},\; \ldots ,\;{{f}_{n}}({{X}_{{fn}}})))]$, which allows us to replenish the knowledge of an AIR on various objects of the PSE based on checking the truth value of the following statement The PSE object${{o}_{j}}({{X}_{j}})$ has functionality ${{f}_{1}}({{X}_{{f1}}}),{{f}_{2}}({{X}_{{f2}}}),\; \ldots ,\;{{f}_{n}}({{X}_{{fn}}})$. This statement is true if the condition ${{X}_{1}} \subseteq {{X}_{j}}$ is met for an arbitrary PSE object${{o}_{j}}({{X}_{j}})$. For example, the AIR can determine such PSE objects that can simultaneously walk, swim, and fly, based on a complex logical addition on a given set of characteristics.

Substitution rule 2. Let the complex logical addition ${{P}_{1}}[{{y}_{1}}({{X}_{1}}),{{f}_{1}}({{f}_{2}}({{f}_{3}},\; \ldots ,\;{{f}_{n}}({{X}_{{fn}}})))]$ and the ordered set of variables $\left\langle {{{y}_{1}}({{X}_{1}}),{{y}_{2}}({{X}_{2}}),{{y}_{3}}({{X}_{3}}), \ldots ,{{y}_{m}}({{X}_{m}})} \right\rangle$ for which the condition C = $({{X}_{1}} \subset {{X}_{2}} \subset {{X}_{3}}, \ldots , \subset {{X}_{m}})$ is fulfilled be given. Then replacing the variable ${{y}_{1}}({{X}_{1}})$ with any of the variables ${{y}_{2}}({{X}_{2}}),{{y}_{3}}({{X}_{3}}), \ldots ,\;{{y}_{m}}({{X}_{m}})$ is admissible. If such a replacement is made in the order determined by condition C, it results in the following branch R_j of the tree G

$$\begin{gathered} {{R}_{j}} = P_{1}^{j}[{{y}_{1}}({{X}_{1}}),{{f}_{1}}({{f}_{2}}({{f}_{3}},\; \ldots ,\;{{f}_{n}}({{X}_{n}})))] \to P_{2}^{j}[{{y}_{2}}({{X}_{2}}),{{f}_{1}}({{f}_{2}}({{f}_{3}},\; \ldots ,\;{{f}_{n}}({{X}_{n}})))] \\ \to \ldots \;P_{m}^{j}[{{y}_{m}}({{X}_{m}}),{{f}_{1}}({{f}_{2}}({{f}_{3}},\; \ldots ,\;{{f}_{n}}({{X}_{n}})))], \\ \end{gathered} $$

where the edges of the branch connecting its adjacent vertices are indicated by arrows.

It should be noted that every logical addition contained in the R_j branch of the tree ${{G}_{h}}$ is a generalization of the formula to its right.

The content of the formulas in the branches R_j of trees G_k, which is extensible based on the substitution rules 1 and 2, makes it possible to supplement the declarative knowledge of the AIR by attribution of the variables contained in them by specific PSE objects.

Let us consider the principle of constructing a model of procedural knowledge of an AIR based on the formulas of the logic of conditionally dependent predicates. Let the following formulas be given:

${{F}_{1}} = {{P}_{1}}({\text{robot}},{{y}_{1}}({{X}_{1}}))$ means to take (robot, object${{y}_{1}}({{X}_{1}})$);

${{F}_{2}} = {{P}_{2}}({\text{robot}},{{y}_{2}}({{X}_{2}}))$ means to come (robot, object${{y}_{2}}({{X}_{2}})$);

${{F}_{3}} = {{P}_{3}}({\text{robot}},{{y}_{3}}({{X}_{3}}))$ means The passage from the location of the robot to the object${{y}_{3}}({{X}_{3}})$ must be free.

Definition 4. The formula ${{F}_{1}}\& {{F}_{2}}\& {{F}_{3}}$ is called the logical addition of the second order of formula ${{F}_{1}}$ and is written as

$${{F}_{4}} = {{P}_{1}}\left[ {{\text{robot}} \to ({{P}_{3}}({{y}_{1}}({{X}_{1}})) \to {{b}_{1}}({{y}_{1}}({{X}_{1}})) \to {{b}_{2}}({{y}_{1}}({{X}_{1}})))} \right]$$

if the condition $({{X}_{2}} \subseteq {{X}_{1}}) \otimes ({{X}_{3}} \subseteq {{X}_{1}})$ is satisfied; this makes it possible to replace the variables ${{y}_{2}}({{X}_{2}})$ and ${{y}_{3}}({{X}_{3}})$ with the variable ${{y}_{1}}({{X}_{1}})$, where

Х₁ is the set of characteristics that PSE objects must possess, Х₁ = {a₁ is the overall dimensions of the object for which the robot’s working body is able to grab it; a₂ is the weight of the object, which should not exceed the carrying capacity of the robot’s arm; an object ${{y}_{1}}({{X}_{1}})$ is not attached to another object and is located at a height within the working area of the robot’s arm};

${{P}_{1}}$ is a logical addition identifier to take an object;

${{b}_{1}}({{y}_{1}}({{X}_{1}}))$ is the action to come to an object${{y}_{1}}({{X}_{1}})$;

${{b}_{2}}({{y}_{1}}({{X}_{1}}))$ is the action to grab and lift an object${{y}_{1}}({{X}_{1}})$.

This formula can be interpreted as follows: if the statement ${{P}_{3}}\left[ {o({{X}_{j}})\& {{b}_{2}}(o({{X}_{j}}))\& {{b}_{1}}(o({{X}_{j}})} \right]$ is true (condition ${{X}_{1}} \subset {{X}_{j}}$ is satisfied and there are no obstacles on the path to this object) for an arbitrary PSE object $o({{X}_{j}})$, then the AIR can come, grab, and lift this object.

Definition 5. If, for arbitrary additions of the second order,

$${{P}_{1}}[{\text{robot}}({{y}_{1}}({{X}_{1}})) \to P_{1}^{*}({{y}_{1}}({{X}_{1}}) \to {{b}_{1}}({{y}_{1}}({{X}_{1}})))];$$

$${{P}_{2}}[{\text{robot(}}{{y}_{2}}({{X}_{2}})) \to P_{2}^{*}({{y}_{2}}({{X}_{2}}) \to {{b}_{2}}({{y}_{2}}({{X}_{2}})))],$$

the condition $({{X}_{1}} \subset {{X}_{2}}) \otimes (P_{1}^{*} = P_{2}^{*}) \otimes ({{b}_{1}} = {{b}_{2}})$ is true, then the first addition is a generalization of the second addition, where $P_{1}^{*}$ and $P_{2}^{*}$ are the conditions that must be fulfilled in the PSE in order for the robot to successfully work out its actions.

For a pair of complements of the second type in which one of them is a generalization of the other, we can also prove statements similar to Statements 1 and 2.

It should be noted that the verification of the feasibility in the PSE of the conditions of each addition of the second type which determine the possibility of successfully working out the corresponding actions, makes it possible to identify the differences between the perceived environment and the required environment for the planned actions. The robot decides that there is a difference between the perceived and the required PSE situation, which must be eliminated in order to successfully work out a specific action of the second type of addition, which is selected during the planning process when the necessary conditions for this are fulfilled in the environment. The procedure for eliminating the differences identified in this way is determined automatically, starting with the position of the last established AIR difference in the process of planning goal-seeking behavior.

It should also be noted that if we add to the structure of the second type of addition a formal description of the results that are achieved by working out the actions included in the substation, we will get the typical behavior firmware (TBF), which allows the AIR to significantly reduce the search space for solutions to various tasks when planning the goal-seeking behavior. Such a reduction in the search space for solutions to the tasks facing the robot is ensured by choosing several effective actions included in the TBF structure at each step of planning the behavior.

Thus, the following two typical constructions of the logic of conditionally dependent predicates should be used to represent the procedural knowledge of the AIR.

1. The second type of additions containing in their structure one action at a time. This allows us to get a flexible model for the representation of procedural knowledge in the form of a set of individual additions. Each such addition includes a description of the required situation, the perception of which in the PSE provides an efficient working out of the corresponding action. However, the use of only such a model for presenting the procedural knowledge of an AIR leads to an increase in the dimension of the decision-finding space in the process of planning goal-seeking behavior.

2. In the form of a TBF, for example, having the following structure (the firmware of the behavior ${{F}_{5}}$ is to transfer an object into the PSE)

$$\begin{gathered} {{F}_{5}} = {{P}_{1}}({\text{robot}},{{y}_{2}}({{X}_{2}}),{{y}_{3}}({{X}_{3}})) \\ \leftrightarrow \;{{P}_{1}}\left[ {{\text{robot}} \to ({{P}_{2}}({{y}_{2}}({{X}_{2}})) \to {{b}_{1}}({{y}_{2}}({{X}_{2}})))} \right. \\ \to \;({{P}_{3}}({{y}_{2}}({{X}_{2}})) \to {{b}_{2}}({{y}_{2}}({{X}_{2}}))) \to ({{P}_{4}}({{y}_{3}}({{X}_{3}})) \\ \to \;{{b}_{3}}({{y}_{2}}({{X}_{2}}),{{y}_{3}}({{X}_{3}})) \to {{b}_{4}}({{y}_{2}}({{X}_{2}}),\left. {{{y}_{3}}({{X}_{3}})))} \right] \Rightarrow {{Z}_{5}}, \\ \end{gathered} $$

where $\leftrightarrow$ is the operation of equivalence of the formulas; P₁ is the TBF identifier to transfer an object; P₂ is the necessary condition There must be a passage in the environment from the location of the robot to the object${{y}_{2}}({{X}_{2}})$ for the effective operation of the action b₁; P₃ is the necessary conditions that must simultaneously be fulfilled in the PSE for the successful operation of action b₂, ${{P}_{3}}$ = {An object ${{y}_{2}}({{X}_{2}})$ is not attached to another object, it has weight and overall dimensions, respectively, of not more than $a_{1}^{*}$ and $a_{2}^{*}$; it is located within the working area of the robot’s arm at height $h{\text{*}}$}; P₄ is the necessary condition The passage must be from the current location of the object${{y}_{2}}({{X}_{2}})$ to the location of the object ${{y}_{3}}({{X}_{3}})$ for the effective operation of actions b₃ and b₄; Z₅ is a structured description of the results of the refinement of the behavior firmware presented, for example, in the form of a semantic network built in the state space or in the form of conditions running in the environment.

However, in the case where there is no TBF in the knowledge model of the robot required to build a behavior plan, there is a need for its automatic generation based on the typical descriptions of individual actions that are selected according to the conditions and the results of their execution specified in their respective second type of additions. Thus, the model for presenting the procedural knowledge of the robot should include both additions of the second type, determining the conditions for successfully testing individual actions, and the TBF formed in accordance with its functional purpose, in order to ensure the efficient functionality of the AIR.

2. THE SPECIFIC CHECKS OF THE SATISFIABILITY OF FORMULAS IN THE LOGIC OF CONDITIONALLY DEPENDENT PREDICATES

We note that, in the general case, there are no generally significant conditionally dependent formulas in the calculus of conditionally dependent predicates, since their truth value is determined from the results of checking the fulfillment of a given condition. We can define only a monotonic set of constants (PSE objects) on which an arbitrary formula or its various additions will take the true value. In other words, each formula, and, more precisely, the sets of characteristics defining the variables entering it, allows us to single out the monotonic region of their allowable values in an arbitrary subject domain, i.e., the values at which this formula becomes true. Thus, it is possible to prove the validity of formulas in the logic of conditionally dependent predicates on a given set of premises (formulas) that define the current PSE situation by analogy with theorems in the logic of first-order predicates.

In the general case, the logic of conditionally dependent predicates allows us to establish the validity or refutation of a particular statement in specific PSE conditions according to the truth of the statement obtained as a result of the admissible valuation of variables in the corresponding formula by objects of this environment. For example, the monotonic domain of definition of a variable in the formula To be (living object${{y}_{i}}({{X}_{i}})$) and be able to fly is a set of objects PSE ${{o}_{j}}({{X}_{j}}) \in O$ for which the condition ${{X}_{i}} \subseteq {{X}_{j}}$ is fulfilled, where the set of characteristics ${{X}_{i}}$ = {characteristics of a living object, to have developed wings, no damage}.

Definition 6. An arbitrary addition of the first or second type is conditionally dependently valid for a given set of constants $A = \{ {{a}_{i}}({{X}_{{ai}}})\}$, $i = 1,m$, if condition ${{X}_{1}} \subseteq {{X}_{{ai}}}$ is true for each ${{a}_{i}}({{X}_{{ai}}}) \in A$ and the variable of these additions.

Let us formulate the property of the satisfiability of the formula B, which determines, for example, the goal of the behavior of the AIR, given irrespective of the specific subject area and containing a second type of addition, on a given set of additions or formulas $W = \{ {{W}_{1}},{{W}_{2}},\; \ldots ,\;{{W}_{i}},\; \ldots ,\;{{W}_{m}}\}$, describing, for example, a generalized model of the current PSE.

The need to check that formula B is a logical consequence of the set of formulas W may arise, for example, in the case when the AIR must find out in the planning process of goal-seeking behavior whether the conditions corresponding to this formula are fulfilled, which ensure the successful completion of the actions contained in it PSE situations.

For example, let the set of true statements $S = \{ {{S}_{1}},{{S}_{2}},\; \ldots ,\;{{S}_{i}},\; \ldots ,\;{{S}_{m}}_{3}\}$ and formula B be given. They determine the actual model of the current PSE conditions and the behavioral goal set by the AIR in the form of an addition F₆, respectively. Suppose a robot, in the process of planning goal-seeking behavior, needs to check the possibility of effectively working out the action of b₁ on its specific object in the current PSE conditions. The validity of the formula B on a given set of statements S, determining the current state of the PSE, is proved to solve this problem.

Statement 3. The actions of AIR in formula B are feasible in the current PSE conditions, i.e., formula B is a logical consequence of a set of true statements S if and only if, for each predicate entering its structure, the set of formulas S contains an expression ${{S}_{i}} \in S$ for which the given predicate serves as its generalization.

Proof. 1. It is obvious that formula B is true on the set of statements S if the complex statement ${{S}_{1}}\& {{S}_{2}}\& ,\; \ldots ,\;\& {{S}_{i}}\& ,\; \ldots ,\;\& {{S}_{m}}\& B{\text{*}}$ is true, where $B{\text{*}}$ is the statement obtained from formula B by denoting variables in its predicates ${{F}_{i}} \in B$ by PSE objects from statements ${{S}_{i}} \in S$, $i = \overline {1,{{m}_{3}}}$ for which these predicates are a logical generalization.

2. According to Statement 2, statement $B{\text{*}}$ is true. Therefore, the statement S₁ & S₂ &, ..., $\& {{S}_{i}}\& ,\; \ldots ,\;\& {{S}_{m}}\& B{\text{*}}$ is also true. Thus, the validity of Statement 3 is proved.

Consequently, the conclusion which allows us to establish that formula B is a logical consequence of formulas S is based on the verification of the fulfillment of an arbitrary formula B, which includes the actions performed by the AIR, on a given set of formulas B that define the current PSE situation.

Example 3. Suppose that an underwater AIR has a technical vision that provides it with the ability to recognize a given set of PSE objects. Let some initial current situation S be observed in the environment: the robot sees a sunken object on the seabed; this object has height h₁; the object $o(X)$ lies on it, which has many characteristics Х, Х = {weight (а₁), overall dimensions (а₂), it is not attached to another object} and the basket (B) of the elevator, having a height of fences h₂ and serving to lift various objects from the seabed.

There are no insurmountable obstacles between the location of the AIR and the object o(X); i.e., there is a free path from the location of the robot to the object o(X). The robot can also freely move from the location of the object o(X) to the elevator. The robot must move the object o(X) and put it in the basket of the elevator.

Thus, the purpose of the behavior for the AIR is given in the procedural form Move the object o(X) to the location of the elevator and drop this object into its basket. To achieve this goal, according to its content, the AIR chooses the TBF ${{F}_{5}}$. This typical firmware allows the AIR to allocate a section in the PSE where it will directly function. The meaning of the variables in the target given to the robot by the PSE objects is given for this. The result is the following set of statements that determine the actual model of the behavior of the AIR in the current situation PSE S*:

to come ((robot, o(X)), (the passage is free));

to grab (robot, o(X)), (not fixed, has weight (${{a}_{1}} \leqslant a_{1}^{*}$) and dimensions (${{a}_{2}} \leqslant a_{2}^{*}$); the height of the object position is (${{h}_{1}} \leqslant h{\text{*}}$));

to come ((robot, B), (the passage is free));

to put (robot, o(X), B), (the height of the basket walls is (${{h}_{2}} \leqslant h{\text{*}}$)).

Consequently, conditions Р₂, Р_3, and Р₄ are fulfilled in the current PSE situation, and all the resulting statements as a result of denoting variables for a given goal are true, since each predicate in formula ${{F}_{5}}$ obviously serves as a generalization of one of the true statements in the original description S of the current problem situation environment. Thus, the TBF ${{F}_{5}}$ is directly implemented in the current PSE conditions, and the AIR only has to work out the actions contained in it in a given order to achieve the goal set before it.

Consider the case when there are insurmountable obstacles between the AIR and the PSE object $o(X)$, as well as between the position of this object and the elevator basket, i.e., when conditions Р₃ and Р₄ of implementing the TBF are not met in the environment. In this case, the robot selects the TBF from memory, which allows it to form the locally optimal route along a straight line to the location of the specified objects built, for example, based on scheduling algorithms for moving in an environment with obstacles [32]. The TBFs formed on the database of algorithms are stored in the AIR’s memory as typical elements of procedural knowledge representation that are selected for implementation in the process of planning behavior by the corresponding identifier the presence of obstacles.

Let us suppose that an AIR needs to obtain new knowledge without reference to the specific conditions of the PSE in the process of forming a plan of goal-seeking behavior to test the validity of formula B, according to Statement 3. The solution of this problem is reduced to the formation of the set of additions ${{W}_{H}} = \{ {{W}_{j}}\}$, $j = \overline {1,k}$ needed to derive the solution of the required task based on the robot’s given knowledge model, which is a set of additions of the second type of W and TBF. To do this, the intellectual AIR solver checks the fulfillment of formula B consisting of logical additions W_H on the given set of formulas W. If formula B turns out to be realizable on the set of formulas W, then the additions W_H are used as typical elements of the procedural knowledge representation of the AIR.

Definition 7. The addition of the second type, for the determination of which the validity of formula B is checked on the given AIR model of knowledge representation, is called the basic addition of this formula.

Definition 8. If the basic addition is false, then formula B is also false, which is a conjunction of the basic addition ${{W}_{j}} \in {{W}_{H}}$ with the set of given formulas defining the conditions that must be fulfilled in the PSE to effectively work out the corresponding action ${{b}_{j}}({{X}_{j}})$.

Definition 9. Formula B is satisfiable on a set of additions W (the logical consequence of formulas W) if and only if, for the given attribution of I variables in these formulas, they take the truth value. In addition, the condition is true that for a basic addition of formula B there is at least one addition ${{W}_{i}} \in W$, which is its generalization.

Statement 4. Formula B is satisfiable on an arbitrary set of formulas W if and only if it takes the true value, and ${{T}_{1}} = \,\,\sim \,{\kern 1pt} ({{W}_{1}}\& {{W}_{2}}\& ,\; \ldots ,\;\& {{W}_{i}}\& ,\; \ldots ,\;\& {{W}_{m}})\& B$ is false for a given attribution of variables I, and the condition that the set of formulas W includes at least one addition of the second type ${{W}_{i}} \in W$, which is a generalization to the basic addition of formula B, which is also true.

Proof. 1. For the attribution

$${{I}_{1}} = \{ {{a}_{1}}({{X}_{{a1}}}),{{a}_{2}}({{X}_{{a2}}}), \ldots ,\;{{a}_{k}}({{X}_{{ak}}})\} ,$$

let formula B be true. Then if we assume that formula B is satisfiable on the set of formulas W, then the formula ${{T}_{1}} = \sim ({{W}_{1}}\& {{W}_{2}}\& , \ldots ,\;\& {{W}_{i}}\& ,\; \ldots ,\;\& {{W}_{m}})\& B$, by definition, must be false. Hence, the formula $\sim ({{W}_{1}}\& {{W}_{2}}\& ,\; \ldots ,\;\& {{W}_{i}}\& ,\; \ldots ,\;\& {{W}_{m}})$ is false, since formula B for the attribution of I₁ is true. Therefore, if formula B is true, then the formula ${{W}_{1}}\& {{W}_{2}}\& ,\; \ldots ,\;\& {{W}_{i}}\& ,\; \ldots ,\;\& {{W}_{m}}$ for the attribution of I₁ is also true, provided that the formula T₁ is false.

2. Let the statement following from the formula ${{W}_{i}} \in W$, which is a generalization of the basic addition of formula B, for the attribution of I₁ be false. Therefore, the statement following from formula B, according to Statement 2 for this meaning, will also be false. Hence, the formula T₁ for the attribution of I₁ will be true, which contradicts the condition that formula B is satisfied on the set of the given additions W. Therefore, formula B, in this case, cannot be fulfilled on the set of formulas W.

3. The validity of Statement 4 clearly follows from steps 1 and 2.

Thus, in terms of conditionally dependent predicates, the proof of the fulfillment of an arbitrary formula B on the given set of additions W is reduced to the attribution of variables in ${{T}_{1}}$ and B by PSE objects, provided that the set W contains an addition, which is a generalization of the basic addition of formula B. Then the conditions are checked that a false statement is formed as a result of such an attribution of the formula T₁, and the statement obtained when these objects attribute variables in formula B is true.

Example 4. Let us assume that the AIR must determine whether it can catch up with a moving object in the PSE. To solve this problem, the robot forms formula B, which includes the following additions: Determine the characteristics of a moving object and Overtake (AIR,${{y}_{j}}({v}\text{*},L\text{*},\gamma \text{*})$), where ${v}{\text{*}}$ is the speed of movement that the object should not exceed; $L{\text{*}}$ is the maximum allowable distance to the object, and $\gamma {\text{*}}$ is the maximum allowable value of the polar coordinates of the meeting point with the object.

The first logical addition of formula B allows the AIR to estimate the following actual characteristics of a moving object: the speed of movement ${v}$, the distance to the object L, and the values of the polar coordinates γ of the meeting point with the object [33]. The truth of the value obtained as a result of a statement is checked after substituting these characteristics of a moving object $o({v},L,\gamma )$ into the basic logical complement Overtake (AIR,${{y}_{j}}({v}\text{*},L\text{*},\gamma \text{*})$). This statement is true if condition $({v} \leqslant {v}\text{*}) \otimes (L \leqslant L\text{*}) \otimes (\gamma \leqslant \gamma \text{*})$ is satisfied for a moving object ${{o}_{i}}({v},L,\gamma )$. In this case, the AIR takes a decision on the expediency of pursuing a moving object and implements the Overtake an object TBF.

3. METHOD FOR CHECKING THE SATISFIABILITY OF FORMULAS IN THE LOGIC OF CONDITIONALLY DEPENDENT PREDICATES

Let us formulate in a general way a method for checking the satisfiability of formulas on a given set of formulas that determine the current PSE situation in the logic of conditionally dependent predicates.

Let two arbitrary n-place formulas D₁ = ${{P}_{1}}({{y}_{1}}(X_{1}^{1}),{{y}_{2}}(X_{2}^{1}), \ldots ,{{y}_{n}}(X_{n}^{1}))$ and D₂ = ${{P}_{2}}({{y}_{1}}(X_{1}^{2}),{{y}_{2}}(X_{2}^{2}), \ldots ,{{y}_{n}}(X_{n}^{2}))$ be given, such that the meaningful words bijectively corresponding to the predicate symbols P₁ and P₂ coincide.

Definition 10. Formula D₁ is a generalization of formula D₂ if the condition

$$\forall {{y}_{i}}(X_{i}^{1}) \in {{D}_{1}}\exists {{y}_{j}}(X_{j}^{2}) \in {{D}_{2}}[(X_{i}^{1} \subset X_{j}^{2}) \oplus (X_{i}^{1} = X_{j}^{2})]$$

is true, where $\oplus$ means that validity of either the left or right side is sufficient to satisfy the initial condition.

We note that in this case, the attribution of variables in the D₂ formula by PSE objects that are allowed for this results in the generation of particular examples for the D₁ formula. If a false statement is formed as a result of an arbitrary attribution of the variables in the formula D₁, then the statement obtained as a result of the same attribution of the variables in the formula D₂ will also be false.

It should also be noted that if the condition

$$\forall {{y}_{i}}(X_{i}^{1}) \in {{D}_{1}}\exists {{y}_{j}}(X_{j}^{2}) \in {{D}_{2}}[(X_{i}^{1} = X_{j}^{2})]$$

is true, then the formulas ${{D}_{1}}$ and ${{D}_{2}}$ are conditionally logically equivalent.

Let two arbitrary formulas also be given:

$${{D}_{3}} = \forall {{y}_{i}}(X_{i}^{j}) \in Y[{{P}_{1}}({{y}_{1}}(X_{1}^{1}),{{y}_{2}}(X_{2}^{1}),\; \ldots ,\;{{y}_{n}}(X_{n}^{1}))\& {{P}_{2}}({{y}_{1}}(X_{1}^{2}){{y}_{2}}(X_{2}^{2}))],\quad i = \overline {1,n} ;\quad j = \overline {1,2} ;$$

$${{D}_{4}} = \forall {{y}_{i}}(X_{i}^{j}) \in Y[{{P}_{3}}({{y}_{1}}(X_{1}^{3}),{{y}_{2}}(X_{2}^{3}))\& {{P}_{4}}({{y}_{1}}(X_{1}^{4}),{{y}_{2}}(X_{2}^{4}))],\quad i = \overline {1,2} ;\quad j = \overline {3,4} .$$

Definition 11. Formula D₃ is a generalization of formula D₄ if the following conditions are true:

(a) Formulas D₃ and D₄ include the same number of predicates;

(b) For each predicate P_i included in the structure of formula D₃, which contains $n_{i}^{1}$ variables, in the structure of formula D₄ there is a predicate of the same name with it ${{P}_{j}}$, including $n_{j}^{2}$ variables, for which one of the following conditions holds:

(1) If $n_{j}^{2} < n_{i}^{1}$, then $\forall {{y}_{j}}(X_{j}^{2}) \in {{P}_{j}}\exists {{y}_{i}}(X_{i}^{1}) \in {{P}_{i}}[(X_{i}^{1} \subset X_{j}^{2}) \vee (X_{i}^{1} = X_{j}^{2})]$.

(2) If $n_{j}^{2} = n_{i}^{1}$, then $\forall {{y}_{i}}(X_{i}^{1}) \in {{P}_{i}}\exists {{y}_{j}}(X_{j}^{2}) \in {{P}_{j}}[(X_{i}^{1} \subset X_{j}^{2}) \vee (X_{i}^{1} = X_{j}^{2})]$.

Suppose there is a set of arbitrary formulas W and formula B, which is a conjunction consisting of an addition of the second type and predicates that determine the conditions under which this formula is true in the PSE model. The following method for solving this problem in the logic of conditionally dependent predicates is proposed in order to establish the validity of the statement that formula B is feasible in the given knowledge representation model consisting of the set of formulas W.

Input variables:$W$ is the set of initial premises; $A = \{ a({{X}_{{ai}}})\}$, $i = \overline {1,{{m}_{1}}}$ are the constants used to attribute variables in the formulas ${{W}_{i}} \in W$ and B; B is the formula whose feasibility is required to be determined on the set of premises W.

Intermediate variables: a pair of formulas $\left\langle {{{W}_{i}},B} \right\rangle$ in which the addition ${{W}_{i}}$ is a generalization of the basic addition of formula B; $W_{i}^{*}$ and B* are the statements obtained by the attribution of the variables in formulas ${{W}_{i}} \in W$and B by the constants $a({{X}_{{ai}}}) \in A$.

Output variables: a false or true statement, obtained by the attribution of variables in the formula ${{T}_{1}} = \sim ({{W}_{1}}\& {{W}_{2}}\& ,\; \ldots ,\;\& {{W}_{i}}\& ,\; \ldots ,\;\& {{W}_{m}})\& B$ with constants $a({{X}_{{ai}}}) \in A$, for which formula B is true.

The method.

1. Start.

2. Check the condition the given set W includes the formula${{W}_{i}} \in W$ which is a generalization of the basic addition of formula B: if the condition is satisfied, then go to step 3, otherwise go to step 7.

3. Form the formula ${{T}_{1}}$.

4. Form the attribution of $I = \{ {{a}_{i}}({{X}_{{ai}}})\}$, $i = \overline {1,w}$, which consists of constants that satisfy the requirements of all variables in formula B, i.e., formula B for the attribution I is true.

5. Replace the variables ${{y}_{j}}({{X}_{j}})$ in the formula ${{T}_{1}}$ with the admissible constants ${{a}_{i}}({{X}_{{ai}}}) \in I$ and obtain the expression ${{D}_{5}} = \sim (W_{1}^{*}\& W_{2}^{*}\& ,\; \ldots ,\;\& W_{i}^{*}\& ,\; \ldots ,\;\& W_{m}^{*})\& B{\text{*}}$ based on this.

6. Check the condition statement D₅is false: if it is true, then formula B is satisfiable on the given set of formulas W, go to step 8; otherwise, go to step 7.

7. Formula B cannot be fulfilled on the initial set of formulas W.

8. End.

Consider the case when the set of formulas W does not contain an addition, which is a generalization of the basic logical addition of formula B. Then, in accordance with step 2 of the proposed method for determining whether the formula B is satisfied, we decide that it is not feasible on the given set of formulas W.

However, the intellectual solver of problems of the AIR using the proposed model of knowledge representation can be endowed with procedures for the automatic generation of formula D_i, which allows generalizing the information available in formulas W. For this, the variable ${{y}_{i}}({{X}_{i}})$ is replaced in the formula ${{W}_{i}} \in W$ in which the content of the predicate symbol coincides with the content of the predicate symbol in the basic addition of formula B, with the variable ${{y}_{j}}({{X}_{j}})$, for which condition $({{X}_{j}} \subset {{X}_{i}}) \otimes ({{X}_{j}} \subset {{X}_{B}})$ is fulfilled, where X_B is the set of characteristics defining the variable in the basic addition of formula B.

Therefore, if it is revealed that formula B is true on a set of formulas in which the premise D_i is a generalization of the logical addition of formula ${{B}_{j}}({{y}_{j}}({{X}_{j}}),{{f}_{i}}({{X}_{{fi}}})) \in B$, then the formula D_i is added to the set of original formulas W, and formula B is regarded satisfiable on the set of formulas $W \cup {{D}_{i}}$ obtained in this way.

Example 5. Assume the robot, in the process of planning goal-seeking behavior, needs to establish the validity of the statement The$o({{X}_{j}})$ PSE object is able to move independently. Suppose that the logical complement The cars$({{X}_{i}})$ are able to move, which is not a generalization of a verified statement, is contained in the declarative model of knowledge representation of an AIR. Then if the declarative model of the knowledge of the robot contains a typical element that defines, in general, all objects that can move using the set of characteristics X_k, then we get the addition Objects (X_k) can move after changing the variable The cars (X_i) to the variable Moving objects (X_k). This logical addition allows the AIR to establish that the object $o({{X}_{j}})$ is able to move independently if the condition ${{X}_{k}} \subseteq {{X}_{j}}$ is fulfilled for it.

4. CONCEPT FOR THE APPLICATION OF THE KNOWLEDGE REPRESENTATION MODEL FOR PLANNING THE GOAL-SEEKING BEHAVIOR OF AN AIR

The proposed model for the presentation and generation of new knowledge allows the AIR to automatically generate a plan of purposeful behavior in an undetermined PSE as follows. First, it is necessary to identify the differences at each step of planning the behavior between the situation perceived in the PSE and the situation required to successfully work out the actions of the TBF selected at this step. Then, the TBF is detected; they contain actions that eliminate these differences. After this, the production rules of the output are automatically generated; they have the following structure: If there is a difference$P_{i}^{*}$, then the actions of the TBF F_i must be implemented to eliminate it. Using the products obtained in this way, the robot automatically builds a plan of behavior that allows it to achieve the goal set in the procedural form by a targeted search in the subtask space based on the conditions and results of working out the actions contained in the selected TBF [26].

Example 6. Assume the conditions P_i necessary for successfully working out the actions of the TBF F_i chosen at the current planning step of the behavior are not fulfilled in the PSE. In other words, there are differences between the current and the required PSE situation, as illustrated by the fact that the conditions P_i are not met in the problem environment and must be eliminated in order to successfully work out the actions included in the structure of the TBF F_i.

In this case, the AIR chooses the TBF F_j, depending on the content of the condition P_i; the actions of this TBF, included in its structure, allow us to eliminate the difference corresponding to this condition. The production output rule $\sim {\kern 1pt} {{P}_{i}}\& {{F}_{j}} \to {{S}_{i}}$ is formed based on this; this means that practicing the actions of the TBF F_j allows us to convert the current PSE situation into situation S_i, in which the condition P_i is satisfied.

Further, if the conditions P_j necessary for practicing the actions included in the structure of the TBF F_j are not fulfilled in the PSE, then the robot proceeds to the next step of behavior planning. At this step, the next TBF is selected according to the content of conditions P_j, etc., until a behavior firmware, the actions of which the AIR can directly work out in the current PSE situation, is revealed. The chain of actions formed in this way makes it possible to eliminate in the PSE the differences that prevent effectively working out the actions of the TBF corresponding to the given behavior goal. At the same time, the procedure for practicing AIR actions in the plan of the goal-seeking behavior thus formed is determined relative to the last distinction taken into account in it.

Statement 5. The evaluation $\beta$ of the complexity of automatically constructing a plan of goal seeking behavior of AIR in an underdetermined PSE based on the proposed model of knowledge representation is determined by the following boundary values:

$$1 \leqslant \beta \leqslant \sum\limits_{i = 1}^n {{{m}_{i}}} .$$

Proof. 1. Let us take the number of automatically generated and applied production inference rules in the process of planning the goal-seeking behavior of an AIR as an indicator of the evaluation of complexity $\beta$.

2. Let the conditions necessary for successful completion of the first productional inference rule be fulfilled after its formation for the action b₂ contained in it in the PSE. In this case, the AIR’s behavior plan will consist of two actions: ${{b}_{2}} \to {{b}_{1}} \to$ the goal is achieved, where b₁ is the action included in the structure of the second type of addition that defines the given goal of the behavior. Therefore, the minimum value of the estimated complexity of the output $\beta$ is determined by the expression $\beta \geqslant 1$.

3. Suppose that there are m_i differences between the current and the desired PSE situation at each ith step of behavior planning; these differences impede the development of the planned actions ${{b}_{i}}$ that need to be eliminated (m_i is the number of conditions that must be fulfilled in the PSE in order to successfully complete the actions ${{b}_{i}}$ of the TBF selected at the ith planning step). Then the AIR will need to form not more than $\sum\nolimits_{i = 1}^n {{{m}_{i}}}$ products in the planning process of goal-seeking behavior to eliminate all the differences observed in the PSE between the perceived and the PSE situations required for the actions, where n is the total number of planning steps. Consequently, the maximum value of evaluation $\beta$ cannot be greater than the value $\sum\nolimits_{i = 1}^n {{{m}_{i}}}$.

4. $1 \leqslant \beta \leqslant \sum\nolimits_{i - 1}^n {{{m}_{i}}}$ follows obviously from steps 1–3.

It should be noted that the mathematical apparatus of fuzzy sets can be used to describe the characteristics of various objects and situations of the PSE, variables in the formulas of the logic of conditionally dependent predicates, and the conditions that are required for the effective development of the planned actions by the AIR. This allows a good generalization of the knowledge given to the robot. For example, all lightweight and small-sized objects in the PSE, which are nearby, i.e., in the working area of the AIR’s manipulator, can be captured by its working body. Thus, the AIR can use the accumulated experience of behavior in the new environmental conditions, similar to the previously encountered conditions, if there is an analogy between different objects and PSE situations [28].

The proposed knowledge representation model also allows organizing the polyphasic behavior of the AIR [4] in a complex and undetermined PSE. In this case, the goal of the behavior of the robot is set in procedural form in the form of interconnected subgoals, the consistent implementation of which in their respective environmental situations provides a solution to the common task set before it. In other words, the plan of purposeful polyphase behavior is formed and the AIR is implemented in stages. The robot moves to a new planning stage in the case when the corresponding behavior goal is achieved at the previous stage.

CONCLUSIONS

The approach proposed in the paper, based on the application of the logic of conditionally dependent predicates, allows us to represent and generate new knowledge of an AIR regardless of the specific subject area in the process of the automatic planning of goal-seeking behavior in a priori undetermined PSEs. This in turn provides the ability of the AIR to adapt in the process of its behavior to the undetermined conditions of the PSE and effectively organize the targeted activities based on this.

The developed method for checking the fulfillment of the formulas in the logic of conditionally dependent predicates is reduced to the attribution of variables in them and to the verification of the truth value of the statements obtained as a result of the given conditions. Thus, it is possible for an AIR to make decisions in real time in the process of purposeful behavior and quickly achieve the goals facing it in difficult PSE conditions.

The further development and application of the proposed model of knowledge representation of an AIR is associated with the organization of instrumental activities based on them by defining, using conditionally dependent predicates, in the process of planning the behavior of such PSE objects, which it can use as tools for efficiently performing certain actions on other environmental objects. This allows the AIR to achieve its goals in the difficult conditions of a real undetermined problem environment.

THE FORMALIZATION LANGUAGE OF THE LOGIC OF CONDITIONALLY DEPENDENT PREDICATES

The subject-predicate conditionally dependent language defines the foundation for the formalization of the logic of conditionally dependent predicates. The proposed conditionally dependent language differs from the well-known subject-predicate language [7] in that the subject variables are set using a number of characteristics that are characteristic of them, providing them with a different degree of generality. The sets of characteristics obtained in this way define application constants (ACs) and conditionally dependent object variables (OVs) of the language of conditionally dependent predicates.

The alphabet of a conditionally dependent subject-predicate language can be determined based on the classification of objects and the characteristics describing them, given in [31], using the following concepts.

The PSE objects. Various objects of the problem environment can be both AC individuals, and these OVs

$a_{i}^{0}(X_{i}^{0})$, $i = \overline {1,{{n}_{1}}}$ are ACs with a zero (E = 0) level of generality;

$y_{i}^{1}(X_{i}^{1})$, $i = \overline {1,{{n}_{2}}}$ are OVs of the kind type with the level of generality E = 1;

$y_{i}^{2}(X_{i}^{2})$, $i = \overline {1,{{n}_{3}}}$ are OVs of the kind genus with the level of generality E = 2;

$y_{i}^{3}(X_{i}^{3})$, $i = \mathop {1,{{n}_{4}}}\limits^{\_\_\_\_\_}$ are OVs of the kind class with the level of generality E = 3,

where the superscript shows the level of generality of the concepts that define the objects of the PSE and the corresponding OV or AC; $X_{i}^{j}$ is the set of characteristics with the help of which in this case the ith subject variables of the jth level of generality are described.

The sets ${{A}_{i}}(F_{A}^{i})$, $i = \overline {1,{{n}_{5}}}$ are variables of the kind conditionally dependent sets, where $F_{A}^{i}$ is the set of characteristics that must be different OVs and ACs to belong to the set ${{A}_{i}}(F_{A}^{i})$, for example, the OV $y_{1}^{1}(X_{1}^{1}) \in {{A}_{1}}(F_{A}^{1})$, if the condition $F_{A}^{1} \subseteq X_{1}^{1}$ is satisfied. In the set $F_{A}^{i}$, superscript i (hereinafter) determines the correspondence between the given set of characteristics and conditionally dependent sets A_i, and subscript A (hereinafter) shows that the set $F_{A}^{i}$ refers to variables of the corresponding kind, in this case to conditionally dependent sets A_i. Conditionally dependent sets are used to isolate monotonic inference plots in a non-monotonic subject domain with respect to the concepts defining their name, for example, flying animals in the subject domain living objects.

The variables ${{P}_{1}},{{P}_{2}},\; \ldots ,\;{{P}_{m}}$ and the $p_{1}^{1},p_{1}^{2},\; \ldots \in {{P}_{1}}$, $p_{2}^{1},p_{2}^{2},\; \ldots \in {{P}_{2}},\; \ldots ,\;p_{m}^{1},p_{m}^{2},\; \ldots \in {{P}_{m}}$ constants of the signs sort characterize the color, weight, geometrical dimensions, shape, chemical composition, and smell of various OVs or ACs. For example, the grade variable shape is defined by the following values: round shape, square shape, etc.

Variables ${{S}_{i}},i = \overline {1,{{n}_{6}}}$, and constants $s_{j}^{i} \in {{S}_{i}}$, $j = \overline {1,{{n}_{7}}}$, of the kind components determine the elements that make up the OVs or ACs. For example, the AIR manipulator consists of a working body, actuators, etc.

Variables ${{B}_{i}}(F_{b}^{i})$, $i = \overline {1,{{n}_{7}}}$ and constants $b_{j}^{i} \in {{B}_{1}}(F_{b}^{i})$, $j = \overline {1,{{n}_{8}}}$ of the kinds permissible actions and abilities denote the skills and actions that can be performed by ACs and OVs (including the AIR) or which can be performed on the given AC or OV, for example, the ability to fly and the action to transfer the object. Here $F_{b}^{i}$ is the set of characteristics that the OV and the AC must have in order for them to have the appropriate skill or, for example, the AIR can perform on all objects of the PSE belonging to the OV $y_{i}^{1}(X_{i}^{1})$ all actions $b_{i}^{j}(X_{i}^{j})$ related to the variable ${{B}_{i}}(F_{b}^{i})$ under the condition $F_{b}^{i} \subseteq X_{i}^{1}$. For example, the AIR can manipulate all objects of the PSE when they have certain dimensions and weight.

The variables ${{\Psi }_{i}}(F_{\psi }^{i})$, $i = \overline {1,{{n}_{9}}}$, and constants $\psi _{j}^{i}(X_{j}^{i}) \in {{\Psi }_{i}}(F_{\psi }^{i})$, $j = \overline {1,{{n}_{{10}}}}$, $F_{\psi }^{i} \subseteq X_{j}^{i}$ of the kind properties denote such characteristics of the OV and AC which determine their functional purpose or the possibility of using an AIR as an auxiliary tool, where $F_{\psi }^{i}$ is the set of characteristics that the OV and AC must have in order to have the ith property. For example, all ACs belonging to the OV $y_{i}^{1}(X_{i}^{1})$ of the kind species have the property $\psi _{j}^{i}(X_{j}^{i}) \in {{\Psi }_{i}}(F_{\psi }^{i})$ if the condition $X_{i}^{j} \subseteq X_{i}^{1}$ is fulfilled.

Variables ${{C}_{i}}(F_{C}^{i})$, $i = \overline {1,{{n}_{{11}}}}$ and constants $c_{j}^{i}(X_{j}^{i}) \in {{C}_{i}}(F_{C}^{i})$, $j = \overline {1,{{n}_{{12}}}}$, $F_{C}^{i} \subseteq X_{j}^{i}$ of the result sort determine either the result of the implementation of an AIR and the corresponding actions on different ACs or OVs, or the ability of an AC or OV to influence other arbitrary objects of a given subject area when they have many characteristics $F_{C}^{i}$; ${{M}_{1}},{{M}_{2}},\; \ldots ,\;{{M}_{n}}$ are predicate symbols.

Operations on OVs or ACs: ${{\varphi }_{1}}(F_{1}^{1},F_{2}^{1})$, ${{\varphi }_{2}}(F_{1}^{2},F_{2}^{2})$, ..., ${{\varphi }_{m}}(F_{1}^{m},F_{2}^{m})$. The operational symbols ${{\varphi }_{i}}(F_{1}^{i},F_{2}^{i})$ define binary operations with the names ${{\varphi }_{i}}$, which are realized between two OVs or ACs when the necessary condition for this is fulfilled. For example, the operation ${{\varphi }_{i}}(F_{1}^{i},F_{2}^{i})$ can be successfully implemented between AC $y_{1}^{0}(X_{1}^{0})$ and $y_{2}^{0}(X_{2}^{0})$, if the condition $(F_{1}^{i} \subseteq X_{1}^{0}) \otimes (F_{2}^{i} \subseteq X_{2}^{0})$ is fulfilled. It should be noted that the variables ${{C}_{i}}(F_{C}^{i})$ and the $c_{i}^{j}(X_{i}^{j})$ constants of the kind result with the names C_i and $c_{i}^{j}$ serve to determine the results of performing operations ${{\varphi }_{i}}(F_{1}^{i},F_{2}^{i})$ with OV or AC pairs, satisfying the required conditions.

Operations. The logic of conditionally dependent predicates uses the following operations.

(a) Logical operations: $\&$ is conjunction, $\vee$ is disjunction, $\to$ is implication, $\leftrightarrow$ is equivalence, and $\bar {M}$ is negation of M.

(b) $\forall$ and $\exists$ are quantifiers according to universality and existence.

(c) The set-theoretic operations: $\in$ is membership; $\mathop \in \limits_\sim$ is conditionally dependent membership, for example $y_{1}^{0}(X_{1}^{0})\mathop \in \limits_\sim y_{1}^{1}(X_{1}^{1})$ if the condition $X_{1}^{1} \subseteq X_{1}^{0}$ is fulfilled; $\subseteq$ is inclusion of one set into another set; $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{ \subset }$ is conditionally-dependent inclusion of one set into another set. For example, the set ${{A}_{1}}(X_{A}^{1})$ all elements of which have characteristics $X_{A}^{1}$ is conditionally dependently included in the set ${{A}_{2}}(X_{A}^{2})$ and denoted by ${{A}_{1}}(X_{A}^{1})\mathop \subset \limits_\sim {{A}_{2}}(X_{A}^{2})$, if condition $X_{A}^{2} \subseteq X_{A}^{1}$ is fulfilled; $\cup$ is the union of sets; and $\cap$ is the intersection of sets.

(d) Comparison operations: = is identity, $\leqslant$ and $\geqslant$ are comparisons less or equal and greater than or equal, respectively.

Symbols. There are bijective correspondences between symbols and language expressions, on the one hand, and the logic model of conditionally dependent predicates, on the other hand.

The $y_{i}^{0}(X_{i}^{0})$ symbols correspond to the ACs which are defined by the $X_{i}^{0}$ characteristics sets. In other words, specific objects of PSE (individuals) with the $y_{i}^{0}$ name are defined by the $X_{i}^{0}$ characteristics set, for example, ТУ134 aircraft numbered 43 (has a fuselage and wings, it can fly, etc.).

The symbols $y_{i}^{1}(X_{i}^{1})$ designate the OV whose domain is defined by the set of ACs similar to each other, satisfying the condition $X_{i}^{1} \subseteq X_{i}^{0}$ according to which they are combined in the OV of the kind type of objects named $y_{i}^{1}$, for example unmanned aerial vehicles K34. Here, $X_{i}^{1}$ is the set of characteristics that individuals must possess in relation to the OV of the $y_{i}^{1}(X_{i}^{1})$ sort species.

Elements $y_{i}^{2}(X_{i}^{2})$ designate the OV whose domain is defined by the set of species similar to each other, satisfying condition $X_{i}^{2} \subseteq X_{i}^{1}$ and, based on this, uniting in the OV of the sort kind of objects with the name $y_{i}^{2}$, for example aircraft type aircraft. Here $X_{i}^{2}$ is the set of characteristics inherent only to all OVs of the sort species, related to the corresponding OVs of the sort genus.

The $y_{i}^{3}(X_{i}^{3})$ symbols denote OVs whose domain is defined by the set of similar varieties of the genus variety, satisfying condition $X_{i}^{2} \subseteq X_{i}^{3}$ and uniting based on this basis into OVs of the class of objects with the name $y_{i}^{3}$, for example, aircraft, where $X_{i}^{3}$ is the set of characteristics common for all aircraft.

Using sets of characteristics, for example, $F_{\psi }^{i}$ and $F_{b}^{j}$, various OVs or ACs can be combined into conditionally dependent OVs or conditionally dependent sets of objects $A(F_{\psi }^{i})$ and $A(F_{b}^{j})$, satisfying the requirements of the sets $F_{\psi }^{i}$ and $F_{b}^{j}$, which are identified with the help of their corresponding compound names, for example, conditionally dependent OV light objects or objects that can be captured and raised, etc. The conditionally dependent OVs and sets constructed in such a way allow us to single out monotonic segments of the decision output in an arbitrary subject area with respect to the given constraints and to ensure based on this the derivation of formulas in the given model of the problem environment that determine the properties, skills, and other characteristics of its various objects. In other words, the sets of characteristics $F_{\psi }^{i}$ and $F_{b}^{j}$ play the role of absolute cause-and-effect constraints that form the acceptable area of decision-making for the AIR in the process of planning purposeful behavior, for example, to replenish knowledge in the process of choosing an effective tool for purposeful activity.

It should be noted that the AIR may also encounter causal constraints, arbitrarily arising in the PSE, in the process of behavior planning. Let us call such restrictions braking characteristics$Z = \{ {{z}_{\chi }}\}$, $\chi = 1,s$. The appearance of the braking characteristics in the OV or AC violates the accepted condition of the validity of the formulas, in the context of the monotonic section of the derivation of true statements, which was previously selected based on the absolute restrictions. For example, all living things with developed wings are combined into many $A({{F}_{a}})$flying living creatures. However, if there is a braking characteristic ${{z}_{\chi }} \in Z$, for example, the appearance of damage, any object from the set $A({{F}_{a}})$ can lose the ability to fly.

Correctly constructed expressions of the subject-predicate language of the logic of conditionally dependent reasoning.

Elementary terms

Elementary terms are defined by symbols of any kind of AC or OV: result, attribute, properties, skills, components, and conditionally dependent sets.

Terms

1. The term is any elementary term.

2. If K₁ is the elementary term of the grade OV or AC, and K₂ is the elementary term of the grade conditionally dependent set, then ${{K}_{1}}\mathop \in \limits_\sim {{K}_{2}}$ is the term subject variable or subject constant that satisfies the requirements of the conditionally dependent set K₂.

3. If K₁ and K₂ are, respectively, elementary terms of the OV or AC variety, and ${{\varphi }_{1}}(F_{1}^{1},F_{2}^{1})$ is the elementary term of a conditionally dependent operation variety, then the expression ${{K}_{1}}{{\varphi }_{1}}(F_{1}^{1},F_{2}^{1}){{K}_{2}}$ is a type term to perform operation${{\varphi }_{1}}$ on the corresponding OV or AC.

4. If K₁ is the elementary term of the OV or AC grade, and $b_{i}^{j}(X_{i}^{j})$ is the elementary term of the grade perform permissible action, then the expression $b_{i}^{j}({{K}_{1}})$ is the term of the grade perform action$b_{i}^{j}(X_{i}^{j})$ on the OV or AC K₁.

5. If K₁ is the elementary term of the OV or AC grade, K₂ is the elementary term of the OV with a higher level of generality, and $\mathop \in \limits_\sim$ is the symbol of the grade conditional affiliation, then ${{K}_{1}}\mathop \in \limits_\sim {{K}_{2}}$ is a term of the grade OV or AC designated K₁meets the requirements (conditions) of PP K₂.

6. If K₁ and K₂ are elementary terms of the OV or AC, respectively, and $\rho$ is a variety constant degree of analogy, then the expression $\rho ({{K}_{1}},{{K}_{2}})$ is the term assessment of the degree of similarity between two OVs or two ACs K₁и K₂.

Atomic Formulas

1. Let $M$ be the predicate symbol $K_{1}^{j}(X_{1}^{j})$, $j = \overline {0,3}$, the terms of the grade OV or AC, and ${{K}_{2}}({{X}_{2}}),{{K}_{3}}({{X}_{3}}),{{K}_{4}}({{X}_{4}}),{{K}_{5}}({{X}_{5}})$ be the terms of the grade conditionally dependent sets, defining respectively the attributes, properties, skills, and components of the OV or AC. Then, if condition ${{X}_{i}} \subseteq X_{1}^{j}$, $i = \overline {2,5}$ is satisfied, expressions of the form $M({{K}_{1}}(X_{1}^{j}),{{K}_{i}}({{X}_{i}})$ are atomic formulas.

2. If ${{K}_{1}}({{X}_{1}})$ and ${{K}_{2}}({{X}_{2}})$ are terms of the same kind, then ${{K}_{1}}({{X}_{1}})$ = ${{K}_{2}}({{X}_{2}})$ is an atomic formula if condition $({{X}_{1}} \subseteq {{X}_{2}}) \otimes ({{X}_{2}} \subseteq {{X}_{1}})$ is met.

3. If ${{K}_{1}}({{X}_{1}})$ and ${{K}_{2}}({{X}_{2}})$ are the terms subject variable, then the expression ${{K}_{1}}({{X}_{1}})\mathop \in \limits_\sim {{K}_{2}}({{X}_{2}})$ is an atomic formula if the condition ${{K}_{2}} \subseteq {{K}_{1}}$ is satisfied, and the OV ${{K}_{1}}({{X}_{1}})$ has a lower degree of generality compared to the OV ${{K}_{2}}({{X}_{2}})$.

4. If K₁ is a term of the result sort, and ${{K}_{2}}({{X}_{2}})$ is a term of the operation or action sort, which can be performed on the software or AC ${{K}_{3}}({{X}_{3}})$; i.e., if condition ${{X}_{2}} \subseteq {{X}_{3}}$ is true, then the expression ${{K}_{2}}({{K}_{3}}({{X}_{3}})) \to {{K}_{1}}$ is an atomic formula, which means that performing the action ${{K}_{2}}({{X}_{2}})$ on the AC or OV ${{K}_{3}}({{X}_{3}})$ produces the result K₁.

Formulas

1. An atomic formula is a formula.

2. If M_i and M_j are formulas, then $\overline {{{M}_{i}}}$${{M}_{i}}\& {{M}_{j}}$, ${{M}_{i}} \vee {{M}_{j}}$, ${{M}_{i}} \to {{M}_{j}}$, and ${{M}_{i}} \leftrightarrow {{M}_{j}}$ are formulas.

3. If M_i is a formula, the term K_i is a OV or AC, and the term K_j is a subject variable with a higher level of generality or conditionally dependent set, then the expressions $\forall {{K}_{i}}\mathop \in \limits_\sim {{K}_{j}}[{{M}_{i}}({{K}_{i}})]$ and $\exists {{K}_{i}}\mathop \in \limits_\sim {{K}_{j}}[{{M}_{i}}({{K}_{i}})]$, $i = \overline {1,m}$ are formulas.

There are no other formulas.

It should be noted that conditionally dependent predicates are not directly interpreted but only their feasibility in a given PSE model is checked in the process of planning the behavior of the AIR. The set of truth values of statements obtained as a result of the designation of formulas of conditionally dependent subject-predicate language, as well as for any logical language, contains two values, true and false.

In the general case, an arbitrary formula M of conditionally dependent predicates’ logic is feasible in a given model of the problem environment or in a given subject area if it contains objects the use of which to denote this formula allows us to get a true statement. If all the objects of a given subject domain satisfy the condition of M, then it forms a monotonic region of satisfiability for the formula.

Let M_i and M_j be formulas of the logic of conditionally dependent predicates. Then the satisfiability of the formulas $\overline {{{M}_{i}}}$, ${{M}_{i}}\& {{M}_{j}}$, ${{M}_{i}} \vee {{M}_{j}}$, ${{M}_{i}} \to {{M}_{j}}$, and ${{M}_{i}} \leftrightarrow {{M}_{j}}$ is related to the truth values of the statements obtained as a result of the meaning M_i and M_j are objects in the problem environment.

1. The formula $\overline {{{M}_{i}}}$ is a negation, which is feasible in a given subject area if the formula M is not feasible.

2. ${{M}_{i}}\& {{M}_{j}}$ is called a conjunction of the formulas M_i and M_j and is executable in a given PSE model if it contains at least one pair of objects the use of which for the designation M_i and M_j allows us to simultaneously get the true statements $M_{i}^{*}$ and $M_{j}^{*}$.

3. ${{M}_{i}} \vee {{M}_{j}}$ is defined as the disjunction of the formulas M_i and M_j, which is feasible in a given PSE model if it contains objects the use of which for the meaning of M_i and M_j makes it possible to obtain at least one true statement $M_{i}^{*}$ or $M_{j}^{*}$.

4. ${{M}_{i}} \to {{M}_{j}}$ is called the implication of the formulas M_i and M_j and it is not feasible in a given PSE model only in the case when it contains only such objects the use of which for the designation M_i and M_j makes it possible to get one true statement $M_{i}^{*}$. Otherwise, this formula is executable in a given model of the problem environment.

5. ${{M}_{i}} \leftrightarrow {{M}_{j}}$ is the equivalence of M_i and M_j, which is feasible in a given PSE model if the formulas M_i and M_j in it are either simultaneously satisfiable or at the same time not realizable.

The expression $\forall {{K}_{i}}\mathop \in \limits_\sim {{K}_{j}}[{{M}_{i}}({{K}_{i}})]$ is an executable formula in a given model of the problem environment if it contains objects, the use of which for the designation of all formulas ${{M}_{i}}({{K}_{i}})$ allows us to obtain the corresponding true statements $M_{i}^{*}$, $i = \overline {1,m}$. Otherwise, this formula is not feasible.

Formula $\exists {{K}_{i}}\mathop \in \limits_\sim {{K}_{j}}[{{M}_{i}}({{K}_{i}})]$ is feasible in a given PSE model if it contains at least one object the use of which to denote these formulas allows us to get at least one true statement $M_{i}^{*}$. If there is no such object, then this formula is not feasible in this subject area.

Thus, the validity of the formulas of the logic of conditionally dependent predicates in a given subject domain can be checked by defining them with the help of its objects by the truth value of the resulting statements.