Trifocal Three-Layer Slotted Waveguide Antenna Array

Abstract

A trifocal planar slotted waveguide antenna array consisting of three layers, the first two of which are planar waveguides and the third is an array of rectangular metal waveguides with paired longitudinal or transverse slots on wide walls, is proposed and studied. A solution to the synthesis problem is used to determine the shape of the mirrors and the position of the slots in rectangular waveguides that provide emission of a plane wave at three positions of the source of a cylindrical wave (feed) in a planar waveguide. The rms aberration of the antenna array optimized in angles of view of 40 and 80 deg when moving the feed along the focal curve is studied, and it is shown that such an aberration is less than that of a three-layer two-mirror and two-layer single-mirror bifocal antenna arrays by a factor of 4.5–11.

INTRODUCTION

Planar multibeam slotted waveguide antenna arrays (AAs) with quasi-optical beam shaping have been considered in several works [1–7]. In the simplest case, such an AA contains two layers that are coupled via a parabolic slot or a system of holes and closed by a parabolic mirror [2, 3]. Feeds are installed in the first layer of the array. However, such an antenna cannot provide a wide-angle multibeam radiation pattern due to phase aberrations when the feed is displaced from the focus of the parabolic mirror. To reduce aberrations, a bifocal waveguide mirror–lens system has been used in [1] as a beam-forming system (BFS), and a trifocal system based on a Rotman microstrip lens has been employed in [4–7]. A two-mirror planar aplanatic BFS has been synthesized and optimized in [8–10] and experimentally studied in [11]. A two-mirror bifocal BFS has been synthesized and investigated in [12]. A three-mirror aplanatic BFS has been synthesized and investigated in [13]. A trifocal waveguide mirror–lens planar BFS with identical waveguide lengths has been analyzed in [14]. However, application of lens and mirror–lens systems with forced refraction leads to a more complicated design and an increase in BFS loss. A bifocal slotted waveguide AA based on a simple two-layer structure with an elliptical mirror has been proposed and investigated in [15]. A multibeam radiation pattern with an angle of view of 80° has been demonstrated. A further increase in the angle of view and the number of beams is limited by the aberrations of the bifocal system.

In this work, we pose and solve the problem of synthesis of the shape of two mirrors and the position of the slots that provide precise focusing at three positions of the feed on the focal curve in the first layer of a three-layer slotted waveguide AA and optimize such positions (foci) to minimize the rms aberration in angles of view of 80° and 40°. We also analyze rms aberrations of the synthesized and optimized antennas and compare the results with the corresponding results for a two-layer single-mirror bifocal AA and a three-layer two-mirror bifocal AA with the slots located on straight lines in the neighboring waveguides.

1 FORMULATION OF THE SYNTHESIS PROBLEM

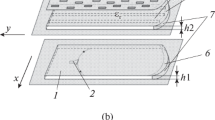
The synthesized AA (Fig. 1) consists of three layers: the first one is planar waveguide 1 with feeds 2 located on the focal line, the second layer is planar waveguide 3 coupled via curved slots 5 and 6 with the first and third layers, and the third one is an array of rectangular waveguides 4 filled with an insulator that are excited through curved coupling slot 6 between the second and third layers. Coupling slots 5 and 6 are located at the edges of planar waveguides, which are closed by mirrors confocal to slots. Periodic paired longitudinal or transverse slots 7 are located in the wide wall of each rectangular waveguide 4.

Fig. 1.

Structure of the three-layer slotted waveguide AA: (1) planar waveguide of the first layer, (2) feed, (3) planar waveguide of the second layer, (4) rectangular waveguide of the third layer, (5)–(7) coupling slots, and (8) and (9) mirrors.

A cylindrical wave emitted by the horn on the first floor propagates along planar waveguide 1, is reflected from first mirror 8, and enters planar waveguide 3 on the second layer through coupling slot 5. Then the wave propagates along planar waveguide 3, is reflected from second mirror 9, and excites the array of rectangular waveguides 4 through coupling slot 6. The fundamental mode that is excited in each rectangular waveguide propagates along the waveguide and emits energy through the slots in the wide wall, so that a narrow beam with a high gain is formed under the condition for in-phase emission of all slots of the antenna array. When the feed moves along the focal curve, the phase relationships between the modes of rectangular waveguides change and, consequently, the antenna beam is scanned. When several feeds are located on the focal curve, the multibeam mode of the AA is implemented.

For the AA synthesis, we must determine the shape of the mirrors (coupling slots) and the positions of the slots in the waveguides that provide emission of a plane wave in three directions when the feeds are located at three foci.

It can be shown that such a problem is equivalent to the 3D problem of the synthesis of a 2D three-mirror system, in which two focal points F₁ and F₂ are symmetric relative to the z axis and located on one side, third point F lies on the z axis, and the second and third mirrors are connected by transmission lines (waveguides) parallel to the z axis (Fig. 2). The following requirement is imposed: after successive reflections from two mirrors of a cylindrical wave from a source located at focus F₁, F₂, or F and after passing through the transmission lines, the eikonals of the fields at the points of intersection of these lines with the third mirror satisfy the conditions

$$\begin{gathered} {{F}_{1}}C + CB + {{t}_{B}} + ({{x}_{M}} - {{x}_{B}})\sin \alpha \\ + \,\,\left| {{{z}_{M}} - {{z}_{B}}} \right|\cos \beta - \left| {{{t}_{M}} - {{t}_{B}}} \right|\cos \beta \\ = {{F}_{1}}P + PM + {{t}_{M}}, \\ \end{gathered} $$

(1)

$$\begin{gathered} {{F}_{2}}D + DA + {{t}_{A}} = {{F}_{2}}N + NQ + {{t}_{Q}} \\ + \,\,({{x}_{Q}} - {{x}_{A}})\sin \alpha + \left| {{{z}_{A}} - {{z}_{Q}}} \right|\cos \beta - \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta , \\ \end{gathered} $$

(2)

$$FP + PQ + {{t}_{Q}} - \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta = FD + DB + {{t}_{B}},$$

(3)

where

$$\begin{gathered} FP = \sqrt {{{{({{x}_{F}} - {{x}_{P}})}}^{2}} + {{{({{z}_{F}} - {{z}_{P}})}}^{2}}} , \\ FD = \sqrt {{{{({{x}_{F}} - {{x}_{D}})}}^{2}} + {{{({{z}_{F}} - {{z}_{D}})}}^{2}}} , \\ PQ = \sqrt {{{{({{x}_{P}} - {{x}_{Q}})}}^{2}} + {{{({{z}_{P}} - {{z}_{Q}})}}^{2}}} , \\ DB = \sqrt {{{{({{x}_{D}} - {{x}_{B}})}}^{2}} + {{{({{z}_{D}} - {{z}_{B}})}}^{2}}} , \\ \end{gathered} $$

$$\begin{gathered} {{F}_{2}}D = \sqrt {{{{({{x}_{{F2}}} - {{x}_{D}})}}^{2}} + {{{({{z}_{{F2}}} - {{z}_{D}})}}^{2}}} , \\ DA = \sqrt {{{{({{x}_{D}} - {{x}_{A}})}}^{2}} + {{{({{z}_{D}} - {{z}_{A}})}}^{2}}} , \\ {{F}_{2}}N = \sqrt {{{{({{x}_{{F2}}} - {{x}_{N}})}}^{2}} + {{{({{z}_{{F2}}} - {{z}_{N}})}}^{2}}} , \\ NQ = \sqrt {{{{({{x}_{N}} - {{x}_{Q}})}}^{2}} + {{{({{z}_{N}} - {{z}_{Q}})}}^{2}}} , \\ \end{gathered} $$

$$\begin{gathered} {{F}_{1}}C = \sqrt {{{{({{x}_{C}} - {{x}_{{F1}}})}}^{2}} + {{{({{z}_{C}} - {{z}_{{F1}}})}}^{2}}} , \\ CB = \sqrt {{{{({{x}_{B}} - {{x}_{C}})}}^{2}} + {{{({{z}_{B}} - {{z}_{C}})}}^{2}}} , \\ {{F}_{1}}P = \sqrt {{{{({{x}_{P}} - {{x}_{{F1}}})}}^{2}} + {{{({{z}_{P}} - {{z}_{{F1}}})}}^{2}}} , \\ PM = \sqrt {{{{({{x}_{M}} - {{x}_{P}})}}^{2}} + {{{({{z}_{M}} - {{z}_{P}})}}^{2}}} , \\ \end{gathered} $$

$\alpha$ is the angle between the z axis and rays F₁O₁ and F₂O₁; t_A, t_Q, t_B, and t_M are the distances from the corresponding points to the line on which the centers of the slots are located, β is the angle of emission of the first spatial harmonic of the leaky wave relative to the waveguide axis (Oz), $\cos \beta = \frac{{\gamma p - 2\pi }}{{kp}}$, γ is the propagation constant of the leaky mode, p is the period of the slots along the waveguide (Oz axis); and k is the propagation constant in free space (see Fig. 2 for the remaining notation).

Fig. 2.

Scheme for the synthesis of mirror shapes and slot positions (see text for details).

When the slots are located at the points of intersection with the third mirror and conditions (1)–(3) are satisfied, the eikonals of the rays from foci at such points plus distances from the points to the plane with the normal are equal to each other.

Thus, the problem of synthesis is reduced to a search for functions z₁(x), z₂(x), and t(x) that satisfy the system of equations (1)–(3).

2 SYNTHESIS OF THE TRIFOCAL THREE-MIRROR SYSTEM

We assume that a ray of the cylindrical wave from the first point of perfect focusing (first focus) F₁ (Fig. 2) is reflected from the first mirror at point C(x_C, z_C) and is incident on the second mirror at point B(x_B, z_B). A ray of the cylindrical wave from the second focus F is reflected from the first mirror at point D(x_D, z_D) and is also incident on the second mirror at point B(x_B, z_B).

We consider the profiles of the central parts of the first and second mirrors (CD and AB, respectively) that represent parabolic functions z₁(x) = b₂x² + b₀ and z₂(x) = a₂x² + a₀, respectively, and determine the positions of points F₁(x_F1, z_F1), F(x_F, z_F), F₂(x_F2, z_F2), C(x_C, z_C), and О₂(x_O2, z_O2) and the distance form point B to the line of the centers of slots t_B.

For the configuration of Fig. 2, we have

$$\alpha = arc{\text{tan}}({{{{x}_{{F1}}}} \mathord{\left/ {\vphantom {{{{x}_{{F1}}}} {({{z}_{{F1}}} - {{z}_{{O1}}})}}} \right. \kern-0em} {({{z}_{{F1}}} - {{z}_{{O1}}})}}),$$

the angle between the z axis and ray F₁C at point C is

$${{\alpha }_{C}} = arc{\text{tan}}({{({{x}_{C}} - {{x}_{{F1}}})} \mathord{\left/ {\vphantom {{({{x}_{C}} - {{x}_{{F1}}})} {({{z}_{C}} - {{z}_{{F1}}})}}} \right. \kern-0em} {({{z}_{C}} - {{z}_{{F1}}})}}),$$

and the angle between the z axis and ray FD at point D is

$${{\alpha }_{D}} = {\text{arctan}}({{({{x}_{D}} - {{x}_{F}})} \mathord{\left/ {\vphantom {{({{x}_{D}} - {{x}_{F}})} {({{z}_{D}} - {{z}_{F}})}}} \right. \kern-0em} {({{z}_{D}} - {{z}_{F}})}}),$$

where ${{x}_{D}} = - {{x}_{C}},\,\,{{z}_{D}} = {{z}_{C}},$ ${{\gamma }_{C}} = {{(90^\circ - {{\alpha }_{C}} - {{\beta }_{C}})} \mathord{\left/ {\vphantom {{(90^\circ - {{\alpha }_{C}} - {{\beta }_{C}})} 2}} \right. \kern-0em} 2}$, ${{b}_{2}} = {{{\text{tan}}{{\gamma }_{C}}} \mathord{\left/ {\vphantom {{{\text{tan}}{{\gamma }_{C}}} {(2{{x}_{C}})}}} \right. \kern-0em} {(2{{x}_{C}})}}$, ${{b}_{0}} = {{y}_{C}} - {{b}_{2}}{{x}_{C}}^{2},$ ${{\gamma }_{D}} = - {{\gamma }_{C}}$, ${{\beta }_{D}} = {{\alpha }_{D}} + 2{{\gamma }_{D}} - 90^\circ$, ${{z}_{B}} = {{x}_{B}}{\text{tan}}{{\beta }_{D}} + {{z}_{D}} - {{x}_{D}}{\text{tan}}{{\beta }_{D}},$ ${{x}_{B}} = ({{z}_{D}} - {{x}_{D}}{\text{tan}}{{\beta }_{D}} - {{z}_{C}} + {{{{x}_{C}}{\text{tan}}( - {{\beta }_{C}}))} \mathord{\left/ {\vphantom {{{{x}_{C}}{\text{tan}}( - {{\beta }_{C}}))} {({\text{tan}}( - {{\beta }_{C}})}}} \right. \kern-0em} {({\text{tan}}( - {{\beta }_{C}})}}$ –${\text{tan}}{{\beta }_{D}})$, ${{a}_{0}} = {{z}_{{O2}}}$; ${{a}_{2}} = {{({{z}_{B}} - {{a}_{0}})} \mathord{\left/ {\vphantom {{({{z}_{B}} - {{a}_{0}})} {x_{B}^{2}}}} \right. \kern-0em} {x_{B}^{2}}}$.

We assume that the ray from focus F is reflected from the first mirror at point P in interval CD. Then, the angle between the z axis and the incident ray at point P is given by

$${{\alpha }_{{FP}}} = {\text{arctan}}({{({{x}_{P}} - {{x}_{F}})} \mathord{\left/ {\vphantom {{({{x}_{P}} - {{x}_{F}})} {({{z}_{P}} - {{z}_{F}})}}} \right. \kern-0em} {({{z}_{P}} - {{z}_{F}})}}),$$

where z_P = z₁(x_P); the angle between the x axis and tangent to the first mirror at point P is represented as

$${{\gamma }_{P}} = {\text{arctan}}(z_{1}^{'}({{x}_{P}})),$$

and the angle between the x axis and the reflected ray at point P is written as

$${{\beta }_{{PQ}}} = 2{{\gamma }_{P}} + {{\alpha }_{{FP}}} - 90^\circ .$$

We assume that the reflected ray is incident on the second mirror at point Q. Figure 2 shows that the following system of equations can be obtained:

$$\left\{ \begin{gathered} {{z}_{Q}} = {{x}_{Q}}{\text{tan}}{{\beta }_{{PQ}}} + {{z}_{P}} - {{x}_{P}}{\text{tan}}{{\beta }_{{PQ}}} \hfill \\ {{z}_{Q}} = {{a}_{2}}{{x}_{Q}}^{2} + {{a}_{0}} \hfill \\ \end{gathered} \right.,$$

(4)

the solution to which is written as

$$\left\{ \begin{gathered} {{x}_{Q}} = \frac{{{\text{tan}}{{\beta }_{{PQ}}} \pm \sqrt {{\text{tan}}\beta _{{PQ}}^{2} - 4{{a}_{2}}{{a}_{0}} + 4{{a}_{2}}{{z}_{P}} - 4{{a}_{2}}{{x}_{P}}{\text{tan}}{{\beta }_{{PQ}}}} }}{{2{{a}_{2}}}} \hfill \\ {{z}_{Q}} = {{a}_{2}}x_{Q}^{2} + {{a}_{0}} \hfill \\ \end{gathered} \right..$$

(5)

The sign of the root is chosen to provide positive value of x_Q.

Using Eq. (3), we obtain

$${{t}_{Q}} = FD + DB + {{t}_{B}} - FP - PQ + \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta .$$

(6)

To determine a new fragment of the first mirror, we assume that the ray from focus F₂ that is incident on the first mirror and reflected at point N in interval DW is incident at point Q on the second mirror. Using Eq. (2), we obtain

$${{z}_{N}} = \frac{{{{A}_{1}} \pm A\sqrt {{{A}_{2}}{{A}_{3}}} + {{A}_{4}}}}{{{{A}_{5}}}},$$

(7)

where

$$\begin{gathered} A = {{F}_{2}}D + DA + {{t}_{A}} - {{t}_{Q}} - ({{x}_{Q}} - {{x}_{A}}) \\ \times \,\,\sin \alpha - \left| {{{z}_{A}} - {{z}_{Q}}} \right|\cos \beta + \left| {{{t}_{A}} - {{t}_{Q}}} \right|\cos \beta , \\ \end{gathered} $$

$$\begin{gathered} {{A}_{1}} = {{A}^{2}}({{z}_{{F2}}} + {{y}_{Q}}) - (x_{{F2}}^{2} - x_{Q}^{2})({{z}_{{F2}}} - {{z}_{Q}}) \\ + \,\,{{z}_{{F2}}}z_{Q}^{2} + z_{{F2}}^{2}{{z}_{Q}} - z_{{F2}}^{3} - z_{Q}^{3}, \\ \end{gathered} $$

$${{A}_{2}} = - {{A}^{2}} + x_{{F2}}^{2} - 2{{x}_{{F2}}}{{x}_{Q}} + x_{Q}^{2} + z_{{F2}}^{2} - 2{{z}_{{F2}}}{{z}_{Q}} + z_{Q}^{2},$$

$$\begin{gathered} {{A}_{3}} = - {{A}^{2}} + x_{{F2}}^{2} - 4{{x}_{N}}({{x}_{{F2}}} + {{x}_{Q}}) + 2{{x}_{{F2}}}({{x}_{Q}} - {{z}_{Q}}) \\ + \,\,4x_{N}^{2} + x_{Q}^{2} + z_{{F2}}^{2} + z_{Q}^{2}, \\ \end{gathered} $$

$${{A}_{4}} = 2{{x}_{{F2}}}{{x}_{N}}{{z}_{{F2}}} - 2{{x}_{{F2}}}{{x}_{N}}{{z}_{Q}} - 2{{x}_{N}}{{x}_{Q}}{{z}_{{F2}}} + 2{{x}_{N}}{{x}_{Q}}{{z}_{Q}},$$

$${{A}_{5}} = 2{{A}^{2}} - 2z_{{F2}}^{2} + 4{{z}_{{F2}}}{{z}_{Q}} - 2z_{Q}^{2},$$

and the sign of the root in expression (7) is chosen to provide positive z_N. Thus, the angle between the z axis and ray F₂N is given by

$${{\alpha }_{{F2N}}} = {\text{arctan}}({{({{x}_{{F2}}} - {{x}_{N}})} \mathord{\left/ {\vphantom {{({{x}_{{F2}}} - {{x}_{N}})} {({{z}_{N}} - {{z}_{{F2}}})}}} \right. \kern-0em} {({{z}_{N}} - {{z}_{{F2}}})}})$$

and the angle between the z axis and ray NQ at point N is represented as

$${{\beta }_{{NQ}}} = {\text{arctan}}({{({{x}_{N}} - {{x}_{Q}})} \mathord{\left/ {\vphantom {{({{x}_{N}} - {{x}_{Q}})} {({{z}_{N}} - {{z}_{Q}})}}} \right. \kern-0em} {({{z}_{N}} - {{z}_{Q}})}}).$$

Figure 2 shows that the angle between the x axis and tangent to the first mirror at point N is written as

$${{\gamma }_{N}} = \frac{{{{\alpha }_{{F2N}}} - {{\beta }_{{NQ}}}}}{2}.$$

(8)

To determine a new fragment of the second mirror, we assume that the ray from focus F₁ that is incident on the first mirror and reflected at point P in interval CD is incident on the second mirror at point M in interval BE. Note that the ray from focus F that is reflected from the first mirror at point N is also incident on the second mirror at point M in interval BE. Thus, the angle between the z axis and ray F₁P is written as

$${{\alpha }_{{F1P}}} = {\text{arctan}}({{({{x}_{P}} - {{x}_{{F1}}})} \mathord{\left/ {\vphantom {{({{x}_{P}} - {{x}_{{F1}}})} {({{z}_{P}} - {{z}_{{F1}}})}}} \right. \kern-0em} {({{z}_{P}} - {{z}_{{F1}}})}}),$$

the angle between the x axis and ray PM at point P is given by

$${{\beta }_{{PM}}} = 2{{\gamma }_{P}} + {{\alpha }_{{F1P}}} - 90^\circ ,$$

the angle between the z axis and ray FN is represented as

$${{\alpha }_{{FN}}} = {\text{arctan}}\left( {{{({{x}_{N}} - {{x}_{F}})} \mathord{\left/ {\vphantom {{({{x}_{N}} - {{x}_{F}})} {({{z}_{N}} - {{z}_{F}})}}} \right. \kern-0em} {({{z}_{N}} - {{z}_{F}})}}} \right),$$

and the angle between the x axis and ray NM at point N is given by

$${{\beta }_{{NM}}} = 2{{\gamma }_{N}} + {{\alpha }_{{FN}}} - 90^\circ .$$

Using Fig. 2, we find the coordinates of point M:

$${{x}_{M}} = \frac{{{{z}_{P}} - {{x}_{P}}{\text{tan}}{{\beta }_{{PM}}} - {{z}_{N}} + {{x}_{N}}{\text{tan}}{{\beta }_{{NM}}}}}{{{\text{tan}}{{\beta }_{{NM}}} - {\text{tan}}{{\beta }_{{PM}}}}},$$

(9)

$${{z}_{M}} = {{x}_{M}}\tan {{\beta }_{{PM}}} + {{z}_{P}} - {{x}_{P}}\tan {{\beta }_{{PM}}}.$$

(10)

With the aid of Eq. (1) for all rays coming from focus F₁ and reflected from the first mirror in interval CD and from the second mirror in interval BE and the rays coming from focus F and reflected from the first mirror in interval DW and from the second mirror in interval BE, we find that

$$\begin{gathered} FD + DB + {{t}_{B}} - \left| {{{t}_{M}} - {{t}_{B}}} \right|\cos \beta \\ = FN + NM + {{t}_{M}}, \\ \end{gathered} $$

(11)

where

$$\begin{gathered} FD = \sqrt {{{{({{x}_{D}} - {{x}_{F}})}}^{2}} + {{{({{z}_{D}} - {{z}_{F}})}}^{2}}} , \\ DB = \sqrt {{{{({{x}_{B}} - {{x}_{D}})}}^{2}} + {{{({{z}_{B}} - {{z}_{D}})}}^{2}}} , \\ FN = \sqrt {{{{({{x}_{N}} - {{x}_{F}})}}^{2}} + {{{({{z}_{N}} - {{z}_{F}})}}^{2}}} , \\ NM = \sqrt {{{{({{x}_{M}} - {{x}_{N}})}}^{2}} + {{{({{z}_{M}} - {{z}_{N}})}}^{2}}} . \\ \end{gathered} $$

Subtracting Eq. (11) from Eq. (1), we obtain

$$B + FN + NM = 0,$$

(12)

where

$$\begin{gathered} B = {{F}_{1}}C + CB + ({{x}_{M}} - {{x}_{B}})\sin \alpha \\ - \,\,{{F}_{1}}P - PM - FD - DB + \left| {{{z}_{M}} - {{z}_{B}}} \right|\cos \beta . \\ \end{gathered} $$

The solution to Eq. (12) is written as

$${{x}_{N}} = \frac{{ \pm B\sqrt {{{B}_{1}}{{B}_{2}}} + {{B}_{3}} + {{B}_{4}}}}{{{{B}_{5}}}},$$

(13)

where

$${{B}_{1}} = - {{B}^{2}} + x_{F}^{2} - 2{{x}_{F}}{{x}_{M}} + x_{M}^{2} + z_{F}^{2} - 2{{z}_{F}}{{z}_{M}} + z_{M}^{2},$$

$$\begin{gathered} {{B}_{2}} = - {{B}^{2}} + x_{F}^{2} - 2{{x}_{F}}{{x}_{M}} + 2{{z}_{F}}{{z}_{M}} \\ + \,\,x_{M}^{2} + z_{F}^{2} - 4{{z}_{N}}({{z}_{F}} + {{z}_{M}}) + z_{M}^{2} + z_{N}^{2}, \\ \end{gathered} $$

$$\begin{gathered} {{B}_{3}} = {{B}^{2}}({{x}_{F}} + {{x}_{M}}) + {{x}_{F}}(x_{M}^{2} - x_{F}^{2} + z_{M}^{2}) \\ + \,\,{{x}_{M}}(x_{F}^{2} + z_{F}^{2} - z_{M}^{2}), \\ \end{gathered} $$

$$\begin{gathered} {{B}_{4}} = 2{{y}_{N}}({{x}_{F}} - {{z}_{M}})({{z}_{F}} - {{z}_{M}}); \\ {{B}_{5}} = 2{{B}^{2}} - 2x_{F}^{2} + 4{{x}_{F}}{{x}_{M}} - 2x_{M}^{2}, \\ \end{gathered} $$

and the sign of the root is chosen to obtain positive x_N.

We use Eqs, (7), (8)–(10) and (12) to find parameters z_N, x_M and z_M, and t_M, respectively. The displacements of point P in interval CD and point Q in interval AB are used to find fragment DW of the first mirror and fragment BE of the second mirror and distance t from the second mirror in interval BE to the line of the centers of the slots.

The procedure is repeated to obtain the next fragments of the mirrors and slot positions.

3 ANALYSIS OF ABERRATIONS OF THE TRIFOCAL PLANAR SLOTTED WAVEGUIDE AA

For the analysis of the normalized rms aberration of the eikonal in the aperture of the trifocal planar slotted waveguide AA for the emission of the leaky wave along the normal to the waveguide (β = 90°), we synthesize two variants of the array for angles of view of 80° and 40°. The rms aberration is calculated as

$$\sigma = \sqrt {{{\sum\limits_{i = 1}^n {{{{\left( {{{L}_{i}} - {{L}_{o}}} \right)}}^{2}}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^n {{{{\left( {{{L}_{i}} - {{L}_{o}}} \right)}}^{2}}} } N}} \right. \kern-0em} N}} ,$$

where L_i is the optical path of the ith ray from the source to the focal point, L₀ is the path of the central ray, and N = 50 is the number of rays in the calculations.

In the synthesis, positions of points F₁(x_F1, z_F1), F(x_F, z_F), F₂(x_F2, z_F2), C(x_C, z_C), and О₂(x_O2, z_O2) and the distance form point B to the line of the centers of the slots t_B are optimized in such a way that the rms aberration in the given angles of view is minimized. Thus, the optimization yields the following parameters

for an angle of view of 80°

$$\begin{gathered} {{x}_{F}}_{1} = - 0.25,\,\,\,\,{{z}_{{F1}}} = - 0.23,\,\,\,\,{{x}_{F}} = 0, \\ {{z}_{F}} = - 0.25,\,\,\,\,{{x}_{{F2}}} = - 0.25,\,\,\,\,{{z}_{{F2}}} = - 0.23, \\ {{x}_{C}} = - 0.08,\,\,\,\,{{z}_{C}} = 0.25,\,\,\,\,{{x}_{{O2}}} = 0, \\ {{z}_{{O2}}} = - 1.02;\,\,\,\,{{t}_{B}} = 0.25; \\ \end{gathered} $$

and the following parameters for an angle of view of 40°

$$\begin{gathered} {{x}_{{F1}}} = - 0.25,\,\,\,\,{{z}_{{F1}}} = - 0.68,\,\,\,\,{{x}_{F}} = 0, \\ {{z}_{F}} = - 0.707,\,\,\,\,{{x}_{{F2}}} = - 0.25, \\ {{z}_{{F2}}} = - 0.68,\,\,\,\,{{x}_{C}} = - 0.05, \\ {{z}_{C}} = 0.25,\,\,\,\,{{x}_{{O2}}} = 0,\,\,\,\,{{z}_{{O2}}} = - 0.52,\,\,\,\,~{{t}_{B}} = 0.25. \\ \end{gathered} $$

Figures 3a and 3b present the dependences of the rms aberration on the angle of view for the first and second variants of the synthesized trifocal planar slotted waveguide AA, respectively, and the corresponding dependences for the two-mirror three-layer bifocal AA with straight lines of the slot positions in the neighboring waveguides and mirror shapes synthesized in [12] and for the single-mirror single-layer bifocal AA [15].

Fig. 3.

Plots of the rms aberration vs. angle of view for (a) synthesis for an angle of view of 80° and (b) synthesis for an angle of view of 40°: (1) trifocal three-layer AA, (2) bifocal three-layer AA, and (3) bifocal two-layer AA.

Figure 3 shows that a two-fold decrease in the angle of view leads to an order-of-magnitude decrease in the rms aberration of the trifocal AA and a decrease by a factor of 2–3 for bifocal AAs. For an angle of view of 80°, the rms aberration of the trifocal three-layer AA of the two-mirror BFS (0.8 × 10^–4) is seven times less than that for the two-layer AA with the single-mirror BFS (5.6 × 10^–4) and is less by a factor of 4.5 than that for the three-layer array with the two-mirror BFS (3.4× 10^–4). For an angle of 40°, the rms aberration of the trifocal three-layer AA with the two-mirror BFS (0.2 × 10^–5) is less by a factor of 11 than that for the two-layer array with the single-mirror BFS (2.2 × 10^–4) and is less by a factor of 7 than that for the three-layer array with the two-mirror BFS (1.4 × 10^–4).

CONCLUSIONS

Based on the results, we draw the following conclusions.

(i) For both angles of view in this work, the minimum rms aberration is obtained for the trifocal three-layer AA, and the maximum rms aberration is obtained for the bifocal two-layer array.

(ii) The rms aberration of the bifocal three-layer AA with a two-mirror BFS is less by a factor of 1.5–2 than that of the two-layer array with a single-mirror BFS and is greater by a factor of 5–7 than that of the trifocal three-layer AA with the two-mirror BFS.

(iii) The positions of the slots of the three-layer trifocal and single-layer bifocal AA depend on emission angle of the leaky wave of the waveguide β (i.e., on the frequency). Therefore, variations in the frequency lead to additional aberrations and, hence, limitation of the working frequency band of the antennas.