Numerous polytypes of silicon carbide, which are wide-band-gap semiconductors characterized by high temperature, mechanical, and radiation resistance, hold much promise as materials for various device structures [1–4]. More recently, they were used as substrates for graphene layers [5]. Although silicon carbide is used widely, its adsorption properties remain understudied. We published our first model description of adsorption of atoms and molecules on SiC with low degrees of coverage (when an adparticle may be considered isolated) in [6, 7]. In the present study, the adsorption of barium atoms on C and Si faces of SiC polytypes is considered. The interest in this adsorption system stems largely from the results presented in [8], where the Ba/SiC/Si(111)-8° heterostructure was examined experimentally and the formation of a new carbon nanostructure was demonstrated.

The model approach to adsorption was detailed in [9, 10]. It should be noted that a free barium atom has two electrons on the outer s shell with the intraatomic Coulomb repulsion acting between them. Since only one electron “contributes” to the adatom–substrate charge transfer, the problem may be reduced to a single-electron one (by analogy with [11], where the adsorption of vanadium on rutile was studied). The adatom state density then takes the following form:

$${{\rho }_{a}}(\omega ) = \frac{1}{\pi }\frac{{\Gamma (\omega )}}{{{{{[\omega - {{\varepsilon }_{a}} - \Lambda (\omega )]}}^{2}} + {{\Gamma }^{2}}(\omega )}}.$$
(1)

Here, ω is an energy variable; εa is the adparticle single-electron level energy; Γ(ω) = πV2ρsub(ω) is the broadening function of the adparticle quasi-level, where ρsub(ω) is the density of states of the substrate and V is the matrix element of the adparticle–substrate interaction; and Λ(ω) = \({{V}^{2}}\int_{ - \infty }^\infty {{{\rho }_{{{\text{sub}}}}}(\omega '){{{(\omega - \omega ')}}^{{ - 1}}}d\omega '} \) is the quasi-level shift function. The simple Haldane–Anderson model [6, 7, 9, 10] is convenient for characterizing the density of states of the semiconductor substrate. In this model, ρsub(ω) = ρs for |ω – E0| ≥ Eg/2 and ρsub(ω) = 0 for |ω – E0| < Eg/2, where E0 = χ + Eg/2 is the energy of the band-gap center relative to vacuum (taken as the reference point) and χ is the electron affinity of a SiC polytype [12]. Then, Γ ≡ πV2ρs = const and Λ(ω) = (Γ/π)ln|(ω – Eg/2)/(ω + Eg/2)|.

The adatom quasi-level energy measured relative to the band-gap center of silicon carbide is εa = –I + e2/4d + E0, where I = 5.21 eV [13] is the Ba atom ionization energy, d is the adsorption bond length, and e is the electron charge [6, 7, 9, 10]. Since the atomic radii of barium and carbon are 2.24 and 0.77 Å [13], d = ra(Ba) + ra(C) = 3.01 Å for adsorption on the C face; in the case of adsorption on the Si face, d = ra(Ba) + ra(Si) = 3.42 Å, since ra(Si) = 1.18 Å [13]. The energy parameters for 3C-, 6H-, and 4H-SiC polytypes and the values of εa are listed in Table 1.

Table 1. Characteristics of the Ba/SiC system: band gap Eg, electron affinity χ, energy εa of the barium adatom quasi-level measured relative to the band-gap center, and band contribution \({{n}_{v}}\) to the occupation number (all energy values are given in eV)
Full size table

Adparticle occupation number na is the sum of band \({{n}_{v}}\) and local nl contributions [6, 7, 9, 10]. It was demonstrated in [9] that valence-band contribution \({{n}_{v}}\) may be calculated using the following approximate formula:

$${{n}_{v}} = \frac{1}{\pi }\operatorname{arccot} \frac{{{{\varepsilon }_{a}} + R}}{\Gamma },\quad R = \frac{{{{E}_{g}}}}{2}\sqrt {1 + \frac{{4\Gamma }}{{\pi {{E}_{g}}}}} .$$
(2)

Adatom quasi-level half-width Γ is typically regarded as a fitting parameter. At Γ = Eg/8, the values of \({{n}_{v}}\) given in Table 1 are obtained. Let us analyze the effect of Γ on the results.

Local state energy ωl, where |ωl| < Eg/2, is determined by solving the ω – εa – Λ(ω) = 0 equation, and the occupation number of this state is

$${{n}_{l}} = {{\bar {n}}_{l}}\Theta ({{E}_{{\text{F}}}} - {{\omega }_{l}}),\quad {{\bar {n}}_{l}} = {{\left( {1 + \frac{\Gamma }{\pi }\frac{{{{E}_{g}}}}{{{{{({{E}_{g}}{\text{/}}2)}}^{2}} - \omega _{l}^{2}}}} \right)}^{{ - 1}}},$$
(3)

where Heaviside function Θ(EF – ωl) ensures that only the contributions of levels lying below the Fermi level (EF) are taken into account [9, 10]. The values of \({{\bar {n}}_{l}}\) are listed in Table 2.

Table 2. Energy ωl of the local level and its occupation number \({{\bar {n}}_{l}}\) at ωl < EF, ionic component \(E_{{ads}}^{{ion}}\) of the adsorption energy, and total adsorption energy Eads for the Ba/SiC system (\(E_{{ads}}^{{ion}} < \) > corresponds to ωl > EF; \(E_{{ads}}^{{ion}} < \), to ωl < EF). All energy values are given in eV
Full size table

Adsorption energy Eads may be presented as a sum of ionic \(E_{{ads}}^{{ion}}\) and metallic \(E_{{ads}}^{{met}}\) components [9, 10]. The ionic component may be estimated as

$$E_{{ads}}^{{ion}} = - \frac{{{{{(Ze)}}^{2}}}}{{4d}},$$
(4)

where Z = 1 – n is the adatom charge (or the adatom–substrate charge transfer). The values of \(E_{{ads}}^{{ion}}\) for unoccupied local levels lying above the Fermi level (\(E_{{ads}}^{{ion}} > \)) and occupied local levels below the Fermi level (\(E_{{ads}}^{{ion}} < \)) are listed in Table 2.

Metallic component \(E_{{ads}}^{{met}}\) of the adsorption energy may be estimated using the Heisenberg uncertainty relation (ΔxΔp ~ ℏ). Assuming that Δx ~ ra(Ba) in an isolated atom and Δx ~ d in the adsorbed state, we obtain kinetic energy gain ΔEkin ~ (ℏ2/2md2)[1 – (ra/d)2], where m is the mass of a free electron. As in [9], it is taken as the simplest order-of-magnitude estimate of the metallic component of the adsorption energy:

$$E_{{ads}}^{{met}} = - \frac{{{{\hbar }^{2}}}}{{2m{{d}^{2}}}}\left( {1 - \frac{{r_{a}^{2}}}{{{{d}^{2}}}}} \right).$$
(5)

\(E_{{ads}}^{{met}}\) = –0.19 eV is obtained for both faces. It is easy now to determine the values of total adsorption ener-gy Eads (Table 2).

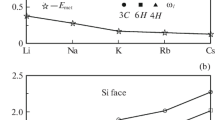
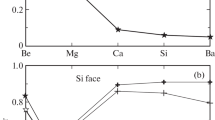
Let us analyze the obtained results. Level εa shifts toward the center of the band gap (while remaining in its upper half) in the 3C → 6H → 4H polytype series. This shift enhances band contribution \({{n}_{v}}\) to occupation number n. Local levels ωl and their occupation numbers \({{\bar {n}}_{l}}\) in the indicated polytype series behave similarly to εa and \({{n}_{v}}\). The difference is that \({{n}_{v}}\) ≪ 1, while the value of \({{\bar {n}}_{l}}\) is close to unity. If the Fermi level lies close to the upper edge of the valence band (p‑SiC), charge Z of a barium adatom is close to +1; if the Fermi level is near the lower edge of the conduction band (n-SiC), Z ~ 0. Therefore, in the former case, ionic component \(E_{{ads}}^{{ion}}\) ~ 1 eV; i.e., it is approximately five times larger in magnitude than metallic component \(E_{{ads}}^{{met}}\). In the latter case, \(E_{{ads}}^{{ion}}\) ~ 0 and Eads ≈ \(E_{{ads}}^{{met}}\). The dependences of calculated values on the quasi-level half-width are presented in Fig. 1. It can be seen that the contributions to occupation numbers \({{n}_{v}}\) and \({{\bar {n}}_{l}}\) depend monotonically and rather weakly on Γ (Fig. 1a). The same is true for energies ωl and \(E_{{ads}}^{{ion}}\). Therefore, the relatively arbitrary setting of Γ does not alter the results qualitatively.

Fig. 1.
figure 1

Adsorption of a barium atom on C and Si faces of polytype 3C of silicon carbide. (a) Dependences of band \({{n}_{v}}\) (circles) and local \({{\bar {n}}_{l}}\) (squares) contributions to the total occupation number on adatom quasi-level half-width Γ. (b) Dependences of ionic contributions \( - E_{{ads}}^{{ion}} < \) (triangles) and \( - E_{{ads}}^{{ion}} > \) (diamonds; the values are multiplied by 10) with their signs reversed and energy ωl of the local level (asterisks) on adatom quasi-level half-width Γ. Open and filled symbols correspond to the adsorption on C and Si faces. \(E_{{ads}}^{{ion}} > \) corresponds to ωl > EF; \(E_{{ads}}^{{ion}} < \), to ωl < EF. The energy interval in (b) is coincident with the upper half of the band gap of 3C-SiC.

Full size image

An alternative estimate of the charge transfer and the Ba atom–substrate binding energy is obtained using the diatomic surface molecule (BaC, BaSi) model and the Harrison binding-orbital method [14, 15]. Energies εh = (εs + 3εp)/4, where εs and εp are the energies of s and p states, of the sp3 orbitals of C and Si atoms are εh(C) = –11.11 eV and εh(Si) = –8.28 eV, since εs(C) = –17.52 eV, εp(C) = –8.97 eV, εs(Si) = ‒13.55 eV, and εp(Si) = –6.52 eV (Herman–Skillman tables of atomic terms [14]). Let us consider the σ bond between the s orbital of a Ba atom and the sp3 orbital of C and Si atoms. Since εs(Ba) = –4.45 eV [14], the polar energies are

$${{V}_{3}}({\text{Ba}}{\kern 1pt} - {\kern 1pt} {\text{C}}) = ({{\varepsilon }_{h}}({\text{C}}) - {{\varepsilon }_{s}}({\text{Ba}})){\text{/}}2 = 3.33\,\,{\text{eV}},$$
$${{V}_{3}}({\text{Ba}}{\kern 1pt} - {\kern 1pt} {\text{Si}}) = ({{\varepsilon }_{h}}({\text{Si}}) - {{\varepsilon }_{s}}({\text{Ba}})){\text{/}}2 = 1.92\,\,{\text{eV}}.$$

The covalent binding energy is V2 = \([({{\eta }_{{ss\sigma }}} + {{\eta }_{{sp\sigma }}}\sqrt 3 ){\text{/}}2]({{\eta }^{2}}{\text{/}}m{{d}^{2}})\) [16], where m is the mass of an electron, ηssσ = 1.32, and ηspσ = 1.42 [15]. Thus, V2(Ba–C) = 1.59 eV and V2(Ba–Si) = 1.23 eV. The bond polarity is defined as αp = \({{V}_{3}}{\text{/}}\sqrt {V_{2}^{2} + V_{3}^{2}} \); therefore, αc(Ba–C) = 0.90 and αc(Ba–Si) = 0.84. Switching to the adsorption problem and assuming Z = αp, we obtain \(E_{{ads}}^{{ion}}\)(Ba–C) = –0.97 eV and \(E_{{ads}}^{{ion}}\)(Ba–Si) = ‒0.74 eV from (4). These values agree fairly well with the \(E_{{ads}}^{{ion}} < \) values from Table 2. Thus, two different approaches indicate that the Ba adatom–substrate binding is markedly ionic in the case of p-SiC.

Unfortunately, we were unable to compare the obtained results with experimental data on the energy of Ba adsorption on SiC. In contrast to the adsorption of metals on metals [17], the adsorption of metals on semiconductors is poorly studied, and no data even on the energy of Ba adsorption on silicon and diamond could be found (although certain data on these (or close) adsorption systems are given in [18–21]). Let us, thus, turn to cesium adsorption. First-principles calculations for the Cs/Si(001) system with coverage degree Θ = 0.5 yield adsorption energies for various adsorption positions falling within the range from ‒1.46 to –2.46 eV [22]. Similar calculations for cesium atoms on graphite yield an adsorption energy of ‒1.42 eV [23]. This indirect validation of the obtained results is the only one available at present.