Recent progress that has been made in the development of high-power microwave generators, in particular, gyrotrons [1, 2], expands the field of their promising applications where controlled radiation spectrum can be essential. For example, the use of gyrotrons as sources of plasma heating radiation in thermonuclear fusion facilities involves the choice of fixed frequencies to compromise between radiation absorption in the central and peripheral plasma regions. However, it has been shown [3] that heating can be much more efficient in the case of using incident microwave radiation with tunable frequency. Another important application of microwave signals with rapidly tunable frequency is related to the possibility of generating short pulses with high peak intensity due to compression of a frequency-modulated signal in dispersive lines, e.g., based on helically corrugated waveguides [4, 5].

In this Letter, we propose to perform frequency tuning in a regime of stimulated Raman backscattering of high-power microwave radiation on an auxiliary weakly relativistic electron beam. In recent years, the Raman backscattering in plasma has been extensively studied as a means of compression and amplification of optical pulses [6–8]. In the case of using electron beams, the Doppler frequency shift effects become significant where the magnitude of frequency tuning is comparable with the frequency of pumping and scattered signal. In the case of a pumping wave cocurrent with the electron beam and the counterpropagating scattered wave, the energy is pumped from the high- to low-frequency radiation and the absolute instability is developing in the scattered radiation. Under these conditions, self-excitation of the system takes place in the absence of external resonators, which provides the possibility of smooth frequency tuning of the scattered (signal) wave by varying the electron beam energy.

Let us consider the model system presented in Fig 1a, in which a cocurrent pumping wave is backscattered in a waveguide on an auxiliary weakly relativistic electron beam into the counterpropagating wave with reduced frequency. It is assumed that the electron beam is focused by strong external magnetic field H0. When the TEn,m mode of the incident pumping wave (subscript i) is scattered into analogous mode of the scattered signal (subscript s), the wave fields can be set by vector potentials expressed as follows:

$${{{\mathbf{A}}}_{j}}({\mathbf{r}},t) = \operatorname{Re} ({{\hat {A}}_{j}}(z){\mathbf{F}}({{{\mathbf{r}}}_{ \bot }}){{e}^{{i({{\omega }_{j}}t - {{h}_{j}}z)}}}),\quad j = i,s.$$
((1))

Here, F(r⊥) = \(\varkappa _{{n,m}}^{{ - 1}}[{{\nabla }_{ \bot }}\psi \times {{{\mathbf{z}}}_{0}}]\) are functions describing transverse field structures in terms of membrane functions ψ = \({{J}_{n}}({{\varkappa }_{{n,m}}}{{r}_{ \bot }})\)exp(inφ), where Jn is the Bessel function, \({{\varkappa }_{{n,m}}}\) = \(\sqrt {k_{j}^{2} - h_{j}^{2}} \) are the transverse wavenumbers, kj = ωj /c, and c is the speed of light. The introduction of a strong guiding magnetic field into the system allows transverse oscillations of electrons in the pumping field to be amplified. The magnitude of magnetic field must be far enough from the value for cyclotron resonance with the pumping wave, while the switching of signal and pumping wave fields should be adiabatically smooth so that

$$({{\omega }_{i}} - {{h}_{i}}{{V}_{{||}}} - {{\omega }_{{{{H}_{0}}}}}){{l}_{{sw}}}V_{{||}}^{{ - 1}} \gg 2\pi ,$$
((2))

where lsw is the length of the switching region, \({{\omega }_{{{{H}_{0}}}}}\) is the gyro frequency, and V|| = β||c is the translational velocity of electrons in the beam. Otherwise, parasitic cyclotron oscillations would be excited which will lead to the pumping wave energy loss.

Fig. 1.
figure 1

Scheme of a model system in which the cocurrent pumping wave is backscattered into the low-frequency counterpropagating wave on an auxiliary weakly relativistic electron beam; (b) longitudinal profiles of wave amplitudes in a stationary generation regime according to the solution of three-wave interaction equations (4) for L = 4 and Ai0 = 1.

Full size image

At a sufficiently large density of electrons in the beam, it can be considered as a medium in which space-charge waves are excited. In the beam absorbing the pumping wave energy under the resonance condition

$${{\omega }_{i}} - {{h}_{i}}{{V}_{{||}}} - {{\omega }_{s}} - {{h}_{s}}{{V}_{{||}}} = \omega {{P}_{{||}}}$$
((3))

(where ωP|| is the longitudinal plasma frequency), a fast space-charge wave is excited with energy having the positive sign. The stimulated Raman scattering on this fast space-charge wave is described by the following system of three-wave equations [9]:

$$\frac{{d{{A}_{b}}}}{{dZ}} = {{A}_{i}}{{A}_{s}},\quad \frac{{d{{A}_{i}}}}{{dZ}} = - {{A}_{b}}{{A}_{s}},\quad \frac{{d{{A}_{s}}}}{{dZ}} = - {{A}_{b}}{{A}_{i}}$$
((4))

with the boundary conditions

$${{A}_{b}}{{{\text{|}}}_{{Z = 0}}} = 0,\quad {{A}_{s}}{{{\text{|}}}_{{Z = L}}} = 0,\quad {{A}_{i}}{{{\text{|}}}_{{Z = 0}}} = {{A}_{{i0}}}.$$
((5))

Since the wave generation takes place provided exact synchronism condition (3), the wave amplitudes in Eqs. (4) can be assumed to be real quantities [9] and expressed in the normalized form as \({{A}_{{i,s}}} = e{{\hat {A}}_{{i,s}}}{\text{/}}2{{\gamma }_{0}}{{m}_{e}}{{c}^{2}}\sqrt {{{G}_{{i,s}}}} \), where Ab is the amplitude of the fast beam wave, Gi,s = \(e{{I}_{b}}T{\text{/}}4{{\gamma }_{0}}{{m}_{e}}{{c}^{2}}{{h}_{{i,s}}}{{\omega }_{c}}r_{w}^{2}N\), Gb = \(T{{r}_{b}}{{\omega }_{c}}c\sqrt {\mu {{\gamma }_{0}}{{m}_{e}}} {\text{/}}\sqrt {8{{V}_{{||0}}}e{{I}_{b}}D} \), Ib is the total beam current, rw is the waveguide radius, rb is the radius of electron beam injection, N is the wave mode norm, Z = \(z\sqrt {{{G}_{i}}{{G}_{s}}{{G}_{b}}} {{\omega }_{c}}{\text{/}}c\), L = \(l\sqrt {{{G}_{i}}{{G}_{s}}{{G}_{b}}} {{\omega }_{c}}{\text{/}}c\), l is the scattering space length, μ = \(\beta _{{||0}}^{{ - 2}}\) is the bunching parameter, ωc = ωi – ωs is the combination frequency,

$$\begin{gathered} D = {{({{\varkappa }_{c}}{{r}_{b}})}^{2}}\frac{{{{I}_{0}}({{\varkappa }_{c}}{{r}_{b}})}}{{{{I}_{0}}({{\varkappa }_{c}}{{r}_{w}})}}({{K}_{0}}({{\varkappa }_{c}}{{r}_{b}}){{I}_{0}}({{\varkappa }_{c}}{{r}_{w}}) \\ \, - {{I}_{0}}({{\varkappa }_{c}}{{r}_{b}}){{K}_{0}}({{\varkappa }_{c}}{{r}_{w}})) \\ \end{gathered} $$

is the space-charge force depression coefficient, \({{\varkappa }_{c}}\) = \(\sqrt {{{{({{h}_{i}} - {{h}_{s}})}}^{2}} - \omega _{c}^{2}{\text{/}}{{c}^{2}}} \) [10], and

$$T = J_{{n - 1}}^{2}({{\varkappa }_{{n,m}}}{{r}_{b}})\frac{{{{\omega }_{i}} - {{h}_{i}}{{V}_{{||}}}}}{{{{\omega }_{i}} - {{h}_{i}}{{V}_{{||}}} - \omega {{H}_{0}}}}$$

is the electromagnetic waves coupling coefficient.

Taking into account the integral relations

$$A_{i}^{2} - A_{s}^{2} = A_{{i0}}^{2} - A_{{s0}}^{2},\quad A_{s}^{2} + A_{b}^{2} = A_{{s0}}^{2},$$
((6))

which represent the law of conservation of the number of radiation quanta, Eqs. (4) reduce to a single equation for the signal wave amplitude:

$$\frac{{d{{A}_{s}}}}{{dZ}} = - \sqrt {A_{{i0}}^{2} - A_{{s0}}^{2} + A_{s}^{2}} \sqrt {A_{{s0}}^{2} - A_{s}^{2}} ,$$
((7))

where As0 = As|Z= 0 is the signal wave amplitude at the output of the scattering region.

In the stationary wave generation regime, the longitudinal profile of the wave amplitude is described by the Jacobi elliptic function (Fig. 1b). Integration of Eq. (7) yields the signal wave amplitude

$${{A}_{s}} = {{A}_{{s0}}}cn[{{A}_{{i0}}}Z,\sqrt R ],$$
((8))

where R = \(A_{{s0}}^{2}{\text{/}}A_{{i0}}^{2}\) is the coefficient of pumping usage (quantum yield) characterizing the number of pumping quanta converted into signal quanta. This value is determined using the relation

$${{A}_{{i0}}}L = K(\sqrt R ),$$
((9))

that follows from expression (8) for Z = L, where K(x) is the complete elliptic integral of the first kind. For R → 0, Eq. (9) yields the condition of self-excitation that has the following form for the lowest longitudinal mode:

$${{A}_{{i0}}}{{L}_{{st}}} = \pi {\text{/}}2.$$
((10))

Switching to physical variables, the starting current is expressed as follows:

$${{I}_{{st}}} = 2{{\pi }^{4}}{{I}_{0}}\frac{{P_{0}^{2}}}{{P_{i}^{2}}}\frac{{\omega _{i}^{2}h_{s}^{2}h_{i}^{2}}}{{{{T}^{4}}\omega _{c}^{4}{{l}^{4}}}}\beta _{{||0}}^{7}\frac{{r_{w}^{8}D{{N}^{4}}}}{{r_{b}^{2}}},$$
((11))

where Pi is the pumping power at the system input, P0 = 8.7 GW, and I0 = 17 kA. Evidently, this current must be significantly lower than the maximum (limiting) vacuum current transferred via a cylindrical waveguide. For a magnetized tubular electron beam in weakly relativistic approximation, this limiting current is given by the following formula [11]:

$${{I}_{{\max }}} = \frac{{17[{\text{kA}}]}}{{2\ln ({{r}_{w}}{\text{/}}{{r}_{b}})}}\beta _{{||0}}^{3}.$$
((12))

The system parameters were estimated for a pumping power of Pi = 1 MW and a wavelength of λi = 2 mm. It was assumed that both the pumping wave and scattered radiation were TE1, 1 modes of the cylindrical waveguide.

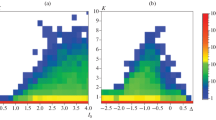
The radius and length of the scattering region were selected to be rw = 6 mm and l = 30 cm, respectively. The magnetic field was set to be 3% different from the resonance value. According to Fig. 2a, there is an optimum beam radius rb, min at which the minimum starting current is achieved. For the above-selected parameter, this value is rb, min = 1.6 mm.

Fig. 2.
figure 2

Plots of (a) starting current vs. electron beam injection radius for TE1, 1 mode scattering and (b) limiting current (dashed curve) and starting current (solid curve) vs. accelerating voltage for rb = 1.6 mm, Pi = 1 MW, λi = 2 mm, rw = 6 mm, and l = 30 cm.

Full size image

Subsequent calculations were performed for the optimum beam radius rb, min indicated above. As can be seen from Fig. 2b, the starting current for accelerating voltages within U = 5–20 kV does not exceed Ist = 6 A and remains much lower than limiting current Imax. Estimation of the quantum yield R by formula (9) shows that, as scattering region length L increases, the coefficient of wave transformation asymptotically tends to unity (Fig. 3a). For example, at an accelerating voltage of U = 10 kV, current I = 3.5 A, and l = 30 cm, the signal wave power at the output is Ps = 700 kW. As the current is increased to I = 5 A, the power reaches Ps = 940 kW.

Fig. 3.
figure 3

Plots of (a) quantum yield vs. length of the scattering region and (b) relative scattered wave frequency tuning magnitude vs. accelerating voltage for the same system parameters as in Fig. 2.

Full size image

The magnitude of frequency tuning (Fig. 3b) is determined from the condition of synchronism (3) and amounts to 20–40% of the pumping frequency for accelerating voltages varied in the interval indicated above. Note that, at an average accelerating voltage of U = 10 kV, modulation of the output radiation frequency within ±3.5% about the central frequency (e.g., for subsequent compression) can be achieved by varying the voltage within ±2.5 kV.

As was noted above, the generation under condition of combination synchronism (3) without exciting parasitic cyclotron oscillations requires adiabatically smooth switching of fields so as to excite only stimulated electron oscillations n the pumping wave field. In the selected range of frequencies and electron beam energies, estimation of characteristic length lsw of the switching region by formula (2) shows that it falls within 2.5–3 cm. Note also that radial electric field Er(r = rw) at the walls of waveguide with the give cross section at pumping wave powers on a megawatt level is about 17 kV/cm and does not exceed the threshold of high-frequency breakdown.

In conclusion, the obtained estimations of parameters showed good prospects of using the proposed model system employing the Raman backscattering for the smooth radiation frequency tuning within 20–40% of the frequency of incident pumping radiation generated by high-power (megawatt) gyrotrons. At the same time, it is evident that implementation of the regime of stimulated Raman backscattering requires using high-density electron beams in the scattering region. Since the beams under consideration have relatively low energies, the emission current from cathode is limited (in the framework of the 3/2 power law). However, with allowance for the fact that the pumping wave energy (rather than the kinetic energy of electrons) is converted into the scattered wave energy, a scheme with partial deceleration of electrons prior to input of the scattering region seems to be promising. In this case, the anode voltage can be rather high so as to ensure a sufficiently large injection current, while the subsequent deceleration of electron beam will provide for the necessary high electron density in the scattering region.

Acknowledgments. This work was supported in part by the Russian Science Foundation, project no. 16-42-01078.