INTRODUCTION

Flow control by means of a corona discharge refers to active electrohydrodynamic methods; it uses the energy of an electric current source. This method is attractive due to its simplicity and reliability, as well as to small sizes of structures, which have no moving parts and are energy efficient. Moreover, in contrast to passive methods, in this case, it is not necessary to change the geometry of the body’s surface. In addition, the magnitude of the effect can be easily regulated by varying the voltage. The time constant for a corona discharge is fractions of microseconds, which is orders of magnitude greater than that for settling of hydrodynamic processes. This opens opportunities for developing feedback control techniques. The theoretical possibility of controlling the flow and aerodynamic characteristics of bodies as a result of the action of electric forces was shown in many experimental and theoretical studies, e.g., [1–4], but this issue requires further study. Several studies are devoted to the control of wing aerodynamics using an electric discharge, while only a few of them are concerned with flow past a cylinder. An overwhelming majority of them are experimental studies. The cylinder is a universal form, suitable for many applications and well studied experimentally; therefore, in our opinion, the study of the effect of a thin (about a millimeter in cross section) jet of electric wind (EW) created by a corona discharge on the flow past a cylinder is not only of practical but also of theoretical interest.

When a viscous medium flows around a cylinder in range of Reynolds numbers Re = 40–105, vortices periodically detach from the body’s surface and a wake, called the Karman vortex street, forms behind the cylinder [5]. Mechanical oscillations caused by the detachment of vortices can lead to vibration, acoustic noise, and, if the vortex shedding frequency coincides with the natural frequency of the structure, to its destruction. Therefore, in the problems of controlling the flow around cylindrical bodies, along with reducing drag force, we can single out a change in the amplitude and frequency of the oscillation of forces acting on the body. This is related to a change in the parameters of the Karman vortex street and the transition of the nonstationary flow regime to the steady state.

For bodies with a high-drag shape, such as a cylinder, the viscous drag is small compared to the pressure drag; therefore, reduction in the drag consists in a reduction in the pressure difference between the fore and aft parts of the body. This problem can be solved by displacing the boundary layer separation point. There are two ways for this: the force from the electric discharge acts along the surface of the body, accelerating air particles of the boundary layer, or acts perpendicularly to the gas motion, attaching the separated boundary layer. The authors of [3] considered the first way. For this, a high-voltage wire electrode was placed at the front stagnation point of the cylinder and a grounded electrode was placed in the aft region. For relatively low Reynolds numbers of 2500 (an incident flow velocity of 0.7 m/s), visualization of the flow with smoke streams showed that switching on the voltage changed the form of the vortex street behind the cylinder: the boundary layer separation points shifted downstream, the vortex street lost its distinct structure, and large vortices were not observed. PIV measurements showed an acceleration in the boundary layer separation region. However, this geometry is not promising for the problem of reducing drag.

In [4], an experimental study of the effect of a corona discharge on a flow past a cylinder for different positions of the discharge electrode was carried out in a wind tunnel. The incident flow velocity varied from 1 to 2 m/s, so that the Reynolds number was in the range of 4000 < Re < 8000. The corona electrode was produced by one or two wires located symmetrically with respect to the plane of symmetry. The position of the wires was characterized by angles θ = 45°, 90°, 135°, and 180°. Visualization of the flow with the help of a smoke wire showed that, depending on the position of the high-voltage electrodes, the boundary layer separation point shifts up- or downstream, increasing or decreasing the size of the wake. The pressure on the cylinder surface was also measured, which confirmed the possibility of controlling the drag force by the position of the electrodes and the magnitude of the corona discharge voltage. From the viewpoint of drag reduction, the most promising positions of the wire are θ = 90° and 180°.

Study [6] is devoted to the numerical simulation of an EHD flow for a system of electrodes with θ = 90° from [4]. A model of a turbulent flow with Reynolds numbers 4000 < Re < 16 000 was considered. The authors confirm that, according to experimental results [4], the size of the turbulent wake behind a cylinder decreases when a corona discharge is switched on.

In this paper, we focus on the specificities of controlling the characteristics of a Karman vortex street behind a cylinder by means of a corona discharge for relatively low Reynolds numbers of 2400 and 3200. Despite the fact that such Reynolds numbers correspond to the transient regime, the wake is characterized by pronounced large vortices with a clear structure, which makes it possible to resolve it by direct numerical modeling. Two variants of the placement of the corona electrodes are considered. In the first case, high-voltage electrodes are located symmetrically above and below the cylinder, creating an EW perpendicular to the main flow. This forced the detached boundary layer to join, reduced the size of the wake, and for some voltages the non-stationary flow led to a stationary one. In the second case, the high-voltage electrode was located behind the cylinder, the EW was directed oppositely to the main flow, increasing the size of the wake, which led to a greater unsteadiness of the flow. The problem was solved using numerical simulation.

1. CORONA DISCHARGE MODEL

A corona discharge arises in systems of electrodes with a small radius of curvature, near which a high electric field is localized. High field strength leads to impact ionization, increasing the number of charged particles around the electrode like an avalanche. A narrow (about 0.1 mm) region near the high-voltage electrode, where ionization processes occur and charged particles of several types, various ions and electrons, interact is called a corona discharge sheath. In the outer zone, outside of the sheath, there are ions of only one sign, which drift toward the opposite electrode under the action of the electric field. When colliding with neutral air molecules, drifting ions transfer their momentum to them, involving them in motion and thus creating an EW.

In the case of a positive high-voltage electrode (positive corona), electrons are formed in a small neighborhood of the sheath due to photoionization [7], are drawn into the sheath, multiply as an avalanche, and are absorbed by the high-voltage electrode. In this case, the flow of positive ions from the corona sheath is directed to the outer zone. The small sizes of the sheath compared to the interelectrode distance make it possible to use a simplified (so-called unipolar) mathematical model of a corona discharge. In the unipolar model, only the external discharge zone is considered, in which charged particles of the same sign drift and the ionization processes in the sheath are replaced by the boundary condition on the high-voltage electrode. As a rule, this condition is chosen based on empirically established regularities and, therefore, traditional models require redefinition of the coefficients with any change in geometry. In the present study, we use an original boundary condition on the high-voltage electrode in the form of a differential equation that specifies the rate of change of the ion flux from the sheath of the corona discharge [8, 9]. The input parameters of the model contain physical quantities amenable to independent measurement, such as the ionization coefficient, ion mobility, ion diffusion coefficient, and the critical number of ionization collisions necessary to initiate the discharge. The model was tested on several problems with an EW for different configurations of electrodes and showed good agreement with the experiment.

The unipolar corona discharge model is described by system (1)–(4). Equation (1) is Poisson’s equation for electric potential φ and the coupling equation for electric field vector E and the potential, where |e| is the absolute value of the electron charge of 1.6 × 10–19 C, ε0 is the dielectric constant of 8.85 × 10–12 F/m, and n is the density of positive ions in the outer zone. Nernst–Planck equation (2) does not contain the source function and takes into account the variation in the ion density due to diffusion with an effective diffusion coefficient D = 10 mm2/s and due to migration in the electric field with an effective mobility of positive ions b = 2.1 × 10–4 m2/(V s).

The birth of positive ions in the sheath of the corona discharge is described by boundary condition (3) on the corona electrode as the rate of change of positive ions flux ∂j0/∂t into the outer zone. Coefficient exp(–M) characterizes the intensity of seed electrons due to photoionization; M is the number of ionization collisions sufficient for ignition of the corona discharge; τ is the transit time of a positive ion from the boundary of the sheath of the corona discharge to the corona electrode of 0.1 ms; m is the number of ionizing collisions along the field line in the sheath of the corona discharge, defined by relationship (4), where α(E) is the effective ionization coefficient, considered as a function of the electric field [7]; and s is the coordinate along the field line:

$$\Delta \varphi = - \frac{{{\text{|}}e{\text{|}}n}}{{{{\varepsilon }_{0}}}},\quad {\mathbf{E}} = - \nabla \varphi ,$$
((1))
$$\frac{{\partial n}}{{\partial t}} + \nabla \cdot ( - D\nabla n + bn{\mathbf{E}}) = 0,$$
((2))
$$\frac{{\partial {{j}_{0}}}}{{\partial t}} = {{j}_{0}}\frac{{\exp ( - M)\exp (m) - 1}}{\tau },$$
((3))
$$m = \int\limits_0^s {\alpha (E)ds.} $$
((4))

2. MODELING THE EHD FLOW

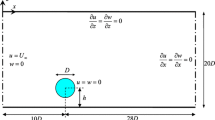
The cylinder–wire electrode system is placed in a wind tunnel with incident air velocity V0. The cylinder of radius R = 3 cm is grounded. To the wire with radius r = 45 μm, high positive voltage U is applied. The wire is placed at distance h = R from the surface of the cylinder. Two variants of the location of high-voltage electrodes relative to the cylinder were considered: (1) a single wire was placed behind the cylinder (θ = 180° in Fig. 1); (2) two wires were placed symmetrically above and below the cylinder (θ = ±90° in Fig. 1). The dimensions of the setup are the same as in experimental study [4].

Fig. 1.
figure 1

Geometry of the model: (1, 2) two variants of the arrangement of high-voltage electrodes relative to the cylinder.

Full size image

The modeling was carried out for plane geometry. The simulation area is shown in Fig. 1; the wires are shown amplified. The tunnel length was ab = 100 cm and the height was ad = 40 cm. Velocities V0 of 0.6 and 0.8 m/s were considered. At such air flow velocities around a cylinder with a switched off corona discharge, the Reynolds number calculated by formula (5) was 2400 and 3200, respectively. For the wire, the Reynolds number did not exceed 5:

$$\operatorname{Re} = \frac{{\rho {{V}_{0}}2R}}{\mu },$$
((5))

where ρ is the air density of 1.2 kg/m3 and μ is the dynamic viscosity of air of 18 μPa s. The flow was described by the Navier–Stokes equations for an incompressible fluid with a bulk electric force (6):

$$\begin{gathered} \rho \left( {\frac{{\partial {\mathbf{V}}}}{{\partial t}} + ({\mathbf{V}} \cdot \nabla ){\mathbf{V}}} \right) \\ = - \nabla \rho + \mu \Delta {\mathbf{V}} + \,{\text{|}}e{\text{|}}n{\mathbf{E}},\quad \nabla \cdot {\mathbf{V}} = 0, \\ \end{gathered} $$
((6))

where V is the velocity of the medium and p is the relative pressure.

System of equations (1)–(4) and (6) was solved by the finite element method in the Comsol Multiphysics software package. The boundary conditions for the simulation are given in Table 1. For the hydrodynamic problem, on walls ab and cd and on the cylinder and wire surfaces, the no-slip condition was imposed. At entrance ad, a velocity perpendicular to the boundary was specified (n is the normal vector to the boundary). Relative pressure p0 at boundary bc (at the exit to the atmosphere) was set to zero. For electrostatics, the non-penetration condition for the electric field was imposed at the outer boundaries of abcd, the cylinder was grounded, and a high positive potential on the wire was specified. For the particle transport equation, at the outer boundaries of the model, the non-penetration condition for positive ions was imposed (j is the ion flux density); on the cylinder, the condition for free passage of ions; and, on the wire, the ion production condition (j0 was calculated from differential Eq. (3)). At the initial moment of time, the voltage on the wire and the input velocity at the entrance were equal to zero, and then they linearly increased to the specified value. In this study, we analyze a quasi-steady solution.

Table 1. Boundary conditions
Full size table

For the finite-element model, a free mesh of triangular elements and a boundary-layer mesh densified near the fluid–solid body interfaces were constructed; the mesh was also densified in the vortex wake region. Analysis of mesh convergence showed that it suffices to consider about 17 000 elements.

3. RESULTS AND DISCUSSION

For the geometry of electrodes considered, the current–voltage characteristic (CVC) of the corona discharge was calculated. As is known [7], the corona discharge has a threshold character; it ignites at certain voltage U0 and further, with increasing voltage U, the CVC of the corona discharge grows quadratically and is described by equation

$$I = KU(U - {{U}_{0}}),$$

where I is the total discharge current. Coefficient K determines the slope of the CVC and depends on the geometry of electrodes and the mobility of positive ions. The ion mobility was set to 2.1 × 10–4 m2/(V s). This value is within the range used in the literature for the effective mobility of positive air ions [7] and agrees well with experimental data [4]. For the case of two wires in the considered geometry, the corona on one electrode burns almost independently of the other. This is confirmed by the fact that, for a system of electrodes with one high-voltage wire, the CVC is about two times lower than for the system of electrodes with two wires. The corona ignition voltage U0 is determined by quantity M: the number of ionization collisions sufficient for the ignition of a corona discharge. In our model, we had M = 11, which corresponds to U0 = 7 kV. The experiment shows [4] that, in such a system of electrodes, breakdown takes place at a voltage of about 31.5 kV.

For the Reynolds numbers under consideration, the air flow around a cylinder is a quasi-periodic process, the character of which may change depending on the position of the electrodes and the magnitude of the voltage. This statement is illustrated by Fig. 2, which shows the velocity distributions near the cylinder at an incident flow velocity of V0 = 0.6 m/s for three variants: Fig. 2a, a classical flow without a corona discharge; Fig. 2b, a rear discharge electrode (θ = 180°) at a voltage of 21.2 kV; and Fig. 2c, two discharge electrodes on top and bottom (θ = 90°) at a voltage of 16.2 kV. In the first case, the classical Karman street is observed; the current periodically detaches from the side surface of the cylinder, and vortices are observed in a wake after the cylinder in a staggered order. In the second case, from the region of corona electrode, a thin EW jet blows to the cylinder, acting on its rear surface and reducing the air drag force. However, as a result of the interaction of the thin EW jet with the incident flow, a distinct annular flow with an increased rotational velocity is formed behind the cylinder. Vortices acquire large sizes, periodically detach from the surface of the cylinder, and drift downstream. In the third case, a discharge area forms near the corona electrodes, which sucks the incoming air flow, displacing the detachment point upstream; the streamlines behind the cylinder are practically mirror-symmetrical to the streamlines in front of the cylinder and the low-pressure region behind the cylinder disappeared. In the upper and lower parts of the cylinder, in the gap between the electrode and the cylinder, two small-scale vortices, detaching bubbles, are formed, and no vortex wake behind the cylinder arises.

Fig. 2.
figure 2

Absolute value of velocity V and streamlines for V0 = 0.6 m/s: (a) U = 0, (b) U = 21.2 kV and θ = 180°, and (c) U = 16.2 kV and θ = 90°.

Full size image

Let us consider in more detail the structure of the resulting flow behind the cylinder for different positions of the corona electrode. Figure 3 shows the calculation results (streamlines and the velocity field) for the flow near the cylinder for the case of two corona electrodes θ = ±90°. In the absence of an external flow (Fig. 3a), a typical pattern of an EW is observed: a thin central jet, normal to the surface of the cylinder, propagates from the corona electrodes. The cross section of the jet is 1–2 mm; the maximum velocity in the stream is typical of corona discharge systems and amounts to 1.5 m/s. This jet, colliding with the cylinder, creates a higher-pressure zone near its surface. After switching on the external air blow, the EW jet drifts downstream and a vortex wake behind the cylinder forms. In Figs. 3b–3d, the incident flow velocity is constant and equal to 0.6 m/s and the voltage increases from 10.2 to 16.2 kV. With increasing voltage, the sizes of the forming vortices decrease and the width of the vortex wake decreases as well. At U = 16.2 kV, the vortices in the interelectrode gap are no more detached by an external flow and the vortex wake behind the cylinder disappears completely. The flow becomes stable, and the shape of the streamlines does not change with time. The lines of the main flow are drawn into the low-pressure region at the corona electrodes, bend around the vortices in the interelectrode gap, and again approach the cylinder surface downstream. The flow appears to be creeping, and the pressure difference between the front and rear walls of the cylinder tends to zero. With a further increase in the velocity of the external flow, the vortices in the interelectrode gap are again displaced to the aft region of the cylinder, forming symmetric recirculation zones. With a further increase in the velocity, the symmetry is broken, the flow becomes unstable, and the vortex street forms again.

Fig. 3.
figure 3

Absolute value of velocity V and streamlines for θ = 90°: (a) V0 = 0 and U = 16.2 kV; (b) V0 = 0.6 m/s and U = 10.2 kV, (c) V0 = 0.6 m/s and U = 12.2 kV, and (d) V0 = 0.6 m/s and U = 16.2 kV.

Full size image

Figure 4 shows the velocities and streamlines for the case of a corona electrode located behind the cylinder. As can be seen from Fig. 4a, in the absence of an external flow, the EW forms a thin jet directed from right to left toward the cylinder. In the presence of an external flow, the EW, directed toward the external flow, contributes to the formation of larger vortices of the Karman street. A nascent vortex under the action of a thin EW jet is pressed against the cylinder. The EW, not letting the vortex be detached, simultaneously spins it up and favors the accumulation of kinetic energy in it. In this case, the detachment period significantly increases due to the action of the EW. In Fig. 2b, we see a large change in the sizes of vortices and maximum velocities in a vortex in comparison with the original Karman street (Fig. 2a). The maximum radius of the vortex observed in this study was more than twice the radius of the cylinder and the maximum rotation velocity of the vortex increased three-fold.

Fig. 4.
figure 4

Absolute value of velocity V and streamlines for θ = 180°: (a) V0 = 0 and U = 16.2 kV, (b) V0 = 0.6 m/s and U = 16.2 kV, (c) V0 = 0.6 m/s and U = 19.2 kV, and (d) V0 = 0.6 m/s and U = 21.2 kV.

Full size image

Figure 5 shows one of the spiral-shaped trajectories of the probe gas volume of gas in the vortex wake (the position of the discharge electrode is indicated by the arrow), as well as the variation along this trajectory of the velocity, Coulomb forces, and pressure forces acting on the probe volume of gas as it moves in the vortex wake. When the probe volume periodically approaches the corona-forming electrode (these time points in the graphs are denoted by t1–t5), the Coulomb force acting on the volume sharply increases, imparting its acceleration. It can be seen in Fig. 5b that, after passing the electrode, the rotational velocity of the vortex abruptly increases under the action of Coulomb and pressure forces. In this case, the mean rotational velocity increases more than twice and then, after the vortex moves away from the electrode, gradually decreases. The vortex enlarged under the action of an EW is an example of a local effect of a corona discharge: since the EW is a thin jet accelerating the vortex only on one side, a flow of large vortices with increased rotation velocity is eventually obtained.

Fig. 5.
figure 5

The effect of the forces acting on a probe volume of gas on its velocity upon its motion in a vortex wake with V0 = 0.6 m/s, U = 24.2 kV, and θ = 180°: (a) spiral trajectory of the probe volume (the arrow indicates the position of the electrode), (b) variation in the velocity of the probe volume along the trajectory, and (c) variation in the projections of the Coulomb forces (Fcoul) and pressure (Fp) on the direction of motion of the probe volume.

Full size image

The drag (Cx) and lift force (Cy) coefficients are defined as

$${{C}_{x}} = \frac{{2{{F}_{x}}}}{{\rho V_{0}^{2}A}},\quad {{C}_{y}} = \frac{{2{{F}_{y}}}}{{\rho V_{0}^{2}A}},$$

where Fx and Fy are the forces acting on the cylinder along the x- and y-axes and A is the midsection of the cylinder.

Figure 6 shows the time dependences of coefficients Cx and Cy. Graphs 1 and 2 in Fig. 6a are the result of a classical Karman vortex street. Periodic oscillations around zero for the lift force and around the mean value of 1.4 for the drag force are observed. The latter value is noticeably overestimated compared to the experimental data on the flow past a cylinder [5, 10]. This discrepancy can be explained by not considering the blockage of the channel. In [11], a correction formula is presented, which gives a correction factor of 1.37. In this case, the corrected value of the drag coefficient Cx = 1.0 becomes closer to the experimental values of 0.9 for Reynolds numbers near 2000. The lift oscillation period is T = 0.46 s; therefore, the Strouhal number determined by formula (7) is 0.22:

$$St = \frac{{2R}}{{{{V}_{0}}T}}.$$
((7))
Fig. 6.
figure 6

Time dependence of Cx and Cy for V0 = 0.6 m/s: (a) θ = ±90°: (1, 2) U = 0, (3) 10.2, (4) 16.2 kV; (b) θ = 180°: (5) U = 16.2 and (6) 26.2 kV.

Full size image

The experimental values of the Strouhal number for the Reynolds numbers considered are 0.21. This comparison seems good enough. The 5 and 10% difference for St and Cx, respectively, can be explained by inaccurate comparison of the experiment and the simulation, e.g., by different conditions at the inlet of the flow. We should also consider that, at the Reynolds numbers under consideration, the flow cannot be considered strictly two-dimensional.

Graphs 3 and 4 in Fig. 6a correspond to the flow around the cylinder with a corona discharge when the electrodes are located above its side surface (θ = ±90°). As the voltage increases to 10.2 kV (graph 3), the amplitude of oscillations and the mean Cx significantly decrease. The oscillation frequency in this case varies only slightly. With an increase in the voltage up to 16 kV (graph 4), fluctuations are almost absent and the mean drag coefficient decreases by an order of magnitude. This case corresponds to the steady flow shown in Fig. 3d.

When the discharge electrode is located behind the cylinder (θ = 180°), the picture is completely different. As shown in Fig. 4, in this case, the vortices are significantly enhanced by the EW. With increasing voltage, the amplitude of oscillations of the drag force increases (Fig. 6b, graphs 5 and 6), its mean value decreases. Moreover, the form of oscillations begins to differ noticeably from the harmonic one and the oscillation frequency decreases (at a voltage of 30 kV, by a factor of 2.5 from the original Karman vortex street). The shape and the amplitude of the oscillations are determined by the vortex accumulation mechanism and the detachment of vortices from the corona electrode. The detachment of the vortex leads to a reduction in the pressure behind the cylinder and an increase in the drag coefficient (the increasing sections of the graph in Fig. 6b). Then, the growth of the vortex on the opposite side of the cylinder begins; the vortex is enhanced by the EW and exerts pressure on the rear part of the cylinder. This leads to a reduction in the drag coefficient (the descending parts of the graph in Fig. 6b). The instability of the wake leads to the formation of additional small vortices near the surface of the cylinder (Fig. 2b), which cause additional weak fast fluctuations of the drag force (Fig. 6b).

Figure 7 shows the dependence of the period-averaged drag coefficient on the voltage at the high-voltage electrode. As can be seen from the figure, the drop in the drag coefficient is significant for each of the two considered arrangements of the corona electrode. However, at θ = ±90°, the effect is manifested at lower voltages (graph 1). In addition, in this case, the reduction in the mean value is accompanied by a reduction on the oscillation amplitude. At θ = 180°, the drag force oscillation amplitude increases due to the formation of large vortices and its mean value decreases. With an increase in the amplitude of the incident flow to 0.8 m/s, the change of the mean drag force by the EW is significantly weaker (graphs 2 and 3). It can be seen that for a number of velocities of the incident flow, it is possible to choose such a voltage at which the EW, depending on the location of the electrodes, compensates completely or on average the effect of the incoming flow. However, for a corona discharge, the voltage increase is limited by the breakdown voltage between the electrodes.

Fig. 7.
figure 7

Drag coefficient Cx vs. voltage: (1) V0 = 0.6 m/s and θ = ±90°, (2) V0 = 0.6 m/s and θ = 180°, and (3) V0 = 0.8 m/s and θ = 180°.

Full size image

CONCLUSIONS

In this study, the flow around a circular cylinder in an unsteady regime at the Reynolds numbers of 2400 and 3200 with an additional volumetric electric force produced by a corona discharge has been studied using computer simulation. The calculation has shown that, in the considered range of parameters, a corona discharge can significantly affect the character of the air flow around the cylinder, shift the position of the boundary layer separation points, and change the characteristics of the Karman vortex street. The effect significantly depends on the position of the corona electrode.

When the discharge electrode was placed behind the cylinder, the corona discharge proved to be able to significantly reduce the vortex formation frequency compared to a Karman vortex street without a corona discharge. In this case, larger vortices with a higher rotational velocity formed. With an increase in the discharge voltage, the vortices accumulate a larger angular momentum, since they are prevented from detaching and are winded up by the EW, which presses them to the cylinder. An increase in the accumulation time leads to a reduction in the mean drag force but, at the same time, the amplitude of the oscillations of the force increases, since the accumulation is followed by detachment, during which the drag force increases. When two discharge electrodes are located symmetrically above and below the cylinder, the picture of the interaction of the corona discharge with the air flow is different. In this case, in the region of corona electrodes, a low-pressure region forms, which sucks the incoming air flow, changing the conditions for the formation of the Karman vortex street. The boundary layer separation point shifts upstream, and the main streamlines condense in the low-pressure region near the corona electrodes and then approach the surface of the cylinder again, and the detached flow is attached again. With increasing voltage, the vortex formation frequency does not change and the size of the wake decreases. For the given conditions, the wake disappeared completely at a voltage of 16.2 kV and the flow became steady and symmetric. The mean and the amplitude of drag force oscillations decreases with increasing voltage of the corona discharge. The corona discharge voltage can be chosen so that the mean drag force will decrease almost to zero. However, with an increase in the incident flow velocity, to achieve such an equilibrium, it is necessary to increase the voltage, which is limited by the breakdown voltage for the chosen electrode system.