Structure of Magnetic Plasma Fluctuations in the Uragan-3M Torsatron at Rare Collision Frequencies

Abstract

Fluctuations of the poloidal component of the plasma magnetic field in the frequency range of 0.5–50 kHz are studied in the Uragan-3M (U-3M) torsatron. Hydrogen plasma is produced and heated by RF fields at frequencies close to that of the ion cyclotron. The studies are carried out using a set of 15 magnetic sensors installed in one of the torus cross sections. RF heating provided the plasma with rare collision frequencies and the presence of the bootstrap current. The study is carried out when the maximum amplitude of magnetic fluctuations is observed and their connection with the plasma energy content is noticeable. Two types of vibrations are observed. In the first type, the current structure rotates with a certain frequency mainly in the direction of the rotation of electrons in the magnetic field, and the amplitude varies slowly with time (the rotating structure). For the second type, the spatial structure does not rotate, but its amplitude changes with a certain frequency (the standing structure). The frequencies of fluctuations and rotations are close for structures with a given poloidal wave number. The standing vibration structures with different poloidal wave numbers in this frequency range are correlated. The maximum amplitude of the rotating structures is observed with m = 2, and for the standing structures with m = 3 and reaches the values of $\tilde {B}$ ≤ 0.3 G in the confinement region. The vibration frequency does not depend on poloidal wave number m for the studied cases; m = 0, 1, 2, 3.

INTRODUCTION

The studies of the magnetic field fluctuations carried out on various toroidal plasma traps stimulated theoretical studies. At present, several instabilities are predicted, which can cause magnetic field fluctuations. These are Alfvén, drift–Alfvén, and drift–sound ones [1]. In addition, the excitation of geodesic acoustic modes (GAMs) [2], toroidally induced Alfvén eigen (TAE) [3], various types of beta-induced Alfvén eigen (AE) [4] and drift–acoustic beta-induced temperature gradient (BTG) modes [5], parametric instabilities due to plasma heating [6], etc., is possible. The heating methods also affect the excitation of drift waves [7], which at finite β values (the ratio of the plasma energy to the energy of the confinement magnetic field) can be accompanied by magnetic field fluctuations. The presence of the longitudinal current in a stellarator magnetic configuration may be accompanied by the excitation of current instabilities (kink- and tearing-modes) [8].

It can be seen from the above studies that plasma instabilities in toroidal magnetic traps depend on many factors and their behavior is very diverse. Therefore, to understand the nature of the instabilities, it is necessary to obtain the maximum possible experimental information on the frequency range, spatial structure, as well as plasma parameters and methods of its heating.

To study the structure of plasma instabilities, it is convenient to use a set of magnetic sensors that are located outside the plasma confinement volume. A set of magnetic sensors provides information on the frequencies and spatial structure of the magnetic field fluctuations associated with these instabilities. The most important disadvantage of magnetic diagnostics is the fundamental inability to determine the localization region of the instability in the plasma volume. Therefore, to determine the localization region of the instability, it is necessary to use other diagnostics.

The purpose of this study is to obtain information about instabilities in the plasma of the U-3M torsatron produced by radio-frequency heating under conditions of rare collisions between plasma particles using a set of magnetic sensors. The study is conducted at the time, when the amplitude of magnetic field fluctuations reaches maximum values, and the energy content growth rate is minimal.

EXPERIMENTAL CONDITIONS

The studies were carried out in the U-3M torsatron [9], when the magnetic field on the geometrical axis of the plasma configuration is B₀ ≈ 0.72 T. The averaged plasma minor radius is a ≈ 0.1 m, and the torus major radius is R ≈ 1 m. The plasma was created and heated in the RF-heating mode [10] at frequencies close to ion cyclotron frequency ω ≈ 0.8ω_ci, where ω_ci is the cyclotron frequency of working gas ions. Hydrogen was used as the working gas. According to the theory, the main mechanism of plasma heating is Cherenkov damping of waves excited in the plasma under conditions of Alfvén resonance on electrons [11]. It is obvious that such a method of energy transfer to plasma electrons favors, especially at rare collision frequencies, the distortion of the distribution function and the appearance of additional conditions for the excitation of instabilities. Since RF waves excited in the plasma have a frequency close to the ion cyclotron, additional heating of ions is possible with corresponding distortions of the distribution function.

For us, the main interest is the mode with low average plasma density n_e ≤ 1 × 10¹⁸ m^–3, with the maximum density on the magnetic axis n_e(0) ≈ 3 × 10¹⁸ m^–3 [12, 13]. In this mode, at the time of studying the structure of magnetic field fluctuations, the average electron and ion temperatures of the plasma column cross section are T_e ≈ 150 eV and T_i ≈ 100 eV [14], respectively, and the current in the plasma was I ≈ 1 kA. At this time the rotational transformation angle produced by this current at the boundary of the plasma column was l(a) ≈ 3 × 10^–2, which is significantly less than the stellarator rotational transformation angle l_st ≈ 0.33. This mode is interesting because the plasma electrons and ions over the collision frequencies are in the “banana” mode that is confirmed by recording the so-called bootstrap current [15].

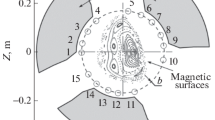
Information on plasma instabilities was obtained using a set of 15 magnetic sensors (coils) recording the poloidal component of the magnetic field and installed in one of the cross sections of the plasma column (Fig. 1). The sensors had a diameter of 6 mm and a length of 16 mm, sensitivity N_S = 180 cm² turns (N is the number of turns in the coil, S is the area of the cross-section of the coil) and were located inside the electrostatic screen. Each coil with a supply cable of about 20 m long allowed recording the change in the magnetic field with the frequency of up to 70 kHz. The signals from the sensors were integrated using a 16-channel electronic integrator. The integration constant was varied in the range τ = 5 × 10^–7–10^–3 s.

Fig. 1.

Location of the magnetic sensors with respect to screw conductors of the magnetic field and magnetic surfaces of the vacuum configuration in this cross section.

The Rogowski belt and the diamagnetic loop were used in addition to magnetic sensors for monitoring the discharge parameters.

To study the structure of magnetic fluctuations (MF), we chose the time of the maximum amplitude of oscillations, which is characterized by a slowdown in the growth of the plasma energy content and the appearance of features on the current. A sharp decrease in the amplitude of the MF is accompanied by an increase in the growth rate of the plasma parameters, which is called the transition to the improved confinement mode in [16, 17].

The energy stored in the plasma at the end of the discharge is about 16 J, and the energy stored in the magnetic field of the plasma current is 6 J, i.e., about 40% of the plasma energy. This indicates the possibility of the appearance of the substantial instability associated with the presence of the current [8].

EXPERIMENTAL RESULTS

Figure 2 shows the time behavior of the energy content of plasma column P, toroidal plasma current I, and the signal from one of the 15 magnetic sensors installed outside the confinement region on the measuring surface of radius b = 16.8 cm. It can be seen in Fig. 2 that 15 ms from the beginning of the discharge there is a noticeable increase in the amplitude of oscillations of the magnetic field and then its sharp decrease by several times. With the increase in magnetic field fluctuations, the growth rate of the energy content decreases. The decrease in the amplitude of oscillations coincides with the sharp increase in the growth rate of the plasma energy content. This time, Fig. 2 is marked with a dashed line.

Fig. 2.

Time behavior of the energy content in the plasma column P, the toroidal plasma current I and the signal recorded by one of the coils $\tilde {B}$(b). The dashed line denotes the time of the sharp decrease in the amplitude of the magnetic field oscillations (t = 15.3 ms).

The time behavior of the signal of a sensor in the interval of 13.5–15.5 ms is shown in Fig. 3. It can be seen in this figure that the magnetic field fluctuations in a given time interval are a set of fluctuations of various frequencies with time-varying amplitude and phases. Namely, the recorded signals have a non-stationary character, and it is impossible to use the standard methods for its processing.

Fig. 3.

Time behavior of the magnetic field fluctuations recorded by one of the sensors in a certain time interval: (a) real implementation; (b) the same realization after the bandpass filter in the range of 20–31.5 kHz.

Due to the fact that it is not correct to speak of a local frequency in this case, we use the concept of a frequency band.

To process the obtained set of signals, the realization were divided into five frequency ranges: δf₁ = 0.5–5 kHz, δf₂ = 5–11 kHz, δf₃ = 11–20 kHz, δf₄ = 20–31.5 kHz, and δf₅ = 31.5–52 kHz. The division into these frequency bands was carried out according to the spectra of realization of all sensors. The digitized signals using band-pass filters were presented as a realization in a certain frequency range. Figure 3 shows as an example the realization in the frequency range of δf₄ = 20–31.5 kHz. The figure shows that this realization is a set of oscillations with approximately the same period. The amplitude of these oscillations varies from minimum to maximum during 2–3 oscillations. The process of changing the amplitude of oscillations consists of successive cycles of the amplitude increase and decrease during 5–7 oscillations, and the amplitude of oscillations becomes larger in each subsequent cycle. It can be seen from Fig. 3 that there are three such cycles, after which, starting from 15.3 ms, the cycles do not repeat. In other frequency bands, the number of cycles can vary from 1 to 5. We will study the structure of fluctuations in the last cycle before the decrease in the MF level.

Further signal processing was as follows. The azimuthal distribution of the signal value over all sensors was plotted at each time in this frequency range. An example of such a distribution for two neighboring points in time in the frequency band of 20–31.5 kHz is shown in Fig. 4. It can be seen from the figure that the poloidal distribution of the value of the magnetic field oscillations on the measuring surface at a given time has a complex form. In addition, this distribution changes over time. There is a rotation of the structure.

Fig. 4.

Distribution of signals from magnetic sensors over the azimuth for two times t = 15.017 and 15.023 ms for the realization in the frequency range of 20–31.5 kHz. The dash in this figure shows the zero level, the dash-dotted line is the z axis of the torus.

Further, the spatial structure of the distribution of the signal into Fourier harmonics was decomposed. An example of such a decomposition is shown in Fig. 5 for time t = 15.017 ms in the frequency band 20–31.5 kHz. The resulting pattern is presented as a set of harmonics with different poloidal wave numbers m = 0, 1, 2, 3, etc. Higher harmonics with wave numbers m > 3 were not considered, since the accuracy of their determination using 15 unevenly located sensors is small, and their amplitude is also small. In addition to the amplitude of this spatial harmonic, its phase with respect to the previous time was also recorded.

Fig. 5.

Decomposition spectrum over poloidal harmonics m of the magnetic field fluctuations (t = 15.017 ms, δf₄ = 20–31.5 kHz).

From the physical point of view, the harmonic with m = 0 represents the oscillations of the magnetic field of the longitudinal plasma current; m = 1 are the oscillations of the dipole current similar to the Pfirsch–Schluter current rotated in space at any arbitrary angle. The structure with m = 2 is an ellipse and with m = 3 it is a triangle.

Attention should be paid to the fact that the considered representation is completely valid only in cylindrical geometry. In a real, albeit sloping torus, as well as in the presence of the displacement of the current surface with respect to the measuring and non-circular shape of the current surface, it is necessary to consider the interconnection of the adjacent poloidal harmonics.

In cylindrical geometry, the knowledge of the value of the amplitude of a certain poloidal harmonic of the magnetic field on the measuring surface makes it possible to determine the value of the magnetic field on the current surface. It is known that in this case the decrease in the magnetic field of a given harmonic is described by the corresponding Macdonald function [18]. In the first approximation, the decrease in the amplitude of the various harmonies is proportional to value (r₀/b)^{m+ 1}. Here, r₀ is the average radius of the current surface and b is the radius of the measuring surface.

The equation of the magnetic surface can be written in cylindrical coordinate system r, ϑ:

$${{r}_{0}} = r + \Delta \cos \vartheta - \delta \cos 2\vartheta .$$

((1))

Here r is the current radius, ϑ is the poloidal angle, Δ is the displacement, and δ is the ellipticity of the magnetic surface, on which currents flow. It is seen in Fig. 1 that the triangularity of the magnetic surfaces is small, and it can be ignored. The expression for the magnetic field on the measuring surface considering toroidality [18] can be presented as

$$\begin{gathered} {{B}_{m}}(b)\cos (m\vartheta + \psi ) = \sum\limits_{n = 0}^3 {{{B}_{n}}({{r}_{0}}){{{\left( {\frac{r}{b}} \right)}}^{{n + 1}}}} \\ \times {{\left[ {1 + \frac{\Delta }{r}\cos \vartheta + \frac{\delta }{r}\cos 2\vartheta } \right]}^{{n + 1}}}\sqrt {1 - \frac{r}{R}\cos \vartheta } \cos (n\vartheta + \psi ), \\ \end{gathered} $$

((2))

where ψ is an arbitrary phase.

If quantities $\frac{\Delta }{r}$; $\frac{\delta }{r}$; and $\frac{r}{R}$ ≪ 1 and assuming that the amplitude of the 3rd harmonic far exceeds the amplitude of the 4th harmonic, which does not contradict the experimental data, expression (2) can be presented as a system of four linear equations for m = 0, 1, 2, 3.

We assume that the oscillation source is located inside the confinement volume on the magnetic surface with the average radius r₀ = 8.4 cm. The Δ and δ values are determined for this surface, and the amplitude of fluctuations was calculated on the basis of the available experimental data for each set of harmonics on the magnetic surface over which the currents flow. The calculations show that in our conditions allowance for the displacement and ellipticity of the magnetic surface, as well as the toroidality does not strongly affect the field amplitude inside the confinement volume.

The results of processing the recorded signals are shown in Fig. 6. The frequency range of δf₃ = 11–20 kHz is chosen as an example. In the figure, the time variation of the phase in the –π to π range and its amplitude are presented for each spatial harmonic. The ${{\tilde {B}}^{2}}$ value is plotted on the y axis.

Fig. 6.

Dependence of the amplitude and phase of the structures with the poloidal wave numbers m = 0, 1, 2, 3 for the frequency range of δf₃ = 11–20 kHz. The dashed line shows the amplitude of the rotating structure.

It can be seen from the data in Fig. 6 that the change in the phase of the structure with m = 0 is presented by the 0 and π values, which correspond to opposite phases of oscillations. The value of the oscillation period can be used to estimate the frequency band in which oscillations occur. Thus, in the time period of t = 14.9–15.0 ms, it is possible to estimate frequency f ≈ 14 kHz from the oscillation period; the oscillations in time period t = 15.05–15.13 ms have a close frequency. For the structure with m = 1, the picture is more complicated. If we consider the situation starting from time t = 14.9 ms, then at first, the structure is observed standing still, the amplitude of which varies with a frequency of f ≈ 14 kHz. However, as the value of the oscillations approaches zero, judging by the phase shift, the structure begins to slowly turn in the direction of the rotation of the electrons in the magnetic field. After the oscillation period, the structure begins to rotate in the opposite direction, and then stops altogether. Further, at t = 15.05–15.2 ms, the structure reappears, in which the oscillations are observed with a period corresponding to a frequency of f ≈ 14 kHz. At the same time, the rotating oscillations appear with the slowly varying amplitude. Its value can be determined from the value of the envelope of the minimum values of oscillations and is indicated by the dashed line. It can be seen that two structures of plasma currents with m = 1 are observed. One structure rotates with a frequency of f ≈ 13.5 kHz in the direction of the electron drift and its amplitude varies slowly with time (dashed line). Another structure stands still (does not rotate) and its amplitude oscillates with a frequency of f ≈ 14 kHz. For magnetic field oscillations with poloidal wave number m = 2, the situation is similar. The amplitude of the standing structure oscillates with a frequency of f ≈ 14 kHz and that of the rotating structure rotates with a variable angular velocity corresponding to a frequency range of f ≈ 14–18 kHz. For a structure with m = 3, only oscillations that are standing still (do not rotate) are observed in a frequency range of δf₃ = 11–20 kHz. The oscillation frequency is about f ≈ 14.5 kHz.

The analysis of all experimental data shows that in this experiment two types of oscillations are observed in a frequency range of f ≈ 0.5–52 kHz. The first type, a structure with a given wave number, stands still (does not rotate) or rotates very slowly. Only its value changes with the recorded frequency. This type of oscillations is observed always. The second type, a structure rotates with a certain frequency and its amplitude varies slightly. The rotation frequency is often not constant in time. Usually, the oscillation frequency of the standing structure is close to the rotation frequency of a structure of the second type. Taking into account that a standing structure when its value approaches zero can quickly turn to a certain angle, it can be assumed that the standing structure stimulates rotation.

The maximum amplitude of fluctuations in the process under study for spatial structures with m = 0, 1, 2, 3 for all detected frequencies is shown in Fig. 7. The positive and negative amplitude values correspond to different directions of rotation of the structure (shaded bars). A positive value corresponds to the rotation in the direction of the rotation of electrons in the magnetic field. Non-shaded bars determine the maximum amplitude of the standing structure. The bar width shows the approximate frequency range of recorded fluctuations.

Fig. 7.

Dependence of the maximum amplitude of fluctuations on the recorded frequency band for spatial structures with different poloidal wave numbers m. Light bars define the standing structures, while the shaded ones define the rotating structures. The positive value of the shaded columns corresponds to the rotation direction of electrons in the magnetic field, and the negative value corresponds to that of ions.

Analysis of the experimental data shows that magnetic field fluctuations in this experiment exist in fairly narrow frequency ranges common to spatial structures with different poloidal wave numbers. Magnetic field fluctuations are recorded in the following frequency ranges: 1.5–2; 6–8; 13–16; 20–27; and 35–43 kHz (Fig. 7).

For the structures with m = 1 and 2, rotation in different directions is observed in the frequency range of 1.5–2 kHz, the amplitudes of which could not be determined. The maximum values of magnetic field fluctuations of standing structures are observed for m = 2 and 3.

In the frequency range of 6–8 kHz, fluctuations are observed in the standing structures with m = 0, 1, 2, 3 and rotating structures with m = 1, 2, 3. It should be noted that all fluctuations of standing structures are interrelated. Namely, their frequencies and phases are close to each other and present a common perturbation for all spatial structures (Fig. 8). The amplitude of the fluctuations inside the confinement region increases with the number of the poloidal mode (Fig. 7). Rotating structures with m = 2 have the maximum amplitude.

Fig. 8.

Amplitudes of fluctuations for four spatial structures with m = 0, 1, 2, 3 in the frequency range of 5–11 kHz on the measuring surface.

For fluctuations observed in the range of 13–16 kHz, the rotation is present only for structures with m = 1 and 2. The standing structures correlate (except for m = 0) and have a maximum amplitude for structures with m = 2 and 3. The amplitudes of rotating structures in this frequency range is less than the amplitudes of standing structures.

In the band of δf₄ = 20–31.5 kHz, fluctuations of standing structures are in the range of 20–22 kHz, except for a structure with m = 2, whose band is 20–27 kHz. The amplitude of the structure with m = 3 reaches maximum value $\tilde {B}$(r₀) ≈ 0.3 G. Only a structure with m = 2 rotates with the frequency of  f_spin = 25–26 kHz, and the amplitude of a rotating structure noticeably exceeds the amplitude of a standing structure.

In the band of δf₅ = 31.5–52 kHz, fluctuations of standing structures are in the range of 40–43 kHz, except for structures with m = 2, where fluctuations are observed in the band of 35–37 kHz and rotation frequency f_spin ≈ 37 kHz. For m = 2, the amplitude of a rotating structure is larger than that of a standing structure. In this frequency range, only the structure with m = 2 rotates. The maximum amplitude has oscillations of a standing structure with m = 3, which reach the value of $\tilde {B}$(r₀) ≈ 0.25G inside the confinement regions.

DISCUSSION

It is shown in Fig. 7 that at the studied time magnetic fluctuations are recorded in the frequency range of f = 1.5–43 kHz. These fluctuations are in five narrow frequency bands, so that Δf/f ≤ 0.25. In each of these frequency ranges, the fluctuation frequency does not depend on poloidal wave number m. Two types of fluctuations are observed: standing structures and structures rotating in the poloidal direction with certain m. The amplitudes of oscillations of standing structures increase with increasing m.

It should be noted that good correlation between standing oscillations with wave numbers m = 1, 2, and 3 is observed in all frequency ranges. In the frequency range of f_r = 6–8 kHz, a correlation is observed even with mode m = 0 (Fig. 8).

Rotating structures are observed for all wave numbers m = 1, 2, 3 (except for m = 0). Only for the structure with m = 3, the amplitude is too small. Rotation is mainly directed towards the electron-diamagnetic drift, except for the case of low frequencies for m = 3. The largest amplitude for a rotating structure is observed for m = 2. In this case, the amplitude of a rotating structure may exceed the amplitude of a standing structure. The rotation frequency is usually close to the oscillation frequency of the standing structure.

We consider frequencies characteristic of the plasma in the frequency range under study. Under conditions of rare collision frequencies, the trapped particles describe a trajectory with a characteristic frequency:

$$f_{j}^{*} = \frac{{{{{v}}_{{Tj}}}l}}{{2\pi R}}{{\left( {\frac{r}{R}} \right)}^{{3/2}}},$$

((3))

where ${{{v}}_{{Tj}}}$ is the thermal velocity of j-type particles, l is the angle of rotational transformation, and r is the current radius. According to Eq. (3), for electrons $f_{e}^{*}$ ≈ 5 × 10² Hz and for ions $f_{i}^{*}$ ≈ 3.5 × 10³ Hz. These frequencies are below or near the lower boundary of frequencies recorded in the experiment.

The expression for the frequency of the diamagnetic drift can be presented in the form

$${{f}_{{dr}}} = - \frac{m}{{2\pi r}}\frac{{c\frac{{\partial p}}{{\partial r}}}}{{e{{n}_{e}}B}}.$$

((4))

Here p = n_ek(T_e + T_i) is the plasma pressure. If it is assumed that the temperature distribution over the radius is uniform, then for the estimates it is possible to use the density distribution measured in a similar mode [12] (Fig. 9). The graph is plotted according to two measured local density values using a Langmuir probe at the boundary of the confinement region and the passage of microwave waves at different frequencies in the plasma center, considering that the integral over the profile should be equal to the average plasma density measured by the interferometer. This distribution is approximated rather well by the expression n_e = n_e(0)[1 – (r/a)^1.5]². Then, for n_e(0) ≈ 3 × 10¹⁸ m^–3, according to expression (4), for m = 1, we obtain the calculated data presented in Table 1.

Fig. 9.

Distribution of the plasma density at the time of the study of the structure of magnetic fluctuations. 〈r〉 is the average radius of the magnetic surface.

Table 1

r/a	0.6	0.7	0.8	0.9
fdr, kHz	25	29	40	61

It is seen that for m = 1 drift frequencies are in the measured frequency range. However, for m = 2 and 3 they exceed significantly those recorded in the experiment. If the non-uniformity of the temperature distribution is considered, then the values will increase even more.

The geodesic acoustic mode (GAM) considering the average curvature of the magnetic field gives frequency value [2]:

$${{f}_{{{\text{GAM}}}}} = \frac{{{{{v}}_{s}}}}{{2\pi R}}\sqrt {2 + {{l}^{2}}(a)} \approx 46\,\,{\text{kHz}}{\text{,}}$$

((5))

where ${{{v}}_{s}}$ is the speed of sound. It can be seen from expression (5) that frequency f_GAM is close to the upper boundary of the recorded frequencies.

The frequency of the TAE mode [3] in our conditions is

$${{f}_{{{\text{TAE}}}}} = \frac{{{{{v}}_{{\text{A}}}}l}}{{4\pi R}} \approx 50\,\,{\text{kHz}}{\text{,}}$$

((6))

where ${{{v}}_{{\text{A}}}}$ is the Alfvén velocity, i.e., the frequency of the TAE mode is also located on the upper boundary of the recorded frequencies.

In plasma, it is also possible to excite the so-called BAE modes (beta induced Alfvén modes) [7], which are the consequence of the coupling of the ideal MHD Alfvén drift and acoustic modes at frequencies less than f_TAE. A variety of BAE modes are the so-called BTG (beta-induced temperature gradient) modes, which were obtained with allowance for the thermal motion of ions [5]. These modes are characterized by frequencies

$$\begin{gathered} {{f}_{{{\text{BTG}}}}} \leqslant \frac{{{{{v}}_{{Ti}}}l}}{{2\pi R}} \approx 6\,\,{\text{kHz}} \\ {\text{and}}\quad {{f}_{{{\text{BTG}}}}} \leqslant \frac{{{{{v}}_{{Ti}}}N}}{{2\pi n{{l}_{0}}}} \approx 57\,\,{\text{kHz}}{\text{,}} \\ \end{gathered} $$

((7))

which are toroidal and three-dimensional satellites. Here, l₀ is the number of starts of the stellarator magnetic field and N is the number of field periods along the facility length. Condition f_BTG < f_TAE is observed only for the case of f_BTG ≤ $\frac{{{{{v}}_{{Ti}}}l}}{{2\pi R}}$ ≈ 6 kHz. This instability is excited if ionic β_i = $\frac{{8\pi {{n}_{e}}k{{T}_{i}}}}{{{{B}^{2}}}}$ > β_cr ≈ 4 × 10^–4 [5] for our conditions. The structure of this instability rotates in the direction of the ionic-diamagnetic drift.

The condition for the development of this instability is

$${{f}_{{dr}}} = {{f}_{{{\text{BTG}}}}} = \frac{{{{{v}}_{{Ti}}}l}}{{2\pi R}}.$$

((8))

In our conditions, $\frac{{{{{v}}_{{ti}}}l}}{{2\pi R}}$ = 6 kHz, which does not coincide with the data for f_dr given in Table 1. Frequencies (7) coincide with the measurement spectrum only at the boundaries of the range of recorded frequencies. The direction of the rotation of the structure is in the opposite direction to the experimental data.

The presence of the longitudinal current in our experiment may be the origin of the excitation of the current instabilities (kink, tearing modes) [8], which develop on the rational magnetic surfaces. Under our conditions, these can be surfaces l = 0.25 (m/n = 4/1; 8/2, etc.), l = 0.33 (r = 10 with m/n = 3/1; 6/2, etc.) and intermediate surfaces with m> 4. Here n is the wave number along the torus. Perturbations with m = 3 are reliably recorded in the experiment. However, it is very difficult to associate it with the development of the current instability because the current density at the interface (r = 10) is zero. Fluctuations with m ≥ 4 are recorded but for 15 irregularly located sensors it is difficult to be sure that such information is reliable, especially since the amplitude of such perturbations is small.

The analysis performed above shows that the obtained information about fluctuations in the plasma of the U-3M torsatron can hardly be explained by the existing theory. These are primarily the presence of five narrowband frequency bands in the 1.5–50 kHz band and the presence of simultaneously standing and rotating structures with similar frequencies. The closest to the measurement results are the so-called GAM and TAE modes, whose frequencies do not depend on the poloidal wave number. However, we do not have theoretical information about the direction of the rotation of these modes and the simultaneous presence of standing and rotating structures with close frequencies among them. In addition, the frequency range of these modes does not coincide with the experimental data.

In [19], it was noted that the so-called transition to the state of the improved confinement is associated with a certain current value. Since the current observed in our experiments is the bootstrap current, then the reference to the β value is observed. The burst in the amplitude of the magnetic field oscillations in the frequency range under study may occur when some limit on β is exceeded. That is, the observed instabilities can be attributed to the so-called beta-induced modes.

CONCLUSIONS

Our studies showed that rather narrowband magnetic fluctuations occur in five frequency ranges in the mode of rare collisions between plasma particles in the presence of the bootstrap current in RF heating conditions in the U-3M torsatron in the frequency range of up to 50 kHz in the plasma volume. These ranges are: 1.5–2; 6–8; 13–16; 20–27; and 35–43 kHz.

The spatial structure of these fluctuations can be presented as poloidal wave numbers with m = 0, 1, 2, 3.

The frequency of magnetic fluctuation observations does not depend on poloidal wave number.

Two types of fluctuations are observed:

—Standing still or very slowly rotating structures in which the magnetic field varies in a certain frequency band.

—Rotating structures, in which the amplitude changes weakly, and the maximum velocity is close to the frequency of fluctuations of a standing structure with a similar poloidal wave number.

The magnetic fluctuation standing structures have a complex spatial configuration (fluctuations with different wave numbers correlate) in this frequency range. These structures have the maximum amplitude of oscillations for the wave numbers with m = 3 and reach values of $\tilde {B}$ ≈ 0.3 G in the confinement region.

Rotating structures may have different poloidal numbers, however, the maximum amplitudes have a structure with m = 2. The rotation direction coincides with the rotation of electrons in the magnetic field, except for the frequency range of 1.5–2 kHz, where the rotation can be in both directions.

It is impossible to fully explain the behavior of magnetic field fluctuations in the confinement volume within the considered theoretical models.